PHYSICAL MODEL FOR RECOGNITION TUNNELING

Abstract

Recognition tunneling (RT) identifies target molecules trapped between tunneling electrodes functionalized with recognition molecules that serve as specific chemical linkages between the metal electrodes and the trapped target molecule. Possible applications include single molecule DNA and protein sequencing. This paper addresses several fundamental aspects of RT by multiscale theory, applying both all-atom and coarse-grained DNA models: (1) We show that the magnitude of the observed currents are consistent with the results of non-equilibrium Green's function calculations carried out on a solvated all-atom model. (2) Brownian fluctuations in hydrogen bond-lengths lead to current spikes that are similar to what is observed experimentally. (3) The frequency characteristics of these fluctuations can be used to identify the trapped molecules with a machine-learning algorithm, giving a theoretical underpinning to this new method of identifying single molecule signals.

1. INTRODUCTION

Electron-tunneling has been proposed^1,2 as a readout system for nanopore sequencing³ of DNA because the tunnel current can be confined to a region as small as the size of a single DNA nucleotide (in contrast to the 4 to 5 nucleotides that are sampled by ion-current measurements). The proposal is that a single stranded DNA molecule would be driven through a nanopore electrophoretically while the sequence is read using the electron tunneling current passing between two closely spaced electrodes (embedded in the pore) as each base passes through the tunnel gap. Tunnel current reads of individual nucleotides have been demonstrated experimentally⁴ but the current distributions measured for the four DNA bases were broad and overlapped considerably. Furthermore, a very small tunnel gap was required (0.8 nm) and this is too small for a single-stranded DNA molecule to pass through. Thermal fluctuations, Brownian motion, and both transverse and electrophoretic fields cause strong fluctuations of instantaneous position of the DNA bases relative to the electrodes. This results in large noise and poor signal-to-noise ratio in the transverse nonresonant tunneling conductance. For example, it was found that the variation in the conductance due to the geometry of the base relative the electrode can easily override the difference between different types of nucleotide^2,5. Therefore, control of the DNA translocation and localization as it threads the nanopore becomes a primary concern for DNA sequencing techniques using synthetic nanopores^6-9. Theoretical calculations predicted significantly increased signal-to-noise ratio in the tunneling reads of the DNA if the electrodes are functionalized with nitrogen so as to promote resonant tunneling through the DNA nucleotides¹⁰. When using a fluidic nanochannel functionalized with a graphene nanoribbon the changes in the conductance of the nanoribbon were deciphered as a result of its interactions with the nucleobases via π–π stacking¹¹. Electron transmission of graphene nanoribon shows characteristic features of physisorbed molecules on it and allows utilization of two-dimensional molecular electronics spectroscopy for a DNA base recognition¹². We have proposed an alternative approach we call recognition tunneling (RT).³ Recognition tunneling has significantly increased discrimination of the electron tunneling signals obtained from each of the DNA bases and is now becoming a good candidate as a “reading head” for DNA sequencing. Unlike nano pore ion-current measurements it is sensitive to single bases. Furthermore, a manufacturable solid state device that reads individual DNA nucleotides was recently demonstrated¹³. In RT, the electrodes of a tunnel gap are functionalized with organic molecular “readers” that form non-covalent contacts with the target molecules (figure 1) but are strongly bonded to the metal electrodes. The weak non-covalent bonding of the “readers” with DNA nucleotides allows for DNA translocation through a pore, but slows down the translocation of the DNA segment through the confining nanopore by some 3 orders of magnitude¹⁴. These non-covalent bonds are strong enough to increase signal-to-noise ratio by imposing constraints on thermal fluctuations^15-18. A special reader molecule has been designed to form distinctive patterns of hydrogen bonds with all four DNA bases. This molecule, 4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide, is referred to as ICA in this paper. Its properties and hydrogen bonding patterns in a RT gap are described elsewhere.¹⁹ The ICA molecule serves to displace contamination and eliminate water molecules and ions from the tunnel current path, as well as holding the target molecule in place transiently. This scheme works well with gaps of about 2 nm,¹⁵ producing characteristic stochastic signals for each of the four DNA bases.¹⁶ The signals are comprised of a series of sharp current spikes. The spike widths are exponentially distributed with characteristic 1/e times of around a ms (experimental measurements are limited in time resolution to about 0.1 ms because of the limited frequency response of the current measuring electronics). Distributions of signal parameters, such as the heights of the current spikes, and of their widths, are still overlapped considerably from one base to another. However, by making use of a number of signal features simultaneously, individual signal spikes can be assigned to each of the DNA bases quite accurately, despite the stochastic nature of the signals. This assignment is done using a machine-learning algorithm called a Support Vector Machine (SVM).¹⁷ More recently, RT has been used to recognize individual amino acids and peptides²⁰ possibly opening the way to sequencing of proteins at the single molecule level.

Figure 1.

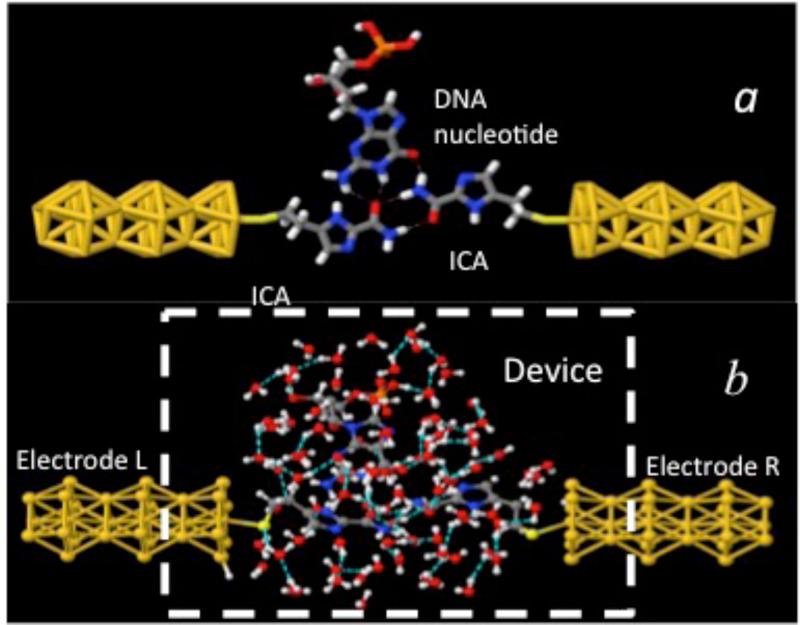
(a) Recognition tunneling. Recognition molecules (ICA) covalently bound to gold electrodes, form transient hydrogen bonds (dashed lines) with a DNA base (Guanosine in this example) to bridge the gap between the electrodes. This complex serves as the model system for the NEGF simulation of the recognition tunneling current signals described here. (b) A much more complex pattern of hydrogen bonds emerges when the complex is embedded in a bath of 90 water molecules. Color key: red-oxygen, white-hydrogen, blue-nitrogen, grey-carbon, yellow-gold atoms.

Despite this progress and promise, there has been almost no theoretical analysis of recognition tunneling. He et al.²¹ have calculated tunnel currents through junctions in which one electrode is functionalized with a cytosine. Their calculations were carried out in the absence of thermal fluctuations, and so do not capture this key feature of RT signals. Furthermore their model system did not include water molecules. Lee and Sankey²² have calculated currents for the ICA-(DNA-base)-ICA complexes bridging a tunnel gap (as in figure 1a). However, these calculations were also carried out at 0K and in the absence of water molecules.

The limited scope of these previous calculations is a consequence of the challenges of modeling the real experiment. The measured fluctuations lie in the ms range, hopelessly beyond the reach of even classical molecular dynamics, let alone the quantum-mechanical calculations required to estimate tunneling currents. One ad hoc attempt to rationalize the form of the RT signal assumed a random walk with a thermal (Gaussian) distribution in one dimension, taking the exponential of displacement as a measure of tunnel current.²³ By choosing parameter values appropriately, the form of the RT signal was reproduced. In this model, the parameters had no obvious relationship to measured physical quantities.

Several big questions remain unanswered: (1) Is the magnitude of the observed signals compatible with electron tunneling? (2) Does a reasonable physical model of the fluctuations predict the form of the RT signal? (3) Do the RT signals in a model system change enough with the chemistry of the target molecule (in the simulation) to allow a machine learning algorithm to identify individual signal spikes with significant accuracy? This latter point is very important, because the machine-learning based analysis of single signal spikes opens up an entirely new approach for analyzing single molecule interactions.

It is not possible to answer these questions with an all-atom, first principles calculation, but, in this paper, we make an attempt on constructing the best approximate models we can in order to address these issues. The goal here is to see if these best estimates resemble the experimental data, or conversely, rule out a mechanism by means of a large disagreement between theory and experiment. In Section 2 we begin with an all-atom quantum-classical molecular dynamics simulation of the motion of hydrated complexes at 300K, taking “snap shots” at short intervals of the atomic configurations and calculating the conductance of each configuration by means of a non-equilibrium Greens function (NEGF).²⁴ These calculations extend only into the ps timescale, and are further complicated by the need to take averages of a wildly fluctuating current in order to begin to approximate the experimental situation where fluctuations are integrated. While there is no a priori reason to suppose that the result can be extrapolated from ps to ms timescales, it is gratifying that the calculated currents fall within about an order of magnitude of the measured currents. Next, we adapt a simplified, coarse-grain model of DNA (the “oxDNA Model”^25-30) to extend classical dynamics simulations into the much longer time scales (covering ns-μs-ms ranges) to extract the hydrogen bond stretching (Section 3) and to develop (Section 4) a simplified representation of ICA molecules interacting with all DNA bases (more specifically, for a single “universal base” interacting with DNA). Using the calculated values of the hydrogen bond stretching over large time spans in the tunneling decay model¹⁹, we calculate the time dependence of the corresponding RT signals (Section 5). The calculated signals bear a strong resemblance to measured RT signals. Finally, in Section 6 we take calculated RT signals for all four bases interacting with the model “ICA” molecule (i.e., the universal base) and analyze them with the support vector machine. Each signal spike can be correctly assigned (A, T, G or C) to an accuracy that approaches 80% for bases where adequate training data was available. This provides a theoretical underpinning for the experimental observation that individual signal spikes can be assigned to better than 90% accuracy if adequate training data are available. Our conclusions are presented in Section 7.

2. QUANTUM-CLASICAL TUNNELING DYNAMICS AND MAGNITUDE OF THE TUNNEL CURRENTS

The quantum tunneling calculations were performed using the simplified geometry shown in figure 1(b). The figure 1(a) illustrates gold wire-electrodes, the ICA reader molecules (attached the electrodes via a sulfur), and a guanosine nucleotide in the initial hydrogen bonded configuration prior to the addition of water. The tunnel gap (sulfur to sulfur) was chosen to be 2 nm. This is smaller than the gap determined using STM break-junction techniques¹⁹ but consistent with more accurate measurements that have recently been made using solid state devices (unpublished data). Starting structures for complexes with the other bases were taken from Liang et al.¹⁹ The structure, as hydrated by 90 water molecules, is shown in figure 1(b). The presence of the water molecules introduces many additional hydrogen bonds, as indicated by dashed lines in figure 1(b). The geometry of the complex, for each of the four bases is optimized and thermalized at 300K with the quantum-classical molecular dynamics approach for their mutual interactions, for the interactions with and among the water molecules and for the gold-electrodes configurations, prior to performing the Quantum-Tunneling Classical Molecular Dynamics (QTCMD)³¹.

The quantum-classical molecular dynamics (QCMD) simulation was performed by the Self-Consistent-Charge Tight Binding Density Functional Theory (SCC DFTB^32-34), using appropriate Slater-Koster parameters.^35,37 We let the system evolve dynamically, using the classical molecular dynamics NVT calculation with a time step of 1 fs, dumping all coordinates each 10 fs. The Andersen thermostat³⁷ was applied, with probability of 0.1 to all particles (except for the gold atoms, which are frozen) to scale the particle velocities to the Maxwell distribution at 300K. Electron transport calculations were carried out (for each of the sets of system coordinates dumped in 10 fs intervals) using the Non-Equilibrium Green's Function method (NEGF-DFTB^38-40,32-34), thus obtaining the time-dependent tunneling signal.

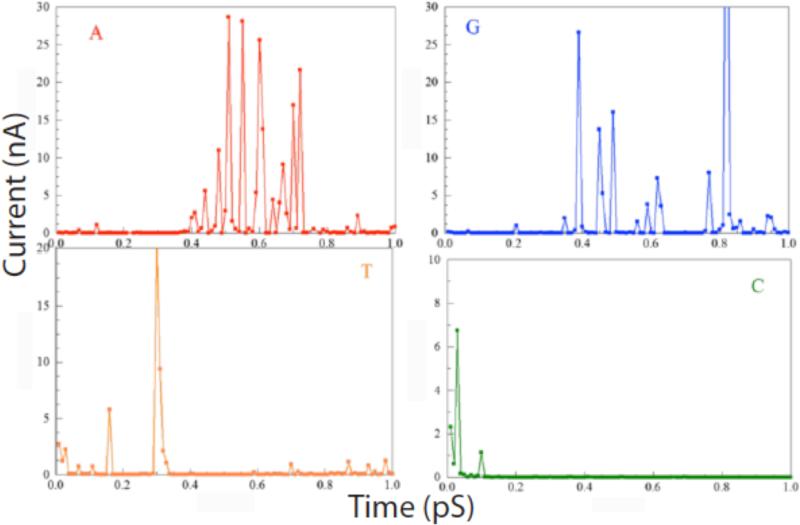
Examples of calculations out to 1ps (for a bias of 0.5V) are shown in figure 2 for all four DNA bases. The currents fluctuate over a wide range, with only the largest peaks visible on these linear plots. These large peaks bear a striking resemblance to the measured spectra but of course the time scale is shorter by over 9 orders of magnitude. Although the classical MD calculations are fast, the computational bottle-neck is the electron transport calculations, which become formidable in presence of water. This is the reason that the all-atom, QTCMD calculations have been performed only within a 1ps interval. The presence of water changes the signal through readers, influencing the frequency and intensity of the peaks. The most important observation here is that the fluctuations of the calculated signal is caused by the thermal fluctuations, and significantly influenced by the presence of water.

Figure 2.

Time-dependent tunnel current calculated for a bias of 0.5 V using combined classical molecular dynamics and quantum-mechanical NEGF calculations of the current for each of the four bases trapped in the tunnel junction by ICA molecules. Red (A), blue (G), yellow (T) and green (C) nucleotides.

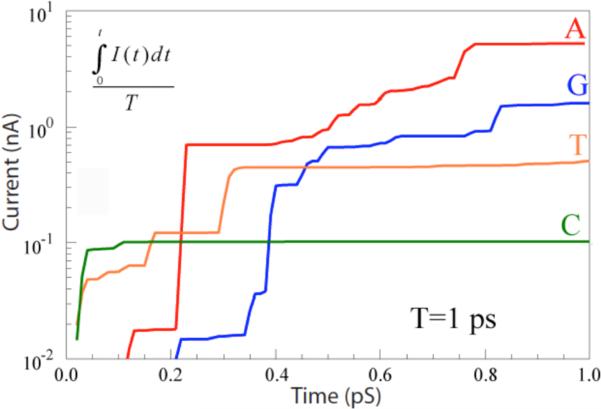
In order to compare with the experimental situation, these currents need to be integrated (as they are in the experiment by the finite response (~0.1 ms) of the electronics). In this present simulation, characteristic bond vibrational times are on the order of 0.1 ps, so a reasonable approximation to the average current can be found by integrating over the 1 ps duration of the simulation. The results of doing this are shown in figure 3. The currents do approach constant values when the time interval for the integral becomes much greater than 0.1 ps. The resulting averaged currents lie in the range from a few nA (Adenosine) to about 100 pA (Cytidine). These values are considerably greater than the tens of pA observed in experiments, but the averages would be likely reduced by other, longer timescale fluctuations beyond the reach of the current simulation. Thus, the magnitude of the measured RT currents are not inconsistent with values calculated for electron tunneling in the presence of strong fluctuations.

Figure 3.

RT currents integrated over 1 ps for the four bases as marked.

3. THE OXDNA MODEL FOR COARSE-GRAINED SIMULATIONS

A first step in order to capture fluctuations out to μs to ms timescales, is a reduction of the system complexity to the coarse-grained model of the interactions of solvated DNA bases. oxDNA^25-30, a coarse-grained DNA model developed by the University of Oxford (and available for public download: https://dna.physics.ox.ac.uk/index.php/Main_Page), is particularly suited for this task.

The model represents DNA as a string of 2-center nucleotides, the centers being sugar-phosphate and base rigidly connected to a nucleotide, which are mutually interacting (see the online Supporting Information, where some further details of the model are given). The potential energy of the system contains both interactions of the nearest-neighbors (nn) nucleotides on the same strand (the sugar-phosphate backbone potential, nn stacking, excluded volume) as well as remaining interactions that can couple different strands (hydrogen bonding V_HB, cross and coaxial stacking). The interactions between nucleotides are schematically shown in figure S1 (Supporting Information).

Since the main focus of the present work is the hydrogen bonding, we focus here on how it is modeled.^25,26 The Watson-Crick base pairing is modeled through the V_HB term of potential, with a radial term dependent on the instantaneous bonding length R, defined by the separation of hydrogen bonding sites. The co-linear alignment of the antiparallel planes of the paired bases has strong preference in the hydrogen bonding interaction (quantified by a set, $\stackrel{‒}{\theta }$, of five angles)

$$V_{HB}=f_1\left(R\right)F\left(\stackrel{‒}{\theta }\right)$$ (1)

Figure S2 shows the radial dependence of the V_HB(R) for randomly chosen sets of $\stackrel{‒}{\theta }$ for the Watson-Crick pairs A-T and G-C. The range of coupling extends to more than 6 Angstroms, while the absolute minimum of the coupling is close to 3.4 Angstroms and is about 0.32 eV for G-C and about 0.23 eV for A-T hydrogen bonding.

4. MODEL OF THE READER-BASE INTERACTION

The oxDNA model represents interactions between DNA molecules – how might it be extended to represent the interactions of the ICA reader molecules with the four bases? At this point, it has not proven possible to make a quantitatively accurate representation of the full ICA-base-ICA complex as shown in figure 1a. Instead, we have extended the oxDNA by a simple model of just one universal molecular reader (i.e., a representation of one of the ICA molecules) interacting with all DNA bases, by implementing a new “base” Z which bonds to all four DNA bases. The base-independent angular modulation of the hydrogen bonding is left as in the oxDNA model. Following the experimental observation, Z-T and Z-A bond strengths (minima in the curves in figure S2) are given the smallest values of 0.23 eV and 0.26 eV respectively, while Z-C and Z-G are assigned somewhat larger values, of 0.292 eV and 0.32 eV, respectively. These assumed H-bond strengths lie between the maximum (G-C) and minimum (A-T) values for the Watson-Crick pairs. The coupling base-pair dependent stacking strength for the Z-A, Z-T, Z-C, Z-G and Z-Z stacking is here taken to be 0.424 eV, which is the average value of all original stacking strengths between the various base pairs.

5. DESCRIPTION OF THE COARSE-GRAINED DYNAMICS

The modified oxDNA model was used to generate the inter-particle forces for a Langevin dynamics simulation of the relative motion between the “Z” readers and DNA bases. In Langevin dynamics the solvent exerts both random forces and dissipative drag on the solute, and the two are related by a fluctuation-dissipation relation to ensure that a steady-state Boltzmann distribution integration of the classical equations of motion into dynamical trajectories includes the effects of the solvent-mediated forces. In this model, each nucleotide (A, T, C, G and “Z”) is a 3D rigid body so that the configuration space spanned by N nucleotides has 12N dimensions in coordinate-momentum space. Pairs of nucleotides interact through the pairwise effective interactions, described in sections 3 and 4. The rigid-body dynamics and description of diffusion in oxDNA are described in detail in the references^25-29 and in the Supporting Information.

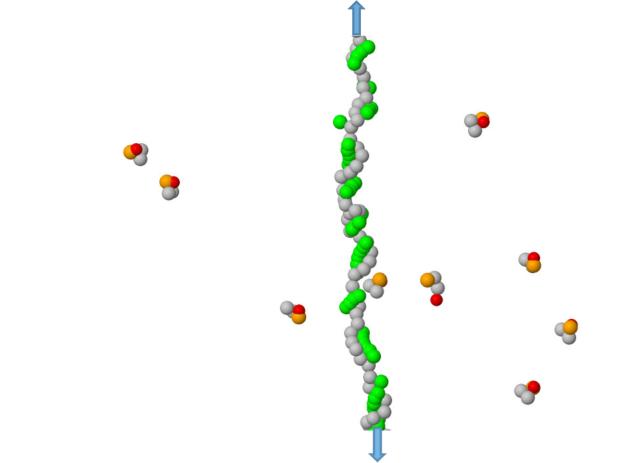
We first tested the model using interactions between DNA bases that Watson-Crick pair to see if the behavior was reasonable (Supplementary Information, figures S4-S6). Armed with this background, we then simulated interactions between the universal “Z” base and the DNA nucleotides. A typical configurations for modeling the Z-nucleotide interactions are shown in figures 4 and S3.

Figure 4.

A typical configuration for detecting the H-bond interactions between ZA dimers and a poly(dG) ssDNA segment (stretched by an applied tension). The DNA bases are shown in green, the Z-bases are red, the A-basis are orange, while phosphorus-sugar groups for bot DNA and ZA dimers are shown in gray. The arrows indicate stretching forces of 24.3 pN imposed to linearize the homopolymer.

The dynamics produces trajectories of the system, which we capture at predefined time intervals. Typical calculations have run for 10⁹ to 10¹⁰ time steps, i.e. tens to hundreds of μs, dumped each 200 steps, i.e., in steps of 1.7 ps. In addition to the trajectories of all particles, we record the components of energy, including the hydrogen bonding energies. Since oxDNA takes into account directional difference of the 3’-5’ and 5’-3’ strand topologies, for the purpose of a correct description of the double-helix association, the smallest DNA segment used for a probe is a dimer. In order to have a single monomer of a dimer bonded to a DNA, we construct the dimer-nucleotides from one Z-base and another DNA base that will not bond to a target homopolymer. Figure 4 shows an example of ZA dimers and poly(dG) (mismatches have zero interaction in the oxDNA model). Both the probes and the DNA are subject to random Brownian forces, resulting in stochastic dynamics of the binding and unbinding of the probes to the DNA, as indicated in figure 4. In the model of a homopolymer interacting with a bath of dimers, it is possible to have several interactions occurring at once. For this reason, we followed the bonding evolution of each probe, obtaining the time-dependent bonding length for each monomer binding event. By analysis of the oxDNA output, from the trajectories and hydrogen bonding energies, we derive the lengths of the hydrogen bonds as functions of time, in steps of 1.7 ps, for each monomer in the dimer probes bonded to the DNA segment. Here, we will focus on interactions between dimers and a DNA homopolymer. (We have also investigated interactions between dimers and heteropolymers, extracting single Z-base interactions from the many types of event that can occur in that case, and obtaining results that were similar to those we present here for the much simpler case of a homopolymer.)

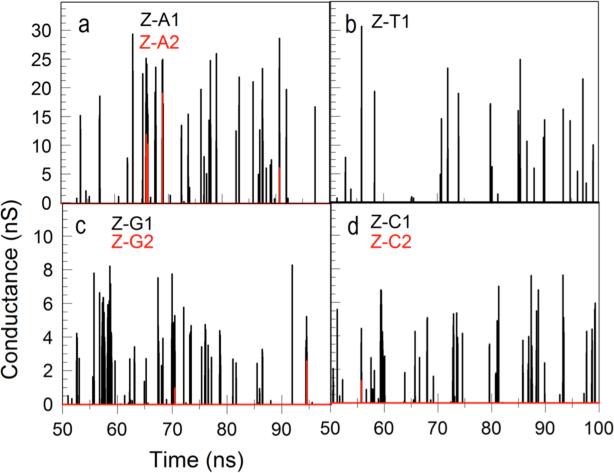
Even in the case of a homopolymer, simultaneous binding of more than one dimer to the target homopolymer may affect the dynamics, so we separate events into single dimer-polymer bindings, double binding events and so on. Thus, for example, events in which a single dimer is bound to a poly(A) are labeled ZA_1, two dimers bound are labeled ZA_2 and so on. Examples of calculated conductance vs. time traces where the different types of binding events are color coded are given in figure 5. We have excluded from these calculations events where dimers interact only with other dimers.

Figure 5.

Conductance vs. time for Z-A (a) Z-T (b), Z-G (c) and Z-C (d) complexes. The multiplicity of each complex is indicated by the color code. We used the same β=3.0 in Eq. 2 for all complexes. The dimer probes contain one Z monomer and one monomer which does not bond the respective DNA polymer. Thus, for polyA and polyT the dimers are ZC, and for polyG and polyC the dimers are ZT. Signals obtained with ZZ dimers are shown in Figs. S7 and S8.

We assume that the tunnel current fluctuations are dominated by the stretching of the hydrogen bonds (as constrained by all the other interactions of the model). Once the time dependent hydrogen bond length was obtained, we used the electronic decay constants, β_G-C, β_A-T for hydrogen bond stretching computed by Lee and Sankey²² to estimate the conductance fluctuations for each bonded monomer, according to

$$G=G_0\exp (-\beta R)$$ (2)

where R is the hydrogen bond length, G₀ is quantum of conductance (77μS) and β_G−C = 3.3A⁻¹ and β_A−_T = 2.6A⁻¹. This is a significant difference, and choosing, for example, to use β_{G_C} for Z-C and Z-G complexes and β_A-T for Z-A and Z-T complexes leads to significant difference in the size (figures S6 and S8) of the corresponding current fluctuation (though we shall see that this does not dominate the SVM analysis). For this reason, we used an identical value for all for interactions (ZA, Z-T, Z-G and Z-C) of β=3.0.

Typical conductance-time traces for Z interacting with each of the four poly-nucleotides, A,T,C and G, are shown in figure 5, estimated at each point of time by equation 2 using the calculated HB distance calculated for each interaction and the same β for all bases. The currents were obtained from the conductance’s assuming an applied voltage bias of 0.5V.

The simulations run out to a fraction of a ms, still not quite the experimentally measured time scale of fluctuations (which are limited to current peaks longer than about 0.1 ms). But the form of the fluctuations bears a striking resemblance to the experimentally measured spectra⁹.

Do these simulated spectra contain enough information to allow identification of the individual nucleotides? This is the subject of the next section.

6. CHEMICAL ANALYSIS FROM SIGNAL PEAK FEATURES

Despite the fact that the experimentally measured RT signals are stochastic, with signal features that are broadly distributed, it turns out experimentally that individual signal peaks can be assigned to particular analytes with remarkable accuracy using a machine-learning algorithm that combines information from many signal features.¹⁷ Is this true of the simulated signals that are the subject of the present paper? This question is important in giving a theoretical underpinning to the observation that single signal spikes can be assigned to individual analytes with high accuracy.^17,20

We used the calculated conductance signals (c.f., figure 5) for homogeneous DNA’s derived from the coarse-grained model described above to answer this question. The code developed for analyzing experimental signals²⁰ begins by identifying each signal spike in the data train by setting a threshold that is a small multiple of the measured instrumental background noise. These simulated spectra have no noise on them and a very large bandwidth, down to the level of the numerical rounding errors. This is an advantage because the machine learning algorithm can be trained with far fewer data points than would be required for noisy experimental data (after selection of the desired monomer binding events, the simulations generated relatively few suitable events - see below). We accept the threshold for the hydrogen bonding inherent in the oxDNA model – the bonding is set to zero if the HB energy is smaller than ~kT (i.e. ~25 mV), so the calculated tunneling currents go precisely to zero when the bonds break. For this reason, no current threshold is required to identify a peak. We did set a time threshold, requiring that the peaks last longer than 8 sample points so that an FFT analysis could be applied. Peaks of 8 or fewer data points were rejected from the analysis. The “spikes” in the simulated data can have a very complex structure (an example is shown in figure S9).

A third difference between theory and experiment lies in the significance of signal amplitudes. These are too variable (from experiment to experiment) to be of much use in classifying experimental data.²⁰ Here, the opposite is true: G’s and C’s are trivially separated from A’s and T’s when a different electronic decay constant used in the simulations. That said, the separation of all four bases, one from the other, was little affected by amplitudes (see below).

In the coarse-grained calculations showed here, we assume that the conductance is mainly determined by the conductance of the hydrogen bonds, dominated by the very large β values associated with hydrogen bond stretching, so the fluctuations in tunnel current reflect length fluctuations of the hydrogen bonds. This is probably a good model for the time dependence of the current. However, the calculated values of conductance (several nS) is significantly larger than the value observed in experiments (tens of pS) at least in part because this simple model does not take account of tunnel current decay owing to the remainder of the molecular structure.

After the selection of peaks lasting longer than 8 data points (~14 ps) a number of peak properties were extracted including amplitude, peak width, and the power spectrum of the peak (for up to a total of 52 signal features as described in our experimental paper¹⁷). We used calculated currents for a homopolymer interacting with a ZX dimer where X is a base that will not pair with the homopolymer. A significant difference between the experiments and simulations lies in the frequency analysis. Because the simulation steps are 1.7 ps, the Nyquist frequency is almost 300 GHz (as opposed to kHz in the experiment). The power spectral density components were calculated as the averages of the FFT data in 51 equal bins (~6 GHz each) from 0 to 300 GHz (referred to as PS1(N) where N is the bin number, 1-51) and then again as the average over 10 equal bins (~30 GHz each). These are referred to as PS2(M) where N runs from 1 to 10. The bins are divided by the total signal power so the values are dimensionless.

We began with the full parameter set, reducing the number of parameters by removing the least significant (in terms of its contribution to classification accuracy) and then repeating the analysis. In this stage of training, a majority (90%) of the data were used to generate support vectors, the classification accuracy of which was tested on the remaining 10% of the data. This procedure was repeated with random sampling to reduce sampling errors. We plotted the assignment accuracy for each of the bases as a function of parameter number and choose a signal-feature set that was optimal for all four bases. The feature set used for all the analyses shown here was PS1(2,3,9,11,40,47,48) and PS2(3,6,10) for a total of 10 signal features.

These trials give the “training” accuracies listed in table 1. These are considerably smaller than the accuracies found in (much bigger) experimental data sets and likely reflect the small number of peaks used in these calculations (A, 928, G, 1862, C, 600 T, 190). In particular, the lifetime of the Z-T complex was the shortest, resulting in a much smaller amount of data for this base with corresponding smaller accuracy. (In contrast, experimental training is done with tens of thousands of peaks.) Nonetheless, the accuracies all exceed the expected random assignment value (of 25%) by a significant amount. This shows that these thermal fluctuations contain significant chemical information even when differences in electronic decay constant are removed.

Table 1.

Accuracies of the SVM classification of the signals for each base for the signal-feature set that produced the most accurate overall classification of the bases.

	A accuracy (%)	G accuracy (%)	C accuracy (%)	T accuracy (%)
Equal beta training	88	83	71	55
Equal beta testing	70	51	55	35
Different beta training	95	80	62	60
Different beta testing	70	76	41	17

“Training” indicates that the cross validation was done on the same simulation.

“Testing” indicates that the cross validation was done with training on one simulation and testing on a different simulation.

The error in the accuracies is approximately ±5%.

It is important to test the robustness of the support vectors with independently simulated data. Our first simulations used homopolymers of 20 nucleotides and a dimer concentration of 10 dimers per box of 10 nm × 10 nm × 10 nm. This generated the training data. We ran a second set of simulations using a homopolymer of 30 nucleotides and a dimer density of 15 in a box of 12 nm × 12 nm × 12 nm. We then used the support vectors generated using the training data and applied them this second set of independently (and slightly differently) generated data. The resulting classification accuracies are referred to as the “testing” results in table 1. The accuracies are, as expected, worse than the training accuracies, but still significantly better than random. (The case of T for different beta's is an exception, and probably a consequence of poor training with the very small number of T signals used – poor training can result in assignment frequency that is worse than random.)

Inspection of table 1 shows that the imposition of different beta values for Z-C, Z-G and Z-T and Z-A (“different beta” in table 1) does little to improve the accuracy of the separation of the four bases, despite the significant differences imposed on Z-G, Z-C vs. Z-A, Z-T current fluctuation amplitudes. Thus, the most significant chemical information appears to be encoded in the time dependence of the current, paralleling what is found with experimental RT data.

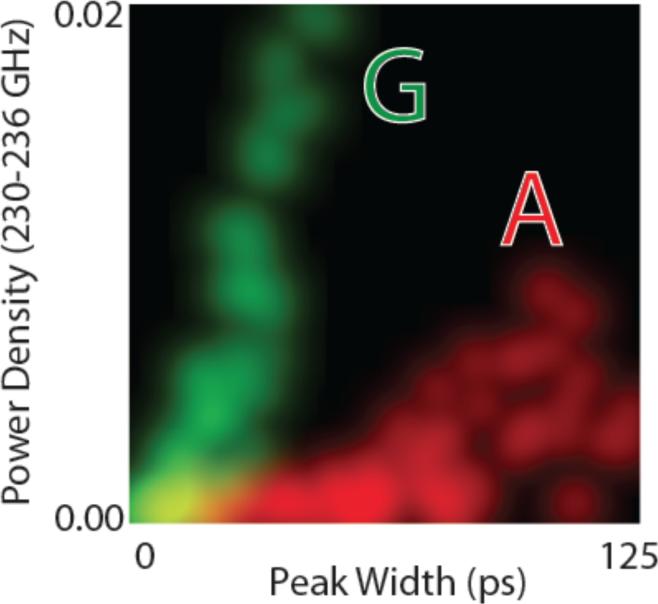
Finally, it is instructive to see how non-linear correlations between signal features lead to enhanced separation of data, as these are key to the enhanced accuracy of the high dimensional analysis of stochastic data enabled by the SVM. Figure 6 shows a two dimensional distribution in which the probability densities of two signal features are plotted together (these are power density in the 40^th bin of the FFT (PS1) and the peak widths at half height). The 1D histograms for each of the signal features correspond to the projection of the brightness of the points onto any one axis. Thus, using peak width alone (for example) only the very longest peaks could be assigned to A (red). However by using the two parameters together, most data points are well separated for A and G. Similar plots for real experimental data can be found in the paper by Zhao et al.¹⁷ Note that PS2(40) data correlate with peak widths (roughly linearly) because the shorter peaks put power density into bins that are even higher in frequency.

Figure 6.

Distribution of a power spectrum component for 230-236 GHz (intensity of points projected onto the vertical axis) against the distribution of peaks widths (intensity of points projected onto the horizontal axis) for Z-A interactions (red) and Z-G interactions (green). This is a color-mixed plot, so that overlapped data produces a yellow color (points are blurred to allow overlap). Note that if the distributions for A and G were plotted with only one parameter as a conventional (1D) histogram, most of the data points would be overlapped. Non-linear correlations between the two signal features result in enhanced separation in this 2D analysis.

7. CONCLUSIONS

To the extent possible within the constraints of current simulation tools, we have demonstrated the following points:

• (1)Thermal fluctuations give rise to sharp current spikes in an all-atom model of a solvated RT complex in a tunnel junction. Water molecules play an important role in these fluctuations.
• (2)The magnitude of the currents calculated for these signal spikes using a non-equilibrium Green’s function is consistent with the experimental data, assuming that the averaging procedure used here can be extrapolated to longer time scales (for a 2 nm tunnel gap, as used in the experiments).
• (3)A coarse grained simulation based on the oxDNA model shows bonding fluctuations out to ms timescales, and generates conductance fluctuations that resemble the experimentally measured RT signals.
• (4)Signal spikes in the RT signals calculated with a simplified model consisting of a single universal base “reading” a ssDNA contain enough information in their shapes alone (i.e., excluding signal amplitudes) for sequence to be read with high accuracy. The amplitudes of the RT signal peaks play a small role in the sequence recognition.

Thus, although it is not possible to generate a rigorous test of a model of RT that incorporates the full atomistic and quantum mechanical details out to the >ms timescales of experiments, the modeling presented in the current paper supports the notion that stochastic thermal fluctuations in a tunnel junction can generate useful chemical information and generate signals of a useful magnitude in a tunnel junction big enough to accommodate a single stranded DNA molecule.