Lamina Cribrosa Microarchitecture in Normal Monkey Eyes Part 1: Methods and Initial Results

Abstract

Purpose.

To introduce quantitative postmortem lamina cribrosa (LC) microarchitecture (LMA) assessment and characterize beam diameter (BD), pore diameter (PD), and connective tissue volume fraction (CTVF) in 21 normal monkey eyes.

Methods.

Optic nerve heads (ONHs) underwent digital three-dimensional (3D) reconstruction and LC beam segmentation. Each beam and pore voxel was assigned a diameter based on the largest sphere that contained it before transformation to one of twelve 30° sectors in a common cylinder. Mean BD, PD, and CTVF within 12 central and 12 peripheral subsectors and within inner, middle, and outer LC depths were assessed for sector, subsector, and depth effects by analysis of variance using general estimating equations. Eye-specific LMA discordance (the pattern of lowest connective tissue density) was plotted for each parameter.

Results.

The ranges of mean BD, PD, and CTVF were 14.0 to 23.1 μm, 20.0 to 35.6 μm, and 0.247 to 0.638, respectively. Sector, subsector, and depth effects were significant (P < 0.01) for all parameters except subsector on CTVF. Beam diameter and CTVF were smaller and PD was larger within the superior-temporal (ST) and inferior-temporal (IT) sectors (P < 0.05). These differences were enhanced within the central versus peripheral subsectors. Beam diameter and CTVF were larger and PD was smaller (P < 0.05) within the middle LC layer. Lamina cribrosa microarchitecture discordance most commonly occurred within the ST and IT sectors, varied by eye, and generally diminished as CTVF increased.

Conclusions.

Our data support previous characterizations of diminished connective tissue density within the ST and IT ONH regions. The clinical importance of eye-specific LMA discordance warrants further study.

Quantitative ONH lamina cribrosa microarchitecture characterization and discordance mapping are used in 21 normal monkey eyes to confirm that connective tissue volume fraction and beam diameter are lowest and pore diameter is largest in the superior-temporal and inferior-temporal ONH sectors.

Introduction

Since Quigley^1,2 and Radius^3,4 first reported larger lamina cribrosa (LC) pore diameters and lower connective tissue density within the superior and inferior regions of the human optic nerve head (ONH), an important literature has characterized the regional structure of the human and monkey LC using histologic,^2–5 electron microscopic,^1,6,7 and, most recently, optical techniques.^8–17 The regions of the LC that are lowest in connective tissue density are important because they appear to correlate with the ONH regions that are most susceptible to age-related¹⁸ (Chauhan BC, IOVS 2014;55:ARVO E-Abstract 4028) and glaucomatous retinal ganglion cell (RGC) axon loss.¹⁸ However, the mechanisms by which they contribute to this susceptibility remain unknown.

We have previously reported our methods for digital three-dimensional (3D) histomorphometric reconstruction (3D HMRN) of the monkey ONH tissues,^19,20 digital isolation of the LC volume,²¹ and digital segmentation of the LC beams.²² Roberts et al.^21,23 used these techniques and employed a continuum finite element modeling approach to divide the LC volume into 45 subvolumes (elements) in which the connective tissue volume fraction (CTVF) and constituent stresses and strains within each element were calculated. In eight eyes of four bilaterally normal monkey eyes, CTVF was significantly correlated with biomechanical stress (positively) and strain (negatively) within each element.²⁴ This finding linked connective tissue density to a potential mechanism of axonal insult²⁵ (connective tissue strain) and proposed CTVF as a clinical imaging target that would predict where connective tissue strain would be greatest in an individual ONH. However, while the predominant orientation of the beams within each element was characterized using the mean intercept length method,²¹ quantifying LC microarchitecture (i.e., LC beam and pore diameter) was not necessary and therefore not performed.

The purpose of the present study was to introduce a 3D method for postmortem quantitative LC microarchitecture (LMA) assessment and use it to characterize LMA in 21 normal monkey eyes of 21 animals. Our method is built upon four new techniques for postmortem 3D histomorphometric characterization of eye-specific ONH anatomy. The first is quantitative, voxel-based 3D LC beam and pore diameter measurement. The second is digital transformation of all LC voxels (with their associated beam or pore diameter) into a common cylinderized space for between-eye comparison. The third is the use of an axis connecting the center of the fovea and Bruch's membrane opening (BMO) centroid (the FoBMO axis) to anatomically orient twelve 30° (clock-hour) ONH sectors.^26,27 The fourth is eye-specific, LMA discordance mapping that identifies the location and extent of those ONH sectors in which the amount of connective tissue is most reduced compared to all other sectors.

The three principal LMA outcome parameters of this report are LC beam diameter (BD), pore diameter (PD), and CTVF.²⁴ Secondary outcome parameters include connective tissue volume (CTV) and LC volume (LV), which are included because they contribute to the calculation (and understanding) of CTVF but are not emphasized because they correlate with it.

Materials and Methods

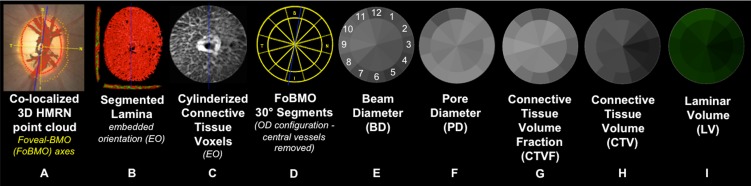
An overview of the method is depicted in Figure 1. Details of each step are outlined in Figures 2 through 8. Within the figures in this report, scaling for BD, PD, CTVF, and CTV has been adjusted so that white suggests more and black suggests less connective tissue. Lamina cribrosa volume is depicted in green because it is not intended to convey connective tissue magnitude or density. All data are reported within 12 FoBMO 30° sectors²⁶; within 12 central and 12 peripheral subsectors (Fig. 1); and within inner (one-third), middle (one-third), and outer (one-third) LC layers (Fig. 5). We use “global” to refer to LMA data for a single ONH that includes all sectors, subsectors, and depths. We use “overall” to refer to LMA data for all 21 eyes considered together. Table 1 contains acronyms and terms with their descriptions.

Figure 1.

Method overview using study eye 7. (A) The foveal-BMO (FoBMO) axis (Fig. 2) is determined and defined to be the nasal-temporal axis of the ONH 3D histomorphometric reconstruction (3D HMRN) (relative to the embedded orientation [EO] of the tissues [embedded vertical axis depicted by blue line]) by colocalizing the reconstructed vessels to a fundus photo (fovea not shown; see Fig. 2). Lamina is isolated (not shown); the beams are segmented (B) (Fig. 3); and each beam voxel and pore voxel has the associated diameter values assigned (Fig. 4). (C) Each voxel is then translated to a common cylinderized space (Figs. 5, 6). (D) The cylinder is rotated to establish FoBMO-oriented 30° (centered on the clinical clock-hours) sectors that straddle the FoBMO nasal-temporal and superior-inferior axes. All left eye data are converted into right eye orientation (Fig. 7). The three principal laminar microarchitecture outcome parameters are (E) beam diameter (BD) (with right eye, clock-hour, 30° sector designations), (F) pore diameter (PD), and (G) connective tissue volume fraction (CTVF). Secondary volumetric outcome parameters include (H) connective tissue volume (CTV) and (I) laminar volume (LV). For all connective tissue and pore parameters, scaling is adjusted so that white suggests more and black suggests less connective tissue. Laminar volume is depicted in green because it is not related to connective tissue. All parameters are reported within 12 central and 12 peripheral FoBMO-oriented 30° sectors (D). A separate analysis considers inner (one-third), middle (one-third), and outer (one-third) laminar layers (not shown). See the appropriate Methods sections and Figures 2 through 7 for detailed explanations of each step.

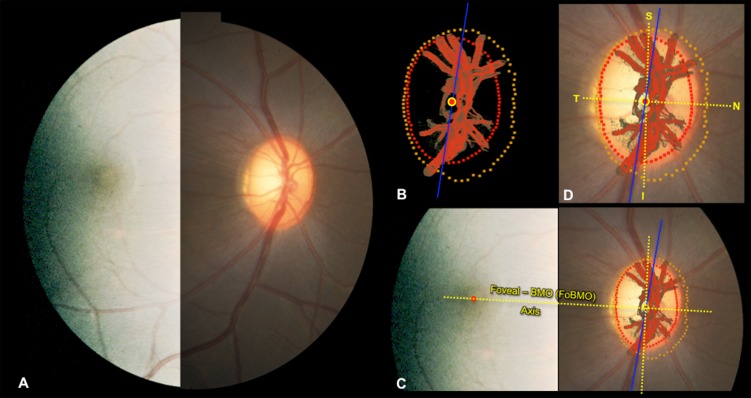
Figure 2.

Estimating the foveal-BMO (FoBMO) axis within the 3D HMRN BMO reference plane of each ONH. (A) A fundus photo (here with brightness enhanced temporally to better show the fovea), confocal scanning laser reflectance image²⁶ (not shown), or postmortem fundus photo (not shown) was used to establish the axis between the fovea and the centroid of BMO for each eye as follows. (B) Delineated neural canal point clouds (BMO, red; ALI, dark yellow) and surfaced central retinal vessels (red) accompanied by the BMO centroid (red circle with yellow outline) and the embedded tissue block vertical (blue line) orientation were colocalized to the clinical fundus photo (C) using the vascular tree and BMO points (see Methods; in this image BMO reference plane is slightly rotated out of the plane of the image to enhance visualization). The center of the fovea ([C] red dot) is assigned to be the center of the dark foveal reflex or the center of the foveal capillaries. The axis connecting the center of the fovea to the BMO centroid (yellow with red center) is the FoBMO axis (C). Using the FoBMO axis as the nasal-temporal (horizontal) midline, a FoBMO vertical axis was established perpendicular to it (C), allowing anatomically consistent, FoBMO superior, inferior, nasal, and temporal landmarks (D) within the BMO reference plane of each studied eye to be established. In this study, LMA was characterized relative to a reference plane based on the anterior LC insertion points (rather than BMO). The FoBMO vertical and horizontal axes were thus projected from the BMO reference plane to the ALI reference plane at the time of cylinderization (see Fig. 5 and Methods). Finally, unlike SDOCT, in which both the FoBMO centroid and foveal center can be determined within SDOCT anatomy at the time of image acquisition, the FoBMO axis within our 3D HMRNs is an estimate because the fovea is not included within the ONH trephine.

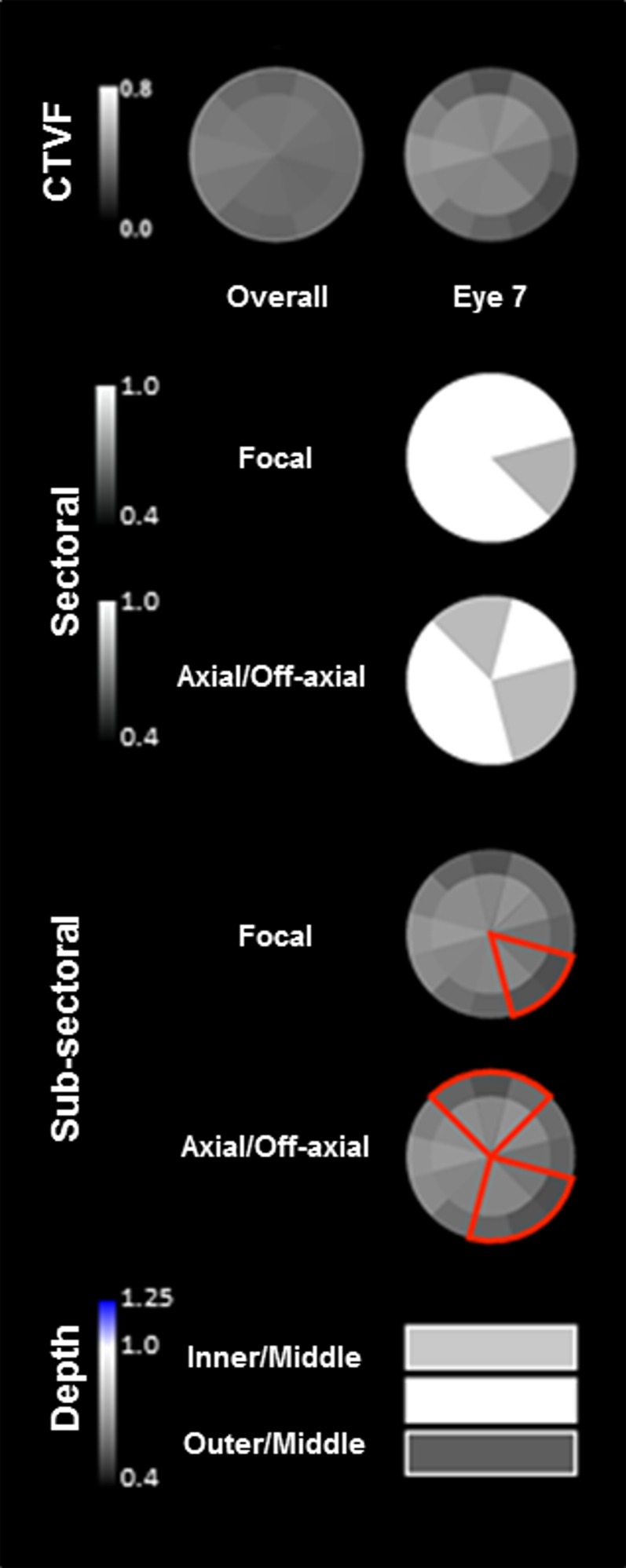
Figure 8.

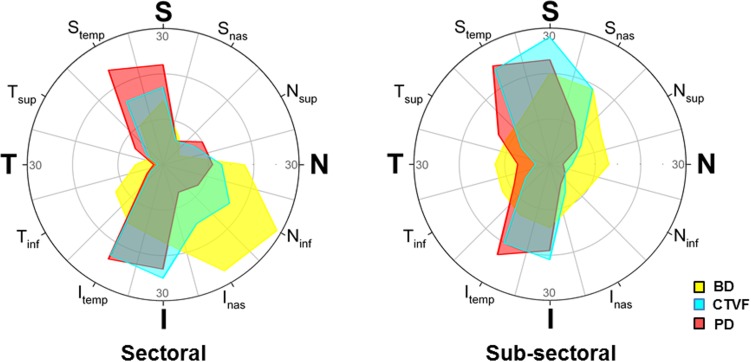
Eye-specific LMA sectoral, subsectoral, and depth discordance mapping in a representative study eye. Overall (left) (all 21 eyes) and eye-specific (study eye 7, right) FoBMO subsectoral CTVF data are shown for study eye 7 in the top row. For CTVF, we define LMA discordance to be present in those sectors in which CTVF is lowest compared to all other sectors of the ONH. Focal (all combinations of two, three, or four adjacent sectors) and axial sectoral discordance (all possible combinations of four, five, or six sectors on either side of BMO centroid—two or three adjacent sectors on one side and two, three, or four adjacent sectors on the other side) are shown in rows 2 and 3. These plots identify the sectoral location and magnitude (grayscale, left) of the greatest discordance from all other sectors (depicted in white). The locations of focal and axial subsectoral discordance are depicted in red in rows 4 and 5. These plots identify those sectors in which the ratio of the peripheral versus central subsectoral CTVF is lowest compared to all other sectors. The magnitude of that ratio is not depicted. The magnitude of inner versus middle and outer versus middle CTVF depth discordance (scale to the left) is depicted in the bottom row. Note that while the superior-temporal (11 and 12) and inferior-temporal (6 and 7) sectors are qualitatively lowest in CTVF in the overall data for all 21 eyes, the nasal, inferior-nasal, and superior sectors are most commonly involved in sectoral and subsectoral discordance in study eye 7.

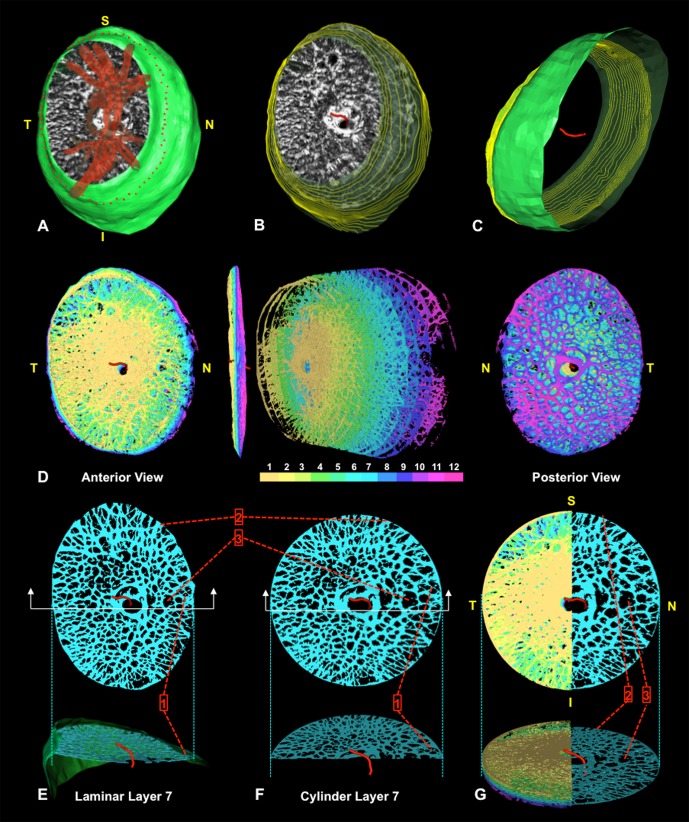
Figure 5.

Transformation of each lamina cribrosa voxel to a common cylinder. (A–G) Screen captures of live data from study eye 7 during cylinderization. (A) Isolated LC segmentation and vessel tree with its neural boundary surface (green) in FoBMO right eye orientation (Fig. 2). The delineated anterior LC insertion (ALI) points are shown in red along the neural boundary surface. (B) Vessel tree removed to reveal the anterior neural boundary centroid spline (red) and neural boundary contours projected as faint yellow lines through the neural boundary surface. (C) View from the underside with the LC removed to reveal the posterior extent of the neural boundary centroid spline relative to the inner neural boundary surface (contours again shown in yellow). The centroid spline passes through the center of mass of each neural boundary contour. (D) To cylinderize the data, each LC voxel is assigned to one of 12 layers. Anterior (left), side (middle left), exploded (middle right), and posterior (right) views are shown. (E) Layer 7 voxels in precylinder orientation depicting specific voxel locations within the LC structure using pointers 1, 2, and 3. Below, the corresponding side cutout view is shown with pointer 1 identifying three pores along the border of the nasal neural boundary. (F, G) Layer 7 voxels after cylinderization. Figure 6 explains the voxel-specific calculations that underlie this transformation. Note the location of three corresponding individual voxel locations shown with pointers in (E–G). Note that the central and peripheral location of voxels precylinderization remain after they are cylinderized. (G) All 12 layers of cylinderized LC voxels are shown to the left of the superior/inferior axis. Layer 7 is isolated to the right. Below is a side view of the same rendering. Note that every beam or pore voxel has a diameter assigned (Fig. 4) prior to cylinderization that is retained throughout the cylinderization process. Voxel size is not modified. Only voxel locations are modified during cylinderization. In polar coordinates (r, θ), θ is held constant while r is adjusted as depicted in Figure 6.

Table 1.

Common Acronyms and Terms With Their Descriptions

Acronyms/Terms	Full Name/Description
ALI	Anterior LC insertion (Supplementary Fig. S1)
ANOVA	Analysis of variance
ASAS	Anterior-most subarachnoid space—the anterior-most extent of the CSF space defined by the dural insertion into the episcleral tissues
ASCO	Anterior scleral canal opening
BD	Beam diameter (Fig. 4)
BM	Bruch's membrane
BMO	Bruch's membrane opening
CSF	Cerebrospinal fluid
CTV	Connective tissue volume—in this study the sum of all connective tissue voxels
CTVF	Connective tissue volume fraction—in this study the ratio of CTV to LV expressed without units
EG	Experimental glaucoma
EO	Embedded orientation—the vertical and horizontal axes of the embedded ONH tissues within the 3D HMRN
FoBMO	Foveal–BMOcentroid
FoBMO axis	For 3D HMRN—a line connecting the estimated center of the fovea in a fundus image and the colocalized 3D HMRN BMOcentroid (Fig. 2)
FoBMO oriented	Using the FoBMO axis as the nasal-temporal midline for ONH 3D HMRN 30° sectoral regionalization (Fig. 1)
GEEGLM	A general linear model fitted with a generalized estimation equation
Global data	Lamina cribrosa data for a single ONH that includes all sectors, subsectors, and depths
HMRN	Histomorphometric reconstruction—stacked, serial digital section images from the stained embedded tissue block surface
ILM	Internal limiting membrane
LC	Lamina cribrosa
LMA	LC microarchitecture—in this study characterized by BD, PD, and CTVF
LV	Lamina cribrosa volume—in this study the sum of all beam and pore voxels
NB	Neural boundary—the boundary that contains the RGC axons as they pass through the wall of the eye (i.e., from BMO through the PSCO)
OD	Right eye
OD configuration	All data from both right and left eyes are presented in right eye configuration (Fig. 6)
ONH	Optic nerve head
OS	Left eye
Overall data	Lamina cribrosa data for all 21 eyes considered together
PD	Pore diameter (Fig. 4)
PSCO	Posterior scleral canal opening
RNFL	Retinal nerve fiber layer
SD	Standard deviation of the mean
SDOCT	Spectral-domain optical coherence tomography

Animals

All animals were treated in accordance with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research. Twenty-one normal eyes of 21 monkeys (9 female, 12 male; 5 cynomolgus, 16 rhesus; 11 right eyes, 10 left eyes; age range, 1.9–21.9 years) were studied. Seventeen eyes were contralateral normal control eyes of animals given chronic unilateral experimental IOP elevations and carried to an early experimental glaucoma (EG) endpoint in the EG eye.^28,29 The remaining four eyes were right eyes from four bilaterally normal animals. Table 2 contains animal and eye data.

Table 2.

Animal and Eye Data

Eye No.*	Animal ID	Wt, kg	Age, y	Species†	Sex‡	Eye§	IOP,‖ mm Hg	BMO Area, 3D HMRN,¶ mm2	No. Section Images#	3D HMRN Voxel Resolution**	BD†† Mean ± SD, μm	PD†† Mean ± SD, μm	CTVF*††	CTV,†† × 106 μm3	LV,†† × 106 μm3
1	23510	4.9	9.5	R	F	R	12	1.180	561	H	14.2 ± 1.3	35.6 ± 3.4	0.247	53.34	215.42
2	AM89‡‡	8.9	21.9	R	M	L	12	1.240	634	H	14.0 ± 1.7	29.8 ± 4.9	0.331	38.07	115.47
3	25341	5.4	1.9	R	M	R	13	1.199	484	H	19.1 ± 3.1	32.6 ± 2.6	0.357	56.79	159.94
4	26161‡‡	3.3	1.4	R	F	L	8	1.057	1018	H	14.9 ± 1.6	26.9 ± 2.5	0.359	37.09	102.30
5	AA3G	8.2	8.3	C	M	L	11	0.885	290	L	18.7 ± 1.5	32.5 ± 3.2	0.363	64.26	178.23
6	7489	5.8	5.8	R	M	R	8	1.722	240	L	18.9 ± 2.2	27.8 ± 2.4	0.377	106.85	283.23
7	AA4C	7.5	8.3	C	M	R	8	1.323	222	L	16.8 ± 3.3	26.0 ± 2.9	0.380	59.44	156.91
8	23533	3.7	8.3	R	F	R	8	1.048	607	H	17.8 ± 2.5	30.7 ± 3.4	0.388	62.39	160.68
9	AA40	7.6	8.1	C	M	L	11	1.360	237	L	18.0 ± 2.1	28.6 ± 2.5	0.388	66.94	175.77
10	514	6	5.2	R	M	R	8	1.195	250	L	20.4 ± 4.9	27.2 ± 3.4	0.402	91.67	223.79
11	23540	5.3	9	R	F	R	13	1.280	524	H	19.6 ± 2.5	29.9 ± 2.8	0.405	76.25	186.94
12	300	6.8	10.3	R	M	R	10	1.059	183	L	18.4 ± 2.5	25.2 ± 2.9	0.410	57.87	137.40
13	5644	7.8	6.2	R	M	R	11	1.312	227	L	19.1 ± 1.7	26.6 ± 2.7	0.411	129.77	312.13
14	AA37	8.2	8.3	C	M	R	10	1.296	290	L	22.5 ± 3.1	26.2 ± 3.1	0.475	100.79	212.50
15	25564‡‡	3.7	2.3	R	F	L	11	1.138	880	H	18.8 ± 2.9	25.2 ± 3.4	0.495	56.67	115.77
16	AA3K	7.2	8.3	C	M	L	13	1.385	320	L	23.0 ± 3.7	24.0 ± 3.5	0.519	90.44	178.23
17	25357‡‡	5.5	2.6	R	M	L	8	1.422	771	H	21.0 ± 2.8	24.2 ± 1.9	0.528	101.07	190.84
18	AO23‡‡	7.2	20	R	F	L	9	1.138	916	H	18.3 ± 1.8	20.0 ± 3.0	0.580	86.34	149.06
19	26072‡‡	4.1	1.5	R	F	R	5	1.311	1192	H	22.9 ± 2.0	20.3 ± 2.2	0.618	120.85	196.70
20	AP02‡‡	5.6	18.6	R	F	L	9	1.368	1016	H	21.9 ± 3.1	20.4 ± 2.3	0.627	89.60	143.67
21	AM76‡‡	8.6	21.9	R	F	L	10	1.570	800	H	23.1 ± 2.6	21.4 ± 2.4	0.638	116.02	182.50
Overall mean, SD		6.3 ± 1.7	8.9 ± 6.5				9.9 ± 2.1	1.261 ± 0.187	555 ± 319		19.1 ± 2.7	26.7 ± 4.2	0.443 ± 0.107	79.17 ± 26.88	179.88 ± 51.26
Summary				16R/5C	9F/11M	11R/10L				9L/12H

^* Study eyes are ordered (left column, 1–21, from smallest [1] to largest [21]) by their CTVF value.

^† R, rhesus; C, cynomolgus.

^‡ F, female; M, male.

^§ R, right; L, left.

^‖ Mean IOP of n = 3 to 5 baseline measurements under ketamine/xylazine anesthesia.

^¶ BMO area as determined by the area of the BMO ellipse within the postmortem 3D histomorphometric reconstruction.

^# Number of serial stained block face section images within the 3D HMRN.

^** H, high; L, low. See Methods.

^†† Values are global for all FoBMO sectors, subsectors, and three laminar layers considered together.

^‡‡ Longitudinal SDOCT data sets of both the control and contralateral EG eye of this animal has been previously reported⁴³ and will be compared to LMA in future reports.

Monkey Euthanasia and Perfusion Fixation

At the time of euthanasia, each study eye had been cannulated with a 27-gauge needle under deep pentobarbital anesthesia and the IOP was set to 10 mm Hg using an adjustable saline reservoir. After a minimum of 30 minutes, the monkey was perfusion fixed via the descending aorta or left ventricle with 1 L 4% buffered hypertonic paraformaldehyde solution followed by 6 L 5% buffered hypertonic glutaraldehyde solution. Following perfusion fixation, IOP was maintained for 1 hour; then each eye was enucleated, all extraorbital tissues were trimmed, and the anterior chamber was removed 2 to 3 mm posterior to the limbus. The posterior scleral shell with intact ONH, choroid, and retina was placed in 5% glutaraldehyde solution for storage.

Low- and High-Resolution 3D Histomorphometric Reconstruction (3D HMRN)

The ONH and peripapillary sclera were trephined (6-mm diameter), embedded in paraffin, and 3D reconstructed using a serial sectioning technique described previously in detail.²⁰ Briefly, a microtome-based system has been developed wherein stain is manually applied to the newly cut block face of an embedded tissue sample and the stained block face is imaged before the next section is cut. The stain is a 1:1 volumetric mixture of ponceau S and acid fuchsin, which allows visualization of exposed connective tissue on the block face surface but does not stain nonconnective tissue structures.

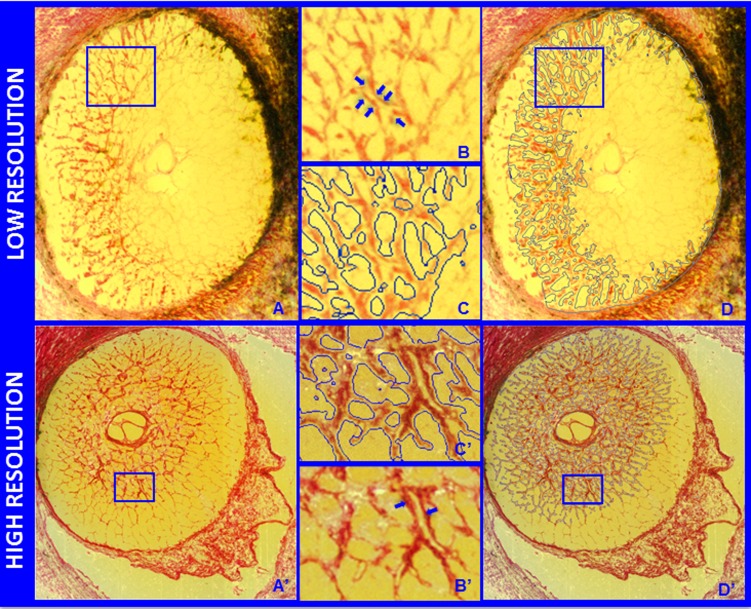
Nine eyes were reconstructed using a “low-resolution” technique.¹⁹ The remaining 12 eyes were reconstructed using a next-generation “high-resolution” technique.²⁰ For low-resolution reconstruction, images were consecutively acquired at 3-μm intervals, stacked, and aligned to produce volumetric data sets (voxel resolution of 2.5 × 2.5 × 3.0 μm) suitable for visualization and morphometric analysis. For high-resolution reconstruction, a voxel resolution of 1.5 × 1.5 × 1.5 μm was captured. All other treatments to the low- and high-resolution eyes were identical.

Lamina Cribrosa Microarchitecture Regionalization and Quantification (Figs. 1–8)

Figure 3.

Representative segmentation endpoints for the low- and high-resolution 3D HMRN data sets. Representative digital section images from a low- ([A] upper) and high- ([A'] lower) resolution 3D HMRN are shown. Magnified regions of unsegmented LC beams are shown in (B, B'), respectively. An LC beam with its central capillary is shown by blue arrows in both (B, B'). Note that an algorithm may easily segment this single beam as two (smaller) beams if the capillary space is considered an LC pore. Because they contain more detail, this is more likely to occur within high-resolution HRMNs. Since our previous report²¹ we adjusted the segmentation algorithm to achieve consistent inclusion of the capillary within the LC beam in both the low- and high-resolution HMRNs of this report by visual inspection ([C, C'], respectively). Note that LC beam segmentation is a 3D process in that data from seven section images on either side of a given section image are included in the assignment of beam borders (D, D'). Once segmented, the algorithm fills in the LC beam capillary space by classifying each capillary lumen as connective tissue. See Figure 4 for a higher-magnified version of LC beam segmentation within (C', D').

Figure 4.

Laminar beam and pore diameter. Within each laminar 3D HMRN reconstruction, beam voxels are segmented (shown within a single section image in [A] and magnified in [B]). All beam voxels are identified as connective tissue (one representative beam voxel is represented by a green dot in [C]). All remaining voxels are “pore” voxels (one representative pore voxel is represented by a purple dot in [C]). Each beam or pore voxel is assigned a beam or pore diameter, which is the diameter of the largest sphere that contains that voxel and fits into either the beam or pore in which it sits (D). Beam or pore diameter for a given beam or region is defined by the population of beam or pore diameters of the constituent voxels.

Figure 6.

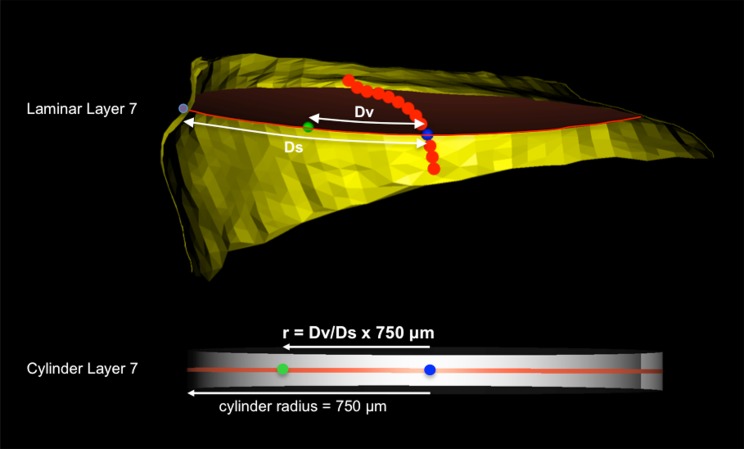
Cylinderization of a representative laminar voxel assigned to layer 7 of study eye 7. Upper: All laminar voxels within laminar layer 7 of the precylinderized lamina are assigned a polar coordinate (Dv, θ) where Dv is the distance along the midlayer reference surface (red) from the neural boundary centroid spline (red dots) centroid (blue dot) and Ds is the radial distance along the surface of the midlayer reference surface from the centroid to the neural boundary (yellow). Lower: Within cylinder layer 7, θ is held constant, but r is proportionally adjusted using the precylinder ratio of Dv/Ds and the cylinder radius of 750 um. Distances Dv and Ds are calculated along a precylinderized reference layer surface contour (curve) that is obtained for every LC voxel. It is not a straight-line measurement in a plane.

Figure 7.

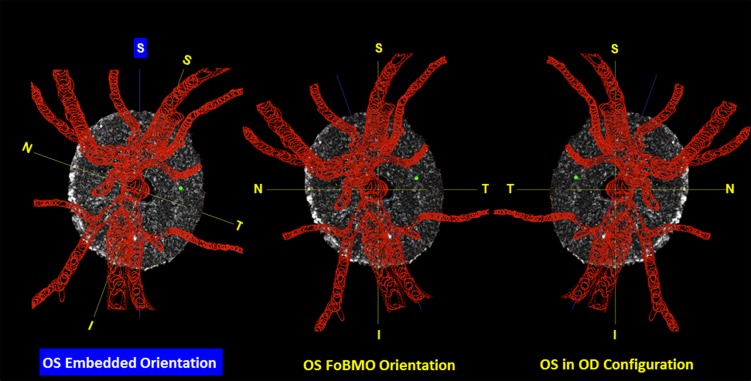
Converting segmented lamina cribrosa from embedded to FoBMO orientation and from left to right eye configuration. Left: The FoBMO vertical axis is established relative to the embedded tissue vertical as depicted for a right eye (OD) in Figure 2. Middle: The embedded data set is rotated (in this eye, counterclockwise 19.8°) to bring the FoBMO vertical optic nerve head anatomy into the vertical coordinate position. Right: FoBMO-oriented left eye (OS) data are translated to FoBMO right eye configuration, by shifting the x-axis location of each voxel to a position that is equal in distance to but opposite in direction from the y- (FoBMO vertical) axis while holding the y- and z-axis positions (not shown) constant. The position of a representative group of surface voxels is shown through each step of the process by a green dot.

Custom software was used to delineate standard anatomic landmarks and surfaces within 40 radial (4.5° interval) digital section images of each 3D HMRN.²⁹ For this study, point clouds from the 40 delineated section images for the following landmarks were utilized: internal limiting membrane (ILM), Bruch's membrane (BM), BMO, anterior scleral canal opening (ASCO), anterior LC insertion (ALI), posterior scleral canal opening (PSCO), anterior-most subarachnoid space (ASAS), anterior and posterior LC and scleral surfaces, the central retinal vessels, and the neural boundary (Supplementary Fig. S1).

Determination of the Foveal-Bruch's Membrane Opening (FoBMO) Temporal-Nasal Axis (Fig. 2)

The importance of the FoBMO axis to the organization of retinal and ONH anatomy has been described in a series of previous reports.^30–37 For this study, we estimated the location of the FoBMO axis relative to the vertical and horizontal axes of the embedded 3D HMRN so as to impose a consistent grid of twelve 30° sectors on the LC anatomy of each eye (Figs. 1, 2). To assess the reproducibility of FoBMO 30° sectoral assignment, the FoBMO axis was estimated in eight eyes from four bilateral normal monkeys (four of these eight eyes were in this study: 1, 3, 8, and 11; Table 2) on three occasions separated by 2 weeks by one author (HY) following the steps in Figure 2. Absolute pairwise differences in the FoBMO axis estimation were calculated for the three repetitions of each eye.

Isolation and Segmentation of the Lamina Cribrosa Connective Tissues (Fig. 3)

To isolate the LV, the delineated points for the anterior and posterior sclera and LC surfaces were fit with B-spline surfaces using custom software based on VTK (VTK Visualization Toolkit; Kitware, Inc., New York, NY, USA) and resampled at a higher point density for additional processing. A Boolean intersection between the anterior and posterior scleral/LC surfaces and the neural canal wall surface was performed to define the boundaries of a volume enclosing the LC space.²¹ This volume definition was then used as a mask to identify all voxels within each 3D ONH reconstruction corresponding to the LV.

The connective tissue voxels within the LV were segmented using a previously described custom 3D segmentation algorithm specifically designed to classify voxels in the LC of our 3D ONH reconstructions as either connective tissue (beam) or nonconnective tissue (pore) voxels.²² Since our previous reports,^21,23,24 we adjusted the segmentation algorithm to consistently segment LC beams in both low- and high-resolution data sets by qualitatively requiring that LC beam capillaries be consistently segmented within the beams (see Fig. 3). Note that once segmented, the algorithm fills in the capillary space within the LC beams by classifying each capillary lumen as connective tissue. The final segmented 3D binary volumes formed the basis for the visualization and quantification procedures used in this study.

Lamina Cribrosa Beam and Pore Quantification (Fig. 4)

Each beam or pore voxel is assigned a beam or pore diameter defined as the diameter of the largest sphere that contains that voxel and fits into either the beam or pore in which it sits (Fig. 4).^38–40 Beam diameter for a given beam or 30° sector is therefore defined by the population of BDs of the constituent voxels. Pore diameter for a given pore or 30° sector is defined by the population of PDs of the constituent voxels.

Transformation of Each LC Voxel to a Common Cylinder (Figs. 5, 6)

A plane is fit to the delineated ALI points (ALI reference plane), and all 3D HMRN data are reoriented relative to the ALI centroid (which becomes x = 0, y = 0, z = 0). The x-, y-, and z-axes are aligned with the ALI plane normal vectors and pass through the ALI centroid. Polar coordinates (p(r, θ)) are then assigned to each LC voxel relative to the ALI centroid. A neural boundary centroid spline (representing the anatomic center of the neural canal; Figs. 5A–C, 6) is generated from the centers of mass of a series of neural boundary contour lines sampled at 3.0-μm (low-resolution 3D HMRN) or 1.5-μm (high-resolution 3D HMRN) intervals parallel to the ALI reference plane. The LC is divided into 12 layers by projecting normal vectors from a uniform 20-μm anterior LC surface grid to the posterior LC surface. The distance between the anterior and posterior LC surfaces on each vector is divided into 12 equal segments, and subsurfaces are fit to each group of vector segments to create LC layers 1 through 12 (anterior [inner] to posterior [outer], respectively). Each LC voxel is then assigned to its closest layer. The position of each voxel within each LC layer is expressed relative to the layer centroid and the neural boundary (Fig. 6, upper). The voxel position within the equivalent cylinder layer is then proportionally assigned (Fig. 6, lower).

Imposing FoBMO 30° Sectoral, Central, and Peripheral Subsectoral and Inner, Middle, and Outer Regions on the Cylinderized Data (Figs. 1, 2, 5, 7)

All LC segmentation as well as beam and pore voxel quantification is performed on “raw” LC data in embedded tissue orientation. After each voxel has been cylinderized, the data are rotated such that the FoBMO vertical and horizontal axes are in the 12 to 6 and the 3 to 9 clock-hour locations, respectively (Fig. 1E). Data for left eyes are transformed to right eye configuration as demonstrated in Figure 7. Data are presented in two ways. (1) Data by sector, subsector, and depth. Each sector is divided into equal volume central and peripheral subsectors and inner (layers 1–4, Fig. 5), middle (layers 5–8, Fig. 5), and outer (layers 9–12, Fig. 5) depth ranges. (2) Full-thickness data without depth. Each sector is divided into equal volume central and peripheral subsectors including all the layers (layers 1–12, Fig. 5). Voxels lying on sectoral or subsectoral boundaries are assigned to the least numbered sector and the central subsector.

Volumetric Parameterization

Following cylinderization of the LC volume (outlined above), data are defined globally and by sector and subsector as follows: LV is defined as the total number of contained beam and pore voxels; CTV is defined as the total number of contained beam voxels; CTVF is defined as the ratio of contained CTV to LV.

Eye-Specific LMA Discordance by Sector, Subsector, and Depth (Fig. 8, Supplementary Figs. S2, S3)

Our strategy for characterizing eye-specific LMA sectoral, subsectoral, and depth discordance builds upon previous attempts to quantify LC pore size and connective tissue density within four quadrants (S, I, N, and T) and their central versus peripheral subquadrants.² For this study, LMA discordance analysis attempts to identify LC sectors, subsectors, or layers that demonstrate a relative decrease in LC connective tissue density compared to the rest of the ONH. Sectoral and subsectoral discordance are based on full-thickness LC data. Depth discordance is assessed for inner, middle, and outer LC layers without regard for sector or subsectors.

More specifically, we define LMA discordance to be present in those sectors in which BD and CTVF are lowest and PD is highest compared to all other sectors of the ONH (Fig. 8). Sectors of low connective tissue density can occur focally (all possible combinations of two, three, or four adjacent sectors on one side of BMO centroid) or axially (all possible combinations of four, five, or six sectors on either side of the BMO centroid—two or three adjacent sectors on one side and two, three, or four adjacent sectors on the other side). Lamina cribrosa microarchitecture discordance is calculated as a ratio of the pooled value from focal or axial sectors versus the pooled value of the rest of the sectors for each parameter within each eye. Axial discordance does not refer to discordance along the z-axis (this is depth discordance or discordance between inner, middle, and outer LC layers). Axial discordance attempts to quantify relationships that are within the plane of the LC and occur along (or just off of) an axis that includes both sides of the BMO centroid—such as the classic superior and inferior pattern of large pores in human and monkey eyes. Focal and axial forms of subsectoral discordance can also be identified in which the ratio of peripheral to central subsectoral connective tissue density is smallest (for BD, CTVF) or largest (for PD). Finally, eye-specific depth discordance or discordance between the inner/middle and outer/middle LC layers can also be compared.

While identifying those sectors in which connective tissue density is greatest is also a form of LMA discordance that may be important, and while our method provides this information, for clarity in this study we identify regions of low connective tissue density only. Figure 8 provides a schematic diagram of our approach for identifying focal and axial sectoral and subsectoral discordance as well as LC depth discordance in a representative study eye. Supplementary Figures S2 and S3 provide a more detailed algorithm for its calculation.

To test the hypothesis that eye-specific sectoral and subsectoral discordance most commonly occurred within the superior, superior-temporal (11, 12), inferior, and inferior-temporal (6, 7) sectors (Fig. 1E), we plotted the frequency of involvement of each sector in sectoral and subsectoral LMA discordance for BD, PD, and CTVF. To test the hypothesis that eye-specific LMA discordance becomes less prominent as global CTVF increases, we looked for an inverse correlation between global CTVF and each eye-specific LMA discordance parameter for BD, PD, and CTVF using linear regression.

Statistical Analysis

A general linear model fitted with a generalized estimation equation (GEEGLM) coded in R (The R Foundation for Statistical Computing, Vienna, Austria) was used to assess the effect of reconstruction resolution (low versus high), monkey species (cynomolgus or rhesus macaque), and age on all parameters (BD, PD, CTVF, CTV, LV). An analysis of variance (ANOVA) that employed a GEEGLM model was used to test the effect of sector (twelve 30°), subsector (central versus peripheral), and depth (inner, middle, outer LC layers) and their interactions on BD, PD, and CTVF, respectively. The effects of sector, subsector, and depth were separately assessed using a GEEGLM model as single factor for LV and CTV parameters.

The ANOVA examines whether each parameter varies by sector, subsector, or depth; however, it does not provide information about pairwise comparisons between individual regions. Therefore, in a secondary analysis, the sectors with the lowest parameter values were compared with all other sectors by GEEGLM models for all parameters. Within each 30° sector, central versus peripheral differences were assessed for each parameter using a GEEGLM model. Pairwise comparisons between inner versus middle and outer versus middle layers were done by GEEGLM models. Hypothesis testing within the eye-specific sectoral, subsectoral, and depth discordance data was carried out as described above.

Results

Animal and Eye Data (Table 2)

Twenty-one normal eyes of 21 monkeys (9 female, 12 male; 5 cynomolgus, 16 rhesus; 11 right eyes, 10 left eyes; age range, 1.9–21.9 years) were studied. Seventeen eyes were contralateral normal control eyes of animals given chronic unilateral experimental IOP elevations and carried to an early EG endpoint in the EG eye. The remaining four eyes were from four bilaterally normal animals (monkeys 1, 3, 8, and 11; Table 2). Additional ocular and demographic data are reported in Table 2. All data are expressed as mean ± SD unless otherwise noted. The effect of resolution (low versus high), age, and species (cynomolgus or rhesus macaque) on each LMA parameter was not significant (P > 0.05),

Reproducibility of FoBMO Axis Assignment

For the eight studied eyes (four from this study: 1, 3, 8, and 11; see Table 2), the maximum absolute difference in the assigned FoBMO axis between any two days was 3.8°. The mean (±SD) absolute difference was 1.23 ± 0.84°. Taken together, these data suggest that the variability of our method for FoBMO 30° sectoral assignment is small compared to the size of each sector.

BD, PD, and CTVF Vary by 30° Sector, Subsector, and Depth

Global values for BD, PD, and CTVF for each eye and each parameter's overall mean value are listed in Table 2. Study eyes are ordered from 1 (global CTVF = 0.247) to 21 (global CTVF = 0.638) by their eye-specific, global CTVF value. Table 3 reports the effects of 30° sectoral, central versus peripheral, and inner, middle, and outer LC regionalization on each parameter based on an ANOVA by GEEGLM. Between-sector differences achieved significance for all five parameters (P < 0.0001 for each). The effect of subsector (central versus peripheral) was significant for BD (P = 0.0024) and PD (P = 0.0011). The effect of LC depth (inner versus middle versus outer) was significant for all five parameters (P < 0.0001 for all except LV [P = 0.003]).

Table 3.

ANOVA Effects of Lamina Cribrosa Regionalization on Each LMA Parameter

Factor	BD*	PD*	CTVF*	CTV†	LV†
Sector	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
Subsector	0.0024	0.0011	0.0940	0.5	0.054
Depth, layer	<0.0001	<0.0001	<0.0001	<0.0001	0.003
Sector:subsector	<0.0001	<0.0001	<0.0001	NA	NA
Sector:depth	<0.0001	1.0000	<0.0001	NA	NA
Subsector:depth	0.0118	0.4244	0.0250	NA	NA
Sector:subsector:depth	1.0000	<0.0001	<0.0001	NA	NA

Sector, 30° (clock-hour) circumferential sectors; subsector, central versus peripheral subsectors; depth, inner versus middle versus outer laminar layers. Bold indicates significant values.

^* ANOVA by GEEGLM with depth, radius, and sector factors and their interactions in one analysis.

^† ANOVA by GEEGLM with depth, radius, and sector as a single factor in three separate analyses.

The interaction between sector and subsector was significant for BD, PD, and CTVF (P < 0.0001 for each). The interaction between sector and depth was significant for BD and CTVF (P < 0.0001 for each). The interaction between subsector and depth was significant for BD (P = 0.0118) and CTVF (P = 0.0250), respectively. The interaction between sector, subsector, and depth was significant for PD and CTVF (P < 0.0001 for each).

Mean BD overall was 19.1 ± 2.7 μm, ranging from 14.0 ± 1.7 to 23.1 ± 2.6 μm among the 21 eyes (Table 2). Beam diameter was smallest inferiorly (3–8 o'clock) and superiorly (12 o'clock) and largest superior nasally (1–2 o'clock) and temporally (9–11 o'clock) (Table 4; Fig. 9). Central mean BD (19.9 ± 1.6 μm) was greater than peripheral mean BD (18.3 ± 2.0 μm) (P < 0.05) (Table 5), and these differences were greatest within the 12, 1, 3, and 6 o'clock sectors (P < 0.05, GEEGLM, Fig. 10). Mid-LC mean BD (20.0 ± 1.8 μm) was greater than inner (17.3 ± 1.8 μm) and outer (18.2 ± 1.7 μm) mean BD (Table 6), which were not different from each other. The character of central versus peripheral differences in mean BD was similar within the inner and middle LC layers but was enhanced within the outer LC, with eight sectors demonstrating significantly smaller peripheral beams (Fig. 10).

Table 4.

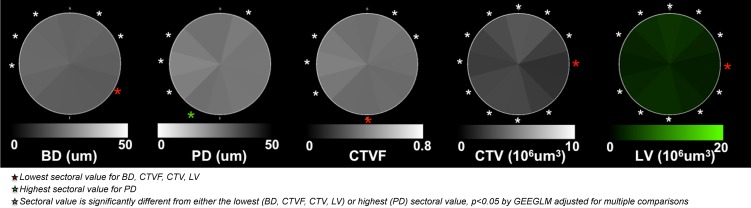
Full-Thickness Lamina Cribrosa Data by 30° Sectors

30° Sector	BD,* μm	PD,* μm	CTVF*	CTV,* ×106 μm3	LV,* ×106 μm3
	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI
1	19.6 ± 1.4†	25.9 ± 1.7‡	0.459 ± 0.045†	8.37 ± 1.33†	18.23 ± 2.33†
2	19.1 ± 1.5†	27.0 ± 1.8	0.442 ± 0.047†	6.08 ± 0.91†	13.74 ± 1.54†
3	18.7 ± 1.7	26.8 ± 2.1	0.434 ± 0.054	4.70 ± 0.76	10.78 ± 1.24
4	17.8 ± 1.7	27.0 ± 2.4	0.417 ± 0.060	4.83 ± 0.85	11.63 ± 1.46†
5	17.9 ± 1.6	26.8 ± 2.7	0.424 ± 0.057	6.01 ± 1.01†	14.29 ± 1.84†
6	18.0 ± 1.4	27.7 ± 2.3	0.411 ± 0.051	6.94 ± 1.09†	16.98 ± 2.06†
7	18.4 ± 1.4	28.4 ± 2.2	0.417 ± 0.051	7.12 ± 1.07†	17.11 ± 1.88†
8	19.6 ± 1.6	25.4 ± 1.9‡	0.468 ± 0.049†	6.88 ± 1.13†	14.72 ± 2.11†
9	20.6 ± 1.8†	23.9 ± 1.9‡	0.501 ± 0.050†	5.89 ± 0.97†	11.80 ± 1.85
10	20.5 ± 1.6†	25.8 ± 2.1‡	0.478 ± 0.047†	6.34 ± 1.05†	13.37 ± 2.15†
11	20.0 ± 1.4†	28.0 ± 2.0	0.437 ± 0.043	7.46 ± 1.20†	17.20 ± 2.58†
12	19.3 ± 1.5	28.0 ± 2.1	0.427 ± 0.044	8.54 ± 1.36†	20.03 ± 2.60†

Bold, lowest sectoral value for parameters BD, CTVF, CTV, LCV; bold italics, highest sectoral value for the parameter PD. CI, confidence interval.

^* Sectoral effect significant for all parameters (P < 0.05, ANOVA); see Table 3.

^† Sectoral value is significantly different from the lowest value, P < 0.05, by GEE adjusted for multiple comparisons.

^‡ Sectoral value is significantly different from the highest value, P < 0.05 by GEE adjusted for multiple comparisons.

Figure 9.

Overall full laminar thickness data for each LMA parameter by 30° sectors. Beam diameter was lowest within sector 4, similarly low within sectors 3, 5, 6, 7, and 12, and significantly higher within sectors 9, 10, 11, 1, and 2. Pore diameter was greatest within sector 7, similarly large within sectors 6, 5, 4, 3, 2, 12, and 11, and significantly smaller within sectors 8, 9, 10, and 1. Connective tissue volume fraction was lowest within sector 6, similarly low within sectors 3, 4, 5, 7, 11, and 12, and significantly higher within sectors 8, 9, 10, 1, and 2. It is important to note that while CTV and LV determine CTVF, their distributions can be quite different. The distribution of total CTV is almost opposite to the distribution of CTVF because LV is greatest superiorly and inferiorly and smallest nasally and temporally.

Table 5.

Full-Thickness Lamina Cribrosa Data by Central Versus Peripheral Subsectors

Radius	Beam Diameter,* μm	Pore Diameter,* μm	CTVF	CTV, ×106 μm3	LV, ×106 μm3
	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI
Central†	19.9 ± 1.6	27.5 ± 2.0	0.451 ± 0.049	38.91 ± 5.95	86.76 ± 11.40
Peripheral†	18.3 ± 2.0	26.0 ± 2.3	0.435 ± 0.052	40.26 ± 6.24	93.12 ± 11.50

^* Central versus peripheral effect significant for these parameters (P < 0.05, ANOVA); see Table 3.

^† All sectors and depths pooled together.

Figure 10.

Central versus peripheral BD, PD, and CTVF by laminar depth. Full-thickness (left) and inner, middle, and outer layer (right) data are shown. Overall, BD is significantly smaller within the peripheral subsectors of sectors 12, 1, 3, and 6. PD is significantly smaller within the peripheral subsectors of sectors 1, 3, 4, and 5. Connective tissue volume fraction is significantly smaller within the peripheral subsectors of sectors 11, 12, and 6. The overall relationships are most consistently present within the middle laminar layer data for each parameter.

Table 6.

Pooled LC Sectoral Data by Inner, Middle, and Outer LC Depth

Depth	BD,* μm	PD,* μm	CTVF*	CTV,* ×106 μm3	LV,* ×106 μm3
	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI	Mean ± 95 CI
Inner†	17.3 ± 1.8‡	27.3 ± 3.0‡	0.381 ± 0.062‡	25.02 ± 4.65‡§	63.16 ± 9.05§
Middle†	20.0 ± 1.8§‖	24.5 ± 2.3§‖	0.519 ± 0.058§‖	33.78 ± 5.38§‖	65.70 ± 9.88§
Outer†	18.2 ± 1.7‡	27.9 ± 2.4‡	0.389 ± 0.059‡	20.37 ± 4.31‡§	51.01 ± 6.80‡§

^* Laminar depth effect significant for all parameters (P < 0.05, ANOVA); see Table 3.

^† All sectors and subsectors pooled together.

^‡ Significantly different from middle.

^§ Significantly different from outer.

^‖ Significantly different from inner.

Mean PD overall was 26.7 ± 4.2 μm, ranging from 20.0 ± 3.0 to 35.6 ± 3.4 μm among the 21 eyes (Table 2). Pore diameter was smallest temporally (8–10 o'clock) and superior nasally (1 o'clock) and largest inferior temporally through nasally (counterclockwise from 7 to 2 o'clock) and superior temporally (11–12 o'clock) (Table 4; Fig. 9). Central mean PD (27.5 ± 2.0 μm) was greater than peripheral mean PD (26.0 ± 2.3 μm) (P < 0.05, ANOVA) (Table 5). However, when considered by sector, central PD was significantly larger than peripheral within the 1, 3, 4, and 5 o'clock sectors only (P < 0.05 by GEEGLM, Fig. 10). Mid-LC mean PD (24.5 ± 2.3 μm) was less than inner (27.3 ± 3.0 μm) and outer (27.9 ± 2.4 μm) mean PD (P < 0.05, Table 6), which were not different from each other. The character and magnitude of central versus peripheral differences in mean PD were similar within all three LC layers. Some reduction in magnitude within the middle and outer layers and larger peripheral superior-temporal pores achieved significance within the 10 o'clock sector of the outer layer only (Fig. 10).

Mean CTVF overall was 0.443 ± 0.107, ranging from 0.247 to 0.638 among the 21 eyes (Table 2). Connective tissue volume fraction was highest temporally (8–10 o'clock) and superior nasally (1–2 o'clock) and lowest inferior temporally through nasally (counterclockwise from 7–3 o'clock) and superior temporally (11–12 o'clock) (Table 4; Fig. 9). Central mean CTVF (0.451 ± 0.049) was not significantly different from peripheral mean CTVF (0.435 ± 0.052) (Table 5). When considered by sector, central CTVF was significantly larger than peripheral within the 11, 12, and 6 o'clock sectors (P < 0.05 by GEEGLM, Fig. 10). Mid-LC mean CTVF (0.519 ± 0.058) was greater than inner (0.381 ± 0.062) and outer (0.389 ± 0.059) mean CTVF (P < 0.05, ANOVA, Table 6), which were not different from each other. The magnitude of central versus peripheral differences in mean CTVF was more pronounced in the inner compared to the middle and outer LC layers. Lower peripheral CTVF was present within the superior-temporal sectors of all three layers (Fig. 10).

Eye-Specific LMA Data and Discordance by Sector, Subsector, and Depth

Eye-specific, subsectoral, full-thickness LC data for all 21 study eyes are displayed in Figure 11. The fact that we chose to order the eyes in this study (1–21) by global CTVF is evident as an increase in white (connective tissue density) from left to right for CTVF (middle row of data).

Figure 11.

Overall and eye-specific full LC thickness LMA data for 21 study eyes in OD configuration. Overall (left) and eye-specific (1–21) data for each LMA parameter are shown. The fact that the study eyes are ordered (1–21) based on global CTVF (see Table 2) can be seen within the CTVF data (row 3), which is darkest (least connective tissue density) in study eye 1 (left) and lightest (most connective tissue density) in study eye 21 (right). Eye-specific LMA discordance can be qualitatively identified for each parameter by noting the regions of greatest (most white) and least (most dark) connective tissue density. Within the BD, PD, and CTVF data, the magnitude of discordance qualitatively appears to diminish as global CTVF increases.

Within the overall sectoral data of Figure 9, BD and CTVF are lowest and PD is greatest within a subset of the superior-temporal (11 and 12 clock-hour) and inferior-temporal (6 and 7 clock-hour) sectors. Beam diameter (sectors 6, 12) and CTVF (sectors 6, 11, and 12) are reduced within the peripheral compared to central subsectors of a subset of these same sectors (Fig. 10). However, peripheral compared to central subsectoral differences also occurred within the nasal sectors for BD and PD. Beam diameter was reduced within the peripheral subsector of sector 3; and for PD, the only peripheral compared to central subsectoral differences that achieved significance were decreases in the peripheral subsectors of sectors 1, 3, 4, and 5 (Fig. 10). Within the eye-specific data (Fig. 11), confirmation of these overall findings is qualitatively most evident within the low CTVF eyes (Fig. 11, left) and becomes less evident in the highest CTVF eyes (Fig. 11, right).

Supplementary Figures S4 through S6 plot the magnitude and location of sectoral, subsectoral, and depth LMA discordance within each study eye. For each parameter, the location, extent, and magnitude of maximum discordance between those sectors in which the connective tissue density is most reduced (i.e., BD [Supplementary Fig. S4] and CTVF [Supplementary Fig. S6] are lowest and PD [Supplementary Fig. S5] is highest compared to all other sectors considered together) are mapped. While the frequency of superior-temporal and/or inferior-temporal connective tissue minima for both focal and axial forms of discordance is apparent, eye-specific variation from these overall patterns is not uncommon. The range of discordance between the inner, middle, and outer LC layers is also displayed. For all three parameters, connective tissue density is most commonly highest within the middle LC layer.

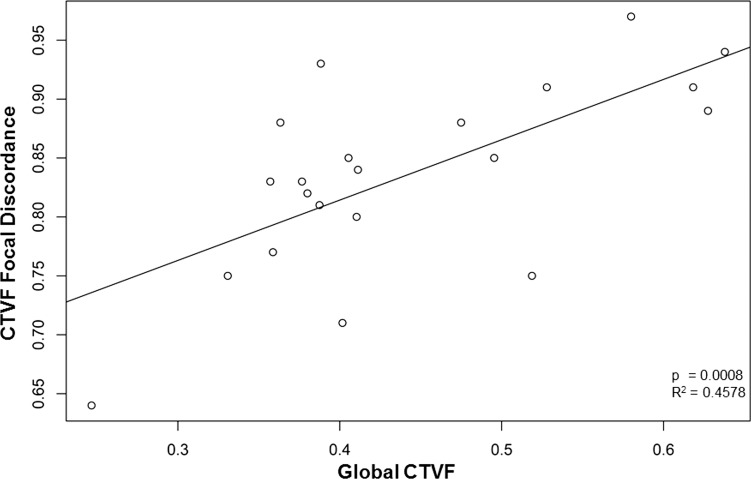
Sectoral and subsectoral discordance is most commonly located within the superior (11, 12)- and inferior (6, 7)-temporal sectors for PD and CTVF (Fig. 12). While this was also true for BD for subsectoral discordance, maximum BD sector discordance most commonly occurred inferior nasally (sectors 4 and 5). The magnitude of LMA discordance significantly diminished as global CTVF increased for a number of parameters (Table 7). We emphasize the correlation for CTVF focal discordance (P = 0.0008, R² = 0.4578) because it is most robust (Fig. 13) within the context of multiple comparisons.

Figure 12.

Frequency of eye-specific LMA sectoral and subsectoral discordance by sector. Among the focal and axial sectoral (left polar plot) and subsectoral (right polar plot) discordance data reported in Supplementary Figures S4 through S6. The frequency with which a given sector was included in a region of maximum discordance is plotted for each parameter. For either sectoral or subsectoral discordance, if a sector was involved in both focal and axial discordance for all 21 eyes, the total number of maximum discordance events would be 42. Data are expressed relative to 30 events because close to the maximum number of sectoral or subsectoral discordance events occur within a single sector (29 events occurred at sector 4 [N_inf] for sectoral BD discordance). These data strongly suggest that eye-specific LMA sectoral and subsectoral discordance occurred most commonly within the superior, superior-temporal, inferior, and inferior-temporal sectors except for BD discordance, which occurred most commonly inferior nasally (sectoral) and superiorly and superior nasally (subsectoral).

Table 7.

Correlation Between LMA Discordance Parameters and Global CTVF

Discordance Type	Discordance Subtype	Discordance Parameter	PValue*	R2
Sectoral†	Focal	BD min ratio	0.2656	0.0648
		PD max ratio	0.6455	0.0114
		CTVF min ratio	0.0008	0.4578
	Axial/off-axial	BD min ratio	0.4005	0.0375
		PD max ratio	0.8989	0.0009
		CTVF min ratio	0.0058	0.3368
Subsectoral‡	Focal	BD CPR max ratio	0.5099	0.0231
		PD CPR min ratio	0.8663	0.0015
		CTVF CPR max ratio	0.0700	0.1625
	Axial/off-axial	BD CPR max ratio	0.3349	0.0490
		PD CPR min ratio	0.5195	0.0222
		CTVF CPR max ratio	0.0091	0.3077
Depth§		BD, PD, and CTVF inner/middle ratios	NS||
		BD, PD, and CTVF outer/middle ratios	NS||

Bold indicates significant values.

^* P values < 0.005 (linear regression) are emphasized in the setting of multiple comparisons.

^† Data from both subsectors pooled together and ratios chosen to identify the sectoral location of least connective tissue density compared to all others.

^‡ Data from the central compared to the peripheral (C/P ratio or CPR) subsector of each sector; ratios chosen to identify the sectoral location where central connective tissue density is greatest and peripheral connective tissue density is least.

^§ Data from the inner, middle, and outer laminar layers pooled together without regard for sectors or subsectors.

^|| Inner/middle and outer/middle ratios were not significantly correlated to global CTVF for any parameter (data not shown).

Figure 13.

Connective tissue volume fraction focal discordance is inversely correlated to global CTVF. For CTVF, focal discordance is maximum (most different from all other sectors considered together) when the discordance ratio (y-axis) is lowest (farthest from 1.0). Within these 21 eyes, as global CTVF increased, the discordance ratio approached 1.0.

Discussion

Our study introduces four new methods for 3D histomorphometric characterization of eye-specific, ONH anatomy in the monkey eye. The first is quantitative, voxel-based 3D LC beam and pore diameter measurement. The second is digital transformation of all LC voxels (with their associated beam or pore diameter) into a common cylinderized space for between-eye comparison. The third is FoBMO-oriented regionalization of postmortem ONH tissues. The fourth is eye-specific LMA discordance mapping.

The principal findings of this report are as follows. Among 21 normal monkey eyes, BD and CTVF were smallest and PD was largest within a subset of the superior-temporal (11 and 12 o'clock) and inferior-temporal (6 and 7 o'clock) sectors. In addition, BD and CTVF were smaller and PD was larger within the peripheral compared to central subsectors of a subset of these same sectors. Beam diameter and PD were smaller and CTVF was not significantly different within the nasal-peripheral compared to central subsectors. Beam diameter and CTVF were greatest and PD was smallest within the middle compared to the inner and outer LC layers. Finally, while eye-specific LMA discordance often varied from the specific relationships outlined above, the superior-inferior and nasal-temporal sectors were the most common site of maximum LMA discordance, which diminished in magnitude as global CTVF increased.

Our 3D, voxel-based method of local diameter measurement is based upon a series of papers that address 3D measurements within images of biological tissues.^38–40 The fact that it is voxel based and 3D provides several theoretical advantages over other, 2D techniques. While the LC is traditionally described as a series of fenestrated connective tissue plates,⁶ we have suggested that it is more like a sponge through which directed pores channel from the inner to the outer LC layers with substantial lateral connectivity between pores.²¹

Because of this interconnectivity, the pores are not commonly full thickness, perpendicular to the LC surface, or consistent in their direction relative to any single cutting plane.⁵ Nor is their direction relative to the LC surface consistent within the central and peripheral LC because the most peripheral pores follow the obliqueness of the adjacent scleral canal wall.⁴¹ Given these anatomic relationships, any single plane sectioning method, especially those designed to capture histologic sections that include intact LC and sclera within a single section, should create sampling artifacts that preferentially affect the size and shape of the peripheral-most pores. These artifacts would be further expected to differentially affect the EG eye of unilateral EG animals, once glaucomatous LC deformation and remodeling occur.²⁵

A central challenge for quantitative intra- and interindividual comparison of any tissue is to make the comparison fairly in the setting of anatomy that can be very different among normal subjects or once changed by disease. The goal of seeking objectivity is to most robustly quantify physiologic variability in all of its forms so as to detect true disease with greater specificity. Transforming eye-specific LC anatomy into a common cylindrical shape (i.e., cylinderization) applies concepts that are common within brain imaging to the ONH LC.⁴² While the focus in this report is to characterize interindividual variability among normal eyes, its development has been driven by our need to compare the LC of profoundly deformed and remodeled EG eyes^21,43,44 to their contralateral normal eyes, which will be the subject of future reports.

To date, there has been no anatomic logic for the assignment of “superior,” “inferior,” “nasal,” and “temporal” to ONH anatomy within postmortem tissues. In most studies this assignment, when described, has been done based on the clinical appearance of the ONH and vascular arcades within in vivo or postmortem fundus images. The logic for using the FoBMO axis to regionalize ONH, retinal nerve fiber layer (RNFL), and macular anatomy has been suggested by previous studies of RNFL anatomy and its relationship to structure–function correlation.^30–37

The implementation of FoBMO orientation for spectral-domain optical coherence tomography (SDOCT) data sets has recently been accomplished both retrospectively^26,28 and at the time of SDOCT data set acquisition²⁷ (Chauhan BC, IOVS 2014;55:ARVO E-Abstract 4028). The present study is, to our knowledge, the first to use the FoBMO axis to regionalize ONH anatomy within postmortem tissues. As such it makes a demarcation from all of our own and other characterizations of the monkey ONH that have been regionalized through clinical inspection of in vivo or ex vivo fundus photos without regard for the fovea.^19,43 As previously demonstrated for SDOCT data sets,²⁶ the reproducibility of retrospective FoBMO 30° sector assignment within postmortem 3D HMRNs in this study was small relative to the size of each 30° sector.

Seventeen of the 21 normal eyes in this report are control eyes from monkeys that were given unilateral chronic IOP elevation in the contralateral eye and carried to early EG.^28,43 Foveal-BMO regionalization in both the control and EG eyes of these animals will allow anatomically consistent LMA comparisons within and between these animals in future reports. It will also allow anatomically accurate and consistent colocalization of longitudinal SDOCT, ONH, and RNFL change²⁸ to underlying LMA EG eye change in the subset of animals from this study for which longitudinal SDOCT change in the EG eye has been reported (see Table 2).²⁸

Our strategy for characterizing eye-specific LMA sectoral, subsectoral, and depth discordance builds upon previous attempts to quantify LC pore size and connective tissue density discordance within four quadrants (S, I, N, and T) and their central versus peripheral subquadrants.^2,15 The parameters we propose are designed to identify the location, sectoral extent, and magnitude of discordance within those sectors in which the amount of connective tissue is most reduced compared to all other sectors considered together. In addition, they quantify LC depth discordance, which has less commonly been addressed in previous publications.^5,15

Our overall results strongly support classic descriptions of LC pore size and connective tissue density distribution,^1–4 with the superior and inferior sectors exhibiting smaller beams, larger pores, and reduced connective tissue density compared to the nasal and temporal sectors, and with these findings further enhanced within the peripheral compared to the central subsectors of these same regions. However, our overall data more tightly focus on the 15° off-axis, superior-temporal and inferior-temporal quadrants (clock-hours 11 and 12; 6 and 7) rather than being axial (i.e., symmetric), which would require all three superior (11, 12, 1) and inferior (5, 6, 7) FoBMO sectors to be equally involved.

The fact that our overall data localize to these four sectors is important for the following reasons. First, in humans, several studies report human glaucoma susceptibility to be greatest within these sectors,^45,46 rather than the broader superior and inferior quadrants. While the FoBMO sectoral susceptibility of the RGC axons in monkey EG has not yet been characterized, it will be the subject of a future report (as mentioned above, see Table 2).²⁶ Second, isolation of these phenomena to four sectors may follow not just from having used 30° sectors (versus 90° quadrants), but also because our FoBMO sectors, being based on ONH and retinal anatomy and applied to cylinderized data, were more consistently assigned in each study eye.

Our findings that PD is smaller and that BD and CTVF are larger in the middle compared to the inner and outer LC layers indirectly support similar findings by Ogden and coauthors⁵ in 17 human cadaver eyes from 17 subjects spanning 25 to 74 years of age. In that study, the lamina scleralis contained approximately 22% more connective tissue between the pores than did the choroidal lamina. Within our LC depth data, CTVF increased 26.6% within the middle (mean of 0.519) compared to the inner (mean of 0.381) LC layers. The two studies are similar in their exclusion of the central vessel connective tissues in their calculations, but are different in species and in the number of LC layers assessed. Ogden and coauthors⁵ separated the LC into choroidal and scleral layers based upon the presence of choroid or sclera adjacent to the most peripheral LC beams within their serial transverse sections. We chose to separate the LC into three layers for two reasons. First, we have previously reported on the differences in anterior (inner) versus posterior (outer) LC insertion migration,⁴⁴ the potential for retrolaminar septal recruitment,²¹ and myelin remodeling (Stowell C, IOVS 2014;55:ARVO E-Abstract 5034) within or adjacent to the outer LC in early monkey EG. We therefore hope to identify early changes in the innermost and outermost LC in early monkey EG in studies that will follow. Second, depth effects in our analysis (Table 6) were more substantial for tripartite compared to bipartite LC layers (data not shown).

Of note, our overall sectoral CTVF data (Fig. 9) support previous reports¹ that CTVF is greatest within the temporal quadrant (sectors 8, 9, and 10) and is similar but slightly lower superior nasally (sectors 1 and 2). However, subsectoral data (Fig. 10) suggest that central versus peripheral differences in CTVF do not achieve significance in either quadrant (full-thickness data). These findings are compatible with the previous literature, which is inconsistent in its support of subsectoral differences within these quadrants, but are different from our own previous CTVF findings²¹ in a subset of seven eyes from the current report. In that study, Roberts et al.²¹ qualitatively reported that CTVF was highest within the superior and central regions and variably lowest within the peripheral elements of the inferior, nasal, and temporal quadrants in seven normal eyes. Five methodological changes likely underlie the CTVF outcome differences in the two reports. First, prior to segmentation, preprocessing of each section image has been simplified to maximize connective tissue voxel identification. Second, the segmentation algorithm used in the earlier report has itself been altered to maximize the inclusion of capillaries within each beam (Fig. 3). Third, to properly characterize their contribution to LC structural stiffness, the central retinal vessel walls were appropriately included in the continuum finite element–based approach of the first report. However, in the present report they have been deliberately removed from the LMA LC volumes so as to avoid confounding our estimates of central BD. Fourth, we use a FoBMO axis-based regionalization method and a 12-sector and 12-subsectoral regionalization strategy, which is different from the previous finite element approach. Fifth, our results are based on data from 21 normal eyes that have been quantitatively and statistically assessed.

Because we detected no effect of data set resolution (low versus high) on the LMA data of this report, we believe that the current BD, PD, and CTVF data most accurately reflect LC beam anatomy in these 21 eyes. However, when overall structural stiffness is being estimated (as in the previous continuum report), inclusion of the central retinal vessel sheaths may be required, and awareness of the implications of doing so on central LC BD and CTVF estimates will be necessary.

Our eye-specific discordance findings commonly demonstrate focal and axial connective tissue density to be least (CTVF and BD to be lowest and PD to be greatest) within sectors of varying size that are related to the superior-temporal and inferior-temporal sectors. However, the location and extent of this discordance are eye specific and are very different from these overall results in a subset of eyes depending upon the parameter. In particular, the presence of focal and axial connective tissue density minima within the nasal and inferior-nasal sectors was not rare (Fig. 8, Supplementary Figs. S4–S6). Within the depth discordance data, while connective tissue density as characterized by all parameters was most commonly greatest within the middle LC layer, in a few eyes the inner LC layer exceeded the middle in connective tissue density by small amounts.

Roberts and coauthors^23,24 have used finite element modeling to suggest that CTVF makes an important contribution to LC structural stiffness and determines the distribution of LC connective tissue stress and strain. Most of the original descriptions of LC beam and pore anatomy hypothesized that small beams and/or large pores may underlie RGC axonal susceptibility.^1–4 While BD, PD, and CTVF are related, they are not equivalent. They represent (BD and CTVF) or are a manifestation of (PD) connective tissue geometry without consideration of connective tissue material/diffusion properties and/or behavior. Refined and validated finite element models that incorporate both geometry and material properties^13,23,24,47 may be required to determine the contribution of each of these three components of LMA to neural and connective tissue susceptibility in glaucoma. However, while such models may be required to predict the level of IOP and the location at which glaucomatous damage will occur in a given eye, eye-specific LMA discordance, alone, may predict the location of RGC axon susceptibility and/or LC connective tissue deformation, remodeling, and failure. If this can be shown to be true in the nonhuman primate (NHP) unilateral EG model, eye-specific LMA discordance characterization using clinical imaging^{8,11,12,14–17} will become important.

Our data and their interpretation are limited by the following considerations. First, our use of the FoBMO axis as the vertical midline for ONH 30° regionalization means that our regional findings are not directly comparable to the regional findings of any previous study. While this is an important limitation, we believe that the logic for adopting FoBMO orientation for all studies of postmortem and in vivo (SDOCT) ONH anatomy is compelling and should improve both within- and between-subject data variability in both fields. Second, even when FoBMO orientation is employed, there is no articulated strategy for imposing a clinically relevant regionalization strategy from the BMO reference plane through the tissues of the prelaminar, laminar, and retrolaminar ONH, which expand⁴¹ and turn toward the chiasm as they pass obliquely through the neural canal. Our cylinderization strategy is intended to address this complex 3D problem, but may introduce artifacts that we have not yet recognized.

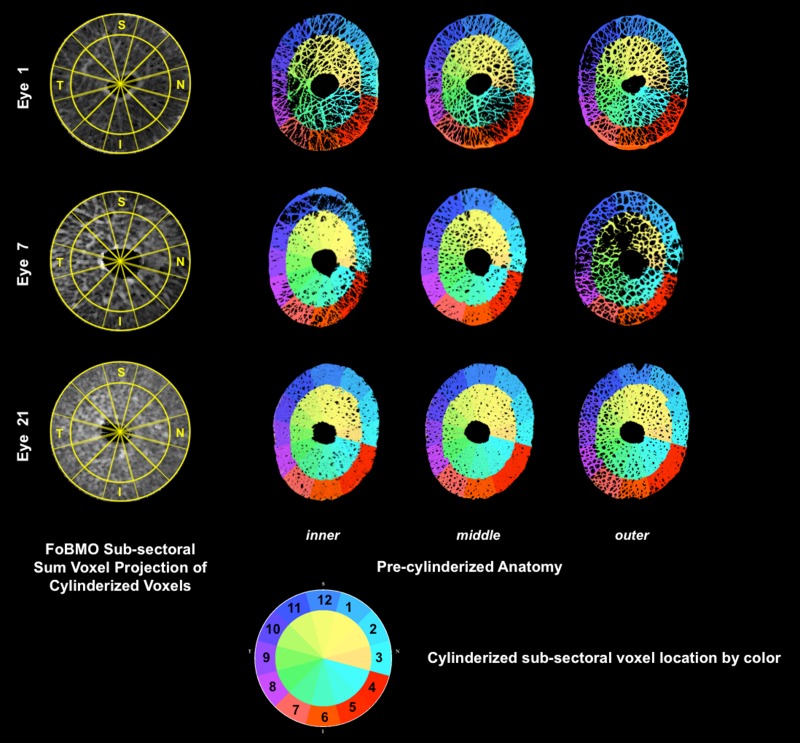
In this regard, our exploration of the subsectoral location of cylinderized voxels projected back into position within the uncylinderized LC anatomy (Fig. 14) is reassuring. Within these projections, the voxel positions appear regionally accurate and the mid-LC layer demonstrates the greatest transverse continuity of LC beam architecture, with variable levels of transverse discontinuity evident within the inner and outer layers of each eye. However, while we believe that this finding represents actual connective tissue discontinuity within the inner and outer LC layers, its regional extent may be overestimated by delineation, surface curve fitting, and segmentation inaccuracies. Delineation inaccuracy can occur if the LC surfaces are delineated “above” or “below” actual biological transverse connectivity. Surface curve fitting inaccuracy can occur because the parametric quadric surfaces that are fit to the anterior LC surface and posterior LC surface point clouds do not necessarily follow the anatomic shape of the anterior and posterior borders of the LC, creating patches of LC that lack transverse continuity. Segmentation inaccuracy can occur if our segmentation algorithm fails to make transverse connective tissue connections where they are biologically present and visible using our 3D delineation techniques. Because all three forms of inaccuracy are likely present within our data, distinctions between inner, middle, and outer LC layers should be conservatively interpreted with these limitations in mind.

Figure 14.

Voxel-specific cylinderized subsectoral assignments projected to precylinderized laminar anatomy in representative low, moderate, and high CTVF Eyes. For all 21 eyes, the cylinderized, subsectoral assignment of each voxel was qualitatively compared to its location within the precylinderized laminar anatomy by coloring each voxel based on its cylinderized subsectoral location (see color chart, lower middle). Comparisons are shown for representative low (eye 1), moderate (eye 7), and high (eye 21) CTVF eyes within inner, middle, and outer laminar layers. Low- (eye 7) and high-resolution (eyes 1 and 21) 3D HMRNs are also represented. Among all 21 eyes, eye 5 had obvious misassignment of voxels on the innermost surface, which involved less than 0.01% of all voxels within the involved subsectors (data not shown). Due to the small number of involved voxels, this was not felt to be significant. Note the lack of transverse connectivity within the outer layer of study eye 7. Contributing causes for this finding are considered in the Discussion.

In summary, our study introduces four methods for 3D histomorphometric characterization of eye-specific ONH LMA, and uses them to characterize sectoral, subsectoral, and depth discordance in BD, PD, and CTVF in 21 normal monkey eyes. Our data support previous characterizations of low connective tissue density within the superior-temporal and inferior-temporal ONH regions in most monkey eyes. They also support enhancement of this effect within the central compared to peripheral subsectors of the same regions and increased connective tissue support within the middle compared to inner and outer LC layers. While eye-specific LMA discordance followed these overall trends, marked individual eye differences from these descriptions were not uncommon, and the magnitude of eye-specific LMA discordance declined as global CTVF increased. The effect of age and other demographic and ocular biometric factors on LMA in an expanded group of 70 normal monkey eyes, as well as characterizations of LMA change in early, moderate, and severe monkey EG, will be the subject of future reports.