Broadband absorption and reduced scattering spectra of in-vivo skin can be noninvasively determined using δ-P₁ approximation based spectral analysis

Abstract

Previously, we revealed that a linear gradient line source illumination (LGLSI) geometry could work with advanced diffusion models to recover the sample optical properties at wavelengths where sample absorption and reduced scattering were comparable. In this study, we employed the LGLSI geometry with a broadband light source and utilized the spectral analysis to determine the broadband absorption and scattering spectra of turbid samples in the wavelength range from 650 to 1350 nm. The performance of the LGLSI δ-P₁ diffusion model based spectral analysis was evaluated using liquid phantoms, and it was found that the sample optical properties could be properly recovered even at wavelengths above 1000 nm where μ_s' to μ_a ratios were in the range between 1 to 20. Finally, we will demonstrate the use of our system for recovering the 650 to 1350 nm absorption and scattering spectra of in-vivo human skin. We expect this system can be applied to study deep vessel dilation induced hemoglobin concentration variation and determine the water and lipid concentrations of in-vivo skin in clinical settings in the future.

1. Introduction

Diffuse reflectance spectroscopy (DRS) is a model-based technique and has been employed to monitor the physiological status of deep and superficial biological tissues [1–4]. For probing deep tissues, such as brain and breast, DRS measurements are generally carried out at large source-detector separations (SDSs) in the range from 20 to 40 mm, while the SDSs for probing superficial tissues are usually within 5 mm. Photon transport models are often used in an inverse fitting procedure to derive the absorption and scattering spectra of samples from the measured diffuse reflectance spectra. Standard diffusion equations (SDEs) derived from the radiative transport equations can be employed to accurately describe photon transport at large SDSs [5, 6]. On the other hand, because the majority of photons are anisotropically scattered at a short SDS setup, rigorous yet complex mathematical models, such as δ-P₁ and P₃ diffusion models, Monte Carlo models, or empirical models have to be employed to relate the sample optical properties to the measurement data [7–10].

Previously, we revealed that a linear gradient line source illumination (LGLSI) geometry could facilitate the use of advanced diffusion models with high order approximation that had closed form solutions for efficient, accurate recovery of the optical properties of superficial samples, even for cases where μ_s'/μ_a was 1.67 [11]. We thoroughly compared the probing depth difference and the sample optical property recovery performance between the LGLSI and the classical 3 mm SDS DRS geometries [11]. Essentially, the LGLSI geometry is equivalent to a one-dimensional planar source and can be achieved by employing a scanning MEMS mirror to manipulate an incident light beam [11]. Compared with a regular planar source, the LGLSI has a greatly reduced source illumination area and notably improved signal to noise ratio. However, because the light source employed in our previously reported system was an intensity modulated laser diode at 780nm, we could only determine the sample optical properties at the laser wavelength. The system would need to employ a bank of laser diodes of different wavelengths to obtain sample absorption and scattering coefficients at various wavelengths.

In this study, we will demonstrate that by adding spectral constraints in the inverse fitting procedure, the LGLSI geometry with a broadband light source can be used to accurately determine the broadband absorption and reduced scattering spectra of samples. Researchers have reported that broadband absorption and scattering spectra could be obtained by applying the spectral analysis to the measured reflectance spectrum [12–14]. In the spectral analysis, spectral constraints, such as spectral signatures of main tissue chromophores and scattering power law, are used to help reduce the measured reflectance to chromophore concentrations and scattering spectra. The recovered chromophore concentrations can in turn be utilized to calculate the sample absorption spectrum. It should be noted that a photon transport model is still required as a forward model in the spectral analysis to relate the sample optical properties to the measured diffuse reflectance spectrum, and the most commonly employed model by far has been based on the SDE which does not work well when μ_s' and μ_a are comparable. Ex-vivo skin studies indicated that skin had μ_s' to μ_a ratios of about 50, 20, and 10 at the wavelengths of 1000, 1200, and 1500 nm, respectively [15]. Since the water content of ex-vivo skin may be substantially lower than that of in-vivo skin, the absorption coefficients as well as μ_s' to μ_a ratios of skin could be underestimated by ex-vivo studies at wavelengths above 1000 nm. This suggests that the validity of SDE becomes more tenuous as the wavelength increases above 1000 nm. Several groups have used different approaches to investigate the in-vivo skin optical property spectra in the wavelength range from 1000 to 1350 nm [16–19], and this wavelength region has been demonstrated to be a crucial region for accurate recovery of the water and lipid concentrations of biological tissues in the studies employing broad wavelength continuous wave light sources [20, 21]. The LGLSI measurement geometry allows the use of the δ-P₁ diffusion model based spectral analysis on the measured diffuse reflectance so that the broadband optical property spectra of samples can be accurately derived within one second even at wavelengths where sample μ_s'/μ_a is close to unity. By employing this method, we efficiently determined in-vivo skin optical property spectra from 650 to 1350 nm.

In the following, we will first introduce the theoretical background of our method in section 2 and describe in detail the experiment design of this study in section 3. Validation of our method by tissue simulating phantoms and in-vivo human skin measurement results will be provided in section 4.

2. Theoretical background

An ideal planar illumination geometry that has infinite lateral extension as shown in Fig. 1(a) can be reasonably assumed to have a circular shape with a radius r (r→∞) and is symmetric with respect to the origin O, as depicted in Fig. 1(b). For such kind of planar illumination geometry with radial symmetry, the ratio of the number of photons entering the sample at r_i to that at r_j is r_i/r_j, where r_i and r_j represent the distances of points i and j to the origin. Thus, a line source whose intensity increases proportionally with the distance from the origin as illustrated in Fig. 1(c) is equivalent to a planar illumination with radial symmetry, which was demonstrated in our previous study [11].

Fig. 1.

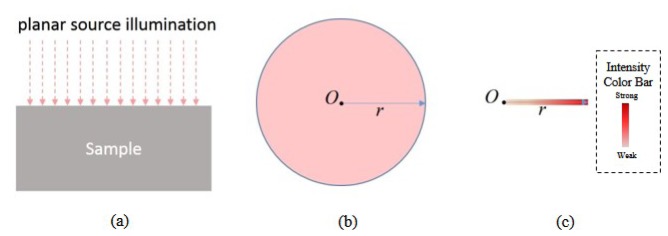
(a) Side view of the planar source illumination geometry. (b) Top view of a planar source with radial symmetry. (c) Top view of a linear gradient line source equivalent to a planar source with radial symmetry. Note that the linear gradient line source is achieved by using a scanning MEMS mirror in this study as illustrated in Fig. 2. The color intensity shown in (c) is proportional to light intensity.

In this study, we adopted the diffusion model that Carp et al. derived for the planar illumination, in which they considered the δ-Eddington phase function in the derivation of diffusion model from the radiative transport equation [22]. The modified model based on the δ-Eddington phase function is usually called the δ-P₁ diffusion model and is well suited to accommodate collimated sources and low scattering media. Carp et al. have provided the detail derivation of the δ-P₁ diffusion model used in this study [22]. We will recapitulate the derivation in the following.

The δ-Eddington phase function has the following form:

$$P_{\delta -P_1}\left(\hat{s}\cdot {\hat{s}}^{\prime }\right)=\frac{1}{4\pi }\left\{2f\delta \left[1-\left(\hat{s}\cdot {\hat{s}}^{\prime }\right)\right]+\left(1-f\right)\left[1+3g^{*}\left(\hat{s}\cdot {\hat{s}}^{\prime }\right)\right]\right\},$$ (1)

where $\hat{s}$ and ${\hat{s}}^{\prime }$ represent the unit vectors of the light propagation before and after scattering, respectively. This phase function includes a Dirac delta function to model the collimated, unscattered component of light. The remainder of light, 1-f, is diffusely scattered according to a P₁ phase function and is composed of an isotropic term and an anisotropic term. The parameters g* and f can be obtained by approximating Eq. (1) to the Henyey-Greenstein phase function, which yields:

$$f=g_{}^2 \text{and} g^{*}=g/(g+1),$$ (2)

where g is the anisotropy factor typically used in the P₁ approximation.

One can obtain the δ-P₁ diffusion equation for a planar source by substituting the δ-Eddington phase function into the RTE:

$$\left[\frac{{\partial }^2}{\partial z^2}-3{\mu }_a{\mu }_t{}^{\prime }\right]{\Phi }_d=-3{\mu }_s{}^{*}\left({\mu }_t{}^{\prime }+{\mu }_t{}^{*}{g}^{*}\right)\exp \left(-{\mu }_t{}^{*}z\right),$$ (3)

where μ_t' = μ_a + μ_s', μ_s* = μ_s(1-f), μ_t* = μ_a + μ_s*, Φ_d is the diffuse fluence rate and c is the speed of light in the medium. By applying the boundary condition at the sample-air interface for Eq. (3), one can obtain the diffuse fluence rate Φ_d.

$${\Phi }_d(z)=E_0(1-R_s)[\alpha \text{exp}(-{\mu }_t^{*}z)+\beta \text{exp}(-{\mu }_{\text{eff}}z)],$$ (4)

where E₀ is the source strength, R_s is the specular reflection coefficient, and μ_eff = (3μ_aμ_t')^1/2. The coefficients α and β are defined as:

$$\alpha =\frac{3{\mu }_s^{*}({\mu }_t^{*}+g^{*}{\mu }_a)}{{\mu }_{\text{eff}}^2-{\mu }_t^{*}{}^2},$$ (5)

and

$$\beta =\frac{-\alpha (1+Ah{\mu }_t^{*})-3Ah{g}^{*}{\mu }_s^{*}}{(1+Ah{\mu }_{\text{eff}})},$$ (6)

where h = 2μ_t'/3, and A can be approximated as A(n) = −0.13755n³ + 4.339n²-4.90366n + 1.6896 with n representing the refractive index of the sample [22]. Finally, the diffuse reflectance at the surface can be determined using the following equation:

$$R_d={\frac{{\Phi }_d(z)}{2A{E}_0(1-R_s)}|}_{z=0}.$$ (7)

3. Materials and Methods

3.1 Linear Gradient Line Source Illumination Geometry

The experimental setup of our broadband LGLSI system is illustrated in Fig. 2 . In the system, a supercontinuum source, which had a power density of about −22 dBm/nm in the 500-1750 nm region (SuperK COMPACT, NKT Photonics, Denmark) projected a collimated light beam onto an aluminum coated MEMS (Micro Electro Mechanical Systems) mirror (Mirrorcle Technologies, CA). The MEMS mirror had 1.2 mm diameter and it could manipulate the light beam to generate the linear gradient pattern as shown in Fig. 1(c). In our previous study, we found that the LGLSI geometry with 10 mm scanning radius was large enough for investigating samples of biological tissue relevant optical properties [11]. Therefore, in this study, the stay time of the light beam at 50 evenly distributed points within the 10 mm scanning radius was designed to be proportional to the distance to the origin. The MEMS mirror had a sample rate of 50000 s⁻¹ and it took around 0.02 s to complete one round of pattern scanning. Besides, since the maximum probing depths of the LGLSI and the classical 3 mm SDS DRS geometries were comparable [11], in this study, after a LGLSI measurement was completed, the light beam was steered to a position that was 3 mm apart from the detector fiber to carry out the 3 mm SDS DRS measurement. The detector fiber was a 480μm diameter low-OH multimode fiber (core diameter = 440μm) with numerical aperture of 0.22. The detection fiber was connected to 1*2 optical switch (Piezosystem jena, MA) to switch between two spectrometers equipped with a back-thinned CCD (QE65000, Ocean Optics, FL; working range from 400 to 1100 nm) and an array of InGaAs photo diodes (NIR512, Ocean Optics, FL; working range from 900 to 1700 nm), respectively. The optical switch and the spectrometer were connected to a computer and were coordinated and controlled by Labview (National Instruments, TX). At each measurement, two reflectance spectra associated with the two spectrometers were sequentially acquired and stored into one file for further data processing. Spectra recorded at wavelengths longer than 1350 nm were removed because the raw data had low counts and were noisy owing to the strong water absorption. Besides, spectra recorded at wavelengths shorter than 650nm were also neglected for the following reasons. First, the intensity of the broadband source was too weak to obtain good quality data below 600 nm. Second, it was reported that the scattering trend of skin at wavelengths shorter than 650 nm was different from that at wavelengths from 650 to 1000 nm [23].

Fig. 2.

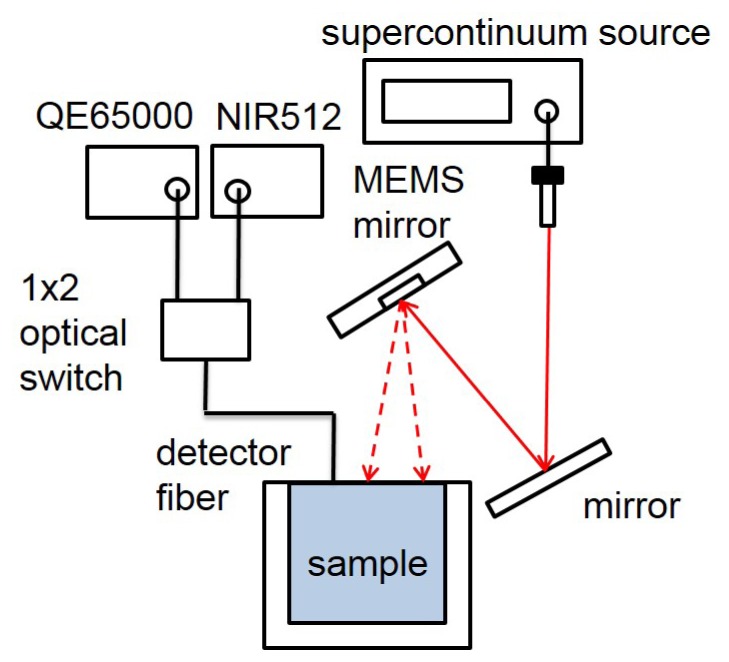
Schematic of the broadband Linear Gradient Line Source Illumination measurement setup.

3.2 Liquid phantom

We made two homogeneous liquid phantoms with known optical properties in this study. These phantoms were fabricated by mixing Lipofundin (Intralipid) 20% (B.Braun Melsungen AG, Germany), Nigrosin solution (MP Biomedical,Inc., Germany) (0.18 g Nigrosin powder in 1000 ml de-ionized water), and de-ionized water. Table 1 lists the recipe of the two liquid phantoms. This recipe was designed to produce phantoms of optical properties mimicking those of human skin which had high absorption at 600 nm (due to hemoglobin and melanin absorption) and low scattering at 1200 nm (as those indicated in refs [15]. and [21]). The two phantoms, LP_a and LP_b, were controlled to have a same μ_s'/μ_a value. We measured the extinction coefficient of the Nigrosin solution using a spectrophotometer. Figure 3 shows the absorption spectra of Nigrosin solution and water from 650 to 1350 nm used in this study. The water absorption spectrum was retrieved from the Oregon Medical Laser Center website [24].

Table 1. The recipe of the liquid phantoms.

Liquid Phantom	Nigrosin (ml)	Lipofundin (ml)	Water (ml)
LP_a	60	30	390
LP_b	50	25	405

Fig. 3.

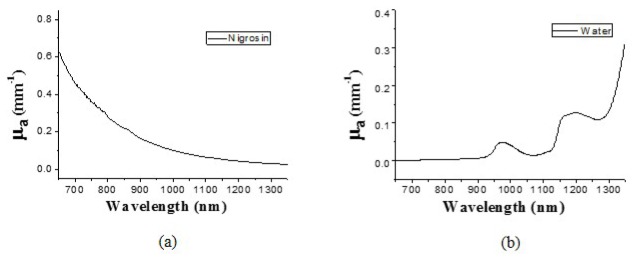
Absorption spectra of (a) Nigrosin solution and (b) water.

3.3 In-vivo skin measurements

In this study, five subjects of skin type III-IV in their twenties were recruited. The protocol was approved by the Institutional Review Board (No. ER-100-332) and written informed consents were obtained from all subjects prior to the measurements. Measurement sites were the volar aspect of forearm. Three measurements were taken on the volar forearm of each subject for each measurement geometry. For each measurement, the subject withdrew the arm from the measurement setup after the measurement and then put back again in the same position for the next measurement.

3.4 Inverse adding doubling (IAD) method

The inverse adding doubling method has been shown to be able to accurately recover μ_a and μ_s' from the reflectance and transmittance measurements of turbid slab samples [25]. We employed this method in this study to define the benchmark absorption and reduced scattering spectra of the two liquid phantoms in the wavelength range from 650 to 1350 nm. The configuration of our integrating sphere measurement system included a supercontinuum laser (SuperK COMPACT, NKT Photonics) which provided a wide output spectrum covering the 450-2400 nm region, an adjustable aperture, a quartz cuvette for containing the liquid phantom, and an integrating sphere (3P-GPS-053-SL, Labsphere, NH). An optical fiber was connected to the exit port of the integrating sphere to collect a part of light and to deliver the light to the two spectrometers (QE65000 and NIR512, Ocean Optics, FL) to record 650 to 1350 nm spectra. Measured sample reflectance and transmittance were processed with the inverse adding doubling algorithm to derive the sample optical property spectra [25].

3.5 Spectral analysis

By properly presuming the wavelength dependence of scattering and absorption properties of samples, the sample optical properties can be determined from a diffuse reflectance spectrum. In the wavelength range of interest here from 650 to 1350 nm, we constrained the reduced scattering coefficient to have a power law dependence on wavelength for both phantoms and skin:

$${\mu }_s{}^{\prime }(\lambda )=A\cdot {\lambda }^{-b},$$ (8)

where A and -b represented the scatter amplitude and scatter power, respectively. Besides, it was assumed that the absorption coefficient of the phantoms was a linear combination of that of Nigrosin solution and water, and could be expressed as:

$${\mu }_{a(phantom)}(\lambda )=C_{\text{Nigroson}}\times {\epsilon }_{\text{Nigroson}}(\lambda )+C_{\text{water}}\times {\epsilon }_{\text{water}}(\lambda ),$$ (9)

where C and ε represented the concentration and the extinction coefficient of a certain substance, respectively. Although Lipofundin contains lipid, the fraction of lipid in our liquid phantoms was around 1%; thus, we did not consider the contribution of lipid to the sample absorption. Similarly, the absorption of skin was assumed to be composed of the following chromophores: oxygenated hemoglobin (HbO₂), deoxygenated hemoglobin (Hb), melanin, water, and lipid, which could be written as:

$$\begin{array}{l}{\mu }_{a(skin)}(\lambda )=C_{{\text{HbO}}_2}\times {\epsilon }_{{\text{HbO}}_2}(\lambda )+C_{\text{Hb}}\times {\epsilon }_{\text{Hb}}(\lambda )+C_{\text{melanin}}\times {\epsilon }_{\text{melanin}}(\lambda )\\ +C_{\text{water}}\times {\epsilon }_{\text{water}}(\lambda )+C_{\text{lipid}}\times {\epsilon }_{\text{lipid}}(\lambda )+baseline.\end{array}$$ (10)

The C parameter has the unit of micro molar for hemoglobin and represents volume fraction for melanin, water, and lipid. In the least-squares fitting process, the A, -b, and C parameters were varied by the program for generating different absorption and reduced scattering spectra, and the optical property spectra were in turn used as the input to the δ-P₁ diffusion model to calculate the diffuse reflectance spectrum. The fitting process kept running iteratively until the program found the best calculated reflectance spectra that matched the measured reflectance spectra, and the A, -b, and C parameters and the corresponding absorption and reduced scattering spectra for the sample were thus determined. The absorption spectra of oxygenated hemoglobin, deoxygenated hemoglobin, melanin, lipid, and water were obtained from the Oregon Medical Laser Center website [24]. It should be noted that a variable DC offset in the skin μ_a spectrum, shown in Eq. (10) as “baseline”, was employed in the least-squares fitting to improve the quality of fitting to the in-vivo skin diffuse reflectance spectrum. Without adding “baseline” in Eq. (10), the spectral analysis performed poorly and fitted spectral shape did not match the spectral shape of the measured diffuse reflectance. This “baseline” might represent the absorption of the skin chromophores that were not taken into account in Eq. (10). Moreover, similar to the algorithm used by Nachabe et al., oxygenated and deoxygenated hemoglobin were not taken into account in the 1000-1350 nm spectral analysis in this study, because they did not possess clear spectral feature in this range [20].

4. Results and discussion

4.1 Phantom measurement results

Phantom experiments were carried out in the LGLSI geometry and in the classical DRS geometry with the 3 mm SDS to understand the performance of our system and the spectral analysis method. We employed phantom LP_b as the calibration phantom to calibrate the system response of the measured diffuse reflectance of the other liquid phantom. Specifically, in the calibration process, by employing Eq. (7) to determine the theoretical diffuse reflectance of LP_b with optical properties determined using the IAD method, the system response can be calculated by dividing the measured diffuse reflectance by the theoretical reflectance of LP_b. Next, the measured reflectance of another sample is divided by the system response to obtain the calibrated reflectance of the sample.

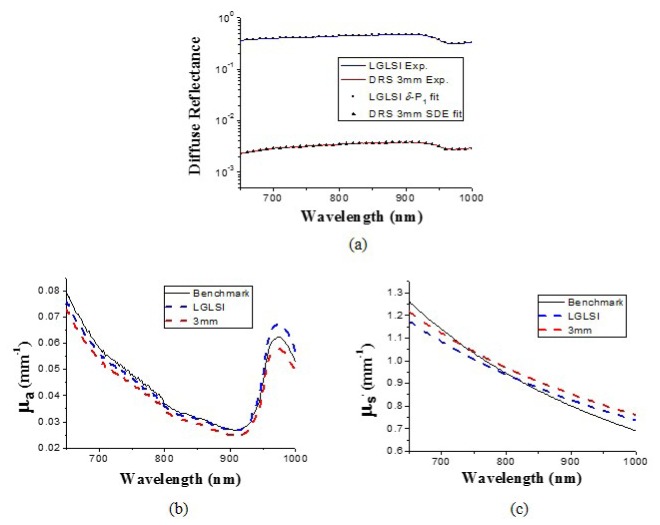
The calibrated diffuse reflectance spectra of LP_a were fit to the δ-P₁ diffusion model Eq. (7) for the LGLSI geometry and SDE for the classical DRS geometry with spectral constraints using the MATLAB (MathWorks, MA) optimization function “lsqcurvefit” to derive the chromophore concentrations and the optical properties of the phantom. The measurement and fit spectra in wavelength region from 650 to 1000 nm are shown in Fig. 4(a) as solid lines and symbols, respectively. In general, a good fitting quality can be observed and the difference between the fit curve and the calibrated reflectance was within 1.0% at all wavelengths. The recovered optical property spectra are illustrated in Figs. 4(b) and 4(c) as blue and red dashed lines for the LGLSI and the classical DRS geometries, respectively. Besides, the benchmark μ_a and μ_s' spectra are depicted in Figs. 4(b) and 4(c) as black lines. It can be seen the optical property spectra recovered from the two measurement geometries share similar trends. The maximal deviations of the recovered μ_a and μ_s' from the benchmark values are 8.3% and 6.8%, respectively, for the LGLSI geometry, and 8.1% and 10.6%, respectively, for the classical DRS geometry. The recovered chromophore concentrations of the liquid phantom are listed in Table 2 . Although water was the dominant component of the liquid phantom and the prominent absorption peak at 980 nm of water could be clear observed, it can be seen in Table 2 that the water recovery errors were not low, and the absorption coefficients recovered using both geometries deviate from the benchmark value at 980 nm as demonstrated in Fig. 4(b). In the 650-1000 nm region, the absorption of Nigrosin solution decreases monotonically with wavelength which is similar to the trend of the scattering power law observed by the sample reduced scattering spectrum. We speculate that the spectral analysis could not clearly differentiate the contribution of the reduced scattering from that of the Nigrosin solution to the reflectance spectrum, and the accuracy of the recovered reduced scattering spectrum was compromised which in turn influenced the accuracy of the water concentration recovery.

Fig. 4.

(a) Diffuse reflectance measured in the LGLSI geometry (blue line) and the 3 mm SDS DRS geometry (red line) in the wavelength range from 650 to 1000 nm for the liquid phantom LP_a, and their respective fitting results (LGLSI: squares, 3 mm SDS DRS: triangles). (b) μ_a and (c) μ_s' spectra of LP_a recovered using the LGLSI geometry (blue dashed lines) and the 3 mm SDS DRS (red dashed lines). The benchmark spectra (black lines) were determined using the IAD method.

Table 2. Chromophore concentrations of liquid phantoms recovered using LGLSI and classical DRS geometries at two wavelength regions.

	650-1000 nm			1000-1350 nm
	Nigrosin(%)	Water(%)		Nigrosin(%)	Water(%)
LGLSI (δ-P1)	11.98	110.54		9.40	99.94
Error (%)	−4.08	11.94		−24.73	1.21
DRS (SDE)	11.49	91.85		7.61	82.28
Error (%)	−8.06	−6.98		−39.06	−16.66

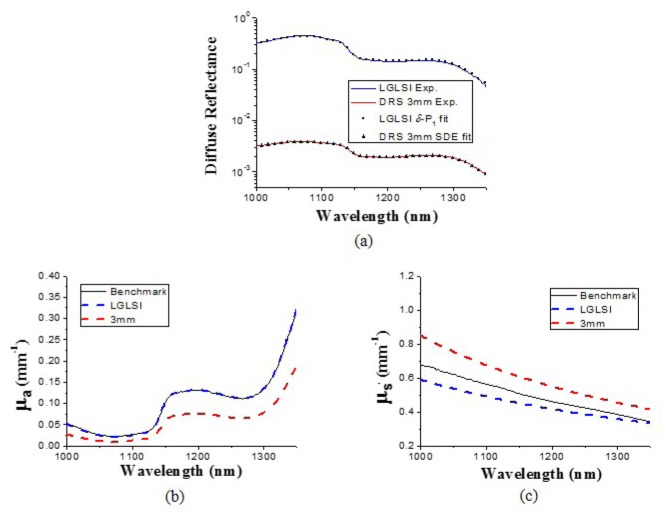
Phantom measurement results at the 1000-1350 nm region are shown in Fig. 5 . The absorption spectrum recovered using δ-P₁ diffusion model agrees very well with the benchmark absorption spectrum with errors less than 5% as illustrated in Fig. 5(b). In contrast, the absorption spectra recovered using the SDE deviates from the benchmark spectrum by as large as 57%. Besides, in Fig. 5(c), the maximal deviations of the reduced scattering coefficients recovered using the LGLSI and the classical DRS geometries are 14% and 26%, respectively. We believe that the large deviation of the optical property spectra recovered using the SDE in the classical DRS geometry from the benchmark values was due to the breakdown of SDE given such a low sample μ_s' to μ_a ratio in this wavelength region. It can be seen in Figs. 5(b) and 5(c) that the SDE overestimated the reduced scattering by 21% and underestimated the absorption by 47% at 1200 nm. The recovered chromophore concentrations in the wavelength range from 1000 to 1350 nm are listed in Table 2. We can observe that the water concentration determined using SDE in the classical 3 mm DRS geometry was smaller than the benchmark value by about 17%, which was caused by the underestimation of the absorption spectrum mentioned above. In this wavelength range, the absorption feature of Nigrosin solution is not prominent and thus not an ideal substance for spectral analysis. Therefore, the two methods could not accurately recover the concentration of Nigrosin solution in this region. On the other hand, the LGLSI geometry with the δ-P₁ diffusion model could precisely determine the water concentration with less than 2% error while the classical DRS geometry with the SDE model had 16% water concentration recovery error.

Fig. 5.

(a) Diffuse reflectance measured in the LGLSI geometry (blue line) and the 3 mm SDS DRS geometry (red line) in the wavelength range from 1000 to 1350 nm for the liquid phantom LP_a, and their respective fitting results (LGLSI: squares, 3 mm SDS DRS: triangles). (b) μ_a and (c) μ_s' spectra of LP_a recovered using the LGLSI geometry (blue dashed lines) and the 3 mm SDS DRS (red dashed lines). The benchmark spectra (black lines) were determined using the IAD method.

From this phantom study, we found that the LGLSI geometry worked in conjunction with the δ-P₁ diffusion model and spectral analysis could precisely recover the sample optical property spectra in the 650-1350 nm region, while the classical DRS geometry with SDE spectral analysis could only properly calculate the sample optical property spectra in the 650-1000 nm region where the sample μ_s' to μ_a ratio was high. To further understand the reason for the poor performance of SDE in the 1000-1350 nm region, we carried out additional Monte Carlo simulations for the classical DRS 3mm SDS geometry at wavelengths of 900 and 1200 nm. When the SDS was 3 mm, the average photon travel lengths were found to be 8.70 and 7.34 mm at the wavelengths of 900 and 1200 nm, respectively. Since the difference between the average photon travel lengths was only 15% at the two wavelengths, the poor performance of the classical 3 mm SDS DRS geometry at 1000-1350 nm range could not mainly caused by the short photon travel lengths in the setup, since this setup performed well in the 650-1000 nm region. Its poor performance could very likely due to the breaking down of the diffusion model at low μ_s'/μ_a conditions. We also carried out phantom measurements using the classical DRS geometry with SDS of 5 mm (data not shown), and we found that its performance was similar to that of the classical 3 mm SDS DRS at 1000-1350nm region where μ_s'/μ_a was between 1 to 20. It could be inferred that the capability of SDE in modeling photon transport in low μ_s'/μ_a conditions could not enhanced by increasing the photon travel length in the sample.

4.2 In-vivo skin measurement results

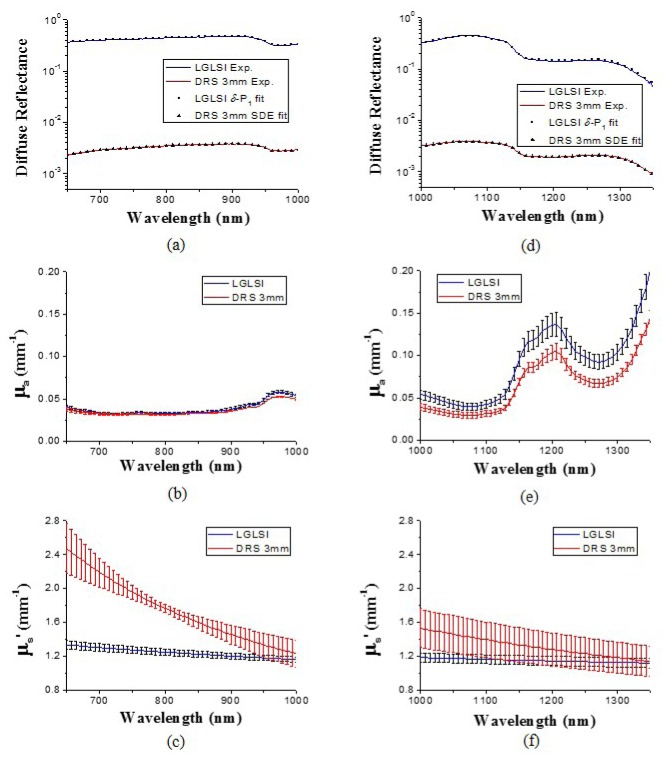
We performed the LGLSI and the classical 3 mm SDS DRS measurements on the volar forearm of five subjects. Three measurements for each measurement geometry were carried out for each subject. The average optical property spectra derived from three LGLSI measurements for one of the subjects are shown in Fig. 6 . The average chromophore concentrations of the five subjects in the wavelength regions of 650-1000nm and 1000-1350 nm are listed in Table 3 and Table 4 , respectively.

Fig. 6.

Diffuse reflectance measured in the LGLSI geometry (blue line) and the 3 mm SDS DRS geometry (red line) for the volar forearm of one of the subjects in the wavelength range from (a) 650 to 1000 nm (b) 1000 to 1350 nm, and their respective fitting results (LGLSI: squares, 3 mm SDS DRS: triangles). (b) μ_a and (c) μ_s' spectra of the volar forearm recovered using the LGLSI geometry (blue lines) and the 3 mm SDS DRS (red lines) in the wavelength range from 650 to 1000 nm. μ_a and μ_s' spectra recovered in the wavelength range from 1000 to 1350 nm are illustrated in (e) and (f), respectively.

Table 3. Average chromophore concentrations and standard deviations of the volar forearm of the five subjects recovered using the LGLSI and the classical 3 mm SDS DRS geometries in the wavelength range from 650 to 1000 nm.

	650-1000 nm
	HbO2(μM)	Hb(μM)	Water(%)	Lipid(%)	Melanin(%)	baseline	A	-b
LGLSI	23.0	5.6	53.8	38.5	0.146	0.021	280.908	-0.613
DRS	± 3.2	± 1.0	± 4.0	± 5.8	± 0.068	± 0.003	± 407.353	± 0.269
	18.3	4.2	48.4	30.9	0.079	0.026	1574948.345	-1.947
	± 5.7	± 3.7	± 2.6	± 4.5	± 0.034	± 0.003	±1920574.124	± 0.202

Table 4. Average chromophore concentrations and standard deviations of the volar forearm of the five subjects recovered using the LGLSI and the classical 3 mm SDS DRS geometries in the wavelength range from 1000 to 1350 nm.

	1000-1350 nm
	Water(%)	Lipid(%)	Melanin(%)	baseline	A	-b
LGLSI	45.3	14.5	0.0	0.018	48.861	0.365
DRS	± 5.1	± 3.5	± 0.0	± 0.004	± 60.856	± 0.257
	40.1	19.4	0.0	0.019	3168845.105	-1.918
	± 3.6	± 4.2	± 0.0	± 0.04	± 5507390.057	± 0.283

Measured reflectance and the fitting results are shown in Figs. 6(a) and 6(d) for 650-1000 nm and 1000-1350 nm wavelength ranges, respectively. Good quality of fitting can be observed in these two figures and the difference between the fit curve and the calibrated reflectance was within 2.6% at all wavelengths. The optical properties determined using the δ-P₁ diffusion model in the LGLSI geometry are shown as blue lines in Figs. 6(b), 6(c), 6(e), and 6(f). The 1000-1350 nm absorption spectrum illustrated in Fig. 6(e) has a dominant peak around 1200 nm caused by strong water absorption which can also be observed in Fig. 3(b).

The reduced scattering spectra are shown in Figs. 6(c) and 6(f) for 650-1000 nm and 1000-1350 nm, respectively. It can be seen that the reduced scattering coefficient gradually decreases with wavelength. Interestingly, the trend and the magnitude of the reduced scattering spectrum determined using the LGLSI geometry in the 650-1000 nm region are not similar to those of in-vivo skin reported earlier by our group [23, 26]; specifically, the magnitude and the scatter power of the reduced scattering spectrum shown here are both lower than those reported earlier. Bashkatov et al. found that the magnitude of scattering and the scatter power of the reduced scattering spectrum of subcutaneous adipose tissue were both lower than those of dermis [15]. Based on Bashkatov’s finding, it was speculated that the reason for different scattering magnitude and trend between this study and our earlier study could result from the probing depth difference between the LGLSI geometry and the modified two-layer geometry used in our earlier studies. We have determined using Monte Carlo simulations the probing depth of the LGLSI geometry and the modified two-layer geometry in current application to be 1.5 mm and 1.0 mm at 900 nm, respectively. It is very likely that the majority of detected photons do not enter the subcutaneous layer in the modified two-layer probing geometry, and this explains the higher magnitude of scattering and the scatter power of the reduced scattering spectrum of skin recovered in the modified two-layer geometry than in the LGLSI geometry. Besides, the probing depth difference between the LGLSI and the modified two-layer geometries can also be observed in the different lipid concentration recovered. We can see that in Table 3 the forearm lipid concentration recovered using the LGLSI geometry is 38.5% which is larger than the 26.1% forearm lipid concentration recovered using the modified two-layer geometry reported in our previous study [23]. Thus, it is logical to assume that the lower magnitude and the scatter power of the reduced scattering spectrum as well as the higher lipid concentration recovered using the LGLSI geometry than those recovered using the modified two-layer geometry could be caused by the larger probing depth of the LGLSI geometry.

Further, it can be seen in Table 4 that the lipid concentration determined using the LGLSI geometry at 1000-1350 nm is 14.5%, which is smaller than the 26.1% lipid concentration recovered using the modified two-layer geometry at 650-1000 nm. We carried out an additional Monte Carlo simulation and found that the maximum probing depth for the LGLSI geometry was 0.9 mm at 1200 nm, which was smaller than the maximum probing depth (1.0 mm) of the modified two-layer geometry at 900 nm. This result supports the fact that the 2-fold difference in the lipid concentrations recovered at 650-1000 nm and 1000-1350 nm regions using LGLSI geometry was very likely caused by the difference in interrogation depth at these two wavelength regions.

The optical property spectra recovered using the classical 3 mm SDS DRS geometry are shown as red lines in Figs. 6(b), 6(c), 6(e), and 6(f). It can be seen in Fig. 6(b) that the absorption spectra recovered using the two methods, shown as red and blue lines, are analogous and have less than 10% difference in the wavelength range from 650 to 1000 nm; in contrast, the reduced scattering spectra determined using the two methods are very different in this wavelength region as depicted in Fig. 6(c). In Table 3, it can be observed that distinctively lower A and –b values were recovered using the LGLSI geometry than those recovered using the classical 3 mm SDS DRS geometry. From the phantom study, we understood that both methods can properly determine the optical properties of samples that are comparable to those of human skin in the 650-1000 nm region. We speculate that one of the reasonable causes for the results shown in Fig. 6(c) would be that the two methods interrogated different depths of skin. In Bashkatov’s study, they measured the reduced scattering spectrum of human subcutaneous adipose tissue and determined that the μ_s' followed a scattering power law in the form of μ_s' = 1050 λ^-0.68 (Fig. 7 in ref [15].). In our previous study, we used the modified two-layer probe to determine the reduced scattering spectrum of human skin and found the scattering power law had the form in μ_s' = 59772 λ^-1.57 (Fig. 9 in ref [23].). In this study, the A and –b values determined using the LGLSI geometry from 650 to 1000 nm were closer to the values reported by Bashkatov et al. for subcutaneous tissue than did those derived from the classical 3 mm SDS DRS geometry [15]. This infers that the probing depth of the LGLSI geometry could go well beyond dermis and a considerable part of the interrogation volume contained the subcutaneous tissue. In contrast, the A and –b values determined using the classical 3 mm SDS DRS geometry were closer to the values reported in ref [23]. for skin than did those derived from the LGLSI geometry. This suggests that the interrogation region of the classical 3 mm SDS DRS geometry is mostly located in the dermis in the 650-1000 nm region.

In the 1000-1350 nm wavelength region, compared to the optical property spectra recovered in the LGLSI geometry, the classical 3 mm SDS DRS geometry recovered lower absorption and higher reduced scattering. A similar phenomenon has been observed in the phantom study as shown in Figs. 5(b) and 5(c), which implied a possible systematic error in the process of simultaneous fitting of the reduced scattering and the chromophore concentrations using the diffusion theory. Moreover, the reduced scattering spectra recovered using the classical 3 mm SDS DRS geometry shown in Figs. 6(c) and 6(f) demonstrate an obvious discontinuity at 1000nm. The facts described above suggest that the credibility of the skin optical properties recovered using SDE in the 1000-1350 nm region was weak.

It is worth noting that the average water concentrations recovered using the LGLSI geometry at 650-1000 nm and 1000-1350 nm were 53.8% and 45.3%, respectively. Although the average water content was slightly higher at 650-1000 nm than at 1000-1350 nm, we found no statistically significant difference between the water concentrations of the five subjects recovered at 650-1000 nm and 1000-1350 nm (p>0.05). Because the probing depth could be influenced by the wavelength region employed, this result suggests that the water distribution in the deep dermis could be depth independent. Furthermore, it can be seen in Table 3 and 4 that the average lipid percentage recovered using LGLSI geometry drops from 38.5% in 650-1000 nm to 14.5% in 1000-1350 nm. We ran student’s t-test and found that the lipid concentrations recovered at 650-1000 nm and 1000-1350 nm in the LGLSI geometry were statistically different (p<0.001). Significantly lower lipid concentration recovered at 1000-1350 nm than at 650-1000 nm suggests that the probing depth of the LGLSI geometry in a layered skin structure reduces greatly in the 1000-1350 nm high absorption, low scattering region. Besides, it can be noted that we recovered zero melanin concentration for both methods in the 1000-1350 nm region. We suspect this was caused by the relatively low absorption of melanin compared to other chromophores in this wavelength region and/or the melanin absorption spectrum was not accurate enough for precise spectral analysis.

5. Conclusion

In this study, we proposed the use of the LGLSI geometry with the δ-P₁ diffusion model based spectral analysis for accurate and efficient determination of broadband optical property spectra of turbid samples. In the phantom study, we showed that while the LGSLI geometry had comparable performance with the 3 mm SDS DRS geometry in the 650-1000 nm region, the LGSLI geometry that employed the δ-P₁ diffusion model outperformed the 3 mm SDS DRS geometry in the 1000-1350 nm region due to the high sample absorption in this wavelength region. We further employed the LGSLI geometry to recover the in-vivo skin optical property spectra and compared the results with those determined using the 3 mm SDS DRS geometry. We found that the two methods produced very different skin reduced scattering spectra, which suggested that their probing depths could be different when applying to investigate in-vivo skin. From our results and the data reported in the literatures, it can be inferred that the LGLSI geometry has a deeper probing depth for skin than does the 3 mm SDS DRS geometry in the 650-1000 nm range, and its interrogation volume may contain a considerable part of subcutaneous tissue. On the other hand, in the 1000-1350 nm wavelength range, the skin optical property recovered using 3 mm SDS DRS geometry could be inaccurate while those recovered using the LGLSI geometry resembles the values reported earlier. In the future, we will integrate the MEMS mirror into a hand-held probe to facilitate performing the LGLSI measurements on in-vivo skin in the clinical setting. The system will be utilized to study skin allergy induced deep vessel dilation using the 650-1000 nm wavelengths and study the water and lipid concentrations of various type of skin diseases using the 1000-1350 nm wavelengths.