Measurements of the thermal coefficient of optical attenuation at different depth regions of in vivo human skins using optical coherence tomography: a pilot study

Abstract

We present detailed measurement results of optical attenuation’s thermal coefficients (referenced to the temperature of the skin surface) in different depth regions of in vivo human forearm skins using optical coherence tomography (OCT). We first design a temperature control module with an integrated optical probe to precisely control the surface temperature of a section of human skin. We propose a method of using the correlation map to identify regions in the skin having strong correlations with the surface temperature of the skin and find that the attenuation coefficient in these regions closely follows the variation of the surface temperature without any hysteresis. We observe a negative thermal coefficient of attenuation in the epidermis. While in dermis, the slope signs of the thermal coefficient of attenuation are different at different depth regions for a particular subject, however, the depth regions with a positive (or negative) slope are different in different subjects. We further find that the magnitude of the thermal coefficient of attenuation coefficient is greater in epidermis than in dermis. We believe the knowledge of such thermal properties of skins is important for several noninvasive diagnostic applications, such as OCT glucose monitoring, and the method demonstrated in this paper is effective in studying the optical and biological properties in different regions of skin.

1. Introduction

Optical coherence tomography (OCT) is a noninvasive imaging technique that has been extensively used for study of the optical properties of superficial layers of biological tissues [1]. Optical properties, such as the absorption coefficient ( ${\mu }_a$), (reduced) scattering coefficient ( ${\mu }_s$) and anisotropy factor that are dependent on the tissue state, can provide possibilities of improved non-invasive diagnosis.

Optical scattering coefficient ${\mu }_s$ at certain depth regions of in vivo human skin is found to have strong correlation with blood glucose and OCT were proposed and demonstrated for non-invasive glucose monitoring by measuring ${\mu }_s$ in such regions [2,3]. Unfortunately, temperature can substantially alter the measured values of ${\mu }_s$ and causes measurement errors. Previous in vivo studies [4] indicated that moderate skin temperature fluctuations on the order of ± 1°C had little effect on accuracy, but substantial change ( ± several degrees Celsius) significantly affected the OCT signal slope. However, no detailed studies have been performed on the temperature-dependent attenuation or scattering coefficient of in vivo human skin in different layers, although such studies may prove important for improving the accuracy and repeatability of OCT based noninvasive glucose monitoring. In addition, the detailed knowledge of the temperature dependencies of the attenuation coefficient ( ${\mu }_t$) in different depth regions of tissues may also be valuable for other noninvasive diagnostic measurements [5–8].

In a previous study, a decreasing of the refractive index and ${\mu }_t$ with increased temperature was observed in the samples of individual vascular wall components [9]. In another study, temperature induced changes in the optical properties of in vitro human dermis and subdermis were studied with a wide wavelength range from 650 nm to 1000 nm [10]. The direction of change with temperature in the optical scattering was found to be different in dermis and in subdermis: ${\mu }_s$ has a negative slope with temperature in subdermis and positive slope in dermis. However, a living human skin tissue with complicated structures and material compositions has an exquisite system of self-regulation, the results from such in vitro experiments may not be useful for the in vivo applications, particularly for OCT based glucose monitoring applications.

The effect of temperature on the absorption and scattering of human skin in vivo was studied with near infrared spectroscopy, and the scattering coefficient ${\mu }_s$ was observed to have a positive slope with temperature between 22°C and 42°C [11]. However, the human skin is a multilayer structure and the optical properties of various skin layers are expected to be different. Near infrared spectroscopy can measure the diffused reflection of light from a tissue at a fixed region of depth, however it cannot obtain optical properties as a function of depth in a particular skin layer. On the other hand, OCT technique can overcome such a limitation and enables in vivo cross-sectional imaging of the tissue microstructure with a spatial resolution on the order of tens of microns. Consequently, it can be used to investigate the temperature-dependent optical properties of skin in different layers in vivo and the results can be directly applied to OCT based glucose measurements.

In this paper, we report our detailed studies of optical attenuation coefficients as a function of temperature in different layers of in vivo human forearm skins, the same body areas used for OCT glucose monitoring [12–15]. We take the advantage of high spatial resolution of a swept-wavelength OCT system to obtain the attenuation coefficients in different skin layers. In order to precisely control the skin temperature, we design and fabricate a micro temperature control chamber integrated with a two dimensional (2D) scanning probe to set the skin in the probe scanning area at any temperature between 28 and 42 degrees with a stability of ± 0.2°C. A programmable temperature controller is used to control the chamber with predetermined temperature variation profile. We propose a novel method of using the correlation map to identify regions in the skin having different degree of correlation with temperature. When ramping the skin temperature up and down, we find that the ${\mu }_t$ in the high correlation regions follows the temperature change closely without any hysteresis in its thermal response. We observe a negative thermal coefficient of attenuation in the epidermis. However in dermis, the slope signs of the thermal coefficient of attenuation are different at different depth regions for a particular subject, however, the depth regions with a positive (or negative) slope are different in different subjects. We further find that the magnitude of the thermal coefficient of ${\mu }_t$ is greater in epidermis than in dermis. We believe that the knowledge of such thermal properties of skins is important for several noninvasive diagnostic applications, especially for OCT glucose monitoring and that the method proposed and demonstrated in this paper is effective for studying the optical and biological properties in different regions of skin.

2. Measurement methods

2.1 Measurement fixture

A commercial fiber-based swept source OCT system from Thorlabs centered at 1300 nm was used in our laboratory experimental investigation. With a coherence length of 6 mm and a wavelength scanning range of 100 nm, the system has a depth measurement range of the back-reflected signals of approximately 3 mm and an axial spatial resolution of 12 μm in air or approximately 8.7 μm in tissue with a refractive index of 1.38 [16]. With a transverse spatial resolution measured around 25 μm, the system can acquire a 3D-OCT image of 3.75 mm × 3.75 mm × 3 mm (x × y × z) comprising 152 pixels × 152 pixels × 512 pixels in 8 seconds. In addition, each A-scan of the OCT image consists of 4 averaged A-scans in order to improve the signal to noise ratio (SNR).

A schematic diagram of the miniature temperature chamber with an optical scanning probe used in this study is shown in Fig. 1(a) . The walls of the chamber are made with thermal insulating materials and two thermal electric coolers (TEC) are placed inside of the chamber for heating and cooling the air inside the chamber. A desk-top programmable temperature controller is place outside of the chamber with wires connecting to the TEC’s to control the temperature inside the chamber with any desired temperature profiles. The OCT optical scanning probe is located at the top of the chamber and there is an opening at the bottom of the chamber for light to go through. The opening is directly in contact with the human skin under test and a temperature sensor connecting to the temperature controller is placed at the edge of the opening to monitor the temperature of the skin and feed the information to the temperature controller, which uses Proportion Integration Differentiation (PID) algorithm to precisely control the skin temperature with a stability of ± 0.2°C in the steady state, as shown in Fig. 1(b). An optical scanning probe is placed on the top of the chamber and the height adjustment screws can be used to adjust the distance between the probe and human skin to focus optical beam onto the surface of skin by an objective lens inside the scanning probe.

Fig. 1.

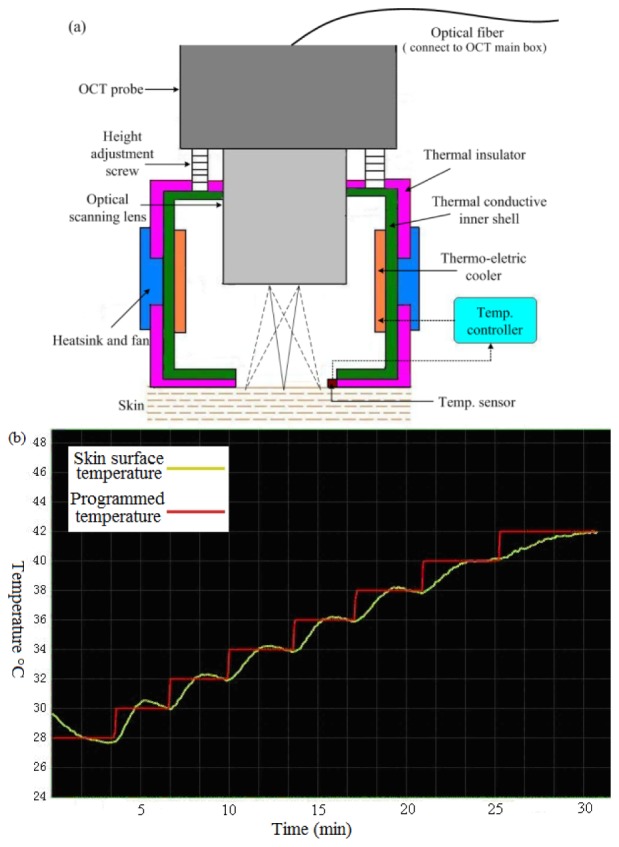
(a) Schematic of a temperature-controlled OCT probe consisting of a miniature temperature chamber with an integrated optical scanning probe; (b) Programmed (red) and measured (green) temperature variation on the surface of a human skin from 28°C to 42°C with 2°C steps. The temperature can be stabilized to be within ± 0.2°C to the programmed setting temperatures in less than 5 minutes.

2.2 Obtaining attenuation coefficient

Figure 2(a) shows a typical OCT volume image of a section of skin taking from the volar side of the forearm of a human subject, while Fig. 2(b) is one-dimensional distribution of back scattered light intensity as a function of depth (the attenuation curve) obtained from Fig. 2(a) using the following steps: 1) identify the skin surface of the OCT volume by an image identification algorithm, and then realign all A-scans of the OCT volume to the surface to reconstruct a new 3D image; 2) Take an average of all A-scans in the reconstructed OCT volume to obtain an one-dimensional signal in order to suppress the speckle noise and minimize motion artifacts so as to improve the measurement precision of backscattering signal of the skin under test. The error bars in Fig. 2(b) indicate the standard deviation of the A-scan data at the selective points with an interval of 100μm. Note that the OCT signals were acquired in the logarithmic scale in dB and the one-dimensional attenuation curve was normalized from the dB intensity. As shown in Fig. 2(b), the OCT attenuation curve has distinctive signatures corresponding to different skin layers to be discussed next. Figure 2(c) is a text book illustration of a typical skin structure, showing the locations of epidermis and different types of dermis.

Fig. 2.

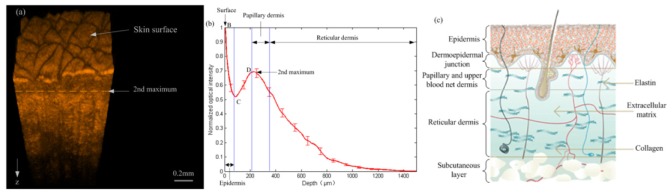
(a) 3D OCT image obtained from the volar side of forearm skin ; (b) One-dimensional distribution of light intensity vs depth obtained by averaging all A-scans in the reconstructed OCT 3D image from (a); (c) Text book illustration of the skin layered structure.

The slope of the normalized one-dimensional attenuation curve at different layers is calculated at the specific depth by using a linear least-square fit method. Within the homogeneous skin layers, the decay of the OCT signal with depth follows the Beer-Lambert law.

$$I=I_0{e}^{-{\mu }_{t}z}$$ (1)

where ${\mu }_t={\mu }_s+{\mu }_a$ is the attenuation coefficient, $I_0$is the incident light intensity, z is the geometric depth inside the tissue. The attenuation coefficient was used as a common parameter to analyze optical properties of skin tissues with OCT in most of literatures [17–21]. Some literatures suggest that in the NIR spectral range, ${\mu }_s$ of most tissues is much greater than ${\mu }_a$, and ${\mu }_t$ can be approximated as ${\mu }_s$ and is a good estimate of the local scattering properties [22–26]. However, in this paper we concentrate on studying the thermal effect on the attenuation coefficient, and choose not to distinguish the relative contributions from scattering and absorption.

2.3 Relationship between attenuation coefficients and skin structure

As shown in Fig. 2(b), the OCT attenuation curve has two maxima resulting from two bright reflection regions, with the skin surface identified as the first reflection maxima B. The region between the first maxima and the local minima C is identified as epidermis [16,27], which is an outer, nonvascular and nonsensitive layer of the human skin. It largely consists of outward moving cells and keratinocytes that are formed by division of cells in the basal layer. With a thickness of 90 to 100 μm, the epidermal layer scatters light strongly, causing the OCT backscattered light to attenuate rapidly with depth.

The layer between the first minima C and the second maxima D in Fig. 2(b) corresponds to a junction of epidermis and upper dermis papillary layer [28]. The second maxima D is caused by the light reflection from dermal fibers and its location is identified as border of dermis [29], which is the second or middle layer of skin that is just below the epidermis. The dermis is divided into two layers. The superficial area adjacent to the epidermis is called the papillary dermis. This layer has a thickness around 120 μm [16] that begins from the second maxima D and contains smaller and more loosely distributed collagen fibers but has more ground substance than in that of the underlying reticular dermis layer. The reticular dermis layer is made of thicker collagen fibers arranged parallel to the surface of the skin. Extracellular matrix and interstitial fluid exist between these fibers, as illustrated in Fig. 2(c). Therefore, the skin can be subdivided into several homogeneous layers in different depths and the effect of temperature on optical attenuation in these layers is expected to be different.

2.4 Experiments on human subjects

The experiments were carried out on 9 volunteers aged 24 to 33 years. The selected subjects were in good health without taking any medication and had no strenuous exercise before the experiment. All experiments reported in this paper were performed within 80 minutes. Because the blood glucose can significantly affect the scattering coefficient of the human skin [12–14], each subject was tested 150 min after meal when his blood glucose was stable [30]. In addition, the blood glucose of each subject was also monitored during the experiment in order to make sure that the blood glucose was stable to minimize its influence on the optical scattering properties. In order to avoid measurement uncertainties of the optical properties of tissue [31] caused by the variations of optical beam’s focal point, special attention is paid to keep the distance between the optical lens of the OCT scanning probe and the skin surface fixed in the experiment. The OCT signals were acquired from the volar side of the forearm skin and the skin area selected for each subject in the experiments generally had no fine hairs and was cleaned before each individual experiment to eliminate the influences of dirt and dead skin particles. The skin temperature was constantly monitored and recorded during the process of data acquisition. Time interval between OCT acquisitions for 3D images was 10 seconds.

Two sets of experiments on the human subjects were performed in our investigation. The first experiment was designed to investigate the response time and repeatability of the temperature-dependent optical properties of the human skin, and was carried out with rapid temperature modulations on the four human subjects. During the experiments, the temperature was varied between 31°C and 39°C back and forth in each circle and repeated three times. The temperature changing rate is approximately 1.5 minutes per degree Celsius. During the measurement the volar side of the forearm of each subject was held in steady and was in contact with the bottom side of the miniature temperature-controlled chamber described in Fig. 1.

The second experiment was performed at a wide range of temperature with a slow temperature variation rate so as to acquire sufficient OCT raw data to quantitatively analyze the correlation between optical scattering properties and temperature of the human skin. Five human subjects were studied in the experimental investigation. The skin surface temperature was raised from 29°C to 41°C with a step of 1°C, and each temperature step was held for 3.5 minutes for acquiring sufficient data points. The time required to raise the temperature by one step (1°C) is about 1.5 minutes.

2.5 Correlation analysis

Because the diversity in skin’s composition, it is reasonable to assume that some regions of the skin are more correlated to temperature variations than other regions. For example, in some regions, the ${\mu }_t$ may increase with temperature (positive correlation region); in some regions it may decrease (negative correlation region); and in other regions it may not change with temperature at all. Therefore, it is important to first quantify the correlation regions of each subject’s skin with temperature before further investigations.

Figure 3 shows the correlation map of the skin in which the vertical axis is the starting position while the horizontal axis represents the depth range from OCT raw data for calculating ${\mu }_t$ at different temperatures of one subject in the first experiment shown in Fig. 4c . For example, the skin surface in Fig. 2(b) corresponds to zero in the vertical axis of Fig. 3, while points C and D correspond to 70 μm and 190 μm in the vertical axis respectively. The point (375, 200) on the correlation map of Fig. 3 represents a value of ${\mu }_t$ calculated in a region starting at 200 μm from the skin surface and ending at a depth of 375 μm from 200 μm.

Fig. 3.

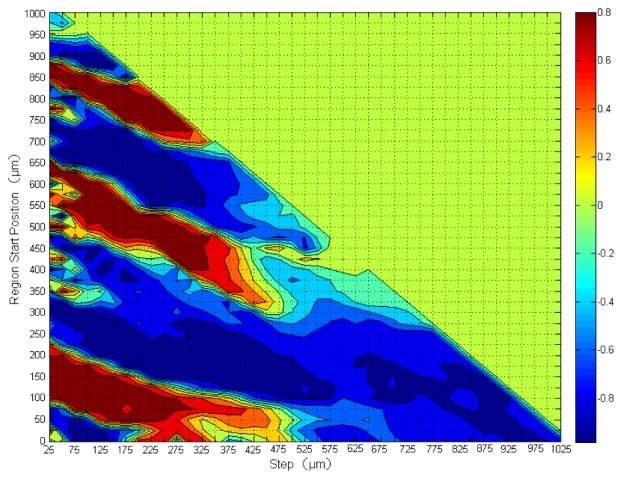
The map of correlation between ${\mu }_t$ and the surface temperature at different depth regions of a human forearm skin from 31°C to 39°C. The color bar on the right indicates the degree of correlation. The vertical axis is the region starting position while the horizontal axis represents the depth range from OCT raw data for calculating ${\mu }_t$ at different temperatures. The deep red regions have the highest positive correlation with the temperature while the deep blue regions have the highest negative correlation. Some regions have little or no correlation with temperatures at all. The color bar represents the magnitude of the correlation coefficient.

Fig. 4.

Measured ${\mu }_t$ as a function of time when the surface temperature of the skin is modulated between 31°C and 39°C. Data were taken on the forearm skin of four different subjects (a-d) in depth regions of the highest degree of correlation with temperature.

As shown in Fig. 2(b), ${\mu }_t$ for each temperature can be calculated for a selected segment with a starting position and a width of multiple of 25 μm (corresponding to 5 data points of OCT raw data). The first starting position is 0, corresponding to the skin surface, and the subsequent starting positions are N × 25 μm (N = 1, 2, 3….). That is, both the starting positions and the range for calculation have an increment of 25 μm.

The correlation between and ${\mu }_t$ and the temperature, R, is obtained using Person product-moment correlation [32]. The Pearson correlation coefficient is a well-established measure of correlation. It reflects the degree of linear relationship between two variables and is denoted by R. The R has range of + 1 (perfect correlation) to −1 (perfect but negative correlation) with 0 denoting the absence of a relationship. Both variables do not need to be measured on the same scale (e.g., one variable can be ratio and one can be interval). Furthermore, the two variables can be measured in entirely different units. Therefore, it is suited to correlation analysis of ${\mu }_t$ and temperature.

$$R=\frac{n{\displaystyle \sum _{i=1}^n{\mu }_{ti}{T}_i-{\displaystyle \sum _{i=1}^n{\mu }_{ti}}{\displaystyle \sum _{i=1}^n{T}_i}}}{\sqrt{n{\displaystyle \sum _{i=1}^n{\mu }_{ti}^2-{({\displaystyle \sum _{i=1}^n{\mu }_{ti}})}^2}}\sqrt{n{\displaystyle \sum _{i=1}^n{T}_i^2-{({\displaystyle \sum _{i=1}^n{T}_i})}^2}}}$$ (2)

where T is temperature and n is the sample point of temperature. In practice, we used a MatLab (MatLab 2008a) function in our calculation [33].

3 Results and discussions

3.1 Temperature response of attenuation coefficient

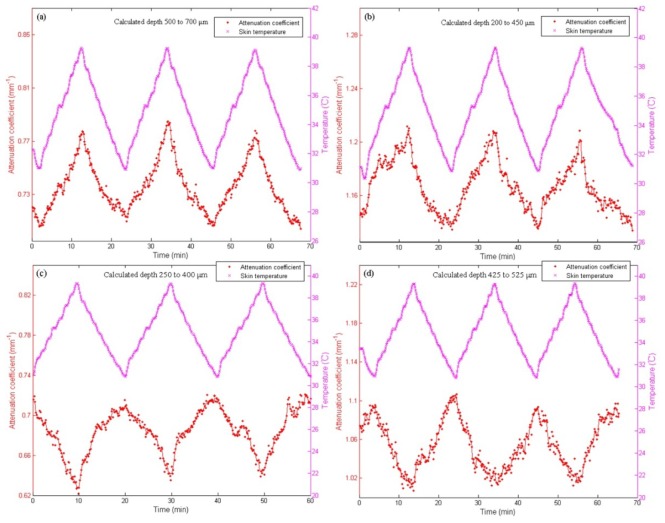
Figure 4 shows the effect of temperature modulation on the ${\mu }_t$ at a most temperature dependent depth region in a human skin in vivo. In the experiment, the miniature temperature chamber was placed on top of the forearm of a subject and the temperature of the skin in contact with the chamber was changed periodically between 31°C and 39°C with a total of 3 cycles. For each subject, we first obtain a correlation map described in Section 2.4 and select a depth region in which ${\mu }_t$ has the highest degree of correlation with temperature to calculate ${\mu }_t$at each temperature, with the results shown in Fig. 4(a) to 4(d) for the four different subjects. In other depth regions with a high degree of correlation, similar dependences of ${\mu }_t$ on temperature are also found. The corresponding correlation maps for the first two subjects are shown in Fig. 5(a) and Fig. 5(b), with high positive correlation regions in red and negative correlation regions in blue.

Fig. 5.

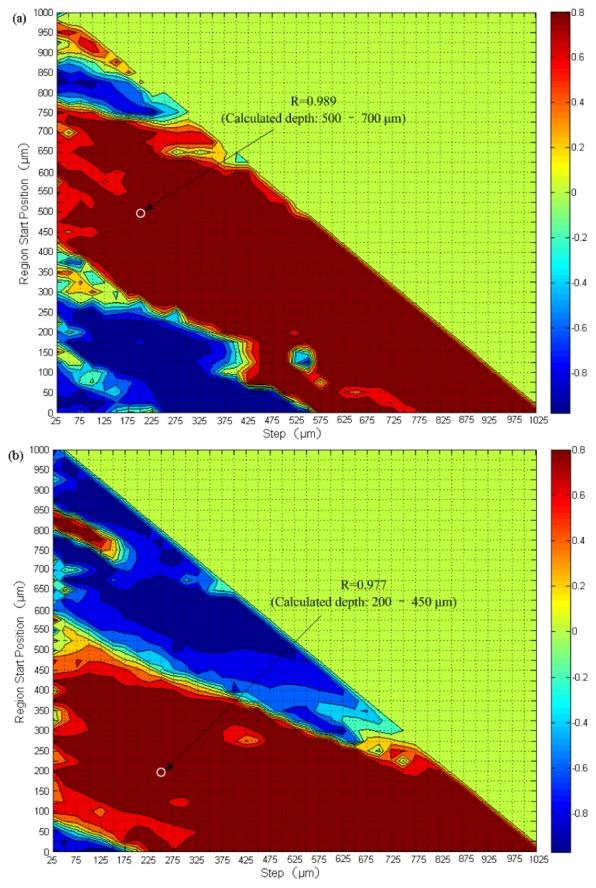
Correlation map between ${\mu }_t$ and temperature at different depth regions of two representative subjects in the first experiment.

It is important to notice that 1) the depth regions of the highest degree of correlation R for different subject are different. For subject 1 in Fig. 4(a), we choose the depth region between 500 to 700 μm with the highest degree of correlation (R = 0.989) to calculate ${\mu }_t$. This positive correlation region shown by the white circle in Fig. 5(a) corresponds to the reticular layer in dermis. For subject 2 in Fig. 4(b), ${\mu }_t$is calculated in the depth region between 200 to 450 μm with the highest degree of correlation (R = 0.977) shown by the white circle in the correlation map (Fig. 5(b)), a region include the junction of papillary layer and reticular layer. For subject 3 (Fig. 4(c)) and subject 4 (Fig. 4(d)), the depth regions with the highest negative temperature correlation between 250 to 400 μm (R = −0.928) and from 425 to 525 μm (R = −0.937) respectively are chosen to calculate ${\mu }_t$. 2) Because it is difficult to measure the temperature inside skin, we use the surface temperature of the skin to obtain the temperature dependence of ${\mu }_t$ in different skin layers, although there should be a temperature gradient along the depth of the skin. In fact, the results of Fig. 4 indicate that the variations of ${\mu }_t$ at different depth regions follow the surface temperature closely without hysteresis in its thermal response, which justify our use of the surface temperature of the skin as the reference to study the thermal coefficients in different skin layers, instead of using the actual temperature for each of the layers. When the positive correlation regions are chosen, such as the cases in Fig. 4(a) and Fig. 4(b), ${\mu }_t$increases with the surface temperature of the skin; while when the negative correlation regions are chosen (Figs. 4(c) and 4(d)), ${\mu }_t$ decreases with surface temperature. 3) The values of ${\mu }_t$ at each temperature are sufficiently repeatable in the three temperature cycles.

One of the major causes for the temperature dependent attenuation is believed to be the dependence of the refractive index mismatch between the scattering centers in the skin, such as papillary and collagen fibers, and the surrounding interstitial fluid. A larger mismatch causes more scattering of light by the scattering centers, and therefore more attenuation of light. Another possible cause is the size change of such scattering centers due to the temperature variations [10,34].

In the upper dermis, the tissue optical properties, such as the scattering coefficient, may also be affected by blood perfusion induced by temperature variations. The venous plexus (upper blood net dermis) is a region below the papillary layer within a layer of 50 - 100 μm in depth. When temperature increases, blood perfusion increases via vasodilation and results in an increased heat dissipation in the skin. On the other hand, decreased skin temperature causes a decrease in blood perfusion. Reflex vasoconstriction substantially decreases convective transfer of heat [35]. Therefore, blood vessels can be vasodilation or vasoconstriction due to temperature variations in tissue, which in turn cause the refractive index mismatch and affect tissue’s optical scattering coefficient.

The Mie theory can be approximated to give the following expression for the scattering coefficient of mixtures of spherical particles for simulating biological tissues [36]:

$${\mu }_s=3.28\pi r^2{\rho }_s{\left(\frac{2\pi r}{\lambda }\right)}^{0.37}{\left(\frac{n_s}{n_m}-1\right)}^{2.09}$$ (3)

where r is the average radius of scattering particles, ${\rho }_s$ is the density of particles, $\lambda$ is the wavelength of light, $n_s$ is the refractive index of scattering particles and $n_m$ is the refractive index of the surrounding medium. It is evident from Eq. (3) that ${\mu }_s$ is mainly affected by the refractive index mismatch between $n_s$ and $n_m$. The refractive index mismatch can be caused by temperature variation, glucose fluctuation and other physiological factors. The ${\mu }_s$ increases as refractive index mismatch increases. Although its accuracy for describing the scattering in different layers of a skin might have not been proven, Eq. (3) still helps to understand quantitatively how the index-mismatch between the scattering centers and the surrounding interstitial fluid in the skin affect the scattering and thus attenuation.

3.2 Epidermis

Figure 6 shows the temperature dependence of ${\mu }_t$ in epidermis for the five subjects (A-E). The temperature coefficient for each subject is obtained using a least-square fit to the experimental data and the value of the slope is used to label each curve. As can be seen in Fig. 6, the values of the temperature coefficients are different for different subjects, but all decrease with temperature and have values in the range from −0.026 to −0.038 mm⁻¹/°C.

Fig. 6.

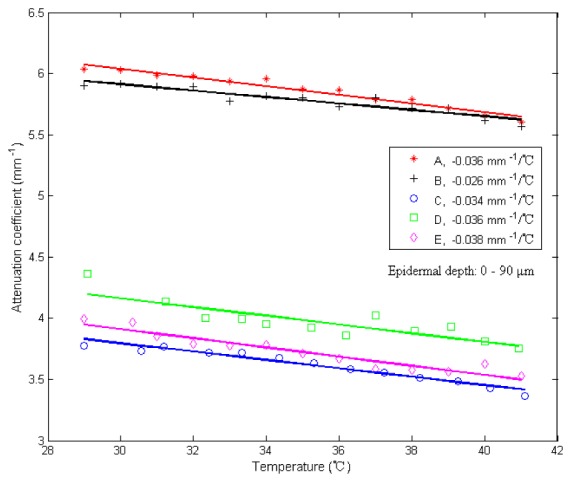
Measured ${\mu }_t$ from epidermis layer of the in vivo human skin (forearm area) versus temperature from 29 to 41°C, calculated in a depth region of 0–90 μm. The letters A through E refer to five different subjects. The solid lines are the least-squares fit to the experimental data of each subject. Each of the fitted slopes was labeled in the legend as its temperature coefficient.

3.3 Dermis

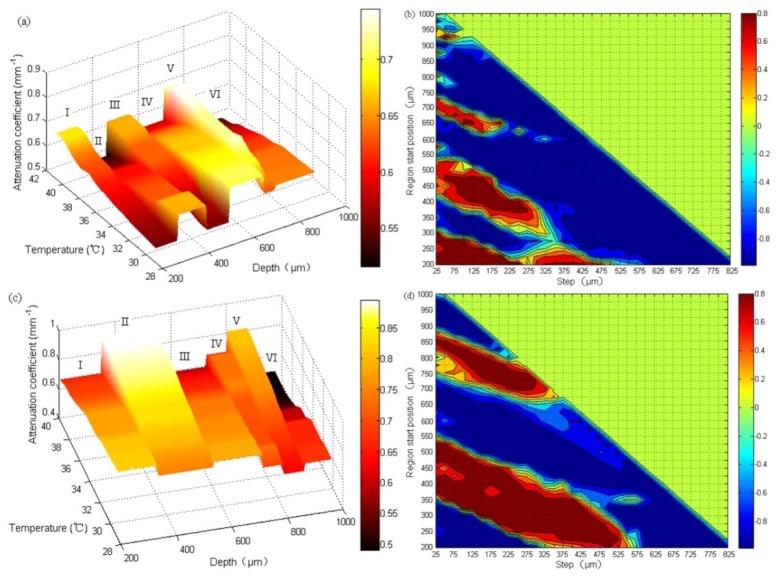
In the dermis layer, the dependence between ${\mu }_t$ and temperature were found to be different at different depth regions for each subject, with some regions of positive slope and others negative. For the five subjects, the regions with positive and negative slopes seemed to vary randomly in the dermis, likely due to biological variability. Figure 7(a) and Fig. 7(c) show the typical temperature dependence of ${\mu }_t$ with temperature at different depth regions in the dermis of two subjects. It is evident that ${\mu }_t$has different slopes with temperature in different depth of regions, with positive slopes in regions I, III, V (Fig. 7(a)) for the first subject and II, IV, V (Fig. 7(c)) for the second subject, while negative slopes in regions II, IV, VI (Fig. 7(a)) for the first subject and I, III, VI (Fig. 7(c)) for the second subject.

Fig. 7.

Attenuation coefficient ${\mu }_t$ as a function of temperature in different depth regions from 29°C to 41°C of two different subjects and their corresponding correlation maps. The color bar in (a) and (c) represents the magnitude of ${\mu }_t$, while the color bar in (b) and (d) represents the degree of correlation. The ${\mu }_t$ as a function of temperature in different depth regions are quite different in the dermis, some having positive slopes while others negative, corresponding to the positive (yellow to red) and negative (green to blue) correlation regions in the corresponding correlation map (b) and (d). In (a) and (c), Roman numbers I-VI are used to differentiate regions with positive and negative slopes, with neighboring regions have opposite slope signs.

As mentioned in Section 3.3, the dependences of ${\mu }_t$ on temperature in different regions in the dermis layer are different. We postulate that regions with positive correlation are made with the same types of tissue while the regions with negative correlation are made a different type of tissue. Therefore, it makes sense to find out the average attenuation coefficient of the issues of the type with positive correlation and the negative correlation respectively. Figure 8 shows the dependence of ${\mu }_t$ on temperature in the regions of positive correlation (a) and negative correlation regions (b) in the dermis for the five subjects. For each subject, ${\mu }_t$ in all the positive (or negative) correlation regions with absolute correlation coefficients greater than 0.9 (corresponding to the deep red and deep blue regions in Fig. 7(b) and Fig. 7(d) were first calculated and then were averaged at each temperature for obtaining an averaged ${\mu }_t$ with the positive (or negative) correlation. Curve-fitting of ${\mu }_t$ vs. temperature curve yields the slope of ${\mu }_t$ as a function of temperature (the temperature coefficient) for each individual subject with its value labeled in the legend. In Fig. 8(a), ${\mu }_t$ increases with temperature and the temperature coefficients range between 0.009 to 0.019 mm⁻¹/°C for all five subjects. Figure 8(b) shows ${\mu }_t$ decreases with temperature with temperature coefficient between −0.010 to −0.020mm⁻¹/°C for the five subjects.

Fig. 8.

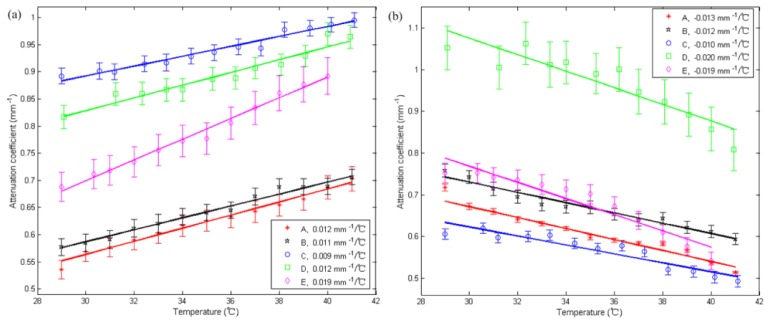
Average ${\mu }_t$ obtained by averaging ${\mu }_t$ of all positive correlation regions (a) and all negative correlation regions (b) in dermis of in vivo human skin versus temperature from 29 to 41°C for the five subjects. The solid lines are calculated by using least-squares fit for the experimental data of the subjects under test. Each of the fitted slopes was labeled in the legend as the temperature coefficient.

The positive or negative correlation region between ${\mu }_t$ and temperature may represents different types of tissues in the dermis. The positive slope may indicate that the refractive index mismatch between the scattering centers and the surrounding interstitial fluid (ISF) increases with temperature, while the negative slope may indicate the mismatch decreases with temperature in the corresponding regions of different biological composition.

4. Summary and discussions

We have investigated the temperature dependence of optical attenuation coefficient of in vivo human skin with optical coherence tomography in this pilot study. We design and build a miniature temperature chamber integrated with an OCT scanning probe for placing on the volar side of the forearm of a testing subject to precisely control the local temperature of the skin under investigation. We propose and demonstrate a method of using the correlation map to calculate the degrees of correlation in different depth regions and identify the depth regions having strong correlation with temperature variations. When the local temperature of the skin is modulated between 31°C and 39°C, we observe that the attenuation coefficient ${\mu }_t$ of each subject follows the temperature variation closely without any hysteresis.

The attenuation coefficients of forearm skins of five different subjects are also measured in a temperature range from 29°C to 41°C. In the epidermis, the temperature dependence coefficients of ${\mu }_t$ of all five subjects are found to be negative, with values between −0.026 to −0.038 mm⁻¹/°C. As for dermis, the signs of thermal coefficient are found to be different at different depth regions. For each subject, the temperature dependence of ${\mu }_t$ is found to change dramatically along the depth, with alternating positive and negative slopes. In the depth regions of positive slope, the temperature coefficients of the five subjects are in the range between 0.009 to 0.019 mm⁻¹/°C, while in the depth regions of negative slope they have the values between −0.010 to −0.020 mm⁻¹/°C.

Our experiments demonstrate the feasibility of using the correlation map and OCT to obtain the detailed information of the optical properties of the skin, such as the attenuation coefficient. We expect that the method and results can be applied to OCT based noninvasive blood glucose sensing and other noninvasive diagnostic measurements, especially for minimizing the influence of temperature on measured values.

Note that with the advantage of OCT, one may study the variation of optical properties, such as the attenuation coefficient, not only in the depth dimension, but also in the lateral dimension. We therefore have investigated such 3D distribution of attenuation coefficient caused by the variations in temperature or glucose, and the results will be published subsequently in separate publications.