Estimation of ROC Curve with Complex Survey Data

Abstract

The receiver operating characteristic (ROC) curve can be utilized to evaluate the performance of diagnostic tests. The area under the ROC curve (AUC) is a widely used summary index for comparing multiple ROC curves. Both parametric and nonparametric methods have been developed to estimate and compare the AUCs. However, these methods are usually only applicable to data collected from simple random samples and not surveys and epidemiologic studies that use complex sample designs such as stratified and/or multistage cluster sampling with sample weighting. Such complex samples can inflate variances from intracluster correlation and alter the expectations of test statistics due to the use of sample weights that account for differential sampling rates. In this paper, we modify the nonparametric method to incorporate sampling weights to estimate the AUC, and employ leaving-one-out jackknife methods along with the balanced repeated replication method to account for the effects of the complex sampling in the variance estimation of our proposed estimators of the AUC. The finite sample properties of our methods are evaluated using simulations, and our methods are illustrated by comparing the estimated AUC for predicting overweight/obesity using different measures of body weight and adiposity among sampled children and adults in the US Hispanic Health and Nutrition Examination Survey.

1. Introduction

The receiver operating characteristic (ROC) curve is frequently used to evaluate diagnostic tests in medical applications and research [1]. The ROC curve is a plot of sensitivity, or true positive rate (TPR) on the vertical axis vs. 1 - specificity, or false positive rate (FPR) on the horizontal axis across all the possible decision thresholds or cutoffs. The TPR is the proportion of patients who have the disease who test positive for it based on a diagnostic test, and FPR is the proportion of people who do not have the disease who will test positive for it based on the same diagnostic test. The curve is useful in (1) evaluating the ability to discriminate between subjects with and without an abnormality of interest, (2) estimating the optimal cut-off point to minimize misclassifying diseased and non-diseased subjects, and (3) comparing of efficacy of two or more medical tests for assessing the same disease. There are several ways to summarize the ROC curve. A widely used summary index is the area under the ROC curve, denoted by AUC, which is bounded between 0.5 and 1. A larger AUC value usually presents a better discrimination of the test between diseased and non-diseased populations.

Both parametric and nonparametric methods have been developed to estimate and compare the AUCs [2-12]. As that parametric approaches require assumptions about the underlying distribution of the data, we will focus this paper on nonparametric methods for estimating the AUC for the ROC curve. Under simple random sampling, Bamber [2] was the first to show that the area under the empirically estimated ROC curve is equal to the Mann-Whitney U-statistic, using the fact that the AUC can be interpreted as the probability that a randomly chosen diseased individual will be larger than or equal to a randomly chosen normal individual. Variance estimation of the estimated AUC has been developed using different approaches [2, 4, 6]. The approach used by Hanley [4], which is based on Bamber's work [2], uses the variance estimation of the Mann-Whitney U-statistic when the observations are not necessarily from continuous distributions [13]. The variance estimation approach of DeLong et al. [6] is based on a structural components method [14], which is equivalent to a jackknife method.

The variances are usually underestimated for surveys with complex sample designs [15] when the sample design is not taken into account in analyses. For example for cluster sample designs ignoring the sample design can result in underestimation of variances because of extra variability from intraclass correlation among observations within the sampled clusters. Also if the sample weighting is improperly accounted for in the variance estimation then biased variance estimation can occur. Therefore, the standard statistical methods of estimation of AUC and its variance that assume simple random sampling are not suitable for data from complex samples. Our objective in this paper is to develop appropriate nonparametric methods for the estimating the AUC and its variance under different sample designs that range from stratified simple random samples to stratified multistage cluster samples.

In section 2, we extend the nonparametric method for estimating the population AUC to properly account for sample weighting under differing complex sample designs. Jackknife and balanced repeated replication (BRR) methods are utilized for variance estimation of our proposed estimator of AUC that account for complex sample design and sample weighting. In section 3, Monte Carlo simulation is performed to compare the accuracy of jackknife and BRR methods. We also discuss informative sample designs where the sample selection probabilities are related to the parameter of interest. We illustrate the estimation of AUC and its variance with an example using the Hispanic Health and Nutrition Examination Survey (HHANES) in section 4 and conclude with a discussion in section 5.

2. Estimation of AUC for complex sampling designs

2.1. Standard nonparametric method

Suppose we have M diseased and N nondiseased subjects and a test applied to each subject where X_i denote the test values of i-th diseased subject, i = 1, 2, ..., M, Y_j denote the test values of j-th diseased subject, j = 1, 2, ..., N. Following Bamber [2], the area under the empirical ROC curve can be expressed as the average over the kernel ψ as

$$\widehat{\theta }=\frac{1}{MN}\sum _{j=1}^N\sum _{i=1}^M\psi (x_i,X_j)$$ (1)

where

$$\psi (X_i,X_j)=\{\begin{array}{cc}1\hfill & Y_j<X_i\hfill \\ \frac{1}{2}\hfill & Y_j=X_i\hfill \\ 0\hfill & Y_j>X_i\hfill \end{array}\phantom{\}}$$

For continuous test values, because the probability of obtaining ties is negligible, it follows that $E\left(\widehat{\theta }\right)=P(Y<X)=\theta$ where θ denotes the population AUC and the expectation is over the joint distribution of the random variables X and Y for test results without specifying the joint distribution. In other words for simple random samples $\widehat{\theta }$ is an unbiased estimator of θ. This nonparametric formula (1) has been routinely applied for simple random samples, but does not directly apply to complex sample survey data where we need to take into account differential sampling rates and other aspects of the sample designs.

2.2. Estimation of AUC for stratified simple random samples

Stratified sampling is commonly applied in surveys where certain characteristics such as gender, race, income, or geographical locations are known for all the units in the population can be used to exhaustively divide the units into disjoint subgroups which are the strata. Stratified simple random sampling (SSRS) is when simple samples are independently selected from each stratum with specified sample sizes.

Suppose we have a finite population of T units (subjects) with strata, such that the number of subjects in the finite population in stratum h is T_h, where T_h = N_h + M_h. N_h and M_h are the number of diseased and nondiseased subjects, and ${\sum }_{h=1}^H{T}_h=T$. A simple random sample of t_h subjects is selected from stratum h so that the total sample size of subjects is $t={\sum }_{h=1}^H{t}_h$. The t_h are fixed constants but the number of disease and nondiseased subjects in the sample in stratum h, m_h, and n_h are random, where t_h = n_h + m_h. In the comparison of diseased and non-diseased pairs of subjects both subjects in a pair may come from the same sampling stratum or from different strata. The joint inclusion probability that diseased and non-diseased subjects will be included in sample s is denoted as π_(hi,h′j), and the joint sample weight is defined as the inverse of joint inclusion probability, w_(hi,h′j) = 1/π_(hi,h′j). Let θ_(h,h′) denote the infinite population AUC for the diseased subjects in h-th stratum and the non-diseased subjects in h′-th stratum, then the AUC can be described as a matrix:

$${\theta }_{(H\times H)}=\left(\begin{array}{cccc}\hfill {\theta }_{(1,1)}\hfill & \hfill {\theta }_{(1,2)}\hfill & \hfill \cdots \hfill & \hfill {\theta }_{(1,H)}\hfill \\ \hfill {\theta }_{(2,1)}\hfill & \hfill {\theta }_{(2,2)}\hfill & \hfill \cdots \hfill & \hfill {\theta }_{(2,H)}\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill {\theta }_{(H,1)}\hfill & \hfill {\theta }_{(H,2)}\hfill & \hfill \cdots \hfill & \hfill {\theta }_{(H,H)}\hfill \end{array}\right)$$

A sample weighted estimator of stratum-pooled AUC for the finite population is:

$${\widehat{\theta }}_U=\frac{1}{\widehat{N}\widehat{M}}\sum _{h=1}^H\sum _{h^{\prime }=1}^H\sum _{j=1}^{T_{h^{\prime }}}\sum _{i=1}^{T_h}{W}_{(hi,h^{\prime }j)}{I}_{(hi,h^{\prime }j)}{\delta }_{hi}(1-{\delta }_{h^{\prime }j})\psi (X_{hi},Y_{h^{\prime }j})={\sum }_{h=1}^H{\sum }_{h^{\prime }=1}^H{\widehat{p}}_h{\widehat{q}}_{h^{\prime }}{\widehat{\theta }}_{(h,h^{\prime })}={\widehat{p}}^T{\widehat{\theta }}_{(H\times H)}\widehat{q}$$ (2)

where for subjects i and j from strata h and h′ respectively, w $\frac{T_h(t_h-1)}{t_h(t_h-1)}$ _(hi,h′j) is $\frac{T_h(T_h-1)}{t_h(t_h-1)}$ if h = h′ or if h = h′, or $\frac{T_h}{t_h}\frac{T_{h^{\prime }}}{t_{h^{\prime }}}$, if h ≠ h′ is the indicator of inclusion of subjects hi and h′j in the sample, and δ_hi is the indicator that is equal to 1 for diseased subjects and 0 otherwise, ${\widehat{p}}^T=({\widehat{p}}_1,\cdots ,{\widehat{p}}_h,\cdots {\widehat{p}}_H)$, where ${\widehat{p}}_h={\widehat{M}}_h∕\widehat{M},{\widehat{q}}^T=({\widehat{q}}_1,\cdots ,{\widehat{q}}_h,\cdots {\widehat{q}}_H)$, where ${\widehat{q}}_h={\widehat{N}}_h∕\widehat{N}$. ${\widehat{\theta }}_{(h,h^{\prime })}$ denotes the estimated AUC for the diseased subjects in h stratum and the non-diseased subjects in h′ stratum, and ${\widehat{\theta }}_{(H\times H)}$ is a H × H matrix estimating θ(H×H). Often the population size T is known or the sample weights are poststratified to known population totals, while the number of diseased subjects M and non-diseased subjects N are unknown but can be estimated by using the sample, i.e., ${\widehat{M}}_h=\frac{m_h}{t_h}{T}_h$ and $\widehat{M}={\sum }_{h=1}^H{\widehat{M}}_h$, ${\widehat{N}}_h=\frac{n_h}{t_h}{T}_h$ and $\widehat{N}={\sum }_{h=1}^H{\widehat{N}}_h$.

Note that the estimator, ${\widehat{\theta }}_U$, for the AUC for the finite population is a ratio estimator, so it is biased but is design consistent for the population AUC because the denominator and numerator are unbiased estimators of the denominator and numerator of (1) for the population.

2.3 Estimation of AUC for stratified multistage cluster sampling

Stratified multistage cluster sampling is a commonly used complex sample design for national household surveys. This type of sample design was used for the HHANES. Without loss of generality we will consider stratified two-stage cluster sampling (STSCS) design since it reflects much of the complexity of three or more stage cluster sampling while allowing for more manageable notation.

We consider STSCS where the first stage cluster sampling is conducted independently for each stratum. The sampling rates within stratum can vary depending on the survey requirements. For example, when the population sizes of the first stage clusters, called primary sample units (PSU), are equal, it is reasonable to employ simple random sampling of the clusters and then an equal sample size simple random sample of second stage units from the sampled PSUs. This type of sample design will result in a self-weighted sample. (i.e., where all the sampled second stage units have the same probability of inclusion in the sample). However when the PSU population sizes are unequal, an unequal probability sampling design of first stage may be employed, for example, probability proportional-to- size (population size of the cluster) sampling (PPS) of the PSUs with approximately equal sample size simple random sampling of seconds stage units from the sample PSUs. This design will also result in a self-weighted sample design. Self-weighted or nearly self-weighted sample designs often produce estimates that have smaller variances than estimates from non-self-weighted sample designs [15].

Suppose the finite population has H strata, each stratum h has K_h PSUs and that the population size of subjects in PSU hg is T_hg = N_hg + M_hg, where N_hg and M_hg are the number of diseased and nondiseased subjects, and k_h is the number of PSUs sampled from stratum h, t_hg be the number of subjects sampled from PSU g in stratum h, and t_hg = n_hg + m_hg where n_hg and m_hg are the number of diseased and nondiseased subjects in the sample from sampled PSU hg.

Under a STSCS design, the joint inclusion probability for sampling a pair consisting of diseased and nondiseased subjects is the product of the probability of sampling the PSUs that these subjects belong to multiplied by the probability that these subjects are sampled from these sampled PSUs. For each pair of diseased and nondiseased sampled subjects, these sampled subjects can be sampled (1) from different strata and different sampled PSUs or (2) from the same stratum but different sampled PSUs or (3) from the same stratum and same sampled PSU. Each of these possible samplings of pairs of diseased and nondiseased subjects can have different joint inclusion probabilities. As before the joint sample weight is defined as the inverse of joint inclusion probability, for example, $w_{(hgi,h^{\prime }{g}^{\prime }j)}=1∕{\pi }_{(hgi,h^{\prime }{g}^{\prime }j)}$ for the selection of i-th subject in g-th cluster within h-stratum and j-th subject in g′-th cluster within h′-stratum. The estimator of the AUC for the finite population, $\widehat{\theta }$, is

$${\widehat{\theta }}_U=\frac{1}{\widehat{N}\widehat{M}}\sum _{h=1}^H\sum _{h^{\prime }=1}^H\sum _{g=1}^{K_h}\sum _{g^{\prime }=1}^{K_{h^{\prime }}}\sum _{j=1}^{T_{h^{\prime }{g}^{\prime }}}\sum _{i=1}^{T_{hg}}{w}_{(hgi,h^{\prime }{g}^{\prime }j)}{I}_{(hgi,h^{\prime }{g}^{\prime }j)}{\delta }_{hgi}(1-{\delta }_{h^{\prime }{g}^{\prime }j})\psi (X_{hgi},Y_{h^{\prime },g^{\prime }j})$$ (3)

where $w_{(hgi,h^{\prime }{g}^{\prime }j)}=\frac{K_h}{k_h}\frac{T_{hg}(T_{hg}-1)}{t_{hg}(t_{hg}-1)}$ if h = h′ and g = g′, or $w_{(hgi,h^{\prime },g^{\prime }j)}=\frac{K_h(K_h-1)}{k_h(k_h-1)}\frac{T_{hg}{T}_{h{g}^{\prime }}}{t_{hg}{t}_{h{g}^{\prime }}}$ if h = h′ and g ≠ g′, or $w_{(hgi,h^{\prime }{g}^{\prime }j)}=\frac{K_h{K}_{h^{\prime }}{T}_{hg}{T}_{h^{\prime }{g}^{\prime }}}{k_h{k}_{h^{\prime }}{t}_{hg}{t}_{h^{\prime }{g}^{\prime }}}$ if h ≠ h′. The formula (3) also can be similarly rewritten in matrix notation as given in (2). Formula (3) can be easily extended for PPS sampling of the PSUs by replacing the inverse of the single inclusion probabilities and joint inclusion probabilities according to the PPS sampling scheme that is used.

2.4. Variance Estimation

In this paper we use a jackknife leaving-one-out method and a BRR method for variance estimation of our AUC estimators. A jackknife variance estimator for data from a STSCS design is:

$${\widehat{V}}_{JK}\left({\widehat{\theta }}_U\right)=\sum _{h=1}^H\left[\frac{k_h-1}{k_h}\sum _{g=1}^{k_h}{({\widehat{\theta }}_{\left(hg\right)}-{\widehat{\theta }}_U)}^2\right]$$ (4)

where k_h PSUs are sampled from stratum h and the ${\widehat{\theta }}_{\left(hg\right)}$ are the estimators of the same functional form as ${\widehat{\theta }}_U$, but computed from the reduced sample by omitting the g-th sampled PSU from stratum h [16].

If the STSCS design can be approximated by a design where two PSUs are sampled from each stratum, then as an alternative to the jackknife method is the BRR method for variance. The BRR variance estimator for our sample weighted estimator of AUC is

$${\widehat{V}}_{BRR}\left({\widehat{\theta }}_U\right)=\frac{1}{L}\sum _{l=1}^L{({\widehat{\theta }}_{\left(l\right)}-{\widehat{\theta }}_U)}^2$$ (5)

where L denotes the number of replicates which is the next multiple of 4 greater than the number of sampling strata H of the sample design and the ${\widehat{\theta }}_{\left(l\right)}$ are estimated using half sample replicates determined by a L × L Hadamard matrix [16].

2.5. AUC estimation for domains

Our proposed methods can be extended to ROC curve analysis of domains by including in the estimators an indicator variable to determine whether or not each sampled subject belongs to the specific domain, e.g., for a sample of both males and females each gender would be a different domain. Note that the population structure and sample design remains the same in the domain estimation, so the sample weights are unchanged. We can apply the jackknife or BRR methods for variance estimation in the same way as before.

3. Simutation study

We conducted limited Monte Carlo simulations to study the empirical finite sample properties of our sample weighted estimators of AUC and the proposed jackknife and BRR variance estimators under SSRS and STSCS designs. In sections 3.1 and 3.2 the sample designs are noninformative for estimating the AUC because the sample weights in each stratum are not related to the stratum-specific AUCs. In section 3.3 we consider informative sample weighting. The simulations are repeated 1000 times where after each sample is selected from the finite population of diseased and nondiseased the finite population is regenerated for the next repetition of the simulation.

3.1. Estimation of AUC and Jackknife Variance Estimation under SSRS Designs

A finite population of size of T = 200,000 is generated with H = 8 strata. The population size of each stratum is set to be the same size (T_h = 25,000). In the context of stratified sampling, we assume that stratum-specific infinite population AUC, θ_h, vary across the strata in the range of θ_h = θ ± 0.05. For example, θ_h are assigned values between 0.90 and 1.0 if θ = 0.95. Similar setups are used when we set the AUC for the infinite population at other values, θ = 0.9, 0.8, 0.7, 0.6 or 0.55 respectively. Assume both diseased and nondiseased subjects' test results are randomly generated as normally distributed with a mean of 5 for diseased subjects for each stratum and a mean determined by θ_h for nondiseased subjects, and the variance is set equal to 1 for both diseased and nondiseased for each stratum. We randomly selected t_h = 30, 60, or 120 samples from each stratum independently so that total sample size across all the sampling strata is t = 240, 480, or 960, respectively.

Table I summarizes the simulation results when the disease prevalence (d) is 0.3. It shows the unweighted estimates are less biased than the weighted estimates. As expected, the weighted jackknife standard errors are slightly and consistently larger than unweighted jackknife standard errors because sample weighting usually inflates the variances. With increasing sample size, the ratios of relative bias for weighted and unweighted standard errors become closer to 1, and the difference between weighted and unweighted RMSEs become smaller.

Table I.

The bias for the estiamte results for SSRS, d = 0.3.

θ	t	Bias1*	Bias2*	Bias(JK1)	Bias(JK2)	RMSE1	RMSE2
0.95	960	−0.0015	−0.0033	1.0205	1.0205	0.0146	0.0150
	480	−0.0039	−0.0071	1.0347	1.0347	0.0206	0.0214
	240	−0.0071	−0.0129	1.0608	1.0606	0.0304	0.0324
0.9	960	0.0010	0.0019	1.0135	1.0089	0.0224	0.0224
	480	−0.0039	−0.0056	0.9847	0.9877	0.0328	0.0331
	240	−0.0063	−0.0096	1.0658	1.0655	0.0460	0.0468
0.8	960	−0.0016	−0.0014	1.0251	1.0282	0.0319	0.0319
	480	−0.0039	−0.0065	1.0128	1.0128	0.0470	0.0474
	240	0.0073	0.0100	1.0369	1.0367	0.0682	0.0688
0.7	960	−0.0003	0.0008	1.0347	1.0347	0.0375	0.0375
	480	−0.0026	0.0030	1.0350	1.0349	0.0544	0.0545
	240	0.0055	0.0084	1.0806	1.0802	0.0771	0.0777
0.6	960	0.0025	0.0031	1.0218	1.0218	0.0413	0.0414
	480	0.0044	0.0046	1.0847	1.0863	0.0557	0.0558
	240	0.0097	0.0123	1.2465	1.2468	0.0717	0.0724
0.55	960	0.0028	0.0034	1.1927	1.1927	0.0359	0.0360
	480	0.0054	0.0088	1.3268	1.3260	0.0459	0.0465
	240	0.0109	0.0142	1.4992	1.4983	0.0599	0.0609

Note:

^*1 = unweighted estimator, 2 = weighted estimator.

$\text{Bias}1=\widehat{\theta }1-\theta$, $\text{Bias}2=\widehat{\theta }2-\theta$, Bias(JK1)=SE(JK1)/SE(EMP1), Bias(JK2)=SE(JK2)/SE(EMP2), SE = standard error, JK = jackknife variance estimate, EMP = empirical variance estimate, RMSE = root of mean squared error.

3.2. Estimation of AUC and Jackknife and BRR Variance Estimation under STSCS Designs

In this section, Monte Carlo simulations are performed to study the estimators of AUC and to compare the accuracy of jackknife and BRR methods for variance estimation of the estimated AUC under STSCS designs. To reflect the sample design of HHANES that we apply our proposed approach in the next section, i.e., we simulate STSCS datasets with unequal strata sizes of PSUs and unequal sizes of PSUs within each stratum. A finite population size T = 200,000 is generated with H = 8 strata (i.e., the number of strata in HHANES), and stratum sizes varying from 15,000 to 35,000. Each stratum is composed of 10 unequal sized PSUs. We let the θ_h vary across the strata in the range of θ_h = θ ± 0.1, where θ is chosen from 0.9 to 0.6 by 0.1. Intra-cluster correlations (ICCs, ρ) for the PSUs vary from ρ = 0 or 0.2. The total sample sizes drawn from the population are, t = 400, 800, or 1200. At the first stage, 2 of 10 clusters are selected without replacement from each stratum by using probability proportional to size (PPS), where the size measure is the PSU population size and a specified number of subjects are chosen from the selected PSU within each stratum.

From Table II, we obtain similar findings as we got from Table I. In addition, we can see that the biases of the jackknife standard errors, particularly for weighted estimators, are consistently slightly smaller than the biases of the standard errors from BRR method. With increasing sample size, the bias of the standard errors decreases and the standard errors from BRR become closer to jackknife standard errors. Overall in this simulation, jackknife variance estimation performs better than BRR variance estimation, as indicated by the jackknife standard errors being closer to empirical standard errors than are the BRR standard errors. Simulations were done for larger numbers of strata i.e., H = 16 and 32, and as expected increasing numbers of strata, which increases the number of degrees freedom for variance estimation, show that both the jackknife and BRR methods perform better, and the BRR variances become closer to jackknife variances (data not shown).

Table II.

Simulation results for the comparison of jackknife method and BRR method for variance estimates under STSCS design, ρ =0 or 0.2.

θ	t	Bias1*	Bias2*	Bias(BRR1)	Bias(BRR2)	Bias(JK1)	Bias(JK2)	RMSE1	RMSE2
ρ = 0
0.9	1200	0.0002	0.0044	1.0103	1.1212	1.0103	1.0505	0.0097	0.0108
	800	−0.0003	0.0070	1.0336	1.2195	1.0336	1.0894	0.0119	0.0142
	400	0.0004	0.0172	1.1059	1.2813	1.0765	1.1711	0.0170	0.0254
0.8	1200	−0.0006	0.0032	1.0519	1.0949	1.0519	1.0730	0.0135	0.0141
	800	0.0004	0.0069	1.0058	1.1086	1.0058	1.0457	0.0172	0.0188
	400	−0.0008	0.0136	1.0398	1.1416	1.0199	1.0892	0.0251	0.0301
0.7	1200	0.0004	0.0037	1.0184	1.0606	1.0184	1.0424	0.0163	0.0169
	800	0.0001	0.0056	1.0049	1.0870	1.0049	1.0531	0.0203	0.0215
	400	0.0005	0.0122	1.0279	1.1677	0.9930	1.0968	0.0287	0.0333
0.6	1200	0.0023	0.0034	1.0479	1.0447	1.0060	1.0279	0.0169	0.0182
	800	0.0042	0.0044	1.1472	1.0848	1.0508	1.0670	0.0201	0.0229
	400	0.0134	0.0103	1.2370	1.1722	1.1575	1.1057	0.0287	0.0347
ρ = 0.2
0.9	1200	−0.0108	−0.0062	1.1715	1.2805	1.1102	1.2000	0.0160	0.0171
	800	−0.0126	−0.0152	1.1750	1.3086	1.0809	1.2057	0.0185	0.0231
	400	−0.0134	−0.0189	1.2751	1.3633	1.1005	1.2245	0.0231	0.0309
0.8	1200	−0.0115	−0.0066	1.1553	1.2623	1.0987	1.1882	0.0191	0.0197
	800	−0.0121	−0.0168	1.2111	1.2963	1.1122	1.2130	0.0217	0.0273
	400	−0.0137	−0.0176	1.2323	1.3115	1.1181	1.2230	0.0289	0.0352
0.7	1200	−0.0084	−0.0053	1.1219	1.2103	1.0698	1.1495	0.0191	0.0201
	800	−0.0091	−0.0113	1.1900	1.2516	1.0950	1.1911	0.0220	0.0252
	400	−0.0102	−0.0145	1.2610	1.4058	1.1397	1.2981	0.0291	0.0344
0.6	1200	−0.0027	0.0022	1.2108	1.2632	1.0723	1.1368	0.0168	0.0191
	800	0.0083	−0.0038	1.2741	1.2937	1.1015	1.1429	0.0214	0.0241
	400	0.0109	−0.0058	1.2857	1.3050	1.2231	1.1880	0.0274	0.0356

Note:

^*1 = unweighted estimator, 2 = weighted estimator.

$\text{Bias}1=\widehat{\theta }1-\theta$, $\text{Bias}2=\widehat{\theta }2-\theta$, Bias(BRR1) = SE(BRR1)/SE(EMP1), Bias(BRR2) = SE(BRR2)/SE(EMP2), Bias(JK1)=SE(JK1)/SE(EMP1), Bias(JK2)=SE(JK2)/SE(EMP2), SE = standard error, EMP = empirical variance estimates, RMSE = root of mean squared error.

3.3 Informative Sampling

In this section we consider informative sampling where the selection probabilities are related to the AUC, i.e., related to the level of sensitivity and specificity. The following simulation study illustrates that unweighted analyses, i.e., ignoring the informativeness of the sample weights, can lead to biased AUC estimation. We consider a STSCS with equal size strata and equal size PSUs. The population parameters are set to: T = 200000, H = 8, K = 100, and θ_h = θ ± 0.1, where θ = 0.9, 0.8, 0.7, or 0.6, ρ = 0 or 0.2. The test results from diseased and nondiseased subjects are normally distributed. The mean for diseased subjects is equal 5 and the variance is equal to 1, while the mean of nondiseased subjects depend on θ_h and the variance is equal to 1.

Total sample size varies from t = 320, 400 to 800, respectively. First, 10 of 100 PSUs are randomly selected from each stratum, then within each stratum a fixed number of subjects are drawn from each selected PSU. The sample size for each stratum th is depended on the value of θ_h. In this simulation, we arbitrarily set the selection probabilities (SP) for each stratum differently, SP = (0.25, 0.25, 0.1, 0.1, 0.1, 0.1, 0.05, 0.05) for the 8 strata, where strata with high θ_h have larger sample sizes.

The results for informative survey sampling for STSCS show that the unweighted estimates of AUC are badly biased, which illustrates the critical role of sample weights in survey data analysis for informative survey sampling (table III). As expected, because of the large sample weights, the weighted standard errors are much larger than the unweighted standard errors.

Table III.

Bias of unweighted estimator under informative sampling, ρ =0 or 0.2.

θ	t	Bias1*	Bias2*	SE(JK1)	SE(JK2)	SE(EMP1)	SE(EMP2)	RMSE1	RMSE2
ρ = 0
0.9	800	0.0329	0.0021	0.0104	0.0231	0.0087	0.0199	0.0339	0.0200
	400	0.0335	0.0014	0.0132	0.0382	0.0109	0.0323	0.0352	0.0323
	320	0.0336	−0.0027	0.0151	0.0396	0.0149	0.0353	0.0368	0.0354
0.8	800	0.0336	0.0014	0.0160	0.0259	0.0153	0.0238	0.0369	0.0239
	400	0.0322	0.0017	0.0214	0.0408	0.0225	0.0376	0.0393	0.0376
	320	0.0339	0.0023	0.0238	0.0392	0.0235	0.0360	0.0412	0.0361
0.7	800	0.0336	0.0027	0.0191	0.0278	0.0217	0.0304	0.0400	0.0305
	400	0.0324	0.0026	0.0265	0.0399	0.0256	0.0351	0.0412	0.0352
	320	0.0337	0.0046	0.0291	0.0424	0.0271	0.0394	0.0432	0.0397
0.6	800	0.0345	0.0026	0.0219	0.0283	0.0230	0.0304	0.0415	0.0305
	400	0.0321	0.0029	0.0293	0.0454	0.0318	0.0410	0.0452	0.0411
	320	0.0347	−0.0074	0.0333	0.0440	0.0320	0.0418	0.0472	0.0424
ρ = 0.2
0.9	800	0.0147	−0.0056	0.0127	0.0236	0.0118	0.0217	0.0189	0.0224
	400	0.0173	−0.0065	0.0156	0.0356	0.0142	0.0321	0.0224	0.0327
	320	0.0214	−0.0102	0.0172	0.0366	0.0154	0.0314	0.0264	0.0330
0.8	800	0.0169	−0.0067	0.0170	0.0264	0.0172	0.0243	0.0241	0.0252
	400	0.0205	−0.0081	0.0236	0.0385	0.0218	0.0347	0.0299	0.0357
	320	0.0218	−0.0113	0.0264	0.0409	0.0260	0.0400	0.0339	0.0416
0.7	800	0.0139	−0.0080	0.0198	0.0279	0.0181	0.0276	0.0229	0.0287
	400	0.0202	−0.0083	0.0277	0.0399	0.0292	0.0371	0.0355	0.0380
	320	0.0218	−0.0112	0.0307	0.0430	0.0309	0.0376	0.0378	0.0393
0.6	800	0.0213	−0.0065	0.0207	0.0285	0.0234	0.0308	0.0316	0.0315
	400	0.0207	−0.0111	0.0289	0.0407	0.0272	0.0314	0.0343	0.0333
	320	0.0224	−0.0118	0.0327	0.0444	0.0348	0.0447	0.0414	0.0462

Note:

^*1 = unweighted estimator, 2 = weighted estimator.

$\text{Bias}1=\widehat{\theta }1-\theta$, $\text{Bias}2=\widehat{\theta }2-\theta$, SE = standard error, JK = jackknife variance estimate, EMP = empirical variance estimate, RMSE = root of mean squared error.

4. Application

4.1. Hispanic Health and Nutrition Examination Survey (HHANES)

The HHANES was conducted by National Center for Health Statistics [17, 18], between 1982 and 1984 to assess the health and nutritional status of Hispanic subjects aged 6 months to 74 years in specific area of the U.S. A four- stage sampling design was used: (1) PSUs consisting of counties or small groups of contiguous counties are sampled from each stratum at the first stage, (2) area segments (a city block or group of blocks in urban areas, or geographic subareas in rural areas) are selected within sampled PSUs at the second stage, (3) households are selected within sampled area segment at the third stage, and (4) subjects are sampled within sampled households at fourth stage of sampling [17]. The PSUs and segments were stratified prior to sample selection. The sample design had 8 pseudo-strata each with 2 pseudo-PSUs. We used the pseudo-strata as strata and pseudo-PSUs as PSUs in the variance estimation as recommended by the National Center for Health Statistics.

We compare the discrimination of three predictors, self-reported body mass index (BMI) and measured triceps skinfold and subscapular skinfold, for classifying subjects as overweight/obese using data from the Mexican-American portion of the HHANES. The measured BMI served as a gold standard [19, 20]. Overweight/obesity was determined for children (aged 2 to 18 years old) by using age- and sex- specific growth charts [21]. For adults (≥ 18 years old) overweight/obesity was defined as having a measure BMI, i.e., weight in kilograms divided by height in meters squared, of greater than or equal to 25.

4.2. Joint inclusion probability

At the last stage of sampling in HHANES the probability of selection of an individual within a sampled household depended on age: 75% for from 6 months to 19 years, 50% for 20 to 44 years and 100% for 45 to 74 years. Those subjects younger than 2 years old are excluded in this data analysis due to undetermined overweight/obese status. Thus, the conditional inclusion probabilities for the sampled subjects within j-th family in i-t PSU from stratum h were = 0.75, 0.5, or 1.0 aged from 2 to 19, 20 to 44, and 45 to 74 years respectively. The final sample weight for each sampled individual (w_hijs) is provided with the HHANES data. These sample weights take into account the inclusion probability at each stage of sampling, i.e., the unequal probability of selection and nonresponse and poststratification adjustments. Therefore, the sample weight for an individual will not equal to the inverse of the inclusion probability, i.e., $w_{hijs}\ne {\left({\pi }_{hij}{\pi }_{s\mid hij}^{∕}\right)}^{-1}$. We approximated inclusion probabilities of the sampled household as [22]:

$${{\pi }_{hij}}^{\ast }={\left(\frac{1}{m_{hij}}\sum _{s=1}^{m_{hij}}{w}_{hijs}{\pi }_{s\mid hij}\right)}^{-1}$$ (6)

where m_hij is the sample size of the hij sampled household. Given the household has been, the joint inclusion probabilities was approximated by assuming Poisson sampling as ${{\pi }_{st\mid hij}}^{\ast }={{\pi }_{s\mid hij}}^{\ast }{{\pi }_{t\mid hij}}^{\ast }$, where ${{\pi }_{s\mid hij}}^{\ast }=w_{hijs}{{\pi }_{hij}}^{\ast }$. Then the joint weight is:

$$w_{(hihs,hijt)}={\left({{\pi }_{st\mid hij}}^{\ast }{{\pi }_{hij}}^{\ast }\right)}^{-1}$$ (7)

4.3. Results

Table 4 compares the discrimination of three predictors for overweight/obese for both un- weighted estimators and weighted estimators. It shows that after taking into account the sample weights, the self-reported BMI (“BMIsf”) has the highest estimated AUC values among the predictors, although the unweighted AUC (“AUC1”) for subscapular skinfold (“SubScap”) is slightly higher than that of self-reported BMI. The triceps skinfold (“Tri- ceps”) has the lowest prediction in this application. Table IV also shows that the weighted jackknife standard errors are slightly larger than unweighted jackknife standard errors due to the sample weights being incorporated in the estimation. Overall the results across the unweighted and weighted estimators are very close, which indicates the sample weighting is not very informative in this example. However there is essentially little loss in precision by using the weighted estimation.

Table IV.

Estimate of AUC for three predictors of overweight/obese.

Predictor	AUC1*	SE(JK1)	AUC2*	SE(JK2)
BMIsf	0.897	4.94E-03	0.911	5.59E-03
SubScap	0.899	3.57E-03	0.893	3.64E-03
Triceps	0.812	5.12E-03	0.789	5.51E-03

^*Note: 1=unweighted estimator; 2=weighted estimator.

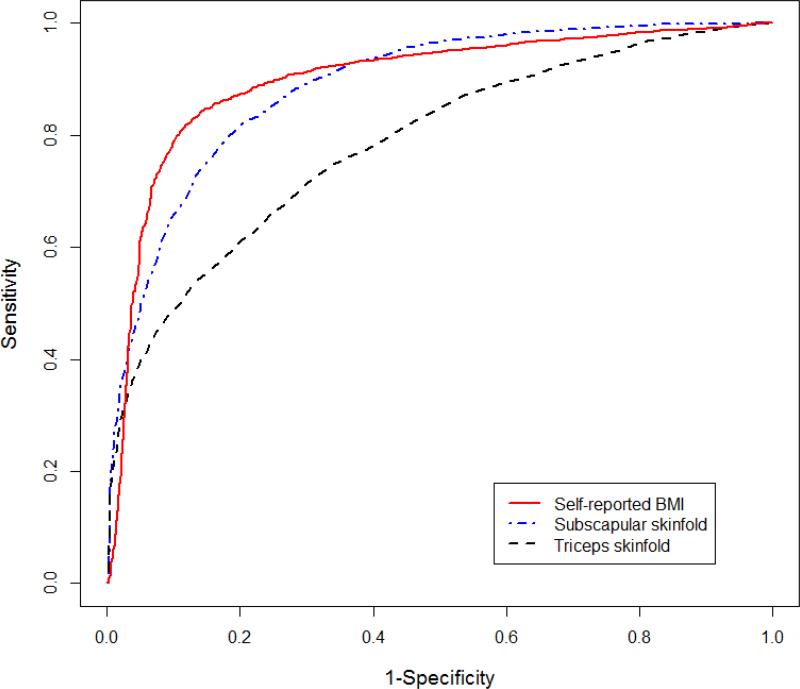
Figure 1 shows the ROC curve for self-reported BMI, subscapular skinfold and triceps skinfold. The ROC curve for subscapular skinfold lies completely above the curve for triceps skinfold, so that the results support that the subscapular skinfold is a better predictor of overweight/obese than the triceps skinfold. Upon examination of the figure, self-reported BMI is not a consistently better predictor across all decision thresholds although self-reported BMI has a higher estimated AUC. The figure implies that self-reported BMI is a better predictor in the range where the sensitivity is above 50% and simultaneously where the specificity is above 70%, which is often the range of interest.

Figure 1.

The comparison of area under ROC curves for self-reported BMI, subscapular skinfold and triceps skinfold.

We applied the extended formula for domain estimation to HHANES data to estimate AUC and its variance for domains of females and males who were 20 - 74 years old to see how prediction of overweight/obese status for our three predictors differ by gender-age-specific domains. Interestingly, all three predictors of overweight/obese for the female domain have better classification than the male domain, for both weighted and unweighted estimators, i.e., AUCs in female domain are larger than those in male domain, and the variances of these three predictors for both weighted and unweighted AUCs in female domain are also smaller (Table V). In both adult male and female domains, the self-reported BMI is the best predictor of overweight/obese among the three predictors in HHANES.

5. Discussion

In survey research, complex sample designs with sample weighting, sample stratification and cluster sampling are commonly implemented. Analyses that do not account for weighting and clustering effects that are induced by the complex survey sampling can be biased and have incorrect standard errors. In this paper, we proposed an extension of the nonparametric method for estimation of the population AUC for complex survey data. The proposed estimator is a ratio estimator, and is consistent for estimating the population AUC. Simulation results indicate that our approach provides consistent estimates of the population AUC and its standard error. Since the estimation is based on paired subjects, the joint sample weights are required, which can be difficult to obtain for complex survey designs, so some assumptions have to be made to derive the joint sampling weights from the sample design information described in the survey documentation. For example in the application of the HHANES data, we made an assumption of Poisson sampling of subjects within each sampled family in the HHANES. It would be desirable for survey organizations to provide on their public use files joint survey weights for estimation problems that require these weights. We applied replication methods for variance estimation, which are conceptually simple and easy to program, but computational intensive for surveys with large numbers of PSUs.

Previous work has considered stratified analyses to adjust the estimate of the AUC for important factors such as center effects in multicenter studies [23] and study effects in meta-analyses [24]. In these papers stratum-specific AUC's are computed and then the AUC's are combined across strata by basically weighting by the inverse of the precision of the stratum-specific AUC's. When the distribution of the test values differ between the stratum, the AUC that is estimated under this type of weighted estimation will, in general, be biased for estimating the AUC for the population, θ. In contrast for SSRS our estimator ${\widehat{\theta }}_U$ differs in that we are obtaining approximately unbiased estimates of the AUC for the population from which the sample is selected. This is accomplished by using the joint and individual sample weights (i.e., the inverse of the joint and single inclusion probabilities) to obtain a weighted number of all pairs of test values of diseased and nondiseased sampled subjects and to obtain weighted numbers of sampled diseased and nondiseased subjects for the numerator and denominator of ${\widehat{\theta }}_U$ in (2), respectively. In other words our estimator ${\widehat{\theta }}_U$ pools the observations across the sampling strata utilizing all pairs of diseased and nondiseased subjects to estimate the population AUC, where as the previous stratified AUC estimators utilize only the pairs of diseased and nondiseased observations for sampled subjects within each stratum for computing the stratum-specific AUC's. Thus ${\widehat{\theta }}_U$ is not a weighted average of stratum-specific AUC's as are previous estimators [23, 24], and the previous estimators of AUC and ${\widehat{\theta }}_U$ will asymptotically agree when the distributions of the test values of the diseased and nondiseased subjects are the same across the strata. Moreover our methods are applicable to more complex sampling designs that combine stratified and multistage cluster sample designs that are not considered by the aforementioned previous work.

In future work, we plan to consider other more computationally efficient approaches for variance estimation, such as Taylor linearization variance estimation. Also we plan on ex- tending the estimation of the AUC for the ROC curves to estimation based on parametric and semi-parametric disease prediction models that are fitted to data from complex sample designs.

Table V.

Estimate of AUC in adult male and female domains.

	Male ≥ 20 yrs				Female ≥ 20 yrs
Predictor	AUC1*	SE(JK1)	AUC2*	SE(JK2)	AUC1*	SE(JK1)	AUC2*	SE(JK2)
BMIsf	0.9348	6.68E-03	0.9362	6.80E-03	0.9645	4.10E-03	0.9652	4.19E-03
SubScap	0.8748	8.99E-03	0.8749	9.19E-03	0.8911	7.46E-03	0.8908	7.64E-03
Triceps	0.7714	1.18E-02	0.7609	1.27E-02	0.8706	8.31E-03	0.8653	8.53E-03

Note: 1=unweighted estimator; 2=weighted estimator.