Evaluating measurement error in readings of blood pressure for adolescents and young adults

Abstract

Readings of blood pressure are known to be subject to measurement error, but the optimal method for combining multiple readings is unknown. This study assesses different sources of measurement error in blood pressure readings and assesses methods for combining multiple readings using data from a sample of adolescents/young adults who were part of a longitudinal epidemiological study based in Cebu, Philippines. Three sets of blood pressure readings were collected at 2-year intervals for 2127 adolescents and young adults as part of the Cebu National Longitudinal Health and Nutrition Study. Multi-trait, multi-method (MTMM) structural equation models in different groups were used to decompose measurement error in the blood pressure readings into systematic and random components and to examine patterns in the measurement across males and females and over time. The results reveal differences in the measurement properties of blood pressure readings by sex and over time that suggest the combination of multiple readings should be handled separately for these groups at different time points. The results indicate that an average (mean) of the blood pressure readings has high validity relative to a more complicated factor-score-based linear combination of the readings.

Introduction

Biomarkers are increasingly included in surveys used by population researchers, and prominent among these biomarkers are blood pressure readings. High blood pressure is related to cardiovascular disease (a leading cause of death around the world), strokes and kidney disease. As population researchers incorporate blood pressure readings into their analyses, it is important to understand the quality of these measurements. The aim of this study is to evaluate measurement error in blood pressure readings at three time points spanning 6 years among adolescents and young adults who were part of a longitudinal epidemiological study.

To help address random fluctuations in blood pressure, it has long been thought that multiple readings of blood pressure are preferable to a single reading (1). In addition to random fluctuations, however, numerous studies have demonstrated that blood pressure readings are influenced by a number contextual factors, including the device used for measurement (2,3), the time of year (4) and potential sources of stress such as the “white coat” effect or the timing of measurement (5) among others. Furthermore, blood pressure readings are subject to recording errors with digit preference the most frequently studied source (3,6–8). Little is known about how these sources of measurement error or the measurement properties of blood pressure readings vary over time or across males and females. Furthermore, little is known about the measurement properties of blood pressure readings among adolescents/young adults participating in an epidemiological study in a low-income country.

Multi-trait, multi-method (MTMM) structural equation models in different groups have been used to evaluate measurement error in blood pressure readings (9). These models decompose the variance in readings of blood pressure into components representing “true” blood pressure, random fluctuations and systematic error. One study using MTMM models with data from elderly patients in Spain found that the second blood pressure reading had the best relationship with “true” blood pressure and that a linear combination of the readings using factor score weights had better measurement properties than an average (mean) of the readings (9).

This study adopts an analytic approach based on MTMM models to evaluate measurement error in blood pressure readings using data from the Cebu Longitudinal Health and Nutrition Survey (10), a longitudinal epidemiological study based in Cebu, Philippines. The analysis is guided by four research questions concerning measurement error that address gaps in our knowledge of the measurement properties of blood pressure readings. First, are there any differences in the measurement properties of the first, second or third readings obtained during a single session? Second, are there any differences in the measurement properties of the three readings across the three waves of data? Third, are there any differences in the measurement properties of the three readings for females and males? Finally, are there any differences in the measurement properties of an average of the three readings compared with a linear combination based on factor scores?

This is the first study to evaluate measurement error in readings of blood pressure: (i) among adolescents/young adults, (ii) with a sample from a low-income country, and (iii) across three waves of data. Given the centrality of blood pressure as a measure of adult health, it is important to understand the measurement properties of blood pressure readings across a range of contexts and how best to operationalize blood pressure for analysis.

Methods

Data

The data for our analysis are drawn from the Cebu Longitudinal Health and Nutrition Survey (CLHNS) (10). The CLHNS began with an initial survey in 1983–1984 of 3327 expectant mothers in 33 randomly selected communities located in the Cebu, Philippines metropolitan area. The mothers and their children were periodically resurveyed to capture processes of infant and adolescent development as well as changing family circumstances. Beginning in the 1998–1999 wave and continuing in the 2002 and 2005 waves of the survey, blood pressure measurements of the participants were collected. During these waves, the adolescents/young adults were respectively aged 14–16, 16–18 and 20–22 in the final wave.

A standard procedure was used for obtaining blood pressure measurements from each of the respondents. During home visits, respondents were measured after a 10-min seated rest. Interviewers trained by physicians took the three measurements using a mercury sphygmomanometer and appropriate cuff sizes. Consent for participation in the study was obtained from the mothers when participants were adolescents and from the participants themselves when they were 18 or older.

Analysis sample

The sample for this analysis consists of 2127 cases (1015 females and 1112 males) with blood pressure readings for at least one of the three waves of data. Over 80% of the cases have blood pressure readings for all three waves. We excluded blood pressure readings from pregnant females. The sample sizes for the individual waves range from 2087 at wave 1 to 1966 at wave 2 and 1812 at wave 3. The adolescents and young adults primarily lived in the Cebu metropolitan area and they ranged in socio-economic resources from poor to reasonably well off.

Blood pressure readings

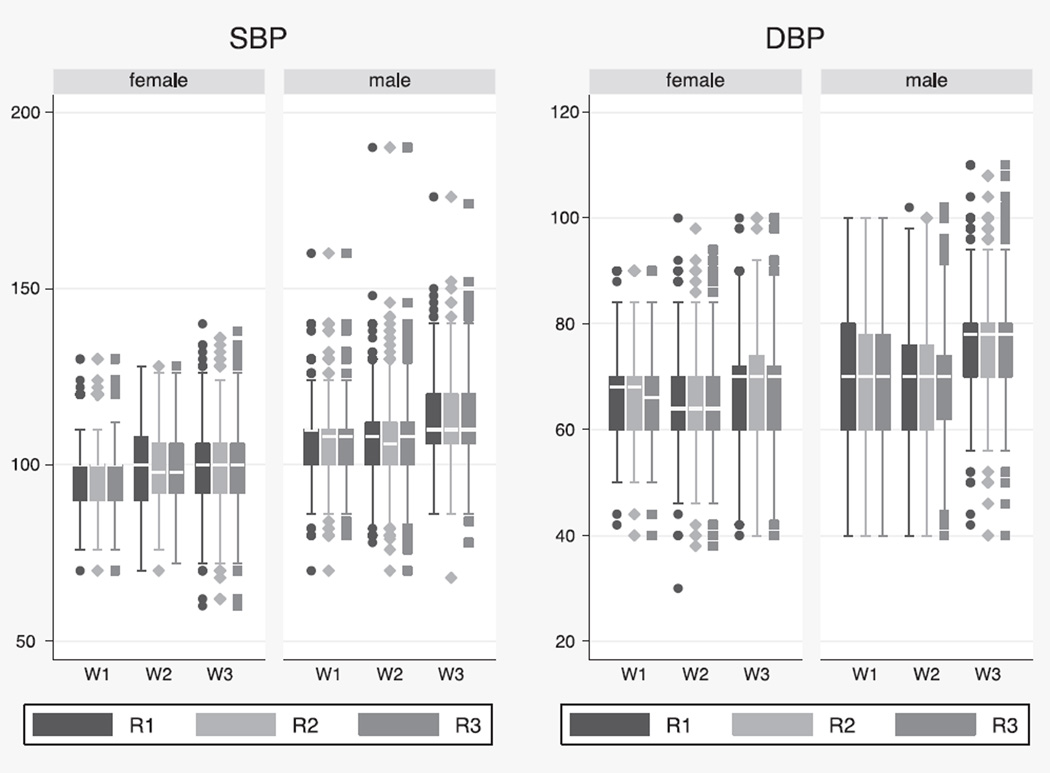
Figure 1 provides box plots to illustrate the distributions of the three readings of systolic and diastolic blood pressure across the three waves of data separately for females and males. For systolic blood pressure among both females and males, we see similar distributions across the three readings within each wave. Across waves, median systolic blood pressure appears to be slightly increasing for females and males and the variance is increasing for females. For diastolic blood pressure, we also observe similar distributions across readings for females and males within waves. Once again, across waves, median diastolic blood pressure appears to be slightly increasing for females and males, particularly by wave 3, and the variance appears to be increasing for females. Blood pressure increases with height as well as weight in children, adolescents and young adults, and would therefore be expected to increase over the period covered by the study.

Figure 1.

Box plots for blood pressure readings over time by sex. W1, W2 and W3 reference waves 1, 2 and 3, and R1, R2 and R3 reference readings.

Analytic approach

We rely on MTMM models to address our research questions concerning the measurement properties of the blood pressure readings. Conceptually, MTMM identify different sources of variation in blood pressure readings that can be attributed to “true” blood pressure (i.e. what the readings are intended to capture), systematic error (e.g. higher or lower readings attributable to a measurement device), and random fluctuations. Multiple-group MTMM models allow for the sources of variation to be identified separately for different population subgroups. Information about the different sources of variation can then be used to assess the extent of measurement error and the measurement properties of blood pressure readings.

For our first analysis, we specify separate MTMM models for females and males and for each wave of blood pressure readings. The two traits in our MTMM models are systolic and diastolic blood pressure. The three methods in our MTMM models are the three readings. The three method factors permit us to capture systematic error in systolic and diastolic readings for each measurement occasion. MTMM models allow us to decompose the variance in each of the individual blood pressure readings into components attributable to “true” systolic or diastolic blood pressure, systematic error associated with each reading occasion, and random error (sometimes referred to as unique factors) associated with each individual reading.

Our MTMM models can be written as

$$x_{ijk}={\mathrm{\alpha }}_{jk}+{\mathrm{\lambda }}_{Tjk}{\xi }_{Tik}+{\mathrm{\lambda }}_{Mjk}{\xi }_{Mij}+{\mathrm{\delta }}_{ijk}$$ (1)

wherex_ijk is the blood pressure reading for traitk (systolic or diastolic blood pressure) with methodj (reading 1, 2 or 3) for theith subject. The ξ_Tik are the latent trait variables representing “true” systolic and diastolic blood pressure. The factor loadings, λ_Tjk, give the effects of underlying blood pressure on the readings. The ξ_Mij are the latent method variables representing the shared variance for the three reading occasions and the factor loadings, λ_Mjk, give the effects of the reading occasions on the readings. The α_jk are intercepts that capture any systematic differences in the means of the blood pressure readings. The δ_ijk are the random error terms for the blood pressure readings that we assume have means of zero and are uncorrelated with the ξ values.

To ensure the model is identified we constrain the factor loadings for the methods factors to equal 1 and we scale the trait factors to the second reading of systolic and diastolic blood pressure respectively by setting these factor loadings equal to 1. We chose the second reading of blood pressure because it has been found to be more reliable than the first or third readings (9). Finally, we constrain the method factors to be uncorrelated with each other and with the latent traits. This set of constraints is consistent with a MTMM model where the number of traits does not equal the number of methods (11). In the following analyses, we refer to this specification as the initial model.

To address our first research question, we impose additional constraints to test for relative bias across the readings. The first set of additional constraints involves setting the remaining free factor loadings for systolic and diastolic blood pressure to equal 1. The second additional set of constraints involves setting the intercepts, α_jk, equal to 0. These restrictions imply that the intercepts and slopes relating the blood pressure reading to the latent blood pressure are the same across the three occasions. We assess the fit of the models using an array of fit statistics and indices, including the overall chi-square test statistic (12), the Bayesian information criterion (BIC) (13,14), the root mean squared error of approximation (15), the Tucker–Lewis index (16) and the comparative fit index (17). The fit statistics and indices preferred the same model in all analyses, so we only report the BIC.

Our second research question concerns testing for measurement invariance across waves. To conduct these tests, we specify a confirmatory factor analysis (CFA) model that combines the preferred MTMM models from the first analysis from each of the waves separately for females and males. In the CFA model, we allow all of the latent trait variables for systolic and diastolic blood pressure across the waves to be correlated, but we maintain the restriction that the method factors at each wave are uncorrelated with each other, with the method factors across waves, and with all of the latent trait variables. We refer to this specification as the initial CFA model.

For this analysis, we maintain all of the cases by using a casewise maximum likelihood estimator (18). To test for measurement invariance across waves we consider two sets of constraints. The first set constrains the random error variances for the respective blood pressure readings to be equal across waves. The second set constrains the variances of the method factors to be equal across waves.

To test for measurement invariance across females and males, we place the preferred CFAs from our second analysis into a multiple-group (MG) framework with groups defined by sex. We continue to use a casewise maximum likelihood estimator to maintain all of the cases in this analysis. The initial MG CFA model allows for all of the free parameters to vary by sex. We consider a similar set of constraints with the analysis of measurement invariance across waves. First, we test whether the random error variances are equal for females and males. Second, we test whether the method factor variances are equal for females and males.

Our final research questions involves assessing the measurement properties of an average of the three readings compared with a weighted average based on factor scores from the best MTMM models from the first analysis. To assess the two approaches to constructing linear combinations of the readings we rely on a measure of validity given by

$$Q=1-\frac{\sum w_{jk}^2{\mathrm{\theta }}_{jk}+\sum w_{jk}^2{\mathrm{\varphi }}_{mj}+\sum 2w_{jk}{w}_{j\prime k}{\mathrm{\varphi }}_{Mj}}{\text{var}(\sum |w_{jk}{x}_{ijk})}$$ (2)

wherew_jk are weights, θ_jk are the error variances for each reading, and φ_Mj are the variances of the method factors (9). The weights are determined by the factor scores or set to appropriate values for the average. For instance, for the average of the three systolic blood pressure readings, when k equals 1 the weights are 1/3 and when k equals 2 the weights are 0.

Results

The first research question concerns whether there are any differences in the measurement properties of the first, second and third readings. We begin by testing for differences in the measurement properties across the readings by first constraining the factor loadings for the latent systolic and diastolic blood pressure variables (the latent trait variables) to all equal 1 and then constraining the intercepts for each of the readings to equal 0.Table I provides model fit statistics for the initial MTMM model and then the two restricted versions of the initial model separately for females and males and for each of the waves.

Table I.

Bayesian information criteria (BICs) for separate multiple-group, multi-trait, multi-method (MTMM) models by sex and wave.

	Female
	Wave 1	Wave 2	Wave 3
M1: initial MTMM model	−32.40	−21.21	−28.91
M2: trait loadings set to 1	−54.00	−43.79	−47.87
M3: M2 + intercepts set to 0	−76.36	−56.68	−69.42
	Male
	Wave 1	Wave 2	Wave 3
M1: initial MTMM model	−17.89	−27.26	−25.73
M2: trait loadings set to 1	−35.35	−44.05	−50.17
M3: M2 + intercepts set to 0	−47.71	−59.56	−62.11

Negative BICs indicate good model fit. A difference in BICs between a restricted and unrestricted model of more than 0 indicates “very strong” support for the restricted model (14).

We find that the initial MTMM models have a good fit with the data for both females and males across all three waves as indicated by the negative BICs. We can compare the BICs across the restricted models – model 2 restricts the trait loadings to equal 1 and model 3 further restricts the intercepts to equal 0. A difference in BICs of more than 10 indicates “very strong” support for the restricted model (14). We find that both setting the trait loadings to 1 and the intercepts to 0 results in models that are consistent with the data and preferred over the models that allow the trait loadings and intercepts to be estimated for females and males at all three waves. These results suggest that there are no differences in the measurement properties with respect to how the three readings relate to “true” blood pressure. We adopt the MTMM models with factor loadings constrained to 1 and intercepts constrained to 0 in the following analyses.

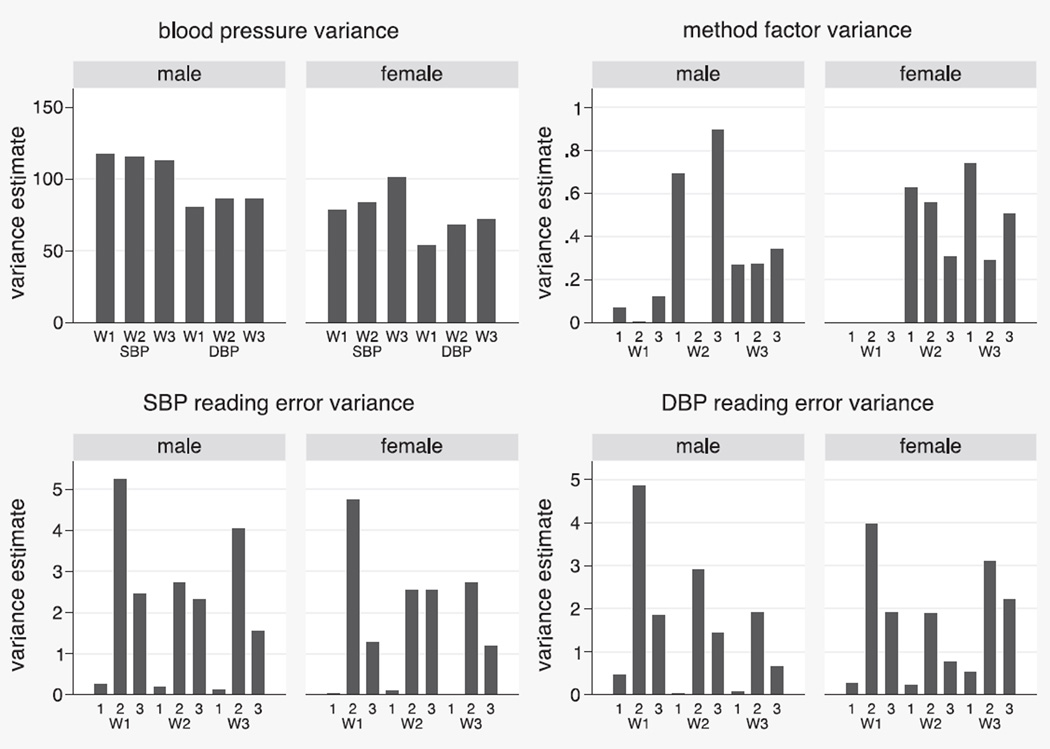
Figure 2 illustrates the estimates for the variances (the y-axis) of “true” blood pressure, the reading occasion method factors (systematic error variance), and the error variances associated with each reading (random error variance) from the preferred MTMM models. The estimated variances of “true” blood pressure are much greater than either the systematic or random error variances for both females and males across all waves. Second, the systematic error variances (method factor variances) are notably less than the individual readings error variances. Third, there is a significant degree of variation among the variance estimates across females and males and over time. We find larger method factor variances at waves 2 and 3 than at wave 1, larger error variances at waves 2 and 3 than at wave 1, and larger error variances for males than females. Fourth, it is notable that there is virtually no method factor variance for females at wave 1. We are unaware of any aspects of the data collection that could explain this pattern, particularly since it is not present among males at the same wave.

Figure 2.

Estimates of variance for “true” blood pressure, method factors and individual readings of blood pressure. The numbers on thex-axis in the panel for method factor variances refer to method factors 1, 2 and 3. The numbers on thex-axis for the SBP and DBP reading error variances refer to readings 1, 2 and 3. W1, W2 and W3 reference waves 1, 2 and 3 in all panels.

The second research question concerns whether the measurement properties of the three readings differ across waves. For this analysis, we specify separate CFA models for females and males that combine the restricted version of the MTMMs from each wave. As with the individual MTMM models, we find that the initial CFA MTMM models have a good fit with the data as indicated by negative BICs (− 782.40 for females and − 747.08 for males). The model fit, however, deteriorates substantially with either constraining all of the method and error variances to be equal over time or just constraining the method variances to be equal over time. For both females and males, the BICs show that the initial CFA MTMM model is very strongly preferred over either of the restricted models. This finding indicates that the extent of systematic and random error variance varies across waves and thus the measurement properties of the three readings are not stable over time.

Our third research question concerns whether the measurement properties of the readings vary by sex. We address this question by specifying a multiple-group version of the CFA MTMM models discussed above with the groups defined by sex. As with the CFA MTMM models we find that the initial model has a reasonable fit with the data (BIC = − 1716.91). Both of the restricted models, however, result in substantially worse model fits. The results indicate that the variances of the error terms and the variances of the method factors are not equivalent for females and males. As discussed above, there is no clear pattern to the variation between females and males. At some waves and for some readings the method factor variance is greater for females, while at some waves and for some readings the method factor variance is greater for males.

Our final research questions concerns whether there are differences in the measurement properties of a simple average of the readings compared with a linear combination of the readings using factor scores.Table II presents the validities for the averages and the weighted averages using factor scores based on the individual MTMM models for systolic and diastolic blood pressure among females and males across the three waves. As one would expect, the validity measures for the weighted averages using the factor scores are all equal to or greater than the validity measures for the averages, but the differences are substantively small. These results indicate that among the adolescents and young adults in the CLHNS a simple average of the three blood pressure readings for females and males across the three waves of data provides a valid measure of blood pressure that performs essentially as well as a weighted average using factor score weights.

Table II.

Comparison of validity measures for average of readings and weighted average of readings using factor scores.

	Average		Factor scores
	SBP	DBP	SBP	DBP
Female
Wave 1	1.000	0.998	1.000	0.998
Wave 2	0.985	0.983	0.986	0.985
Wave 3	0.993	0.990	0.993	0.992
Male
Wave 1	0.999	0.999	1.000	1.000
Wave 2	0.987	0.986	0.989	0.988
Wave 3	0.993	0.994	0.993	0.994

Discussion

This study was motivated by four research questions: (i) Are there any differences in the measurement properties of the first, second, or third readings of blood pressure done at approximately the same time? (ii) Are there any differences in measurement properties of the three readings across the three waves of data? (iii) Are there any differences in measurement properties of the three readings across females and males?, and (iv) Are there any differences in the measurement properties of an average of the three readings compared with a weighted average based on factor scores?

With respect to the first question, we do not observe any systematic differences in the measurement properties of the first, second and third readings for females or males across each of the three waves of data. This contrasts with past studies that suggest the second reading is the most reliable (9). The contrast in findings may be due to two sources: (1) our analysis relies on a younger population than in past studies, which could have less variance in blood pressure readings and (2) the blood pressure readings in our analysis have such high validity that it is not easy to distinguish a best reading. In light of the contrasting results with past studies, a conservative approach is to maintain data for all blood pressure readings and combine the multiple readings rather than relying on a single reading (e.g. the second reading).

We do find, however, that the there are differences in the measurement properties across the three waves of data and for females and males. In particular, we observed larger method factor variances at waves 2 and 3 than at wave 1, but otherwise few systematic patterns among the method factor variances. We also observed larger reading error variances at waves 2 and 3 than at wave 1, particularly at wave 2. Furthermore, in general, males had larger error variances than females, which is likely a function of greater variation in heights among males. Thus, our results suggest that it is important to attend to potential differences in measurement properties over time and by sex. In particular, researchers should recognize that the reliability of blood pressure readings in longitudinal studies is likely to vary over time and across different subgroups of the population.

Our final research question concerned how well different linear combinations of the readings capture underlying “true” blood pressure and whether there are any differences in using a simple average (mean) as opposed to a weighted average based on factor score weights. We find that the both a simple average and a weighted average using factor scores have quite high validity, and therefore do a good job of reflecting the underlying “true” blood pressure. In addition, we find that the simple average of the readings performs essentially as well as the weighted average based on factor score weights. This result is also different than that found in an analysis of an elderly population in Spain and suggests that it may not be necessary to develop weighted averages of blood pressure readings based on factor scores for some sources of data (9). When in doubt, researchers can use the methods outlined in this analysis to examine the measurement properties of blood pressure readings (or multiple readings of other bio-markers) in their own data.

It is important to be aware of several limitations of this study. First, the study examines a sample of adolescents and young adults ranging in age from 15 to 21 residing in a low-income country and may not generalize to other populations. Second, the study relies on data initially gathered in the late 1990s when validated automatic blood pressure devices were not available. It is possible that newer devices for measuring blood pressure when collecting readings for an epidemiologic survey would exhibit less measurement error and/or different patterns of measurement quality.

Conclusions

Blood pressure readings are required to measure rates of hypertension among different populations. The results of this study demonstrate that the measurement quality of blood pressure readings can vary over time and across different subpopulations in longitudinal epidemiological surveys. Furthermore, this study suggests that researchers should keep all of the blood pressure readings (as opposed to keeping just the second reading) and consider different approaches to combining the readings (e.g. taking the average or using factor scores) before estimating hypertension rates.