Neural Coding of Sound Envelope in Reverberant Environments

Abstract

Speech reception depends critically on temporal modulations in the amplitude envelope of the speech signal. Reverberation encountered in everyday environments can substantially attenuate these modulations. To assess the effect of reverberation on the neural coding of amplitude envelope, we recorded from single units in the inferior colliculus (IC) of unanesthetized rabbit using sinusoidally amplitude modulated (AM) broadband noise stimuli presented in simulated anechoic and reverberant environments. Although reverberation degraded both rate and temporal coding of AM in IC neurons, in most neurons, the degradation in temporal coding was smaller than the AM attenuation in the stimulus. This compensation could largely be accounted for by the compressive shape of the modulation input–output function (MIOF), which describes the nonlinear transformation of modulation depth from acoustic stimuli into neural responses. Additionally, in a subset of neurons, the temporal coding of AM was better for reverberant stimuli than for anechoic stimuli having the same modulation depth at the ear. Using hybrid anechoic stimuli that selectively possess certain properties of reverberant sounds, we show that this reverberant advantage is not caused by envelope distortion, static interaural decorrelation, or spectral coloration. Overall, our results suggest that the auditory system may possess dual mechanisms that make the coding of amplitude envelope relatively robust in reverberation: one general mechanism operating for all stimuli with small modulation depths, and another mechanism dependent on very specific properties of reverberant stimuli, possibly the periodic fluctuations in interaural correlation at the modulation frequency.

Introduction

Temporal fluctuations in the amplitude envelope of physical signals, or amplitude modulations (AMs), are crucial to the neural representation of the environment across sensory modalities. For instance, in the visual system, AMs in luminance or color spectrum play an important role in motion perception and figure/ground segregation (Blake and Lee, 2005). AMs are ubiquitous in natural sounds (Attias and Schreiner, 1997; Nelken et al., 1999; Singh and Theunissen, 2003) and are particularly important for speech intelligibility. Speech reception in quiet is fairly robust to degradations in spectral information, as long as AMs are preserved (e.g., Shannon et al., 1995, 1998). Speech intelligibility in noise and reverberation can approximately be predicted from physical measurements of the transmission of AMs (Houtgast et al., 1980; Steeneken and Houtgast, 1980).

Reverberation presents a challenge to the processing of sound envelopes, as reflections from boundary surfaces combine with the original signal to attenuate AMs by filling in the gaps in the signal envelope. While this degradation occurs in natural environments, such as forests (Richards and Wiley, 1980), it is especially relevant to everyday spoken communication in rooms. Although speech reception performance of human subjects is degraded in the presence of extreme reverberation (e.g., Payton et al., 1994; Neuman et al., 2010), it remains robust for normal-hearing listeners in moderate reverberation (e.g., Poissant et al., 2006; Sato et al., 2007; Yang and Bradley, 2009), suggesting that the auditory system may possess compensation mechanisms that counteract the attenuation of envelope modulations in reverberation. Psychophysical experiments provide evidence for such compensation mechanisms in AM detection (Zahorik et al., 2011, 2012) and speech reception (Watkins, 2005; Brandewie and Zahorik, 2010, 2013).

Previous studies of the coding of sound by auditory neurons typically presented acoustic stimuli either through headphones or in anechoic space, and rarely included reverberation representative of everyday rooms. A few studies of the auditory brainstem (Sayles and Winter, 2008; Sayles et al., 2015) and midbrain (Devore et al., 2010; Kuwada et al., 2014) have shown that the neural coding of temporal envelope can be substantially degraded by realistic reverberation. On the other hand, Kuwada et al. (2012, 2014) showed that, for neurons in the rabbit inferior colliculus (IC), the neural modulation gain (the ratio of the modulation depth of the neural response to the modulation depth of the acoustic stimulus) tends to be larger in reverberation than in anechoic conditions, consistent with a possible neural compensation mechanism.

To further investigate neural mechanisms underlying reverberation compensation, we recorded from single units in the IC of unanesthetized rabbit in response to sinusoidally amplitude modulated (SAM) broadband noise in simulated anechoic and reverberant environments. The IC is a key processing stage for AM coding because IC neurons exhibit stronger synchronization and sharper firing rate tuning to AM frequency than subcollicular neurons (Joris et al., 2004). Although reverberation degraded both rate and temporal coding of AM in the IC, our results suggest the existence of two distinct compensation mechanisms: one that enhances temporal coding for all stimuli with small modulation depths, and the other one linked to very specific acoustic characteristics of reverberant stimuli.

Materials and Methods

Surgical preparation

Surgical procedures to prepare female Dutch-belted rabbits (Oryctolagus cuniculus) for chronic unanesthetized recordings from single units in IC were based on the techniques of Kuwada et al. (1987), Nelson and Carney (2007), and Devore and Delgutte (2010), and were approved by the Institutional Animal Care and Use Committees of the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology.

Animals underwent two separate aseptic surgeries before being used for chronic single-unit recordings. In the first surgery, animals were anesthetized with an intramuscular injection of acepromazine (1 mg/kg), ketamine (44 mg/kg), and xylazine (6 mg/kg). Supplemental doses of ketamine (15 mg/kg) and xylazine (2 mg/kg) were administered as necessary based on pedal withdrawal and corneal reflexes. Part of the skull was exposed to affix a stainless steel cylinder and brass head bar using stainless steel screws and dental acrylic. Ear molds were made with vinyl polysiloxane impression material (Reprosil, Patterson Dental). After ∼1 week recovery from surgery, rabbits were habituated to the experimental setup until they could remain attached by the head post for 2–3 h while being presented acoustic stimuli through speakers connected to the ear molds.

Once they were habituated to the setup, rabbits underwent a second aseptic surgical procedure to perform a small craniotomy. Animals were anesthetized either by intramuscular injection of a mixture of acepromazine, ketamine, and xylazine as described for the first procedure, or by inhalation of isoflurane. Isoflurane anesthesia was induced by placing the animals in a hermetic Plexiglas box ventilated with a 1 L/min flow of isoflurane (5% mixture in oxygen) and then maintained throughout the procedure with mask delivery of a 0.5–1 L/min flow of isoflurane (1–2.5% mixture in oxygen). Isoflurane concentration was adjusted to maintain a suppressed pedal withdrawal reflex and high oxygen blood saturation. A small (∼1–2 mm diameter) craniotomy was performed ∼10 mm posterior from bregma and 3 mm lateral from the midline. A topical antibiotic (bacitracin) was applied to the exposed dura, and the cylinder filled with a sterile elastopolymer (Sammons-Preston). During the course of several months of recording sessions, additional surgeries were done periodically to clean the exposed dura off of scar tissue and/or slightly enlarge the craniotomy.

Acoustic stimuli

Virtual auditory space.

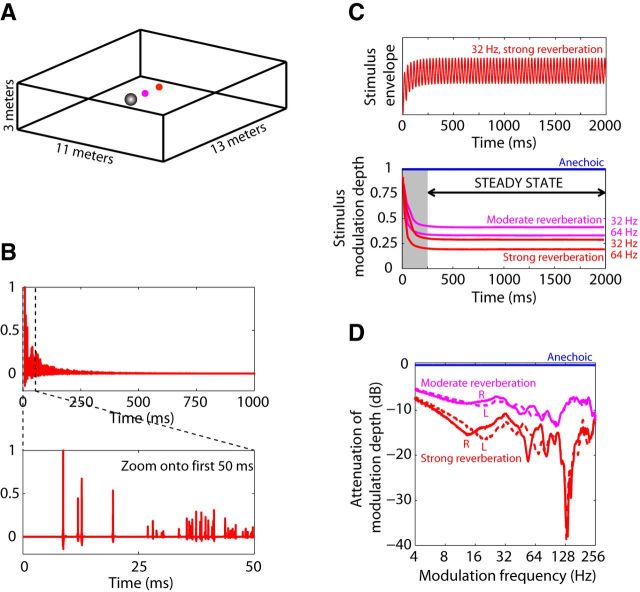
We simulated binaural room impulse responses (BRIRs) using the room-image method (Allen and Berkley, 1979; Shinn-Cunningham et al., 2001) with room dimension and simulation parameters similar to those of Devore et al. (2009). The virtual room measured 11 × 13 × 3 m, and the rabbit head was modeled by a rigid sphere, 12 cm in diameter, placed near (but not exactly at) the center of the room. The ears were represented by two receivers placed on the sphere at ±90° azimuth relative to the median vertical plane (Fig. 1A). The use of a spherical head model ensures that the acoustic reflections in the BRIRs contain both interaural time and level difference cues.

Figure 1.

Virtual reverberant stimuli. A, Geometry of the virtual room. Reverberant binaural room impulse responses (BRIRs) were simulated using the image method for a source positioned at 0° azimuth either 1.5 m (“moderate” reverberation, magenta) or 3 m (“strong” reverberation, red) away from the model spherical head (gray). B, Example BRIR (right channel, strong reverberation). The direct sound is followed by superimposed reflections with approximately exponential energy decay. Detail reveals individual early reflections. C, Time course of modulation depth at the ear in reverberant and anechoic stimuli. Anechoic stimulus modulation depth is nearly 1 throughout the entire stimulus duration, whereas reverberant stimulus modulation depth decays after stimulus onset to reach a plateau by 250 ms. D, Binaural room modulation transfer functions (MTFs) describe the attenuation of amplitude modulation between a source and each ear due to reverberation. MTFs were computed in the steady-state part of the reverberant stimuli (see Materials and Methods). Anechoic MTFs (blue) are flat at 0 dB attenuation. Moderate (magenta) and strong (red) reverberant MTFs are <0 dB and frequency dependent. MTFs for left (solid lines) and right (dashed lines) ears were similar at most modulation frequencies.

BRIRs were simulated for a source positioned at 0° azimuth and at distances of 1.5 and 3 m from the center of the sphere. We chose an azimuth of 0° because it is the most relevant azimuth for speech communication; reflections, however, can come from all directions. The direct-to-reverberant energy ratio was 0 dB for the 1.5 m distance (“moderate reverberation”) and −6 dB for the 3 m distance (“strong reverberation”). T60 (the time elapsed before the sound pressure level of reflections decays by 60 dB) was 1.1 s. Anechoic impulse responses were obtained by isolating the first peak (direct sound) from the reverberant BRIRs. Figure 1B shows the right channel of the BRIR for the strongly reverberant condition, with a detail of the first 50 ms where the direct sound and individual reflections can be resolved. For a given source–receiver distance, the energy in the reverberant BRIR was larger than the energy of the corresponding anechoic BRIR because of the addition of reverberant energy. To control for sound pressure level, both channels of a reverberant BRIR pair were scaled by a common factor chosen so that the energy in the contralateral channel of the reverberant BRIR matched that of the anechoic BRIR.

Virtual auditory space stimuli were created by convolving SAM broadband noise tokens with the left and right BRIRs (Fig. 1B). The standard sound source had a modulation depth of 1, but lower modulation depths were also used in the anechoic condition to characterize how the modulation depth in the neural response depends on input modulation depth.

Characterization of the AM degradation in the stimulus due to reverberation.

Two complementary measures were used to characterize the attenuation of AM produced by reverberation: the steady-state room modulation transfer function (Fig. 1D) and a characterization of the time course of modulation depth for reverberant stimuli with a given modulation frequency (Fig. 1C).

The definition of modulation depth requires some care because, while our anechoic stimuli always had a sinusoidal envelope, this was not the case for the reverberant stimuli due to distortions introduced by reverberation (see Fig. 9A). Consistent with prior studies (Houtgast et al., 1980; Schroeder, 1981), modulation depth for a stimulus with modulation frequency f_m was defined using the discrete Fourier transform (DFT_env) of the envelope, as follows:

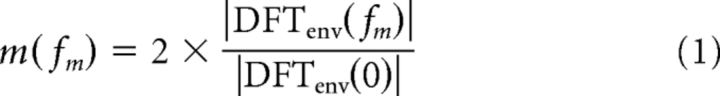This definition amounts to finding the best fitting sinusoid, then computing the ratio of the peak amplitude of this sinusoid to the DC component. If the stimulus has a sinusoidal envelope, this definition is consistent with the traditional definition. In practice, fluctuations in the broadband noise carrier make it hard to define the envelope of AM noise for a single noise token, so we created 50 reverberant stimuli for each modulation frequency, by convolving our BRIRs with 50 different tokens of SAM broadband noise (each with a modulation depth of 1 and of 2 s duration), then averaging the full-wave rectified reverberant stimuli across all noise tokens to obtain the amplitude envelope. Equation 1 was applied to the steady-state part of the average envelope.

Figure 9.

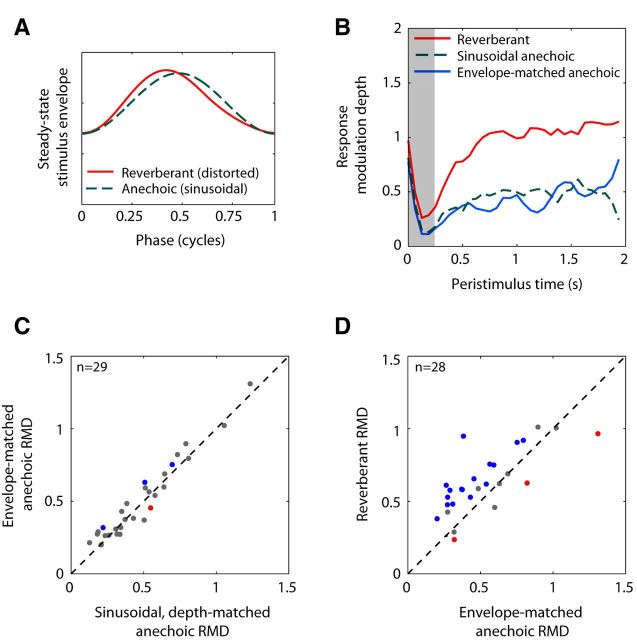
Effect of envelope distortions created by reverberation on RMD. A, Average envelope cycle for reverberant stimulus (f_m = 32 Hz, strong reverberation) and depth-matched anechoic stimulus. Reverberation distorts the sinusoidal envelope of the anechoic stimulus. B, Time course of RMD to reverberant stimulus (solid red), envelope-matched anechoic stimulus (solid blue), and depth-matched anechoic stimulus with sinusoidal envelope (dashed green) in one IC neuron (BF = 4 kHz, f_m = 16 Hz). RMDs were computed over 1 period bins (62.5 ms) and smoothed with a 3 point moving average filter. C, Scatter plot of RMD to envelope-matched anechoic stimulus against RMD to sinusoidal, depth-matched anechoic stimulus for 29 IC neurons. Blue dots indicate envelope-matched anechoic RMD significantly greater than sinusoidal anechoic RMD. Red dots indicate envelope-matched anechoic RMD significantly lower than sinusoidal anechoic RMD. D, Scatter plot of RMD to reverberant stimulus against RMD to envelope-matched anechoic stimulus for 28 neurons with significant reverberant RMDs. Blue dots indicate reverberant RMD significantly greater than envelope-matched anechoic RMD. Red dots indicate reverberant RMD significantly lower than envelope-matched anechoic RMD.

The attenuation of modulation depth between the source and each receiver due to reverberation was quantified by the room modulation transfer function (MTF) (Fig. 1D), defined as the ratio of the modulation depth of the reverberant stimulus at the receiver to the modulation depth of the sound source as a function of modulation frequency f_m. Because the modulation depth at the source was always 1, the room MTF in dB was simply:

Reverberation is a dynamic process: The earlier portion of a reverberant AM stimulus is more modulated than the later portion because reverberant energy gradually builds up over time after stimulus onset. The time course of modulation depth for our 2 s reverberant stimuli (Fig. 1C) showed a sharp initial decay, followed by a plateau after 250 ms. To measure this time course, we obtained a smooth envelope by averaging the full-wave rectified reverberant waveforms generated from 50 different tokens of SAM noise as described above, and then computed the envelope modulation depth on a cycle-by-cycle basis using Equation 1. Specifically, the envelope DFT was computed over a sliding temporal window with a width equal to the modulation period, in increments of 1 ms.

Because the time course of modulation depth in reverberant stimuli reached an asymptote after 250 ms, all of our steady-state analyses (including acoustic and neural MTFs) were performed over a window beginning after an integer number of modulation cycles ≥250 ms following stimulus onset, and extending up to the end of the 2 s stimulus. This steady-state interval always included an integer number of modulation cycles.

Hybrid anechoic stimuli matching selected acoustic properties of reverberant stimuli.

Our reverberant AM stimuli differ from anechoic stimuli not only in modulation depth, but also in other acoustic properties, including envelope waveform, interaural correlation, and spectral coloration. To determine which of these properties best explain the differences in neural responses to anechoic and reverberant stimuli that we observed, we synthesized a series of hybrid anechoic AM stimuli that matched reverberant stimuli in one or more of these acoustic properties (Table 1). These stimuli are called “anechoic” because they were generated using anechoic BRIRs rather than reverberant BRIRs.

Table 1.

Characteristics of the hybrid stimuli matching certain properties of reverberant stimuli

Stimulus	Modulation depth	Envelope shape	Mean IACC
Standard anechoic	1	Sinusoidal	1 (diotic)
Reverberant	<1	Distorted	0.74 (strong); 0.85 (moderate)
Depth-matched anechoic	Contralateral matches reverberant	Sinusoidal	1 (diotic)
Envelope-matched	Contralateral matches reverberant	Contralateral matches reverberant	1 (diotic)
IACC-matched	Contralateral matches reverberant	Sinusoidal	Matches reverberant

Depth-matched anechoic stimuli.

The simplest hybrid stimulus was a 2 s SAM broadband noise that had a modulation depth matching that of the reverberant stimulus in the ear contralateral to the recording site during the steady-state portion of the stimulus. Contrary to the reverberant stimuli, which are dichotic, these depth-matched anechoic stimuli were presented diotically.

Envelope-matched anechoic stimuli.

Reverberation introduces small distortions in the sinusoidal envelopes of the anechoic stimuli (see Fig. 9A). To investigate the effect of these envelope distortions, we synthesized hybrid stimuli having not only the same modulation depth but also the same average envelope shape as the reverberant stimuli during the steady-state portion. Average envelope shape was extracted for each reverberant condition and each modulation frequency f_m by taking 50 tokens of reverberant SAM noise, full-wave rectifying, low-pass filtering (third-order Butterworth filter with cutoff frequency 5 × f_m), and averaging across tokens. The resulting envelope was divided into nonoverlapping 1 period time segments, and all the segments during the steady-state portion of the stimulus (≥250 ms) were averaged together. The average envelope cycle in the ear contralateral to the IC was used to modulate a 2 s broadband noise, which was subsequently filtered with the anechoic BRIRs and presented diotically.

Interaural cross-correlation (IACC)-matched anechoic stimuli.

Because our modulated sound source was positioned at 0° azimuth, the signals at the two receivers on the spherical head were identical in the anechoic condition, so that the peak IACC was always 1. In contrast, the signals at the two receivers were decorrelated in the reverberant conditions because most reflections reached the two receivers with different delays and amplitudes (see Fig. 10A). The mean interaural coherence in the steady-state portion (≥250 ms) of our stimuli was 0.85 in moderate reverberation, and 0.74 in strong reverberation, for all f_m. To investigate the effect of this decorrelation on the neural response, we synthesized anechoic stimuli that had both the same interaural coherence and the same modulation depth as the reverberant stimuli. A Gram–Schmidt orthogonalization procedure (Culling et al., 2001) was used to create a pair of broadband noises with a specified interaural coherence. The pair of noise carriers were then modulated so as to match the modulation depths of the reverberant stimuli, and finally the modulated noises were convolved with the anechoic BRIRs. These hybrid stimuli thus match the reverberant stimuli in both modulation depth and average interaural coherence.

Figure 10.

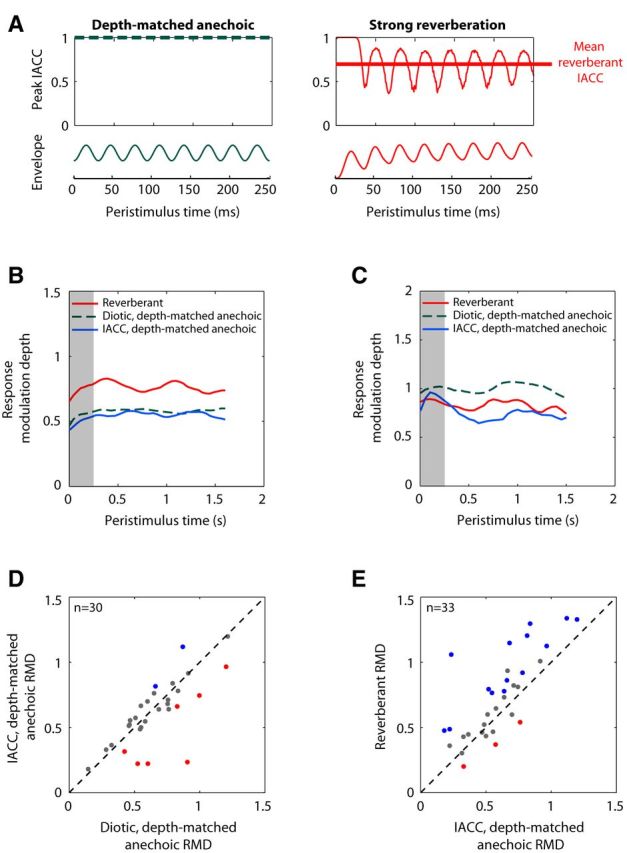
Effect of interaural decorrelation introduced by reverberation on RMDs. A, Time course of interaural coherence (the peak IACC across interaural time differences) and amplitude envelopes for reverberant stimulus (f_m = 32 Hz, strong reverberation) and depth-matched anechoic stimulus. IACC was computed over 780 μs windows (40 windows/cycle). Only the first 250 ms of each stimulus is represented. Reverberation reduced the mean interaural coherence (thick red line) and introduced periodic fluctuations at the modulation frequency. B, Time course of RMD to reverberant stimulus (solid red, f_m = 64 Hz), diotic, depth-matched anechoic stimulus (dashed green), and anechoic stimulus with matched mean IACC and modulation depth (solid blue) in an IC neuron (BF = 10.5 kHz). RMDs were computed over ∼391 ms time bins with 90% overlap and smoothed with a 3 point moving average. In this neuron, the decrease in mean IACC had little effect on RMD. C, Same as in B for another neuron (BF = 3.6 kHz) using f_m = 128 Hz. RMDs were computed over 500 ms time bins with 90% overlap and smoothed with a 3 point moving average. In this neuron, static decorrelation significantly decreased RMD and could partly account for the reverberant disadvantage. D, Scatter plot of RMD to IACC-matched anechoic stimulus against RMD to diotic, depth-matched, anechoic stimulus for 30 neurons. In 7 neurons (red dots), RMD was significantly lower for the decorrelated stimulus than for the diotic stimulus; and, in 2 neurons (blue dots), RMD was significantly greater in the decorrelated case. E, Scatter plot of RMD to reverberant stimulus against RMD to IACC-matched anechoic stimulus for 33 neurons. In 14 neurons (42%), RMD was significantly greater in the reverberant condition (blue dots); and in 3 neurons (9%), RMD was significantly smaller in the reverberant condition (red dots).

Neural recording procedures

Recording sessions took place in an electrically shielded, vibration-isolated, sound-attenuating chamber. At the beginning of a recording session, the animal head was secured to the head post, and the elastopolymer cap covering the craniotomy was removed. The inside of the cylinder and exposed dura were flushed with sterile saline, and a few drops of a topical anesthetic (Marcaine) were applied to the surface of the dura. The two ear molds were inserted into the animal's pinnae, and two Beyer-Dynamic (DT-48) sound speakers were coupled to ∼5 mm diameter sound delivery plastic tubes encased in the ear molds. A probe-tube microphone (Etymotic ER-7C) was used to measure sound pressure near the tympanic membrane in response to broadband chirp stimuli and compute the transfer function of the acoustic system. Inverse filters compensating for this transfer function were digitally created. All sound stimuli were generated by a 24-bit D/A converter (National Instruments, NIDAC 4461) at a sampling rate of 50 kHz and filtered by the inverse filters.

We recorded from single units in the IC using either epoxy-coated (A-M Systems) or custom made, glass-coated tungsten electrodes. Electrodes were descended vertically into the IC using a remote-controlled hydraulic micropositioner (Kopf 650). Neural activity from the electrode was amplified, bandpass filtered (0.3–3 kHz), and sampled at 100 kHz using a 16-bit A/D converter (National Instruments, PXI-6123). Custom software was used to measure spike times by threshold crossing and save them to disk.

Experimental sessions typically occurred 6 d/week for up to 3 months in each IC. During recording sessions, animals were monitored with a video system, and sessions were interrupted if they showed any sign of discomfort. At the end of each session, the exposed dura was flushed with sterile saline and covered with bacitracin to prevent infection. A new elastopolymer cap was then made to protect the craniotomy.

After the last recording session from an animal, electrical lesions were made while the animal was under anesthesia to determine the anatomical location of our recordings. Lesions were made with 10 μA DC current applied for 30–45 s in locations spanning the region where recordings were performed, and the locations of the lesions within the IC were subsequently verified histologically.

Neural measurement paradigms

A search stimulus (40 Hz SAM broadband noise presented diotically at 60 dB SPL) was played while descending the microelectrode through the brain toward the IC (identified by the presence of sound-evoked multiunit activity). Single units were defined as neural activity for which all action potentials shapes were very similar, with a peak amplitude at least 3 times above the noise floor, and interspike interval histograms showing a refractory period ≥1 ms. Only single units that had physiological responses consistent with a location in the central nucleus of the IC (best frequency sequence consistent with tonotopic organization and nonhabituating responses across trials) were studied.

Upon isolating a single unit, a rate-level function was measured using 200 ms diotic broadband noise bursts presented in random order at levels between 0 and 70 dB SPL (5–10 repetitions), from which the rate threshold was estimated visually. Then, the neuron's best frequency (BF) was determined using either an iso-rate tracking algorithm (Kiang and Moxon, 1974) or by presenting tone pips just above threshold and with frequencies spanning 4 octaves centered around the BF of single units previously isolated nearby. All subsequent SAM noise stimuli were presented at 15–20 dB above the broadband noise threshold.

Neural modulation transfer functions (MTFs).

Neural responses to SAM broadband noise were measured as a function of f_m for both anechoic and reverberant stimuli to construct neural MTFs. Stimuli were 2 s long, followed by a 1 s silent interval, and presented 3–5 times each in random order. The sound source was SAM broadband noise with a modulation depth of 1 (using a different noise token for every trial) with f_m varied over 4–256 Hz (octave spacing, plus 45, 90, and 180 Hz). Either the moderate or the strong reverberant condition was studied first, and the other reverberant condition was studied subsequently, time permitting. Presentation order was randomized across f_m and between anechoic and reverberant conditions.

Modulation input–output functions (MIOFs).

Because reverberation attenuates AM in the stimulus, it is important to characterize how neural responses vary with modulation depth to understand the effects of reverberation. We therefore measured neural responses to SAM broadband noise with fixed f_m, as a function of modulation depth to construct a neural MIOF. The 2 s SAM noises were convolved with the anechoic BRIRs. We typically used 5–12 modulation depths between 0 and 1, each presented five times in random order with a 1 s silent interval between stimuli. The modulation frequency was chosen to elicit both a large firing rate and strong phase-locking to the modulation. The most frequently used f_m were 16–90 Hz (median 64 Hz). In a few experiments, we measured MIOFs for several f_m. In these experiments, the stimuli were presented randomly across modulation depths and f_m.

Time course of response to reverberant and hybrid stimuli.

In some experiments, we measured responses to reverberant stimuli at a given f_m for a large number of trials (up to 71) to characterize the detailed time course of response for comparison with the time course of modulation depth in the reverberant stimulus. Again, the stimuli were 2 s long with a 1 s silent interstimulus interval, and f_m was chosen to elicit both a large firing rate and strong phase-locking to the modulation. The reverberant stimuli were interleaved with anechoic stimuli at the same f_m but with different modulation depths, and also with hybrid stimuli that matched the reverberant stimuli for certain acoustic properties (as described under Acoustic stimuli). Up to nine different stimulus conditions were randomly interleaved in this paradigm.

Data analysis

Only well-isolated single units were included in our dataset. A first step in many of our analyses was to isolate the “steady-state” part of the neural response by excluding spikes occurring in a time window containing the smallest integer number of modulation cycles ≥250 ms after the onset of the 2 s stimuli. This was done both to eliminate the prominent onset response observed in many neurons, and to allow sufficient time for reverberant energy to build up and reach a quasi steady-state after stimulus onset (Fig. 1C).

Response modulation depth and neural modulation gain.

A major goal of our study was to characterize how reverberation alters the temporal coding of AM in IC neurons. To use the same metrics as previous studies of AM coding by auditory neurons (e.g., Møller, 1972; Frisina et al., 1990; Joris and Yin, 1992; Kuwada and Batra, 1999; Krishna and Semple, 2000; Joris et al., 2004; Kuwada et al., 2014), we used Fourier analysis of period histograms (PH) based on the modulation period to define the response modulation depth (RMD) to a stimulus with modulation frequency f_m, as follows:

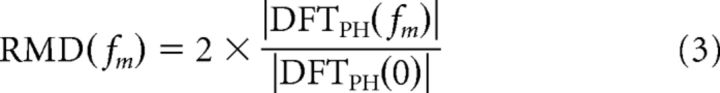This definition of RMD closely parallels the definition of modulation depth for the acoustic stimulus (Eq. 1) and amounts to fitting a sinusoid to the period histogram and then expressing the amplitude of the best-fitting sinusoid relative to the mean firing rate. RMD is mathematically equivalent to twice the “vector strength,” also known as the “synchronization index,” a widely used measure of neural phase-locking to periodic waveforms (Goldberg and Brown, 1969; Johnson, 1980). RMD can take values between 0 and 2, with 1 corresponding to a 100% modulated sinusoid. Values >1 mean that no spikes occur over a fraction of the stimulus period.

In practice, to avoid any numerical errors resulting from binning spike times to construct period histograms, RMD was computed directly from the spike times, by treating each spike as a unit vector whose angle is defined by its phase of occurrence within the modulation cycle. The vector strength is the mean resultant vector over all spikes. The period histograms in Figure 2A are shown for illustrative purposes only, and were not used for computing RMD.

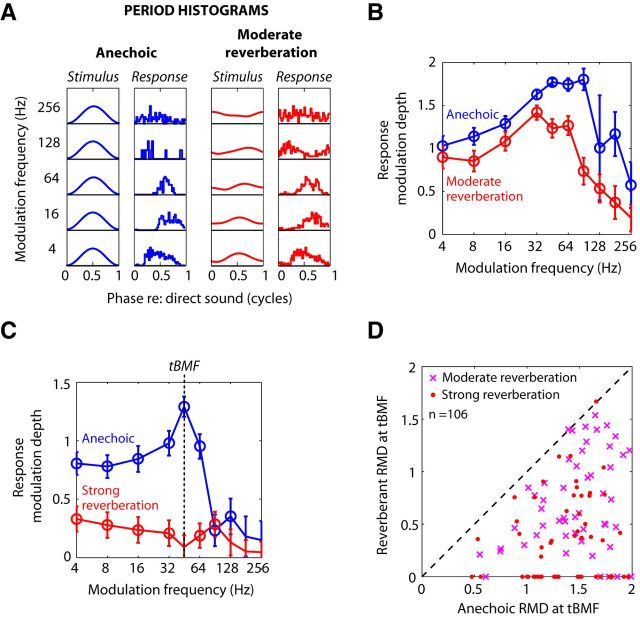
Figure 2.

Effects of reverberation on temporal coding of amplitude modulation. A, Envelopes of anechoic (left, blue) and moderately reverberant stimuli (right, red) and corresponding temporal response patterns (period histograms) from one neuron (BF = 3.8 kHz) for 5 modulation frequencies. B, Neural temporal modulation transfer function (tMTF) constructed from the same neuron represent the response modulation depth (RMD) against modulation frequency. Error bars indicate ±2 SDs estimated based on a von Mises distribution (see Materials and Methods). RMDs that were significantly greater than 0 (Rayleigh test of uniformity, p < 0.05) are marked with an open circle. C, tMTFs from another neuron (BF = 3.9 kHz). Strength of temporal coding of AM was quantified by the RMD at the best modulation frequency of the anechoic tMTF (tBMF). D, Scatter plot of RMD at tBMF for reverberant stimuli against RMD for anechoic stimuli for a sample of 110 IC neurons. Points for which anechoic RMD was not significant (4 of 110) are not shown. Reverberant RMDs that were not statistically significant are shown along the lower axis.

The ratio of RMD to stimulus modulation depth is the “neural modulation gain,” which is often expressed in decibels. A modulation gain >1 (0 dB) means that the modulation in the neural response is stronger than that in the acoustic stimulus. In Results, we compare neural modulation gains for reverberant and acoustic conditions.

A Rayleigh test of uniformity (Mardia, 1972) was used to assess the statistical significance (p < 0.05) of the RMD. Additionally, the standard deviation of the RMD was estimated for each f_m using an approximate formula described by Mardia and Jupp (1999; their Eq. 4.8.18). Both the Rayleigh statistic and the standard deviation estimate only depend on the vector strength and the total spike count. To compare RMDs from one neuron between two different stimulus conditions, we used the test for equality of concentration parameters for von Mises distribution (Mardia and Jupp, 1999; their p. 133), which is a circular-statistics analog of the F test for equality of variances for Gaussian distributions. To compare RMDs across the neuronal population between two stimulus conditions, we used nonparametric rank-based tests (Wilcoxon). Because these tests are invariant to a monotonic transformation of the data (such as a logarithm), the results do not depend on whether RMD is expressed on a linear scale or in dB.

Acoustic and neural degradations in AM.

In many neurons, we find that the neural modulation gain is larger for reverberant stimuli than for anechoic stimuli (see also Kuwada et al., 2014). Using the definition of modulation gain as the ratio of RMD to the modulation depth of the stimulus at the ear m, this relationship can be written as follows:

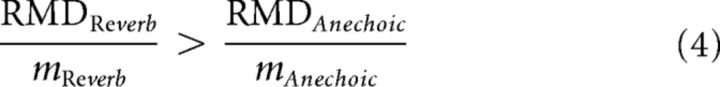Rearranging terms, we obtain the following:

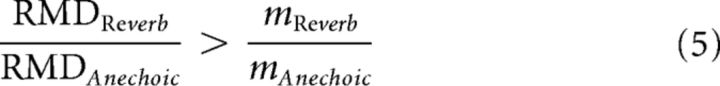The ratio on the right of Equation 5 represents the attenuation of AM in the acoustic stimulus introduced by reverberation, which can be obtained by evaluating the room MTF evaluated at f_m. Similarly, the ratio on the left of Equation 5 represents the degradation in temporal neural coding of AM caused by reverberation. Thus, Equation 5 means that the neural degradation in AM coding is smaller than the attenuation of AM introduced by reverberation in the stimulus (i.e., there is a neural compensation for the effect of reverberation). This further implies that the finding of a larger neural modulation in the reverberant condition than in the anechoic condition can be interpreted as evidence for a neural compensation mechanism. In the following, we will adopt this interpretation without making any further use of the degradation ratios defined in Equation 5.

Neural modulation transfer functions.

Neural modulation transfer functions were used to characterize both temporal and rate coding of AM in anechoic and reverberant conditions. Temporal MTFs (tMTFs) represent the RMD as a function of f_m. tMTFs were computed for both anechoic and reverberant conditions using SAM noise with a modulation depth of 1 at the source.

Rate MTFs (rMTFs) were computed for each room condition as the average firing rate during the steady-state window as a function of f_m. The strength of envelope frequency representation in the rMTF was quantified by a signal-to-noise ratio (SNR) metric based on ANOVA (Hancock et al., 2010). Specifically, the SNR is the ratio of the variance in firing rate attributable to changes in f_m, to the variance in firing rate across multiple repetitions of the same stimulus, averaged across all f_m. The SNR was compared between anechoic and reverberant conditions to assess the degradation in rate coding of f_m by reverberation.

Modulation input-output functions (MIOFs).

MIOFs for anechoic stimuli were constructed by plotting RMD as a function of stimulus modulation depth for a given f_m, after removing the spikes occurring before 250 ms. A scaled incomplete beta function was fitted to the data points as a function of modulation depth using a weighted least square procedure. The incomplete beta function provides both compressive and expansive shapes that encompass the diversity of MIOFs measured. Goodness of fit was assessed by the coefficient of determination r². We analyzed and used MIOFs only when r² was >0.5. This criterion excluded 3 neurons (of 94), where synchronization was poor and variability was large. For the 91 neurons that passed this criterion, the fit was usually very good (median r² was 0.98; range, 0.55–0.99). The mean slope of the MIOF (in dB/dB) was estimated by plotting the fitted curve in double logarithmic coordinates, computing the slope for each modulation depth, and averaging over all depths above the minimum depth at which RMD became significant.

The fitted MIOF was also used to predict the RMD to a reverberant stimulus under the assumption that the reverberant RMD is the same as the RMD of an anechoic stimulus having the same modulation depth at the ear. Specifically, if m_r represents the modulation depth of a reverberant stimulus, then the predicted reverberant RMD was obtained by evaluating the curve fitted to the MIOF at m_r. Predicted RMDs were compared with measured RMDs for reverberant stimuli.

Time course of response modulation depth.

When a sufficient number of stimulus presentations were tested, we characterized the time course of temporal coding of AM for the reverberant stimuli for comparison with the time course of modulation depth in the reverberant stimulus (see Fig. 1C). The time course of the neural modulation was obtained by separately computing RMD in sliding time windows whose duration was an integer number of modulation cycles. The number of cycles was chosen for each neuron so that RMD would be significant (Rayleigh test of uniformity, p < 0.05) in at least 95% of all time bins for a given condition. In the examples shown (see Figs. 7, 8, 9, and 10), the bin width ranged from 44 to 500 ms, depending on f_m and spike count. To smooth out fluctuations in RMD, the windows sometimes overlapped by 50%, and the time course was further smoothed with a rectangular moving-average filter (usually with a 3 point span).

Figure 7.

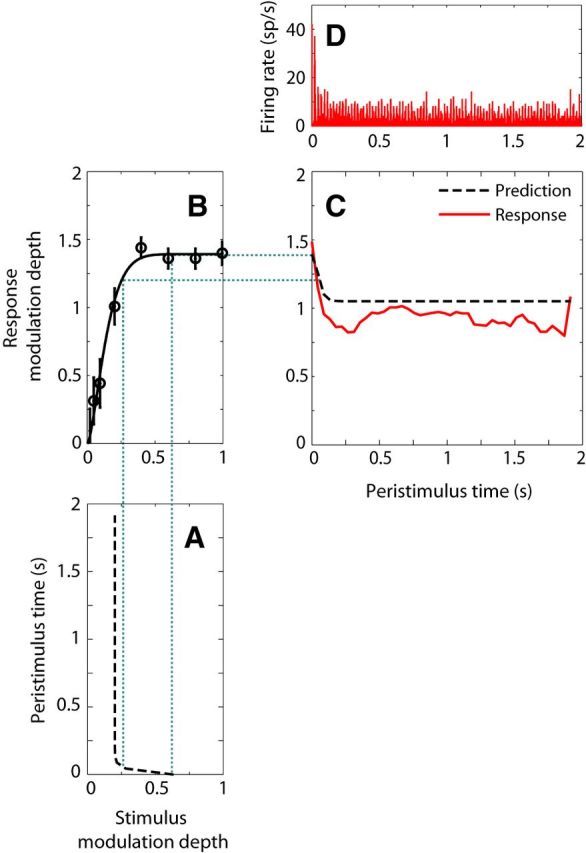
Time course of reverberant RMD and prediction from the MIOF and time course of stimulus modulation depth in one IC neuron (BF = 8 kHz). A, Time course of modulation depth for the reverberant stimulus after simulated cochlear filtering (f_m = 45 Hz, strong reverberation). Modulation depths were computed in 2 period bins (∼44 ms) and fitted with the sum of two decaying exponentials. B, MIOF with remapped abscissa to take into account the effect of cochlear filtering. Open circles represent significant RMD (Rayleigh test of uniformity, p < 0.05). Solid line indicates least-square fit with an incomplete beta function. C, Reverberant RMD (red, solid line) and prediction (black, dashed line) from the time course of stimulus modulations (A) and the MIOF (B). RMDs were computed over 2 period bins (∼44 ms) and smoothed with a 7 point moving average filter. In this example, the MIOF predicted the reverberant response fairly well. D, Peristimulus time histogram of the reverberant response (10 bins/period).

Figure 8.

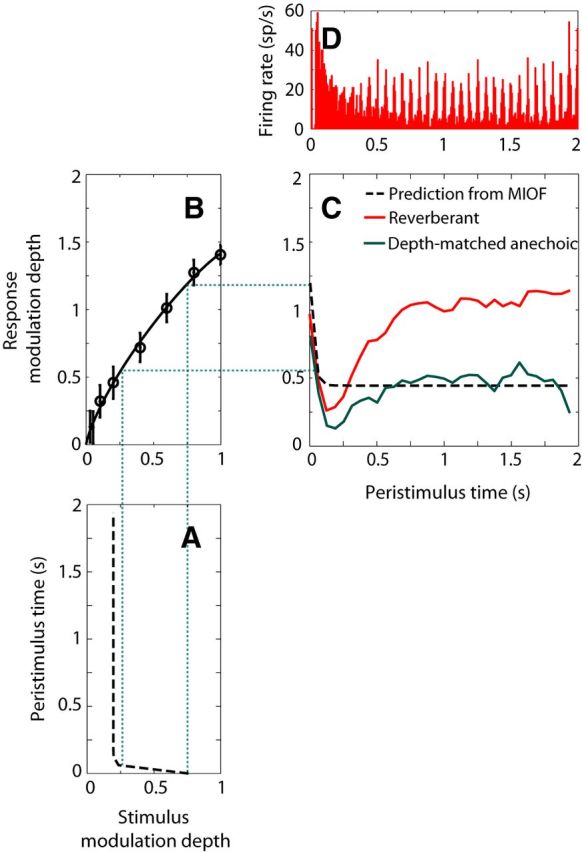
Same as in Figure 7 for another IC neuron (BF = 4 kHz, same example as Fig. 5A) that showed a strong reverberant coding advantage for f_m = 16 Hz. A, Time course of modulation depth for the reverberant stimulus after simulated cochlear filtering, computed over 1 period bins (62.5 ms). B, MIOF taking into account cochlear filtering. C, Time course of reverberant RMD and prediction from MIOF, computed over 1 period bins, and smoothed with a 3 point moving average. In this case, the reverberant RMD (C, red line) was significantly larger (p < 0.05) than the prediction from the MIOF (dashed line) over the steady-state portion of the stimulus. The time course of RMD to a depth-matched anechoic stimulus (C, green solid line) showed a similar initial dip followed by recovery as for the reverberant RMD. D, Peristimulus time histogram of the reverberant response.

Results

We measured responses of single units in the IC of unanesthetized rabbits to a SAM broadband noise source presented in simulated anechoic and reverberant environments using a virtual acoustic room. Our main focus is on the temporal coding of AM for reverberant stimuli and whether it can be predicted from responses to anechoic stimuli that possess certain acoustic characteristics of reverberant stimuli. Our results are based on recordings from 195 well-isolated single units in 7 rabbits.

Reverberation degrades temporal coding of amplitude modulation

The virtual auditory space stimuli were SAM broadband noise with a modulation depth of 1 produced by a sound source located 1.5 or 3 m away from a spherical head, in a medium-size virtual room (Fig. 1A). The direct-to-reverberant (D/R) energy ratio was 0 dB for the 1.5 m source-to-receiver distance (“moderate reverberation”) and −6 dB for the 3 m distance (“strong reverberation”). Reverberation degraded the modulation depth of the stimuli in a modulation frequency-dependent fashion, as illustrated by the room modulation transfer functions (Fig. 1D). Intuitively, reflections from the walls, ceiling, and floor overlap with the source stimulus waveform (Fig. 1B), thereby partially filling the gaps in the envelope of the SAM stimulus and reducing its modulation depth.

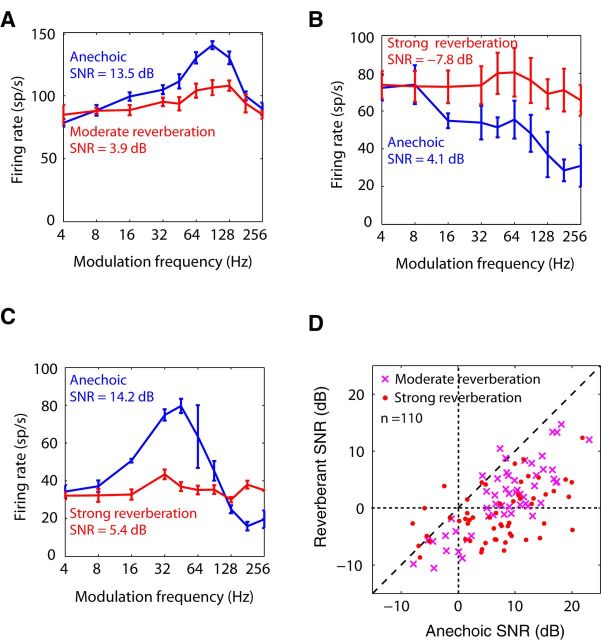
We measured neural responses to both anechoic and reverberant virtual auditory space stimuli (Fig. 1; see Materials and Methods) as a function of modulation frequency to characterize the effects of reverberation on the coding of AM in 110 single units. Figure 2A, B illustrates the temporal coding of AM for anechoic and reverberant stimuli in an example neuron. The period histograms for the anechoic condition (Fig. 2A, blue) show strong phase-locking to the modulated sound source for f_m up to 64 Hz and weaker phase-locking at 128 and 256 Hz. Moderate reverberation decreased the modulation depth of the stimulus waveform at the ear (Fig. 2A, red). The modulation depth of the neural response was also decreased compared with the anechoic condition, although it remained relatively robust at the lower f_m. In some cases (e.g., for f_m at 16 and 64 Hz), the period histogram for the reverberant condition shows more pronounced modulation than the acoustic stimulus, suggesting a possible neural compensation.

To quantify the modulations in the neural response, we used a metric based on Fourier analysis of period histograms that has been widely used in previous studies of AM coding by auditory neurons (e.g., Møller, 1972; Frisina et al., 1990; Joris and Yin, 1992; Kuwada and Batra, 1999; Krishna and Semple, 2000; Joris et al., 2004; Kuwada et al., 2014). Plotting this “response modulation depth” (RMD; see Materials and Methods) in the anechoic condition as a function of f_m to construct a tMTF (Fig. 2B, blue) reveals a bandpass shape, with a best temporal modulation frequency (tBMF: the frequency of maximum RMD) near 90 Hz. The reverberant tMTF (Fig. 2B, red) also has a bandpass shape, but with a lower high-frequency cutoff and decreased RMDs at all f_m relative to the anechoic condition. This decrease in RMD is qualitatively consistent with the attenuation of AM produced by reverberation in the acoustic stimulus at the ear.

Anechoic and reverberant tMTFs are shown for another neuron in Figure 2C. The anechoic tMTF is narrowly tuned to a tBMF near 45 Hz. In this neuron, reverberation had a dramatic effect on temporal coding of AM, and the degradation in RMD was highly dependent on f_m, resulting in a much flattened reverberant tMTF with very low RMD at all f_m.

Consistent with previous studies of the IC that used unanesthetized preparations (e.g., Nelson and Carney, 2007; Ter-Mikaelian et al., 2007; Kuwada et al., 2014), anechoic tMTFs in our neuronal sample had a variety of shapes, most commonly bandpass, low-pass, or all-pass over the range of modulation frequencies investigated. Anechoic tBMFs ranged from 4 to 180 Hz, with a median of 45 Hz, similar to other studies in unanesthetized rabbit (e.g., Nelson and Carney, 2007, their Fig. 3). In general, reverberation tended to increase the tMTF bandwidths.

Figure 3.

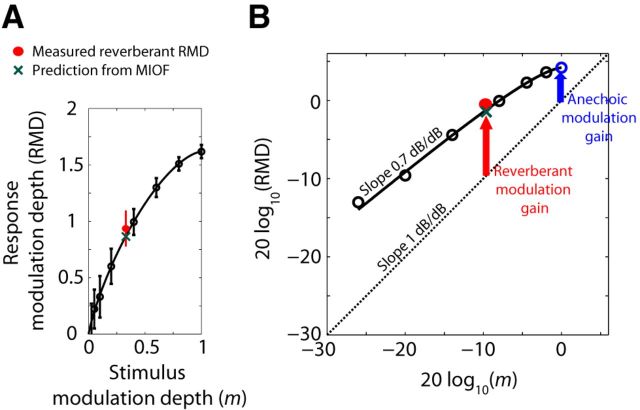
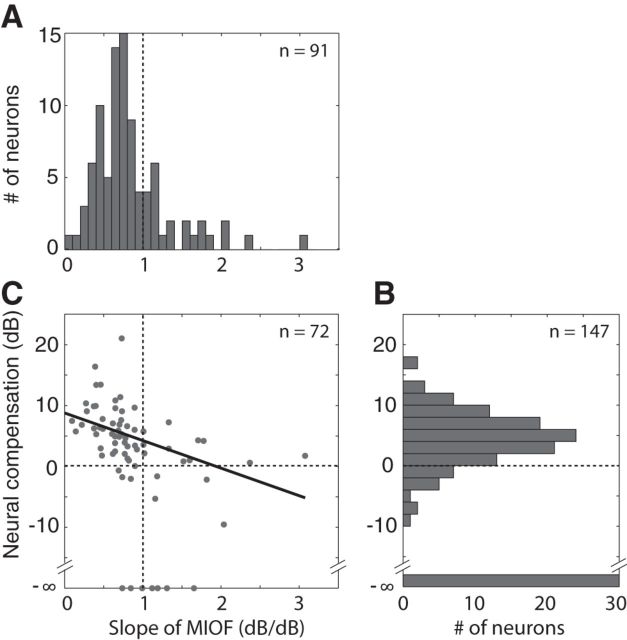
The compressive shape of modulation input-output functions (MIOFs) partially compensates for the attenuation of AM caused by reverberation. A, MIOF from an IC neuron (BF = 4.2 kHz) for f_m = 64 Hz, showing RMD (mean ± 2 SD) as a function of stimulus modulation depth. Thick black line indicates least-squares fit with an incomplete beta function (see Materials and Methods). Green cross represents prediction of reverberant RMD from the MIOF. Red dot indicates measured reverberant RMD. B, MIOF from the same neuron plotted in dB. Dashed line with slope of 1 dB/dB represents identity (0 dB neural modulation gain). The neural modulation gain in the reverberant condition (vertical red arrow) is greater than than the neural modulation gain in the anechoic condition (vertical blue arrow). The difference between reverberant and anechoic modulation gains, or neural compensation, results from the compressive shape of the MIOF (average slope: 0.7 dB/dB).

To quantify the effect of reverberation on temporal coding of AM, we compared the anechoic and reverberant RMDs at the anechoic tBMF. In the example of Figure 2B, the anechoic RMD at tBMF was 1.29, and dropped to a value that was not statistically significant in reverberation. Across our neuronal sample (Fig. 2D), reverberation significantly decreased the median RMD (p < 0.001, Wilcoxon signed rank test). The median decrease in RMD at the tBMF was ∼−0.85 (−9 dB). The median decrease in RMD in strong reverberation (−1.00 or −13 dB) was significantly more negative than the decrease in moderate reverberation (−0.67 or −7.5 dB) (p < 0.01, Wilcoxon rank sum tests). This difference is qualitatively consistent with the lower magnitude of the room MTFs in strong reverberation compared with moderate reverberation (Fig. 1D). When the degradation in AM coding by reverberation was assessed for all tested modulation frequencies rather than just at the anechoic tBMF, the median degradation across the neuronal sample was also highly significant (p < 0.001, Wilcoxon signed rank test) both in moderate reverberation (−0.32 or −4.2 dB) and in strong reverberation (−0.38 or −8.2 dB). There was no significant dependence of neural degradation on BF in our sample. This is in contrast to Kuwada et al. (2014) who found greater degradation for BF ≤2 kHz. Differences in the room characteristics between the two studies may play a role.

Neural compensation and the compressive shape of MIOFs

The observed decrease in RMD in the reverberant conditions relative to the anechoic condition is to be expected because reverberation attenuates AM in the stimulus at the ear. A key question is how the neural degradation in AM coding caused by reverberation compares with the AM attenuation in the stimulus. To address this question, we characterized how RMD varies with the modulation depth of an anechoic stimulus (i.e., we measured neural MIOFs). MIOFs were measured for anechoic SAM broadband noise with modulation depths varying between 0 and 1 in 91 IC single units (see Materials and Methods). MIOFs were usually measured at one f_m, chosen to elicit both a large firing rate and strong phase-locking to the modulation.

Figure 3A (black symbols) shows the MIOF from an example neuron, measured for a 64 Hz f_m. In this example, RMD increased monotonically with stimulus modulation depth with a gradually decreasing slope (i.e., the MIOF was compressive). When the data are replotted in double logarithmic coordinates (Fig. 3B), RMD in dB increases nearly linearly with stimulus modulation depth in dB, with an average slope of 0.7 dB/dB. This linear relationship means that the MIOF is approximately a power function with an exponent of 0.7; that the exponent is <1 implies that the MIOF has a compressive shape.

Assuming that the RMDs for both anechoic and reverberant stimuli only depend on the modulation depth of the stimulus at the ear, we can predict the reverberant RMD from the MIOF and the room MTF. For this f_m, the modulation depth of the moderately reverberant stimulus at the ear was 0.33 (−9.6 dB), which, based on the MIOF in this neuron, should elicit an RMD of 0.87 (−1.2 dB) (Fig. 3A,B, green crosses). The measured RMD for the reverberant stimulus (red dots) did not significantly differ from the prediction (p > 0.05, test of equality of concentration parameters for von Mises distributions; Mardia and Jupp, 1999). This result is representative of approximately half the neurons in our sample.

To further quantify the effect of reverberation on the neural coding of AM, it helps to introduce the neural modulation gain, the ratio of the modulation depth in the neural response (RMD), to the modulation depth of the acoustic stimulus. Figure 3B compares the neural modulation gains for anechoic and reverberant conditions for one neuron using a 64 Hz f_m. Because the ordinate is in dB, the neural modulation gain for a given stimulus is the vertical distance from the dashed diagonal line representing identity (0 dB gain) to the corresponding data point (RMD in dB). Here, the neural modulation gain for the reverberant condition is +9.0 dB (Fig. 3B, red arrow), where the positive sign indicates that the modulation is more pronounced in the neural response than the acoustic stimulus. This reverberant gain is larger than the +4.2 dB neural modulation gain for the anechoic condition (blue arrow). For this neuron, the difference in modulation gains between reverberant and anechoic conditions is a consequence of the compressive shape of the MIOF. Because the slope of the compressive MIOF (0.7 dB/dB) is smaller than the 1 dB/dB slope of the identity line, the neural modulation gain decreases with increasing stimulus modulation depth. Because the reverberant stimulus has a lower modulation depth than the anechoic stimulus, a compressive MIOF will yield a larger neural modulation gain in the reverberant condition than in the anechoic condition for neurons such as that of Figure 3 where the reverberant RMD can be predicted from the anechoic MIOF.

In Materials and Methods (Eqs. 4 and 5), we show that the finding of a larger neural modulation gain for the reverberant condition than for the anechoic condition also means that reverberation causes a smaller degradation in the neural coding of AM than the attenuation of AM in the acoustic stimulus (i.e., there is a form of neural compensation for the effect of reverberation). We thus define the dB difference between the reverberant neural modulation gain and the anechoic neural modulation gain as the “neural compensation.” For the neuron of Figure 3, the reverberant modulation gain was +9.0 dB and the anechoic gain was +4.2 dB, so the neural compensation is +4.8 dB. In this neuron, the positive compensation is linked to the compressive shape of the MIOF.

Figure 4B shows the distribution of neural compensation across the sample of neurons for which both anechoic and reverberant RMDs were obtained at the same f_m (n = 147; data from both strong and moderate reverberant conditions are included). In 30 of these neurons, the neural compensation could not be determined because the reverberant RMD was not statistically significant; these are shown at −∞ in Figure 4B. The neural compensation was positive in 101 of the 117 remaining cases (86%), suggesting that the attenuation in stimulus modulation depth due to reverberation was partially compensated at the level of the IC. The median neural compensation across the 117 neurons was +4.6 dB, which is significantly greater than 0 (p < 0.001, Wilcoxon signed rank test). There was no significant correlation between neural compensation and BF across the neuronal sample. There was also no simple relationship between neural compensation and f_m, although there was a tendency for the neural compensation to be larger at those f_m where the attenuation of AM in the acoustic stimulus was larger.

Figure 4.

Population summary showing the dependence of the neural compensation on MIOF compression. A, Distribution of the mean slope of the MIOF in log–log coordinates across the 91 neurons in which MIOFs were measured. B, Distribution of the neural compensation at tBMF across the 147 cases from 125 neurons for which both anechoic and reverberant RMDs were obtained (measurements were made at both D/R or at 2 modulation frequencies in 22 neurons). Data points for which reverberant RMDs were not statistically significant are shown at −∞ dB. C, Neural compensation against MIOF slope in the 72 neurons for which both types of data were available. Solid line indicates linear regression.

We have argued that the neural compensation is related in part to the compressive shape of the MIOF such that neurons exhibiting the most compressive MIOFs should show a large compensation. As predicted, most MIOFs had a compressive shape, as their mean slopes in log–log coordinates were <1 dB/dB (Fig. 4A). The median slope across the sample of 91 neurons in which a MIOF was measured was 0.73 dB/dB, which is significantly smaller than 1 (p < 0.001, Wilcoxon signed rank test). This result is consistent with previous reports that the modulation gains of IC neurons tend to decrease with increasing stimulus modulation depth (Krishna and Semple, 2000; Nelson and Carney, 2007). Consistent with our hypothesis, there was a significant negative correlation between MIOF slope and neural compensation among the 72 neurons in which both metrics were obtained (Fig. 4C; r = −0.49, p < 0.001). There are two reasons why the correlation between MIOF slope and neural compensation is not higher. First, MIOFs cannot be represented by a single slope because they are not perfectly linear on double logarithmic coordinates. Second, for approximately half the neurons, the measured RMD to reverberant stimuli differed significantly from the prediction based on the MIOF, an important point to which we return in the next section.

Although the vast majority of IC neurons had compressive MIOFs, there was considerable diversity in MIOF shapes among our neurons. Some neurons, such as those of Figures 3A and 8B, had gently compressive shapes such that RMD grew without saturating up to the maximum stimulus modulation depth of 1. This pattern is dominant in auditory nerve fibers (Joris and Yin, 1992) and most ventral cochlear nucleus neurons (Rhode, 1994; Sayles et al., 2013), and has also been reported in some IC neurons (Nelson and Carney, 2007). The MIOFs of other IC neurons (see, e.g., Fig. 7B) grew steeply for low modulation depths and then showed a hard saturation at input modulation depths of 0.3–0.5. This saturating pattern has been reported in ventral cochlear nucleus onset neurons (Rhode, 1994), in superior olivary complex neurons that show an inhibitory rebound after tonal stimulation (Kuwada and Batra, 1999), and in transient responding neurons of the ventral nucleus of the lateral lemniscus (Batra, 2006). Thus, there may be a trend toward stronger MIOF compression in the ascending auditory pathway, although there is considerable variability at each site.

Some neurons show a reverberant coding advantage over anechoic stimuli matched for modulation depth

For the neuron in Figure 3, the RMD to a reverberant stimulus could be predicted from the MIOF measured with anechoic stimuli, suggesting that RMD was entirely determined by the stimulus modulation depth at the ear regardless of whether the stimulus was anechoic or reverberant. Not all neurons behaved this way. The neuron of Figure 5A had a gently compressive MIOF for 16 Hz anechoic stimuli (black dots and fitted curve), with an average slope of 0.71 dB/dB when plotted in log–log coordinates, similar to the neuron of Figure 3. Yet the RMD to the strongly reverberant stimulus (red circle) exceeded the prediction from the MIOF (green cross) by ∼0.52 (+6.9 dB), and the difference was highly significant (p < 0.001, test of equality of concentration parameters for von Mises distributions). Such neurons exhibit a “reverberant coding advantage” over anechoic stimuli having the same modulation depth at the ear.

Figure 5.

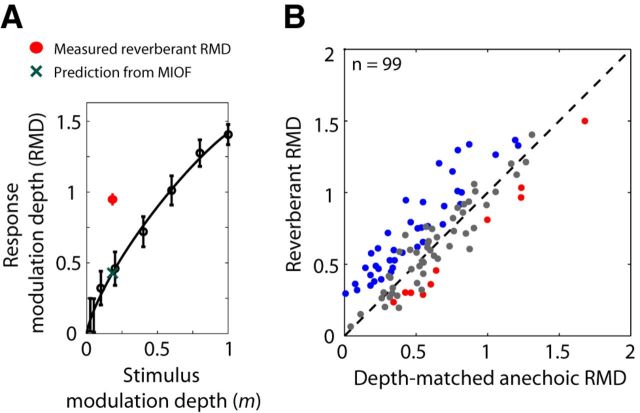
In a population of neurons, reverberant stimuli had a coding advantage over anechoic stimuli after controlling for stimulus modulation depth. A, MIOF from an IC neuron (BF = 4 kHz) for f_m = 16 Hz, showing RMD (mean ± 2 SD) as a function of stimulus modulation depth. Thick black line indicates least-squares fit with an incomplete beta function (see Materials and Methods). Green cross represents prediction of reverberant RMD from the MIOF. Red dot indicates measured strong reverberant RMD. In this example, measured reverberant RMD is significantly greater than the prediction from the MIOF. B, RMD to reverberant stimuli against RMD for diotic, anechoic stimuli with matched modulation depths in the contralateral ear for 99 neurons. In 59 neurons, RMDs were measured in response to depth-matched anechoic stimuli interleaved with the reverberant stimuli. In the 40 other neurons, anechoic data were not collected at the depth of the reverberant stimulus, so the depth-matched anechoic RMD was calculated by taking the value from a curve fit to the MIOF. In both cases, reverberant and depth-matched anechoic RMDs were computed in the steady-state portion of the stimulus (>250 ms). In 39% of the neurons, reverberant RMDs were significantly larger than RMDs for depth-matched anechoic stimuli (blue). In 10% of the neurons, reverberant RMDs were significantly smaller than RMDs for depth-matched anechoic stimuli (red).

We compared measured RMDs to reverberant stimuli with predictions from responses to anechoic stimuli across our sample of neurons (Fig. 5B). Such predictions were obtained in two ways. For neurons in which a MIOF was measured, the fitted curve (see Materials and Methods) was interpolated at the modulation depth of the reverberant stimulus to obtain the prediction (Fig. 3A, green cross). In other neurons, we directly measured responses to anechoic stimuli whose modulation depths matched those of reverberant stimuli (see Materials and Methods). Across the sample of IC neurons, there was a strong correlation (r = 0.84, p < 0.001) between reverberant RMDs and predictions from responses to depth-matched anechoic stimuli (Fig. 5B), confirming that the modulation depth at the ear is an important determinant of temporal coding of AM for reverberant stimuli. For 51% of the neurons (Fig. 5B, gray dots), the difference in RMD between reverberant and depth-matched anechoic conditions was not statistically significant (p > 0.05, test of equality of concentration parameters for von Mises distributions). However, in 39% of neurons (example neuron in Fig. 5A, and blue dots in Fig. 5B), the reverberant RMD was significantly greater than the RMD for the depth-matched anechoic stimulus. The median reverberant coding advantage for these neurons was 0.22 (+3.7 dB). A smaller number of neurons (10%, Fig. 5B, red dots), showed the opposite effect, where the RMD to the reverberant stimulus was significantly lower than the RMD for the depth-matched anechoic stimulus; the median difference between reverberant and matched anechoic RMDs for these neurons was −0.18 (−2.9 dB).

The finding of a reverberant advantage (or disadvantage) in almost half the neurons means that acoustic properties of reverberant stimuli other than the modulation depth of the stimulus at the ear influence the temporal coding of AM in reverberation for these neurons. Before presenting results of experiments aimed at identifying what other stimulus properties influence reverberant RMDs, we first show that the reverberant advantage cannot be accounted for by cochlear filtering or by the dynamics of reverberant energy.

Cochlear filtering does not account for the reverberant coding advantage

Our method for matching the modulation depth of an anechoic stimulus to that of a reverberant stimulus controls for the modulation depth of the broadband stimulus waveform presented in the ear canal, but does not take into account possible differential effects of cochlear filtering on the two types of stimuli. In general, filtering will alter the modulation depth of AM signals, with the effect size depending primarily on the duration of the filter impulse response relative to the modulation period (Houtgast et al., 1980). Although reverberant and depth-matched anechoic stimuli both undergo the same cochlear filtering, the spectral distortion introduced by the reverberant BRIR may result in differential effects of cochlear filtering on modulation depth for the two stimuli. This effect, in turn, might yield an apparent reverberant advantage (or disadvantage) in the responses of frequency-selective IC neurons that receive predominant inputs originating from a given cochlear place.

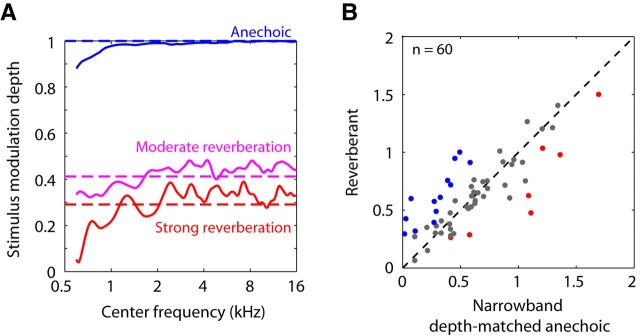
To test for this possibility, the effect of cochlear filtering on modulation depth was simulated by processing our anechoic and reverberant stimuli with gammatone filters having equivalent rectangular bandwidths matching those of frequency tuning curves from rabbit auditory nerve fibers (Borg et al., 1988). Modulation depths at the filter output were computed as a function of filter center frequency. Results are shown in Figure 6A for f_m = 32 Hz; results for other f_m were qualitatively similar. For the anechoic stimulus with a modulation depth of 1 (blue), simulated cochlear filtering reduced the modulation depth somewhat at low center frequencies (<1.2 kHz) but had little effect at higher frequencies, where most of our neurons' BFs are located. For reverberant stimuli, modulation depths after simulated cochlear filtering also deviated most from the broadband modulation depths (dashed lines) for low center frequencies, but there were additional fluctuations as a function of center frequency, even in the range >1 kHz. In strong reverberation, these fluctuations reached peak amplitudes of 34% (2.5 dB difference in modulation depth). These fluctuations likely result from the distortions in spectral fine structure introduced by the reverberant BRIRs on the SAM noise stimulus.

Figure 6.

Effect of cochlear filtering on temporal coding of reverberant stimuli. A, Modulation depths of anechoic and reverberant stimuli with f_m = 32 Hz after processing by gammatone filters of equivalent rectangular bandwidths matching those of rabbit auditory nerve tuning curves (Borg et al., 1988). Modulation depths are plotted against filter center frequency. Dashed lines indicate modulation depths of the broadband noise stimulus in the ear canal. B, Scatter plot of reverberant RMD against RMD of depth-matched anechoic stimulus after simulated cochlear filtering for 60 IC neurons for which both a BF and a MIOF were measured. In 22% of the neurons, reverberant RMDs were significantly larger than RMDs for narrowband depth-matched anechoic stimuli (blue). In 12% of the neurons, reverberant stimuli had a significant coding disadvantage over narrowband depth-matched anechoic stimuli (red).

A two-step method was used for testing whether the differences in RMD apparent in Figure 5 between reverberant stimuli and depth-matched anechoic stimuli (the reverberant advantage and disadvantage) could be accounted for by the effects of cochlear filtering. This test was applied to all 60 neurons for which the MIOF, the reverberant RMD, and the BF had all been measured. The first step was to remap the abscissa of the measured MIOF to represent the modulation depth at the output of the simulated cochlear filter centered at the neuron's BF, rather than the modulation depth in the ear canal. In the second step, the remapped MIOFs were evaluated at the modulation depth of the reverberant stimulus after cochlear filtering around the BF to generate a prediction for the reverberant RMD. For most neurons, the differences between the original RMD predictions based on broadband modulation depths and the revised predictions taking into account cochlear filtering were small (median absolute difference 0.043, standard deviation 0.055). This was expected given that differences between filtered and unfiltered stimulus modulation depths were moderate and that the compressive nature of MIOFs would tend to further attenuate these differences.

Figure 6B shows a scatter plot of measured reverberant RMDs against the revised predictions from the anechoic MIOF taking into account cochlear filtering. Measured and predicted reverberant RMDs did not significantly differ (p > 0.05) in 40 of the 60 neurons (67%, gray dots). In 13 neurons (22%, blue dots), reverberant stimuli had a significant coding advantage over depth-matched anechoic stimuli, whereas in 7 neurons (12%, red dots), reverberant stimuli had a significant coding disadvantage. Therefore, in one-third of the neurons (20 of 60), the measured RMD for reverberant stimuli significantly differed from the predictions derived from depth-matched anechoic stimuli after taking into account cochlear filtering. This fraction compares to 41% (25 neurons) when using the original method based on broadband modulation depths to predict reverberant RMDs in the same sample of 60 neurons. These results suggest that cochlear filtering cannot explain the observed differences in temporal coding between reverberant and depth-matched anechoic stimuli.

Time course of reverberant responses

So far, we have described the temporal coding of AM for reverberant stimuli in the “steady-state” (>250 ms after stimulus onset). However, reverberation degrades the modulation depth of AM stimuli in a time-dependent fashion (Fig. 1C): Unlike anechoic stimuli for which modulation depth is constant, the modulation depth of a reverberant stimulus sharply decreases over the first 250 ms of the stimulus before reaching a plateau, consistent with the buildup of reverberant energy over time. Devore et al. (2009) found that IC neurons have more reliable directional sensitivity to azimuth in the early portion of a reverberant stimulus, when sound localization cues are minimally degraded by acoustic reflections. They further showed that firing rate adaptation emphasized the early part of the response when localization cues are reliable, over the later response when cues are strongly degraded, thereby partially counteracting the degradation of sound localization cues by reverberation. We hypothesized that a similar mechanism might operate for the temporal coding of AM, such that the coding would be better in the early portion of the reverberant stimuli, when the stimuli show stronger modulation.

To test whether the time course of temporal coding of AM in reverberation mirrors the time course of AM in the reverberant stimulus, we compared the time course of RMD for the reverberant stimulus to a prediction based on the time course of modulation depth in the stimulus as transformed by the MIOF, assumed to operate instantaneously. The effect of cochlear filtering on stimulus modulation depth was taken into account for these analyses in the same way as in the previous section. Figure 7 shows results from an example neuron. The time course of modulation depth in the 45 Hz reverberant stimulus (Fig. 7A) was characterized, as is typical, by a sharp decay over the first 250 ms of the stimulus followed by a plateau. The MIOF for this neuron (Fig. 7B) increased steeply for modulation depths <0.3, before saturating to an RMD of ∼1.4. We used the MIOF and the time course of stimulus modulation depth to predict the time course of the reverberant RMD (Fig. 7C, black dashed line). The prediction resembles the time course of modulation depth in the reverberant stimulus, consistent with the monotonicity of the MIOF, although the predicted RMD exceeds the stimulus modulation depth because the neural modulation gain is >1. The peristimulus time histogram of the measured reverberant response in this neuron (Fig. 7D) shows a peak in firing rate near stimulus onset, followed by phase-locking to the 45 Hz modulation frequency throughout the entire 2 s duration of the stimulus. This phase-locking was quantified by the RMD (Fig. 7C, red solid line), which shows a sharp decay, followed by a plateau at an RMD of ∼1. In this neuron, the time course of the reverberant RMD was reasonably well predicted by the time course of modulation depth in the reverberant stimulus as transformed by the MIOF.

Figure 8 shows results from another neuron, using f_m = 16 Hz, where the reverberant RMD and the MIOF-based prediction differed markedly. The MIOF (Fig. 8B) had a nonsaturating profile with smaller modulation gains than in Figure 7. The decaying time course of modulation depth in the reverberant stimulus (Fig. 8A) was mirrored in the prediction of RMD (Fig. 8C, black dashed line), which reached a plateau at ∼0.4. The measured RMD for the reverberant stimulus (Fig. 8C, red line) also showed a sharp decay near stimulus onset but, in contrast to the prediction, increased between 200 ms and 1 s to reach a high plateau of ∼1.1. This increase in modulation depth following the initial dip is clearly visible in the peristimulus time histogram as well (Fig. 8D). In this example, the MIOF poorly predicted the time course of reverberant RMD, and the measured RMD was substantially higher than the prediction (i.e., there was a large reverberant coding advantage). Unexpectedly, this advantage was larger in the later portion of the response, when the modulation depth of the reverberant stimulus has decayed to a minimum.

The neurons in Figures 7 and 8 both showed an initial decay in RMD for reverberant stimuli. Such a decay was frequently (but not consistently) observed across our neuronal sample. To test whether this decay reflects the temporal profile of stimulus modulations, we also measured the time course of RMD for an anechoic stimulus whose modulation depth matched the steady-state modulation depth of the reverberant stimulus in a subset of neurons. If the sharp initial decay of the reverberant RMD reflected the time course of stimulus modulation, then RMD should be constant for this depth-matched anechoic stimulus, which has a constant modulation depth throughout the stimulus. However, for the neuron of Figure 8, the time course of RMD for the depth-matched anechoic stimulus (Fig. 8C, green line) showed a similar initial decay and recovery as for the reverberant stimulus, despite the flat profile of stimulus modulations in the anechoic case. This suggests that the initial decay results from intrinsic dynamic properties of the neuron rather than from the decay of stimulus modulations.

We compared the reverberant RMD computed in a short time window at stimulus onset (with width equal to the smallest integer number of modulation cycles >20 ms) to the “ongoing” RMD computed over the remainder of the response across our sample of neurons. On average, onset RMD was larger than ongoing RMD (Wilcoxon signed rank test, p < 0.001) consistent with the decaying time course of stimulus modulations. However, the same analysis performed on the static, depth-matched anechoic stimuli led to a similar onset preference. Across the neuronal sample, onset preferences for reverberant and depth-matched anechoic stimuli were highly correlated (r = 0.86, p < 0.001), suggesting that they were shaped by intrinsic properties of the neuron rather than by the time course of modulation depth in the acoustic stimulus.

Responses to hybrid anechoic stimuli that match select properties of reverberant stimuli

In the preceding sections, we have shown that neither the time course nor the steady-state value of RMD for reverberant stimuli can consistently be predicted from the stimulus modulation depth at the ear, as transformed by the MIOF. Approximately one-third of the neurons showed a significant steady-state reverberant advantage (or disadvantage) over anechoic stimuli matched for modulation depth, and, in some neurons, the time course of reverberant RMD followed a different trend from that of modulation depth in the reverberant stimulus (see, e.g., Figs. 8C and 10C). Reverberation alters not only modulation depth, but also other stimulus properties, such as envelope shape and interaural cross-correlation, and also introduces spectral coloration and interaural envelope disparities. We tested the influence of some of these acoustic properties on RMD in an attempt to explain the observed differences in RMD between reverberant and depth-matched anechoic stimuli. Our approach was to create hybrid anechoic stimuli (Table 1) that possessed selected properties of reverberant stimuli as well as matched modulation depths, and compare the neural responses to these hybrid stimuli with responses to reverberant stimuli.

Envelope distortion

One difference between reverberant and depth-matched anechoic stimuli that might explain the reverberant advantage/disadvantage is the shape of the amplitude envelopes. Anechoic stimuli have a sinusoidal envelope throughout the stimulus duration (Fig. 9A). In contrast, reverberation slightly distorted the envelope, making the average envelope period more asymmetric and somewhat peakier than a sinusoid (Fig. 9A). For all modulation frequencies and both reverberation strengths, the deviations from a sinusoidal envelope were small. However, because the shape of the envelope is known to have notable effects on responses of IC neurons (Sinex et al., 2002; Krebs et al., 2008; Zheng and Escabí, 2008), we tested the possibility that envelope distortions introduced by reverberation might be responsible for the observed RMD differences between reverberant and depth-matched anechoic stimuli.

To test this hypothesis, we extracted the average envelope period in the steady-state portion of the reverberant stimulus and used this average envelope to modulate broadband noise (see Materials and Methods). The resulting modulated noise was then filtered by the anechoic room impulse response, resulting in a hybrid anechoic stimulus with the same modulation depth and average envelope waveform as the reverberant stimulus. This hybrid stimulus was presented diotically. Figure 9B shows data from one neuron (f_m = 16 Hz, same neuron as in Fig. 8), in which RMD was significantly larger for the reverberant stimulus (red solid line) than for the sinusoidal, depth-matched anechoic stimulus (green dashed line). The RMD for the envelope-matched anechoic stimulus (blue solid line) was very similar to that for the sinusoidal anechoic stimulus, and much lower than the RMD to the reverberant stimulus, suggesting that envelope distortions cannot explain the large reverberant advantage in this neuron.

Across the sample of neurons (Fig. 9C), RMDs for envelope-matched anechoic stimuli were highly correlated with RMDs for sinusoidal, depth-matched anechoic stimuli (r = 0.97, p < 0.001) and the median RMDs did not significantly differ between the two stimulus conditions (p = 0.09, Wilcoxon signed rank test). Only 4 of 29 neurons had significant differences in RMD between the two conditions (p < 0.05, test of equality of concentration parameters), but even in these cases, differences were small (∼0.1). On the other hand, median RMDs across the population were significantly greater for reverberant stimuli than for envelope-matched stimuli (Fig. 9D; median difference, 0.14; Wilcoxon signed rank test, p = 0.004). Fifteen of 28 neurons showed a significant reverberant coding advantage over the envelope-matched, anechoic condition (Fig. 9D, blue dots). Together, these tests indicate that the small envelope distortions created by reverberation do not explain the observed reverberant advantages and disadvantages.

Interaural cross-correlation (IACC)

Because our sound source was located at 0° azimuth, the signals at the two ears were identical in the anechoic condition and therefore the IACC was always 1. In the reverberant case, the superimposed reflections from different directions occur at different times and with different amplitudes at the two ears, resulting in substantial decorrelation of the binaural signals (IACC < 1). The effect of reverberation on the time course of short-time IACC (computed over time windows of 780 μs) is illustrated in Figure 10A for 32 Hz modulations. The short-time interaural coherence (the peak IACC across interaural time differences) of the anechoic stimulus was nearly 1 throughout the stimulus duration (Fig. 10A, left, dashed line). In contrast, the interaural coherence of the reverberant stimulus starts near 1 at stimulus onset (before decorrelating reflections reach the ears) and then decays before settling in an oscillatory pattern at the 32 Hz modulation frequency (Fig. 10A, right, thin red line). The mean interaural coherence in the oscillating part of the stimuli was 0.74 in strong reverberation (thick red line) and 0.85 in moderate reverberation for all modulation frequencies.

To test the possibility that the decrease in mean IACC caused by reverberation may be responsible for the observed differences in RMD between reverberant and depth-matched anechoic stimuli, we synthesized hybrid stimuli for which both the mean interaural coherence and modulation depth matched those of the reverberant stimuli in the steady state (see Materials and Methods). Figure 10B, C shows data from two neurons. In the first neuron (Fig. 10B), the reverberant RMD (red line) was significantly larger than RMD to the IACC-matched stimulus (blue line), whereas the latter was very similar to the RMD to the diotic, depth-matched anechoic stimulus (green, dashed line). Therefore, in this neuron, mean IACC did not greatly influence the RMD, so that differences in IACC could not explain the substantial reverberant advantage. In contrast, in the neuron of Figure 10C, which showed a reverberant disadvantage, the RMD to the IACC-matched anechoic stimulus was significantly lower than the RMD to the diotic anechoic stimulus and was similar to the RMD for the reverberant stimulus, suggesting that decorrelation contributed to the reverberant disadvantage in this neuron.

Across the sample of neurons (Fig. 10D), the IACC-matched RMDs were strongly correlated with the diotic anechoic RMDs (r = 0.74, p < 0.001) and the median RMDs were not significantly different between the two conditions (p = 0.38, Wilcoxon signed rank test). Nevertheless, decorrelation significantly decreased RMD in 7 of 29 neurons (red dots) and also increased RMD in 2 neurons (blue dots). Overall, RMD was significantly altered by a static decorrelation in nearly one-third of the neurons, and the decrease in RMD resulting from decorrelation relative to the diotic stimulus could be quite substantial (>0.2 in some neurons). On the other hand, the median RMD across the population was significantly greater in the reverberant condition than in the IACC-matched condition (Fig. 10E; median difference, 0.11; Wilcoxon signed rank test, p < 0.001), and the reverberant RMD was significantly greater than the RMD for the IACC-matched, anechoic stimulus in 14 of 33 neurons (Fig. 10E, blue dots). Together, these tests indicate that, although decorrelation influences RMD in some neurons, the differences in RMD between reverberant and depth-matched anechoic stimuli cannot be entirely accounted by the effects of static decorrelation.

One limitation of this test is that our IACC-matched anechoic stimulus only reproduced the average IACC over the later part of the reverberant stimulus but did not include the periodic fluctuations in IACC at the modulation frequency (Fig. 10A). This important point is addressed in the Discussion.

Other properties of reverberant stimuli

We further tested the effect of other acoustic properties, alone or in combination, that differed between reverberant and anechoic stimuli. For the sake of brevity, only a selection of these tests is described here and the results are presented in minimal detail.

In addition to decorrelating the temporal fine structures of the binaural signals, reverberation also introduces interaural envelope disparities (IEDs), small differences between the envelopes of the left and right ear input signals. Specifically, reverberation introduces a small envelope interaural phase difference (∼0.01 cycle in moderate reverberation and ∼0.03 cycle in strong reverberation) and a small difference in modulation depth across the two ears (∼0.03 on average in both reverberant conditions). The effects of IED were tested by creating hybrid stimuli that had the same envelope shape in each ear (and therefore the same IEDs) as the reverberant stimuli. Comparing neural responses between these IED-matched stimuli and diotic depth-matched stimuli showed a small effect of IED in some neurons, but the effects were too small to explain the reverberant advantage overall.

Filtering by the reverberant BRIRs introduces spectral coloration to the broadband noise carrier, which has a flat power spectrum in the anechoic condition. Specifically, the frequency responses of the reverberant BRIRs consist of the superposition of a large number of spectral notches at frequencies corresponding to the inverse of the intervals between individual reflections. When analyzed over bandwidths matching those of cochlear filters in rabbit (Borg et al., 1988), the power spectra of reverberant stimuli rarely deviated by >1 dB from the spectrum of the anechoic stimulus. We tested the effect of spectral coloration by creating hybrid anechoic stimuli that had both the same power spectrum and the same modulation depth as the reverberant stimuli. For the most part, RMDs for these colored stimuli were similar to RMDs for flat-spectrum, anechoic stimuli, suggesting that coloration had very little influence on AM coding in our neurons.

Reverberation degrades rate coding of amplitude modulation

In the previous sections, we focused on the effect of reverberation on the temporal coding of AM. Because the firing rates of many IC neurons are tuned to specific modulation frequencies (e.g., Langner and Schreiner, 1988; Joris et al., 2004), modulation frequency may also be coded in the firing rates of IC neurons. To investigate the effect of reverberation on rate coding of modulation frequency, rMTFs were constructed by plotting the average firing rates to both anechoic and reverberant stimuli against f_m. Results from three neurons are shown in Figure 11A–C, illustrating the diversity of rMTFs encountered. In Figure 11A, the anechoic rMTF was bandpass with high firing rates and a best modulation frequency (rBMF) of 90 Hz; in Figure 11B, the rMTF was lowpass; and in Figure 11C, it was bandpass with lower firing rate than in Figure 11A and an rBMF near 45 Hz. The anechoic rBMFs from these neurons are representative of the range encountered in our sample (4–256 Hz with a median at 32 Hz) and are consistent with previous studies in unanesthetized animals (Nelson and Carney, 2007; Ter-Mikaelian et al., 2007).

Figure 11.

Effects of reverberation on neural representation of modulation frequency by average firing rate. A–C, Rate modulation transfer functions (rMTF; mean firing rate ± 2 SEs) for anechoic (blue) and reverberant (red) stimuli in three IC neurons. Strength of modulation frequency representation in the rMTF was quantified by a signal-to-noise ratio (SNR) metric based on ANOVA (see Materials and Methods). A, BF = 0.8 kHz. B, BF = 3.9 kHz. C, BF = 8 kHz. D, Scatterplot of neural SNR in reverberant condition against SNR in anechoic condition across 110 neurons.

For these three neurons, reverberation could either decrease (Fig. 11A) or increase (Fig. 11B) the firing rates to SAM stimuli, or both increase and decrease firing depending on f_m (Fig. 11C). In all three cases, the net effect of reverberation was to flatten the rMTF, thereby degrading the rate coding of f_m. To quantify this degradation, we used a signal-to-noise ratio (SNR) metric for rate coding of f_m based on ANOVA (see Materials and Methods). The larger the variance in mean firing rates across f_m (signal), the larger the SNR. The larger the variance in firing rate across repetitions of a given f_m (noise), the lower the SNR. In Figure 11A, the SNR was 13.5 dB in the anechoic case, and dropped to 3.9 dB in moderate reverberation, consistent with the flattening of the rMTF. In Figure 11B, C, reverberation also lowered the SNR by ∼10 dB. Across the sample of neurons (Fig. 11D), reverberation significantly lowered the SNR (p < 0.001, Wilcoxon signed rank test), indicating a degradation in rate coding of AM. The median degradation in SNR across the population was −7.3 dB. Unexpectedly, the median degradation in strong reverberation (−8.7 dB) did not significantly differ from the median degradation in moderate reverberation (−6.7 dB) (p = 0.084, Wilcoxon rank sum test). We could not assess whether IC neurons would show a reverberant advantage in rate coding of AM paralleling the observed temporal coding advantage because responses to depth-matched anechoic stimuli were not measured at a sufficient number of modulation frequencies.

Discussion

Using single-unit recordings from the IC of unanesthetized rabbit, we found that reverberation degrades the neural coding of amplitude modulation for broadband noise stimuli. However, in most neurons, the degradation in temporal coding was smaller than the attenuation of AM in the acoustic stimulus, and this form of compensation was largely explained by the compressive shape of the transformation from stimulus modulation depth into neural modulations (MIOF). Additionally, in a subset of neurons, the reverberant stimuli had a significant temporal coding advantage or (more rarely) disadvantage over anechoic stimuli after matching the modulation depths at the ear. Together, these results suggest the existence of both reverberation-specific and nonspecific compensation mechanisms that maintain temporal envelope coding in reverberant environments.

Use of virtual auditory space stimuli

The room-image method used to generate reverberant stimuli provided the key characteristics of reverberant impulse responses measured in real rooms (Hartmann et al., 2005; Shinn-Cunningham et al., 2005), including a direct sound, individual early reflections from room surfaces, and the dense superposition of late reflections arriving from many directions. The spherical model used for the rabbit head ensured that our stimuli contained binaural cues, although this model somewhat underestimates interaural-level differences (Kim et al., 2010). Several studies support the resemblance of simulated reverberation to acoustic measurements in rooms (Allen and Berkley, 1979; Shinn-Cunningham et al., 2001). Furthermore, only small perceptual differences are found when comparing speech samples convolved with simulated and measured BRIRs with matched acoustic parameters (Zahorik, 2009).

Yet, a limitation of our study is the use of a single room and a single source direction for all our experiments. It will be important in further work to investigate similar questions using more than one direction and additional room characteristics (Kuwada et al., 2014). However, given that BRIRs depend in a complex manner on room characteristics and the positions of the sound source and the listener within a room, any reverberation compensation mechanism that may exist in the auditory system is likely to operate robustly in most rooms rather than being tuned to the detailed characteristics of specific rooms.

Importance of MIOFs for AM coding in reverberation

In a vast majority of IC neurons, the neural modulation gain was larger for reverberant stimuli than for acoustic stimuli, resulting in a positive “neural compensation” (Fig. 4). This means that reverberation did not degrade the neural coding of modulation as much as it attenuated the modulation in the acoustic stimulus. The finding of larger neural modulation gains for reverberant stimuli is consistent with the report by Kuwada et al. (2012, 2014) when the distance to the sound source is sufficiently large. However, because Kuwada et al. (2014) did not compare RMDs to reverberant stimuli with RMDs to anechoic stimuli having the same modulation depth at the ear, it is not possible to determine from their results whether the observed compensation can simply be accounted for by the reduced modulation depth of reverberant stimuli and the compressive shape of MIOFs, which results in higher modulation gains for stimuli with smaller modulation depths.

Across our sample, neurons with more compressive MIOFs tended to show a greater amount of reverberant compensation (Fig. 4). Moreover, there was a strong correlation between the RMD for reverberant stimuli and RMD for anechoic stimuli having matched modulation depth at the ear, which incorporate the effect of MIOF compression (Fig. 5B). Together, these results suggest that the compressive shapes of most MIOFs are a major determinant of neural reverberant compensation in the IC. A compressive MIOF means that the neural modulation gain decreases with increasing modulation depth of the stimulus. Decreasing modulation gains with increasing depth have been reported in previous studies of the neural coding of SAM tones in the auditory nerve (Joris and Yin, 1992), ventral cochlear nucleus (Rhode, 1994; Sayles et al., 2013), superior olivary complex (Kuwada and Batra, 1999), ventral nucleus of the lateral lemniscus (Batra, 2006; Zhang and Kelly, 2006), and IC (Rees and Møller, 1983; Müller-Preuss et al., 1994; Krishna and Semple, 2000; Nelson and Carney, 2007). Our results extend these findings to broadband noise carriers and demonstrate their importance to robust AM coding in reverberation.

A compressive MIOF enhances the neural representation of the small modulations that occur in reverberant settings relative to the larger modulations occurring in anechoic spaces, but the mechanism is not specific to reverberation. Compressive MIOFs will also enhance the neural coding of AM in other common conditions that result in small modulation depths, such as the presence of background noise or other competing sounds. Even though our anechoic stimuli were always presented diotically, this mechanism is likely to be effective for both monaural and binaural stimulation, as most of the studies that reported decreasing neural modulation gains in IC neurons (Krishna and Semple, 2000; Nelson and Carney, 2007) used monaural stimulation of the contralateral ear.

That compressive MIOFs are observed in auditory nerve fibers (Joris and Yin, 1992) suggests the compression may be partly of cochlear origin. If so, the reduced cochlear compression frequently associated with sensorineural hearing loss (e.g., Moore and Oxenham, 1998; Oxenham and Bacon, 2003) may contribute to the degradation in speech reception commonly experienced by hearing impaired listeners in reverberant environments (Nábělek and Pickett, 1974; Duquesnoy and Plomp, 1980; Payton et al., 1994).

Reverberant advantage over anechoic stimuli with matched modulation depth

Although stimulus modulation depth was a primary determinant of temporal coding of AM in reverberation for a majority of neurons, in 30%–50% of the neurons, the RMD for reverberant stimuli significantly differed from the RMD for anechoic stimuli with matched modulation depths at the ear, and these deviations were more often than not in the direction of a coding advantage for reverberant stimuli (Fig. 5B). Simulations of cochlear filters in rabbit suggested that these deviations cannot be accounted for by any differential effects of cochlear filtering on anechoic versus reverberant stimuli (Fig. 6B).

The existence of a reverberant advantage or disadvantage means that the temporal coding of AM is influenced by other properties of reverberant stimuli besides their modulation depth at the ear. To identify acoustic properties that contribute to the reverberant advantage/disadvantage, we measured neural responses to hybrid stimuli that possessed selected features of reverberant stimuli. We specifically tested the effects of envelope distortion, spectral coloration, interaural envelope disparities, and average interaural coherence. None of these reverberant features, either solely or in combination, could account for the reverberant advantage/disadvantage, although envelope disparities and IACC influenced RMD in some neurons.

The hybrid stimuli designed to test the effect of IACC matched the mean IACC of the reverberant stimuli but did not reproduce the fluctuations in short-time IACC at f_m that occur in reverberation (Fig. 10A). These IACC fluctuations arise because, near a peak of the stimulus envelope, the reverberant stimulus is more dominated by the direct sound, and therefore the IACC is relatively high; conversely, near a trough of the envelope, reverberant energy from the previous modulation cycle dominates the reverberant stimulus, thereby decreasing IACC.

We suggest that the interaction between the fluctuations in IACC and the envelope modulation at the same f_m may influence the temporal coding of AM by IC neurons for reverberant stimuli. Binaural neurons in IC (Joris et al., 2006) and the dorsal nucleus of the lateral lemniscus (Siveke et al., 2008) phase-lock to modulations in the IACC of unmodulated broadband noise. This sensitivity to fluctuations in IACC is likely to arise at the sites of primary binaural interaction in the superior olivary complex although this has not been experimentally tested. That the reverberant advantages and disadvantages in our IC neurons were relatively modest is consistent with the small size of IACC fluctuations in the reverberant stimuli (0.08–0.36 depending on f_m and distance to the source). Across our sample of neurons, there was a significant correlation (r = 0.44, p = 0.01) between the reverberant coding advantage/disadvantage and the depth of IACC modulation in the reverberant stimulus, suggesting that these neurons were sensitive to IACC fluctuations at the depths present in the reverberant stimuli.

The interaction between amplitude modulations and fluctuations in IACC can potentially account for both the reverberant coding advantage and the less common disadvantage because the effect of the interaction will depend on the type of neural sensitivity to interaural time differences (ITD). In neurons with “peak-type” sensitivity to ITD, firing rate grows with increasing IACC, whereas firing rate varies inversely with IACC in “trough-type” neurons (Shackleton et al., 2005; Devore and Delgutte, 2010). If the modulations in amplitude and IACC occur nearly in phase in the reverberant stimulus (which is the case for low f_m), the two forms of modulations will act in synergy for a peak-type neuron, thereby leading to a reverberant coding advantage, whereas the effects of the two modulations will be antagonistic for trough-type neurons, leading to a reverberant disadvantage. Further work is needed to directly test this hypothesis. Investigating these effects using more than one source direction will be important as IACC and its fluctuations depend strongly on azimuth.

Kuwada et al. (2014) observed larger neural modulation gains for reverberant stimuli than for anechoic stimuli using monaural stimulation as well as binaural stimulation. This observation is consistent with our proposed binaural mechanism based on sensitivity to IACC fluctuations if the neural compensation observed by Kuwada et al. (2014) in the monaural condition results from MIOF compression. The modulation depths of reverberant and anechoic stimuli must be matched to assess whether there is a genuine reverberant coding advantage.

Whatever the mechanisms underlying the reverberant coding advantage in IC neurons, the existence of such neurons is consistent with reports of a reverberant advantage in human detection of AM (Zahorik et al., 2011, 2012). These authors found that modulation detection thresholds for SAM broadband noise presented in simulated reverberation could be 4–6 dB lower than predicted from AM detection thresholds in anechoic condition and the room MTF. This reverberant advantage was more pronounced for binaural presentation than for monaural presentation, consistent with our hypothesis that sensitivity to dynamic IACC may play a role. Other studies have reported binaural benefits for modulation detection (Danilenko, 1969) and speech reception (Koenig, 1950; Moncur and Dirks, 1967; Helfer, 1994; Libbey and Rogers, 2004; Brandewie and Zahorik, 2010) in reverberant conditions. Together, these results suggest that binaural processing plays an important role for speech reception in reverberation and that the mechanisms underlying the reverberant advantage for the neural coding of AM may also play a role for speech reception.

Conclusion

Using single-unit recordings from the auditory midbrain of unanesthetized rabbit, we identified two distinct mechanisms that partially compensate for the attenuation of amplitude modulation caused by reverberation in the acoustic inputs to the ears. The first one is a general mechanism linked to the compressive shapes of MIOFs. This mechanism may be partly of peripheral origin and is likely to play a role in any task that involves the detection of small modulations against a background sound. The second mechanism, found in approximately one-third of the neurons, is very specifically linked to the acoustic properties of reverberant stimuli. Although this was not tested in our experiments, we suggest that this second mechanism may result from an interaction between neural sensitivities to AM and dynamic IACC. Both mechanisms have correlates in human psychophysics.