On Optimal Treatment Regimes Selection for Mean Survival Time

Abstract

In clinical studies with time-to-event as a primary endpoint, one main interest is to find the best treatment strategy to maximize patients’ mean survival time. Due to patient’s heterogeneity in response to treatments, great efforts have been devoted to developing optimal treatment regimes by integrating individuals’ clinical and genetic information. A main challenge arises in the selection of important variables that can help to build reliable and interpretable optimal treatment regimes since the dimension of predictors may be high. In this paper, we propose a robust loss-based estimation framework that can be easily coupled with shrinkage penalties for both estimation of optimal treatment regimes and variable selection. The asymptotic properties of the proposed estimators are studied. Moreover, a model-free estimator of restricted mean survival time under the derived optimal treatment regime is developed and its asymptotic property is studied. Simulations are conducted to assess the empirical performance of the proposed method for parameter estimation, variable selection, and optimal treatment decision. An application to an AIDS clinical trial data set is given to illustrate the method.

1. Introduction

Personalized medicine has received much attention in treating complex diseases, such as cancer, AIDS, and mental disorders. Numerous studies have been dedicated to finding optimal treatment regimes in the past. A treatment regime is a rule of assigning patients to a specific treatment according to their characteristics, such as demographic information, clinical measurements, genetic information, and etc. An optimal treatment regime is supposed to produce the best clinical outcome on average if all the patients are treated accordingly. Personalized medicine has aroused great interest among clinicians, statisticians, and public policy makers.

In the literature, various approaches have been proposed to estimate optimal treatment regimes, such as Q-learning [1, 2] and A-learning [3, 4, 5]. Recently, [6] proposed a robust estimation method for the mean response under a given treatment regime based on the inverse probability of propensity scores weighted (IPW) estimation and extended it to the augmented IPW estimation with the double robustness. Then, an optimal treatment regime is obtained by directly maximizing the estimated mean response over all possible treatment regimes in a specified class. The outcome weighted learning (OWL) proposed by [7] transforms the problem of maximizing the estimated mean response over all possible treatment regimes into minimizing the associated weighted classification error, which is solved by weighted support vector machine. In addition, [8] proposed a general framework for estimating the optimal treatment regimes from a classification perspective.

In many clinical studies, a primary endpoint is time-to-event and a main interest is to find the best treatment regime to maximize patients’ mean survival time. For example, in our motivating study from the AIDS Clinical Trials Group Protocol 175 (ACTG175) [9], a primary endpoint was time to first ≥ 50% decline in CD4 count, an AIDS-defining event or death, recorded in days. Patients were randomized to four treatment groups and showed difference in survival between treatment groups. Moreover, in many clinical studies, a large amount of prognostic factors may be available, such as genetic information, clinical measures, as well as some social, environmental and behavior characteristics. However, not all of them are useful for selecting the best treatment for patients. This urges the need to integrate variable selection with optimal treatment regime estimation since it can lead to a parsimonious, interpretable and reliable treatment rule for practical use. In the context of classical regression settings, shrinkage methods, such as least absolute shrinkage and selection operator (LASSO) penalty [10], smoothly clipped absolute deviation (SCAD) penalty [11] and adaptive LASSO penalty [12], have been widely used for variable selection due to their superior empirical and theoretical properties. However, they are less studied in the estimation of optimal treatment regimes. One main challenge is that in the context of optimal treatment regimes, we are interested in the interaction between treatments and predictors, but not the baseline effects of predictors. Recently, there are a few developments for variable selection in deriving optimal treatment regimes. For example, [13] introduced the concepts for predictive variables (predictors with important baseline effects) and prescriptive variables (predictors interacting with treatments), and developed a ranking method for selecting qualitative interactions. [14] developed a l₁-penalization method for selecting both predictive and prescriptive variables in a regression model and studied the theoretical properties of the obtained optimal treatment regimes. [15] proposed a least square loss-based selection framework for uncensored responses, which was shown to be robust to misspecification of the baseline effects of predictors and able to incorporate various shrinkage penalties naturally. To our knowledge, variable selection in optimal treatment regimes for censored survival outcomes has not been well studied in literature.

In this article, we extend the method of [15] to the estimation and selection of optimal treatment regimes for mean survival time. In particular, we propose an inverse probability of censoring weighted least squares estimation with adaptive LASSO penalty for variable selection. As in [15], the new method does not require the correct specification of the baseline effects since it properly adjust for propensity scores as in the A-learning estimation. We further generalize the proposed optimal treatment regime learning scheme for two treatments to the case of multiple treatments. To evaluate the optimality of the estimated optimal treatment regime, we develop a model-free method to estimate the restricted mean survival time under the derived optimal treatment regime and study its associated inference.

The remainder of the paper is organized as follows. In Section 2, we introduce the proposed model, estimation and variable selection methods for deriving optimal treatment regimes. In addition, we develop a model-free estimator for the restricted mean survival time under the derived optimal treatment regime. The asymptotic properties of the proposed estimators are also presented. Section 3 assesses the empirical performance of the proposed estimators by simulation studies. Section 4 demonstrates the application of the method to a data set from the AIDS Clinical Trials Group Protocol 175 (ACTG175) [9]. We conclude the paper with discussions in Section 5.

2. Proposed Method

2.1. Notations and model assumptions

Let 𝒜 = {0, 1, 2, …, k} represent the set of k + 1 available treatments. Consider a clinical trial with n subjects, each of whom receives one treatment from 𝒜. Define A_i as the actual treatment received by the ith subject and A_(j)i as the indicator of subject i taking treatment j, i.e., A_j,i = I(A_i = j), j = 0, ⋯, k. For subject i, let Y_i denote the survival or log survival time of interest, C_i denote the corresponding censoring time, and X_i = (X_1i, …, X_pi)^T denote the p-dimensional baseline covariates. The observed data then consist of (Ỹ_i, δ_i, X_i, A_i), i = 1, ⋯, n, where Ỹ_i = Y_i ∧ C_i, δ_i = I(Y_i ≤ C_i) and a ∧ b = min(a, b).

Let $Y_i^{*}(j)$ be the potential survival or log survival time of subject i if he or she were given treatment j, j ∈ 𝒜. Our goal is to find the optimal treatment regime to maximize the mean survival time. Here, a treatment regime g is a function that maps the sample space of X to 𝒜. For any treatment regime g, we have $Y^{*}(g(X))={\sum }_{j=0}^k{Y}^{*}(j)I\{g(X)=j\}$. Therefore, the optimal treatment regime g^opt is defined by

$$g^{\mathit{\text{opt}}}(X)=\text{arg}\underset{g\in 𝒢}{\text{max}}E\{Y^{*}(g(X))\},$$

where 𝒢 is the functional space for g.

As in [16], we make the following two commonly used assumptions:

• (C1)(Consistency assumption) Y = ∑_j∈𝒜 I (A = j)Y* (j);
• (C2)(No unmeasured confounders assumption) A⊥{Y* (j)}_j∈𝒜|X.

Under conditions (C1) and (C2), we can show that

$$E\{Y^{*}(g(X))\}=E_X[\sum _{j=0}^{k}E(Y|A=j,X)I\{g(X)=j\}].$$

It follows that g^opt(x) = argmax_j∈𝒜E{Y|A = j, X = x}.

To estimate the optimal treatment regime, we consider a semiparametric regression model for Y_i,

$$E(Y_i|X_i,A_i)=h_0(X_i)+A_{1,i}{\beta }_1^T{\mathrm{X̃}}_i+\cdots +A_{k,i}{\beta }_k^T{\mathrm{X̃}}_i,$$ (1)

where ${\mathrm{X̃}}_i={(1,X_i^T)}^T$ and h₀ is an unspecified baseline mean function. It is easy to show that the optimal treatment regime under model (1) is

$$g(X;\beta )=\{\begin{array}{cc}{\text{argmax}}_{j\in \{1,\dots ,k\}}{\beta }_j^T\mathrm{X̃},\hfill & {\text{if max}}_{j\in \{1,\dots ,k\}}{\beta }_j^T\mathrm{X̃}>0;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (2)

where $\beta ={({\beta }_1^T,\dots ,{\beta }_k^T)}^T={({\beta }_{1,0},\dots ,{\beta }_{1,p},\dots ,{\beta }_{k,0},\dots ,{\beta }_{k,p})}^T$. Here, we restrict the optimal treatment regime to a class of linear functions of covariates for its simplicity and easy interpretation in practical use. However, the proposed idea can be extended to other functionals to meet the need of more complicated estimation and selection procedures.

2.2. Estimation and selection for optimal treatment regimes

When there is no censoring and only two treatments, [15] proposed a general framework for selecting important predictors in optimal treatment regimes. The approach does not require the correct specification of the baseline mean function and is therefore robust. In this work, we generalize their estimation framework to incorporate censoring and multiple treatments. Specifically, we handle censoring by the inverse probability of censoring weighted (IPCW) technique as widely studied in the literature [17, 18, 19, 20, 21]. As usual, we make the independent censoring assumption, i.e., C⊥(Y, X, A). Let G(·) denote the survival function of censoring times. We propose to estimate the optimal treatment regime by minimizing the following loss function:

$$L_n(\beta ,\gamma )=\frac{1}{n}\sum _{i=1}^n\frac{{\delta }_i}{Ĝ(Y_i)}{[Y_i-\varphi (X_i;\gamma )-\sum _{j=1}^k{\beta }_j^T{\mathrm{X̃}}_i\{A_{j,i}-{\pi }_j(X_i)\}]}^2$$ (3)

with respect to β and γ, where π_j(x) = P(A_i = j|X_i = x) is the propensity score, Ĝ(·) is the Kaplan-Meier estimator of G, and φ(x; γ) is a posited parametric function. Let (β̃, γ̃) denote the minimizer of (3) and β₀ be the true value of β.

In some studies such as randomized clinical trials, the propensity scores are known by design. However, in non-randomized studies, the propensity scores are usually unknown and need to be estimated based on a posited model, e.g. a multinomial logistic regression. In this paper, we focus on the case with the propensity scores known in priori. Various parametric functions can be used for φ(·; γ). Here, for simplicity, we consider the constant model φ(x; γ) = γ and linear model φ(x; γ) = γ^T x. As shown in the following theorem, regardless of the choice of φ(·; γ), the estimator β̃ is always consistent and asymptotically normal as long as the propensity scores are correctly specified.

The independent censoring assumption can be relaxed in (3), but it then needs to model the censoring time distribution, say by a proportional hazards (PH) model, and replace the Kaplan-Meier estimator by the survival function estimator obtained under the posited PH model. In our simulations, we conducted sensitivity analysis to assess the performance of the proposed estimators when the independent censoring assumption is violated. Based on our limited simulation study results, the proposed estimators are quite robust to the violation of the independent censoring assumption.

Theorem 1. Assume that the propensity scores are correctly specified and conditions (A1)–(A5) in Appendix hold. We have that $\sqrt{n}(\mathrm{\beta ̃}-{\beta }_0)\underrightarrow{d}N(0,\mathrm{\Sigma })$ as n → ∞.

The proof of Theorem 1 is given in Appendix. Based on Theorem 1, the optimal treatment regimes can be consistently estimated by g(X; β̃). When the dimension of covariates is high, selection of important variables for deriving optimal treatment regimes becomes crucial to achieve personalized medicine, since it can lead to more reliable and practically useful treatment rules. The proposed weighted loss function given in (3) can be easily coupled with various shrinkage penalties, such as LASSO [10], SCAD [11], adaptive LASSO [12, 22] and minimax concave penalty [23], for variable selection. Here we use the adaptive LASSO penalty and solve

$$\underset{\beta }{\text{min}}{L}_n(\beta ,\mathrm{\gamma ̃})+{\lambda }_n\sum _{j=1}^k\sum _{l=0}^p{w}_{j,l}|{\beta }_{j,l}|.$$ (4)

where we set $w_{j,l}^{-1}=|{\mathrm{\beta ̃}}_{j,l}|$, j = 1, …, k, l = 0, …, p.

For computation, we point out that the proposed weighted loss can be represented as a least squared loss. Specifically, define ${𝕐}_i=\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{Y_i-\varphi (X_i;\mathrm{\gamma ̃})\}$ and ${𝕏}_i={({\mathrm{X̃}}_i^T\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{A_{1,i}-{\pi }_1(X_i)\},\dots ,{\mathrm{X̃}}_i^T\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{A_{k,i}-{\pi }_k(X_i)\})}^T$. Then $L_n(\beta ,\mathrm{\gamma ̃})=n^{-1}{\sum }_{i=1}^n{({𝕐}_i-\beta \prime {𝕏}_i)}^2$. Thus, the optimization in (4) is equivalent to a penalized least squares estimation with the adaptive LASSO penalty. The whole solution path of the proposed estimators can be obtained by the LARS algorithm [24]. Let β̂(λ) denote the resulting estimator for fixed λ. To choose the tuning parameter λ, we propose to use the BIC-type criteria as studied in [15], that is, choosing λ that minimizes L_n(β̂(λ), γ̃)/L_n(β̃, γ̃) + d(λ) log(n)/n, where d(λ) is the number of non-zeros in β̂(λ).

Denote the solution to (4) by β̂. Then the estimated optimal treatment rule is g(X; β̂). Next, we establish the asymptotic properties of β̂. Without loss of generality, write ${\beta }_0={({\beta }_{(1),0}^T,{\beta }_{(2),0}^T)}^T$, where β_(1),0 is a vector of non-zero coefficients with length s and β_(2),0 = 0. Accordingly, write $\mathrm{\beta ̂}={({\mathrm{\beta ̂}}_{(1)}^T,{\mathrm{\beta ̂}}_{(2)}^T)}^T$.

Theorem 2. Assume that conditions in Theorem 1 hold, and $\sqrt{n}{\lambda }_n\to 0$ and nλ_n → ∞ as n → ∞. We have

1. (sparsity) P(β̂₍₂₎ = 0) → 1;

2. (asymptotic normality) $\sqrt{n}({\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0})\underrightarrow{d}N(0,{\mathrm{\Sigma }}_S)$ as n → ∞.

The expression of Σ_S and the proof of Theorem 2 are given in the Appendix.

2.3. Nonparametric evaluation of estimated treatment regime

In practice, it is of great interest to nonparametrically estimate the mean survival time for a given treatment regime, since it can help to asses its optimality and compare with other treatment regimes. Under model (1), the mean survival time under the true optimal treatment regime is given by V₀ = E{Y*(g(X; β₀))}. However, for most clinical studies with limited follow-up time, the support of censoring times is usually shorter than that of survival times of interest. As a consequence, the mean survival time is not estimable based on censored survival data. Alternatively, it has been proposed to estimate the restricted mean survival time (RMST) since it is an easily interpretable and clinically meaningful measure for censored survival data [25, 26, 27]. Specifically, the RMST under a treatment regime g is defined by V^L(g) = E{Y* (g) ∧ L}, where L is a constant such that P(Ỹ ≥ L) > 0. Therefore, the RMST is the mean of survival times for all potential study subjects followed up to time L.

Let $V_0^L=E\{Y^{*}(g(X;{\beta }_0))\wedge L\}$. Given our estimated optimal treatment regime g(X; β̂), we now derive a model-free method to estimate $V_0^L$. Recently, for uncensored responses, [6] proposed an inverse propensity scores weighted estimation method to estimate the mean response given a treatment regime g. Specifically, E{Y* (g)} can be consistently estimated by solving the following equation:

$$\sum _{i=1}^n\frac{I\{A_i=g(X_i)\}}{{\pi }_{A_i}(X_i)}[Y_i-E\{Y^{*}(g)\}]=0,$$

where ${\pi }_{A_i}(X_i)={\sum }_{j=0}^{k}I(A_i=j){\pi }_j(X_i)$. The above estimating equation for E{Y* (g)} does not require the model assumptions on the response variable Y. This motivates us to consider the following equation to estimate V^L (g) with censored survival data:

$$\sum _{i=1}^n\frac{{\delta }_i^L}{Ĝ(Y_i^L)}\frac{I\{A_i=g(X_i)\}}{{\pi }_{A_i}(X_i)}\{Y_i^L-V^L(g)\}=0,$$ (5)

where $Y_i^L=Y_i\wedge L$ and ${\delta }_i^L=I(Y_i^L\le C_i)={\delta }_i+(1-{\delta }_i)I({Ỹ}_i\ge L)$. Therefore, an estimator of V^L (g) is given by

$${\mathrm{V̂}}^L(g)=\frac{{\sum }_{i=1}^n\frac{{\delta }_i^L}{Ĝ(Y_i^L)}\frac{I\{A_i=g(X_i)\}}{{\pi }_{A_i}(X_i)}{Y}_i^L}{{\sum }_{i=1}^n\frac{{\delta }_i^L}{Ĝ(Y_i^L)}\frac{I\{A_i=g(X_i)\}}{{\pi }_{A_i}(X_i)}}.$$

This leads to an estimator of $V_0^L$, denoted by ${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)={\mathrm{V̂}}^L(g(·,;\mathrm{\beta ̂}))$. In the following theorem, we establish the asymptotic distribution of ${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)$.

Theorem 3. Assume that conditions in Theorems 1 and 2 hold. We have, as n → ∞, $\sqrt{n}\{{\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)-V_0^L\}\underrightarrow{d}N(0,{\sigma }^2)$.

The proof of Theorem 3 is given in Appendix. The asymptotic variance σ² has a very complicated analytical form, and its estimation based on the usual plug-in method is difficult since ${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)$ is not a smooth function of β̂. Here, we use the bootstrap method for estimating σ² in our numerical studies. In addition, we can compare a given treatment regime g with the estimated optimal treatment regime g(X; β̂) in terms of ${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)-{\mathrm{V̂}}^L(g)$, and use the bootstrap method to assess the significance of the difference.

3. Simulation Studies

3.1. Low dimensional examples with p = 10

We considered the following models with 2 or 4 treatments, i.e. k = 1 or 3:

• Model I: two treatments with quadratic baseline.

  $$Y_i=\text{log}(T_i)=1+0.5({\gamma }_1^T{X}_i)({\gamma }_2^T{X}_i)+A_{1,i}{\beta }_1^T{\mathrm{X̃}}_i+{\epsilon }_i,$$

  where γ₁ = (1, −1, 0₈)^T, γ₂ = (1, 0₂, −1, 0₅, 1)^T and β₁ = (1, 1, 0₇, −0.9, 0.8)^T.
• Model II: four treatments with quadratic baseline and common important factors across treatments.

  $$Y_i=\text{log}(T_i)=1+0.5({\gamma }_1^T{X}_i)({\gamma }_2^T{X}_i)+\sum _{j=1}^3{A}_{j,i}{\beta }_j^T{\mathrm{X̃}}_i+{\epsilon }_i,$$

  where γ₁ = (1, −1, 0₈)^T, γ₂ = (1, 0₂, −1, 0₅, 1)^T, β₁ = (1, 1, 0₇, −0.9, 0.8)^T, β₂ = (1, 0.7, 0₇, 0.8, −1)^T and β₃ = (1, −1, 0₇, 1, 0.9)^T.

• Model III: the same as model II but with different important factors across treatments, i.e., β₁ = (1, 1, 0₇, −0.9, 0.8)^T, β₂ = (1, 0₂, 1, 0.8, 0₅,−0.9)^T and β₃ = (1, −0.9, 0₆, 1, 0.8, 0).

For each model, the covariate vector X = (X₁, …, X_p)^T is generated from a multivariate normal distribution with mean 0, variance 1 and correlation Corr(X_j, X_k) = 0.5^|j−k|, and the error term is from a normal distribution with mean 0 and standard deviation 0.5. In addition, subjects are randomized to one of the available treatments with equal probabilities. Therefore, the propensity score is 0.5 with two treatments and 0.25 with four treatments. Censoring times are generated as log(C_i) ~ unif(0, τ_c), where τ_c is chosen to achieve 15% and 40% censoring rates respectively. For each scenario, we run 500 replications with sample size of n = 400 and 800.

We consider two choices for the posited parametric function ϕ(X; γ):

• Choice 1 (constant model): ϕ(X; γ) ≡ γ.

• Choice 2 (linear model): ϕ(X; γ) ≡ γ^T X̃.

To evaluate the estimation accuracy of the proposed estimator, we report the mean squared error of β̂, i.e. MSE = ‖β̂ − β₀‖². To evaluate the variable selection performance, we report the number of non-zero coefficients incorrectly identified as zero (denoted by “Incor0”), the number of correct zero coefficients identified (denoted by “Corr0”), the proportion of exactly selecting the correct model (denoted by “Exact”) and the proportion of covering all the important variables (denoted by “Cover”). Note that the number of zero coefficients is 7 under Model I, and is 21 under Models II and III. To assess the accuracy of the estimated optimal treatment regimes, we report the average percentage of making correct decisions (PCD) over 500 runs, where PCD is defined as $n^{-1}{\sum }_{i=1}^{n}I\{g(X_i;\mathrm{\beta ̂})=g(X_i;{\beta }_0)\}$. For comparison, we also report the average PCD for the estimated optimal treatment regime g(X; β̃) without penalization.

The estimation, selection and PCD results for Models I–III are summarized in Table 1. Based on the results, we have several observations. First, the estimation, selection and PCD results improve as sample size increases and the censoring rate decreases as expected. Second, when the censoring rate is low (15%), Incor0 are close to 0, Corr0 are close to the true number of zero coefficients, and the coverage frequencies (Cover) are high in most cases. The selection frequencies of the correct model (Exact) are also reasonable under Model I, but much lower under Models II–III. Under the higher censoring (40%) case, the overall selection performance becomes worse but is still reasonable with Choice 2. Third, Choice 2 with the linear model for ϕ(X; γ) generally shows better performance than Choice 1 with the constant model, and the improvement may be substantial under the heavy censoring situation. Fourth, with regard to PCD, both the unpenalized and penalized estimates of optimal treatment regimes perform reasonably well, with PCD above 85% for all the cases. In addition, the penalized estimates generally have slightly better PCD than the unpenalized estimates, but the gain is not significant.

Table 1.

Estimation, selection and PCD results for Models I–IV (CR denote the censoring rate; the numbers in parentheses are the standard errors of MSE).

					Selection				PCD (%)
Model	Choice	CR	n	MSE	Incor0	Corr0	Exact	Cover	Unpenalized	Penalized
I	1	15%	400	0.262 (0.011)	0.02	6.29	0.510	0.976	91.5	93.3
			800	0.121 (0.005)	0	6.51	0.650	1	93.6	95.3
		40%	400	1.065 (0.033)	0.26	4.89	0.092	0.784	85.5	86.0
			800	0.782 (0.026)	0.11	4.89	0.134	0.902	88.1	89.1
	2	15%	400	0.172 (0.007)	0	6.26	0.520	0.998	92.7	94.3
			800	0.083 (0.004)	0	6.52	0.652	1	94.5	96.0
		40%	400	0.563 (0.021)	0.07	4.99	0.160	0.936	89.2	90.2
			800	0.390 (0.014)	0.02	5.10	0.172	0.984	91.2	92.3
II	1	15%	400	1.271 (0.037)	0.26	17.82	0.068	0.782	87.0	89.2
			800	0.562 (0.016)	0.05	19.10	0.224	0.956	90.7	93.0
		40%	400	2.302 (0.053)	0.65	14.84	0.006	0.564	83.3	84.6
			800	1.327 (0.036)	0.20	15.52	0.012	0.848	87.2	88.7
	2	15%	400	1.139 (0.035)	0.21	17.89	0.070	0.816	87.8	90.1
			800	0.482 (0.014)	0.03	18.96	0.202	0.976	91.3	93.6
		40%	400	1.900 (0.046)	0.41	14.73	0.012	0.682	84.5	86.0
			800	1.047 (0.028)	0.10	15.75	0.010	0.916	88.3	89.9
III	1	15%	400	1.171 (0.035)	0.15	18.05	0.090	0.868	87.9	89.5
			800	0.465 (0.013)	0.01	19.10	0.230	0.994	91.6	93.4
		40%	400	2.543 (0.059)	0.53	14.28	0.002	0.614	82.6	83.3
			800	1.514 (0.040)	0.13	15.27	0.020	0.880	86.6	87.8
	2	15%	400	0.958 (0.028)	0.09	17.84	0.106	0.918	89.0	90.7
			800	0.379 (0.011)	0.00	19.19	0.248	0.996	92.4	94.1
		40%	400	1.916 (0.048)	0.28	14.34	0.004	0.768	84.9	86.2
			800	1.123 (0.029)	0.05	15.49	0.018	0.946	88.3	89.7
IV	1	15%	400	0.418 (0.018)	0.06	44.59	0.226	0.948	83.1	91.2
			800	0.164 (0.007)	0	45.54	0.430	1.000	87.4	94.7
		40%	400	1.599 (0.036)	0.38	36.11	0.002	0.690	75.8	80.5
			800	0.999 (0.024)	0.08	37.84	0.014	0.928	80.9	86.4
	2	15%	400	0.324 (0.012)	0	42.50	0.124	0.996	84.8	91.8
			800	0.102 (0.004)	0	45.43	0.384	1.000	89.0	95.5
		40%	400	1.268 (0.031)	0.06	28.23	0	0.944	79.4	83.4
			800	0.513 (0.013)	0.01	37.28	0.016	0.994	85.2	90.3

3.2. Large dimensional examples with p = 50

To show the effectiveness of the proposed method for high dimensional covariates, we consider the following model with p = 50. The estimation, selection and PCD results are summarized in Table 1.

• Model IV: two treatments with quadratic baseline.

  $$Y_i=\text{log}(T_i)=1+0.5({\gamma }_1^T{X}_i)({\gamma }_2^T{X}_i)+A_{1,j}{\beta }_1^T{\mathrm{X̃}}_i+{\epsilon }_i,$$

where γ₁ = (1, −1, 0₄₈)^T, γ₂ = (1, 0₂, −1, 0₅, 1, 0₄₀)^T and β₁ = (1, 1, 0₇, −0.9, 0.8, 0₄₀)^T.

In Model IV, the number of zero coefficients is 47. The proposed method still demonstrates competitive performance. Overall, we have observed the same patterns as in the low dimensional cases, except that the PCDs of the penalized estimators now exhibit considerable enhancement compared with those of the unpenalized estimators; it demonstrates the advantage of the penalization method when dealing with high dimensional covariates.

3.3. Sensitivity analysis

In our proposed method, the independence censoring assumption is made and Kaplan-Meier estimator is used for estimating the survival function of censoring times. However, this assumption may be restrictive for practical applications. To evaluate the performance of the proposed method when the independence censoring assumption is violated, we conduct sensitivity analysis. Specifically, we reran all the simulations under the same conditions except that censoring times are now generated from log(C_i) = τ_c + η^TX_i + e_i, where e follows the standard extreme value distribution, and τ_c is chosen to obtain the desired censoring rates of 15% and 40%. For Model I, we set η = (1, 0₂, 1, 0₆)^T; for Model II and III, set η = (1, 0₄, 1, 0₄)^T; for Model IV, set η = (1, 0₄, 1, 0₄₄)^T.

The results from sensitivity analysis are given in Tables 2. The findings are very similar to those in independence censoring cases reported previously. Although the coefficient estimation and variable selection become slightly worse when the independence censoring assumption is violated, the PCDs of our proposed methods are very comparable to those given in Table 1. In summary, based on the limited sensitivity analysis we have conducted, the proposed method appears to be insensitive to the violation of the independence censoring assumption. However, in general, our method requires the independent censoring assumption for its validity.

Table 2.

Sensitivity analysis results for Models I–IV.

					Selection				PCD (%)
Model	Choice	CR	n	MSE	Incor0	Corr0	Exact	Cover	Unpenalized	Penalized
I	1	15%	400	0.382 (0.017)	0.04	5.84	0.310	0.962	90.1	91.6
			800	0.221 (0.011)	0.01	5.83	0.346	0.992	91.9	93.5
		40%	400	0.940 (0.037)	0.20	4.67	0.052	0.856	84.7	85.5
			800	0.662 (0.023)	0.06	4.55	0.054	0.948	86.5	87.4
	2	15%	400	0.254 (0.011)	0.01	6.03	0.392	0.988	92.0	93.4
			800	0.145 (0.006)	0.00	6.19	0.504	1	93.9	95.2
		40%	400	0.512 (0.019)	0.06	5.17	0.168	0.944	89.5	90.7
			800	0.371 (0.014)	0.01	5.24	0.190	0.988	91.3	92.5
II	1	15%	400	1.666 (0.049)	0.39	17.01	0.038	0.720	85.5	87.5
			800	0.819 (0.029)	0.09	18.15	0.120	0.924	89.3	91.4
		40%	400	2.934 (0.074)	0.80	14.15	0.000	0.472	80.8	81.7
			800	1.791 (0.057)	0.30	14.70	0.008	0.756	85.1	86.5
	2	15%	400	1.216 (0.036)	0.23	17.46	0.040	0.822	87.5	89.6
			800	0.588 (0.019)	0.04	18.51	0.172	0.962	90.9	93.0
		40%	400	1.915 (0.042)	0.37	14.59	0.004	0.720	84.3	85.7
			800	1.103 (0.028)	0.09	15.87	0.026	0.928	88.3	90.0
III	1	15%	400	1.464 (0.043)	0.22	17.10	0.036	0.800	86.9	88.2
			800	0.715 (0.026)	0.04	18.02	0.114	0.964	90.3	92.0
		40%	400	2.870 (0.070)	0.56	14.13	0.004	0.590	81.4	82.0
			800	1.745 (0.051)	0.17	14.49	0.006	0.850	85.3	86.4
	2	15%	400	1.179 (0.034)	0.14	17.14	0.050	0.882	88.4	89.9
			800	0.588 (0.019)	0.02	18.30	0.152	0.980	91.5	93.1
		40%	400	2.084 (0.045)	0.33	14.21	0.004	0.722	84.2	85.2
			800	1.301 (0.031)	0.07	15.17	0.024	0.936	87.9	89.2
IV	1	15%	400	0.539 (0.020)	0.09	43.21	0.114	0.922	82.4	89.8
			800	0.276 (0.011)	0.01	44.04	0.180	0.992	86.0	92.9
		40%	400	1.534 (0.043)	0.31	35.63	0.002	0.754	76.1	80.9
			800	0.979 (0.036)	0.10	36.91	0.006	0.914	80.0	84.8
	2	15%	400	0.369 (0.012)	0.01	41.86	0.072	0.994	84.9	91.5
			800	0.180 (0.006)	0.00	44.70	0.288	1.000	88.8	94.5
		40%	400	1.154 (0.029)	0.05	29.97	0.004	0.946	80.1	84.3
			800	0.508 (0.015)	0.01	38.08	0.028	0.992	85.5	90.4

3.4. Estimation of RMST

In this subsection, we conduct simulations to evaluate the performance of the proposed nonparametric estimator ${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)$ of the MRST under the obtained optimal treatment regime given in Section 2.3. For simplicity, we choose L = τ_c, the log of the maximum follow-up time. We have $V_0^L=3.88$ under the 15% censoring rate, and $V_0^L=3.31$ under the 40% censoring rate, which are calculated by simulating survival times of 400, 000 subjects following the true optimal treatment regime. We only present the results for Model IV with 4 treatments, p = 10 and n = 800. For each case, 200 bootstrap samples are used for variance estimation. For each bootstrap sample, we recalculate the Kaplan-Meier estimator of the censoring survival function and the adaptive LASSO estimator of β₀. The results are summarized in Table 3. We report the mean and standard deviation (SD) of our estimates, the estimated standard error (SE), and the coverage probability (CP) of Wald-type 95% confidence intervals for $V_0^L$. From the simulation results, we observe that our estimates are nearly unbiased for $V_0^L$, the bootstrap standard errors are close to the Monte Carlo standard deviations, and the CPs are also reasonably close to the nominal level, when the censoring rate is low. When the censoring rate is 40%, the bootstrap standard error tends to be underestimated and the CPs are lower than the nominal level. One possible reason is that the bootstrap variance for the proposed adaptive LASSO estimator of β₀ tends to be underestimated under heavy censoring.

Table 3.

Estimation results for RMST.

CR	$V_0^L$	Choice	Estimate	SD	SE	CP
15%	3.88	1	3.88	0.14	0.14	0.95
		2	3.87	0.14	0.14	0.94
40%	3.31	1	3.33	0.20	0.17	0.89
		2	3.32	0.21	0.17	0.90

4. Real Data Analysis

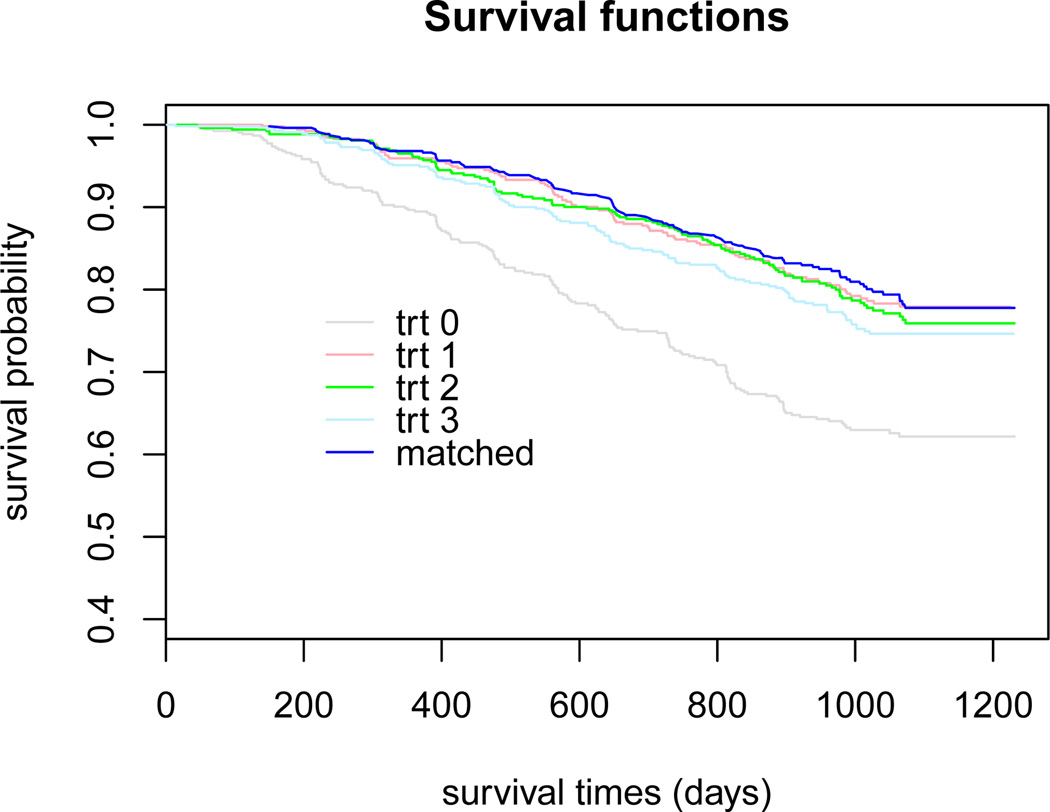
For illustration, we apply our method to the HIV data from AIDS Clinical Trials Group Protocol 175 (ACTG175) [9]. In ACTG175, 2137 HIV-infected subjects were randomized to receive one of the four treatments: zidovudine (ZDV) monotherapy (treatment 0), ZDV + didanosine (ddI) (treatment 1), ZDV + zalcitabine (treatment 2) and ddI monotherapy (treatment 3). The primary endpoint was time to the first ≥ 50% decline in CD4 count, an AIDS-defining event or death, recorded in days. Among 2137 subjects, 75.6% of them were censored due to the end of trial or loss to follow-up. In Figure 1, we plotted the Kaplan-Meier survival curves for the four treatment groups. From the plots, it can be seen that treatments 1, 2 and 3 have clearly better survival than treatment 0; treatments 1 and 2 have very comparable survival curves, which are slightly better than treatment 3.

Figure 1.

The Kaplan-Meier survival curves for four treatment groups and patients following the estimated optimal treatment regime with the linear model for baseline.

As in [28] and [29], besides the treatment indicators, we considered 12 covariates, including 5 continuous variables: age (years), weight (kg), Karnofsky score (scale of 0–100), CD4 count (cells/mm³) at baseline and CD8 count (cells/mm³) at baseline, and seven binary covariates: hemophilia (0=no, 1=yes), homosexual activity (0=no, 1=yes), history of intravenous drug use (0=no, 1=yes), race (0=white, 1=non-white), gender (0=female, 1=male), antiretroviral history (0=naive, 1=experienced), and symptomatic status (0=asymptomatic, 1=symptomatic). The goals are to derive the optimal treatment regime to maximize the mean log survival time and to select important predictors that are needed for deriving the optimal treatment regime.

As in simulations, we consider both the constant model and the linear model for the baseline function ϕ(X; γ), and conduct variable selection using the adaptive LASSO estimation. The final estimated coefficients β̂ are given in Tables 4 and 5, respectively. For the constant model fit, the optimal treatment regime is determined by comparing the following four functions

1. 0;

2. 0.275 − 0.003 * wtkg − 9.83 × 10⁻⁵ * cd40 + 1.57 × 10⁻⁴ * cd80+ 0.316 * drugs;

3. −1.634 + 0.021 * karnof − 4.70 × 10⁻⁴ * cd40 + 0.080 * hemo + 0.048 * race;

4. −0.010 + 1.20 × 10⁻⁴ * cd80 − 0.100 * gender + 0.140 * str2;

while for the linear model fit, the optimal treatment regime is determined by comparing

1. 0;

2. 0.466 − 0.005 * wtkg + 9.64 × 10⁻⁵ * cd80 + 0.233 * drugs;

3. −1.443 + 0.018 * karnof + 0.050 * hemo;

4. −0.021 + 1 × 10⁻⁴ * cd80 − 0.031 * gender + 0.144 * str2 − 0.099 * symptom.

Table 4.

Estimated coefficients for interactions using the constant model for baseline

Variable Name	Treatment 1	Treatment 2	Treatment 3
intercept	0.275	−1.634	−0.010
age	0	0	0
wtkg	−0.003	0	0
karnof	0	0.021	0
cd40	−9.83E-5	−4.70E-4	0
cd80	1.57E-4	0	1.20E-4
hemo	0	0.080	0
homo	0	0	0
drugs	0.316	0	0
race	0	0.048	0
gender	0	0	−0.100
str2	0	0	0.140
symptom	0	0	0

Table 5.

Estimated coefficients for interactions using the linear model for baseline

Variable Name	Treatment 1	Treatment 2	Treatment 3
intercept	0.466	−1.443	−0.021
age	0	0	0
wtkg	−0.005	0	0
karnof	0	0.018	0
cd40	0	0	0
cd80	9.64E-5	0	1E-4
hemo	0	0.050	0
homo	0	0	0
drugs	0.233	0	0
race	0	0	0
gender	0	0	−0.031
str2	0	0	0.144
symptom	0	0	−0.099

The optimal treatment rule is

$$\{\begin{array}{cc}\mathrm{Z}\mathrm{D}\mathrm{V}\text{monotherapy},\hfill & \text{if}(\mathrm{a})\text{is maximum};\hfill \\ \mathrm{Z}\mathrm{D}\mathrm{V}+\mathrm{d}\mathrm{d}\mathrm{I},\hfill & \text{if}(\mathrm{b})\text{is maximum};\hfill \\ \mathrm{Z}\mathrm{D}\mathrm{V}+\text{zalcitabine},\hfill & \text{if}(\mathrm{c})\text{is maximum};\hfill \\ \mathrm{d}\mathrm{d}\mathrm{I}\text{monotherapy},\hfill & \text{if}(\mathrm{d})\text{is maximum}.\hfill \end{array}$$

Based on the constant model fit, one would assign 1 subject to treatment 0, 729 subjects to treatment 1, 1216 subjects to treatment 2, and 193 subjects to treatment 3. Based on the linear model fit, one would assign 644 subjects to treatment 1, 1383 subjects to treatment 2, and 112 subjects to treatment 3. These results agree with the Kaplan-Meier curves given in Figure 1, since treatment groups 1, 2 and 3 have significantly better survival than treatment group 0, and treatment groups 1 and 2 are slightly better than group 3. Moreover, for comparison, we plot the Kaplan-Meier survival curve for patients whose received treatments agree with those given by the estimated optimal treatment regime with the linear model for baseline (denoted by “match”). From the plot, we note that the survival curve following the optimal treatment regime stays above all other four survival curves for individual treatment groups, confirming that the obtained optimal treatment regime can lead to better survival compared with each individual treatment.

In addition, we calculate the restricted mean log survival time following different treatment strategies based on the estimation method derived in Section 2.3. As in simulations, we take L as the log of maximum follow-up time. Specifically, the restricted mean log survival time under the estimated optimal treatment regimes with the constant fit and the linear fit are 6.44(0.045) and 6.43(0.047), respectively. The numbers in the parentheses are the associated standard errors obtained via 500 bootstraps. For comparison, we also compute the restricted mean log survival time for treatment groups 0, 1, 2 and 3, which are 6.13(0.049), 6.37(0.045), 6.38(0.054) and 6.30(0.049), respectively. The estimated restricted mean log survival time under the derived optimal treatment regimes are larger than the restricted mean log survival time of each individual treatment group. To assess whether the differences are significant, we obtain the 95% confidence intervals for the differences between the restricted mean log survival time under the optimal treatment regime $(V_0^L)$ and the restricted mean log survival time of each individual treatment group (denoted by V^L(j), j = 0, 1, 2, 3, i.e. g(X) ≡ j) via 500 bootstraps. Two types of confidence intervals are considered: Wald-type confidence interval and percentage based confidence interval (i.e. using the 2.5% and 97.5% quantiles of the bootstrapped differences). The results are given in Table 6. Based on the results, we observe that all the confidence intervals stay above 0, showing the significant increase of the restricted mean log survival time under the estimated optimal treatment regimes compared with each individual treatment.

Table 6.

95% confidence intervals for the differences of restricted mean log survival time

	constant fit
	$V_0^L-V^L(0)$	$V_0^L-V^L(1)$	$V_0^L-V^L(2)$	$V_0^L-V^L(3)$
Wald	(0.26, 0.52)	(0.04, 0.26)	(0.03, 0.26)	(0.10, 0.33)
percentile	(0.26, 0.51)	(0.05, 0.27)	(0.04, 0.26)	(0.10, 0.34)
	linear fit
Wald	(0.25, 0.51)	(0.03, 0.26)	(0.03, 0.25)	(0.09, 0.33)
percentile	(0.25, 0.51)	(0.03, 0.27)	(0.03, 0.27)	(0.09, 0.33)

In above analyses, the estimation of the optimal treatment regime and its associated evaluation used the same dataset, which may cause some overfitting. However, note that the estimation and selection of the optimal treatment regime for the mean log survival time is based on the assumed semiparametric regression model, while the evaluation of the estimated optimal treatment regimes are fully nonparametric. Specifically, we used two measures: (1) Kaplan-Meier curves for matched subjects; (2) the nonparametric estimator of restricted mean survival time based on matched subjects. Both measures do not use the assumed model when comparing different treatment regimes, and thus can still provide fair comparisons. In addition, we conducted 10 random splits of the original data to half training and half testing data. Using the training data, we estimated the sparse optimal treatment regime based on the proposed method with the posited constant baseline effect. Then, we compared the estimated optimal treatment regime with other simple treatment regimes based on the estimated restricted mean log survival times using the proposed nonparametric estimators. The averages and standard deviations (given in parenthesis) are 6.40 (0.035), 6.13 (0.047), 6.36 (0.035), 6.35 (0.049) and 6.33 (0.055) for the estimated optimal treatment regime, and treatment groups 0, 1, 2, and 3, respectively. This also supports that the estimated optimal treatment regime improves the restricted mean log survival time comparing with single treatment groups.

5. Discussion

In this paper, we propose an ICPW-based loss function to estimate the optimal treatment regime that maximizes the mean log survival time with multiple treatments. The proposed estimation method is robust in the sense that it can consistently estimate the optimal treatment regime regardless of the form of the posited baseline model as long as the treatment-covariates interactions and propensity scores are correctly specified. However, a more comprehensive choice for the baseline model usually can improve the estimation efficiency and accuracy. In addition, the new loss function can be easily coupled with shrinkage penalties, such as adaptive LASSO, to select important variables that are related to the optimal decision. The resulting sparse estimates can lead to parsimonious optimal treatment regimes with easy interpretation and can improve the accuracy of optimal treatment decision, especially in high dimensional cases.

In our current estimation framework, the adaptive LASSO penalties are added to each individual regression coefficient. With multiple treatments, i.e. k > 1, regression coefficients are naturally grouped. For example, coefficients β_j,l, j = 1, ⋯, k are all associated with covariate X_l, l = 0, ⋯, p, where X₀ ≡ 1 corresponding to the intercept. In practice, it is of great interest to consider variable selection with certain group structures. Specifically, we may consider the following penalized estimation:

$$\underset{\beta }{\text{min}}{L}_n(\beta ,\mathrm{\gamma ̃})+{\lambda }_n\sum _{l=0}^p{(\sum _{j=1}^k{w}_{j,l}|{\beta }_{j,l}|)}^{\frac{1}{2}}.$$

The penalty in the above equation adopts the weighted group L₁ norm, which encourages group selection and also allows the selection of individual covariates within groups, which shares the spirit of the group bridge penalty [30] and the hierarchical group lasso [31].

Furthermore, in this paper, we focus on the estimation and selection of optimal treatment regimes at one decision point. For many complex diseases, such as cancer, AIDS and mental disorders, clinicians may make a series of treatment decisions based on patients’ evolving status of the disease, i.e. a dynamic treatment process. It is therefore of great interest to extend the proposed method to the estimation and selection for optimal dynamic treatment regimes, which is a challenging problem and warrants future study.

Appendix

We need the following regularity conditions to establish the theorems.

• (A1)The vectors (Y_i, C_i, X_i, A_i), i = 1, …, n are independently and identically distributed. In addition, the censoring time C_i is independent of Y_i, A_i and X_i.
• (A2)The values of β and γ belong to a compact set, the vector of covariates X has a convex support, and ϕ(X, γ) is continuously differentiable with respect to γ.
• (A3)There exists a constant τ such that P(C = τ) > 0, P(C > τ) = 0 and P(Y ≥ τ) > 0.
• (A4)The matrix $\partial {(m_{i,1}^{\beta }{(\beta ,\gamma ,G)}^T,\dots ,m_{i,k}^{\beta }{(\beta ,\gamma ,G)}^T,m_i^{\gamma }{(\beta ,\gamma ,G)}^T)}^T/\partial {({\beta }^T,{\gamma }^T)}^T$ is negative definite, and the equation $E\{m_i^{\gamma }({\beta }_0,\gamma ,G)\}=0$ has a unique solution γ*, where the definitions of $m_{i,j}^{\beta }(\beta ,\gamma ,G)$ and $m_i^{\gamma }(\beta ,\gamma ,G)$ are given by (6) and (7) in the proof of Theorem 1.
• (A5)The matrix U defined in the proof of Theorem 1 is finite and non-singular.

Condition (A3) is assumed to simplify theoretical arguments and is satisfied in many clinical studies with an administrative censoring. In practice, τ can be chosen as the maximum of follow-up time. To ensure (A3) in general situations, as suggested by [21], an artificial censoring time L can be introduced to truncate censoring times, that is, C* = C ∧ L. Then (A3) is automatically satisfied with truncated censoring times. Conditions (A4) and (A5) are assumed to ensure the consistency and asymptotic normality of the proposed estimators.

7.1. Proof of Theorem 1

To simplify notations, define V_ij = A_j,i − π_j(X_i), G_i = G(Y_i), Ĝ_i = Ĝ(Y_i), and

$$m_{i,j}^{\beta }(\beta ,\gamma ,G)=\frac{{\delta }_i}{G(Y_i)}\{Y_i-\varphi (X_i;\gamma )-\sum _{l=1}^k{\beta }_l^T{\mathrm{X̃}}_i{V}_{il}\}{\mathrm{X̃}}_i{V}_{ij},j=1,\dots ,k,$$ (6)

$$m_i^{\gamma }(\beta ,\gamma ,G)=\frac{{\delta }_i}{G(Y_i)}\{Y_i-\varphi (X_i;\gamma )-\sum _{l=1}^k{\beta }_l^T{\mathrm{X̃}}_i{V}_{il}\}\frac{\partial \varphi (X_i;\gamma )}{\partial \gamma }.$$ (7)

Since Ĝ(·) is a consistent estimator of G(·), we can show that

$$\frac{1}{n}\sum _{i=1}^n{m}_{i,j}^{\beta }(\beta ,\gamma ,Ĝ)\stackrel{p}{\to }E\{m_{i,j}^{\beta }(\beta ,\gamma ,G)\},j=1,\dots ,k,\frac{1}{n}\sum _{i=1}^n{m}_i^{\gamma }(\beta ,\gamma ,Ĝ)\stackrel{p}{\to }E\{m_i^{\gamma }(\beta ,\gamma ,G)\},$$

uniformly for β and γ in a compact set. Based on condition (A3), we have that for large n, (β̃^T, γ̃^T)^T are the unique solutions to the equations ${\sum }_{i=1}^n{m}_{i,j}^{\beta }(\beta ,\gamma ,Ĝ)=0$, j = 1, …, k, and ${\sum }_{i=1}^n{m}_i^{\gamma }(\beta ,\gamma ,Ĝ)=0$. In addition, it is easy to show that, for any γ, β₀ are the unique solutions to the equations $E\{m_{i,j}^{\beta }(\beta ,\gamma ,G)\}=0$, for j = 1, …, k. Therefore, by (A3), β₀ and γ* are the unique solutions to the equations $E\{m_{i,j}^{\beta }(\beta ,\gamma ,G)\}=0$, j = 1, …, k, and $E\{m_i^{\gamma }(\beta ,\gamma ,G)\}=0$. This implies that $\mathrm{\beta ̃}\stackrel{p}{\to }{\beta }_0$ and $\mathrm{\gamma ̃}\stackrel{p}{\to }{\gamma }^{*}$.

Next, we prove the asymptotic normality. Define $m_i(\beta ,\gamma ,G)={(m_{i,1}^{\beta }{(\beta ,\gamma ,G)}^T,\dots ,m_{i,k}^{\beta }{(\beta ,\gamma ,G)}^T,m_i^{\gamma }{(\beta ,\gamma ,G)}^T)}^T$. By the first order Taylor expansion, the fact that $\sqrt{n}\{{Ĝ}_i(Y_i)-G(Y_i)\}=O_p(1)$ and some empirical process approximation techniques, we have

$$0=\sum _{i=1}^n{m}_i(\mathrm{\beta ̃},\mathrm{\gamma ̃},Ĝ)=\sum _{i=1}^n{m}_i({\beta }_0,{\gamma }^{*},G)+\sum _{i=1}^n\frac{\partial m_i({\beta }_0,{\gamma }^{*},G)}{\partial G}\{{Ĝ}_i(Y_i)-G(Y_i)\}+\{\sum _{i=1}^n\frac{\partial m_i({\beta }_0,{\gamma }^{*},G)}{\partial {\beta }^T}\}(\mathrm{\beta ̃}-{\beta }_0)+\{\sum _{i=1}^n\frac{\partial m_i({\beta }_0,{\gamma }^{*},G)}{\partial {\gamma }^T}\}(\mathrm{\gamma ̃}-{\gamma }^{*})+o_p(n^{1/2}).$$

In addition, by the martingale integral representation of $\sqrt{n}\{{Ĝ}_i(Y_i)-G(Y_i)\}$, we have

$$n^{-1/2}\sum _{i=1}^n\frac{\partial m_i({\beta }_0,{\gamma }^{*},G)}{\partial G}\{Ĝ(Y_i)-G(Y_i)\}=n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\frac{{\sum }_{j=1}^n{m}_j({\beta }_0,{\gamma }^{*},G)Y_j(u)}{{\sum }_{j=1}^n{Y}_j(u)}\mathrm{d}{M}_i^c(u)+o_p(1)=n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\frac{{\mu }_1(u,{\beta }_0,{\gamma }^{*},G)}{y(u)}\mathrm{d}{M}_i^c(u)+o_p(1),$$

where τ is the maximum follow-up time, Y_i(u) = I(Ỹ_i ≥ u), $Y_i(u)=I({Ỹ}_i\ge u),N_i^c(u)=(1-{\delta }_i)I({Ỹ}_i\le u),M_i^c(u)=N_i^c(u)-{\int }_0^{u}I({Ỹ}_i\ge s)\mathrm{d}{\mathrm{\Lambda }}^c(s)$ with Λ^c(·) being the cumulative hazard function for censoring time, y(u) = P(Ỹ_i ≥ u) and μ₁(u, β₀, γ*,G) = E{m_i(β₀, γ*, G)Y_i(u)}.

Let U = E{−∂m_i(β₀, γ*,G)/∂(β^T, γ^T)^T}. After some algebra, we have

$$U=\left[\begin{array}{cc}{U}_{11}\hfill & 0\hfill \\ 0\hfill & U_{22}\hfill \end{array}\right],$$

where U₁₁ is a (p + 1)k × (p + 1)k matrix with the (ij)th block matrix being E[−π_i(X){1 − π_j(X)}X̃X̃^T], i = 1, …, k, j = 1, …, k, and $U_{22}=E[\frac{\partial \varphi (X,{\gamma }^{*})}{\partial \gamma }\frac{\partial \varphi (X,{\gamma }^{*})}{\partial {\gamma }^T}]$. Then, we have

$$\sqrt{n}\left(\begin{array}{c}\hfill \mathrm{\beta ̂}-{\beta }_0\hfill \\ \hfill \mathrm{\gamma ̂}-{\gamma }^{*}\hfill \end{array}\right)=U^{-1}{n}^{-1/2}\sum _{i=1}^n\{m_i({\beta }_0,{\gamma }^{*},G)+{\int }_0^{\tau }\frac{{\mu }_1(u,{\beta }_0,{\gamma }^{*},G)}{y(u)}\mathrm{d}{M}_i^c(u)\}+o_p(1).$$

By the central limit theorem, $\sqrt{n}(\mathrm{\beta ̂}-{\beta }_0,\mathrm{\gamma ̂}-{\gamma }^{*})$ converges in distribution to a normal random vector with mean 0 and variance-covariance matrix U⁻¹ΩU⁻¹.

7.2. Proof of Theorem 2

Recall that ${𝕐}_i=\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{Y_i-\varphi (X_i;\mathrm{\gamma ̃})\}$ and ${𝕏}_i={({\mathrm{X̃}}_i^T\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{A_{1,i}-{\pi }_1(X_i)\},\dots ,{\mathrm{X̃}}_i^T\frac{{\delta }_i}{\sqrt{Ĝ(Y_i)}}\{A_{k,i}-{\pi }_k(X_i)\})}^T$. Then $L_n(\beta ,\mathrm{\gamma ̃})=n^{-1}{\sum }_{i=1}^n{({𝕐}_i-\beta \prime {𝕏}_i)}^2$. The optimization (4) becomes the penalized least squares estimation subject to the adaptive LASSO penalty. Since Ĝ(t) is a $\sqrt{n}$-consistent estimator of the censoring survival function G(t), and $E\{\frac{{\delta }_i}{G(Y_i)}\}=1$, following the similar arguments used in [12] and [22] for the adaptive LASSO estimation, we can prove the asymptotic results given in Theorem 2. The details are omitted here.

7.3. Proof of Theorem 3

Recall that

$${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)=\frac{{\sum }_{i=1}^n\frac{{\delta }_i^L}{Ĝ(Y_i^L)}\frac{I\{A_i=g(X_i;\mathrm{\beta ̂})\}}{{\pi }_{A_i}(X_i)}{Y}_i^L}{{\sum }_{i=1}^n\frac{{\delta }_i^L}{Ĝ(Y_i^L)}\frac{I\{A_i=g(X_i;\mathrm{\beta ̂})\}}{{\pi }_{A_i}(X_i)}}.$$

By the first order Taylor expansion, the fact that $\sqrt{n}\{{Ĝ}_i(Y_i)-G(Y_i)\}=O_p(1)$ and some empirical process approximation techniques, we have

$${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)={\mathrm{V̂}}_0^L(\mathrm{\beta ̂},G)+\frac{\partial {\mathrm{V̂}}_0^L(\mathrm{\beta ̂},G)}{\partial G}(Ĝ-G)+o_p(n^{-1/2}).$$

Define $J_i={\delta }_i^{L}I\{A_i=g(X_i;\mathrm{\beta ̂})\}/{\pi }_{A_i}(X_i)$. Then

$$n^{1/2}\frac{\partial {\mathrm{V̂}}_0^L(\mathrm{\beta ̂},G)}{\partial G}(Ĝ-G)=n^{1/2}\sum _{i=1}^n{\int }_0^L\frac{{\sum }_{j=1}^n\frac{J_j{Y}_j^L{Y}_j(u)}{G(Y_j^L)}{\sum }_{j=1}^n\frac{J_j}{G(Y_j^L)}-{\sum }_{j=1}^n\frac{J_j{Y}_j^L}{G(Y_j^L)}{\sum }_{j=1}^n\frac{J_j{Y}_j(u)}{G(Y_j^L)}}{{({\sum }_{j=1}^n\frac{J_j}{G(Y_j^L)})}^2{\sum }_{j=1}^n{Y}_j(u)}\mathrm{d}{M}_i^c(u)+o_p(1).$$

In addition, we have

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}{n}^{-1}\sum _{j=1}^n\frac{J_j}{G(Y_j^L)}=\underset{n\to \infty }{\text{lim}}{n}^{-1}\sum _{j=1}^n\frac{{\delta }_i^{L}I\{A_i=g(X_i;{\beta }_0)\}}{G(Y_j^L)}=E\left[\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}\right]=1, \\ \underset{n\to \infty }{\text{lim}}{n}^{-1}\sum _{j=1}^n\frac{J_j}{G(Y_j^L)Y_j^L}=\underset{n\to \infty }{\text{lim}}{n}^{-1}\sum _{j=1}^n\frac{{\delta }_i^{L}I\{A_i=g(X_i;{\beta }_0)\}{Y}_j^L}{G(Y_j^L)}=E\left[\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}{Y}_j^L}{{\pi }_{A_i}(X_i)}\right]=V_0^L. \end{gathered}$$

Similarly, we have ${\mu }_2(u)\equiv {\text{lim}}_{n\to \infty }{n}^{-1}{\sum }_{j=1}^n\frac{J_j{Y}_j^L{Y}_j(u)}{G(Y_j^L)}=E[\{Y^{*}(g(X,{\beta }_0))\wedge L\}I\{Y^{*}(g(X,{\beta }_0))\ge u\}]$ and ${\mu }_3(u)\equiv {\text{lim}}_{n\to \infty }{n}^{-1}{\sum }_{j=1}^n\frac{J_j{Y}_j(u)}{G(Y_j^L)}=P\{Y^{*}(g(X,{\beta }_0))\ge u\}$. Therefore,

$$n^{1/2}\frac{\partial {\mathrm{V̂}}_0^L(\mathrm{\beta ̂},G)}{\partial G}(Ĝ-G)=n^{-1/2}\sum _{i=1}^n{\int }_0^L\frac{{\mu }_2(u)-V_0^L{\mu }_3(u)}{y(u)}\mathrm{d}{M}_i^c(u)+o_p(1).$$

In addition, by some empirical process approximation techniques, it can be shown that ${\mathrm{V̂}}_0^L(\beta ,G)\stackrel{p}{\to }E\{Y^{*}(g(X,\beta ))\wedge L\}\equiv V(\beta )$ uniformly for β in a compact set. Here, V (β) is a smooth function of β. By Theorem 2, we have P(β̂₍₂₎ = 0) → 1 and $\sqrt{n}({\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0})\stackrel{d}{\to }N(0,{\mathrm{\Sigma }}_S)$. Write $\beta ={({\beta }_{(1)}^T,{\beta }_{(2)}^T)}^T$ accordingly and let υ(β) denote the derivative of V (β) with respect to β₍₁₎. Then, we have

$${\mathrm{V̂}}_0^L(\mathrm{\beta ̂},G)-{\mathrm{V̂}}_0^L({\beta }_0,G)-\upsilon ({\beta }_0)({\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0})=o_p(\Vert {\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0}\Vert ).$$

It follows that

$$\sqrt{n}\{{\mathrm{V̂}}_0^L(\mathrm{\beta ̂},Ĝ)-V_0^L\}=\sqrt{n}\{{\mathrm{V̂}}_0^L({\beta }_0,G)-V_0^L\}+\upsilon {({\beta }_0)}^T\sqrt{n}({\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0})+n^{-1/2}\sum _{i=1}^n{\int }_0^L\frac{{\mu }_2(u)-V_0^L{\mu }_3(u)}{y(u)}\mathrm{d}{M}_i^c(u)+o_p(1).$$

Finally,

$$\sqrt{n}\{{\mathrm{V̂}}_0^L({\beta }_0,G)-V_0^L\}=\frac{n^{-1/2}{\sum }_{i=1}^n\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}(Y_i^L-V_0^L)}{n^{-1}{\sum }_{i=1}^n\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}}=n^{-1/2}\sum _{i=1}^n\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}(Y_i^L-V_0^L)+o_p(1),$$

since $E\left[\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}\right]=1$. In addition, we can write $\sqrt{n}({\mathrm{\beta ̂}}_{(1)}-{\beta }_{(1),0})=n^{-1/2}{\sum }_{i=1}^n{\xi }_i+o_p(1)$, where ξ_i’s are i.i.d. mean-zero random vectors. Therefore,

$$\sqrt{n}\{{\mathrm{V̂}}_0^L({\beta }_0,G)-V_0^L\}=n^{-1/2}\sum _{i=1}^n[\frac{{\delta }_i^L}{G(Y_i^L)}\frac{I\{A_i=g(X_i;{\beta }_0)\}}{{\pi }_{A_i}(X_i)}(Y_i^L-V_0^L)+\upsilon {({\beta }_0)}^T{\xi }_i+{\int }_0^L\frac{{\mu }_2(u)-V_0^L{\mu }_3(u)}{y(u)}\mathrm{d}{M}_i^c(u)]+o_p(1),\equiv n^{-1/2}\sum _{i=1}^n{\eta }_i+o_p(1),$$

which converges in distribution to a mean-zero normal random variable with the variance ${\sigma }^2=E({\eta }_i^2)$.