Why post progression survival and post relapse survival are not appropriate measures of efficacy in cancer randomized clinical trials

Abstract

Comparisons of post relapse survival (PRS) and post progression survival have been used to measure efficacy in some cancer clinical trials. These comparisons are an attempt to account for second-line therapies and to identify benefits that do not translate in longer overall survival. However, the use of PRS comparisons can be misleading (either a longer or shorter PRS may indicate a benefit, depending on the circumstances) and can result in biased estimates (because of selection). Here we describe the problems surrounding PRS comparisons and propose alternative approaches to deal with non-randomized therapies administered after progression to the experimental treatment.

Cancer trials of experimental therapies often use as the primary outcome overall survival—time from randomization to death— or either disease-free survival (DFS)—time from randomization to the earliest of relapse or death—in the adjuvant setting or progression-free survival (PFS) —time from randomization to the earliest of tumor progression or death—in the advanced disease setting.

Post relapse survival (PRS)—time from relapse to death—or post-progression survival (PPS)—time from progression to death—is another outcome that has been reported in clinical trials^1–5 and observational studies^6,7 as a complement to overall survival and, occasionally, as the main result.^1,3,5 Several pooled analyses of trials have studied the correlation of PRS/PPS, also referred to as “post disease-free survival”² and “treatment failure survival”,⁶ with PFS^8–11 and overall survival.^12–15

It has been argued that using PRS/PPS helps elucidate the survival benefit of new drugs,^10,14,15 that PPS can be a better surrogate for overall survival than PFS,¹⁰ and that differences in PRS/PPS may explain why DFS/PFS benefits do not always translate into overall survival benefits.^8,9,11 However, analyses that incorporate PRS/PPS may be misleading, biased, or both, as we describe below. For brevity, we focus on PRS, but the same reasoning applies to PPS.

The use of PRS as a complement to overall survival may be misleading

Consider a randomized trial that compares an experimental and a control adjuvant therapy in localized colon cancer. For simplicity, suppose that all patients relapse during the follow-up (below we discuss the more realistic setting in which not all patients relapse during the follow-up). The primary outcome is overall survival but investigators wish to add PRS to their analyses.

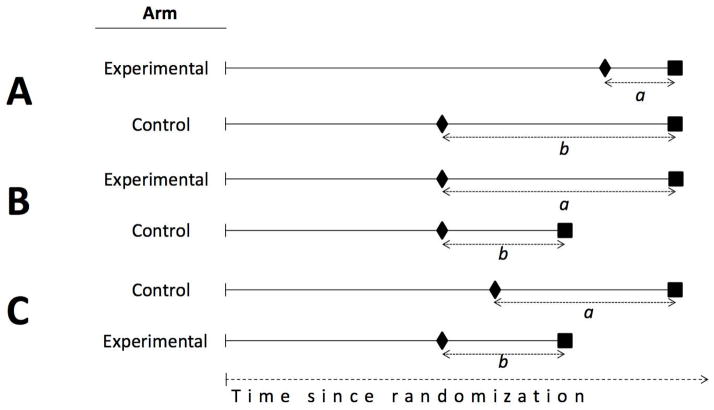
First, suppose that the experimental therapy has no effect on overall survival but increases time to relapse (Figure 1A). Because time to relapse plus PRS equals overall survival, the experimental arm must necessarily have a shorter PRS than the control arm. That is, a shorter PRS indicates a beneficial effect of the experimental treatment in postponing relapse. An example was a randomized trial in localized colon cancer² that found a longer relapse-free survival (hazard ratio: 0.72, 95% CI 0.41–0.92), but a shorter PRS (hazard ratio: 1.61, 95% CI 1.06–2.46), for fluorouracil plus oxaliplatin versus control treatment in high-risk stage II colon cancer.

Figure 1.

Three hypothetical scenarios in which, compared with control, the experimental treatment has an impact on DFS/PFS (Scenario A), overall survival (Scenario B), or both (Scenario C), with PRS/PPS being either shorter (Scenarios A,C) or longer (Scenarios B). Diamonds represent disease relapse or progression and squares represent death.

Second, suppose that the experimental therapy increases overall survival but does not affect the time to relapse¹⁶ (Figure 1B). Because time to relapse plus PRS equals overall survival, the experimental arm must necessarily have a longer PRS than the control arm. That is, a longer PRS indicates a beneficial effect of the experimental treatment because of longer survival after relapse.

These two simple examples show how misleading the PRS may be when taken in isolation. The experimental therapy may be superior to the control therapy whether it increases or decreases the PRS, depending on the effect of the experimental therapy on overall survival and time to relapse. PRS becomes even harder to interpret when the experimental therapy affects both overall survival and time to relapse (Figure 1C). For example, a phase III trial evaluating the addition of cetuximab to perioperative chemotherapy for the treatment of potentially operable colorectal liver metastases, reported both a shorter PFS and a shorter PPS for the experimental arm. Here a shorter PPS indicates a detrimental effect of the experimental treatment⁵.

In summary, even if all patients were observed to relapse during the follow-up, the difference in PRS between the experimental and the control groups is insufficient to decide which treatment provides a greater clinical benefit.

The use of PRS may lead to biased estimates

In practice not all patients relapse during the follow-up. An analysis based on PRS is a subgroup analysis that includes only individuals who do relapse during the follow-up. However, the variable that defines the subgroup, time to relapse, is a post-randomization variable, and thus individuals in PRS analyses are selected based on a post-randomization variable. This selection may introduce bias^17,18 because the individuals in the experimental and control arms may not be comparable after relapse even if they were comparable at baseline.

To see this, consider the following example. Suppose that, consistent with empirical findings in colon cancer,² oxaliplatin-based adjuvant therapy increases the time to relapse but not overall survival compared with a control therapy. Also suppose there exist some prognostic factors (e.g., tumor-specific characteristics) with independent effects on relapse time and overall survival. For example, very aggressive tumors can produce early relapse and, independently, paraneoplasic syndromes (e.g., procoagulative status, cachexia-anorexia) that increase the risk of an early death. Other prognostic factors with effects on both relapse time and overall survival may include characteristics of the patients (e.g., overall health status, immune competence) and the health care delivery system (e.g., resources for cancer treatment and surveillance).

Now consider a PRS analysis that selects only individuals with a relapse during the follow-up. This “relapsing population” is different from the one that was originally randomized. Specifically, it has a different distribution of risk factors than the original one because patients less susceptible to relapse are less likely to be included. Worse, relapsing individuals in the experimental and control arms may no longer be comparable: because individuals in the experimental arm are less likely to have a relapse than those in the control arm, it follows that individuals who relapse in the experimental arm have, on average, risk factors for relapse so strong than they can overcome the delaying effect of the experimental therapy. By restricting the analysis to relapsing individuals, those with the worst prognosis are selected for the experimental arm, whereas those who would normally relapse are selected for the control arm. That is, relapsing individuals in the experimental and control arms do not have a comparable risk profile. The causal diagram¹⁹ in Figure 2 represents this setting.

Figure 2. Causal diagram representing the built-in selection bias in a PRS analysis.

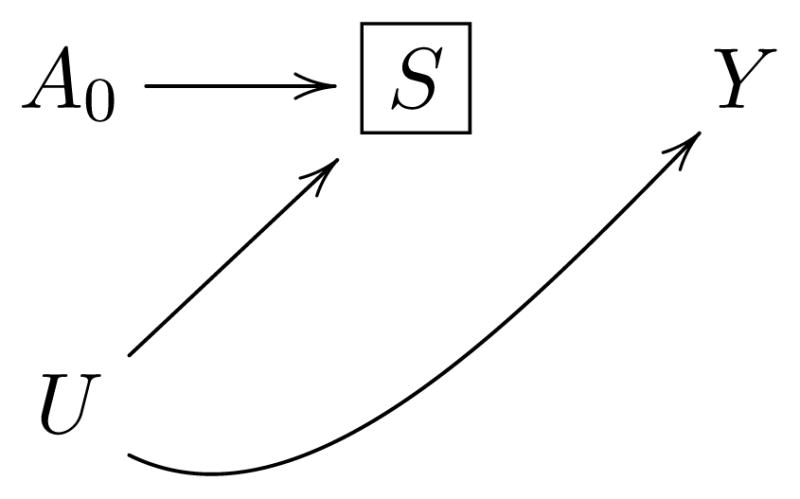
Using the example of localized colon cancer²: A₀ represents assignment to oxaliplatin-based adjuvant chemotherapy, S disease relapse, Y death, and U unmeasured risk factors for relapse and death. Selecting the subset of relapsing patients implies conditioning on a variable S (represented by the box around S) that is affected by the treatment of interest A₀, which generally induces a non-causal association between A₀ and Y through the unmeasured factors U ¹⁷ (technically, S is a collider on which we are conditioning by selecting relapsing patients).

In summary, the benefits of randomization are lost when the analysis is restricted to those who relapse because, even if the therapy does not affect any patient’s overall survival, we might find a shorter PRS in relapsing individuals in the experimental arm compared with the control arm. Bias due to the selection of individuals with relatively worse prognosis in the experimental arm might invalidate the estimates.

Alternatives to PRS-supplemented analyses

Differences in overall survival between the experimental and control groups may be obscured by the use of non-randomized therapies after relapse or progression. The use of PRS is a flawed attempt to overcome this problem.

Ideally, non-randomized therapies would be controlled by design. The protocol of cancer trials would specify fixed therapeutic strategies to be followed after relapse/progression (or would assign them randomly). For example, suppose we randomize patients with localized colon cancer to either (i) adjuvant 5-FU followed by oxaliplatin-based chemotherapy at progression, irinotecan-based chemotherapy +/− antiEGFR (depending on KRAS mutational status) as second line therapy and Regorafenib as third line therapy, or (ii) adjuvant 5-FU plus oxaliplatin (the experimental drug) followed by the same sequence of treatments. An intent-to-treat analysis of this trial would validly estimate the relative effect of assignment to oxaliplatin versus the control therapy on overall survival under the specified sequence of post-progression treatments.

However, if the above protocol cannot be implemented for practical reasons or if patients do not adhere to the specified sequence of treatments, an alternative is to statistically adjust for the use of non-randomized therapies. That is, one needs to treat the randomized trial partly as an observational study,²⁰ to estimate the effect that would have been estimated if all patients had adhered to the protocol. Estimating these “per-protocol effect” requires two steps.

First, investigators need to record information on therapies received by the patients after relapse/progression, and on prognostic factors that affect the choice of therapy, e.g. performance status, comorbidities, frailty scale, toxicity, center, type of health insurance coverage, bone marrow, liver and renal function. This information has to be recorded every time that treatment is susceptible to be changed (e.g., at each follow-up visit). Because post-randomization data on treatment and clinical factors is not always systematically collected in cancer trials, the trial protocol will need to pre-specify the data that will be recorded and the procedures to do so during the conduct of the study.

Second, the protocol also needs to specify how the post-randomization data will be used in the statistical analysis. Conventional statistical methods cannot appropriately adjust for post-randomization variables, as illustrated by the causal diagram in Figure 3. In contrast, causally-explicit methods (like inverse probability weighting, g-estimation, and the g-formula) can appropriately adjust for post-randomization variables.

Figure 3. Causal diagram representing confounding for non-randomized therapies.

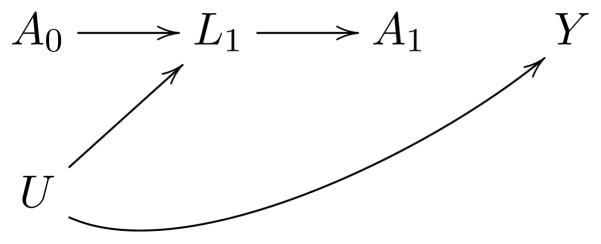
A₀ represents assignment to the experimental arm, A₁ the non-randomized treatment received at disease relapse, Y death, L₁ prognostic factors that affect the clinicians’ choice of A₁ (e.g. performance status, comorbidities, frailty scale, toxicity, center, type of health insurance coverage, bone marrow, liver and renal function), and U the unmeasured determinants of those factors and of death. Conventional statistical methods adjust for the factors L₁ by conditioning on them, e.g., adding them as covariates in an outcome regression model, which will generally induce selection bias in the estimates.

Let us return to our example about the effect of oxaliplatin as adjuvant treatment. One approach to estimate the per-protocol effect of the experimental therapy on overall survival would be the following. First, censor patients at the time they deviate from the therapeutic strategy specified in the protocol, e.g. patients starting FOLFOX plus bevacizumab as third line therapy would be censored at the time they start that new regime. Note that patients stopping or modifying their assigned treatment for clinical reasons (e.g., toxicity) cannot be considered to deviate from protocol as the trial protocol should allow for such changes. Second, use the information recorded on post randomization treatment and covariates to model, at each time during the follow-up, the probability of remaining on protocol (i.e., the probability of being uncensored) conditional on past treatment and covariate history. Third, compute subject-specific, time-varying inverse probability weights based on the estimated probabilities. Finally, fit a weighted survival model in which each subject is assigned the corresponding inverse probability weight at each time ^21–23. If a weighted Cox model is fitted, this approach will estimate the hazard ratio that would have been observed had all clinical trial participants followed their assigned, pre specified therapeutic strategy until the end of the study.²³ This approach can also easily incorporate adjustment for selection bias due to differential loss to follow-up.

Unfortunately, causally-explicit methods like the one described above are not free of potential bias as they depend critically on assumptions that are inherently unverifiable. Specifically, these methods require that all pre- and post-randomization prognostic factors that affect either treatment choices or lost to follow-up are correctly measured and modeled. In our example, the causal estimate might be invalid if health insurance coverage, which impacts both survival and treatment adherence, were not correctly measured and adjusted for.

Conclusion

Effect estimates based on PRS/PPS are hard to interpret and are affected by a built-in selection bias. From the perspective of patients and clinicians, estimates based on DFS or overall survival are obviously relevant, but estimates based on PRS/PPS may be misleading. Investigators interested in overcoming the problems raised by non-randomized therapies may elect a more principled approach: estimating appropriately adjusted (per-protocol) effects on overall survival.

Novelty & Impact.

• Post relapse survival and post progression survival have been used to measure efficacy in some cancer clinical trials.

• Their use can be misleading and can result in biased estimates.