Effects of countermovement depth on kinematic and kinetic patterns of maximum vertical jumps

Abstract

Although maximum height (H_max), muscle force (F), and power output (P), have been routinely obtained from maximum vertical jumps for various purposes, a possible role of the countermovement depth (H_cmd) on the same variables remains largely unexplored. Here we hypothesized that (1) the optimum H_cmd for maximizing H_max exists, while (2) an increase in H_cmd would be associated with a decrease in both F and P. Professional male basketball players (N=11) preformed maximum countermovement jumps with and without arm swing while varying H_cmd ± 25 cm from its preferred value. Although regression models revealed a presence of optimum H_cmd for maximizing H_max, H_max revealed only small changes within a wide range of H_cmd. The preferred H_cmd was markedly below its optimum value (p < .05). However, both F and P sharply decreased with H_cmd, while F also revealed a minimum for H_cmd close to its highest values. Therefore, we conclude that although the optimum H_cmd should exists, the magnitude of its effect on H_max should be only minimal within a typical H_cmd range. Conversely, F and P of leg muscles assessed through maximum vertical jumps should be taken with caution since both of them could be markedly confounded by H_cmd.

INTRODUCTION

It has been generally accepted that maximum vertical jumps could provide a reliable and sensitive assessment of various kinematic and kinetic variables (Markovic et al., 2004, Moir et al., 2004, Moir et al., 2005, Sheppard et al., 2008). Therefore, vertical jumps have been widely used not only for training purposes, but also for testing the velocity, force, and power production capacity of leg muscles both in athletes (Cormie et al., 2011, Cuk et al., 2014, Nedeljkovic et al., 2009, Sheppard et al., 2008, Vuk et al., 2012) and in various patient and elderly populations (Rittweger et al., 2004, Runge et al., 2004). A variety of vertical jumps have been employed, including those with and without a preceding countermovement, arm swing, or external loads.

The concentric phase of the natural countermovement vertical jump is inevitably performed with a preceding eccentric phase that lowers the body center of mass to a certain countermovement depth (H_cmd). The changes in H_cmd markedly affect conditions for muscle actions, and consequently the patterns of various mechanical variables that can be obtained from vertical jumps (Bobbert, 2012, Bobbert et al., 2008, Samozino et al., 2012, Vanrenterghem et al., 2004). Nevertheless, the effect of H_cmd on vertical jumps remains largely neglected in literature. Namely, a typical implicit presumption has been that the tested subjects are able to select the movement pattern (such as assessed by H_cmd) that maximizes the jump height (Moir et al., 2004) and, thereafter, to reproduce it over a series of consecutive trials. As a consequence, both the differences among various populations (Nuzzo et al., 2010, Pazin et al., 2011, Vuk et al., 2012) and the effects of the applied interventions (Cormie et al., 2011, Markovic et al., 2013) on various variables obtained from vertical jumps have been usually attributed to the differences in force and power producing ability of leg muscles, rather than to the differences between the jumping kinematic patterns.

The above discussed disregard of the possible role of H_cmd in vertical jumps has been partly supported by a robust and stable pattern of muscle activation that could be only moderately tuned to the differences in H_cmd (Bobbert and van Soest, 2001, Van Soest et al., 1994). This phenomenon could explain the findings of some experimental and modeling studies suggesting that H_max could be relatively insensitive to H_cmd (Bobbert et al., 2008, Domire and Challis, 2007, Selbie and Caldwell, 1996). Conversely, in addition to empirical and research evidence suggesting that subjects repeatedly select a particular H_cmd and adjust it to the external load (Markovic and Jaric, 2007b, Markovic et al., 2011, Markovic et al., 2014) and effort (Vanrenterghem et al., 2004), some studies have suggested that H_cmd could have a marked effect on H_max (Kirby et al., 2011, Salles et al., 2011). This discrepancy could be explained by a larger range of H_cmd manipulated in the cited studies, as compared with the studies that did not reveal the effect of H_cmd on H_max (Bobbert et al., 2008, Domire and Challis, 2007, Selbie and Caldwell, 1996).

Therefore, one could conclude that we still do not know whether and to what extent H_cmd affects H_max in vertical jumps. Namely, it appears that H_cmd has never been directly manipulated to assess its effect on H_max (Ziv and Lidor, 2010). As a consequence, it remains possible that a number of both the research findings and the outcomes of various testing procedures based on maximum vertical jumps have been confounded by the changes in H_cmd.

In addition to the jumping performance assessed through H_max, there is some evidence suggesting that H_cmd could also affect other variables frequently obtained from vertical jumps. For example, the ground reaction force (F) has often been recorded to assess the effects of various mechanical conditions, as well as to evaluate the outcomes of various strength training procedures (Domire and Challis, 2007, Hori et al., 2007, Markovic et al., 2011, Markovic et al., 2013, Samozino et al., 2014). However, the results of some experimental and modeling studies suggest that the maximum F (F_max) could decrease with an increase in H_cmd (Kirby et al., 2011, Markovic et al., 2014, Salles et al., 2011). In addition, it is well known that the changes in muscle length associated with differences in H_cmd could affect the muscle stretch-shortening cycle performance [c.f., (Cormie et al., 2010)]. An important consequence could be the effect of H_cmd on the muscle power output (P). Namely, the maximum jumping performance (i.e., H_max) may not only require high P of leg muscles (Cormie et al., 2011, Samozino et al., 2012), but H_max could also be a measure of P normalized for body size (Harman et al., 1991, Markovic and Jaric, 2007a, Nedeljkovic et al., 2009). However, a H_cmd associated decrease in P has been reported in literature (Kirby et al., 2011, Salles et al., 2011).

Recent studies have also shown that a jump training associated increase in H_max may not be associated with a comparable increase in F and P due to increased H_cmd (Markovic et al., 2011, Markovic et al., 2013). Therefore, there is convincing evidence that in addition to kinematic, H_cmd could also affect the kinetic pattern of vertical jumps and therefore decouple F and P output of leg muscles from jumping performance (Markovic et al., 2014, Samozino et al., 2012). Nevertheless, we still do not know the magnitude of that effect within a wider range of H_cmd, as well as whether it could be different for F and P. The main aim of the present study is to explore the effects of H_cmd on kinematic and kinetic patterns of maximum vertical jumps. Our first hypothesis was that there would be an optimum H_cmd for maximizing H_max. Our second hypothesis was that both F and P would decrease with an increase in H_cmd. The expected results could be of importance for interpreting the outcomes of various training and testing procedures based on vertical jumping, as well as for gaining a general understanding of the effect of H_cmd on the various mechanical variables typically obtained from vertical jumping.

METHODS

Subjects

Due to the aims of the study, the subjects were required to be exceptionally familiar with vertical jumps performed under different mechanical conditions (Ziv and Lidor, 2010). Therefore, we recruited 11 elite male basketball players (I National league level; age 21.8 ± 2.9 years). We purposefully avoided recruiting the players taller than 2 m because of the prominent scaling effects that their body size could have on both the kinematic and kinetic jumping patterns (Jaric, 2003, McMahon, 1984). Their body mass (86.2 ± 7.1 kg) and body height (192.9 ± 6.0 cm) were assessed by a digital scale and standard kinanthropometer, respectively. Percent of body fat (8.5 ± 4.2 %) was assessed by the bioelectric impedance method (In Body 720; South Korea). None of the subjects reported recent injuries to the musculoskeletal apparatus. The study was conducted in accordance with the Declaration of Helsinki and all subjects signed informed consent approved by the Institutional Review Board.

Experimental protocol

The study was carried out through the familiarization and experimental session separated by at least three days of rest. The anthropometric measures were taken prior to the familiarization session, but the sessions were otherwise identical. They were preceded by a standard warm-up procedure (5 min cycling, 5 min stretching, and 2 sets of 5 submaximal jumps) followed by 2 blocks of 20–23 (see further text for detailed explanations) maximum countermovement jumps performed either without (CMJ) or with an arm swing (CMJA). The countermovement depth (H_cmd) of both jumps was manipulated with respect to the initially self-determined preferred H_cmd. Specifically, the jumps were performed with small, preferred and large H_cmd. Both the sequence of jumps and the sequence selected H_cmd were randomized. The subjects were instructed to avoid any strenuous exercise one day prior to the experiment.

Testing procedures

The blocks of trials for each jump (i.e., CMJ and CMJA) were initiated by 5 maximal jumps that were used for the determination of reference values for all variables. Thereafter, subjects performed 3 sub-blocks of maximum jumps in a random sequence that served for data collection. Specifically, they performed 5 jumps from the preferred H_cmd, as well as 5 or more jumps from either small or large H_cmd. For the preferred H_cmd, subjects were solely instructed to jump as high as possible. The sub-block of jumps performed from the preferred served for the assessment of reliability. Regarding the sub-blocks performed from the small and large H_cmd, subjects were instructed to jump as high as possible either “by going less deep” or “by going deeper into the squat”, respectively.

In both sub-blocks, the experimenters specifically targeted H_cmd to be between 10 and 20 cm different from its reference value obtained from first 5 trials. Whenever the individual trials revealed a H_cmd out of the target interval, the subject was instructed to correct it in the subsequent trial, while the instruction regarding the maximization of jump height was always reiterated. Note that the entire procedure of H_cmd manipulation was based on a series of pilot experiments conducted with the aim to provide an H_cmd approximately equally distributed within the range up to ± 25 cm with respect to the preferred H _cmd. The trials that did not fall within this range (about 1 per subject) were repeated.

About 15 s of rest were allowed between two consecutive trials, 2 min between the sub-blocks, and 5 min between CMJ and CMJA blocks. According to both the subject reports and to previous studies that applied similar protocols (Markovic et al., 2011, Markovic et al., 2013, Pazin et al., 2011), fatigue was never an issue.

Data analyses

A force plate (AMTI BP600400; USA) was mounted and calibrated according to the manufacturer’s specifications. The custom-designed software (LabVIEW, National Instruments, Version 11.0, Austin, TX, USA) was used to record and process the vertical component of the ground reaction force (F) at the sampling frequency of 1000 Hz. The change in the vertical position of the subject’s center of mass was calculated by consecutive integrations of the acceleration signal obtained from F. Each individual set of data was checked and corrected if integration drift appeared. In addition to the maximum displacement of the center of mass during the eccentric (i.e., the countermovement depth; H_cmd) and flight (jump height; H_max) phase of the jump, we also recorded the maximum F (F_max) and calculated P as its maximum (P_max) and average value (P_avg) power from the concentric jump phase as a product of F and velocity of the center of mass.

Statistical analyses

Descriptive statistics were calculated for all experimental data as mean and standard deviation (SD) values. To evaluate the reliability of H_max and H_cmd, we calculated the intraclass correlation coefficients (ICC), coefficients of variation (CV), and standard errors of measurement (SEM) together with the corresponding 95% confidence intervals (95% CI). Repeated measures one-way analysis of variance (ANOVA) was also used for detection of possible systematic bias among five consecutive trials.

To assess the effect of H_max on all dependent variables, we applied both a linear and second-order polynomial regression model on individual, as well as on the group data. When needed, the correlation coefficients and the corresponding 95% CI were used for testing the differences between the applied regression models. Due to its particular importance, the effect of H_cmd on H_max will be presented through both the individual and group data. The maxima of polynomial regressions were used to assess the optimum H_cmd that maximizes the H_max. One-group t-test was used to assess the differences between the optimum and preferred H_cmd. The same test was used to compare the Z-transformed correlation coefficients obtained from the 2 jump types. The effect of H_cmd on the remaining dependent variables (i.e., F_max, P_max, and P_avg) will only be presented through the group data. However, note that the selection of the models (i.e., the polynomial for F_max and linear for P_max and P_avg) was based on the individual data. Alpha was set to 0.05 for all comparisons. All statistical tests were performed using SPSS 16.0 (SPSS Inc, Chicago, IL, USA) and Office Excel 2003 (Microsoft Corporation, Redmond, WA, USA).

RESULTS

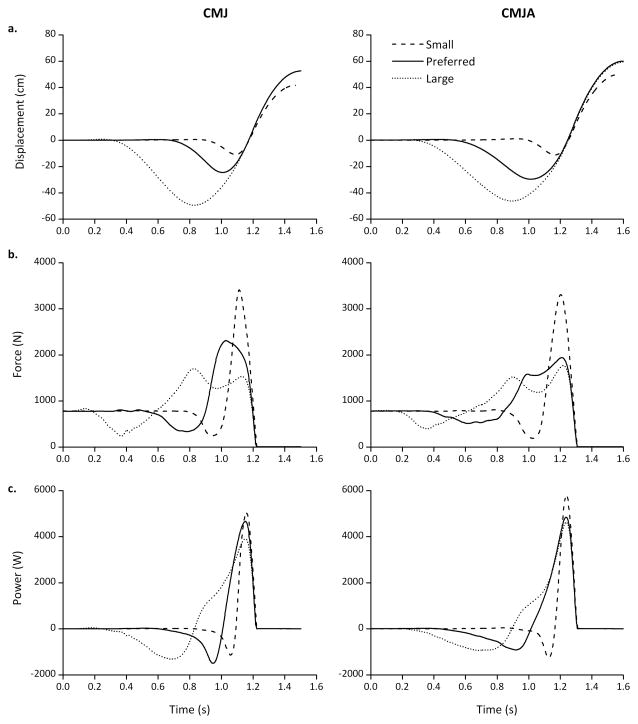
The typical time series of the dependent mechanical variables obtained from a representative subject when performing jumps from the small, preferred, and large countermovement depth (H_cmd) for 2 jump types are shown in Figure 1. Note that an increase in H_cmd was associated with a decrease in both the maximal ground reaction force (F_max) and the maximal power (P_max). Conversely, the jump height (H_max) was comparable for the preferred and large H_cmd suggesting that the optimum H_cmd could be somewhere in between these two values.

Figure 1.

Time series of the height of the center of mass (a), ground reaction force (b) and power output (c) recorded from the maximum countermovement jumps performed without (CMJ) and with arm swing (CMJA) when the instructed countermovement depth was smaller (dashed line), preferred (solid line) and larger (dotted line). Data are aligned with respect to the instant of take-off.

Descriptive statistics and intra-trial reliability coefficients of H_cmd and H_max observed from the sub-block of jumps performed from the preferred H_cmd are presented in Table 1. In general, most of the data suggest a high reliability of the evaluated variables. However, the comparison of 95% CI of the depicted variables also reveal higher reliability of H_max than of H_cmd. No significant differences among five consecutive trials were recorded in any of the evaluated variables.

Table 1.

Reliability analysis of the jump height and preferred countermovement depth (all data in cm; n = 11).

	CMJ		CMJA
	Hmax	Hcmd	Hmax	Hcmd
	Mean±SD	Mean±SD	Mean±SD	Mean±SD
Trial 1	36.9± 3.7	33.2± 5.3	43.3±3.6	31.0±4.2
Trial 2	37.3± 3.3	33.2±4.9	43.2±3.6	30.6±2.5
Trial 3	37.8± 3.6	33.4± 4.7	43.7±3.4	30.0±3.9
Trial 4	38.0± 3.6	33.3± 4.0	43.3±4.2	30.8±3.0
Trial 5	37.8± 3.7	33.9± 4.3	44.2±3.2	30.6±4.4
F	2.48	0.23	0.78	0.25
p	0.06	0.91	0.54	0.91
ICC (95% CI)	0.92 (0.82–0.98)	0.82 (0.65–0.94)	0.83 (0.65–0.95)	0.61 (0.35–0.85)
CV (95% CI)	2.2 (1.7–2.9)	5.7 (4.6–7.7)	3.9 (3.1–5.3)	9.0 (7.2–12.1)
SEM (95% CI)	0.8 (0.6–1.1)	1.9 (1.5–2.5)	1.6 (1.3–2.2)	2.5 (2.1–3.4)

CMJ - countermovement jump without arm swing; CMJA - countermovement jump with arm swing; H_max - jump height; H_cmd - countermovement depth; ICC - intraclass correlation coefficient; CV - coefficient of variation; SEM - standard error of measurement; 95% CI - 95% confidence interval

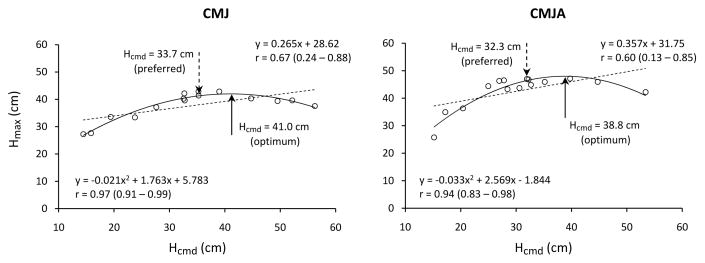
Although we explored the relationships of all dependent variables with H_cmd (see further text for details), of particular importance should arguably be the relationship between H_cmd and H_max. Figure 2 presents both regression models applied to the data of the representative subject. Note that both jumps reveal the correlation coefficients of the polynomial model that are above 95% CI of the corresponding linear model. Of importance could also be that the preferred values of H_cmd were smaller than the optimum ones that were assessed by the maxima of the polynomial models.

Figure 2.

Individual data of the jump height (H_max) observed from CMJ and CMJA trials of representative subjects performed with different countermovement depths (H_cmd). Both linear and second-order polynomial models are fitted, while the dashed and solid arrows indicate the preferred and optimum Hcmd, respectively. Note that both jumps reveal the polynomial correlation coefficient above the 95% CI of the linear coefficient, while the preferred H_cmd is below the optimum one.

When all individual data are taken together, the median correlation coefficients (range) were r = 0.68 (0.26–0.82) and r = 0.45 (-0.08–0.78) for the linear, and r = 0.94 (0.82–0.98), and r = 0.83 (0.55–0.94) for the polynomial model applied on CMJ and CMJA data, respectively. All 11 individual relationships per jump obtained through the polynomial model were significant (p < 0.05), while the linear model revealed 7 and 4 significant individual relationships for CMJ and CMJA, respectively. The correlation coefficients of both models proved to be higher for CMJ than for CMJA(p < 0.05). Of more importance could be that the observed coefficients of correlation for the polynomial model were above the 95% CI of the corresponding linear model in 9 out of 11 and in 8 out of 11 sets of individual data for the CMJ and CMJA, respectively. All polynomial regressions were concave providing maxima that corresponded to the optimum H_cmd that enables maximization of H_max. Collectively, these findings justified applying the polynomial model on the group data (see further text). Finally, the individual sets of data also show that the preferred H_cmd was 8.2 ± 3.2 and 4.0 ± 3.4 cm below its optimum value in CMJ and CMJA, respectively (both p < 0.05; one-group t-test).

Figure 3 illustrates the main findings of the present study obtained from the group data. Specifically, the data obtained from all 15 jumps of each subject are shown through their differences from the reference values (i.e., the data observed from their first 5 jumps performed from the preferred H_cmd; the reference values averaged across the subjects are shown along the main axes).

Figure 3.

Maximum jump height (ΔH_max; panels a), maximum ground reaction force (ΔF_max; panels b), and the maximum (ΔP_max; panels c) and average power output (ΔP_avg; panels d) as a function of the countermovement depth (H_cmd; the axis label shown at the bottom of the figure) obtained from all subjects performing CMJ and CMJA jumps. All data are presented relative to the corresponding reference values observed from the sub-block of trials performed from the preferred H_cmd (averages across the subjects are shown aside). Polynomial and linear regressions with the correlation coefficients and corresponding 95% CI are also shown. Vertical arrows indicate the optimum H_cmd that maximizes H_max.

Regarding H_max (Figure 3a), the findings were in line with the data observed from individual subjects. The polynomial model revealed either high (r = 0.86 in CMJ) or moderate (r = 0.65 in CMJA) relationships, while the data as a whole also suggest that the preferred H_cmd were smaller than the optimum H_cmd (33.4 vs 41.6 cm in CMJ, and 30.6 vs. 34.7 cm in CMJA, respectively). However, of importance here could also be that the fitted polynomial regressions were relatively flat. As a result, the subjects lost on average only about 0.9 and 0.3 cm of their H_max due to the preferred H_cmd being 8.2 and 4.0 cm smaller than the optimum one in CMJ and CMJA, respectively.

Regarding the group data of the 3 remaining dependent variables, Figure 3b reveals a strong polynomial relationship of F_max with H_cmd in both jumps. Although the regression models revealed a minimum, F_max changes almost two-fold within the tested H_cmd range. However, since the minimum appears close to the maximum values of H_cmd, it appears that F_max decreases over the most of the tested H_cmd range. Finally, Figures 3c and 3d reveal a strong (all r > 0.85) and approximately linear H_cmd associated decrease in both P_max and P_avg. Note also that the regression slopes lines are almost two-fold higher in CMJA than in CMJ.

DISCUSSION

Within the present study we tested maximum vertical countermovement jumps performed from the preferred, as well as from both a lower and higher countermovement depth (H_cmd). Independently of whether the arm swing was used or not, the data were mainly in line with our predictions. Regarding our first hypothesis, although the magnitude of the effect of H_cmd on H_max could be relatively weak within a wide range of H_cmd change, an optimum H_cmd for maximizing the jump height (H_max) could exist.

Interestingly, the preferred H_cmd consistently remained below the optimum one across both the subjects and jumps. Regarding the second hypothesis, both the peak (P_max) and averaged power output (P_avg) does decrease with H_cmd in a rather linear fashion, while a generally similar trend of the maximum ground reaction force (F_max) may have a ceiling, if not a minimum, for H_cmd well above its optimum values. The polynomial regression models of the tested jumps revealed an optimum H_cmd for maximizing H_max that could be somewhat greater than their preferred value of about 31–33 cm. Therefore, our findings generally suggest that the optimum H_cmd does exist.

However, note also that the regression curves appeared to be relatively flat. For example, they suggest that H_max drops less than 5 cm when H_cmd varies up to about ± 20 cm from its optimum value. This interval is almost one order of magnitude above the variance of H_cmd typically observed from consecutive vertical jumps of either the same subjects (see Table 1) or from physically active individuals (Cuk et al., 2014, Markovic et al., 2004, Markovic et al., 2013). Moreover, although the tested top-level basketball players should have been familiar with vertical jumps performed from a wide range of H_cmd, one could also question their coordination when jumping with preceding H_cmd, which differs as much as 25 cm from their preferred values (Selbie and Caldwell, 1996, Vanrenterghem et al., 2004). As a result, a part of the already modest drop in H_max observed at the limits of the tested H_cmd interval could partly originate from a suboptimal jumping coordination rather than only from suboptimum H_cmd per se. Therefore, we conclude that although the optimum H_cmd exists, H_max could also be only moderately sensitive to H_cmd variations within its ‘natural’ range of change. This finding is in line with modeling studies that also revealed a lack of a meaningful effect of H_cmd on H_max (Bobbert et al., 2008, Domire and Challis, 2007, Selbie and Caldwell, 1996). The observed phenomenon could also explain a relatively low reliability of H_cmd as compared with H_max. Namely, H_max is apparently the main performance variable of maximum vertical jumps and therefore it should directly reflect a presumably high level of jumping skill in the tested subjects. Conversely, H_cmd has only a marginal effect on the task performance and, therefore, it does not need to be stabilized as an important component of the tested skill. Overall, the discussed findings suggest a limited role of H_cmd in performance tested through maximum countermovement jumps. A general implication of the discussed finding could be that the lack of control of H_cmd should not be seen as a limiting factor in use of CMJ in various modeling and in-depth studies of the design and function of lower limb muscles (Bobbert, 2014).

Despite the discussed low sensitivity of H_max to the variations of H_cmd, of potential importance is that the subjects quite consistently preferred a smaller H_cmd than the optimum one. To our knowledge, this finding is a novel one and we do not have the data to interpret it. Nevertheless, one could speculate that a possible cause of preferring a smaller H_cmd could be a need for the minimization of effort since a prescribed decrease in jumping effort is associated with gradually reduced H_cmd (Vanrenterghem et al., 2004).

Specifically, the preferred jumping kinematic pattern could be selected for a ‘dual task’ aimed both to maximize performance (i.e., H_max) and minimize effort. Alternatively, one could also hypothesize on another type of dual task. Namely, in addition to maximize H_max, the goal of the task in a number of athletic activities is also to jump as quickly as possible, which requires a smaller H_cmd. For example, the ‘quickness’ of jumps is often of crucial importance for success in sport games, such as basketball, volleyball, or soccer. Nevertheless, note also that by preferring a H_cmd that was considerably smaller than the optimum one, the tested subjects on average lost less than 1 cm of their H_max.

While H_max proved to be relatively insensitive to broad variations of H_cmd, both F_max and the power output assessed through P_avg and P_max showed strong dependence on H_cmd in both types of the tested jumps. F_max revealed not only almost a two-fold difference within the tested H_cmd range, but also a minimum for H_cmd that was well above its preferred values. This is mainly in line with previous findings suggesting that F_max may decrease with H_cmd (Kirby et al., 2011, Markovic et al., 2014, Salles et al., 2011). The observed phenomenon could originate from two independent mechanisms. The first one could be based on a reduced leverage of leg extensors unavoidably associated with an increase in H_cmd (Bobbert, 2012). This should reduce F_avg that is obtained from the entire movement range. In addition, a deeper H_cmd should also result in relatively higher velocities at joint angles when subjects typically exert high F. Consequently, the force-velocity property of the active muscles should result in a decreased F_max. Regarding the second mechanism, note also that changes in H_cmd inevitably affect the performance of the SSC through the altered muscle lengths, as well as have an effect on position of body segments and movement ranges, which should all affect F_max and, consequently, P (Cormie et al., 2010). Both discussed mechanisms should lead to the observed negative relationship between H_cmd and either F_max or F_avg.

Both measures of muscle power output also revealed an approximately linear decrease associated with an increase in H_cmd. This result is in line with a number of findings observed from previous studies (Kirby et al., 2011, Salles et al., 2011). Since P is a product of F and velocity, the main cause of the observed phenomenon could be decreased F_max and F_avg associated with increased H_cmd. Namely, since the jumping velocity (and, therefore, H_max) is only slightly affected by H_cmd, P_max and P_avg should be predominantly dependent upon F_max and F_avg, respectively. Note also that increased H_cmd inevitably leads to prolonged concentric jump phase. Therefore, for the jumping velocity and H_max to remain virtually unaltered, P has to decrease. Nonetheless, our results revealed an exceptionally pronounced effect of H_cmd on both P variables that could apparently originate from a much larger H_cmd range tested in the present study. Of particular importance here could be a general difference in trends between H_max and both P_max and P_avg. Namely, while H_max shows a maximum, albeit not a prominent one, both P_max and P_avg markedly decrease over the entire range of H_cmd. This seemingly explains why a generally strong relationship between jumping performance and leg muscle power (Harman et al., 1991, Markovic and Jaric, 2007a, Nedeljkovic et al., 2009) could be decoupled by changes in H_cmd (Markovic et al., 2014, Samozino et al., 2012).

Taken together, our findings related to the effect of H_cmd on both F and P collectively suggest that the variables such F_max, P_max and P_avg should be used with caution in the assessments of training interventions applied to increase F and P of leg muscles. Namely, although both muscle strength and power are frequently targeted by various athletic training interventions aimed to increase movement performance, their direct measures could be strongly confounded by H_cmd. Note that several studies have revealed a marked increase in H_cmd associated with training based on loaded maximum jumps (Cormie et al., 2010, Markovic et al., 2011, Markovic et al., 2013) which inevitably confounded evaluation of the effectiveness of the applied procedure based on directly measured F and P. Conversely, further research is needed to elucidate whether the observed increase in F and P associated with decreased H_cmd could be of importance for optimization of the training based on maximum vertical jumps

Although most of the observed findings appeared to be consistent across the two jump types, two differences between them need to be addressed. First, we found that the relationship between H_cmd and H_max was weaker in CMJA than in CMJ. We do not have the data to explain the observed finding, but it could be plausible to speculate on the role of arm swing used in CMJA, but not in CMJ. Specifically, the arm swing could not only add to the variance of the movement kinematics (and thus reduce strength of the discussed relationship), but also provide additional means of adaptation to differences in H_cmd. Second, higher rates of a decrease in P with an increase in H_cmd suggests that H_cmd decouples P from H_max, and that it does this more in CMJA than in CMJ (see regression slopes in Figure 3). This directly implies that the performance of CMJ could be a more valid predictor of muscle power as compared to CMJA and, therefore, recommended for routine assessments of leg muscle power.

CONCLUSION

We found that although the optimum value of countermovement depth exists, its role in the maximum jumping performance could be fairly small. Therefore, the countermovement depth could often be neglected in both training and testing procedures based on maximum vertical jumps, as well as in the analyses of jumping techniques and its optimizations. Conversely, due to a marked effect of countermovement depth, both the force and power output observed from vertical jumps should be taken with caution. This could be particularly important when using maximum vertical jumps for the assessment of strength and power of leg muscles, as well as for testing the outcomes of various strength training and rehabilitation interventions. Future research could generalize the present finding to other populations, examine causes of a relative insensitivity of jumping performance to the changes in countermovement depth, and explore the origin of the observed difference between the preferred and optimum countermovement depth.

ABREVIATIONS

CMJ

countermovement jump without arm swing

CMJA

countermovement jump with arm swing

H_cmd

countermovement depth

H_max

jump height

F

force outpu

F_max

maximum force outputl

P

power output

P_avg

average power output

P_max

maximum power output

Biographies

Radivoj Mandic received his M.S. degree in kinesiology from Belgrade University. He is currently a Ph.D. student and a teaching and research assistant at the Faculty of Sport and Physical Education of the Belgrade University, Serbia. His main research interest is control of human movements, as well as the selection of youth in sport.

Sasa Jakovljevic received his M.S. (1995) and Ph.D. degrees (2000) in sports sciences from the University of Belgrade, School of Physical Culture, Serbia. Currently he is a Professor at the Faculty of Sport and Physical Education, University of Belgrade. His main research interests are various aspects of team sports training, especially in basketball, technology of sports training and sports biomechanics.

Slobodan Jaric received the M.S. degree in biomedical engineering in 1981 and a Ph.D. in kinesiology in 1986 from Belgrade University. He worked as an Assistant, Associate Professor and a Research Professor at the Belgrade University until 1999, and as an Associate Professor at the National Institute for Working Life and the Umea University in Sweden between 1999 and 2002. Currently he is a Professor of motor control at the University of Delaware and an Adjunct Professor of the Belgrade and Zagreb University. His research interest includes motor control, biomechanics of human movements, and sports biomechanics.