A structured population model suggests that long life and post-reproductive lifespan promote the evolution of cooperation

Abstract

Social organization correlates with longevity across animal taxa. This correlation has been explained by selection for longevity by social evolution. The reverse causality is also conceivable but has not been sufficiently considered. We constructed a simple, spatially structured population model of asexually reproducing individuals to study the effect of temporal life history structuring on the evolution of cooperation. Individuals employed fixed strategies of cooperation or defection towards all neighbours in a basic Prisoner’s Dilemma paradigm. Individuals aged and transitioned through different life history stages asynchronously without migration. An individual’s death triggered a reproductive event by one immediate neighbour. The specific neighbour was chosen probabilistically according to the cumulative payoff from all local interactions. Varying the duration of pre-reproductive, reproductive, and post-reproductive life history stages, long-term simulations allowed a systematic evaluation of the influence of the duration of these specific life history stages. Our results revealed complex interactions among the effects of the three basic life history stages and the benefit to defect. Overall, a long post-reproductive stage promoted the evolution of cooperation, while a prolonged pre-reproductive stage has a negative effect. In general, the total length of life also increased the probability of the evolution of cooperation. Thus, our specific model suggests that the timing of life history transitions and total duration of life history stages may affect the evolution of cooperative behaviour. We conclude that the causation of the empirically observed association of life expectancy and sociality may be more complex than previously realized.

Introduction

Most biological species age and different species age at different rates. These observations are explained by the evolutionary theory of aging with the declining force of natural selection at older ages based on extrinsic mortality and reproductive schedule (Hamilton, 1966). For social species, and particularly humans, this basic theory has been refined to account for inclusive fitness effects through resource transfers (Bourke, 2007; Lee, 2003). A specific example is the “Grandmother Hypothesis”, explaining the expansion of female post-menopausal lifespan (Hawkes et al., 1998). Transfers can take the form of resources and information and may explain why many social species, including humans, are exceptionally long-lived and exhibit post-reproductive lifespans (Carey and Judge, 2001). However, a comprehensive explanation of the association between longevity and sociality may be more complicated (Carey, 2001a; Carey and Judge, 2001) and post-reproductive lifespan may exist for other reasons (Cohen, 2004; Packer et al., 1998).

The inverse causality may have influenced the co-evolution of sociality and longevity: Longer-lived species or species with post-reproductive lifespan may be more likely to evolve cooperation and ultimately sociality, creating potentially positive feedback loops in the association between life history and social evolution. The effect of life history on social evolution has been explored by several theoretical studies that mainly focus on the role of age-dependent dispersal [reviewed in (Lehmann and Rousset, 2010)] and the role of local kin competition that may negate kin-selected benefits of altruistic behaviour (Debarre et al., 2014; Taylor, 1992). Increased survival resulting in overlapping generations, has also been demonstrated to promote altruistic behaviour (Taylor and Irwin, 2000). The specific life history of cetaceans and humans have been analysed to explain the emergence of a post-reproductive life span (Johnstone and Cant, 2010). However, we are unaware of a study that systematically explores the effect of the temporal structure of life histories, namely the durations of the pre-reproductive, reproductive, and post-reproductive life span in a simple, general model.

Modelling the effect of particular life history structures on the evolution of cooperation allows for unbiased testing of the separate effects of pre- and post-reproductive lifespan, reproductive stage, and total duration of life without the additional life-history parameters that may influence the coevolution of sociality and longevity in any particular species. Sociality may protect individuals, particularly during maturation, from a variety of factors and thus decrease extrinsic mortality (Keller and Genoud, 1997). Maturation time is correlated with sociality (Hatchwell, 2009) and with longevity (Ricklefs, 2010). In empirical data sets such correlations hinder the investigation of independent effects of specific life history variables. For example, no association between sociality and longevity was detected in North American birds when external mortality and maturation time were statistically accounted for (Blumstein and Moller, 2008). Prolonged maturation time is also associated with longevity in other taxa (Ridgway et al., 2011) but its effects on the evolution of cooperation and sociality are unclear.

The evolution of cooperation is commonly modelled in the general game theoretical framework by a two-person game called Prisoner’s Dilemma (Nowak, 2012). The simple form of the Prisoner’s Dilemma (PD) predicts no evolution of cooperation because a non-cooperator (= defector) receives a higher fitness pay-off from a pairwise interaction with another individual than a cooperator, regardless of whether the other individual cooperates or not (Axelrod, 1984). Relative to cooperation, the predicted defection behaviour leads to fitness costs at the group level but persists due to individual selection. However, several extensions of the PD have been developed that can explain the emergence and maintenance of cooperation in a population (see for example Nowak, 2006) and these extensions serve to increase the realism of the underlying model for most biological systems (Lewis and Dumbrell, 2013).

The extensions that generally favour cooperation include repeated interactions (Axelrod, 1984) and the introduction of spatial population structure (Nowak and May 1992, Killingback & Doebeli, 1996, Nakamaru et al., 1997, van Baalen & Rand, 1998, Nakamaru et al., 1998, Mitteldorf & Wilson, 2000, Ifty et al. 2004, Nakamaru, N., Iwasa, Y., 2005, Lieberman et al. 2006, Ohtsuki et al., 2006), particularly in the form of scale-free networks (Santos et al., 2006a). In some cases, however, the spatial structure inhibits the cooperation (Hauert & Doebeli, 2004).

Although some exceptions exist, most Metazoans age with important functional consequences (Finch, 1990). Thus, a third biologically significant extension of reiterated PD games that has recently received significant attention is the phenomenon of ageing. Older age may lead to more information that can enhance an individual’s strategy transfer capability (Szolnoki et al., 2009). Alternatively, ageing leads to a decrease in vitality and thus increases the likelihood of being replaced (Liu et al., 2012). Both processes promote the evolution of cooperation by increasing the population heterogeneity, particularly when individuals are born young and grow older during the simulation (Liu et al., 2012; Szolnoki et al., 2009). Age as a co-evolutionary process has also demonstrated benefits for the evolution of cooperation when it influences the strategy adoption of an individual’s neighbours (Wang et al., 2012). These studies of aging demonstrate an impact of ageing on the evolution of cooperation but allow horizontal transmission of strategies (Liu et al., 2012; Szolnoki et al., 2009; Wang et al., 2012) which is more appropriate for cultural than for genetic evolution (Danchin et al., 2004). Specifically, this approach deemphasizes the role of biological ageing and its link to mortality and reproductive schedules, which are central to the understanding of the evolution of ageing and life-history (Finch, 1990; Hamilton, 1966). The life-history of most biological species can be divided into pre-reproductive, reproductive, and post-reproductive stages that differ fundamentally with respect to fitness consequences and thus their impact on the evolution of cooperation (Finch, 1990) and any other traits.

To specifically investigate the link between different life-history structures and the evolution of cooperation in a general biological context, we constructed a spatial model that relied solely on vertical transmission, replacing individuals that die of old age with young, biological offspring from neighbouring individuals (Ross et al., 2013). We incorporated an age-dependent life-history structure with pre-reproductive, reproductive, and post-reproductive periods of varying lengths and study their effect on the long-term evolutionary dynamics of cooperators and defectors. This biologically realistic division in reproductive and non-reproductive phases resulted in an unsaturated population model that is difficult, if not impossible to solve analytically (Debarre et al., 2014). Our simulation results suggested that the total duration of life and the ratio of reproductive to non-reproductive stages are important for the evolution of cooperation. Furthermore, we found consistent evidence that the duration of post-reproductive and reproductive, but not pre-reproductive life-history stages, favour the evolution of cooperation.

Methods

For our simulation analyses we built a spatially organized population model in C++, in which stationary individuals can occupy the nodes of a 128 × 128 square lattice with periodic boundaries. Each of the 16384 nodes in this two-dimensional lattice is connected to eight neighbouring nodes (Moore neighbourhood size of one). Although neighbourhood size itself can influence the evolution of cooperation (Zhu et al., 2013) we keep this parameter constant for simplicity. The neighbourhood size of eight behaves more deterministically than smaller neighbourhood sizes (Ross et al., 2013), is biologically relevant and computationally manageable. Cooperative or non-cooperative interactions can occur only pairwise with the direct neighbours (Figure 1) and lead to fitness payoffs for each of the two interactants. We chose a simplified PD payoff matrix with 1 < b ≤ 2, following (Santos et al., 2006b) and (Szolnoki et al., 2009).

$$\begin{array}{ccc}\hfill \hfill & \hfill \mathit{\text{Cooperate}}\hfill & \hfill \mathit{\text{Defect}}\hfill \\ \hfill \mathit{\text{Cooperate}}\hfill & 1& 0\\ \hfill \mathit{\text{Defect}}\hfill & b& 0\end{array}$$ (I)

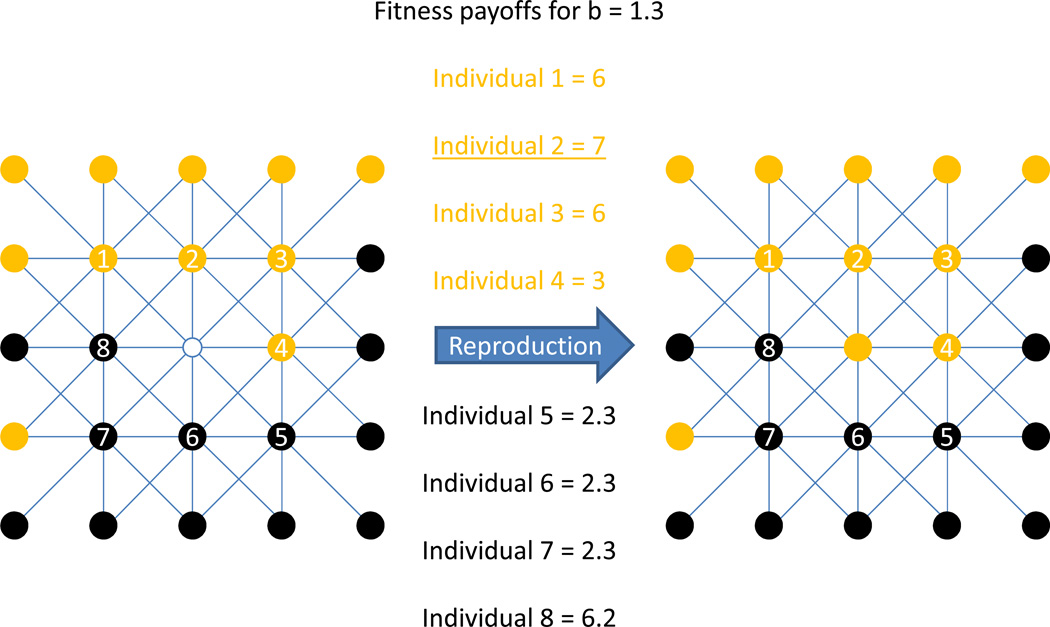
Figure 1.

The spatial population structure and functioning of our model is shown in a small example. Multiple cooperative individuals (yellow) are in contact with multiple defecting individuals (black). The fitness consequences of all pairwise interactions of the eight numbered individuals are given. In this case, individual #2 (underlined) has the highest fitness payoff and would therefore be the most likely to fill the central empty node (white) with a biological offspring that pursues a cooperative strategy.

The model implements a stochastic updating procedure of nodes by randomly selecting one specific node from the entire population at a time. If this node is occupied by an individual, this individual ages and progresses to the next life cycle stage with the probability $d_x^{-1}$, where d_x is the expected duration of the current life cycle stage x in terms of (reproductive) seasons. Alternatively, the individual maintains its current status and remains in the life cycle stage with the probability $1-d_x^{-1}$. For example, an individual is currently in the reproductive stage and the average duration for this stage (d_repro) equals five seasons. This individual has a 1/5 probability to age out of the reproductive stage each time it is selected for an update. The transition from the final life cycle stage leads to the death of the individual. Thus, the total duration of life is expected to be d_life = ∑d_x. This stochastic procedure ensures that individuals in the population age in a biological sense at a variable rate (Finch and Kirkwood 2000), transitioning through the life cycle stages that are assumed in different model variations. These model variations incorporate pre-reproductive, reproductive, and post-reproductive stages of varying length. The duration of the pre-reproductive stage (d_pre) and post-reproductive stage (d_post) varies from 0 to 6 seasons, whereas the reproductive stage (d_repro) varies from 1 to 6 seasons because the simulated population simply collapses without any reproduction.

A transition event from the final life-cycle stage leads to death of the organism and results in an empty node. When such an empty node is selected during the simulation for updating, the surrounding neighbours are assessed for their reproductive status. If no neighbour in the reproductive stage exists, the focal node remains unoccupied. Otherwise, all reproductive neighbours compete for producing one offspring at that node. This offspring starts in the first life cycle stage, inherits the parental strategy (cooperation or defection), and employs that strategy throughout its life. Reproductive competition is probabilistic: Each reproductively active neighbour has a probability to be selected for reproduction (Ps) according to its evolutionary fitness (f_i) relative to the fitness of the other reproductive individuals surrounding the empty node $(Ps=\frac{f_i}{\sum f_i})$.

This fitness is a function of the cumulative payoffs from PD games that the individual plays instantaneously with all its own neighbours. Based on the payoff matrix defined in (I), the fitness of an individual after interactions with its immediate neighbours can be determined by summing the number of cooperative neighbours, which is represented by c in (II) and (III). For defectors, c is multiplied by the defector’s benefit (b) defined previously in (I). According to the above payoff matrix (I),

$$\text{the fitness of a cooperator is}{f}_{\mathit{\text{coop}}}=1+c$$ (II)

$$\text{ane the fitness of a defector is}{f}_{\mathit{\text{def}}}=1+bc$$ (III)

A baseline fitness of 1 is assumed for all individuals, ensuring that reproduction can occur for individuals even without cooperative neighbours.

During the simulations, each update of a specific node represents a single step in a long-term Monte-Carlo process. Each node is updated once on average over 16384 steps because there are 16384 nodes. The 16384 steps are defined as one season although not every individual will have been updated. The total duration of life in terms of seasons (d_life) multiplied by the number of simulation steps per season defines a generation. Each simulation was performed over 5000 generations (G_max = 5000), starting with a solid, small (8 × 8) cluster of cooperators in a predominantly defecting population. The initial frequency of cooperators p_c was thus 0.4% (Ross et al., 2013). The initial age of each individual was determined probabilistically (Ross et al., 2013). All possible model variations were evaluated for three parameter values (b = 1.1, b = 1.3, and b = 1.5) in 100 independent simulations each.

For each simulation, we recorded final population density (PD), whether cooperation or defection strategies were fixed (p_c = 1 or p_c = 0, respectively), and in how many generations (G) fixation occurred. When no strategy was fixed after 5000 generations, G = 5000. Some of these cases may have been due to very slow fixation times, but visual inspection of a few select cases suggest periodic behaviour of the system in the majority of these cases. However, the simulations are without analytical solution and therefore, we cannot be certain. Additionally, we found that accounting for this periodicity with G = ∞ distorts our calculated averages. We defined fixation speed for cooperators G_c = G for all cases of p_c > 0.

In order to quantify the evolutionary potential of cooperation with one numerical expression, we combined the final proportion of cooperators, p_c, and the fixation speed G into a novel variable M, the evolutionary potential of cooperators. M was defined as following. For 1 p_c = 1, we set $M=1-\frac{G}{G_{\mathit{\text{max}}}}$ and for p_c = 0 we defined $M=-(1-\frac{G}{G_{\mathit{\text{max}}}})$. For simulations that did not result in a fixed strategy after 5000 generations M = 0. Thus, the average of M for a particular model variation had a theoretical range from −1 (all 100 simulations lead to the fixation of defection in the first generation) to +1 (all simulations lead to the fixation of cooperation in the first generation).

The 100 independent simulations of each of the 294 model variations (0 to 6 pre-reproductive seasons × 1 to 6 reproductive seasons × 0 to 6 post-reproductive seasons) for three values of b resulted in a total of 88200 simulations. Thus, differences between specific model variations could be statistically tested in addition to evaluating the absolute and relative effects of d_pre, d_repro, d_post, and d_life.

Results and Discussion

Across all simulations, linear regression analyses indicated significant effects of the independent variables d_pre, d_repro, and d_post on the speed of the spread of cooperation, G_c, the final proportion of cooperators in the population, p_c, and consequently the evolutionary potential for cooperation, M (Table 1). The effects of the duration of life history stages differed between G_c and p_c and depended on the relative benefit to defect, b. For high b values, the overall effect of d_pre on the evolution of cooperation was negative and that of d_post was positive, while their effects at lower b and the effects of d_repro for all b were less pronounced (Table 1). Inspection of the data indicated further non-linearities and interactions among d_pre, d_repro, and d_post, requiring the following, more detailed examination of the results.

Table 1.

Overall effects^* of the duration of the pre-reproductive, reproductive, and post-reproductive life history stages (independent variables) on the different simulation outcomes (dependent variables) for different defector incentives (b)

Dependent Variable	Independent Variables	b = 1.1	b = 1.3	b = 1.5
Proportion of cooperators at the end of simulation	Pre-reproductive stage	β = 0.06, p < 0.001	β = −0.004, p = 0.426	β = −0.20, p < 0.001
	Reproductive stage	β = 0.27, p = 0.002	β = 0.27, p < 0.001	β = 0.05, p < 0.001
	Post-reproductive stage	β = −0.16, p < 0.001	β = −0.06, p < 0.001	β = 0.54, p < 0.001
Time to fixation of cooperators	Pre-reproductive stage	β = 0.58, p < 0.001	β = 0.21, p < 0.001	β = 0.38, p < 0.001
	Reproductive stage	β = −0.42, p < 0.001	β = 0.12, p < 0.001	β = 0.32, p < 0.001
	Post-reproductive stage	β = −0.30, p < 0.001	β = −0.61, p < 0.001	β = −0.72, p < 0.001
Cooperation score	Pre-reproductive stage	β = 0.02, p = 0.004	β = −0.10, p < 0.001	β = −0.29, p < 0.001
	Reproductive stage	β = 0.30, p < 0.001	β = 0.22, p < 0.001	β = 0.05, p < 0.001
	Post-reproductive stage	β = −0.14, p < 0.001	β = 0.21, p < 0.001	β = 0.44, p < 0.001
Population size	Pre-reproductive stage	β = 0.28, p < 0.001	β = 0.28, p < 0.001	β = 0.28, p < 0.001
	Reproductive stage	β = 0.79, p < 0.001	β = 0.79, p < 0.001	β = 0.79, p < 0.001
	Post-reproductive stage	β = 0.20, p < 0.001	β = 0.20, p < 0.001	β = 0.20, p < 0.001

^*Multiple regression analysis, standardized regression coefficient β and significance value p are given.

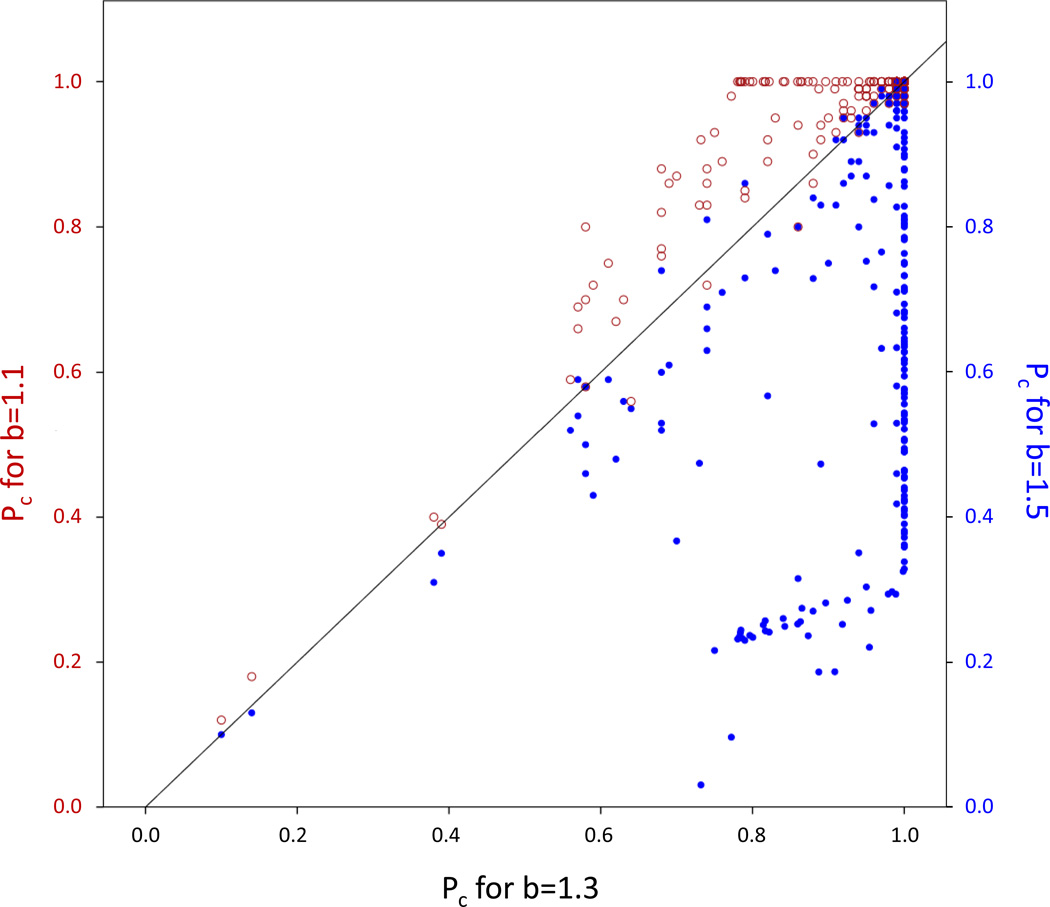
The final proportion of cooperators, p_c, and the number of generations until fixation of cooperators, G_c, in specific life history scenarios were modestly correlated across the different values of b, with higher b resulting overall in smaller final proportions of cooperators (Figure 2) and slower spread of cooperators (Figure 3). Specifically, 56 of the 215 life history structures that invariably resulted in fixation of cooperation for b = 1.1 exhibited p_c averages that were smaller than 1 for b = 1.3. Similarly, 110 of the 159 life history structures that invariably resulted in fixation of cooperation for b = 1.3 resulted in range of p_c values below 1 for b = 1.5. Thus, the benefit to defect predictably decreases both measures of evolutionary success of cooperation in our simulation.

Figure 2.

The average proportion of cooperators at the end of the simulation, p_c, shows a medium correlation between models that were run with different benefits to defect (b). As expected, p_c was generally higher for b = 1.1 than for b = 1.3 (red hollow circles) and generally lower for b = 1.5 (blue solid circles) but several exceptions exist (below and above the diagonal, respectively).

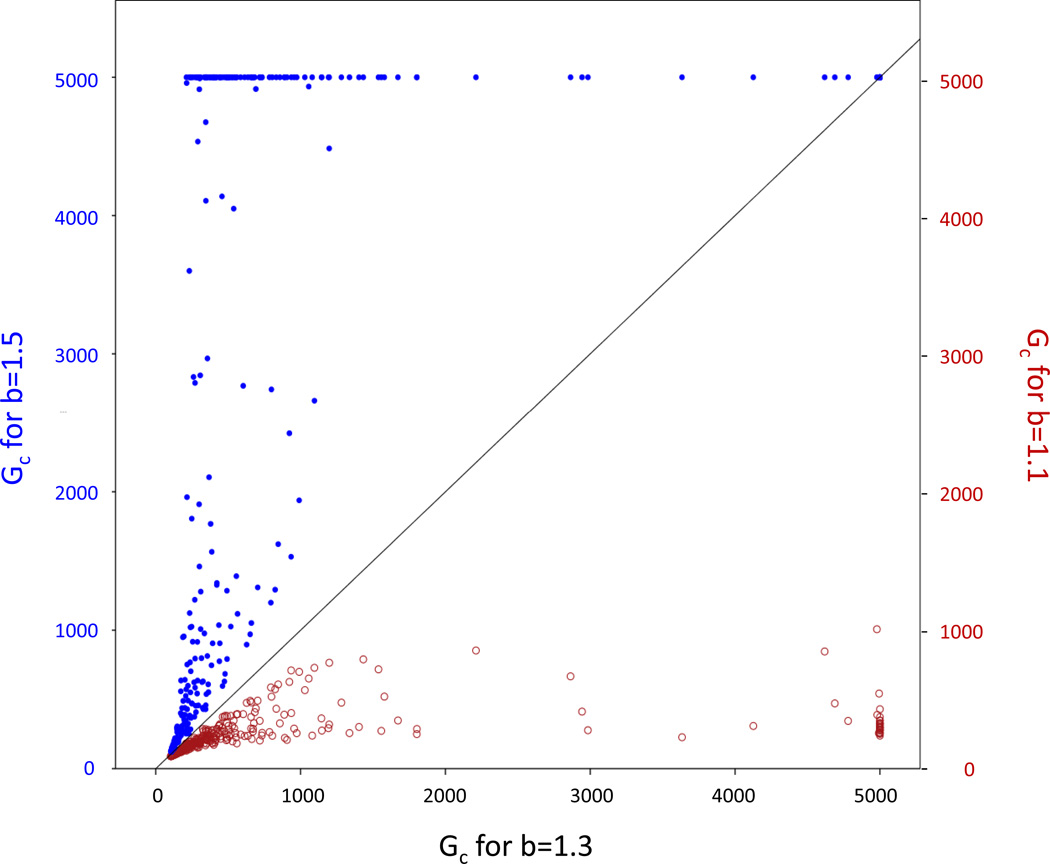
Figure 3.

In simulations that led to the persistence of cooperators, the average time to their fixation G_c was smaller for b = 1.1 than for b = 1.3 (red hollow circles) and larger for b = 1.5 (blue solid circles) without exception. A number of scenarios led to coexistence of cooperators and defectors and G_c = 5000 was defined in these cases because 5000 generations was the limit of each individual simulation.

However, in several exceptional cases the average final proportion of cooperators for b = 1.3 was higher than for b = 1.1 or lower than for b = 1.5 (red circles below or blue dots above the diagonal in Figure 2, respectively). A closer inspection of these unexpected results revealed that these scenarios were characterized by long post-reproductive stages, while scenarios that showed a much higher p_c for b = 1.1 than for b = 1.3 had almost never a post-reproductive stage. The absence of a post-reproductive stage was also typical for scenarios that resulted in much higher p_c values for b = 1.3 than for b = 1.5. In contrast, scenarios that resulted in higher p_c values for b = 1.5 than for b = 1.3 were characterized by short reproductive stages.

In contrast to previous analytical studies (Lehmann and Rousset, 2010) our simulation approach enabled us to explore our model empirically, resulting in a more nuanced picture of the complex evolutionary outcomes in a spatial, multigenerational population model. However, it is more difficult to explain our observations than to explain effects in an analytical study. The counter-intuitive effect that led to higher p_c averages with increasing benefit to defect can only be explained by effects of the life history structure on the clustering of cooperators and defectors in the population. Presumably, under these circumstances a higher b resulted in tighter clustering of individuals with identical strategies, allowing cooperators to initially survive and later expand better than in scenarios with a smaller advantage to defect (Ifti et al., 2004; Szabo and Toke, 1998). This interpretation is supported by the fact the speed of cooperator fixation was always negatively affected by increasing b (Figure 3), including the scenarios that showed higher proportions of cooperators at the end of the simulations for increasing b.

Regardless of the mechanism, the finding that specific life history structures inverse the typical effect of the defector’s benefit in our structured population model indicates that incorporating reproductive and non-reproductive life history periods in game theoretical modelling may be important. This insight corroborates the well-established fact that the timing of reproduction relative to dispersal affects inclusive fitness and thus the evolution of cooperation and altruism (Lehmann and Rousset, 2010).

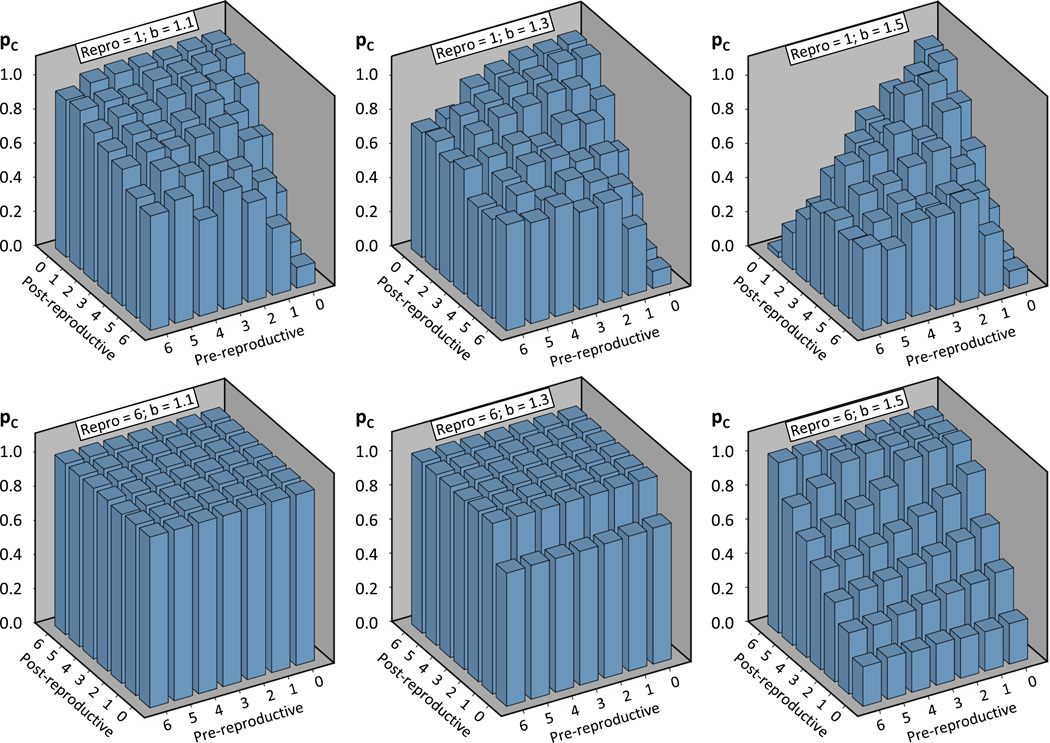
The final proportion of cooperators in individual simulations ranged from 0 to 1 with most values at the extremes of this range. Initially, we used parametric, linear analyses to evaluate overall effects among the different scenarios consistently. This approach was justified by our large sample size and the central limit theorem (Kallenberg, 1997). However, some of the data showed non-linearities. Therefore, additional, visual inspection of the average p_c values for specific life history scenarios was used to reveal the following trends: When the reproductive stage was relatively short (e.g., Figure 4 - upper graphs), d_post had mostly a negative impact on p_c, particularly with b < 1.5. The effect of d_pre depended on d_post in these cases, increasing p_c when d_post was large and decreasing p_c when d_post was small. These results reflect higher success of the cooperators in short-lived species without a post-reproductive lifespan than with post-reproductive lifespan, especially when the benefit to defect is not very high. Furthermore, the results suggested that a prolonged pre-reproductive stage could impede the evolution of cooperation, unless it is paired with a long post-reproductive stage in species with a short reproductive period. Overall, maximal p_c values for short reproductive stages were observed when d_pre and d_post were small. An association of small d_pre, d_repro, and d_post is common in actual biological species, while prolonged pre- and post-reproductive stages are rarely found in species that have a short period of reproduction.

Figure 4.

The average proportion of cooperators in the simulated population was strongly influenced by the benefit to defect (b), the average duration of pre-reproductive, reproductive, and post-reproductive life span, as well as interactions between these four independent variables. To illustrate the main findings the interactive effects of b, pre-, and post-reproductive lifespan are shown here for the shortest (top row) and the longest (bottom row) reproductive duration. Note that the post-reproductive axis is inverted between the rows to improve the visualization of the results.

With a sufficiently long reproductive stage d_post increased p_c and d_pre decreased it consistently (e.g., Figure 4 - lower graphs). Consequently, the scenarios with the highest p_c values were observed for long post-reproductive and short pre-reproductive stages, although p_c was close to its maximum value in many cases for d_repro = 6, which made these effects of d_pre and d_post less apparent. These results match the observation that many social species are relatively long-lived and some exhibit a post-reproductive lifespan (Bourke, 2007; Cohen, 2004; Johnstone and Cant, 2010). Several species, particularly social insects, also have shorter pre-reproductive, developmental stages than their non-social counterparts (Page and Peng, 2001). Thus, some observations correspond well to our model results of an association between long reproductive and post-reproductive life, fast development, and the evolution of cooperation and sociality. In contrast, the classic hypothesis that explains the evolution of long life and post-reproductive lifespan as a consequence of social evolution, predicts a prolonged developmental stage in social species for resource and information transfer to occur (Carey and Judge, 2001; Lee, 2003).

The proportion of simulations that resulted in a fixation of cooperation despite a defector’s benefit was relatively high, with 96.3% for b = 1.1, 85.6% for b = 1.3, and 46.8% for b =1.5. None of the evaluated scenarios led invariably to the extinction of the cooperators, which is remarkable given that the benefit to defect was as high as 50%. The rigid spatial structure without a migratory phase (Nowak and May, 1992) and overlapping generations (Taylor and Irwin, 2000) both increase the assortment of genotypes, facilitating the evolution of cooperation in our simulations. Fixation of defection in singular simulations occurred due to a rapid stochastic extinction of the small initial cluster of cooperators. The small cluster was designed to mimic the real-life scenario of the initial evolutionary dynamics of an incipient cooperative strategy.

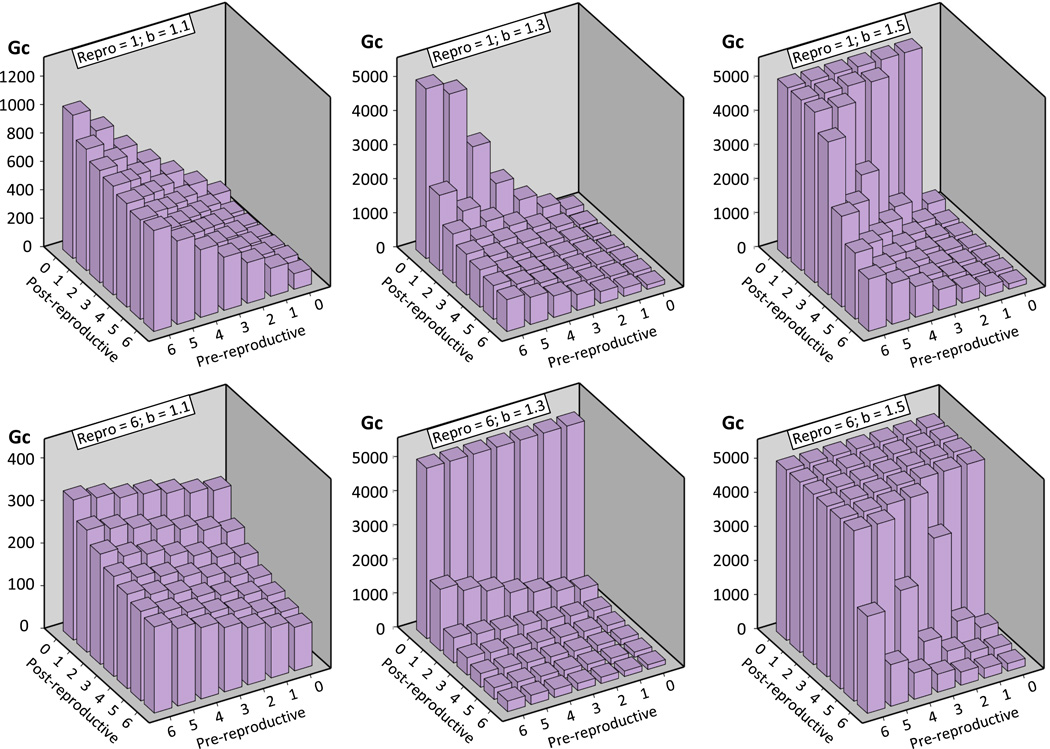
Stochastic extinction was less likely to occur when cooperators spread rapidly, but the speed of fixation of cooperators, G_c, constitutes a second, independent measure of the evolutionary potential of cooperation in our model: Evolutionary success is affected by how fast a particular strategy spreads because the selective environment may change over time (Levins, 1968). Overall, G_c was significantly affected by d_pre, d_repro, and d_post (Table 1). While d_repro showed variable effects that depended on the duration of the other two life stages, d_pre consistently increased G_c and d_post consistently decreased G_c. Thus, the smallest G_c values (fastest fixation of cooperators) were found for small d_pre and large d_post, irrespective of d_repro (e.g., Figure 5).

Figure 5.

The average number of generations until fixation of cooperators (G_c) or their coexistence with defectors (G_c = 5000) in the simulated population was strongly influenced by the benefit to defect (b), the average duration of pre-reproductive, reproductive, and post-reproductive life span, as well their interactions. To illustrate the increase by b and pre-reproductive lifespan, the decrease with increasing post-reproductive lifespan, and the variable effect of the reproductive duration, average simulation outcomes are shown here for the shortest (top row) and the longest (bottom row) reproductive duration.

The two strategies coexisted for 5000 generations in numerous simulations, most commonly when d_repro and b were high. Our simulation proceeds stochastically, which should result in the eventual fixation of one strategy in every case. However, we cannot rule out that the prolonged persistence of cooperation and defection is due to periodic or static patterns of coexistence (Nowak and May, 1992) because we did not follow individual simulations across generations. Regardless of the exact nature of the prolonged co-existence, our outcome contrasts with the conclusion of most analytical models that cannot incorporate the network complexity and spatio-temporal dynamics of the simulated system.

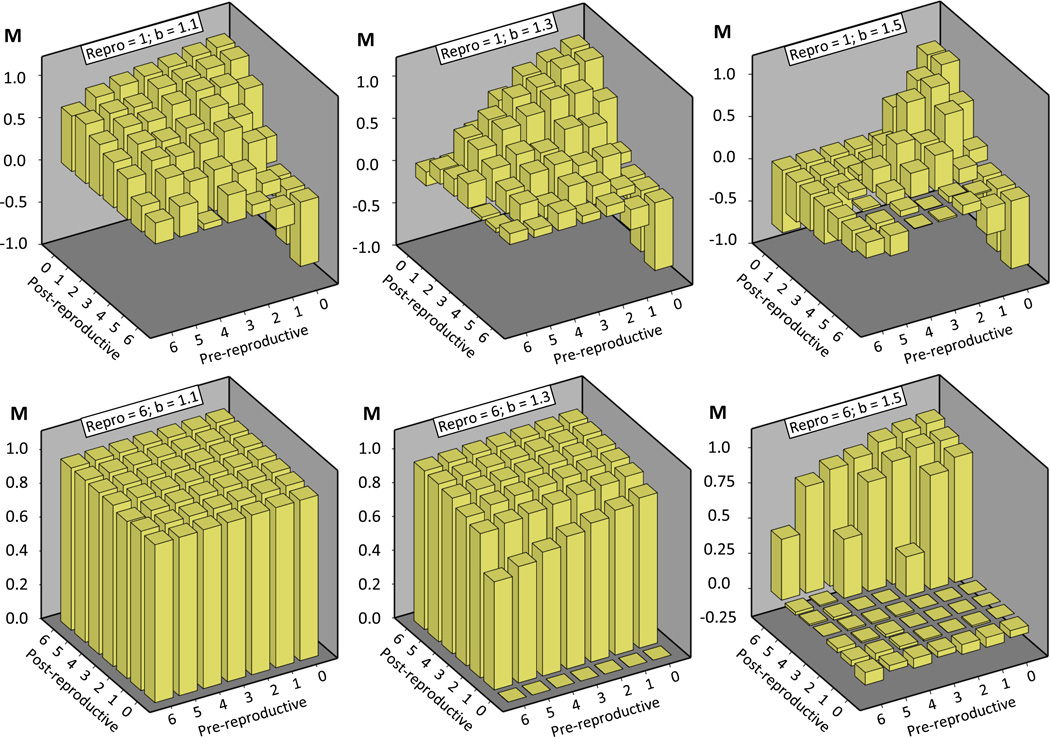
Negative averages of M, the evolutionary potential of cooperators, were observed in 14.3% of all 294 scenarios. These scenarios were characterized by a large difference between d_pre and d_post in combination with high b or small d_repro (e.g., Figure 6). The remaining scenarios had positive M averages, indicating an evolutionary advantage of cooperators in our square lattice population, particularly for low b and large d_repro. For large b and sufficiently large d_repro, M was increased by increasing d_post and decreasing d_pre. Scenarios with a shorter reproductive stage showed variable effects of d_pre and d_post, resulting in maxima of M for low to intermediate values of d_pre and d_post (e.g., Figure 6). Globally, the highest values of M were attained for small d_pre and b, and large d_repro and d_post.

Figure 6.

The evolutionary potential of cooperation (M) was computed by combining the final proportion of cooperators and the rate of fixation of either strategy. The M score was significantly influenced by the benefit to defect (b), the average duration of pre-reproductive, reproductive, and post-reproductive life span, as well their interactions. To illustrate the main findings, average M for each scenario is plotted as a function of the pre- and post-reproductive lifespans for separate b values (increasing from left to right) and for the shortest (top row) and longest (bottom row) reproductive duration.

These outcomes for M resemble the results obtained for p_c, but they are even stronger evidence that particular life-history structures can favour the evolution of cooperation in our model. The most influential life-history characteristics with this effect are a long reproductive phase and a post-reproductive lifespan, which characterizes many social species (Bourke, 2007). Social vertebrates in particular also have typically a prolonged developmental period (Carey and Judge, 2001), which does not match the overall negative association of a prolonged pre-reproductive stage with the evolution of cooperation in our model. However, the effect of d_pre is less pronounced (e.g., Figure 6) and may be outweighed by the effects of the other two stages, given a sufficiently tight correlation between d_pre, d_repro and d_post in biological species. Thus, a positive association between the duration of a pre-reproductive stage and cooperation may evolve indirectly.

The effect of the two summary statistics, total duration of life (d_life) and the relative length of the reproductive stage, was evaluated in a second set of analyses. Both variables showed significant overall effects on all measured outcomes of the simulations. The evolution of cooperation increased with increasing d_life, while the proportion of time spent reproducing only showed a positive association with the evolution of cooperation for the two lower b values (Table 2). Thus, a long life could favour the evolution of cooperation, particularly in conjunction with a prolonged reproductive period, if our specific model results can be generalized. This result suggests that the correlation of longevity and sociality may be explained by the positive effect of long life on the evolution of cooperation in structured populations. While all of our model variations exhibit generational overlap, longevity increased the potential for overlap in our model. Thus, our results corroborate and extend previous studies that specifically studied generational overlap (Taylor and Irwin, 2000).

Table 2.

Overall effects^* of the total duration of life and proportion of time spent in the reproductive stage (independent variables) on the different simulation outcomes (dependent variables) for different defector incentives (b)

Dependent Variable	Independent Variables	b = 1.1	b = 1.3	b = 1.5
Proportion of cooperators at the end of simulation	Duration of life	β = 0.16, p < 0.001	β = 0.18, p < 0.001	β = 0.21, p < 0.001
	Proportion of reproductive stage	β = 0.29, p = 0.002	β = 0.27, p < 0.001	β = −0.07, p < 0.001
Time to fixation of cooperators	Duration of life	β = −0.22, p < 0.001	β = −0.13, p < 0.001	β = 0.08, p < 0.001
	Proportion of reproductive stage	β = −0.50, p < 0.001	β = 0.23, p < 0.001	β = 0.39, p < 0.001
Cooperation score	Duration of life	β = 0.18, p < 0.001	β = 0.23, p < 0.001	β = 0.11, p < 0.001
	Proportion of reproductive stage	β = 0.32, p < 0.001	β = 0.16, p < 0.001	β = −0.004, p = 0.492
Population size	Duration of life	β = 0.83, p < 0.001	β = 0.83, p < 0.001	β = 0.83, p < 0.001
	Proportion of reproductive stage	β = 0.43, p < 0.001	β = 0.43, p < 0.001	β = 0.43, p < 0.001

^*Multiple regression analysis, standardized regression coefficient β and significance value p are given.

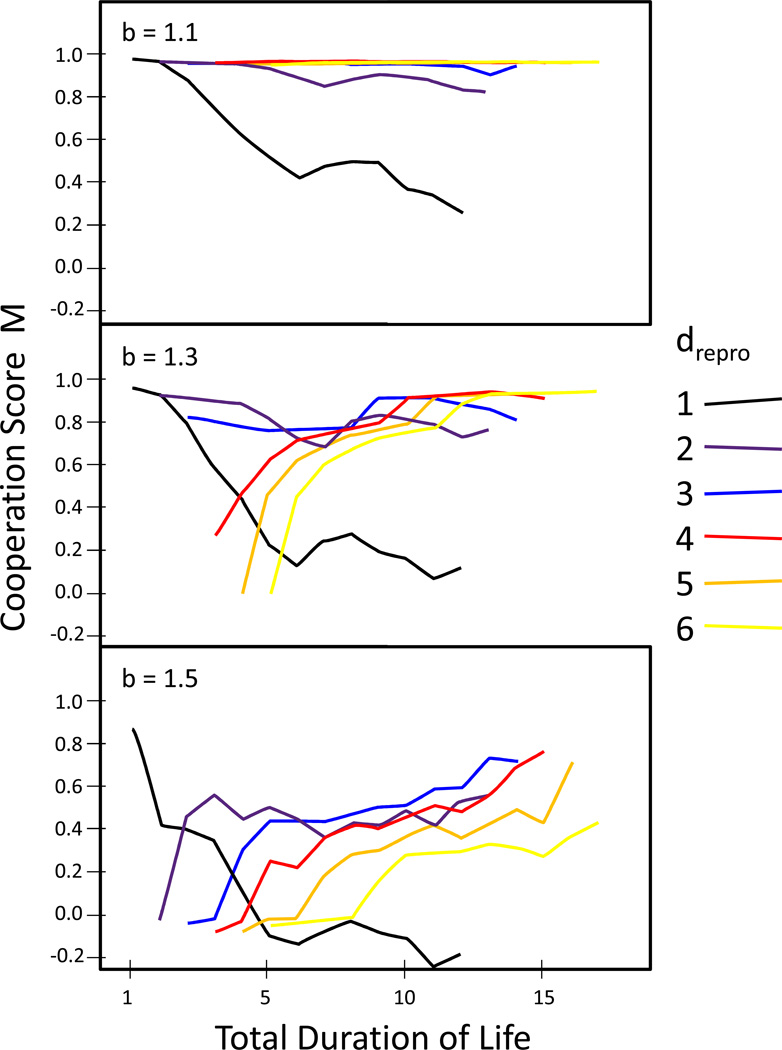
The addition of non-reproductive stages, resulting in an overall longer life for a given reproductive duration, led to an increase in the cooperation score, M, except for scenarios with very short reproductive stages which showed the opposite trend (Figure 7). The increase in M was least apparent for b = 1.1 because M was close to its maximum for all d_repro > 2. Thus, in relatively long-lived species, the prolongation of pre- and post-reproductive lifespan might have facilitated the evolution of cooperative behaviour further. The non-reproductive phases may provide increased opportunity for altruistic behaviour to occur, with the potential for cost/benefit asymmetries that may provide additional benefits for cooperation to evolve. For example, the cost of cooperating may be relatively low for a post-reproductive individual and the benefit of receiving cooperation may be proportionally high for a pre-reproductive, developing individual. Thus, mutually reinforcing interactions between cooperation and longevity may occur (Carey, 2001a), instead of social cooperation simply causing the evolution of longevity and post-reproductive lifespan.

Figure 7.

The evolutionary potential of cooperators M is shown in separate panels for the three evaluated values of the defectors’ benefit b. Scenarios were separated by reproductive duration (dark to light in ascending order) and show the average effect of prolonged life expectancy by adding non-reproductive s (pre- and post-reproductive) stages. While M decreases for very short reproductive durations, the addition of non-reproductive stages increases the evolutionary potential of cooperation for most scenarios.

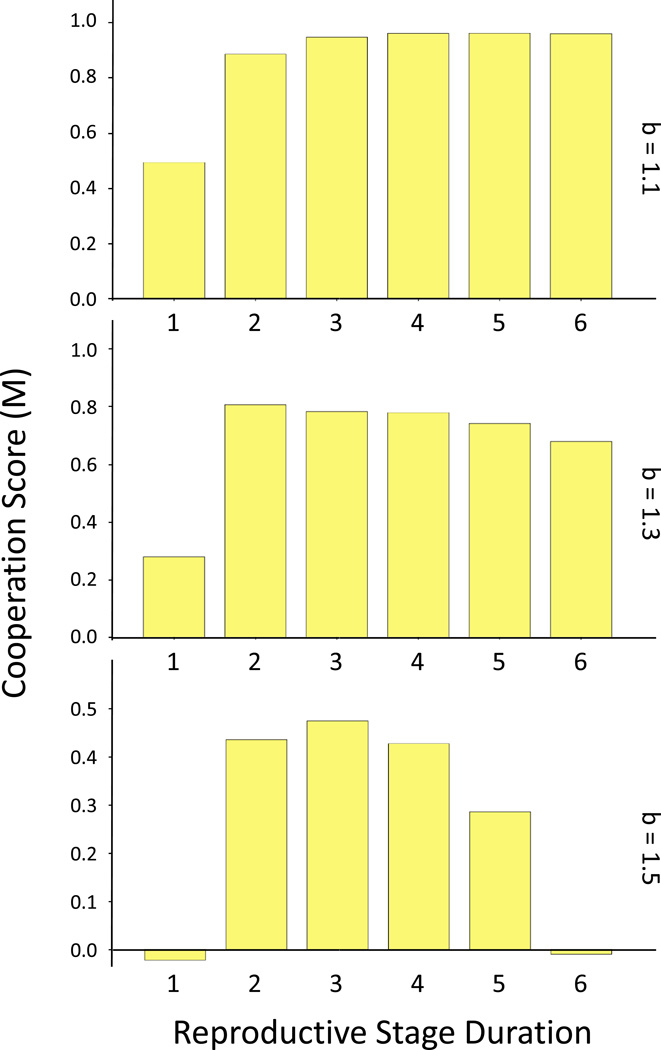
When d_life was constrained, intermediate values of d_repro maximized M (Figure 8), a result of the combination of the positive effect of d_repro and of adding non-reproductive stages when d_repr was sufficiently large. Longer reproductive stages further increased M but only when the total life duration was also allowed to increase. These results limit the length of post-reproductive lifespan that can increase the likelihood of cooperation for a given total duration of life. The effect may be partly explained by more generation overlap (Taylor and Irwin, 2000) but inspection of the raw results suggested that the decreased extinction risk resulting from longer reproductive phases was also influential. Fewer reproductive opportunities per individual increased the stochasticity of the system, benefitting the initially predominant defector strategy.

Figure 8.

For a given life expectancy, intermediate values of reproductive duration were most conducive for the evolution of cooperation, a combined effect of the positive effect of the duration of the reproductive stage and the benefit of adding post-reproductive lifespan.

On the one hand, the evaluated ranges for d_pre, d_repro and d_post cover only a small portion of values that can be observed in biological species. Many vertebrate and some invertebrate species exceed a reproductive duration of six years and a total life expectancy of 18 years (Tacutu et al., 2013). In addition, our models makes some restrictive assumptions with regard to the spatial population structure, the Prisonner’s Dilemma paradigm used, and we employed a compact cluster of cooperators at the beginning of each simulation. However, our findings may suggest important general principles. Reassuringly, our model behaved consistently at the upper limits of the evaluated parameter space.

On the other hand, biological species do not occupy the entire parameter space evaluated. When present, post-reproductive lifespan is typically shorter than reproductive lifespan, while pre-reproductive lifespan is highly variable, ranging from <5% of the total duration of life in some organisms, such as honey bee queens (Page and Peng, 2001), to >95% in other species, such as mayflies, cidadas, or salmon (Carey, 2001b; Finch, 1990). The former group contains some social species, while cooperative behaviour and sociality are conspicuously absent in the latter group, in agreement with our modelling results. Social vertebrates, including humans, have a more moderate ratio of developmental to reproductive duration, typically with a relatively long reproductive stage. Our model suggests that such a life history structure may be favourable, although not the most conducive, for the evolution of cooperation. Given our assumptions, cooperation commonly displaced defection in scenarios with long life and somewhat shorter pre- and post-reproductive stages.

The average final population density, PD, for the different scenarios varied between 8171 and 15411 individuals on the 16384 nodes (49.9 – 94.1% occupancy). Linear regression analysis indicated that PD was mostly increased by d_repr and to a lesser extent by d_pre and d_post (Table 1), resulting in a strong positive association between d_life and PD and a moderate positive association between the proportion of life spent reproductive and PD (Table 2). This effect is due to empty population nodes that arose by the death of an individual without replacement because no reproductive individual surrounds the empty node. Incorporation of PD as an independent variable in our overall analyses of the effects of d_pre, d_repro, and d_post did not change our main results qualitatively, with the exception that the positive impact of d_repro on p_c and M was statistically accounted for by PD. Thus, the effects of life history structure on population density may indirectly affect the evolution of cooperation (Matsuda, 1987). In any case, our conclusions with regards to the effect of pre- and post-reproductive duration seem robust. The strong positive effect of d_life in our specific model supports our initial hypothesis that life history may not only be a consequence of social evolution but also facilitate it (Carey, 2001a) and indirect effects of d_life on population density may aid in this effect. More sophisticated modelling would be required to dissociate the direct and indirect effects of life history, for example by accounting for the typically lower reproductive rates in long-lived species.

Conclusions

In accordance with previous studies (Debarre et al., 2014; Nakamaru et al., 1997; Nowak, 2012), our simulation models suggest that cooperation can evolve in structured populations. A few previous studies have explicitly taken aging into account (Johnson et al., 2002; Szolnoki et al., 2009; Liu et al. 2012) and the effect of dispersal and reproductive timing on the evolution of cooperation are well-established (Lehmann and Rousset, 2010). However, our focus on the reproductive schedule in a life history context uniquely emphasizes the potential interactions between biological aging and social evolution. For the first time, we have systematically investigated how partitioning of the life course into pre-reproductive, reproductive, and post-reproductive phases influences the evolution of cooperation. Our model was conceptually quite simple and employed several specific assumptions that may limit the generality of our results. However, practically the study system was too complex to be solved analytically, requiring this simulation approach. Although the model could be refined in multiple ways, such as asymmetrical costs and benefits of cooperation (Johnson et al., 2002), it provides an important step in our understanding of the potential interactions between life history and social evolution.

Our study challenges the widely-held view that the taxonomic association of sociality with longevity and post-reproductive lifespan is solely explained by life history evolution in response to social organization. Indicating significant effects of life history structure on the evolutionary potential of cooperative behaviour, our study suggests that the direction of a causal link between social and life history evolution needs to be carefully re-evaluated and may differ among specific cases. Post-reproductive lifespan in particular could have evolved for different reasons (Cohen, 2004; Packer et al., 1998) and subsequently led to cooperation, extended kin selection, and sociality. Particularly, the early evolution of social insects provides scenarios where life history and sociality may have mutually reinforced each other (Carey, 2001a) and our model indicates that such feedback from life-history to behaviour is theoretically plausible.

• Social organization correlates with longevity across animal taxa which has been explained by selection for longevity by social evolution.

• We constructed a simple, spatially structured population model of aging individuals, implementing a basic Prisoner’s Dilemma paradigm to study the effect of life history structure on the evolution of altruism.

• Complex interactions among the effects of the duration life history stages and the benefit to defect affected the evolutionary potential of cooperation.

• Overall, a long post-reproductive stage promoted the evolution of cooperation, while a prolonged pre-reproductive stage has a negative effect and the total length of life also increased the probability of the evolution of cooperation.

• We conclude that the timing of life history transitions and total duration of life history stages may affect the evolution of cooperative behaviour and that the causation of the empirically observed association of life expectancy and sociality may be more complex than previously realized.