Abstract
In high-throughput studies, an important objective is to identify gene-environment interactions associated with disease outcomes and phenotypes. Many commonly adopted methods assume specific parametric or semiparametric models, which may be subject to model mis-specification. In addition, they usually use significance level as the criterion for selecting important interactions. In this study, we adopt the rank-based estimation, which is much less sensitive to model specification than some of the existing methods and includes several commonly encountered data and models as special cases. Penalization is adopted for the identification of gene-environment interactions. It achieves simultaneous estimation and identification and does not rely on significance level. For computation feasibility, a smoothed rank estimation is further proposed. Simulation shows that under certain scenarios, for example with contaminated or heavy-tailed data, the proposed method can significantly outperform the existing alternatives with more accurate identification. We analyze a lung cancer prognosis study with gene expression measurements under the AFT (accelerated failure time) model. The proposed method identifies interactions different from those using the alternatives. Some of the identified genes have important implications.
Keywords: Gene-environment interaction, robust rank estimation, penalization, marker identification
Introduction
High-throughput profiling has fundamentally changed the paradigm of research and practice of multiple diseases. Multiple types of genetic, epigenetic, genomic, and proteomic measurements have been generated. To avoid confusion, we use the generic terminology “gene”, which matches the gene expression data analyzed in this article but note that the proposed method is also applicable to other types of genetic and genomic measurements. For complex diseases such as cancer and diabetes, the risk and progression are associated with the combined effects of genes, clinical and environmental risk factors, and their G × E (gene-environment) interactions. For the identification of important interactions, there are multiple families of approaches, including for example the joint approach and stratification approach. For comprehensive discussions, we refer to Hunter [2005], North and Martin [2008], Thomas [2010] and others. In this article, we focus on the statistical modeling approach, where interactions are described using the products of variables in statistical models. In general with high-dimensional measurements on genes, there are two types of analyses [Witten and Tibshirani 2010]. The first conducts marginal analysis and analyzes one gene at a time, and the other describes the joint effects of all genes in a single model. The proposed method conducts marginal analysis, which is still more popular than the joint analysis in G × E interaction studies.
Denote Y as a disease outcome or phenotype. It can be a continuous marker, categorical disease status, or survival time. Denote Z = (Z1, …, Zp) as the p genes and X = (X1, …, Xq) as the q clinical/environmental risk factors. Assume n iid observations. The most popular statistical modeling approach proceeds as follows. (1) For k = 1, …, p, fit a parametric or semiparametric model . For example with a binary Y, ϕ can be the logistic model. αkl’s, γk, and βkl’s are the unknown regression coefficients. As usually q ≪ n, for each k, this step can be carried out using standard techniques and software. Denote pkl as the p-value of β̂kl, the estimate of βkl. (2) With {pkl: k = 1, …, p, l = 1, …, q}, conduct multiple comparison adjustment. Approaches such as the FDR (false discovery rate) can be applied to identify significant interactions. Multiple existing approaches belong to this category [Hunter 2005; Thomas 2010]. Different approaches may have minor differences in terms of statistical models, hypothesis testing methods, and multiple comparison adjustment techniques.
The above approach has the following limitations. With p genes, it is likely that some of the p models are mis-specified. Although in principle it is possible to conduct model diagnostics, to the best of our knowledge, there is no study actually examining the validity of all p regression models. There are a few robust methods. A popular one is the multifactor dimensionality reduction (MDR) [Moore et al. 2006], which provides a powerful approach to detect nonlinear interactions among discrete attributes that are predictive for discrete outcomes. However, it cannot be directly adapted to continuous outcomes or discrete outcomes associated with continuous attributes. Other robust methods may share a similar limitation of restricted applicability. In addition, most of the existing methods use significance level to identify interactions. For some estimates, for example the rank estimate proposed in this study, computing the p-values can be computationally tedious. Moreover, as shown in our simulation study, the significance based methods may have less satisfactory performance.
In this article, we analyze high-throughput data and search for important gene-environment interactions. A statistical modeling approach is adopted, which detects interactions by conducting estimation with βkl’s. A new method is developed to overcome some limitations of the existing methods. Specifically, we assume a general semiparametric transformation model, which makes much weaker model assumptions and hence can be less sensitive to model mis-specification. Correspondingly, a rank-based estimation approach is proposed. This modeling and estimation framework can accommodate continuous, categorical, and censored survival data and includes many commonly adopted models as special cases. We propose using penalization for estimation. In general, for data with a small to moderate sample size, penalization can lead to more reliable estimates. More importantly, for the present problem, penalization can identify important interactions along with estimation, without relying on the significance level. Thus it provides an alternative strategy for identifying interactions. For computational feasibility, a smoothed penalized rank estimation is developed. Simulation study and data analysis are conducted to examine performance of the proposed method.
Robust Modeling and Rank Estimation
Semiparametric transformation model
We use notations similar to those in the above section. For gene k(= 1, …, p), consider the model
| (1) |
where Wk = (X, Zk, ZkX)′, αk = (αk1, …, αkq)′ is the unknown coefficient vector for clinical and environmental factors, γk is the main gene effect, βk = (βk1, …, βkq)′ corresponds to G × E interactions, and . Model (1) is a semiparametric transformation model where the form of the transformation function gk is left unspecified, making the model assumptions much weaker than the existing ones. For identifiability, it is assumed that gk is monotone (without loss of generality, monotone increasing). Under the approach described in the Introduction section, different genes usually have the same ϕ. Here different genes are allowed to have different transformation functions, making this model much more flexible.
For a continuous outcome, model (1) includes as a special case. When gk(t) = t and gk(t) = log(t), this model reduces to the additive and multiplicative error models, respectively. When gk(t) takes the form of a power function and εk follows a normal distribution, we obtain the Box-Cox transformation model. For categorical data, model (1) includes many commonly adopted generalized linear models, for example the logistic model and probit model for binary data and Poisson model for count data. For survival data, model (1) accommodates transformation models (which include the Cox model, accelerated failure time (AFT) model, exponential and other parametric models, etc) and the additive risk model. Thus model (1) indeed has broad applications.
Rank estimation
In principle, it is possible to build estimating equations and simultaneously estimate gk and θk. However, nonparametric estimation of gk can be computationally expensive. A small scale simulation to be presented below also shows that it may lead to inferior results. For the identification of important interactions, only θk is of interest. In this study, we adopt the rank-based estimation [Han 1987; Khan and Tamer 2007], which can avoid estimating gk.
With n iid subjects, use the subscripts i and j to denote the ith and jth subjects, respectively. For gene k(= 1, …, p), consider the estimate θ̂k = argmaxθk O(θk), with the objective function O(·) defined as follows. (a) When Y is continuous,
| (2) |
where I(·) is the indicator function. (b) When Y is categorical, first consider a binary outcome. Denote D and H as the index sets for diseased (Y = 1) and healthy (Y = 0) subjects with sizes nD and nH, respectively. Then
| (3) |
O(θk) is the empirical AUC (area under curve) under the ROC (receiver operating characteristics) framework [Pepe 2004]. With multi-category data, the construction of rank estimates may follow Pepe [2004] and followup studies. (c) When Y is a right-censored survival outcome, denote C as the censoring time. One observes (V = min(Y, C), Δ = I(Y ≤ C)), where Δ is the event indicator. Here
| (4) |
which is closely connected with the integrated time-dependent AUC [Li and Ma 2011]. Under more complex censoring patterns (for example interval censoring), it is also possible to develop rank estimation [Li and Ma 2011]. However, such data are rarely encountered in genomic data analysis and hence not further discussed.
In the above rank-based objective functions, θk is only identifiable up to a constant. Without loss of generality, we assume that |αk1| = 1, k = 1, …, p. With a slight abuse of notations, we still use θk to denote the remaining coefficients (αk2, …, αkq, γk, βk1, …, βkq)′. Although there are some minor differences, the objective functions in (2), (3), and (4) all belong to the MRC (maximum rank correlation) framework. Their asymptotic behaviors can be established following Han [1987] and Sherman [1993], and computationally they can be solved using similar algorithms.
Penalized Identification of G × E Interactions
For the identification of important G×E interactions, we propose the following penalization method. For gene k = 1, …, p, compute
| (5) |
where ρ(·) is the penalty function. Interactions (and main effects) corresponding to the nonzero components of θ̂k’s will be identified as associated with response. In this study, we consider the MCP penalty [Zhang 2010], where and . λ > 0 is the tuning parameter, and γ > 1 is the regularization parameter. Many other penalties can be used to replace MCP, including for example the Lasso family, bridge, SCAD, and others. Studies under simpler data and model settings suggest that MCP can outperform Lasso and several other penalties and have similar performance as bridge, SCAD, and others. As the main goal is not to compare different penalties, we focus on the MCP and will not further discuss the other penalties.
O(θk) is not differentiable. Straightforwardly maximizing O(θk) is an NP-hard problem. A few computationally effective methods have been proposed including the tree-based method and the more recent forward selection method in Li et al. [2011]. However, the high dimensionality of genes and more importantly MCP penalization make computation in this study nontrivial. To tackle the computation problem, we adopt the approximation proposed in Ma and Huang [2005]. Specifically, in O(θk) is approximated with , where is the sigmoid function. We denote the smoothed approximation of O(θk) as Os(θk). The smoothed counterpart of (5) is proposed as
| (6) |
and referred to as the smoothed penalized rank estimate (SPRE). Performance of the approximation and hence the estimate depend on σn. The asymptotic behavior of σn has been studied in Ma and Huang [2005]. Numerical studies in Ma and Huang [2005] and followup studies show that, as long as σn is small, the smoothed rank estimate is not very sensitive to its value. In our numerical study, we set and find satisfactory results. In practice, one may need to experiment with a sequence of σn values and find one that is small enough (so that the estimate does not change significantly when it gets smaller) but not too small (so that the approximation is still stable).
Penalization is imposed. Here it serves two purposes. First, it achieves the identification of important interactions along with estimation. There is no need to further compute the significance level. Using the results in Sherman [1993], we can establish the asymptotic behaviors of θ̂k. In our numerical study, we demonstrate that it is possible to compute a p-value for the rank estimate. However, it can be computationally expensive especially when the number of genes or environmental factors is large or the sample size is moderate to low (so that the asymptotic results are not sensible, and computationally expensive methods such as bootstrap have to be adopted). Second, in general, with a small to moderate sample size, penalization can lead to more stable estimates. In the proposed penalized estimation, the tuning parameter λl’s do not depend on k. Thus, the same degree of penalization is imposed on all genes, leading to a fair comparison. For a gene, the first q − 1 λl’s correspond to the effects of clinical/environmental risk factors. Our main goal is to select important interactions and gene effects. As the clinical/environmental risk factors are usually pre-selected as important and have a low dimensionality, in this study, the first q −1 effects are not subject to penalization, and we set λl = 0 for l = 1, …, q − 1. In practice, when it is suspected that there may be “noisy” clinical/environmental factors, prescreening or penalization can be conducted. All interactions and main effect will be subject to the same amount of penalty, that is, λq = … = λ2q. Following Liu et al. [2013], the penalty can be revised to respect the “main effect, interaction” hierarchy. Such an extension is of less interest under the present setup and will not be pursued.
Under low-dimensional settings, Song and Ma [2010] studies penalized rank estimation. The present data settings are much more complicated, and the MCP penalty is adopted, which may outperform the Lasso penalties in Song and Ma [2010]. Liu et al. [2013] identifies important interactions using penalization. However, that study assumes specific data generating models, which are subject to mis-specification.
Computation
With fixed λl and γ, optimization in (6) can be solved using the coordinate descent algorithm, which proceeds as follows. For each k: (a) Initialize θk. Sensible initial values include component wise zero and the unpenalized estimate. (b) For l = 1, …, 2q, optimize (6) with respect to θkl (the lth component of θk), with θkm(m ≠ l) fixed at its current value θ̃km. (c) Repeat Step (b) until convergence. In our numerical study, we use the ℓ2-norm of the difference between two consecutive estimates less than 0.001 as the convergence criterion. Convergence is achieved for all simulated and real data, usually within 20 iterations.
Consider optimization with respect to θkl in Step (b). Denote R(θkl) as the terms in (6) that involve θkl. Denote θ̃k = (θ̃k1, …, θ̃k,2q). To simplify the optimization in (6), we propose using a local linear approximation of the penalty. More specifically, we approximate ρ(θkl; λl) with . Let Ȯs(θkl|θk,−l) and Ös(θkl|θk,−l) be the first and second partial derivatives of Os at θkl. Here θk,−l is θk with the lth element removed. Overall, we approximate R(θkl) at θ̃kl by the following function
| (7) |
Below we show the derivatives of Os for right censored survival data. Results for other types of data can be derived in a very similar manner. Let and . Simple calculation shows that for each θkl (l = 1, …, 2q),
and
Since is upper-bounded by ξ = 0.1, maximizing R(θkl) is equivalent to maximizing its minorization
and the solution is
where , bkl = akθ̃kl − Ȯs(θ̃k|θ̃k,−l), and .
In the overall objective function, Os is continuously differentiable and regular in the sense of Tseng [2001]. The MCP penalty is separable. Thus, the above algorithm converges to a coordinate-wise maximum of Os, which is also a stationary point.
Parameter path
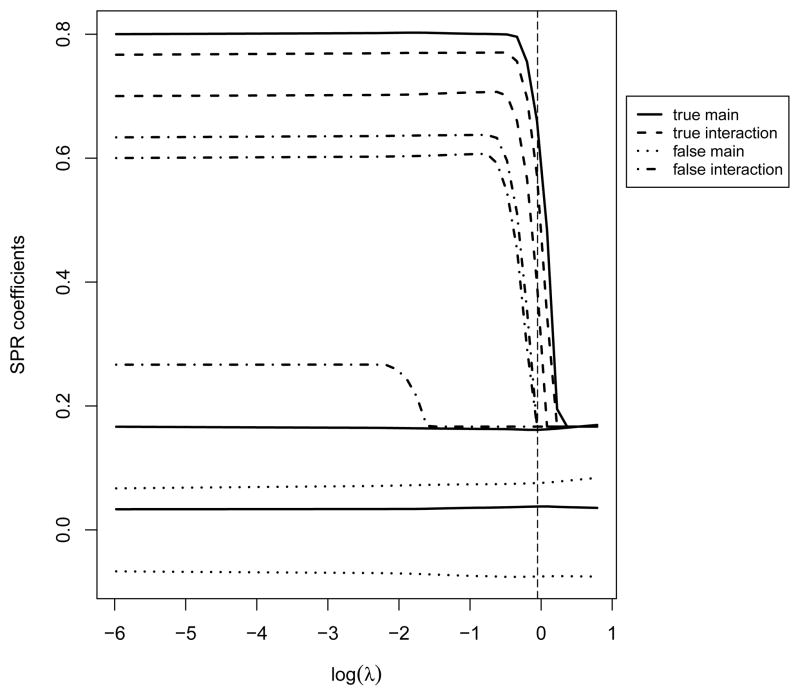
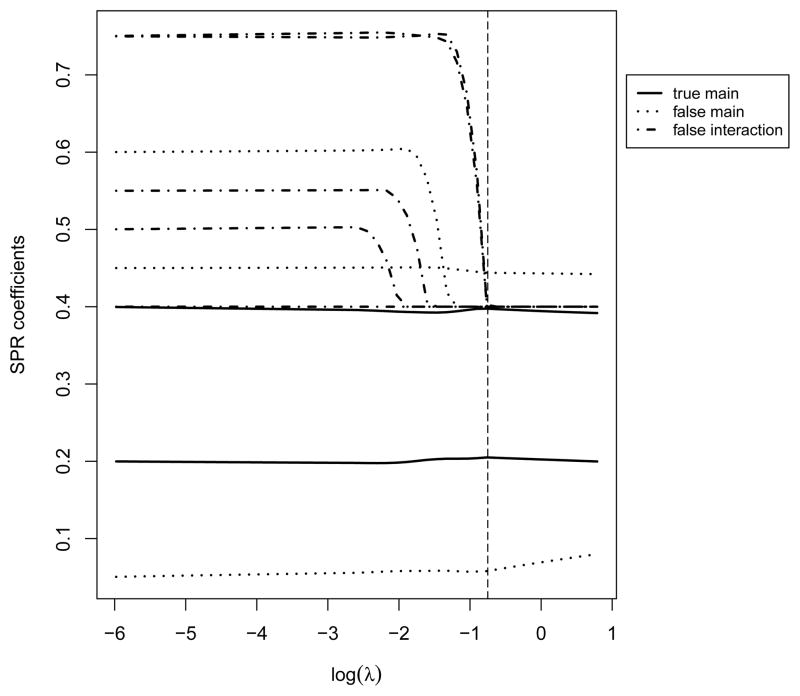
Parameter path provides a way of visualizing the estimates as a function of tuning. We analyze one simulated dataset with a continuous response under the linear regression model with Error 2. The number of genes is p = 1000, and the correlation structure is AR(0.8). More detailed settings are described in the next section. When the number of clinical/environmental risk factors is not too large and the sample size is not too small, as in our simulation, we recommend using the unpenalized estimates as the initial values. This type of “warm starts” allows for more stable estimates and faster convergence. In Figure 1 (Appendix), we show the parameter paths for a gene with a nonzero main effect and two important interactions. In Figure 2 (Appendix), we show those for a gene with no important main effect or interaction. The parameter paths overall look “similar” to other penalized estimates. A nonzero effect may enter the model earlier under a larger λl, and more important effects (with larger coefficients) may enter earlier. The intuition is that many penalization methods including the proposed one are closely related to thresholding. This can be partly seen from the above coordinate descent algorithm. With a high level of thresholding (large penalty), important effects may enter the model, while less important ones may not. Thus by examining the parameter paths (whether an effect, main or interaction, enters early or late), we may draw conclusions on the relative importance of effects. More definitive conclusions on performance of the proposed method will be drawn based on larger scale simulations in the next section.
Tuning parameter
The MCP penalty involves two tunings, λ and γ. For γ, Zhang [2010] and Breheny and Huang [2011] suggest examining a small number of values (in particular including 1.8, 3, 6, and 10) or fixing its value. In our numerical study, we find that the performance is not very sensitive to γ and set γ = 6. In practice, one may need to experiment with multiple γ values, examine the sensitivity of estimate, and select using data-dependent methods. The value of λ plays a more important role: with a smaller λ, more interactions will be identified. Following Tibshirani [2009] and others, it is possible to determine the value of λ data-dependently, using for example cross validation. In Figure 1 and 2 (Appendix), we also plot the λ values selected using 2-fold cross validation. However, it should be noted that with high-dimensional data, the selection of optimal tuning is still an ongoing effort especially in marginal analysis, and it can be more sensible and “safer” to examine performance under a sequence of tunings as opposed to one fixed value [Meinshausen and Buhlmann 2010; Liu 2013b]. In our simulation and data analysis, we start with the smallest λ value under which all gene effects (main and interaction) are zero. We then gradually reduce λ. At each λ value, we examine the set of identified interactions. In simulation, as the set of true positives is known, we are able to compute the true/false positive rates. With a sequence of λ values, as a comprehensive measure, we are able to compute the AUC (area under curve) under the ROC (receiver operating characteristics) framework for binary data and time-integrated AUC for censored survival data. The same discussions and evaluation approach are applicable to penalty functions other than MCP. In addition, for the alternative methods described in the next section (and many of the existing G×E interaction analysis methods), we can vary the cutoffs and compute (time-integrated) AUC in a similar manner.
Simulation
As specific examples, we consider continuous and right censored survival responses. In particular, we consider the following three scenarios: (a) a continuous response under a linear regression model; (b) a survival response under the accelerated failure time (AFT) model, where ; and (c) a survival response under the transformation model with the transformation function other than log. Here , with g(t) = t3, t5, t, and t1/3. For all three models, we consider three different error distributions: (a) Error 1 has a standard normal distribution. (b) Error 2 has a 0.7N(0, 1) + 0.3Cauchy(0, 1) distribution. That is, it is partly contaminated. And (c) Error 3 has a t-distribution with one degree of freedom. This distribution has a long tail. For each subject, we simulate five normally distributed clinical and environmental risk factors. The expressions of p = 500 or 1000 genes are simulated from a multivariate normal distribution. Two correlation structures are considered here. The first is the auto-regressive correlation where the correlation between genes j and k is ρjk = ρ|j−k| with ρ = 0.2 and 0.8, corresponding to weak and strong correlations, respectively. We also consider two banded correlation scenarios. Under the first scenario, ρjk = 0.33 if |j − k| = 1, and ρjk = 0 otherwise. Under the second scenario, ρjk = 0.6 if |j − k| = 1, ρjk = 0.33 if |j − k| = 2, and ρjk = 0 otherwise. There are a total of 2500 or 5000 G×E interactions. Seven main effects, three from environmental risk factors and four from genes, and twenty interactions have nonzero coefficients and are associated with the response. The coefficient of the first main effect is set as 1, and the rest nonzero coefficients are generated from Unif[0.2, 0.8]. For the two survival scenarios, we generate the censoring times independently. The censoring distributions are adjusted so that the censoring rates are about 20%.
We analyze the simulated data using the proposed SPRE. In addition, we also conduct benchmark analyses. In the first set of analysis, we take the commonly-adopted model-based goodness-of-fit measures and employ the same penalization as with SPRE. Specifically, for the continuous response, we consider penalized least squares (PeLS, Table 1). For the survival response under the AFT model, we consider penalized AFT (PeAFT, Table 2). For more details on penalized estimation under the AFT model, we refer to Huang and Ma [2010]. For the survival response under the transformation model, we consider penalized Cox (PeCOX, Table 3), where the goodness-of-fit measure is the log partial likelihood function. In the second set of analysis, we adopt the rank estimation. The marginal p-value, which is the most popular ranking statistic, is used to rank and select important interactions. This approach is referred to as “Sig” (for significance) in Table 1–3.
Table 1.
Simulation for a continuous response under the linear regression model. PeLS: penalized least squares. Sig: significance based analysis. In each cell, AUC based on 100 replicates (mean in the first row, standard deviation in the second row).
| p | AR(0.2) | AR(0.8) | Band1 | Band2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| PeLS | Sig | SPRE | PeLS | Sig | SPRE | PeLS | Sig | SPRE | PeLS | Sig | SPRE | ||
|
|
|||||||||||||
| 500 | Error 1 | 0.911 | 0.928 | 0.826 | 0.945 | 0.995 | 0.954 | 0.917 | 0.936 | 0.838 | 0.928 | 0.962 | 0.885 |
| 0.034 | 0.029 | 0.056 | 0.046 | 0.004 | 0.036 | 0.034 | 0.027 | 0.056 | 0.038 | 0.024 | 0.048 | ||
| Error 2 | 0.739 | 0.755 | 0.791 | 0.806 | 0.889 | 0.936 | 0.750 | 0.769 | 0.800 | 0.778 | 0.824 | 0.849 | |
| 0.126 | 0.126 | 0.058 | 0.127 | 0.137 | 0.055 | 0.127 | 0.133 | 0.060 | 0.124 | 0.135 | 0.053 | ||
| Error 3 | 0.595 | 0.614 | 0.710 | 0.613 | 0.742 | 0.897 | 0.601 | 0.624 | 0.722 | 0.632 | 0.650 | 0.793 | |
| 0.089 | 0.077 | 0.067 | 0.107 | 0.147 | 0.076 | 0.098 | 0.088 | 0.064 | 0.114 | 0.127 | 0.074 | ||
|
| |||||||||||||
| 1000 | Error 1 | 0.929 | 0.942 | 0.815 | 0.945 | 0.998 | 0.956 | 0.934 | 0.950 | 0.825 | 0.934 | 0.971 | 0.876 |
| 0.029 | 0.027 | 0.037 | 0.047 | 0.002 | 0.034 | 0.029 | 0.024 | 0.034 | 0.037 | 0.015 | 0.035 | ||
| Error 2 | 0.659 | 0.667 | 0.776 | 0.751 | 0.798 | 0.949 | 0.667 | 0.679 | 0.796 | 0.707 | 0.731 | 0.850 | |
| 0.128 | 0.130 | 0.045 | 0.146 | 0.175 | 0.029 | 0.130 | 0.137 | 0.048 | 0.132 | 0.153 | 0.042 | ||
| Error 3 | 0.601 | 0.616 | 0.691 | 0.683 | 0.763 | 0.869 | 0.601 | 0.612 | 0.706 | 0.644 | 0.673 | 0.767 | |
| 0.073 | 0.055 | 0.067 | 0.132 | 0.147 | 0.074 | 0.074 | 0.075 | 0.061 | 0.095 | 0.105 | 0.070 | ||
Table 2.
Simulation for a right censored survival response under the AFT model. PeAFT: penalized AFT. Sig: significance based analysis. In each cell, time-integrated AUC based on 100 replicates (mean in the first row, standard deviation in the second row).
| p | AR(0.2) | AR(0.8) | Band1 | Band2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| PeAFT | Sig | SPRE | PeAFT | Sig | SPRE | PeAFT | Sig | SPRE | PeAFT | Sig | SPRE | ||
|
|
|||||||||||||
| 500 | Error 1 | 0.736 | 0.818 | 0.768 | 0.834 | 0.976 | 0.898 | 0.739 | 0.816 | 0.775 | 0.739 | 0.867 | 0.820 |
| 0.064 | 0.047 | 0.050 | 0.067 | 0.020 | 0.065 | 0.060 | 0.051 | 0.065 | 0.081 | 0.061 | 0.053 | ||
| Error 2 | 0.613 | 0.668 | 0.732 | 0.716 | 0.861 | 0.881 | 0.635 | 0.689 | 0.741 | 0.658 | 0.739 | 0.799 | |
| 0.107 | 0.099 | 0.056 | 0.156 | 0.151 | 0.064 | 0.115 | 0.120 | 0.053 | 0.122 | 0.138 | 0.067 | ||
| Error 3 | 0.531 | 0.575 | 0.676 | 0.602 | 0.703 | 0.824 | 0.539 | 0.586 | 0.705 | 0.565 | 0.609 | 0.741 | |
| 0.077 | 0.080 | 0.050 | 0.114 | 0.143 | 0.090 | 0.080 | 0.057 | 0.064 | 0.093 | 0.106 | 0.098 | ||
|
| |||||||||||||
| 1000 | Error 1 | 0.732 | 0.800 | 0.770 | 0.816 | 0.978 | 0.898 | 0.753 | 0.822 | 0.786 | 0.788 | 0.896 | 0.810 |
| 0.060 | 0.057 | 0.055 | 0.080 | 0.029 | 0.086 | 0.075 | 0.060 | 0.045 | 0.070 | 0.043 | 0.063 | ||
| Error 2 | 0.651 | 0.721 | 0.745 | 0.715 | 0.875 | 0.889 | 0.653 | 0.736 | 0.766 | 0.673 | 0.778 | 0.843 | |
| 0.096 | 0.088 | 0.056 | 0.119 | 0.150 | 0.072 | 0.089 | 0.094 | 0.066 | 0.111 | 0.130 | 0.049 | ||
| Error 3 | 0.543 | 0.555 | 0.707 | 0.616 | 0.735 | 0.856 | 0.542 | 0.582 | 0.727 | 0.579 | 0.640 | 0.776 | |
| 0.064 | 0.081 | 0.056 | 0.084 | 0.139 | 0.070 | 0.068 | 0.072 | 0.055 | 0.058 | 0.084 | 0.084 | ||
Table 3.
Simulation for a right censored survival response under the transformation model. PeCOX: penalized Cox. Sig: significance based analysis. In each cell, time-integrated AUC based on 100 replicates (mean in the first row, standard deviation in the second row).
| p | t3 | t5 | t | t1/3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| PeCOX | Sig | SPRE | PeCOX | Sig | SPRE | PeCOX | Sig | SPRE | PeCOX | Sig | SPRE | ||
|
|
|||||||||||||
| 500 | Error 1 | 0.647 | 0.566 | 0.721 | 0.652 | 0.571 | 0.730 | 0.642 | 0.565 | 0.717 | 0.652 | 0.570 | 0.721 |
| 0.048 | 0.052 | 0.077 | 0.059 | 0.058 | 0.076 | 0.043 | 0.056 | 0.076 | 0.054 | 0.055 | 0.076 | ||
| Error 2 | 0.594 | 0.556 | 0.742 | 0.597 | 0.550 | 0.747 | 0.586 | 0.536 | 0.748 | 0.572 | 0.548 | 0.743 | |
| 0.062 | 0.041 | 0.061 | 0.056 | 0.046 | 0.055 | 0.059 | 0.051 | 0.060 | 0.056 | 0.044 | 0.060 | ||
| Error 3 | 0.548 | 0.544 | 0.713 | 0.548 | 0.542 | 0.715 | 0.544 | 0.547 | 0.716 | 0.545 | 0.552 | 0.719 | |
| 0.050 | 0.044 | 0.074 | 0.052 | 0.048 | 0.070 | 0.052 | 0.051 | 0.071 | 0.051 | 0.051 | 0.071 | ||
|
| |||||||||||||
| 1000 | Error 1 | 0.662 | 0.580 | 0.740 | 0.666 | 0.571 | 0.746 | 0.647 | 0.582 | 0.739 | 0.654 | 0.576 | 0.738 |
| 0.059 | 0.048 | 0.065 | 0.063 | 0.058 | 0.063 | 0.057 | 0.049 | 0.064 | 0.049 | 0.043 | 0.065 | ||
| Error 2 | 0.575 | 0.552 | 0.733 | 0.574 | 0.548 | 0.735 | 0.578 | 0.548 | 0.728 | 0.581 | 0.564 | 0.737 | |
| 0.070 | 0.044 | 0.061 | 0.075 | 0.045 | 0.058 | 0.074 | 0.051 | 0.063 | 0.078 | 0.044 | 0.063 | ||
| Error 3 | 0.540 | 0.519 | 0.677 | 0.540 | 0.513 | 0.675 | 0.536 | 0.517 | 0.676 | 0.529 | 0.520 | 0.679 | |
| 0.061 | 0.037 | 0.083 | 0.059 | 0.039 | 0.083 | 0.061 | 0.040 | 0.086 | 0.053 | 0.038 | 0.089 | ||
Simulation first suggests that the proposed method is computationally feasible. Under fixed tunings, for one gene, the analysis takes 0.46 seconds on a regular desktop computer. For the continuous response (Table 1), when the errors have a normal distribution, the significance based method has the best performance. For example when p = 500 under the AR(0.2) correlation structure, the AUC values are 0.911 (PeLS), 0.928 (Sig) and 0.826 (SPRE). This result is as expected. Using classic likelihood theories, one can prove that the least squares estimation with normal error and so the significance based method are the most efficient. The PeLS is slightly worse because of the shrinkage caused by penalization. The proposed method is robust. As with other robust methods, it can be less efficient. The loss of efficiency can be clearly seen from Table 1 under Error 1. However, when the errors are contaminated or have a long tail, the proposed method can significantly outperform the alternatives. For example when p = 500 under the second banded correlation structure and Error 3, the AUC values are 0.632 (PeLS), 0.650 (Sig), and 0.793 (SPRE). Under the second simulation scenario, although the model has a similar form as the linear regression model for continuous data, right censoring leads to significantly different estimation and inference procedures [Huang and Ma 2010]. Observations made in Table 2 are similar to those in Table 1. In Table 3, we observe that SPRE has the largest AUC under all simulation scenarios. For example with p = 500, g(t) = t3, and Error 1, the AUC values are 0.647 (PeCOX), 0.566 (Sig), and 0.721 (SPRE), respectively. In addition, PeCOX outperforms Sig, which may also justify the use of penalization.
The proposed method avoids estimating gk’s. We conduct a small scale simulation and compare the proposed method against the following alternative. For gene k, gk is estimated using the nonparametric method for single index models provided in R package np. Specifically, the functions npindexbw and npindex are used. The same penalty as with the proposed method is imposed for selection. We consider the scenario with a continuous response under the transformation model and Error 1. The nonparametric method is computationally expensive. For each gene, its computer time is about 7.72 times that of the proposed method. To reduce computational burden, we consider only five environmental factors and ten genes. Summary statistics in Table 5 (Appendix) clearly shows the superiority of the proposed method.
Analysis of a Lung Cancer Prognosis Study
Lung cancer is the leading causes of cancer death for both men and women in the United States. Gene profiling studies have been extensively conducted, searching for markers associated with prognosis. The progression of lung cancer is a complex process, involving the contributions of multiple clinical and environmental risk factors, genetic mutations and defects, and their interactions. Individual lung cancer profiling studies have small sample sizes and may lead to unreliable results. To increase sample size, following Xie et al. [2011], we collect and analyze three independent datasets. The UM (University of Michigan Cancer Center) dataset has a total of 175 patients, among whom 102 died during follow-up. The median follow-up was 53 months. The HLM (Moffitt Cancer Center) dataset had a total of 79 patients, among whom 60 died during follow-up. The median follow-up was 39 months. The CAN/DF (Dana-Farber Cancer Institute) dataset has a total of 82 patients, among whom 35 died during follow-up. The median follow-up was 51 months. We refer to Xie et al. [2011] and references therein for more detailed information.
A total of 22,283 probe sets were profiled in all three datasets. Gene expression normalization is first conducted for each dataset separately. To improve comparability, across-datasets normalization is also conducted. To reduce computational cost, and as genes with higher variations are often of more interest, the probe sets are ranked using their variations, and the top 2,500 are screened out for downstream analysis. For the expression of each gene in each dataset, the mean is normalized to zero, and the variance is normalized to one. The following demographic and clinical factors are analyzed: age (centered to mean zero and rescaled to variance one), gender (male is used as reference), smoke (current/former or never; never is used as reference), chemo (chemotherapy treatment), and stage. They include the most commonly measured prognostic factors.
We apply the proposed SPRE and provide the results in Table 4. For each gene, the regression coefficient of age’s main effect is set as −1.0 (we have experimented with 1 and found that −1 leads to an overall larger objective function). As described above, with the proposed method, the number of identified important main effects and interactions depends on the tuning parameter. The results in Table 4 correspond to one specific tuning value which leads to 30 identified genetic effects (main and interaction combined). Results under other tunings are available from the authors.
Table 4.
Analysis of the lung cancer data using SPRE: identified main effects and interactions.
| Gene name | main effects | interactions | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| age | gender | smoke | chemo | stage | gene | age | gender | smoke | chemo | stage | |
| XIST | −1.00 | −1.21 | −0.56 | −0.29 | −3.89 | 2.43 | |||||
| ALB | −1.00 | 0.60 | 0.05 | −0.28 | −3.41 | 3.57 | 2.49 | ||||
| APOA2 | −1.00 | 0.47 | 0.01 | −0.36 | −3.11 | 4.02 | |||||
| ANXA10 | −1.00 | 0.32 | 0.16 | −0.49 | −3.70 | −2.93 | −2.99 | ||||
| AHSG | −1.00 | 0.54 | 0.46 | −0.51 | −3.27 | 2.46 | 3.14 | ||||
| EIF1AY | −1.00 | 2.33 | 2.46 | −0.35 | −2.34 | 3.45 | 2.53 | ||||
| CXCL5 | −1.00 | 0.52 | 2.25 | −0.13 | −3.56 | 3.51 | |||||
| TF | −1.00 | 0.31 | −0.24 | −0.62 | −3.33 | −2.58 | |||||
| AGR2 | −1.00 | 1.30 | −0.71 | −0.62 | −3.09 | 3.08 | |||||
| IL8 | −1.00 | 0.54 | 0.83 | −0.35 | −3.01 | 2.42 | |||||
| HBG1 | −1.00 | 1.06 | −0.07 | −0.30 | −2.51 | −2.91 | |||||
| CXCL5 | −1.00 | 0.66 | 1.06 | −0.35 | −3.46 | 3.30 | |||||
| CALB1 | −1.00 | 0.31 | 0.23 | −0.30 | −2.73 | −4.09 | |||||
| IGFBP1 | −1.00 | 0.27 | −0.11 | −0.34 | −3.18 | −2.60 | |||||
| MGP | −1.00 | 0.93 | 1.61 | −0.32 | −2.65 | −2.72 | |||||
| KDM5D | −1.00 | −0.42 | 3.24 | −1.00 | −3.75 | 2.87 | |||||
| CALB1 | −1.00 | 0.79 | 0.44 | −0.39 | −3.45 | 3.63 | −2.63 | ||||
| SLC6A10P | −1.00 | 0.65 | 0.42 | −0.21 | −2.58 | 2.60 | |||||
| FAM134B | −1.00 | 1.14 | 0.97 | −0.86 | −4.29 | 2.57 | |||||
| ZIC1 | −1.00 | 0.85 | 1.36 | −0.42 | −2.92 | 2.95 | |||||
| FOXG1 | −1.00 | 0.35 | 0.05 | −0.46 | −3.02 | −2.58 | |||||
| CEL | −1.00 | 0.55 | −0.15 | 0.01 | −3.31 | −2.87 | |||||
| FABP1 | −1.00 | 0.68 | 0.47 | −0.34 | −2.14 | 2.84 | |||||
| SFRP1 | −1.00 | 0.74 | 1.71 | −1.12 | −4.25 | 5.50 | |||||
| FOSL1 | −1.00 | 0.75 | 1.41 | −0.28 | −2.44 | 2.45 | |||||
Most of the identified interactions are between genes and smoking status. There are also a few interactions with age and stage. There is one interaction with gender, but no interaction with chemotherapy. In our literature search, we find very few lung cancer studies on G×E interactions. Thus we cannot definitively say whether the identified interactions are meaningful or not. However there are more results on the functionalities of genes, which may provide some insights into the identified effects. The most interesting finding is perhaps SFRP1 (Secreted frizzled related protein 1). SFRP1 is an antagonist of the transmembrane frizzled receptor, a component of the Wnt signaling pathway, and has been suggested to be a candidate tumor suppressor in several human malignancies including lung cancer. Fukui et al. [2005] demonstrates that the SFRP1 gene is frequently downregulated by promoter hypermethylation and suppresses tumor growth activity of lung cancer cells. Other interesting findings include genes that play important roles in the regulation of cell growth, differentiation, and migration. Gene IGFBP1 encodes a protein which is a member of the insulin-like growth factor binding protein family, and binds both insulin-like growth factors and circulates in the plasma, which promotes cell migration. Its important role in lung cancer has been suggested by Chang et al. [2002] and Lee et al. [2002]. Gene AHSG has several important functionalities, including endocytosis, brain development, and formation of bone tissue. It encodes the serum glycoprotein AHSG blocks, whose levels are significantly altered in serum from patients with squamous cell carcinoma of the lung [Dowling et al. 2012]. Swallow et al. [2004] also suggests that AHSG may play an important role in tumor progression. AGR2 is a proto-oncogene that may play a role in cell migration, cell differentiation, and cell growth. Pizzi et al. [2012] shows its overexpression in lung adenocarcinoma. IL 8 acts as a promoter of human non-small cell lung cancer (NSCLC) tumor growth through its angiogenic properties [Kunkel et al. 1991]. We have also identified several genes that have been implicated in the development and progression of several other cancers. For example, it has been reported that low ANXA10 expression is associated with disease aggressiveness in bladder cancer [Munksgaard et al. 2011]. The protein encodes by CXCL5 belongs to the CXC chemokine family, which plays a paramount role in tumor progression [Raman et al. 2007; Speetjens et al. 2008]. FAM134B has been associated with Wilms tumor. Considering the interconnections among different cancer types, it may be of interest to study their functions in lung cancer.
We have also applied the alternative methods. Results using PeAFT (Table 6), PeCOX (Table 7), and Sig (Table 8) are provided in Appendix. For these three methods, the number and set of identified interactions also depend on tunings. We only provide results for a specific tuning value, and more extensive results are available from the authors. We can see that different methods identify significantly different sets of main effects and interactions. We have also examined “longer lists” of identified effects and reached the same conclusion. With our limited knowledge on the genetic effects, it is hard to say whether the SPRE identified interactions are more sensible. The simulation results and biological implications described above may partly support SPRE.
Discussion
In the literature, there are a large number of statistical methods for detecting gene-environment interactions. However, most of them assume specific models and rely on the notion of significance level for ranking the relative importance of effects. Advancing from the existing studies, we adopt a robust approach which does not assume a specific model form. The proposed modeling framework and rank estimation include quite a few commonly encountered data and model settings as special cases. To facilitate computation, a smooth approximation is introduced. Different from the existing methods, the proposed SPRE uses penalization as a way of estimation and, more importantly, for identifying important interactions. The proposed method has roots in the MRC estimation and penalized marker selection. However, this study is among the first to apply such techniques in high-throughput G×E interaction studies. In simulation, we show that under certain scenarios, the proposed method can significantly outperform the model-based penalization method and the commonly used significance-level based method. In the analysis of a lung cancer prognosis study, the proposed method identifies interactions (and main effects) different from the alternatives. Some of the identified genes have been shown to have important implications.
The proposed method has limitations. Computationally, it is more expensive than the existing methods. This is the price paid for robustness and penalization. However, as the analysis can be conducted in a highly parallel manner, the computational cost is in fact acceptable. The significance level based methods can be coupled with multiple comparison adjustment methods such as the FDR and Bonferroni. With the proposed method, the notion of significance is not directly relevant. Most of the existing penalization methods examine results under a specific tuning parameter value. In principle, we can follow Tibshirani [2009] and use, for example, cross validation to determine such a tuning value, as shown in Figure 1 and 2. However, we believe it is more sensible to examine a sequence of tuning parameter values. Under such an approach, effects entering earlier (under larger tunings) are deemed as more important. In simulation, we have examined a total of 72 different settings. The proposed method is potentially applicable to a large number of data and model settings, but it is impossible to examine all of them in one study. In Table 1 under Error 1, the proposed SPRE is less competitive. This is not surprising. Under such a simulation setting, we can prove that the model-based method is more efficient than the robust method. Under other settings, the superiority of the proposed method is obvious. In data analysis, the proposed method identifies a different set of important interactions. More bioinformatics and biological analyses are needed to fully comprehend the identified interactions.
Figure 1.
Parameter paths for a gene with important interactions. The vertical line corresponds to λ selected using 2-fold cross validation.
Figure 2.
Parameter paths for a gene without important interaction. The vertical line corresponds to λ selected using 2-fold cross validation.
Supplementary Material
Acknowledgments
We thank the editor, associate editor, and two referees for careful review and insightful comments, which have led to a signicant improvement of this article. This research was supported by NIH grants CA165923, CA152301 and CA142774, National Social Science Foundation of China (13CTJ001), and National Bureau of Statistics Funds of China (2012LD001).
References
- 1.Breheny P, Huang J. Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. The Annals of Applied Statistics. 2011;5(1):232. doi: 10.1214/10-AOAS388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chang YS, Wang L, Liu D, Mao L, Hong WK, Khuri FR, Lee HY. Correlation between insulin-like growth factor-binding protein-3 promoter methylation and prognosis of patients with stage i non-small cell lung cancer. Clinical Cancer Research. 2002;8(12):3669–3675. [PubMed] [Google Scholar]
- 3.Dowling P, Clarke C, Hennessy K, Torralbo-Lopez B, Ballot J, Crown J, Kiernan I, O’Byrne KJ, Kennedy MJ, Lynch V, et al. Analysis of acute-phase proteins, ahsg, c3, cli, hp and saa, reveals distinctive expression patterns associated with breast, colorectal and lung cancer. International Journal of Cancer. 2012;131(4):911–923. doi: 10.1002/ijc.26462. [DOI] [PubMed] [Google Scholar]
- 4.Fukui T, Kondo M, Ito G, Maeda O, Sato N, Yoshioka H, Yokoi K, Ueda Y, Shimokata K, Sekido Y. Transcriptional silencing of secreted frizzled related protein 1 (sfrp1) by promoter hypermethylation in non-small-cell lung cancer. Oncogene. 2005;24(41):6323–6327. doi: 10.1038/sj.onc.1208777. [DOI] [PubMed] [Google Scholar]
- 5.Han AK. Non-parametric analysis of a generalized regression model: the maximum rank correlation estimator. Journal of Econometrics. 1987;35(2):303–316. [Google Scholar]
- 6.Huang J, Ma S. Variable selection in the accelerated failure time model via the bridge method. Lifetime Data Analysis. 2010;16:176–195. doi: 10.1007/s10985-009-9144-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hunter DJ. Gene-environment interactions in human diseases. Nature Review Genetics. 2005;6:287–298. doi: 10.1038/nrg1578. [DOI] [PubMed] [Google Scholar]
- 8.Khan S, Tamer E. Partial rank estimation of duration models with general forms of censoring. Journal of Econometrics. 2007;136(1):251–280. [Google Scholar]
- 9.Kunkel SL, Standiford T, Kasahara K, Strieter RM. Interleukin-8 (il-8): the major neutrophil chemotactic factor in the lung. Experimental Lung Research. 1991;17(1):17–23. doi: 10.3109/01902149109063278. [DOI] [PubMed] [Google Scholar]
- 10.Lee HY, Chun KH, Liu B, Wiehle SA, Cristiano RJ, Hong WK, Cohen P, Kurie JM. Insulin-like growth factor binding protein-3 inhibits the growth of non-small cell lung cancer. Cancer Research. 2002;62(12):3530–3537. [PubMed] [Google Scholar]
- 11.Li J, Ma S. Time-dependent ROC analysis under diverse censoring patterns. Statistics in Medicine. 2011;30(11):1266–77. doi: 10.1002/sim.4178. [DOI] [PubMed] [Google Scholar]
- 12.Li M, Ye C, Fu W, Elston RC, Lu Q. Detecting genetic interactions for quantitative traits with U-statistics. Genetic Epidemiology. 2011;35(6):457–468. doi: 10.1002/gepi.20594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu J, Huang J, Zhang Y, Lan Q, Rothman N, Zheng T, Ma S. Identification of gene-environment interactions in cancer studies using penalization. Genomics. 2013 doi: 10.1016/j.ygeno.2013.08.006. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu J, Wang K, Ma S, Huang J. Accounting for linkage disequilibrium in genome-wide association studies: a penalized regression method. Statistics and Its Interface. 2013b;6:99–115. doi: 10.4310/SII.2013.v6.n1.a10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ma S, Huang J. Regularized ROC method for disease classification and biomarker selection with microarray data. Bioinformatics. 2005;21:4356–4362. doi: 10.1093/bioinformatics/bti724. [DOI] [PubMed] [Google Scholar]
- 16.Meinshausen N, Buhlmann P. Statbility selection. JRSSB. 2010;72:417–73. [Google Scholar]
- 17.Moore JH, Gilbert JC, Tsai CT, Chiang FT, Holden T, Barney N, White BC. A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility. J Theor Biol. 2006;241(2):252–261. doi: 10.1016/j.jtbi.2005.11.036. [DOI] [PubMed] [Google Scholar]
- 18.Munksgaard P, Mansilla F, Eskildsen AB, Fristrup N, Birkenkamp-Demtroder K, Ulhoi BP, Borre M, Agerbak M, Hermann G, Orntoft TF, et al. Low anxa10 expression is associated with disease aggressiveness in bladder cancer. British Journal of Cancer. 2011;105(9):1379–1387. doi: 10.1038/bjc.2011.404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.North KE, Martin LJ. The importance of gene-environment interaction: implications for social scientists. Sociological Methods Research. 2008;37:164–200. [Google Scholar]
- 20.Pepe MS. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford University Press; USA: 2004. [Google Scholar]
- 21.Pizzi M, Fassan M, Balistreri M, Galligioni A, Rea F, Rugge M. Anterior gradient 2 overexpression in lung adenocarcinoma. Applied Immunohistochemistry & Molecular Morphology. 2012;20(1):31–36. doi: 10.1097/PAI.0b013e3182233f9f. [DOI] [PubMed] [Google Scholar]
- 22.Raman D, Baugher PJ, Thu YM, Richmond A. Role of chemokines in tumor growth. Cancer letters. 2007;256(2):137–165. doi: 10.1016/j.canlet.2007.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sherman RP. The limiting distribution of the maximum rank correlation estimator. Econometrica. 1993;61:123–137. [Google Scholar]
- 24.Song X, Ma S. Penalised variable selection with U-estimates. Journal of Nonparametric Statistics. 2010;22(4):499–515. doi: 10.1080/10485250903348781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Speetjens FM, Kuppen PJ, Sandel MH, Menon AG, Burg D, van de Velde CJ, Tollenaar RA, de Bont HJ, Nagelkerke JF. Disrupted expression of cxcl5 in colorectal cancer is associated with rapid tumor formation in rats and poor prognosis in patients. Clinical Cancer Research. 2008;14(8):2276–2284. doi: 10.1158/1078-0432.CCR-07-4045. [DOI] [PubMed] [Google Scholar]
- 26.Swallow CJ, Partridge EA, Macmillan JC, Tajirian T, DiGuglielmo GM, Hay K, Szweras M, Jahnen-Dechent W, Wrana JL, Redston M, et al. α2hsglycoprotein, an antagonist of transforming growth factor β in vivo, inhibits intestinal tumor progression. Cancer research. 2004;64(18):6402–6409. doi: 10.1158/0008-5472.CAN-04-1117. [DOI] [PubMed] [Google Scholar]
- 27.Thomas D. Methods for investigating gene-environment interactions in candidate path-way and genome-wide association studies. Annual Review of Public Health. 2010;31:21–36. doi: 10.1146/annurev.publhealth.012809.103619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tibshirani RJ. Univariate shrinkage in the Cox model for high dimensional data. Statistical Applications in Genetics and Molecular Biology. 2009;8(1):1–18. doi: 10.2202/1544-6115.1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tseng P. Convergence of a block coordinate descent method for nondifferentiable minimization. Journal of Optimization Theory and Applications. 2001;109:475–494. [Google Scholar]
- 30.Witten DM, Tibshirani R. Survival analysis with high-dimensional covariates. Statistical Methods in Medical Research. 2010;19:29–51. doi: 10.1177/0962280209105024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xie Y, Xiao G, Coombes K, Behrens C, Solis L, Raso G, Girard L, Erickson H, Roth J, Hey-mach J, Moran C, Danenberg K, Minna J, Wistuba I. Robust gene expression signature from formalin-fixed paraffin-embedded samples predicts prognosis of non-small cell lung cancer patients. Clin Cancer Res. 2011;17(17):5705–5714. doi: 10.1158/1078-0432.CCR-11-0196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang CH. Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics. 2010;38(2):894–942. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.