Identifying gene-environment and gene-gene interactions using a progressive penalization approach

Abstract

In genomic studies, identifying important gene-environment and gene-gene interactions is a challenging problem. In this study, we adopt the statistical modeling approach, where interactions are represented by product terms in regression models. For the identification of important interactions, we adopt penalization, which has been used in many genomic studies. Straightforward application of penalization does not respect the “main effect, interaction” hierarchical structure. A few recently proposed methods respect this structure by applying constrained penalization. However, they demand very complicated computational algorithms and can only accommodate a small number of genomic measurements. We propose a computationally fast penalization method that can identify important gene-environment and gene-gene interactions and respect a strong hierarchical structure. The method takes a stagewise approach and progressively expands its optimization domain to account for possible hierarchical interactions. It is applicable to multiple data types and models. A coordinate descent method is utilized to produce the entire regularized solution path. Simulation study demonstrates the superior performance of the proposed method. We analyze a lung cancer prognosis study with gene expression measurements and identify important gene-environment interactions.

Introduction

In genomic studies, gene-environment and gene-gene interactions can have important implications beyond main effects. Identifying important interactions, especially gene-gene interactions, is challenging because of the high dimensionality of genomic measurements. We refer to Hunter [2005], Caspi and Moffitt [2006] and others for a survey. A large number of methods have been developed for identifying interactions. We refer to Cordell [2009] and Thomas [2010] for comprehensive reviews. The discussions below and proposed method are applicable to multiple types of genomic measurements. We use the generic term “gene” which matches the gene expression data analyzed in this article.

For identifying gene-environment interactions, a family of methods first conducts marginal analysis of genes while using environmental factors as control variables, and then expands the model by adding gene-environment iteration terms if a gene is marginally significant. Such methods are simple and have low computational cost. However, they can only analyze a small number of genes at a time. For gene-gene interactions, such methods are also applicable. Dong et al. [2007] developed an entropy-based model for gene-gene interactions. However, an overwhelming number of possible iteration terms still poses a major challenge. Wakefield et al. [2010] developed a Bayesian mixture model with a mixture prior. Machine learning models offer a flexible nonparametric approach. Some machine learning techniques such as the tree-based methods [Breiman, 2001] can naturally capture interactions during the tree splitting process. A limitation of the nonparametric methods is that the resulted models are difficult to summarize and draw conclusion.

We take a statistical modeling approach under which interactions are represented by product terms in regression models. We incorporate all main effects and their second order interactions in a single statistical model, which differs from the marginal approach and may better reflect disease biology. With a large number of effects, only a small subset is expected to be associated with the outcome variable. To identify important interactions and main effects, we propose using penalization [Tibshirani, 2011], which has been extensively adopted in genomic data analysis. When the number of genes is large, straightforwardly analyzing interactions (especially gene-gene interactions) is computationally prohibitive. In addition, the “main effect, interaction” hierarchical structure (which is described in detail in the next section) may not be respected. Recently, Bien et al. [2013] developed a Lasso-based penalization method for gene-gene iterations that enforces a hierarchical constraint on the optimization problem. For gene-environment interactions, Liu et al. [2013] proposed using the group MCP penalty in addition to MCP penalties on individual interactions to reinforce the hierarchical structure. However, both methods need to solve a large optimization problem and hence suffer high computational cost.

The overall framework of this study is similar to that of some recently published studies. That is, the statistical modeling approach is adopted to describe interactions, and penalization is adopted for selecting important interactions. Our goal is to develop a practically feasible method that has lower computational cost and hence can accommodate a large number of genes. In addition, the proposed method respects the hierarchical structure. To this end, we develop a progressive penalization method. The proposed method only requires computation cost comparable to a main effect penalized method. It can be viewed as a stagewise (as opposed to stepwise) model fitting that takes advantage of the hierarchical structure. Its applicability is relatively independent of the data and model types. It thus fills the gap of published studies.

Penalized interaction model

Let Y denote the response variable such as a disease outcome or phenotype. Let Z = (Z₁, …, Z_q) be the q clinical/environmental risk factors, and X = (X₁, …, X_p) be the p genes. Consider the following models for gene-environment (G × E) interactions

$$Y~\varphi \left(\sum _{k=1}^q{\alpha }_k{Z}_k+\sum _{j=1}^p{\beta }_j{X}_j+\sum _{j,k}{\theta }_{jk}{X}_j{Z}_k\right),$$ (1)

and gene-gene (G × G) interactions

$$Y~\varphi \left(\sum _{j=1}^p{\beta }_j{X}_j+\sum _{j,k}{\gamma }_{jk}{X}_j{X}_k\right),$$ (2)

where ϕ is the known link function, α_k’s and β_j’s are the main effects of clinical/environmental factors and genes respectively, and θ_jk’s and γ_jk’s are the interaction effects.

A hierarchical structure is assumed to avoid the presence of interaction terms when the corresponding main effects are not identified as important [Peixoto, 1987]. There are two types of hierarchical structures. A strong hierarchical structure assumes that an interaction term can be identified only when both of the corresponding main effects are identified. In contrast, a weak hierarchical structure assumes that an interaction term can be identified when at least one of the two corresponding main effects is identified. In this article, we mainly focus on the strong hierarchical structure which can be expressed by adding the following constraints to models (1) and (2) respectively:

$$G\times E\text{interaction}\text{model}:{\theta }_{jk}\ne 0\Rightarrow {\beta }_j\ne 0\text{and}{\alpha }_k\ne 0,\forall j,k,$$ (3)

$$G\times G\text{interaction}\text{model}:{\gamma }_{jk}\ne 0\Rightarrow {\beta }_j\ne 0\text{and}{\beta }_k\ne 0,\forall j,k.$$ (4)

For the G× G interaction model, Bien et al. [2013] provided extensive arguments for favoring the strong hierarchy and gave a simple example to show that violating the strong hierarchy amounts to “postulating a special position for the origin [MacCullagh and Nelder, 1989]”. Another reason that we prefer the strong hierarchical structure is that in the G × E interaction model, Liu et al. [2013] and references therein suggested that as the clinical/environmental factors are usually important and have a low dimensionality, they can always be present, making the weak hierarchical structure less meaningful. Moreover, the constrained optimization problem of the strong hierarchical G × G interaction model is computationally more challenging [Bien et al., 2013].

Let α = (α₁, …, α_q)′, β = (β₁, …β_p)′, Θ_{p × q} = {θ_ij}, and Γ_{p × p} = {γ_ij}. With n iid observations, denote L(·) as the loss function, which can be the negative log-likelihood function or from an estimating equation.

For the G × E interaction model, consider the constrained penalized estimate

$$\begin{array}{l}(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }},\widehat{\mathbf{\Theta }})=\underset{\alpha \in R^q,\mathit{\beta }\in R^p,\mathbf{\Theta }\in R^{p\times q}}{\mathit{argmin}}L(\mathit{\alpha },\mathit{\beta },\mathbf{\Theta })+{\rho }_1(\mathit{\beta })+{\rho }_2(\mathbf{\Theta })\\ s.t.{\beta }_j=0\Rightarrow {\Vert {\mathbf{\Theta }}_j\Vert }_{\infty }=0,\text{for}j=1,\dots ,p.\end{array}$$ (5)

ρ₁(·) and ρ₂(·) are the penalty functions. Θ_j = {θ_jk, k = 1, …, q}. ${\Vert {\mathbf{\Theta }}_j\Vert }_{\infty }=\underset{k}{\mathit{max}}\{\mid {\theta }_{jk}\mid \}$. As the clinical/environmental risk factors are usually important and have a low dimensionality, they are treated as control factors, and α is not subject to penalization.

For the G × G interaction model, a similar constrained penalized estimate is defined as:

$$\begin{array}{c}(\widehat{\mathit{\beta }},\widehat{\mathbf{\Gamma }})=\underset{\mathit{\beta }\in R^p,\mathbf{\Gamma }\in R^{p\times p}}{\mathit{argmin}}L(\mathit{\beta },\mathbf{\Gamma })+{\rho }_1(\mathit{\beta })+{\rho }_2(\mathbf{\Gamma })\\ s.t.{\gamma }_{jk}={\gamma }_{kj},\text{and}{\beta }_j=0\Rightarrow {\Vert {\mathbf{\Gamma }}_j\Vert }_{\infty }=0,\text{for}j=1,\dots ,p,\end{array}$$ (6)

where Γ_j = {γ_jk, k = 1, …, p}. Moreover, an intercept term α₀ can be added to both models without receiving penalization. Solving the constrained optimization problems (5) and (6) is nontrivial. A few methods have been proposed to solve them by applying tricks to the penalty terms or constraints to avoid the undesirable formulation. Bien et al. [2013] proposed to use ||Γ_j||₁ ≤ |β_j| instead of the hierarchical constraint in (6) and further used a convex relaxation to achieve the strong hierarchy. For model (5), Liu et al. [2013] applied the group MCP penalty to the vector (β_j, Θ_j) to force group-in and group-out selection and guarantee hierarchy, and added another MCP penalty to individually penalize each element of Θ_j. However, when p is moderate to large, these methods require optimization with respect to a huge number of input parameters, which can be computationally overwhelming.

Progressive penalization

The proposed method is motivated by the observation that under the strong hierarchical constraint, we do not need to optimize the input parameter θ_ij (or γ_ij) unless its corresponding main effect β_j is nonzero. However, since we do not know in advance which β_j’s are nonzero, we can perform the optimization in a stagewise fashion. That is, we allow β̂_j to move by a small amount each time. And once β̂_j ≠ 0, we consider the corresponding θ̂_ij’s (or γ̂_ij’s) by allowing them to diverge from 0. Notice that in each step, this seemingly simple idea gives us a control of the number of input parameters in optimization, which can significantly reduce computational cost.

Many computational methods have been developed to solve penalization problems [Efron et al., 2004; Beck and Teboulle, 2009]. Among them, the coordinate descent method [Friedman et al., 2010] is the most convenient under our framework. With a fixed step size (which is usually small) and only updating one coordinate at a time, we are able to gradually expand the interaction effects (or the corresponding θ̂_ij’s and γ̂_ij’s) according to the status of β̂_j’s.

For simplicity of notation, we first describe the proposed method for a continuous response variable under the linear regression model, where the loss function is the sum of squared errors. Extensions to other data and model types are described later in this section. In principle, a variety of penalties can be adopted for ρ₁ and ρ₂, including for example bridge, MCP, SCAD and others. We adopt the Lasso penalty, which is strictly convex and computationally and theoretically well understood. In addition, adopting the Lasso penalty can facilitate a direct comparison with Bien et al. [2013]. Adopting other penalties may demand revising the computational algorithm. But the principle of the proposed method is still applicable. Below we describe the details of the proposed method for the G × E interaction model. The G × G interaction model can be analyzed with minor modifications, and details are provided in the Adaption section. We now specify the optimization problem (5) for a regression model with the Lasso penalty. With n iid observations, denote Y as the n × 1 vector composed of the responses and Z and X as the n × q and n × p design matrices for X and Z, respectively. Use subscript i to denote the ith observation. Consider

$$\begin{array}{c}\underset{\mathit{\alpha }\in R^p,\mathit{\beta }\in R^p,\mathbf{\Theta }\in R^{p\times q}}{\mathit{Minimize}}\frac{1}{2}{\Vert \mathbf{Y}-\mathbf{Z}\mathit{\alpha }-\mathbf{X}\mathit{\alpha }-{\left(\sum _{j,k}{\theta }_{jk}{X}_{1,j}{Z}_{1,k},\dots ,\sum _{j,k}{\theta }_{jk}{X}_{n,j}{Z}_{n,k}\right)}^{\prime }\Vert }_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1+\lambda {\Vert \mathbf{\Theta }\Vert }_1\\ s.t.{\beta }_j=0\Rightarrow {\Vert {\mathbf{\Theta }}_j\Vert }_{\infty }=0,\text{for}j=1,\dots ,p.\end{array}$$ (7)

|| · ||₂ is the ℓ₂-norm. The subscript “2” is suppressed unless necessary. λ is the data-dependent tuning parameter. In principle, we can have different tunings for β and Θ. We apply the same degree of penalization for computational simplicity. Below with a slight abuse of notation, we use Σ_j,k θ_jkX_jZ_k to denote the vector (Σ_j,k θ_jkX_1,jZ_1,k, …, Σ_j,k θ_jkX_n,jZ_n,k)′

Algorithm

Define a small stepsize s > 0, and a sufficiently large tuning parameter λ⁽⁰⁾. Assume that Y is centered and both X and Z are normalized. Record the mean of Y as ȳ. In numerical study, we set s = 10⁻⁴, and λ⁽⁰⁾ to be the maximum absolute partial derivatives of β_j’s at the initial value of parameter estimates, which will be defined below.

• Step a) Initialize α⁽⁰⁾ = 0_{q × 1}, β⁽⁰⁾ = 0_{p × 1}, Θ⁽⁰⁾ = 0_{p × q}, and the intercept term ${\alpha }_0^{(0)}=\overline{y}$ if necessary.

• Step b) At iteration m ∈ {1, …, M}, consider the activated main effect set ${\mathcal{A}}_m=\{j:{\beta }_j^{(m-1)}\ne 0\}$, which is ∅, an empty set, at m = 1. To respect the hierarchical structure, for the interaction parameters Θ_j, we only update them if j ∈ 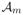. Conceptually, it is equivalent to solving the following optimization problem that involves input parameters α, β and {Θ_j : j ∈ }:

  $$\underset{\mathit{\alpha }\in R^q,\mathit{\beta }\in R^p,\mathbf{\Theta }\in R^{p\times q}}{\mathit{Minimize}}\frac{1}{2}{\Vert \mathbf{Y}-\mathbf{Z}\mathit{\alpha }-\mathbf{X}\mathit{\alpha }-\sum _{j\in ,{\mathcal{A}}_m,k=1,\dots ,q}{\theta }_{jk}{X}_j{Z}_k\Vert }^2+{\lambda }^{(m)}{\Vert \mathit{\beta }\Vert }_1+{\lambda }^{(m)}\sum _{j\in {\mathcal{A}}_m}{\Vert {\mathbf{\Theta }}_j\Vert }_1.$$ (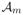8)
  1. Since α is not subject to penalization, we first obtain its least square estimate

     $${\mathit{\alpha }}^{(m+1)}={({\mathbf{Z}}^{\top }\mathbf{Z})}^{-1}{\mathbf{Z}}^{\top }\left(\mathbf{Y}-\mathbf{Z}{\mathit{\alpha }}^{(m)}-\mathbf{X}{\mathit{\beta }}^{(m)}=\sum _{j\in {\mathcal{A}}_m,k=1,\dots ,q}{\theta }_{jk}^{(m)}{X}_j{Z}_k\right),$$

     where Z^⊤ is the transpose of Z.

  2. Calculate the residual under the current parameter estimates

     $${\mathbf{r}}^{(m)}=\mathbf{Y}-\mathbf{Z}{\mathit{\alpha }}^{(m+1)}-\mathbf{X}{\mathit{\beta }}^{(m)}-\sum _{j\in {\mathcal{A}}_m,k=1,\dots ,q}{\theta }_{jk}^{(m)}{X}_j{Z}_k.$$
  3. Search for the coordinate among the main effects β and the activated interactions {Θ_j : j ∈ 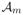} that gives the most negative value of the partial derivatives. Move a small step s towards that direction. To be more specific, the partial derivatives are

     $$\frac{\partial }{\partial {\beta }_j}L=-\sum _{i=1}^n{r}_i^{(m)}{X}_{ij},\text{for}j=1,\dots ,p,$$ (9)
     and

     $$\frac{\partial }{\partial {\theta }_{jk}}L=-\sum _{i=1}^n{r}_i^{(m)}{X}_{ij}{Z}_{ik},\text{for}j\in {\mathcal{A}}_m\text{and}k=1,\dots ,q.$$ (10)

     Update the parameter estimate according to the following two cases:

     • If $\underset{j}{max}\{\mid \frac{\partial }{\partial {\beta }_j}L\mid \}\ge \underset{j\in {\mathcal{A}}_m,k}{max}\{\mid \frac{\partial }{\partial {\theta }_{jk}}L\mid \}$, let $\widehat{j}=\underset{j}{argmax}\{\mid \frac{\partial }{\partial {\beta }_j}L\mid \}$, and update the ĵth main effect parameter estimate by letting ${\beta }_{\widehat{j}}^{(m+1)}={\beta }_{\widehat{j}}^{(m)}+\mathit{sign}(\frac{\partial }{\partial {\beta }_{\widehat{j}}}L)$. All other estimates are unchanged.

     • Otherwise, let $(\widehat{j},\widehat{k})=\underset{j\in {\mathcal{A}}_m,k}{argmax}\{\mid \frac{\partial }{\partial {\theta }_{jk}}L\mid \}$ and update the interaction parameter ${\theta }_{\widehat{j}\widehat{k}}^{(m+1)}={\theta }_{\widehat{j}\widehat{k}}^{(m)}+\mathit{sign}(\frac{\partial }{\partial {\theta }_{\widehat{j}\widehat{k}}}L)·s$. All other estimates are unchanged.

     When estimating the intercept term is necessary, let

     $${\widehat{\alpha }}_0^{(m+1)}=\overline{y}-\frac{1}{n}{\left|\mathbf{Z}{\mathit{\alpha }}^{(m+1)}-\mathbf{X}{\mathit{\beta }}^{(m+1)}-\sum _{j\in {\mathcal{A}}_m,k=1,\dots ,q}{\theta }_{jk}^{(m+1)}{X}_j{Z}_k\right|}_1.$$
• Step c) To produce the entire solution path, let

  $${\lambda }^{(m+1)}=min\left\{{\lambda }^{(m)},\underset{j}{max}\{\mid \frac{\partial }{\partial {\beta }_j}L\mid \},\underset{j\in {\mathcal{A}}_m,k}{max}\{\mid \frac{\partial }{\partial {\theta }_{jk}}L\mid \}\right\}.$$

  Evaluate whether the updated parameter estimates result in a decreased L. We enforce multiple stopping rules: λ^(m+1) is sufficiently small (10⁻⁴), or there are more than n nonzero parameters. Otherwise, go back to Step b) with m = m + 1.

At the initial stage where m = 0, the activated main effect set 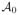is empty. The optimization problem (8) is nothing but to fit a main effect model with only α and β. In the first update, the most “beneficial” β_j enters the model and thus activates q interaction terms corresponding to X_j. Under the hierarchical structure, a nonzero interaction term corresponds to a nonzero main effect. Under mild data and model conditions, the ℓ₁ penalization can identify the true main effects with a high probability. Once the important main effects are incorporated in the model, the corresponding interaction terms are invoked and considered. Under the selection consistency of ℓ₁ penalization, the important interaction terms can be selected. More arguments are provided in Appendix.

Compared to other penalization methods, the strength of the proposed method lies in its computational advantage. At the first iteration, we only deal with p parameters as opposed to p × q. Since the ℓ₁ penalization selects at most n nonzero parameters, in the worst case, we deal with p + n × q parameters. For G × G interactions which we specify below, we need to deal with at most p + n(n + 1)/2 parameters. Note that this number can be reduced with an early stopping rule for λ, since the Lasso solution for extremely small values of λ can be unstable and should not be used. Compared with most of the existing methods such as the all-pairwise Lasso or hierarchical Lasso [Bien et al., 2013] where we always optimize over p × p parameters, the computational advantage is significant.

Adaption

The proposed method can be adapted to identify important G × G interactions under the strong hierarchical structure. Rewrite optimization (8) in Step b) as

$$\underset{\mathit{\beta }\in R^p,\mathbf{\Theta }\in R^{p\times p}}{\mathit{Minimize}}\frac{1}{2}{\Vert \mathbf{Y}-\mathbf{X}\mathit{\beta }-\sum _{j,k\in {\mathcal{A}}_m,k<j}{\gamma }_{jk}{X}_j{X}_k\Vert }^2+\lambda {\Vert \mathit{\beta }\Vert }_1+\lambda \sum _{j\in {\mathcal{A}}_m}{\Vert {\mathbf{\Gamma }}_j\Vert }_1.$$ (11)

In G × G interactions, γ_jk = γ_kj. To avoid redundancy, we add the constraint that k < j. The rest of the proposed procedure only needs minor modifications. The trivial details are omitted here.

Consider other types of data and models, for example binary data under the logistic regression model and right censored survival data under the Cox model. Here the loss function is the negative log-likelihood function. Consider for example G × G interactions. An iterative algorithm proceeds as follows: (i) Initialize β̂ = 0 and Γ̂ = 0. (ii) At the current estimate (β̂, Γ̂), make Taylor expansion of the loss function. Keep the linear and quadratic terms. (iii) Call the algorithm developed for linear regression. (iv) Repeat Step (ii) and (iii) until convergence. In Step (ii), we can also resort to an MM (Minorize-Maximization) algorithm.

Simulation study

We apply the proposed method to both G × E and G × G interaction settings in regression. Both settings respect the strong hierarchical structure. Let Z ~ norm(0, Σ_{q × q}) where ${\mathrm{\sum }}_{ij}={\rho }_Z^{\mid i-j\mid }$. Two types of G factors are considered, including continuous with X ~ norm(0, Σ_{p × p}) where ${\mathrm{\sum }}_{ij}={\rho }_X^{\mid i-j\mid }$ and binary by further discretizing X as I(X > 0). We consider

$$G\times E\text{Model}:Y=\sum _{k=1}^q{\alpha }_k{Z}_k+\sum _{j=1}^p{\beta }_j{X}_j+\sum _{j,k}{\theta }_{jk}{X}_j{Z}_k+\epsilon ,$$

and

$$G\times G\text{Model}:Y=\sum _{j=1}^p{\beta }_j{X}_j+\sum _{j\ne k}{\gamma }_{jk}{X}_j{X}_k+\epsilon .$$

ε follows a standard normal distribution, and ρ_X = ρ_Z = 0.3. For the G × E model, we set q = 10. Two different scenarios for each model are considered: the first scenario has 15 nonzero main effects and 5 nonzero interactions, and the second scenario has 10 nonzero main effects and 10 nonzero interactions. All of the nonzero α_k, β_j, θ_jk, and γ_jk parameters are independently generated from Uniform (0.5, 1). p = 500, 1000 and n = 150, 250.

Beyond the proposed method, we also apply several alternatives. Notice that not all methods can be applied to both the G × E and G × G models. The all-pairwise Lasso method directly applies the Lasso penalization to both main effects and all second-order interactions, without considering the hierarchical structure. It can be realized using the R package glmnet. The hierarchical Lasso method [Bien et al., 2013] is applied to the G × G model. It is realized using the R package hierNet. Our simulation setting has a larger p than in Bien et al. [2013], and we find that enforcing the strong hierarchical structure using hierNet is not computationally feasible for large-scale simulations. Thus, we only implement the weak hierarchical method in Bien et al. [2013]. Two multiple testing procedures are included in the analysis of G × E model. Both procedures apply a marginal test to each main effect, while the first procedure test pairwise interaction effects marginally, and the second procedure tests interaction effects conditioning on the main effects. Moreover the second method is forced to select a main effect if any of its corresponding interaction terms is selected. It shares similarity with the entropy-based methods such as Dong et al. [2007] where the response is binary. We abbreviate the two multiple testing procedures as MT and MT +, respectively. Due to high computational cost, we do not apply these two procedures to the G × G model.

We evaluate marker identification accuracy by plotting the (partial) ROC curves and comparing the partial area under the ROC curve (pAUC). The ROC curves are constructed by restricting the number of false positives at 80. Model sizes of the three penalization methods (proposed, all-pairwise, and hierNet) are controlled by the tuning parameter λ, while the multiple testing procedures MT and MT + select variables with the smallest p-values. We also compare the true positive rates under model size 20 and 40. For each of the three penalization methods, we also choose the λ value that yields the smallest mean prediction error on an independently generated testing dataset (with 500 samples) and report the fitted model results under this λ value. Simulation results are summarized in Tables 1, 2, 5 and 6, and Figures 1–4.

Table 1.

G × E Model with continuous X

Scenario 1: 15 main effects, 5 interactions.
n	p	Method	pAUC (sd)	TP20 (sd)	TP40 (sd)	TP.best(sd)	FP.best(sd)	MSE.best(sd)
150	500	Proposed	0.82 (0.11)	11.90 (2.38)	16.66 (2.71)	18.96 (1.81)	92.48 (21.97)	5.08 (1.85)
		All-pairwise	0.58 (0.12)	7.79 (1.89)	11.15 (2.43)	14.99 (3.03)	95.04 (26.01)	8.49 (2.04)
		MT	0.40 (0.08)	6.08 (1.98)	8.05 (1.84)	-	-	-
		MT+	0.39 (0.08)	5.96 (1.54)	7.88 (1.72)	-	-	-
150	1000	Proposed	0.70 (0.13)	10.18 (2.36)	13.94 (2.91)	16.84 (2.60)	94.09 (23.42)	7.09 (2.24)
		All-pairwise	0.45 (0.11)	6.24 (1.96)	8.90 (2.33)	11.93 (3.06)	90.59 (27.16)	10.12 (1.94)
		MT	0.32 (0.09)	4.85 (1.73)	6.37 (2.01)	-	-	-
		MT+	0.32 (0.08)	4.91 (1.61)	6.42 (1.75)	-	-	-
250	500	Proposed	0.97 (0.03)	17.58 (1.61)	19.88 (0.61)	19.97 (0.30)	85.11 (29.76)	1.97 (0.46)
		All-pairwise	0.93 (0.04)	14.94 (2.04)	18.73 (1.41)	19.99 (0.10)	134.92 (31.32)	2.66 (0.55)
		MT	0.66 (0.09)	10.97 (1.90)	12.98 (2.01)	-	-	-
		MT+	0.65 (0.08)	10.68 (1.63)	12.84 (1.87)	-	-	-
250	1000	Proposed	0.96 (0.05)	16.70 (1.81)	19.61 (1.23)	19.83 (0.82)	99.38 (33.91)	2.25 (0.78)
		All-pairwise	0.87 (0.06)	13.04 (1.89)	17.47 (1.90)	19.83 (0.45)	154.31 (30.82)	3.25 (0.83)
		MT	0.58 (0.07)	9.46 (1.66)	11.33 (1.69)	-	-	-
		MT+	0.58 (0.07)	9.25 (1.49)	11.55 (1.62)	-	-	-

Scenario 2: 10 main effects, 10 interactions.
n	p	Method	pAUC (sd)	TP20 (sd)	TP40 (sd)	TP.best(sd)	FP.best(sd)	MSE.best(sd)
150	500	Proposed	0.71 (0.17)	10.47 (2.85)	14.35 (3.65)	16.77 (3.61)	84.08 (27.85)	6.66 (2.64)
		All-pairwise	0.53 (0.13)	7.24 (2.16)	10.28 (2.76)	14.14 (2.98)	96.97 (28.82)	8.98 (2.28)
		MT	0.40 (0.10)	6.18 (2.06)	7.76 (2.22)	-	-	-
		MT+	0.36 (0.08)	5.37 (1.72)	7.15 (1.80)	-	-	-
150	1000	Proposed	0.61 (0.17)	8.69 (2.79)	11.82 (3.55)	15.26 (3.91)	89.48 (29.56)	7.98 (2.45)
		All-pairwise	0.43 (0.11)	6.24 (1.96)	8.35 (2.25)	11.23 (2.98)	85.83 (30.24)	10.50 (1.95)
		MT	0.36 (0.09)	5.57 (1.70)	7.12 (1.99)	-	-	-
		MT+	0.31 (0.08)	4.80 (1.61)	6.42 (1.80)	-	-	-
250	500	Proposed	0.96 (0.04)	16.73 (2.01)	19.64 (1.12)	19.96 (0.40)	87.28 (30.11)	2.09 (0.56)
		All-pairwise	0.91 (0.04)	14.01 (1.84)	18.43 (1.38)	19.99 (0.10)	135.35 (30.43)	2.92 (0.67)
		MT	0.67 (0.08)	11.05 (1.76)	13.20 (1.89)	-	-	-
		MT+	0.62 (0.08)	10.04 (1.66)	12.18 (1.76)	-	-	-
250	1000	Proposed	0.93 (0.09)	15.54 (2.91)	19.02 (2.20)	19.92 (0.49)	112.62 (44.25)	2.47 (0.88)
		All-pairwise	0.86 (0.08)	12.86 (2.48)	17.04 (2.30)	19.79 (0.64)	154.44 (35.14)	3.56 (1.39)
		MT	0.61 (0.09)	9.96 (2.10)	12.12 (1.93)	-	-	-
		MT+	0.56 (0.09)	9.08 (1.76)	11.01 (1.92)	-	-	-

The pAUC is calculated up to 80 false positive nonzero parameters. TP20 and TP40 denote the true positives under model size 20 and 40, respectively. TP.best, FP.best, and MSE.best correspond to the model that yields the best prediction MSE.

Table 2.

G × G Model with binary X

Scenario 1: 15 main effects, 5 interactions.
n	p	Method	pAUC (sd)	TP20 (sd)	TP40 (sd)	TP.best(sd)	FP.best(sd)	MSE.best(sd)
150	500	Proposed	0.73 (0.08)	9.73 (1.35)	14.38 (1.81)	17.80 (1.99)	79.68 (26.77)	2.08 (0.30)
		All-pairwise	0.17 (0.05)	3.03 (1.29)	3.43 (1.16)	3.91 (1.17)	115.69 (31.45)	2.81 (0.36)
		hierNet	0.55 (0.07)	8.60 (1.23)	10.76 (1.54)	14.77 (1.40)	185.33 (30.34)	2.55 (0.33)
150	1000	Proposed	0.68 (0.09)	9.12 (1.46)	13.33 (2.16)	16.85 (2.21)	80.02 (27.19)	2.41 (0.45)
		All-pairwise	0.13 (0.04)	2.30 (1.10)	2.67 (0.87)	2.89 (1.08)	118.61 (32.77)	3.32 (0.46)
		hierNet	0.48 (0.08)	7.66 (1.45)	9.53 (1.78)	13.70 (1.54)	203.72 (33.04)	2.92 (0.50)
250	500	Proposed	0.82 (0.04)	10.57 (1.21)	16.18 (1.09)	19.7 (0.59)	89.36 (21.52)	1.57 (0.15)
		All-pairwise	0.22 (0.04)	4.25 (0.96)	4.67 (0.81)	4.78 (0.79)	156.73 (35.41)	2.00 (0.22)
		hierNet	0.74 (0.06)	12.39 (1.25)	14.53 (1.16)	17.3 (1.30)	251.08 (54.58)	1.86 (0.22)
250	1000	Proposed	0.82 (0.03)	10.36 (1.26)	16.04 (1.07)	19.61 (0.61)	93.44 (28.13)	1.67 (0.14)
		All-pairwise	0.22 (0.03)	4.20 (0.95)	4.59 (0.67)	4.69 (0.67)	175.64 (45.15)	2.27 (0.25)
		hierNet	0.67 (0.07)	11.40 (1.38)	13.14 (1.45)	16.49 (1.36)	288.39 (48.12)	2.02 (0.23)

Scenario 2: 10 main effects, 10 interactions.
n	p	Method	pAUC (sd)	TP20 (sd)	TP40 (sd)	TP.best(sd)	FP.best(sd)	MSE.best(sd)
150	500	Proposed	0.89 (0.04)	13.23 (1.27)	18.73 (1.33)	19.35 (0.83)	53.19 (20.73)	1.74 (0.18)
		All-pairwise	0.38 (0.07)	6.90 (1.52)	7.96 (1.60)	8.16 (1.46)	102.62 (30.29)	2.51 (0.40)
		hierNet	0.50 (0.05)	8.89 (1.11)	9.92 (1.09)	11.59 (1.44)	161.62 (37.58)	2.40 (0.30)
150	1000	Proposed	0.88 (0.05)	13.38 (1.56)	18.43 (1.35)	19.01 (1.01)	54.46 (22.83)	1.89 (0.25)
		All-pairwise	0.35 (0.07)	6.49 (1.70)	7.38 (1.58)	7.57 (1.54)	114.82 (30.74)	2.92 (0.51)
		hierNet	0.47 (0.04)	8.41 (1.00)	9.34 (1.05)	10.90 (1.10)	176.15 (38.47)	2.68 (0.35)
250	500	Proposed	0.93 (0.02)	13.87 (1.20)	19.77 (0.49)	19.89 (0.31)	56.29 (22.81)	1.45 (0.14)
		All-pairwise	0.49 (0.03)	9.39 (0.94)	10.14 (0.75)	10.19 (0.84)	123.27 (28.87)	1.75 (0.21)
		hierNet	0.62 (0.07)	11.01 (1.12)	12.21 (1.46)	14.46 (1.70)	193.03 (66.23)	1.85 (0.22)
250	1000	Proposed	0.92 (0.02)	13.66 (1.06)	19.73 (0.54)	19.85 (0.40)	57.41 (18.30)	1.50 (0.13)
		All-pairwise	0.48 (0.03)	9.13 (1.03)	9.83 (0.76)	9.76 (0.79)	139.38 (39.54)	1.93 (0.21)
		hierNet	0.58 (0.05)	10.49 (0.84)	11.45 (1.08)	13.37 (1.66)	222.41 (69.30)	1.98 (0.21)

The pAUC is calculated up to 80 false positive nonzero parameters. TP20 and TP40 denote the true positives under model size 20 and 40, respectively. TP.best, FP.best, and MSE.best correspond to the model that yields the best prediction MSE.

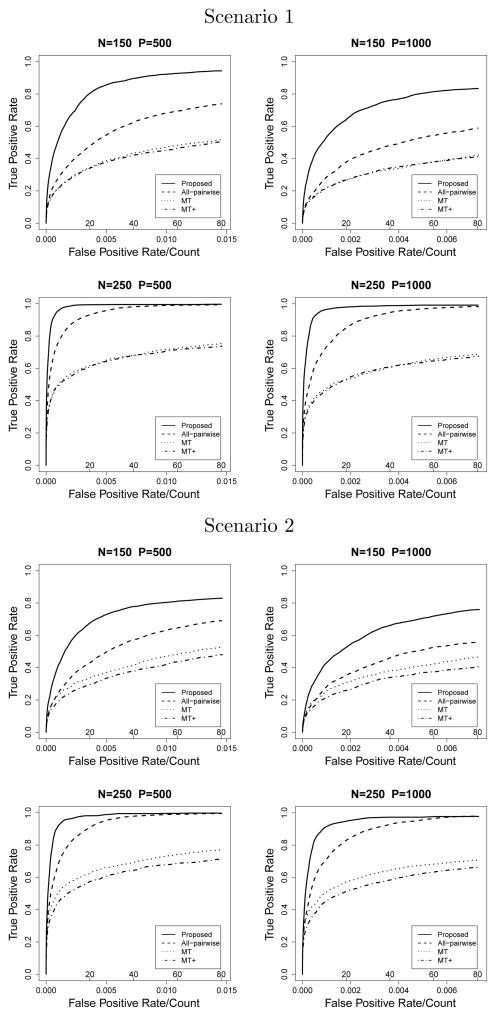
Figure 1.

G × E Model with continuous X

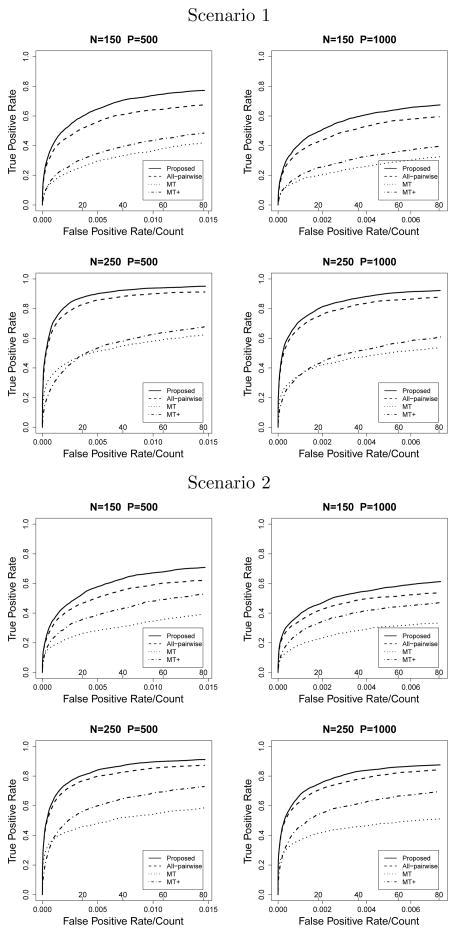
Figure 4.

G × G Model with continuous X

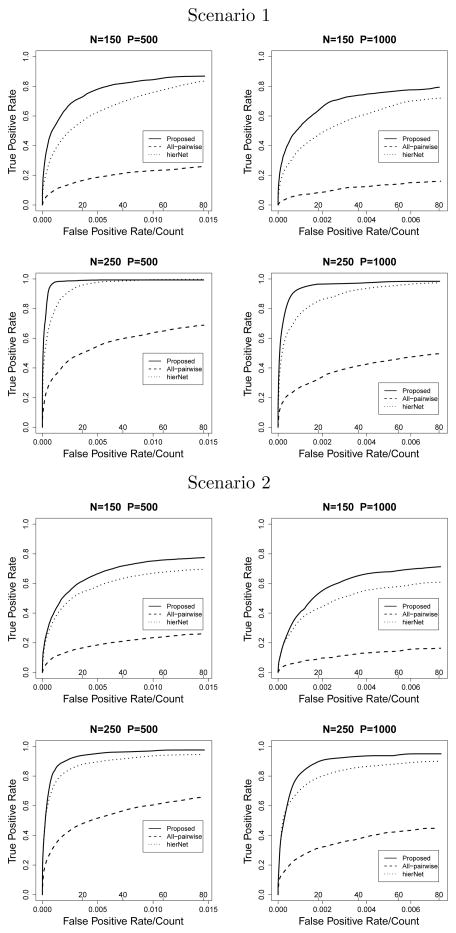
The proposed method has the highest pAUCs under all simulation settings. For the G × E model, the two multiple testing procedures fall behind the proposed method and all-pairwise lasso. For the G × G model, with a large number of variables, the all-pairwise lasso performs the worst.

In the G × E model, scenario 1 with continuous X, n=250 and p=500, the proposed method selects on average 17.58 true nonzero variables when the model size is 20, while the all-pairwise lasso and two multiple testing procedures select 14.94, 10.97 and 10.68 on average, respectively. When the model size is increased to 40, the proposed method selects almost all true nonzero variables (19.88). A similar pattern is found in scenario 2 with continuous X where more interaction terms are involved. All methods perform worse when X is binary. In scenario 2, with n = 250 and p = 500, the proposed method selects on average 16.39 true nonzero variables when the model size is 40, while the other three methods selects 15.71, 9.75, and 12.03 true nonzero variables, respectively.

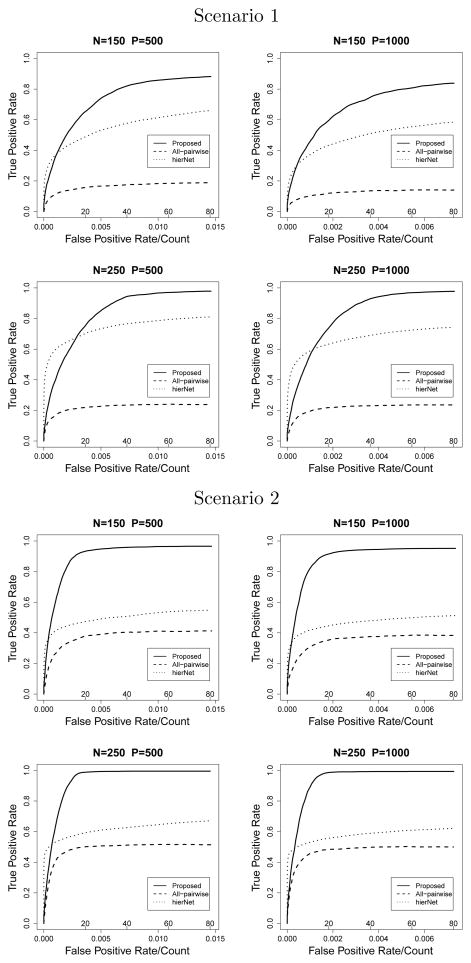
In the G × G model, the proposed method also shows significant improvement over hierNet and all-pairwise lasso. When X is continuous, under scenario 1, n = 250 and p = 1000, the proposed method selects 19.36 true nonzero variables when the model size is 40, while hierNet selects 17.30 and all-pairwise lasso selects 7.80 on average. The average MSE from the best fitted model is 2.37 with the proposed method, which is 73% of that of hierNet. All methods perform slightly worse under scenario 2, however, the pattern is similar. When X is binary, the ROC plots (Figure 2) show interesting results. In scenario 1, n=250, the hierNet method quickly identifies about 60% of the true nonzero parameters without false positives, however, the ROC curve falls flat afterwards. This is also reflected by the “best λ” model in Table 2, where hierNet can only identify 16.49 true nonzero parameters even with over 200 false positives. In contrast, the ROC curve of the proposed method grows steadily and approaches 1 eventually. The “best λ” model identifies almost all of the nonzero parameters (19.61) with 93.44 false positives, which is less than half of hierNet under the same setting. This pattern is observed in scenario 2, however with little difference between the two methods at small false positive values. And hierNet falls behind quickly when the model size increases, which yields pAUC just slightly larger than half of the proposed method.

Figure 2.

G × G Model with binary X

The proposed method has much lower computational cost. For the G × G model with n = 250 and p = 1000, the hierNet (where the computational core of the R package is written in C) takes over 2 hours to compute a single solution path (50 λ values without cross-validation). The strong hierarchy option implemented in hierNet takes much longer to compute and does not seem feasible under our simulation settings, which is the reason why we use the weak hierarchy option. The proposed method and all-pairwise Lasso both take a few minutes on the same desktop computer, while our code is written completely in R.

Analysis of lung cancer prognosis data

Lung cancer is the leading cause of cancer death for both men and women in the United States. Non-small-cell lung cancer (NSCLC) is the most common type of lung cancer, constituting approximately 85% of the cases. Gene profiling studies have been widely conducted on lung cancer, searching for markers associated with prognosis. As individual studies usually have small sample sizes (which may lead to unreliable results), we follow Xie et al. [2011] and analyze data from four independent studies. The DFCI (Dana-Farber Cancer Institute) study had a total of 78 patients, among whom 35 died during followup. The median followup time was 51 months. The HLM (Moffitt Cancer Center) study had a total of 76 patients, among whom 59 died during followup. The median followup time was 39 months. The MI (University of Michigan Cancer Center) study had a total of 92 patients, among whom 48 died during followup. The median followup time was 55 months. The MSKCC (Memorial Sloan-Kettering Cancer Center) study had a total of 102 patients, among whom 38 died during followup. The median followup time was 43.5 months. Affymetrix U133 plus 2.0 arrays were used to measure gene expressions. After simple processing, data on 22,283 probe sets are available for analysis. A robust method is used to conduct across-datasets gene expression normalization. We refer to Xie et al. [2011] for more detailed experimental information.

There are five clinical covariates, namely age, gender, smoke, chemotherapy, and stage. Among them, age is a continuous variable and is normalized. Gender, smoke, and chemotherapy are binary. Stage has three levels. We create two binary indicator variables for stage II and III, with stage I as baseline. We also consider fixed effects for study sites. DFCI is used as baseline. Our goal is to identify genes and their interactions with the clinical risk factors (site effects not included for interactions) that are associated with prognosis. Such interactions are not “typical” G × E interactions, however, are also of significant interest. In principle, the proposed method can analyze all of the gene expressions. As genes with higher variations are often of more interest, the probe sets are ranked using their variations, and the top 2500 are screened out for analysis. We also include the probe sets that correspond to the 59 genes identified in Xie et al. [2011]. For each gene expression and each dataset separately, the mean is normalized to zero, and the variance is normalized to one.

Multiple survival models are potentially applicable. For this specific data, Liu et al. [2013] adopted the AFT (accelerated failure time) model for gene expressions (ignoring clinical/environmental factors) and showed that it has satisfactory performance. As there is a lack of model diagnostic tool for high-dimensional data, we focus on the AFT model without further discussing other models. The AFT model assumes that

$$\mathit{log}(T)={\alpha }_0+\sum _{k=1}^q{\alpha }_k{Z}_k+\sum _{j=1}^p{\beta }_j{X}_j+\sum _{j,k}{\theta }_{jk}{X}_j{Z}_k+\epsilon ,$$

where T is the survival time and α₀ is the intercept. Denote C as the censoring time and Y = min(T, C). A weighted-least-squares (WLS) estimation approach is described in Stute [1993] and adopted in Liu et al. [2013] and other studies. Denote {w_i, i = 1, …, n} as the jumps in the Kaplan-Meier estimate. The WLS objective function is

$$\frac{1}{2}\sum _{i=1}^n{w}_i{\left(\mathit{log}(Y^{(i)})-{\alpha }_0-\sum _{k=1}^q{\alpha }_k{Z}_k^{(i)}-\sum _{j=1}^p{\beta }_j{X}_j^{(i)}-\sum _{j,k}{\theta }_{jk}{X}_j^{(i)}{Z}_k^{(i)}\right)}^2.$$ (12)

Here the superscript “(i)” denotes the ith ordered observation (sorted using the observed times). With the above simple objective function, the proposed algorithm is applicable with very minor modifications in the derivative calculation.

The hierNet method used in simulation cannot handle G × E interactions, while the all-pairwise Lasso can be used in a similar AFT model setting. With practical data, the tuning parameter selection approach described in simulation is no longer applicable. We thus resort to cross validation. The all-pairwise Lasso selects only 2 main effects and 1 interaction effect. With the extreme complexity of lung cancer prognosis, such results do not seem informative. The proposed method identifies 60 main gene effects and 28 interactions, which seem more sensible. We also apply the two multiple testing methods. As they conduct marginal analyses, the estimates are not directly comparable to those under joint analyses. Thus in Appendix (Tables 7, 8, and 9), we present the p-values for the top 88 effects, matching the number of important findings with the proposed method. Results using the proposed method are provided in Table 3 and 4. The estimates for the main effects of clinical factors and sites are 0.008 (age), 1.319 (gender), −0.221 (smoke), 0.545 (chemo), −0.258 (stage II), −0.653 (stage III), −0.174 (site HLM), 0.136 (site MI), and 0.509 (site MSKCC), respectively. The qualitative results are meaningful. For example, we observe a detrimental effect of smoking and a beneficial effect of chemo. Higher-stage patients have shorter survival. We also observe certain differences across sites which may be caused by the differences in patient characteristics.

Table 3.

Analysis of lung cancer data: identified main and interaction gene effects.

Gene	Main Effects	Interactions
		Age	Gender	Smoke	Chemo	Stage I	Stage II
CPS1	−0.003						0.005
CXCL13	0.007				−0.065
PAEP	0.054
PSPH	−0.015	0.000			0.024	0.016
TESC	−0.005		0.103
FMO5	0.031
IL8	−0.027
CA12	−0.008					0.003
ID1	−0.024
DPP4	0.023
DUSP4	−0.013
ZNF238	0.003
KIAA0101	−0.026	0.002
CXCL3	−0.018				0.101
CPB2	0.131	0.003					0.030
NELL1	0.010
NR0B1	0.004
COL21A1	0.062
HIST1H1C	0.002
AHCYL2	−0.074
KCNE4	0.054
CX3CL1	0.013
C4B	0.046
KRT5	0.001
EIF1AY	0.754		1.302
SERPINE1	−0.055
GGTLC1	0.030
SERPINB3	0.004
GABRP	0.003					−0.014
MSTP9	−0.065

Table 4.

Analysis of lung cancer data: identified main and interaction gene effects (continued).

Gene	Main Effects	Interactions
		Age	Gender	Smoke	Chemo	Stage I	Stage II
EGFL6	−0.006
BEX4	0.004
C4BPB	0.068	0.003					0.076
THBD	−0.016
WNT5A	0.003
LY6D	−0.001		−0.014
TRIM2	0.024
LOC642799	−0.052
EFNB2	−0.006			−0.049
NFIB	0.047
XK	−0.031			0.102	0.055
TWF1	0.010
PTPLA	−0.201				0.054
HDGFRP3	0.120
TFPI	−0.025
HDGFRP3	0.037
GK	−0.122			0.247		0.137
SLCO2A1	−0.001		0.048
ARL4C	−0.042
NFAT5	−0.048
LOC100134401	0.081
CEL	−0.171
NDRG1	−0.026
CLDN8	0.034				−0.028
SNRPN	0.001						0.031
NFIB	0.005
AGA	0.090
H3F3A	0.118
NBN (202905 x at)	−0.139
NBN (217299 s at)	−0.042	0.004		0.072			−0.155

We observe interactions between genes and all clinical factors. In the literature, research on G × E interactions in lung cancer remains limited. It is difficult to determine objectively whether the identified interactions are biologically sensible. Among the identified genes, six of them were identified in Xie et al. [2011]. The difference is caused by the differences in modeling and estimation procedure and the accommodation of interactions. We search NCBI and find that the identified genes may have important implications. Some are related to the hallmarks of cancer such as cell cycle, apoptosis, and invasion. A few genes have been associated with multiple cancers, while others have been associated with lung cancer only.

Briefly, mutations in the gene encoded by CPS1 have been associated with susceptibility to persistent pulmonary hypertension. The protein encoded by IL8 is a member of the CXC chemokine family. This chemokine is one of the major mediators of the inflammatory response. IL8 has been studied extensively in the literature. This gene is believed to play a role in the pathogenesis of bronchiolitis, a common respiratory tract disease caused by viral infection. Several other genes that belong to the CXC chemokine family are also identified, including CXCL13 and CXCL3. Serum CXCL13 has been shown to positively correlate with prostatic disease and prostate cancer cell invasion. CX3CL1 is a member of CX₃C chemokine family. It is reportedly known to act on inflammatory conditions in immune diseases and associated with multiple types of tumors. Carbonic anhydrases (CAs) participate in a variety of biological processes, including respiration and saliva. Gene CA12 has been found to be overexpressed in renal carcinomas. The protein encoded by ID1 may play a role in cell growth, senescence, and differentiation. DPP4 is associated with immune regulation and plays an important role in tumor biology. Its levels on the cell surface or in the serum increase in some neoplasms. KIAA0101 transcript has been found to be overexpressed in the great majority of lung cancers. Patients with tumors displaying high-level KIAA0101 expression have significantly shorter survival. High concentrations of the SERPINE1 gene product are associated with thrombophilia. EGFL6 encodes a member of the epidermal growth factor (EGF) repeat superfamily. Members of this superfamily are often involved in the regulation of cell cycle, proliferation, and developmental processes. Its expression has been detected in lung and meningioma tumors. WNT5A belongs to the WNT gene family. The encoded proteins of this gene family have been implicated in oncogenesis and in several developmental processes, including regulation of cell fate and patterning during embryogenesis. EFNB2 encodes a member of the ephrin (EPH) family, which have been implicated in mediating developmental events, especially in the nervous system and in erythropoiesis. Gene TWF1 has high enrichment scores in multiple cancer cells, such as lung, colon, ovary, and kidney cancers. It has also been found to be involved in breast cancer cell invasion. The protein encoded by PTPLA is a member of the PTP family that are known to be signaling molecules that regulate a variety of cellular processes. TFPI is a major inhibitor of tissue factor-initiated coagulation. Evidence indicates that this gene plays an important role in cancer biology. The product of NFAT5 is a member of the nuclear factors of activated T cells family of transcription factors. Proteins belonging to this family play a central role in inducible gene transcription during immune response. The protein encoded by NDRG1 is a cytoplasmic protein involved in stress responses, hormone responses, cell growth, and differentiation. Expression of NDRG1 may be a prognostic indicator for several types of cancer, including lung cancer. Differential expression of CLDN8 has been observed in colorectal carcinoma and renal cell tumors. Two probe sets of the same gene NBN are identified. The encoded NBN protein is associated with the repair of double strand breaks which pose serious damage to a genome. Mutations in this gene are associated with microcephaly, growth retardation, immunodeficiency/recurring infections and cancer predisposition.

Discussion

In the study of complex diseases, the identification of important G × E and G × G interactions has significant implications. The penalization technique has been adopted in several studies. In this article, we have developed a progressive penalization method, which advances from some of the existing studies by respecting the “main effect, interaction” hierarchical structure, by having a much lower computational cost, and by having better identification and prediction performance. This method assumes the strong hierarchical condition. If this condition does not hold, then the method will either fail to identify important interactions or cause a large number of false positives in the main effects. Although the algorithm is presented for a linear regression model, we expect the progressive penalization strategy to be broadly applicable. For the Lasso penalty which is strictly convex, we provide in Appendix ad hoc arguments on the asymptotic validity of the proposed method. The arguments can be adapted to other models as most of the commonly used loss functions are convex. With alternative penalties that are not convex, the arguments need to be revised. Simulation shows that the computational cost of the proposed method can be several orders lower than the alternatives, making it applicable to data with a much larger number of genes which cannot be handled using the alternatives. Simulation also shows the superior performance of the proposed method. We analyze lung cancer prognosis data with gene expression measurements. The types of responses in simulation and data analysis may seem quite different. However, under the AFT model, the loss function in data analysis has a weighted least squares form, where the weights do not depend on the unknown parameters. Thus the simulation results can be used to support application of the proposed method to censored data under the AFT model. In the simulation study, there is a considerable number of false positives. The over-selection of Lasso has been rigorously proved and demonstrated in a large number of numerical studies. False positives may be reduced by conducting Lasso iteratively or replacing Lasso with other penalties. To make a fair comparison with hierNet, such a strategy is not pursued. In addition, our analysis faces a dramatically large number of working variables. A large number of publications have shown that interactions are extremely difficult to identify. We observe significant improvement over the existing methods, which justifies value of the proposed method. In data analysis, our brief literature review suggests that the identified genes have important implications. More downstream analysis is needed to fully comprehend the identified genes and their interactions. Given the simulation results, some of the findings can be false positives and need to be filtered out.

Figure 3.

G × E Model with binary X