Abstract
Rapid developments in neural interface technology are making it possible to record increasingly large signal sets of neural activity. Various factors such as asymmetrical information distribution and across-channel redundancy may, however, limit the benefit of high-dimensional signal sets, and the increased computational complexity may not yield corresponding improvement in system performance. High-dimensional system models may also lead to overfitting and lack of generalizability. To address these issues, we present a generalized modulation depth measure using the state-space framework that quantifies the tuning of a neural signal channel to relevant behavioral covariates. For a dynamical system, we develop computationally efficient procedures for estimating modulation depth from multivariate data. We show that this measure can be used to rank neural signals and select an optimal channel subset for inclusion in the neural decoding algorithm. We present a scheme for choosing the optimal subset based on model order selection criteria. We apply this method to neuronal ensemble spike-rate decoding in neural interfaces, using our framework to relate motor cortical activity with intended movement kinematics. With offline analysis of intracortical motor imagery data obtained from individuals with tetraplegia using the BrainGate neural interface, we demonstrate that our variable selection scheme is useful for identifying and ranking the most information-rich neural signals. We demonstrate that our approach offers several orders of magnitude lower complexity but virtually identical decoding performance compared to greedy search and other selection schemes. Our statistical analysis shows that the modulation depth of human motor cortical single-unit signals is well characterized by the generalized Pareto distribution. Our variable selection scheme has wide applicability in problems involving multisensor signal modeling and estimation in biomedical engineering systems.
Index Terms: Brain–computer interface (BCI), brain–machine interface (BMI), feature selection, modulation depth (MD), neural decoding, neural interface, state-space model, tetraplegia, variable selection
I. Introduction
Neural interfaces, also referred to as brain–machine interfaces (BMI) or brain–computer interfaces (BCI), offer the promise of motor function restoration and neurorehabilitaion in individuals with limb loss or tetraplegia due to stroke, spinal cord injury, limb amputation, ALS, or other motor disorders [1]. A neural interface infers motor intent from neural signals, which may consist of single-unit actions potentials (or spikes), multiunit activity (MUA), local field potentials (LFP), electrocorticograms, or electroencephalograms (EEG). The movement intention may then be converted into action by means of restorative (e.g., functional electrical stimulation) or assistive technology (e.g., a computer cursor, robotic arm, wheelchair controller, or exoskeleton). Recent clinical studies have demonstrated the potential of chronically implanted intracortical neural interface systems for clinical rehabilitation of tetraplegia [2]–[4].
Recent advances in neural interface technology have led to the possibility of simultaneously recording neural activity from hundreds of channels, where a channel may refer to a single unit or an electrode on a microelectrode array. The features, or variables, derived from these signals may constitute a much larger space, e.g., each LFP variable comprising power from one of several frequency bands in the signal recorded at each electrode. The problem is compounded since typical neural decoding algorithms, such as a cascade Weiner filter or a point-process filter, use multiple parameters per input variable. A large parameter space can severely affect the generalizability of the model due to overfitting. Additionally, model calibration and real-time decoding can become computationally prohibitive and impracticable. The need for a computationally efficient variable selection scheme becomes even more pronounced when a neural interface employs frequent filter recalibration [5] to combat neural signal nonstationarity [6].
To address this issue, signal dimensionality reduction has been a topic of considerable interest in neural interface system design. Dimensionality reduction by variable selection, also referred to as feature selection or signal subset selection, involves ranking and identifying the optimal subset of signals on the basis of their signal-to-noise ratio, information content, or other characteristics important from an estimation and detection viewpoint [7]. The goal of variable selection is to eliminate low-information channels, resulting in improved computational efficiency and generalization capability. The variable selection process involves finding the optimal tradeoff between model complexity and performance.
A common approach to variable selection involves a linear transformation to an optimal basis, such as with principal components analysis (PCA) [8]– [10], independent components analysis [11], or factor analysis [12]. Projection-based techniques such as these disconnect the resulting abstract features from their underlying neurophysiological meaning, making intuitive understanding difficult. Also, since all input channels are used to compute the projections by linear combinations, they must all be recorded and preprocessed. Furthermore, techniques such as PCA do not take the behavioral correlation into account, so the largest principal components may be unrelated to the task conditions [1]. It is, therefore, of interest to study selection methods devoid of such transformations, instead operating in the original space of the physical channels. Several such variable selection algorithms have been explored in the context of neural interfaces with lower complexity than the NP-hard exhaustive search method. An example is greedy search or stepwise regression, which consists of forward selection [9], [13], [14] or backward elimination (random [15] or selective neuron dropping [16], [17]).
Alternatively, information-theoretic metrics such as Shannon mutual information have been used for channel ranking [13], [18], [19]. Methods for computing mutual information have been presented both for continuous-time neural signals [20] and for spike-trains using point process models [21], [22]. Mutual information computation, however, not only requires prohibitively large amounts of data, but reduced-complexity approaches that compute bounds on mutual information may be highly erroneous due to inaccurate assumptions [23]–[25]. Furthermore, information-theoretic measures may not necessarily predict filter-based decoding performance of a variable subset, especially in neural interface applications. An alternative to information-theoretic analysis for channel ranking is decoding analysis [25]. Pearson’s correlation coefficient and coefficient of determination are common measures of task-related information used for variable selection in decoding analysis. Strictly speaking, these are valid only for linear regression or reverse correlation models and not for Bayesian or other models. Extensions of such Gaussian regression measures to generalized linear models have been presented [26]. Although some of the highest information carrying channels are identified consistently irrespective of the ranking method, the differences can sometimes be significant [16]. From a complexity viewpoint, such decoding-based measures may be unsuitable for practical and real-time systems since they require repeating the decoding analysis with each individual channel or subset for the purpose of performance-based ranking, increasing the selection algorithm’s computational complexity with the input signal dimensionality.
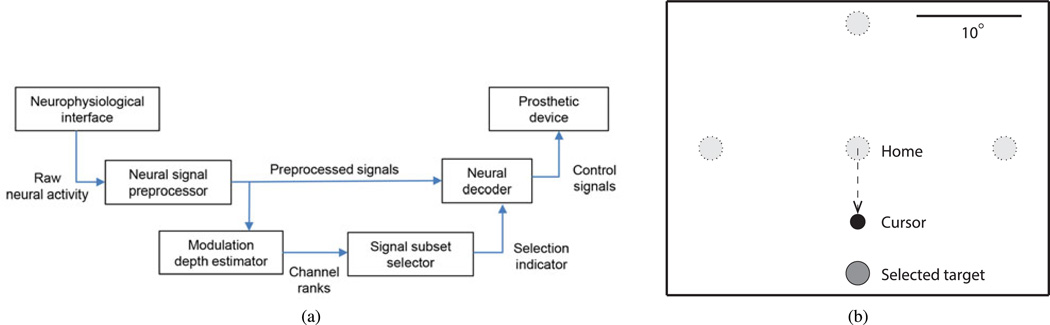
We introduce a highly efficient variable selection scheme based on the state-space formulation, which is consistent with commonly used Bayesian decoding techniques such as the Kalman filter [27].Within this Gaussian linear dynamical framework, we estimate the modulation depth (MD) of a channel as the ratio of its task-dependent response to its spontaneous activity and noise. As such, MD can be used to quantify each variable’s relative importance to decoding in a neural interface and to identify the optimal variable subset [see Fig. 1(a)]. In the next section, we present a mathematical description of the MD estimation procedure for state-space models, followed by its application to channel selection in neural interfaces for people with tetraplegia.
Fig. 1.
Schematic representation of variable selection scheme and behavioral task design for neural recordings. (a) Decoder in a neural interface with optimal variable subset selection based on MD ranking. (b) Open-loop center-out-back task for recording neural activity under motor imagery, with four peripheral targets and a computer-controlled cursor. Bounding rectangle represents the computer screen, and scale bar is in units of visual angle.
II. System Model and Methods
We use a state-space model to estimate intended movement kinematics from neural activity during performance of a 2-D motor imagery task. We denote the vector time series of observations (e.g., single-unit binned spike rates) at time t with m-dimensional vector y(t), where m is the number of channels (e.g., single units). Assuming a velocity encoding model for primary motor cortical neurons [28], [29], we represent the intended movement velocity by the n-dimensional latent variable, x(t), to be estimated from spike-rates y(t) using a state-space paradigm. We consider the intended velocity in the 2-D Cartesian coordinate system, i.e., n = 2 in our case, while m represents the neuronal ensemble size. We estimate the MD of each of the m channels as described below.
A. Dynamical System Model
We consider a continuous-time linear time-invariant (LTI) Gaussian dynamical system model consisting of a latent multivariate random process, x(t), with Markovian dynamics, related to multivariate observations, y(t). We can express this state-space model as
| (1) |
| (2) |
where t ∈ ℝ+, x(t) is the n-dimensional state vector, y(t) is the m-dimensional observation vector, ω(t) is the n-dimensional process noise vector, ν(t) is the m-dimensional measurement noise vector, and F(t) and H(t) are the n × n system matrix and n × m observation martix, respectively. The noise processes have mean zero, i.e., ℰ {ω(t)} = ℰ {ν(t)} = 0. The noise covariances are ℰ {ω(t)ω′(τ)} = Qcδ(t − τ), ℰ {ν(t)ν′(τ)} = Rcδ(t − τ), and ℰ {ω(t)ν′(τ)} = 0, where δ(·) is the Dirac delta function and (·)′ denotes matrix transpose. We assume that Qc is a symmetric positive semidefinite matrix and Rc is a symmetric positive definite matrix. We assume that the observations are zero mean, i.e., ℰ {y(t)} = 0.
B. Modualtion Depth Estimation
We consider (2) and define Hx(t) as the signal and ν(t) as the noise in our model. We further define the MD of a channel as its signal-to-noise ratio (SNR), i.e., the ratio of the signal and noise covariances. For our multivariate state-space model, we denote the m × m signal and noise covariance matrices by Λs (t) and Λn (t), respectively. Then, the m × m time-varying SNR matrix of observations y(t) is
| (3) |
where the n × n matrix Pc (t) is defined by x(t) ~ 𝒩 (μc (t), Pc (t)).
The definition in (3) extends the notion of SNR of a discrete-time single-input single-output state-space model, derived in [30], to that of a continuous-time multiple-input multiple-output state-space model. The (i, j)th and (j, i)th elements of the symmetric matrix Λs (t) represent the signal covariance between ith and jth channels at time t. Similarly, the (i, j)th and (j, i)th elements of Λn (t) represent the noise covariance between channels i and j. If channels i and j have uncorrelated noise, then R is a diagonal matrix. Then, the (i, j)th element of S(t) represents the signal covariance of channels i and j relative to the noise covariance of channel j, whereas the (j, i)th element represents the signal covariance of channels i and j relative to the noise covariance of channel i. Irrespective of the structure of Λs (t) and Λn (t), the ith diagonal element of S(t) represents the SNR of the ith channel at time t.
For the homogeneous LTI differential equation ẋ(t) = Fx(t), the fundamental solution matrix is Φ(t) such that ẋ(t) = Φ(t)x(0), where the state-transition matrix Φ(t, τ) = Φ(t)Φ−1 (τ) represents the system’s transition to the state at time t from the state at time τ and Φ(t, 0) = Φ(t). For the dynamical system in (1), the state transition matrix Φ(t, τ) = eF(t−τ) only depends on the time difference t − τ. The solution to the nonhomogeneous differential equation (1) is
| (4) |
| (5) |
The covariance matrix of x(t) in (4) is given by [31]
| (6) |
C. Model Discretization
We can discretize the system model in (5) by sampling at tk = kΔt = tk−1 + Δt for k = 1, …, K, so that
| (7) |
We define the state-transition matrix Φ = eFΔt, so the equivalent discrete-time system can be represented by
| (8) |
| (9) |
where k ∈ ℤ+, ℰ {w[k]} = ℰ {v[k]} = 0, ℰ {w[k]w′[l]} = Qdδ[k, l], ℰ {v[k]v′[l]} = Rdδ[k, l], and δ[·, ·] is the Kronecker delta function. The state x[k] is a Gaussian random variable initialized with x[0] ~ 𝒩 (μd[0], Pd[0]).
From the power series expansion for a matrix exponential
| (10) |
We can write the covariance of x[k + 1] in (8) as [30]
| (11) |
The equivalent discrete-time SNR can be written by discretizing (3) and substituting the discrete-time covariances, so that
| (12) |
Note that for the above continuous-time and discrete-time system models to be equivalent, we use the approximation Qd ≈ QcΔt andRd ≈ Rc/Δt, neglecting 𝒪(Δt2) terms [32], [33]. Under this condition, the continuous- and discrete-time covariance matrices are equal, i.e., Pc(t) = Pd[k] [34].
Next, we consider certain classes of linear dynamical systems that occur frequently in practice and that admit special forms for MD estimation.
D. Steady-State System
On differentiating (6), using the relation Φ̇(t, t0) = FΦ(t, t0), and solving, we obtain [31]
| (13) |
For a stable LTI continuous-time system at steady state, we can write (13) as limt→∞ Ṗc(t) = 0 [27], [30]. Thus, the steady-state covariance, P̄c = limt→∞ Pc(t), is given by the continuous-time algebraic Lyapunov equation
| (14) |
If λi(F) + λj (F) ≠ 0 ∀ i, j ∈ {1, …, n}, where λi(F) denotes an eigenvalue of F, the solution to the above equation is given by [34]
| (15) |
Similarly, let us consider the discrete-time covariance in (11). The system is stable if |λi(Φ)| < 1 ∀ i ∈ {1, …, n}, where λi(Φ) denotes an eigenvalue of Φ. For a stable LTI system, the steady-state covariance, limk→∞ Pd[k] = P̄d, can be obtained from (11) and expressed in terms of the discrete-time algebraic Lyapunov equation or Stein equation
| (16) |
If λi(Φ)λj (Φ) ≠ 1 ∀ i, j ∈ {1, …, n}, the solution to the above equation is given by [34]
| (17) |
We can solve (15) and (17) numerically using, for example, the Schur method [35].
The steady-state SNR, S̄ = limk→∞ S[k], can therefore be expressed in terms of discrete-time system parameters as
| (18) |
E. Time-Variant System
The expression in (12) gives the instantaneous SNR of the observations at the kth time-step. It can be used to estimate the SNR of a time-varying or nonstationary system. Then, we express the state transition matrix as Φ[k + 1, k], the observation matrix as H[k], and the process noise covariance matrix as Qd[k]. The time-varying state covariance of a state-space system propagates as [30]
| (19) |
By recursive expansion of the above equation and using the property , we can write
| (20) |
If the process noise is wide-sense stationary, then Qd [k] = Qd, and the above equation simplifies to
| (21) |
The above expressions provides an estimate of the state covariance at time k in terms of the initial state covariance and the process noise covariance.
F. Trajectory SNR Estimation
So far, we have considered SNR estimation for two classes of linear dynamical systems: the instantaneous SNR S[k] for a time-varying system, and the steady-state SNR S̄ for a time-invariant and stable sytem. These quantities provide measures of instantaneous information flow between the two multivariate stochastic processes under consideration, namely x[k] and y[k]. Following the nomenclature used in recent work on mutual information estimation for point process data [36], we refer to this measure as the marginal SNR. We now consider the alternate problem of information flow between the entire trajectories of the random processes, as opposed to the instantaneous (marginal) measure. To rephrase, the trajectory SNR is a measure of the SNR conditioned on the entire set of observations for k = 1, …, K. This formulation is useful for SNR estimation by offline, batch processing of data for a time-varying system.
Given the time-varying observation matrix H[k] and state-transition matrix Φ[k], and assuming the noise processes w[k] and v[k] are zero mean and stationary with covariance matrices Qd and Rd, respectively, we can obtain the m × m trajectory SNR matrix as
| (22) |
where ℋ = [H[1], …, H[K]] is an m × nK block matrix and
| (23) |
is an nK × nK block matrix. Here, Pd[i, j] denotes the covariance between x[i] and x[j] for i, j ∈ {1, …, K}, i ≠ j, defined as [30]
| (24) |
G. Colored Measurement Noise
We consider the case that the multivariate measurement noise v[k] in our state-space model (9) is a colored noise process. We assume that v[k] is zero mean and stationary. According to Wold’s decomposition theorem, we can represent v[k] as an m-dimensional vector autoregressive process of order p, i.e., VAR(p), given by
| (25) |
where ζ[k] is an m-dimensional zero-mean white noise process with covariance ℰ {ζ[i]ζ′[j]} = Wδ[i, j], and ψi is an m × m VAR coefficient matrix. We can express the above VAR(p) process in VAR(1) companion form as
| (26) |
where 𝒱[k] is the mp × 1 vector
| (27) |
Z[k] is the mp × 1 whitened noise vector
| (28) |
with covariance ℰ {Z[i]Z′[j]} = diag {Wδ[i, j], 0}, Ψ is the mp × mp VAR(p) coefficient matrix
| (29) |
and Im denotes the m × m identity matrix.
With this formulation, we can augment the state-space with 𝒱[k] so that the augmented state vector has dimensions (n + m) × 1 and is given by 𝒳[k] = [x′[k], 𝒱′[k]]′ [33]. The SNR estimation methodology described earlier can then be applied directly. It should be noted that when using this state augmentation approach for noise whitening, the parameter space can increase substantially if the measurement noise is modeled as a high-order VAR process, which may result in overfitting. The optimal VAR model order, p, can be estimated using standard statistical methods based on the Akaike Information Criterion or Bayesian Information Criterion (BIC).
H. Uncorrelated State Vector
We now consider the special case that the n states, represented by the random n-dimensional vector x[k] at discrete time k, are mutually uncorrelated. Practically, this situation may occur in neural interface systems when, for example, the decoder’s state vector has three components representing intended movement velocity in 3-D Cartesian space. Then, we have Φ = diag {ϕ1,1 …, ϕn,n} and Qd = diag {q1,1 …, qn,n}. The steady-state covariance of the state, given by (17), simplifies to
| (30) |
where we have used the formula for the Neumann series expansion for a convergent geometric series, and the fact that λi(ΦΦ′) = λi(Φ)λi(Φ), and therefore |λi(ΦΦ′)| < 1 so that ΦΦ′ is stable. We can write (30) as
| (31) |
The diagonal elements in P̄d then correspond to the covariances of a set of n mutually independent first-order autoregressive processes each with autoregression coefficient ϕi,i and white noise variance qi,i for i = 1, …, n. For this asymptotically stable system with a diagonal state-transition matrix, the steady-state SNR in (18) can be obtained as
| (32) |
When Rd is also diagonal, the SNR of the ith channel is given by the ith diagonal element of S̄ for i = 1, …, m, i.e.,
| (33) |
Note that if the state vector consists, for example, of position, velocity, and acceleration in Cartesian space, the condition of independence is violated due to coupling between the states, which is reflected in the nonzero off-diagonal entries of Φ [33].
The SNR expressions (12) and (32) include the sampling interval, Δt, since the quantities on the right-hand side correspond to the discrete-time system representation. We now show that if the SNR estimate is converted to the original continuous-time representation, Δt factors out of the SNR equation. To demonstrate this, we transform the discrete-time variables in (32) into the corresponding continuous-time variables by substituting Φ = I + FΔt, Qd = QcΔt, and Rd = Rc/Δt, neglecting higher order terms 𝒪(Δt2), so that
| (34) |
The variables in the above expression correspond to the continuous-time system model. The above expression shows that the SNR is consistent when derived using equivalence relations for continuous- and discrete-time systems.
III. Results
In our neural interface system model, the 2-D state vector x[k] consisted of the horizontal and vertical components of computer cursor movement velocity at discrete time k. We aggregated single-unit spikes (action potentials) within nonoverlapping time-bins of width Δt = 50 ms to obtain binned spike-rates, y[k], which we centered at 0 by mean subtraction. Since this system exhibits short-term stability and convergence [27], we assumed time-invariant state-space system matrices {Φ, H, Qd, Rd}. Using the Neural Spike Train Analysis Toolbox (nSTAT) [37], we obtained maximum-likelihood estimates of the system parameters as part of filter calibration with training data. We used the expectation-maximization (EM) algorithm for state-space parameter estimation, which we initialized with ordinary least squares (OLS) parameter estimates obtained using the procedure described in [27]. As a result of OLS-based parameter initialization, the EM algorithm consistently converged in under five iterations. We estimated the steady-state SNR matrix S̄, and the MD si = [S̄]i,i for channels i = 1, …, m, using (18). To prevent numerical errors, we set the constraint S̄ ≥ 0.
This clinical study was conducted under an Investigational Device Exemption and Massachusetts General Hospital IRB approval. Neural data were recorded using the BrainGate1 neural interface from clinical trial participant S3, who had tetraplegia and anarthria resulting from a brainstem stroke that occurred nine years prior to her enrollment in the trial. A 96-channel microelectode array was surgically implanted chronically in the motor cortex in the area of arm representation. The data presented in this paper were recorded in separate research sessions conducted on five consecutive days, from Day 999 to Day 1003 postimplant. A center-out-back motor task with four radial targets was developed in which the participant observed and imagined controlling a computer cursor moving on a 2-D screen [see Fig. 1(b)]. A single target, selected pseudorandomly, was highlighted, the computer-controlled cursor moved toward the target and then back to the home position with a Gaussian velocity profile. This constituted one trial, and this process was repeated 36 times within four blocks for a total of about 6 min in each session. This motor imagery task was performed under the open-loop condition, i.e., the participant was not given control over cursor movement during this epoch. The cursor position and wideband neural activity were recorded throughout the task duration. The neural data were bandpass filtered (500 Hz–5 kHz) and spike-sorted to identify putative single units. For decoding analysis, these data were used to calibrate a steady-state Kalman filter [27] and estimate the imagined movement velocity of the cursor using leave-one-out cross validation.
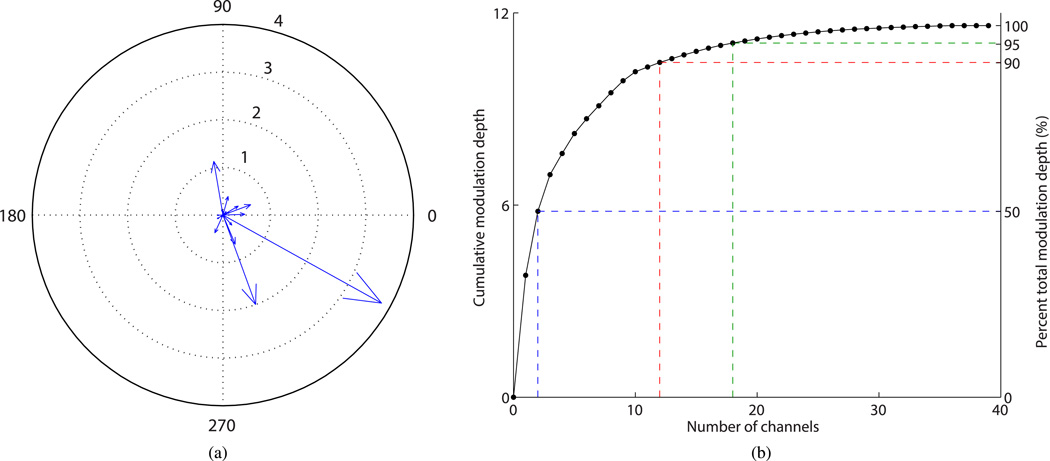
We investigated the MD characteristics of an ensemble of single units. Unless otherwise specified, the representative results presented below are from the session conducted on day 1003 postimplant. The neural data from the session consisted of the spiking activity of m = 39 putative single units isolated by spike-sorting. We estimated the MD of each of the 39 channels and found its magnitude to be highly asymmetrical across channels [see Fig. 2(a)]. The MD of the best (most strongly modulated) channel (s = 3.8) was nearly twice as high as that of the next best channel (s = 2.0). We estimated the MD distribution skewness as 3.5 (unbiased estimate, bootstrap).
Fig. 2.
MD of human motor cortical single-unit spike rates. (a) Distribution of MD (radial length) and preferred direction (angle) of 39 individual channels (single units) recorded in one research session. (b) Cumulative MD as a function of optimal subset size. Blue, red, and green dashed lines: number of channels required to achieve at least 50%, 90%, and 95% of total MD, respectively.
We defined the preferred direction of the ith channel in the 2-D Cartesian space as θ̄i = tan−1 (hi,2/hi,1). The preferred directions of the channels appeared to be distributed approximately uniformly in the [0, 360°) range when the MDs [radial lengths in Fig. 2(a)] were disregarded. MD, however, is instrumental in informing us that only a small number of channels are principally relevant for decoding, and the preferred-direction spread of those high MD channels is of key importance. The preferred directions of three best channels were estimated as 330°, 290°, and 100°, respectively. Although the preferred directions of the most strongly modulated channels did not form an orthogonal basis in 2-D Cartesian space, they were not clustered together. This result suggests that for this task, a small number of channels, with large MD and substantial spread in preferred direction, may be adequate for representing movement kinematics in this 2-D space.
We studied the increase in total MD with increasing ensemble size by analyzing the cumulative MD curve [see Fig. 2(b)], obtained by adding successive values of MD sorted in descending order. As the MD distribution is highly nonuniform, the increase in ensemble size follows the law of diminishing returns. We found 2, 12, and 18 channels to yield 50%, 90%, and 95%, respectively, of the total MD obtained with all 39 channels.
To address the problem of optimal subset selection for decoding in a neural interface, we studied the effect of ensemble size on decoding performance. When only the most strongly modulated channel was used for decoding, the decoded trajectory was restricted to a unidimensional axis [see representative trial in Fig. 3(a)]. This 150–330° axis was defined by the preferred direction of the corresponding channel [see Fig. 2(a)]. When the two best channels were used for decoding, the trajectory estimate spanned both spatial dimensions. The trajectory estimate improved with more channels but the improvement associated with an increase in selected subset size rapidly saturated. For the trajectory estimate in Fig. 3(a) obtained by decoding open-loop motor imagery data, the neural activity remarkably reflects the outward movement, reversal of direction, and inward movement phases along the correct axis even in the absence of feedback control.
Fig. 3.
Decoding using optimal channel subset. (a)Open-loop center-out-back task with rightward peripheral target (gray circle). Blue line: computer cursor trajectory from home position outward to target and back; red line: cursor trajectory estimated by decoding neural activity of the m best channels ranked by MD; black rectangle: computer screen location and dimensions; scale bar in units of visual angle. (b) Decoding of the system’s hidden state (imagined cursor velocity) from neural activity using m best channels. The trials, each of 12 s duration, start with target onset at time 0. Blue arrow: direction of selected target relative to home position.
We compared the velocity estimates obtained with a single (most strongly modulated) channel, five of the most strongly modulated channels, and all 39 channels [see Fig. 3(b)]. In trials where the cursor movement axis was closer to the preferred direction of the strongest channel, the single-channel decoder provided reasonable velocity estimates [see Trials 1 and 4 in Fig. 3(b)]. The reason was that the horizontal projection of the encoding vector of that channel [shown in Fig. 2(a)] provided significant movement information. On the other hand, the single-channel decoder performed poorly in trials with movement along the vertical axis (Trials 2 and 3), orthogonal to the dominant component of the encoding vector for that channel, as expected. With five channels, the decoded velocity was qualitatively indistinguishable from that obtained with the entire ensemble.
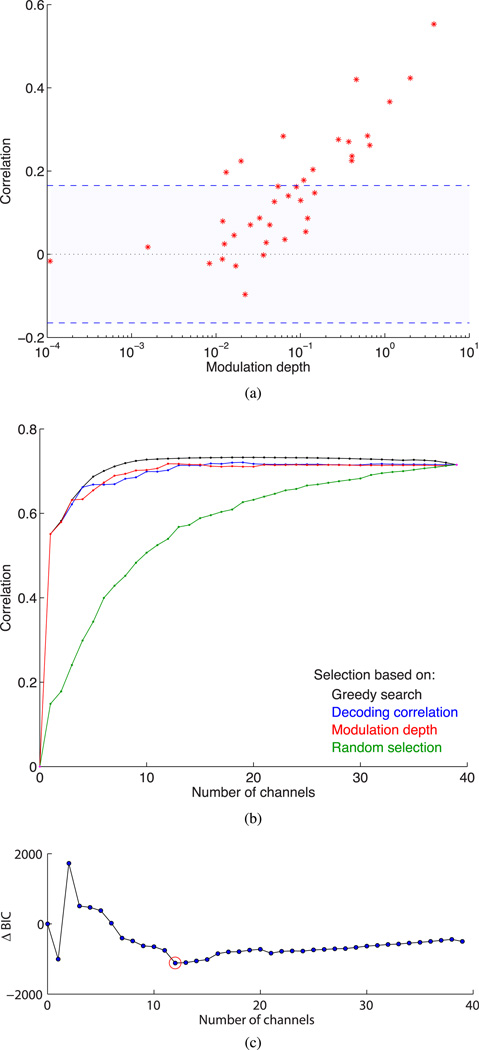
To characterize quantitatively the relation between MD and decoding performance of a given channel, we analyzed the vector field correlation between true (computer-controlled) and decoded 2-D cursor velocity. We used each channel individually to calibrate the filter and decode under cross validation, and computed the correlation [see Fig. 4(a)]. To obtain chance-level correlation, we generated surrogate data by bootstrapped phase randomization. The most strongly modulated channels provided significantly larger decoding correlation than weakly modulated channels. The single-channel correlation appeared to follow an exponential relationship with MD for a few channels in the high MD regime, but did not have a significant relationship in the low MD regime. This result shows that channel ranks are not independent of the evaluation criteria, in this case correlation and MD, as also reported in [16].
Fig. 4.
Effect of neural channel MD on decoding performance. (a) Relation of MD to open-loop decoding correlation of true computer cursor velocity with velocity estimate obtained by decoding each neural channel individually. Shaded region: 95% CI of chance-level decoding correlation. (b) Improvement in decoding correlation with increasing channel subset size chosen using the specified scheme. (c) Normalized BIC as a function of channel subset size chosen by MD. Red circle: optimal subset size with lowest BIC.
To study the implications of channel ranks on decoding performance, we compared the true and decoded state correlation obtained with a subset of channels selected on the basis of MD and of individual channel correlation [see Fig. 4(b)]. The strongest modulated channel alone provided a correlation of over 0.5, and the correlation exceeded 90% of its limiting value of 0.7 with five highest MD channels (see Table I). We also evaluated the decoding correlation achieved with greedy selection and random selection to obtain upper and lower bounds on performance, respectively. Decoding performance of channel subsets chosen by correlation and MD ranking performed almost identically despite differences in the individual channel ranks noted above. The decoding performance of these two schemes was nearly as good as that of greedy selection but substantially better than random selection; this difference reduced as the selected subset size increased. We investigated the optimal model order in terms of the tradeoff between decoding accuracy and model complexity using the BIC. The addition of each channel contributed three parameters to our 2-D velocity decoding model according to (2), namely a row to H and a main diagonal element to R. Based on BIC, the optimal subset size was 12 channels [see Fig. 4(c)], which matches the number of channels that contribute 90% of the total MD [see Fig. 2(b)]. The nonsmooth and nonmonotonic BIC curve reflects the fact that the relative improvement in decoding performance on increasing the neural channel subset size is highly irregular when the subset size is small; increasing the subset from 1 to 2 channels does not reduce the estimation error as much as it increases the parameter space, and so on.
TABLE I.
Comparison of Execution Time and Decoding Correlation (Using Selected Five of the Available 39 Channels) of Various Selection Schemes on a Standard Personal Computer
| Selection Scheme | Execution Time, mean±s.e. (s) | Correlation |
|---|---|---|
| Greedy search | 1.8 × 103 ± 7.2 | 0.69 |
| Decoding correlation | 1.2 × 102 ± 3.8 × 10−1 | 0.67 |
| MD | 4.7 × 10−4 ± 1.4 × 10−5 | 0.65 |
| Random selection | 5.8 × 10−6 ± 9.4 × 10−8 | 0.35 |
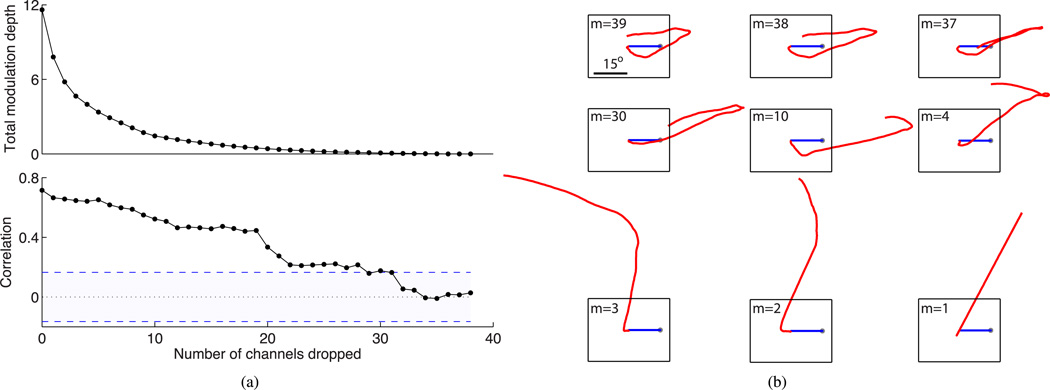
We investigated the phenomenon of loss of the most informative channels and the decoder sensitivity to such loss. This situation may occur in practice due to relative micromovements of the recording array and single units [6].We found that decoding performance deteriorates progressively as the highest MD channels are removed from the decoder, as expected, but the detrimental effect on decoding correlation is particularly dramatic when the number of high-information channels dropped is small (see Fig. 5). This result shows that although a small number (say m = 5) of the highest modulated channels are sufficient to obtain accurate decoding (see Fig. 3), the system is fairly resilient to the loss of highly modulated channels and suffers only a small loss in decoding performance that could be easily compensated under feedback control.
Fig. 5.
Effect of dropping some of the highest modulated channels on decoding performance. (a) Decrease in total MD (top) and open-loop decoding correlation between true and estimated cursor velocity (bottom) when the specified number of the best channels are removed from the neural decoder. Shaded region: 95% CI of chance-level decoding correlation. (b) Open-loop center-out-back cursor trajectories decoded from m channels with the lowest MD. Blue lines: computer cursor trajectory; red lines: imagined velocity decoded from neural channel subset; black rectangle: computer screen.
MD estimation has substantially lower algorithmic complexity than ranking based on decoding correlation, greedy search, or exhaustive search, all of which involve multiple iterations of decoding analysis with the entire dataset. As a practical measure of complexity, we compared the time taken to perform subset selection using various schemes on our computing platform (Desktop PC with 2xQuadCore Intel Xeon 3.2-GHz processor, 24-GB RAM, Windows 8.1 operating system, running MATLAB software). We did not consider exhaustive search in this analysis due to its prohibitive complexity, so greedy search was the most complex scheme in our analysis and served as the performance benchmark. Decoding correlation-based selection had an order of magnitude lower complexity than greedy search while MD based selection was seven orders of magnitude lower (see Table I). The complexity of the MD scheme was within two orders of magnitude of that of random selection, the simplest approach possible. Thus, MD offers vastly reduced computational complexity than other schemes with only a small cost in performance and thus offers a superior selection mechanism.
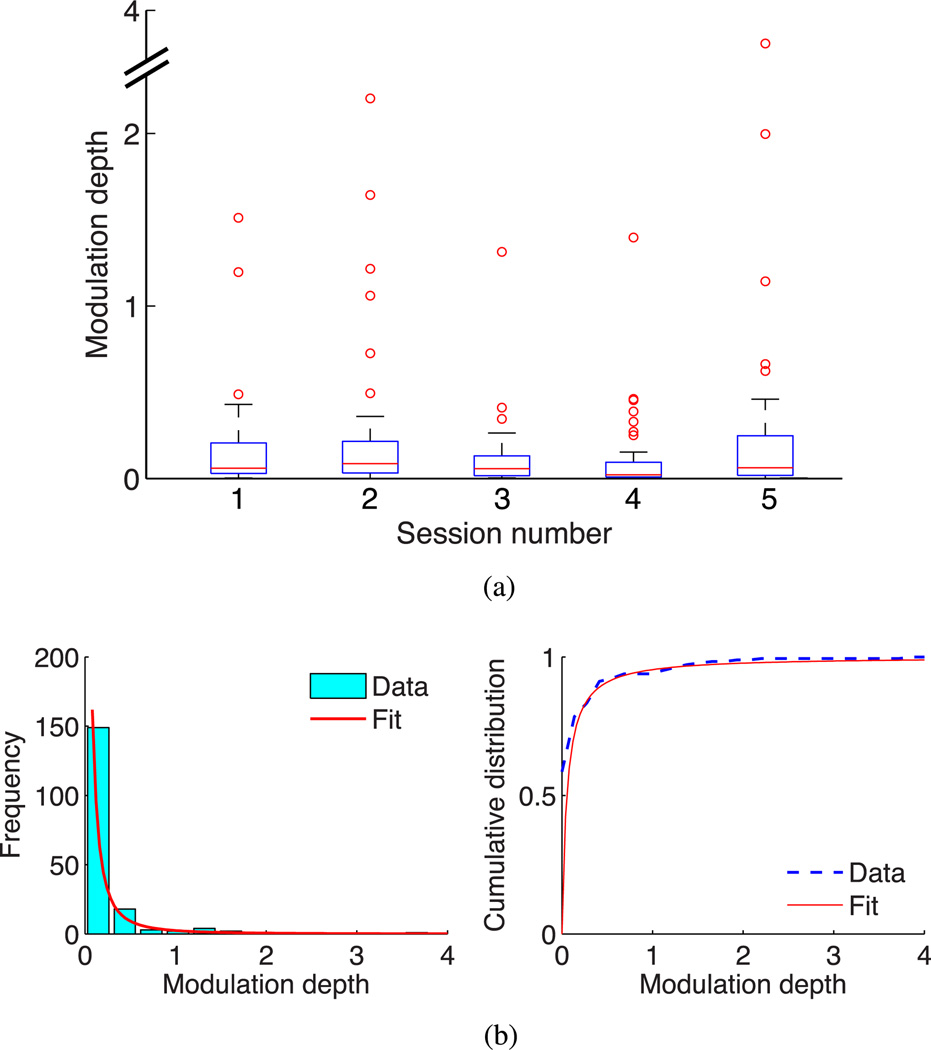
In order to verify that our analysis of MD characteristics was generalizable across sessions, we analyzed the MD distribution in each of the five sessions. The observation of a long-tailed distribution was consistent across sessions [see Fig. 6(a)]. A small number of outliers, i.e., channels with MD several times higher than the median MD, were observed in each session. We characterized the statistical properties of the MD by estimating the best-fit distribution. For this analysis, we pooled together the MD data from all five sessions and estimated the probability distribution from the normalized histogram. Since the MD distribution was highly asymmetric, we used Doane’s formula to compute the optimal number of histogram bins. We investigated a number of candidate probability distributions to obtain accurate statistical description of the data. We obtained maximum-likelihood parameter estimates for each candidate distribution and conducted the Anderson–Darling test with the null hypothesis that the data were sampled from the estimated distribution. Of the distributions that passed the test with the null hypothesis at the 5%significance level, we found that the generalized Pareto distribution provided the best fit (p = 0.714), followed by the Weibull distribution (p = 0.074). The alternative hypothesis was found to be true for the lognormal, exponential, extreme value, Gaussian, and several other distributions (p < 10−6). Based on these results, we conclude that the generalized Pareto distribution provides the most accurate statistical characterization of MD with maximum likelihood estimates of shape parameter k = 0.93 [0.64, 1.22] and scale parameter σ = 0.06 [0.04, 0.08] (mean and 95% confidence intervals). This is illustrated by the close agreement of the generalized Pareto probability density with the data [see Fig. 6(b)]. The Pareto distribution, originally formulated to describe unequal distribution of wealth among individuals, is widely used for modeling asymmetric, peaky data in many applications. In our analysis, the significant positive value of parameter k reflects heavy-tailed behavior, i.e., the presence of a small number of highly modulated channels. We also analyzed MD statistics for each session individually and found the generalized Pareto distribution to provide the best fit to the data in each of the five sessions, followed by the Weibull distribution, confirming our earlier observations.
Fig. 6.
Statistical characterization of single-unit MD. (a) Distribution of MD of various channels in each of five research sessions. Red line: median; box: interquartile range [q1, q3]; whiskers: extreme points that are not outliers and lie within the range q3 ± 1.5 (q3 − q1); red circles: outliers. (b) (Left) Histogram of MD data from five research sessions, along with the scaled best-fit generalized Pareto probability density function. (Right) Cumulative distribution function of MD data and best-fit generalized Pareto distribution.
IV. Discussion
We have presented a simple and efficient method for estimating the MD of a channel in a multivariate state-space system. This definition of MD is an extension of the notion of a single-input single-output state-space system’s SNR [30] to a multivariate system. It is analogous to dimensionless SNR and is consistent across sensorimotor tasks, behavioral state variables, neural signals, and sample rates, due to which it can be used for comparative analysis of a variety of system configurations and experimental conditions. MD can be used as a metric to rank channels and select the optimal subset in a neural interface system. It can be used to analyze and compare the information content and decoding potential of multiple neural signal modalities, such as binned spike-rates and LFP, and also signals recorded from different areas in the brain. The total MD summed across the ensemble could be used in conjunction with a pre-specified threshold to determine whether the information quality is poor and filter recalibration should be initiated.
Most of the computational procedures required to estimate MD are performed as part of the standard Kalman filter calibration process and therefore incur little additional computational cost. The only additional computation required to obtain the SNR matrix, S, consists of relatively simple matrix operations, i.e., matrix multiplications involving the measurement noise covariance matrix that usually has a diagonal structure. Compared to alternative approaches for computing channel modulation measures and ranks, such as those involving neural decoding with correlation-based greedy subset selection, our method has substantially lower computational complexity. It is, therefore, highly suited to real-time neural decoding and high-throughput offline analyses with high-dimensional state or observation vectors or large number of temporal samples. The low computational cost makes repeated estimation of MD possible as may be required during online real-time decoding for performance monitoring or closed-loop recalibration [5]. In a nonstationary setting, the time-varying form of the system SNR and MD can provide an instantaneous measure of signal quality.
MD estimation may be useful in a wide range of systems neuroscience applications beyond movement-related neural interfaces. It is widely applicable to analyses of neural systems involving a set of behavioral correlates and multichannel recordings. Our framework can be applied directly, for example, to an experiment measuring sensory response of a primary visual cortex neuron to a visual stimulus, and the MD then quantifies the response evoked in that neuron by the stimulus applied, leading to a tuning curve estimate for that neuron. Repeating this analysis across a neuronal ensemble can help in comparative analysis of neuronal tuning properties. This approach can be applied to any neuroscience experiment in which the underlying system can be expressed in the form of a state-space model, comprising both intracortical (spike-rate, multiunit threshold crossing rate, analog MUA, or LFP), epicortical (elecrtrocorticogram), or epicranial (EEG or functional magnetic resonance imaging) neural signals.
Our state-space formalism can be modified to incorporate a temporal lead or lag between the latent state and the neural activity. Motor cortical single-unit spike signals typically lead movement by about 100 ms in able-bodied monkeys [38] and are more variable in humans with paralysis [29], and similarly LFP beta rhythm leads movement due to its encoding of movement onset information [39]. Such temporal effects can be analyzed through the covariance structure of model residuals or the likelihood function, and the optimal lags can be included in the observation equation on a per-channel basis, after which MD can be estimated in the usual manner.
The channel-wise MD computation does not take into account cross-channel covariance, which may be substantial for certain signals. For example, LFPs recorded intracortically using a microelectrode array may exhibit significant spatial correlation in the lower frequency bands due to the proximity of the electrodes [40]. The same challenge is encountered with various other measures of neural modulation and ranking, such as correlation and coefficient of determination. In the case of highly correlated signals, one possible solution could be to first reduce signal dimensionality by projection to an orthogonal basis, and then compute the MDs of the resulting set of features.
V. Conclusion
We have presented a framework for estimating the MD of observation variables in a multivariate state-space model for neural interfaces and other applications. This MD estimator is closely related to the Kalman filtering paradigm and is suitable for channel ranking in a multichannel neural system. In contrast with greedy selection and information-theoretic measures, our state-space MD estimation scheme has high computational efficiency and thus provides a method for real-time variable subset selection useful for closed-loop decoder operation. Due to these characteristics, our MD estimation and ranking scheme is highly suitable for both offline neuroscience analyses and online real-time decoding in neural interfaces. This approach will enable optimal signal subset selection and real-time performance monitoring in future neural interfaces with large signal spaces.
Acknowledgment
The authors would like to thank participant S3 for her dedication to this research. They are also grateful to J. D. Simeral for assistance with data collection, and to I. Cajigas and P. Krishnaswamy for their useful comments and suggestions.
This work was supported in part by the Department of Defense (USAMRAA Cooperative Agreement W81XWH-09-2-0001), Department of Veterans Affairs (B6453R, A6779I, B6310N, and B6459L), National Institutes of Health (R01 DC009899, RC1 HD063931, N01 HD053403, DP1 OD003646, TR01 GM104948), National Science Foundation (CBET 1159652), Wings for Life Spinal Cord Research Foundation, Doris Duke Foundation, MGH Neurological Clinical Research Institute, and MGH Deane Institute for Integrated Research on Atrial Fibrillation and Stroke. The pilot clinical trial, in which participant S3 was recruited, was sponsored in part by Cyberkinetics Neurotechnology Systems. The BrainGate clinical trial is directed by Massachusetts General Hospital. The contents do not necessarily represent the views of the Department of Defense, Department of Veterans Affairs, or the United States Government.
Biographies

Wasim Q. Malik (S’97–M’00–SM’08) received the Ph.D. degree in electrical engineering from the University of Oxford, Oxford, U.K., and completed the postdoctoral training in computational neuroscience from the Massachusetts Institute of Technology, Cambridge, MA, USA, and Harvard Medical School, Boston, MA.
He is an Instructor in Anesthesia at Harvard Medical School and Massachusetts General Hospital, Boston. He holds visiting academic appointments at the Massachusetts Institute of Technology, Cambridge, and Brown University, Providence, RI, USA. He is also affiliated with the Center of Excellence for Neurorestoration and Neurotechnology, Department of Veterans Affairs, Providence. His current research interests include signal-processing algorithms for clinical brain–machine interfaces, neuromusculoskeletal modeling, and two-photon neuroimaging.
Dr. Malik received the Career Development Award from the Department of Defense, the Lindemann Science Award from the English Speaking Union of the Commonwealth, and the Best Paper Award from the Automated Radio Frequency & Microwave Measurement Society. He was a Member of the U.K. Ofcom’s Mobile and Terrestrial Propagation Task Group. He serves as an international expert for the national science and technology research councils of Norway, Romania, and Chile, and as an Expert on the use of information and communication technologies for the health sector in the Scientific&Technological Policy panel of the European Parliament & Commission. He is a Member of the New York Academy of Sciences, the Society for the Neural Control of Movement, and the Society for Neuroscience. He is the Chair of the IEEE Engineering in Medicine and Biology Society, Boston Chapter.

Leigh R. Hochberg received the M.D. and Ph.D. degrees in neuroscience from Emory University, Atlanta, GA, USA.
He is an Associate Professor of Engineering, Brown University, Providence, RI, USA; an Associate Director of the Center of Excellence for Neurorestoration and Neurotechnology, Department of Veterans Affairs, Providence; a Neurologist at Neurocritical Care and Acute Stroke Services at Massachusetts General Hospital (MGH), Boston, MA, USA; and a Senior Lecturer on Neurology, Harvard Medical School, Boston. He directs the pilot clinical trial of the BrainGate2 Neural Interface System, which includes the collaborative BrainGate research team at Brown, Case Western Reserve University, MGH, Providence VAMC, and Stanford University. His research interests include developing and testing novel neural interfaces to help people with paralysis and other neurologic disorders.

John P. Donoghue (M’03) received the Ph.D. degree from Brown University, Providence, RI, USA, and completed the postdoctoral training from the National Institute of Mental Health, Bethesda, MD, USA.
He is the Henry Merritt Wriston Professor of Neuroscience and Engineering, and the Director of the Institute for Brain Science, Brown University. He is also the Director of the Center of Excellence for Neurorestoration and Neurotechnology, Department of Veterans Affairs, Providence, RI. He was the Founding Chair of Brown’s Department of Neuroscience, serving from 1992 to 2005. His research focuses on understanding how networks of neurons represent and process information to make voluntary movements. He translated his basic research and technical advances in brain recording to create the BrainGate neural interface system, designed to restore movement in those with paralysis.
Dr. Donoghue is a Fellow of the American Academy of Arts and Sciences and the American Institute for Medical and Biological Engineering. He has served on boards for the National Institutes of Health, the National Science Foundation, and the National Aeronautics and Space Administration. He received the 2007 German Zulch Prize, an NIH Javits Neuroscience Investigator Award, and the Discover Magazine Award for Innovation. His work has been published in Nature and Science magazines and featured by the British Broadcasting Corporation, the New York Times, and the television news magazine “60 Min.”

Emery N. Brown (M’01–SM’06–F’08) received the B.A. degree from Harvard College, Cambridge, MA, USA, the M.D. degree from Harvard Medical School, Boston, MA, and the A.M. and Ph.D. degrees in statistics from Harvard University, Cambridge.
He is the Edward Hood Taplin Professor of Medical Engineering at the Institute for Medical Engineering and Science and a Professor of computational neuroscience at the Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology; the Warren M. Zapol Professor of Anaesthesia at Harvard Medical School; and an Anesthesiologist at the Department of Anesthesia, Critical Care and Pain Medicine, Massachusetts General Hospital. His statistical research interests include the development of signal-processing algorithms to study neural systems. His experimental research uses systems neuroscience approaches to study the mechanisms of general anesthesia.
Dr. Brown was a Member of the NIH BRAIN Initiative Working Group. He received the National Institute of Statistical Sciences Sacks Award for Outstanding Cross-Disciplinary Research, an NIH Director’s Pioneer Award, and an NIH Director’s Transformative Research Award. He is a Fellow of the American Statistical Association, a Fellow of the American Institute of Medical and Biological Engineering, a Fellow of the American Association for the Advancement of Science, a Fellow of the American Academy of Arts and Sciences, a Member of the Institute of Medicine, and a Member of the National Academy of Sciences.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Wasim Q. Malik, Department of Anesthesia, Critical Care and Pain Medicine, Massachusetts General Hospital, Harvard Medical School Boston, MA 02115 USA; with the Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA02139 USA; with the School of Engineering, and the Institute for Brain Science, Brown University, Providence, RI 02912 USA; and with the Center for Neurorestoration and Neurotechnology, Rehabilitation R&D Service, Department of Veterans Affairs Medical Center, Providence, RI 02908 USA (wmalik@mgh.harvard.edu).
Leigh R. Hochberg, Center for Neurorestoration and Neurotechnology, Rehabilitation R&D Service, Department of Veterans Affairs Medical Center, Providence, RI 02908 USA, with the Department of Neurology, Massachusetts General Hospital, Harvard Medical School, Boston, MA 02115 USA; and with the School of Engineering, and the Institute for Brain Science, Brown University, Providence, RI 02912 USA (leigh_hochberg@brown.edu)
John P. Donoghue, Center for Neurorestoration and Neurotechnology, Rehabilitation R&D Service, Department of Veterans Affairs Medical Center, Providence, RI 02908 USA, and also with the Department of Neuroscience, and the Institute for Brain Science, Brown University, Providence, RI 02912 USA (john_donoghue@brown.edu).
Emery N. Brown, Department of Anesthesia, Critical Care and Pain Medicine, Massachusetts General Hospital, Harvard Medical School, Boston, MA 02115 USA, and also with the Institute for Medical Engineering and Science, and the Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139 USA (enb@neurostat.mit.edu).
REFERENCES
- 1.Wolpaw JR, Wolpaw EW, editors. Brain-Computer Interfaces. New York, NY, USA: Oxford Univ. Press; 2012. [Google Scholar]
- 2.Hochberg LR, Serruya MD, Friehs GM, Mukand J, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006 Jul.442(7099):164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- 3.Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, Haddadin S, Liu J, van der Smagt P, Donoghue JP. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012 May;485(7398):372–375. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ, McMorland AJ, Velliste M, Boninger ML, Schwartz AB. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet. 2013 Feb.16(381):557–564. doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Orsborn AL, Dangi S, Moorman HG, Carmena JM. Closed-loop decoder adaptation on intermediate time-scales facilitates rapid bmi performance improvements independent of decoder initialization conditions. IEEE Trans. Neural Syst. Rehabil. Eng. 2012 Jul.20(4):468–477. doi: 10.1109/TNSRE.2012.2185066. [DOI] [PubMed] [Google Scholar]
- 6.Perge JA, Homer ML, Malik WQ, Cash S, Eskandar E, Friehs G, Donoghue JP, Hochberg LR. Intra-day signal instabilities affect decoding performance in an intracortical neural interface system. J. Neural Eng. 2013 Jun.10(3) doi: 10.1088/1741-2560/10/3/036004. art. no. 036004, [Online]. Available: http://iopscience.iop.org/1741-2552/10/3/036004/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guyon I, Elisseeff A. An introduction to variable and feature selection. Amer. J. Mach. Learn. Res. 2003;3:1157–1182. [Google Scholar]
- 8.Hu J, Si J, Olson BP, He J. Feature detection in motor cortical spikes by principal component analysis. IEEE Trans. Neural Sys. Rehabil. Eng. 2005 Sep.13(3):256–262. doi: 10.1109/TNSRE.2005.847389. [DOI] [PubMed] [Google Scholar]
- 9.Vargas-Irwin C, Shakhnarovich G, Yadollahpour P, Mislow JM, Black MJ, Donoghue JP. Decoding complete reach and grasp actions from local primary motor cortex populations. J. Neurosci. 2010 Jul.30(29):9659–9669. doi: 10.1523/JNEUROSCI.5443-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kao JC, Nuyujukian P, Stavisky S, Ryu SI, Ganguli S, Shenoy KV. Investigating the role of firing-rate normalization and dimensionality reduction in brain-machine interface robustness; Proc. IEEE Eng. Med. Biol. Conf; Osaka, Japan. 2013. Jul. pp. 293–298. [DOI] [PubMed] [Google Scholar]
- 11.Laubach M, Wessberg J, Nicolelis MAL. Cortical ensemble activity increasingly predicts behaviour outcomes during learning of a motor task. Nature. 2000 Jun.405(6786):567–571. doi: 10.1038/35014604. [DOI] [PubMed] [Google Scholar]
- 12.Santhanam G, Yu BM, Gilja V, Ryu SI, Afshar A, Sahani M, Shenoy KV. Factor-analysis methods for higher-performance neural prostheses. J. Neurophysiol. 2009 Aug.102(2):1315–1330. doi: 10.1152/jn.00097.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhuang J, Truccolo W, Vargas-Irwin C, Donoghue JP. Decoding 3-D reach and grasp kinematics from high-frequency local field potentials in primate primary motor cortex. IEEE Trans. Biomed. Eng. 2010 Jul.57(7):1774–1784. doi: 10.1109/TBME.2010.2047015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ajiboye AB, Simeral JD, Donoghue JP, Hochberg LR, Kirsch RF. Prediction of imagined single-joint movements in a person with high-level tetraplegia. IEEE Trans. Biomed. Eng. 2012 Oct.59(10):2755–2765. doi: 10.1109/TBME.2012.2209882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wessberg J, Stambaugh CR, Kralik JD, Beck PD, Laubach M, Chapin JK, Kim J, Biggs SJ, Srinivasan MA, Nicolelis MAL. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000 Nov.408(6810):361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- 16.Sanchez JC, Carmena JM, Lebedev MA, Nicolelis MAL, Harris JG, Principe JC. Ascertaining the importance of neurons to develop better brain-machine interfaces. IEEE Trans. Biomed. Eng. 2004 Jun.51(6):943–953. doi: 10.1109/TBME.2004.827061. [DOI] [PubMed] [Google Scholar]
- 17.Singhal G, Aggarwal V, Soumyadipta A, Aguayo J, He J, Thakor N. Ensemble fractional sensitivity: A quantitative approach to neuron selection for motor tasks. Comput. Intell. Neurosci. 2010 Feb.2010 doi: 10.1155/2010/648202. [Online]. Available: http://hindawi.com/journals/cin/2010/648202/cta/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang Y, Sanchez JC, Principe JC. Selecting neural subsets for kinematics decoding by information theoretical analysis in motor brain machine interfaces; Proc. Int. Joint Conf. Neural Netw; Atlanta, GA, USA. 2009. Jun. pp. 3275–3280. [DOI] [PubMed] [Google Scholar]
- 19.Brostek L, Eggert T, Ono S, Mustari MJ, Buttner U, Glasauer S. An information-theoretic approach for evaluating probabilistic tuning functions of single neurons. Front. Comput. Neurosci. 2011 Mar.5(15):1–11. doi: 10.3389/fncom.2011.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Magri C, Whittingstall K, Singh V, Logothetis NK, Panzeri S. A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings. BMC Neurosci. 2009 Jul.10:81. doi: 10.1186/1471-2202-10-81. [Online]. Available: http://www.biomedcentral.com/1471-2202/10/81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Barbieri R, Frank LM, Nguyen DP, Quirk MC, Solo V, Wilson MA, Brown EN. Dynamic analyses of information encoding in neural ensembles. Neural Comput. 2003 Feb.16(2):277–307. doi: 10.1162/089976604322742038. [DOI] [PubMed] [Google Scholar]
- 22.Pillow JW, Ahmadian Y, Paninski L. Model-based decoding, information estimation, and change-point detection techniques for multineuron spike trains. Neural Comput. 2011 Jan.23(1):1–45. doi: 10.1162/NECO_a_00058. [DOI] [PubMed] [Google Scholar]
- 23.Brown EN, Kass RE, Mitra PP. Multiple neural spike train data analysis: State-of-the-art and future challenges. Nat. Neurosci. 2004 May;7(5):456–461. doi: 10.1038/nn1228. [DOI] [PubMed] [Google Scholar]
- 24.Rozell CJ, Johnson DH. Examining methods for estimating mutual information in spiking neural systems. Neurocomputing. 2005 Jun.65/66:429–434. [Google Scholar]
- 25.Quiroga RQ, Panzeri S. Extracting information from neuronal populations: Information theory and decoding approaches. Nat. Rev. Neurosci. 2009 Mar.10(3):173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- 26.Czanner G, Sarma SV, Eden UT, Brown EN. Proc. World Congr. Eng. London, U.K.: 2008. Jul. A signal-to-noise ratio estimator for generalized linear model systems; pp. 2672–2693. [Google Scholar]
- 27.Malik WQ, Truccolo W, Brown EN, Hochberg LR. Efficient decoding with steady-state Kalman filter in neural interface systems. IEEE Trans. Neural Syst. Rehabil. Eng. 2011 Feb.19(1):25–34. doi: 10.1109/TNSRE.2010.2092443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moran DW, Schwartz AB. Motor cortical representation of speed and direction during reaching. J. Neurophysiol. 1999 Nov.82(5):2676–2792. doi: 10.1152/jn.1999.82.5.2676. [DOI] [PubMed] [Google Scholar]
- 29.Truccolo W, Friehs GM, Donoghue JP, Hochberg LR. Primary motor cortex tuning to intended movement kinematics in humans with tetraplegia. J. Neurosci. 2008 Jan.28(5):1163–1178. doi: 10.1523/JNEUROSCI.4415-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mendel JM. Lessons in Estimation Theory for Signal Processing, Communications, and Control. 2nd ed. Englewood Cliffs, NJ, USA: Prentice-Hall; 1995. [Google Scholar]
- 31.Grewal MS, Andrews AP. Kalman Filtering: Theory and Practice Using MATLAB. 3rd ed. Hoboken, NJ, USA: Wiley-IEEE Press; 2008. [Google Scholar]
- 32.Smith MWA, Roberts AP. An exact equivalence between the discrete- and continuous-time formulations of the Kalman filter. Math. Comput. Simul. 1978 Jun.20(2):102–109. [Google Scholar]
- 33.Simon D. Optimal State Estimation. Hoboken, NJ, USA: Wiley; 2006. [Google Scholar]
- 34.Troch I. Solving the discrete Lyapunov equation using the solution of the corresponding continuous Lyapunov equation and vice versa. IEEE Trans. Autom. Control. 1988 Oct.33(10):944–946. [Google Scholar]
- 35.Laub AJ. A Schur method for solving algebraic Riccati equations. IEEE Trans. Autom. Control. 1979 Dec.AC-24(6):913–921. [Google Scholar]
- 36.Pasha SA, Solo V. Computing the trajectory mutual information between a point process and an analog stochastic process; Proc. IEEE Eng. Med. Biol. Conf; 2012. pp. 4603–4606. [DOI] [PubMed] [Google Scholar]
- 37.Cajigas I, Malik WQ, Brown EN. nSTAT: Open-source neural spike train analysis toolbox for Matlab. J. Neurosci. Methods. 2012 Nov.211(2):245–264. doi: 10.1016/j.jneumeth.2012.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J. Neurophysiol. 2004 Jan.91(1):515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
- 39.Donoghue JP. Bridging the brain to the world: A perspective on neural interface systems. Neuron. 2008 Nov.60(3):511–521. doi: 10.1016/j.neuron.2008.10.037. [DOI] [PubMed] [Google Scholar]
- 40.Hwang EJ, Andersen RA. The utility of multichannel local field potentials for brain-machine interfaces. J. Neural Eng. 2013 Aug.10(4) doi: 10.1088/1741-2560/10/4/046005. art. no. 046005, [Online]. Available: http://iopscience.iop.org/1741-2552/10/4/046005/ [DOI] [PMC free article] [PubMed] [Google Scholar]