While crystallization phase diagrams are excellent tools to conceptualize phase relations in protein solutions, they need to be used appropriately and to be compatible with their physicochemical meaning.
Keywords: crystallization, phase diagrams, non-ideal mixtures, thermodynamics, excess properties
Abstract
Crystallization phase diagrams are frequently used to conceptualize the phase relations and also the processes taking place during the crystallization of macromolecules. While a great deal of freedom is given in crystallization phase diagrams owing to a lack of specific knowledge about the actual phase boundaries and phase equilibria, crucial fundamental features of phase diagrams can be derived from thermodynamic first principles. Consequently, there are limits to what can be reasonably displayed in a phase diagram, and imagination may start to conflict with thermodynamic realities. Here, the commonly used ‘crystallization phase diagrams’ are derived from thermodynamic excess properties and their limitations and appropriate use is discussed.
1. Introduction
Macromolecular crystallization, as the self-assembly of complex and irregular molecules into a regular periodic lattice, is an inherently improbable and complex phenomenon. Crystallization is in essence the separation of an ordered crystalline phase from a metastable solution. For this improbable process to take place, certain conditions (illustrated in Fig. 1 ▶) must be met.
(i) The protein must be inherently crystallizable. This primary requirement unique to each protein expresses the simple fact that when the periodic intermolecular contacts necessary for self-assembly into a regular lattice cannot be formed under any circumstances, any protein-rich phases separating from the protein solution will not be a crystal. An example of an adverse protein property might be the presence of large flexible regions that prevent the molecules from forming the required three-dimensional periodic crystal contact network.
(ii) Thermodynamic conditions must establish necessary conditions for crystallization. Formation of a crystal must in principle be thermodynamically possible. This means that in a system of a given chemical composition, a stable, protein-rich phase in the form of a crystal, in equilibrium with its growth solution, must exist. For the process to occur spontaneously, the free energy of crystallization, ΔG C, must be negative. The above requirement for the existence of a stable equilibrium phase establishes a necessary – but not sufficient – macroscopic condition for crystallization. We rarely know a priori at which chemical composition or at which temperature of the system a stable crystal can form, hence the need to screen each protein construct against a chemically diverse set of crystallization reagents.
(iii) Kinetics determine whether the thermodynamically possible outcome will actually be realised. Even if the macroscopic conditions for the formation of a crystal are thermodynamically possible, the kinetic processes leading to the formation of a stable crystal must be favourable so that the thermodynamically possible macroscopic scenario can actually become reality: the enabling microscopic processes take place under kinetic control.
While condition (i) is an invariable inherent property of each individual protein construct and is not predictable, conditions (ii) and (iii) can be discussed in general physicochemical terms.
Figure 1.
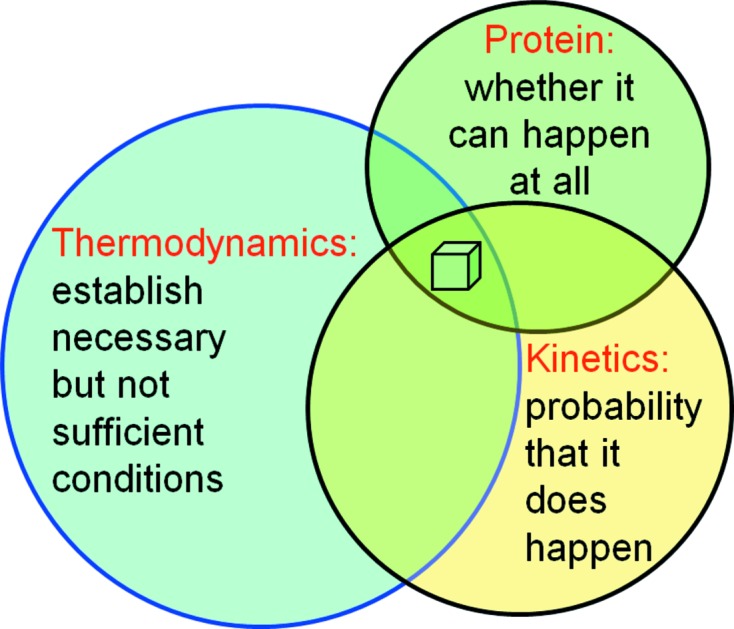
Fundamental factors determining protein crystallization. The protein properties determine whether the process of crystal formation is in principle possible; thermodynamics establish the necessary but not sufficient macroscopic conditions (reagents and temperature) for crystallization, and the kinetics and dynamics of the microscopic processes determine whether a possible scenario actually becomes reality.
1.1. Phases and phase separation
In thermodynamic lingo, a phase is simply a macroscopically homogeneous state of matter, without any assumptions about its microscopic nature. In the common scenario of crystallization of proteins from an aqueous solution, thermodynamics dictate that a metastable, supersaturated protein solution will eventually – even if it takes geological timeframes – revert towards equilibrium by separating into a stable saturated protein solution and a protein-rich phase. What the nature of this protein-rich phase actually is depends on the phase equilibria in the given chemical system. Precipitates, oils and also crystals all represent possible outcomes for protein-rich phases. In §3 metastability and supersaturation in protein solutions will be discussed, and McPherson (1999 ▶) provides a summary of practical means of achieving supersaturation.
1.2. Kinetic processes
The actual realisation of the possible outcomes of a crystallization experiment depends critically on the controlling kinetics. Nucleation and crystal growth are dynamic microscopic processes determining the kinetics (see McPherson & Kuznetsov, 2014 ▶), and they are in general much harder to control and to adjust than macroscopic thermodynamic conditions, which are defined by easily controllable parameters such as the mother liquor (drop) and reservoir composition and volumes, temperature and pressure. Even in space, thermodynamic phase equilibria do not change. The outcome, however, of the experiment in a microgravity environment (∼10−6 g) can differ for example as a result of the practical absence of buoyancy-driven convection (DeLucas et al., 1989 ▶) and the absence of gravity-induced sedimentation of impurities on the crystal surface (Koszelak et al., 1995 ▶). In addition, kinetic processes are by definition time-dependent; for example, the speed at which supersaturation is reached affects nucleation, or slower crystal growth may give better quality crystals. Thermodynamics is ignorant of such microscopic subtleties.
Very little is known a priori about each specific protein as far as optimal crystallization conditions are concerned. While we only can guess where the (extremely narrow) phase fields of stable crystals may be located (for further details, see §3.9), we can use the crystallization phase diagrams as a conceptual aid and an operational playground for imagination when analysing or designing crystallization experiments. In the following, we will investigate what these crystallization phase diagrams actually are, where they originate from and how we can use them to understand protein crystallization. We will also realise that not every line casually drawn in a phase diagram is meaningful or physico-chemically justified.
2. Types of phase diagrams
Phase diagrams in general depict the state of matter under the variation of certain conditions. They may visualize many different dependencies, such as simple pressure–volume (P/V) isotherms or pressure–composition (P/x) diagrams. The phase diagrams that we commonly encounter in macromolecular crystallization are temperature–composition (T/x) and composition–composition (x/x) phase diagrams. They all serve different purposes and contain different information, but they are related to each other. Common to them is that they are all thermodynamic phase diagrams; that is, they inform us about phase equilibria, but out of principle they cannot provide any information about the microscopic kinetics leading to these phase equilibria.
2.1. Temperature–composition diagram example: the lipid cubic phase
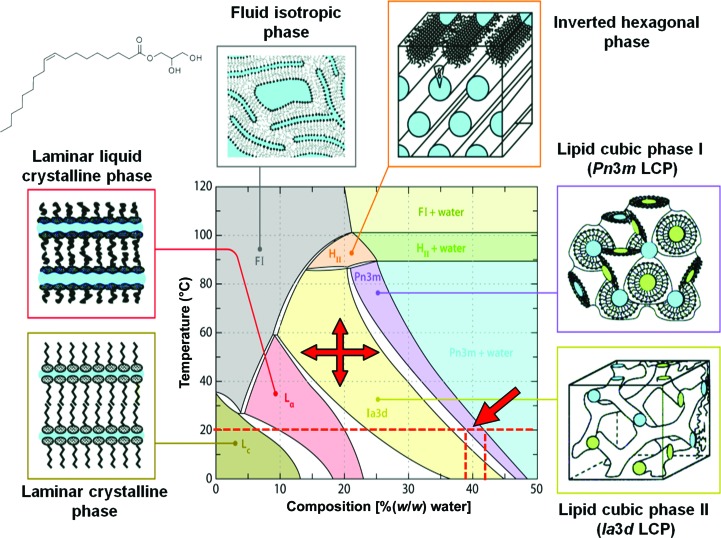
To determine T/x diagrams, mixtures of the components are prepared and equilibrated at a given temperature and constant pressure, and the nature and the relative amounts of phases are established point by point by painstaking experimental labour (often by crystallographic methods in the case of condensed phases). From the sum of these data, the phase fields and composition lines in the phase diagram are established. Such experimentally determined T/x diagrams can be quite complex and they are also reasonably accurate and reliable. Fig. 2(a) of Qiu & Caffrey (2000 ▶) shows well the large number of samples (defined by a specific chemical composition and temperature) that need to be analysed to obtain a complete T/x phase diagram.
The carefully established phase diagram for monoolein [1-(cis-9-octadecenoyl)-rac-glycerol] and water versus temperature (Fig. 2 ▶) is an excellent example of a specific T/x diagram that is useful in macromolecular crystallography. Here, the weight percent (or a similar composition measure, such as the molar fraction x) of monooolein and water is plotted against the temperature. This phase diagram informs us where a stable region (phase field) for the formation of the lipid cubic (meso)phase (LCP) exists. We consult this diagram and similar ones to estimate the proper ratio of protein solution to monoolein for a given temperature when preparing an LCP for a crystallization experiment (Caffrey & Cherezov, 2009 ▶; Caffrey, 2015 ▶). Note that in Fig. 2 ▶ the composition is given in %(w/w); therefore, proper factors must be applied when converting to volumes (Aherne et al., 2012 ▶).
Figure 2.
Temperature–composition phase diagram of the monoolein–water system. Stable phase fields and two-phase regions are shown in different colours. The Gibbs phase rule (derived in many standard thermodynamics texts) mandates that in T/x diagrams single-phase fields are always separated from each other by a two-phase field (white). At 20°C, the practically useful lipid cubic mesophase with Pn3m structure (dark blue) has a homogeneity range around 38–43%(w/w) water (arrow). The small inset at the top left is the structural formula of monoolein [1-(cis-9-octadecenoyl)-rac-glycerol]. Strictly speaking, even this useful diagram is not a true thermodynamic equilibrium T/x diagram but rather an ‘operational’ phase diagram, because it also shows the liquid crystal phase fields extending below about 17°C, where the phases are in fact metastable (i.e. undercooled). The closest approximation to an actual equilibrium phase diagram of the monoolein–water system is represented by Fig. 2(b) in Qiu & Caffrey (2000 ▶). Redrawn with permission from Qiu & Caffrey (2000 ▶).
One can also recognize from Fig. 2 ▶ that some phase fields can have a fairly large homogeneity range; for example, the Pn3m LCP can form at room temperature between about 38 and 43%(w/w) water. The formation of this LCP is therefore reasonably forgiving as far as hitting the exact compositional conditions is concerned; protein crystals, in contrast, have extremely narrow phase fields (§3.9).
2.2. Composition–composition diagrams for protein solutions
In the case of protein crystallization from aqueous solutions, we are in general interested how the system must develop at a given constant temperature and constant pressure so that it can, at least in principle, produce crystals. To aid our understanding, we draw a simple x/x diagram showing the relationship between protein concentration and precipitant concentration in an aqueous solution. The principal chemical components of the system are (i) water, (ii) protein and (iii) a third pseudo-component, into which we pool all other mother-liquor (drop) constituents such as buffer, precipitating agent and various additives under the collective term ‘reagent’. The relative reagent ratios remain constant for a given system. As derived in §3.7, such a diagram is in fact the water-rich corner of an isothermal section of a pseudo-ternary phase body. Ignoring the water as a third, dependent, component, one might even call these x/x diagrams ‘pseudo-pseudo-binary’ (Fig. 3 ▶).
Figure 3.
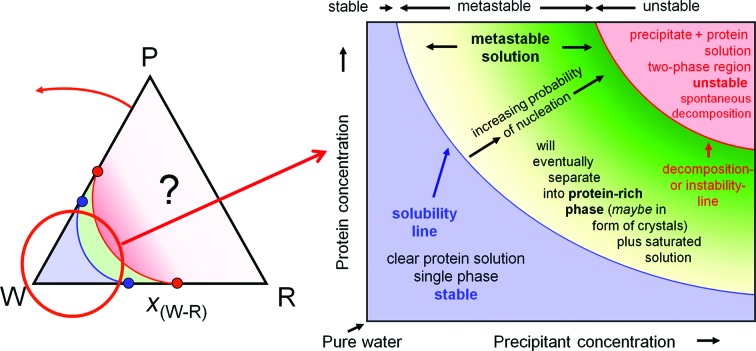
Framework and components of a crystallization phase diagram. The ‘crystallization phase diagram’ is a useful operational framework for visualizing processes during crystallization. It is derived from the water-rich corner of an isothermal section of a pseudo-ternary phase body water–protein–reagent. As such, the thermodynamic information it can contain is at the same time fundamentally defined but limited in scope, and is rarely specifically known with any certainty. Kinetics and temporal development are not part of the phase diagram, but can, with caution, be visualized in the context of the thermodynamic phase diagram.
We use these crystallization diagram frameworks shown in Fig. 3 ▶ to describe an almost unknown specific thermodynamic situation, and in addition imaginatively decorate this non-information with kinetic scenarios. We generally do not know where exactly the solubility lines are, where the phase fields for stable crystals are located in a given system and what other phases may or may not exist. Nonetheless, there are certain fundamental and universal properties that one can at least theoretically justify and use to extract useful information and at the same time keep imagination in check. Cautiously used within their limitations, these ‘operational’ phase diagrams can be a valuable aid to understanding the crystallization process. It is important to distinguish when thermodynamic information, which is a legitimate part of a thermodynamic phase diagram, is augmented with ‘operational’ assumptions of kinetic processes, which are not derivable from macroscopic thermodynamic equilibria.
3. Thermodynamic foundations of phase diagrams
The reason why we have different forms of matter and states or phases is non-ideality. An ideal world, devoid of any interactions, would be a rather boring perfect mixture of dimensionless and non-interacting particles: the definition of an ideal gas. Interactions between the atoms and the fact that they have finite dimensions lead to non-ideality, which is the origin of everything interesting. It is therefore necessary that we examine the basis of thermodynamics in non-ideal multi-component systems by introducing the concept of thermodynamic excess properties, in particular the excess chemical potential.
3.1. Closed versus open systems
A well-sealed cell in a hanging-drop crystallization experiment will approximate a closed system (the closed cell does not exchange matter with the outside), but the crystallization drop itself will be an open system and undergo a change of composition by acquiring water (or other volatile components) and will eventually revert to the defined system equilibrium, given sufficient time or favourable kinetics. A crystallization experiment with a leaky tape (or diffusion of components through plate plastics) will be open to the environment and will eventually dry out and ultimately be in equilibrium with the atmosphere of the crystallization laboratory.
In a crystallization experiment, we are interested in obtaining stable crystals in equilibrium with their mother liquor. The key thermodynamic conditions that we need to understand to appreciate the role of thermodynamics in biomolecular crystallization are therefore (i) phase stability, (ii) phase equilibria and (iii) the response of the system to variation of composition.
To facilitate the derivation of phase diagrams, a minimum of thermodynamic formalism is needed. General physical chemistry textbooks (for example, Atkins & DePaula, 2009 ▶) and specific textbooks on phase thermodynamics (for example, Lupis, 1983 ▶) provide complete introductions and derivations, and Appendix A provides a mini-review limited to the context necessary to formally derive thermodynamic phase diagrams of multi-component systems.
3.2. Introduction to stability, metastability and phase equilibria
The simplest case of an ideal versus a real system (an ideal versus a real gas) allows the introduction of the important concept of conditions for phase stability, as well as instability and metastability.
In the most simple physical situation corresponding to (1), the internal energy U of a fixed amount n of ideal gas at a constant temperature T is simply given by the product of the energy-conjugated pair of variables pressure P and volume V
The intensive variable P is therefore inversely proportional to the extensive variable V (see §A1 for definitions). The pressure–volume phase diagram of an ideal gas at a given temperature is then described according to (1) by a hyperbolic function (inset at the top right in Fig. 4 ▶).
Figure 4.
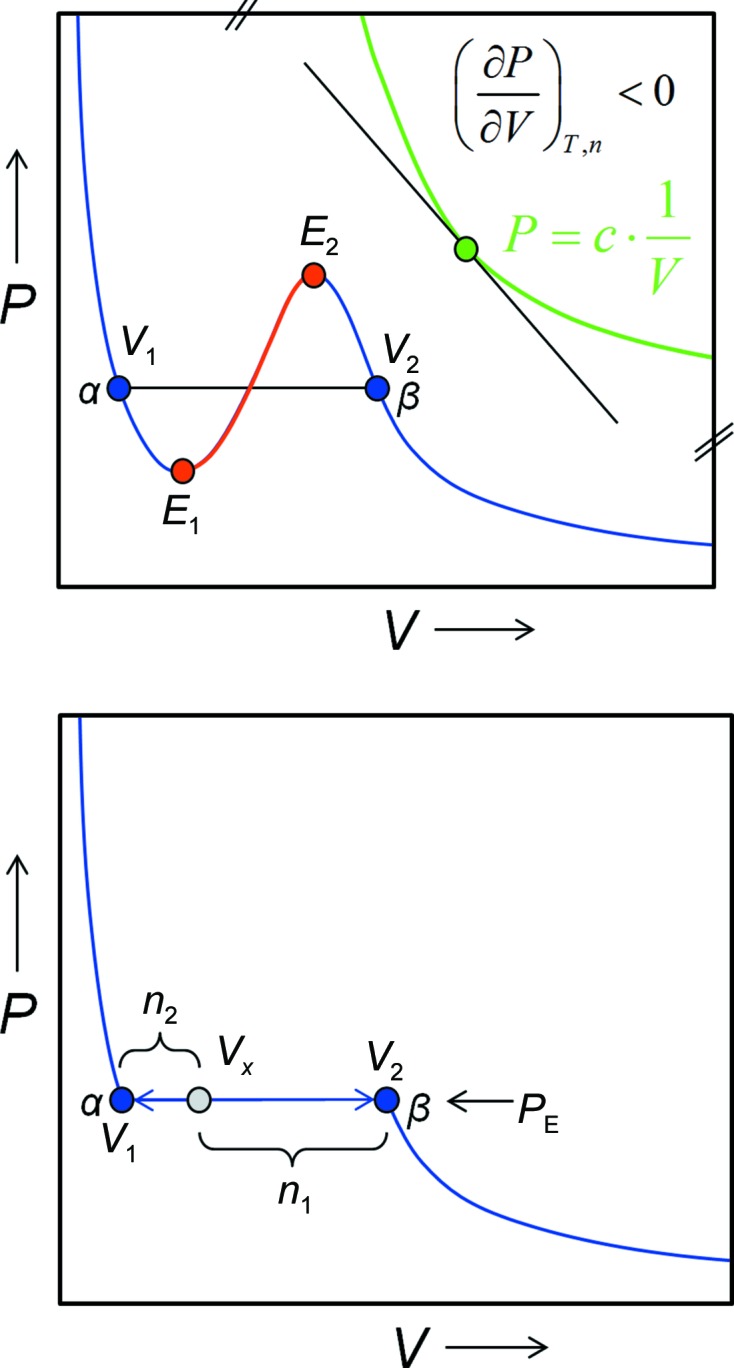
Ideal versus real states and non-ideality induced metastability. Top panel: the top right portion of this P/V phase diagram shows the hyperbolic PV isotherm (green) for an ideal gas. The slope of the graph is always negative, with the first derivative (dP/dV) < 0 being a requirement for physical phase stability. Non-ideality gives rise to the blue PV isotherm for a van der Waals gas. States located on the red branch E 1 E 2 of the isotherm are unstable and will spontaneously decompose into a two-phase mixture (gas α plus liquid β). In a real gas scenario, V 1 represents the boiling point and V 2 the dew point. Metastable supercooled vapour can exist between V 2 and E 2, and superheated liquid between V 1 and E 1, but both metastable phases will eventually (time and/or kinetics permitting) also decompose into a stable two-phase liquid–gas mixture. The bottom panel shows how the ratio of the amounts of the liquid phase and the gas phase coexisting at the equilibrium pressure P E is derived by the lever rule as n 1/n 2.
3.2.1. Conditions for phase stability
As the inset at the top right in Fig. 4 ▶ shows, at any point on the P/V isotherm the tangent has a negative slope, i.e. at constant temperature the pressure in a given amount of ideal gas always and invariably decreases when the volume increases. The opposite effect, namely that the volume of matter increases when the pressure is raised, clearly never happens and is physically impossible. Therefore,
is an invariable thermodynamic condition for (material) phase stability. In the case of crystallization, we will have to extend these conditions and introduce compositional phase stability in multi-component systems (§3.5).
3.2.2. Nonideality
Real atoms have dimensions and interact with each other, and such a simplified van der Waals gas can be described by
where a is an interaction constant increasing the pressure and b a measure for finite particle volume. R is the gas constant.
3.2.3. Virial coefficients and particle interaction
Non-ideality of a system can also be accounted for by an expansion of virial coefficients. It is obvious that some form of attractive interactions between protein molecules is necessary for self-assembly into a crystal, but the intermolecular interaction should not be too strong (leading perhaps to rapid formation of precipitates) and also not too weak (insufficient intermolecular interaction). Such a favourable range of interactions is indeed observed as a ‘crystallization window’ by analysing the second viral coefficient B 2 by means of light scattering (Wilson & DeLucas, 2014 ▶; Wilson, 2003 ▶). However, as a thermodynamic measure, the range of B 2 reflects a necessary thermodynamic condition, but cannot inform us with certainty about the actual outcome of the experiment.
3.2.4. Instability
The graph of a real gas isotherm from (3) is shown in the left part of Fig. 4 ▶. What immediately becomes obvious is that owing to (3) now being third-order in V, the graph has acquired an inflection point flanked by two extrema E 1 and E 2. If we follow the curve, we realise that the function inside the two extrema does violate our condition for phase stability (2): any state between E 1 and E 2 violating the stability criterion (∂P/∂V) < 0 will therefore spontaneously and invariably decompose into equilibrium phases α defined by P E·V 1 (liquid) and β defined by P E·V 2 (gas) in relative amounts determined by the initial composition and the lever rule. This process is called spontaneous decomposition. In the case of the real gas, state V 1 represents the end point of the single-phase liquid state α (almost incompressible, small volume) and state V 2 represents the end point of a single-phase gas β. The same situation of spontaneous formation of two phases is true for unstable protein solutions as derived in §3.4.
3.2.5. Equilibrium conditions
At the equilibrium pressure P E, states between V 1 and V 2 can only be in equilibrium if both phases have the same internal energy U. It follows that the phases must be present in relative amounts following the lever rule corresponding to the location of the initial state on the two-phase coexistence line (Fig. 4 ▶).
3.2.6. Metastability
The most interesting parts of Fig. 4 ▶ are the branches of the blue curve between V 1 and E 1 and E 2 and V 2. They are not yet violating the stability criterion (2) because it still holds that (∂P/∂V)T,n < 0, but at the same time the blue branches do not represent an equilibrium state. Such a system can exist until perturbed, and it is metastable. For macromolecular crystallization, the interesting part is if and how (by which pathway) a system represented by a metastable, supersaturated solution can return to the equilibrium of a stable protein-rich phase coexisting with saturated protein solution. To understand the phase relations, we need to accomplish two important expansions: (i) to make the fundamental equations of state depend on some practically manageable natural variables which we can hold constant while we vary the composition of our system and (ii) to introduce chemical composition into our equations of state.
The fundamental equation of state so faithfully introduced in freshman physical chemistry in energy form as a sum of energy-conjugated products of paired extensive and intensive variables Ei and Ii,
or in its differential form,
is inconvenient for condensed matter: we neither have an ‘entropometer’ in the laboratory nor do we know how to keep the extensive variable S constant with an ‘entropostat’, and most condensed systems (including protein solutions) expand or contract upon temperature change, making it impossible to keep V constant.
3.3. Legendre transformation: dependence on intensive variables
A most useful consequence of the equation of state being a homogeneous function (Appendix A ) is the fact that we can readily transform (4), the fundamental equation in energy form U(S, V), by two successive Legendre transformations (§A3) into the Gibbs (free) energy G(P, T). In differential form,
The Gibbs (free) energy G is extremely useful to describe thermodynamic systems as it depends only on the easily controllable intensive variables T and P. The moment that we can keep T and P constant, which is easily accomplished experimentally, the Gibbs energy of a system solely depends on its composition. This is exactly what we need to know in order to establish a phase diagram, provided that we can we account for the dependence of the Gibbs energy on chemical composition.
3.4. Introduction of the material composition into the equation of state
The introduction of the material composition into the equation of state is, at least formally, quite straightforward. The chemical potential μ (§A2) and the amount n of species i in the system again form an energy-conjugated intensive–extensive product, the chemical energy, again in differential form
This function dG(P, T, ni) is definitely something that we can work with as experimental scientists, because we can easily keep T and P constant (i.e. dP and dT are zero), and then the state of our system depends only on its chemical composition,
3.5. Reaction of a system to compositional change: the chemical potential
Applying the Legendre transformation to the fundamental equations, we derive in §A3 the definition for the chemical potential of component i as its partial molar Gibbs energy,
In practice, mean (average) molar properties of a system are easier to measure than the individual partial molar properties. Changing from the number of species n to the molar fraction,
allows the expression of (8) in terms of the mean molar Gibbs energy 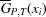 . Applying Legendre’s tangent representation (27) to
. Applying Legendre’s tangent representation (27) to 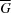 we obtain the relation between the partial molar Gibbs energy (chemical potential) and the mean molar Gibbs energy
we obtain the relation between the partial molar Gibbs energy (chemical potential) and the mean molar Gibbs energy 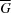 in an N-component system,
in an N-component system,
If we plot for a binary (two-component) system the mean molar Gibbs energy 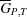 as a function of the molar fraction x
2 (x
1 = 1 − x
2), we would obtain in the ideal case a linear relationship; that is, a line connecting
as a function of the molar fraction x
2 (x
1 = 1 − x
2), we would obtain in the ideal case a linear relationship; that is, a line connecting 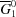 and
and 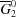 , the mean molar Gibbs energies of the pure components (Fig. 5 ▶).
, the mean molar Gibbs energies of the pure components (Fig. 5 ▶).
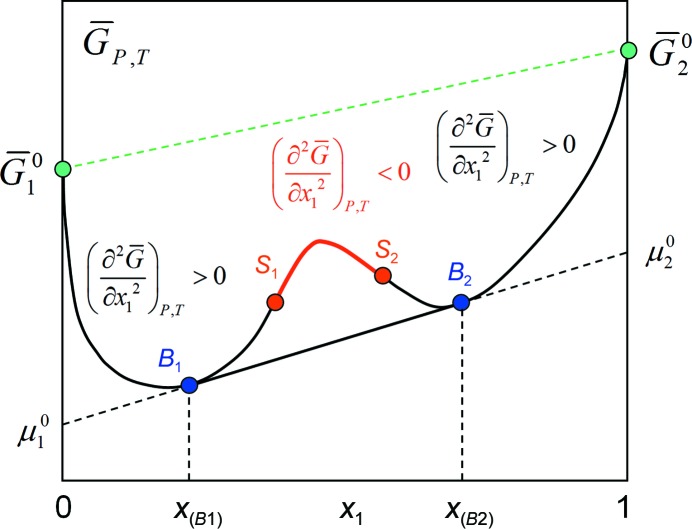
Figure 5.
Partial molar Gibbs energy or chemical potential versus composition: the 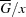 diagram. Deviations from ideality lead to excess partial molar properties, which are the origin of the metastability and instability of multi-component systems. The red branch of the curve violates the stability criterion, and such a state must spontaneously decompose into equilibrium phases α and β in amounts corresponding to the lever rule. The blue branches B
1
S
1 and S
2
B
2 represent metastable states which, given enough time and/or favourable kinetics, will also return to equilibrium with phases α and β in amounts corresponding to the lever rule.
diagram. Deviations from ideality lead to excess partial molar properties, which are the origin of the metastability and instability of multi-component systems. The red branch of the curve violates the stability criterion, and such a state must spontaneously decompose into equilibrium phases α and β in amounts corresponding to the lever rule. The blue branches B
1
S
1 and S
2
B
2 represent metastable states which, given enough time and/or favourable kinetics, will also return to equilibrium with phases α and β in amounts corresponding to the lever rule.
3.5.1. Again: non-ideality
In real systems, non-ideality does lead to so-called excess partial molar properties. For example, negative excess partial volumes mean that a volume contraction of the system occurs during mixing, as is in fact observed and measureable, for example, in water–ethanol mixtures. Similar deviations from the ideal linear model owing to the interaction of system components occur for the chemical potential μ and we can define the chemical excess potential Δμex as
where μi 0 is the chemical potential of pure component i. Although only in rare cases is the excess chemical potential in fact measureable, it will interesting to see how the presence of these excess properties leads to the much sought-after x/x crystallization diagrams (§3.5).
3.5.2. Again: equilibrium
Let us now examine the simple case of a non-ideal, two-component system. Equilibrium conditions demand that the chemical potential of each component i of each phase is the same. For two phases α and β in equilibrium,
Using the relation (11) between mean molar and partial molar Gibbs energy and the equilibrium condition (13), we obtain for a two-component system
which means (i) that two phases in equilibrium have to have the same slope in the 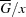 diagram and (ii) that the intercept is the chemical potential of the component i in phase α and β, respectively, as illustrated in Fig. 5 ▶.
diagram and (ii) that the intercept is the chemical potential of the component i in phase α and β, respectively, as illustrated in Fig. 5 ▶.
3.5.3. Again: metastability
Legendre transformation of the general stability conditions from internal energy U to Gibbs energy G yields
which simply states that the second derivative or the curvature of 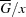 , that is the change of the first derivative, always has to be positive. Inspecting the
, that is the change of the first derivative, always has to be positive. Inspecting the 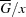 diagram in Fig. 5 ▶, we recall the same scenario as in the P/V isotherm (Fig. 4 ▶): we can recognize metastable states between B
1 and S
1 and between S
2 and B
2 because they comply only with the stability condition (15) and not with the equilibrium condition (14). States between S
1 and S
2 again are absolutely unstable and spontaneous spinodal decomposition must occur into a phase rich in component 1 (α) and one with less of component 1 (β). Note that this scenario is valid for all kinds of phases: at no point have we made any assumption about the nature of the phases formed.
diagram in Fig. 5 ▶, we recall the same scenario as in the P/V isotherm (Fig. 4 ▶): we can recognize metastable states between B
1 and S
1 and between S
2 and B
2 because they comply only with the stability condition (15) and not with the equilibrium condition (14). States between S
1 and S
2 again are absolutely unstable and spontaneous spinodal decomposition must occur into a phase rich in component 1 (α) and one with less of component 1 (β). Note that this scenario is valid for all kinds of phases: at no point have we made any assumption about the nature of the phases formed.
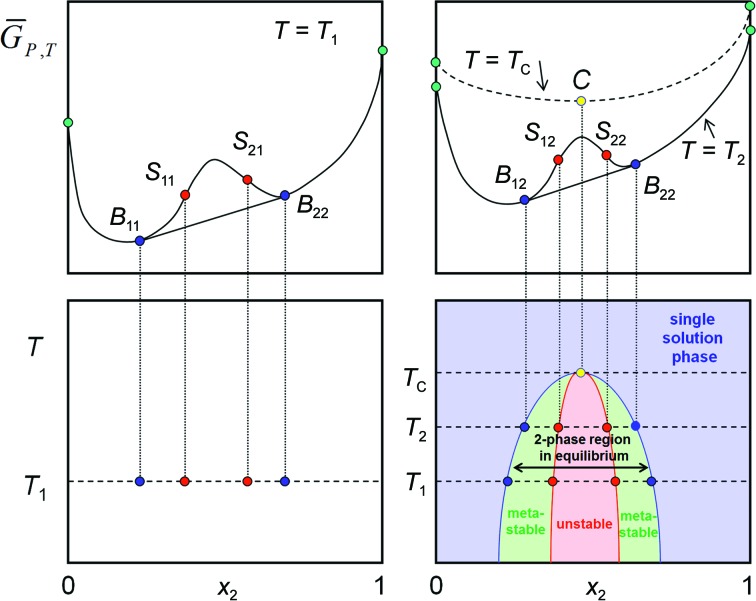
3.6. The next step: constructing the T/x diagrams
Fig. 5 ▶ contains a single 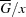 isotherm, but we can (at least on paper) determine further isotherms at different temperatures. Our simple example system depicted in Fig. 5 ▶ shows a miscibility gap in a two-component system at a given temperature T
1 below the critical temperature. With increasing temperature, the mutual solubility of the components increases while the system approaches a more ideal state, until at the critical isotherm the system remains single phase over the entire composition range. We can project the binodal equilibrium points and the spinodal decomposition points of each
isotherm, but we can (at least on paper) determine further isotherms at different temperatures. Our simple example system depicted in Fig. 5 ▶ shows a miscibility gap in a two-component system at a given temperature T
1 below the critical temperature. With increasing temperature, the mutual solubility of the components increases while the system approaches a more ideal state, until at the critical isotherm the system remains single phase over the entire composition range. We can project the binodal equilibrium points and the spinodal decomposition points of each 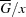 isotherm onto the corresponding temperature levels and obtain the complete T/x phase diagram, in which metastable and unstable regions are easily recognized (Fig. 6 ▶).
isotherm onto the corresponding temperature levels and obtain the complete T/x phase diagram, in which metastable and unstable regions are easily recognized (Fig. 6 ▶).
Figure 6.
Constructing the T/x diagram. The complete T/x diagram of a simple two-component system with a miscibility gap is obtained by projecting binodal equilibrium points and the spinodal decomposition points from each 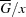 isotherm onto corresponding isotherms of a temperature–composition (T/x) diagram. The blue solubility line delineates the phase boundary of the single solution phase region. The left boundary phases are rich in component 2 and the right boundary phases are rich in component 1. In thermodynamic equilibrium, the region between the solubility lines is a two-phase mixture of the two boundary phases in ratios according to the lever rule. A metastable phase region exists between the binodal coexistence line (or solubility line; blue) and the spinodal decomposition line (red). In the red instability region, instantaneous spinodal decomposition into the corresponding boundary phases must take place.
isotherm onto corresponding isotherms of a temperature–composition (T/x) diagram. The blue solubility line delineates the phase boundary of the single solution phase region. The left boundary phases are rich in component 2 and the right boundary phases are rich in component 1. In thermodynamic equilibrium, the region between the solubility lines is a two-phase mixture of the two boundary phases in ratios according to the lever rule. A metastable phase region exists between the binodal coexistence line (or solubility line; blue) and the spinodal decomposition line (red). In the red instability region, instantaneous spinodal decomposition into the corresponding boundary phases must take place.
In the final step, we need to transfer the information contained in the T/x diagram into our desired crystallization phase diagrams.
3.7. From T/x to isothermal sections: pseudo-ternary composition diagrams
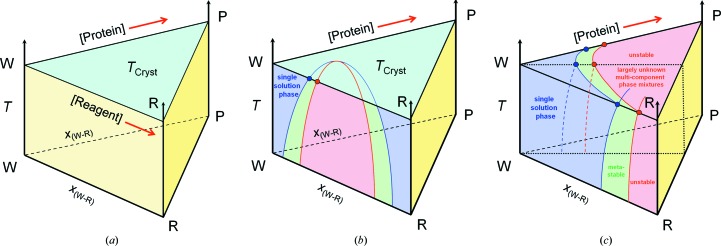
The systems that we have treated so far are general two-component systems. As outlined in §2.2, a crystallization diagram describes a system with at least three components: water W, protein P and a reagent pseudo-component R that includes everything else from buffer via precipitants to additives etc. The system we are dealing with is therefore actually pseudo-ternary, and phase relations can be presented in a ternary phase body with axes T, W, P and R. An isothermal section then is a phase triangle, with the pure components W, P and R located at the three corners. The sum or ‘stack’ of all isothermal sections forms the ternary body shown in Fig. 7 ▶(a).
Figure 7.
The ternary phase body T/(W, R, P). (a) The horizontal isothermal sections through the ternary body are the basis for the pseudo-ternary phase diagrams that we are actually interested in. (b) The ‘walls’ of the ternary body are simply the corresponding T/x diagrams that we have already constructed in §3.5 from the set of 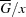 diagrams. (c) Given a set of corresponding pseudo-binary T/x sections and focusing on the water-rich region, the interesting part of the complete isothermal section can be constructed. In general, not much is known experimentally and with certainty past the solubility lines in the case of protein solutions. Areas in the right-hand region of the isothermal section are unknown and of limited practical interest.
diagrams. (c) Given a set of corresponding pseudo-binary T/x sections and focusing on the water-rich region, the interesting part of the complete isothermal section can be constructed. In general, not much is known experimentally and with certainty past the solubility lines in the case of protein solutions. Areas in the right-hand region of the isothermal section are unknown and of limited practical interest.
3.7.1. Constructing the crystallization phase diagram
We realise that the ‘walls’ of the ternary body are actually (pseudo-) binary T/x diagrams. If we project our simple binary mixture T/x diagram constructed in Fig. 6 ▶ onto the corresponding wall of the ternary body, we obtain a solubility point and an instability point on the selected isothermal section (Fig. 7 ▶ b). Focusing now on the water-rich corner and only the water-rich sections of a set of appropriate pseudo-binary T/x diagrams, we can construct the entire water-rich part of the isothermal section W, P, R (Fig. 7 ▶ c). Such a scenario is not unrealistic, because in general and at best we can determine solubility lines for the protein in this region, but the rest of the phase relations are neither easily accessible by experiment nor crucial in our situation of crystallization from an aqueous, water-rich, solution. For example, the line R–P would correspond to a mixture of solid protein with solid precipitate, representing at best the extreme but otherwise uninformative case of a completely dried-out crystallization drop as the end point in a failed vapour-diffusion experiment open to the laboratory environment.
3.8. From ternary section to rectangular phase diagram
In practice, we are not interested in the regions of almost pure solid protein nor are we interested in any water-poor/solid reagent mixtures. Our focus of interest lies in the water-rich corner of the isothermal pseudo-ternary sections. One therefore zooms in to a ‘orthogonalized’ rectangular presentation (often preferred in chemical engineering when one component, such as the water in our case, is in excess) of this partial water-rich close-up area of the isothermal section to obtain our phase diagram as previously sketched in Fig. 3 ▶ and now filled with the information that we could derive from thermodynamic first principles. The path to the final crystallization phase diagram is visualized in Fig. 8 ▶.
Figure 8.
Final gestation of the crystallization phase diagram. The crystallization phase diagram can be directly derived as the water-rich corner of a pseudo-ternary isothermal section of a ternary phase body. The lack of knowledge and detail of the water-poor regions is indicated by the question mark in the phase triangle. The gradient fill of the metastable solution indicates its increasing degree of supersaturation.
3.8.1. Solubility line
The most likely experimentally accessible feature in the phase diagram is the solubility line, which determines the maximum equilibrium protein concentration [P]max at any given reagent concentration [R]. Such lines have been determined for lysozyme, catalase and other model systems; for reviews, see, for example, McPherson, (1982 ▶), Ducruix & Giegé (1999 ▶) and Asherie (2004 ▶). The solubility line derived for the diagram in Fig. 8 ▶ is in fact qualitatively presenting the solubility line for a protein in a polyethylene glycol (PEG) solution. The solubility S of a protein in PEG generally follows a logarithmic law (see figures in McPherson, 1982 ▶; Rupp, 2009 ▶),
and when plotted linearly the logarithmic curve approximates the solubility line drawn in Fig. 8 ▶. The situation is considerably more complex for salt solutions, where salting-in effects can occur and the solubility lines can exhibit a maximum. Fig. 3-14 in Rupp (2009 ▶) illustrate such a scenario, although with the caveats discussed in §5 and a somewhat improbable spinodal decomposition line.
3.9. The location of the protein crystal phase fields
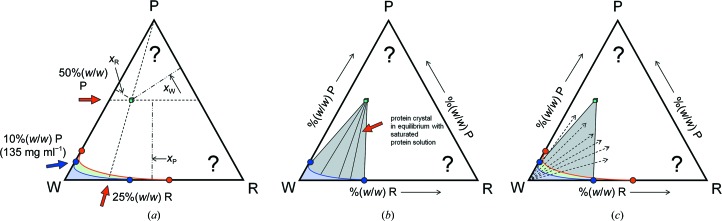
Given that we have now established the pseudo-ternary isothermal section as our area of operation, we can ask where the phase fields of protein crystals would be located. Let us assume that we are dealing with a typical average crystal of 50% solvent content and that the mother liquor that it grew from contained 25% PEG. Given that the protein specific density is about 1.35 g cm−3 or 1350 mg ml−1 (Quillin & Matthews, 2000 ▶), the protein concentration in this crystal would be around 600–700 mg ml−1. This is very, very far from the solubility limit for normal proteins, which is in the range from a few to several tens of milligrams per millilitre1. We realise that such phase fields must lie very far away towards the distant protein-rich corner in the ternary phase diagram in Fig. 9 ▶.
Figure 9.
Location of crystal phase fields. (a) Assuming a crystal with 50% solvent content at 25% PEG, the crystal contains 50% protein, 12.5% PEG and 37.5% water. The phase point can be located in the phase diagram as follows. All concentrations with a fixed absolute amount of a component P are on lines parallel to the opposite side (WR). Lines indicating a fixed ratio of W:R lead towards the remaining component (P). The intersection of these two lines is the sought-after phase point (or field, if any homogeneity range exists) of the crystal. The sum of the three fractions xi is constrained to one. (b) In equilibrium, i.e. the end point of the crystallization experiment, the crystal will coexist in equilibrium with saturated protein solution with concentration [W, P, R] as defined by the corresponding coexistence line originating from the solubility line. (c) In this panel, the equilibrium information is combined with the existence region of the metastable supersaturated phase (green). If only a single component such as water is removed in a vapour-diffusion experiment, the initial ratio of P:R remains constant and therefore the path which the experiment takes leads away from the water corner. The arrows indicate only the direction of the pathways in a vapour-diffusion experiment (described in detail in Fig. 10 ▶). Note that the actual experimental path must invariably end at the red spinodal decomposition line. Outside of the grey two-phase field indicating saturated solution–protein crystal equilibria, spontaneously formed mixtures of the corresponding boundary phases exist. We can see that the actual experimental workspace will be very compressed towards the water corner; note the unusually protein high solubility in this particular example.
Nonetheless, if the situation was as clear-cut and simple as depicted in Fig. 9 ▶ and kinetics did not matter, we would always succeed in obtaining a crystal once we had the right chemical composition of our system and a stable crystal and its phase field exist. We also do not have to precisely hit the crystal phase field starting from the water corner in a vapour-diffusion experiment; if this were the case, the drop-ratio variation would be an incredibly dominant factor in each crystallization trial, and we would have to ‘experimentally extrapolate’ from a very small accessible area far off in the water corner to a tiny phase field with very little homogeneity, and this phase field is hidden deep in the protein-rich, unknown part of the phase diagram. Such an ‘experimental extrapolation’ would be almost certain to fail. Drop-ratio variation is certainly a useful parameter for optimization (McPherson & Cudney, 2014 ▶), but many protein crystals, regardless of their actual solvent content, grow fine from 1:1 protein:precipitant drops.
Tie lines (lines of coexistence) between protein solution and crystal extend in principle from each point on the solubility line to the crystal (Fig. 9 ▶ b). This is a necessity because during crystal formation the solution slowly depletes in protein [recall that we form a protein-rich phase (600–700 mg ml−1) out of a very dilute protein solution of a few milligrams per millilitre] and the composition of the solution returning to equilibrium changes accordingly. §4 discusses a simple example of a vapour-diffusion experiment in greater detail.
Nonetheless, because the path (coexistence lines) towards the crystal changes during protein depletion, any unknown phase that lies in between the current solution and the crystal phase field may intercept an emerging coexistence line. All of a sudden, despite promising initial crystals, we may obtain only precipitate. The reverse can also be true, and while we initially find only precipitate, crystals may form later. If the crystal is more stable than the precipitate, it may grow in size while the other protein-rich precipitate phase disappears. Note that this is simply a matter of phase stability, and is not the same as Ostwald ripening (Ostwald, 1897 ▶; small crystals disappearing with the gain of larger crystals of the same sort growing larger), which requires the introduction of surface energy into our state equations as a kinetic phenomenon, and the presence of diffusion for it to take place. The introduction of plausible kinetic scenarios as far as they are necessary for the utilization of the phase diagram as a conceptual tool is discussed in the following section.
4. A basic vapour-diffusion experiment process visualized in a crystallization phase diagram
4.1. Some knowns…
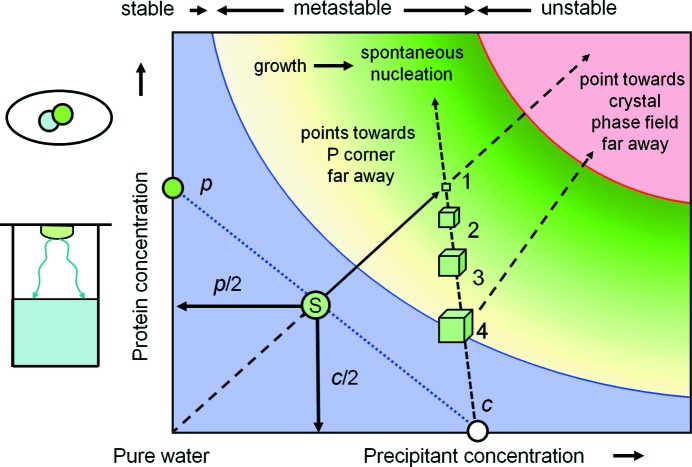
Fig. 10 ▶ shows a typical instance of an operational crystallization phase diagram. It is intended to describe a hanging-drop vapour-diffusion crystallization experiment. Firstly, let us examine what we do know from thermodynamics: (i) given a protein:precipitant drop ratio of 1:1 the starting point S of the experiment is clearly defined, and (ii) when solely water is removed from the drop by vapour diffusion into the reservoir, the solution will proceed from S away from the water corner. We also know the end result: (iii) given a practically infinite-size reservoir, the precipitant concentration in the drop in equilibrium will be c. We also know that (iv) a metastable zone will exist and that (v) with increasing supersaturation the probability for spontaneous nucleation increases. This is just another way to express increasing thermodynamic instability.
Figure 10.
The classical case of vapour diffusion. The diagram represents the simplest possible scenario of a vapour-diffusion experiment. A detailed discussion of the figure is provided in §4.
While we do not know how and when nucleation occurs, the level of supersaturation clearly can never exceed the experimental limit defined by the reservoir precipitant concentration c. Once nucleation occurs, the solution will deplete in protein while the crystal grows. This depletion happens along the tie line towards the protein corner, because predominantly P disappears from the solution. This line is almost (but only almost) a vertical line in the rectangular diagram, as we are looking just at the very water-rich corner of the ‘orthogonalized’ phase triangle. At the end of the process, the crystal, whose phase field actually is far off the diagram, is in equilibrium with saturated solution at the intersection of the tie line from c to P and the solubility line (point 4). That we draw the large crystals there is simply an aid to visualization (it looks like that in the drop); it is not their true location in the thermodynamic phase diagram. The phase field for a crystal is far remote, as Fig. 9 ▶ illustrates.
4.2. …and many unknowns
It goes without saying that the described scenario is oversimplified, and nucleation can occur at different levels of supersaturation, multiple protein-rich phase fields can and will exist, and the pathways can be considerably more complex than the minimalistic situation depicted here. For example, a transiently forming phase can itself be metastable, or during the development of the system towards equilibrium another protein-rich phase or crystal may become more stable. There is nothing that this diagram can tell us about the actual time line of the development of the system. Very important information affecting the experimental outcome, such as the dynamics and the formation of pre-nucleation assemblies as demonstrated by time-dependent DLS experiments (Meyer et al., 2012 ▶), are absent in such a phase diagram.
5. Summary: the use and limitations of crystallization phase diagrams
The exact thermodynamic derivation of the isothermal W–P–R phase diagram section allows a few fundamental principles to be stated that apply irrespective of the details and the degree of knowledge about a specific system. One needs to keep in mind that the derivation presented here introduced only the absolute minimum complexity necessary for a multi-component system to exhibit distinct phase separation. The reality of a macromolecular crystallization experiment is almost always significantly more complex. Unfortunately, very little is known a priori and with certainty in our complex real systems.
(i) The almost trivial first statement is that the system obviously must be non-ideal. Non-ideality is the basis for excess partial molar properties, and in multi-component systems of sufficient non-ideality the phenomena of metastability, supersaturation and compositional instability will occur. The exact location of these regions can in principle be experimentally determined; however, in the case of macromolecular crystallization only few model systems have been examined in such detail.
(ii) The most likely experimental accessible feature in the phase diagram is the solubility line, which determines the maximum equilibrium protein concentration [P]max at any given reagent concentration [R]. The commonly plotted curved solubility line approximates a logarithmic law as is typical for PEGs. The situation is considerably more complex for salt solutions, where salting-in effects occur and the solubility lines exhibit a maximum.
(iii) When solutions exceed the respective solubility limit, the system may remain single phase, but is now supersaturated and metastable. With increasing supersaturation, the probability of spontaneous nucleation in the system increases, upon which it will return to equilibrium. The nucleation is probability a kinetic property, and amongst other parameters depends on the degree of supersaturation (García-Ruiz, 2003 ▶).
(iv) At a certain point the supersaturation approaches the spinodal decomposition line, whereupon the system spontaneously separates into a protein-rich phase and saturated protein solution. As at this level of supersaturation, the process must happen instantaneously; the formation of ordered material such as crystals is almost impossible. For some model proteins such as lysozyme, extreme and atypical supersaturation of several 100 mg ml−1 have been established, but in general the supersaturation limit for protein solutions is significantly lower.
(v) The ‘thermodynamically legal’ playground in this type of diagram is the metastable state between the solubility line and the decomposition line. The position of the latter is in general unknown, but it can be expected that in typical cases it is not too far from the solubility line, which should be considered when drawing such lines. Thermodynamically, there is no justification to subdivide the metastable region into a ‘metastable’ and a ‘labile’ zone by drawing any hard lines. While the intention is (presumably) to indicate increasing probability of nucleation and thus of phase separation as a result of increasing instability, there is no thermodynamic justification for a dividing line suggestive of distinctly different phases. The term ‘more metastable’ may intuitively express this fact but is not part of the thermodynamic vocabulary. The system simply becomes more supersaturated and more unstable. Even the dashed lines drawn for example in the diagrams in Rupp (2009 ▶) should be avoided in favour of a gradient fill (Figs. 8 ▶ and 10 ▶) or a similar continuous transition.
(vi) Crystals must be located in stable phase fields in equilibrium with the solubility line. A priori, it is in general unknown (1) whether such phase fields exist in a given chemical system and (2) where (at what ratio of W, P and R) these phase fields are located in the case that they do exist. We are trying to screen for (1) by varying the chemical composition of [R] and within a given compositional system (2) for variation of parameters affecting the kinetic behaviour or the pathway through the diagram.
(vii) Thermodynamics notwithstanding, the equilibrium states that we desire cannot be reached if the kinetics are unfavourable. The degree of supersaturation is one of the few thermodynamic parameters that can be clearly linked to higher nucleation probability (García-Ruiz, 2003 ▶). Microseeding (Bergfors, 2003 ▶; D’Arcy et al., 2007 ▶, 2014 ▶), for example, exploits the effect that more sparse nucleation can be induced at lower supersaturation, where slower growth may lead to fewer and better crystals. The role of kinetics and the underlying dynamic microscopic phenomena and transient phases (Meyer et al., 2012 ▶) in determining the path and the practical outcome of a crystallization experiment can hardly be overemphasized.
(viii) Temperature changes bring us into a different isothermal section. A small temperature change may or may not vary the phase equilibria dramatically. Solubility may either decrease or increase with temperature changes. In contrast, owing to their dependency on kT, kinetic effects generally slow down at lower temperature.
6. Conclusions
Crystallization phase diagrams are a valuable aid for visualizing the possible phase relations and pathways through the crystallization maze. Their origin in the thermodynamics of non-ideal multi-component systems with miscibility gaps establishes limits as to which features can be drawn in such diagrams that are fundamentally correct (but not necessarily known) and where, in the spirit of parsimony, creativity should be restrained. To quote Confucius from his Analects, ca. 500 BC:
When you know a thing, to hold that you know it; and when you do not know a thing, to allow that you do not know it – this is knowledge.
Acknowledgments
BR acknowledges financial support from k.-k. Hofkristallamt, Vista, California, USA and the European Union under a FP7 Marie Curie People Action grant PIIF-GA-2011-300025 (SAXCESS). Martin Caffrey, Trinity College, Dublin, Ireland, contributed helpful comments and the phase diagram in Fig. 2.
Appendix A. Mini-review of thermodynamics
A1. Fundamental equations
A1.1. Fundamental equation
In its most general form, a thermodynamic state Φ of a macroscopic system is defined by the sum of products of energy-conjugated pairs of intensive variables I and extensive variables E,
Extensive variables depend on the amount of matter involved (for example, volume V, entropy S and amount of species ni), while intensive variables such as pressure P, temperature T or chemical potential μi do not change as a function of the amount of material involved. From an experimental point of view, thermodynamic functions that depend on easy-to-control intensive variables are the most useful.
The reaction of the system to change is described by the perfect (complete) differential of (17) as a differential fundamental equation
A1.2. Homogeneity of the fundamental equation
An important property of the thermodynamic fundamental equations is that they are scale-invariant homogeneous functions of degree k = 1, i.e.
for which Euler’s homogenous function theorem holds that
The homogeneity condition (19) is necessary for the application of Legendre transforms in §3.3, and relation (20) is used in §3.5 when we establish the chemical potential as the property determining the phase relations in a multi-component system.
A2. The chemical potential
The chemical potential μ and the amount n of species i in the system again form an energy-conjugated intensive–extensive product: the chemical energy (the definition of μ is formally derived via equations 25 and 26).
It follows from (17) that
or in differential form,
As used in §3.5, the deviations from the simple, ideal linear relationship between the chemical potential and the number of particles are fundamental for phase formation in non-ideal systems. The question is how to make (21) and (22) useful to derive crystallization phase diagrams.
A2.1. Definition of the chemical potential
The fact that the fundamental equation of state in energy form U is homogeneous leads via (20) to the relation
Therefore, for the variables S, V and ni in a multi-component system,
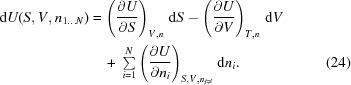 |
Comparing the last term in (24) with that in (22), we can establish a relation between the chemical potential and the compositional change in the system,
from which the definition of the chemical potential follows:
Unfortunately, this is not yet a practically useful relation. What is needed is a thermodynamic equation of state that does not depend on hard-to-control extensive variables.
A3. Legendre transformation
A most useful consequence of the equation of state being a homogeneous function is the fact that we can apply a Legendre transformation Λ. In principle, Λ replaces a given function Φ with the envelope of its tangents:
Formally, Λ is a bijective transformation which allows us to substitute one of the less useful extensive variables by its – from an experimental point of view more useful – conjugated intensive variable without loss of information:
We wish to eliminate the impractical entropy first, and transform
This first Legendre transform is the Helmholtz energy A. It is useful in statistical thermodynamics of gases, but not for our purpose, as it still depends on the extensive and, in condensed matter, hard-to-control extensive variable V.
A3.1. The second Legendre transformation of U(S, V, n) leads to the Gibbs energy G(P, T, n)
The second Legendre transformation of the fundamental equation in energy form U(S, V, n) is extremely useful as it yields the Gibbs (free) energy G(P, T, n), which depends only on the easily controllable intensive variables T and P and the chemical composition defined by n. The moment that one can keep T and P constant, which is easily accomplished, the Gibbs energy of the system solely depends on its composition, which is exactly what we need to obtain a phase diagram:
A handy tool to remember the Legendre transforms of the thermodynamic fundamental equations and its partial derivatives and Maxwell relations is the SUV–VAT diagram or the thermodynamic (Gibbs) square (Fig. 11 ▶).
Figure 11.
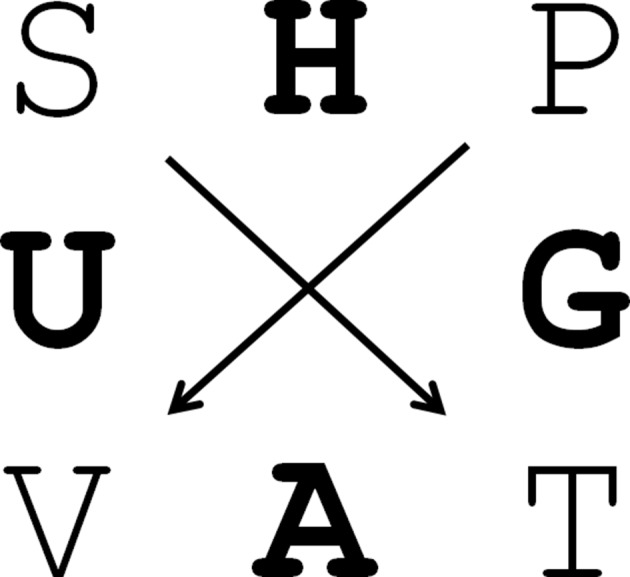
The thermodynamic square: one of the most useful mnemonics in thermodynamics. In the centre of each side is the thermodynamic function, indicated in bold, flanked by its variables. Starting from U, A and H are the first Legendre transforms in T and P, respectively, and G is the second transform in both P and in T. The derivatives of the functions are obtained by following the arrows. An opposite direction indicates a negative sign.
We can directly read from the Gibbs square that G is a function of (T, P) and, for example, that (∂G/∂T)P = −S or (dG)P = −SdT. Reading the diagram, we can therefore immediately write down the entire equation of state for G,
dG(P, T, ni) is definitely something that we can work with as experimental scientists, because we can easily keep T and P constant, and the state of our system then depends only on its composition. Under transformation, the definition of the chemical potential as function of G then becomes, in analogy to (26),
which is the partial molar Gibbs energy of component i. The transformation from partial to mean molar properties via the Legendre tangent representation (27) is provided in the main section §3.5. When drawing 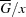 diagrams, note that
diagrams, note that 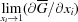 = ∞.
= ∞.
Footnotes
The hardy perennial of physicochemical investigations, lysozyme, is actually not a good model for such contemplations because it can be supersaturated to extreme levels of several hundred milligrams per millilitre, almost corresponding to the concentration of the protein in its crystals.
References
- Aherne, M., Lyons, J. A. & Caffrey, M. (2012). A fast, simple and robust protocol for growing crystals in the lipidic cubic phase. J. Appl. Cryst. 45, 1330–1333. [DOI] [PMC free article] [PubMed]
- Asherie, N. (2004). Protein crystallization and phase diagrams. Methods, 34, 266–272. [DOI] [PubMed]
- Atkins, P. & DePaula, J. (2009). Physical Chemistry, 9th ed. New York: W. H. Freeman & Co.
- Bergfors, T. (2003). Seeds to crystals. J. Struct. Biol. 142, 66–76. [DOI] [PubMed]
- Caffrey, M. (2015). A comprehensive review of the lipid cubic phase or in meso method for crystallizing membrane and soluble proteins and complexes. Acta Cryst. F71, 3–18. [DOI] [PMC free article] [PubMed]
- Caffrey, M. & Cherezov, V. (2009). Crystallizing membrane proteins using lipidic mesophases. Nature Protoc. 4, 706–731. [DOI] [PMC free article] [PubMed]
- D’Arcy, A., Bergfors, T., Cowan-Jacob, S. W. & Marsh, M. (2014). Microseed matrix screening for optimization in protein crystallization: what have we learned? Acta Cryst. F70, 1117–1126. [DOI] [PMC free article] [PubMed]
- D’Arcy, A., Villard, F. & Marsh, M. (2007). An automated microseed matrix-screening method for protein crystallization. Acta Cryst. D63, 550–554. [DOI] [PubMed]
- DeLucas, L. J. et al. (1989). Protein crystal growth in microgravity. Science, 246, 651–654. [DOI] [PubMed]
- Ducruix, A. & Giegé, R. (1999). Crystallization of Nucleic Acids and Proteins. Oxford University Press.
- García-Ruiz, J. M. (2003). Nucleation of protein crystals. J. Struct. Biol. 142, 22–31. [DOI] [PubMed]
- Koszelak, S., Day, J., Leja, C., Cudney, R. & McPherson, A. (1995). Protein and virus crystal growth on International Microgravity Laboratory-2. Biophys. J. 69, 13–19. [DOI] [PMC free article] [PubMed]
- Lupis, C. H. P. (1983). Chemical Thermodynamics of Materials. New York: Elsevier.
- McPherson, A. (1982). Preparation and Analysis of Protein Crystals. New York: Wiley.
- McPherson, A. (1999). Crystallization of Biological Macromolecules. New York: Cold Spring Harbor Laboratory Press.
- McPherson, A. & Cudney, B. (2014). Optimization of crystallization conditions for biological macromolecules. Acta Cryst. F70, 1445–1467. [DOI] [PMC free article] [PubMed]
- McPherson, A. & Kuznetsov, Y. G. (2014). Mechanisms, kinetics, impurities and defects: consequences in macromolecular crystallization. Acta Cryst. F70, 384–403. [DOI] [PMC free article] [PubMed]
- Meyer, A., Dierks, K., Hilterhaus, D., Klupsch, T., Mühlig, P., Kleesiek, J., Schöpflin, R., Einspahr, H., Hilgenfeld, R. & Betzel, C. (2012). Single-drop optimization of protein crystallization. Acta Cryst. F68, 994–998. [DOI] [PMC free article] [PubMed]
- Ostwald, W. (1897). Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 22, 289–330.
- Qiu, H. & Caffrey, M. (2000). The phase diagram of the monoolein/water system: metastability and equilibrium aspects. Biomaterials, 21, 223–234. [DOI] [PubMed]
- Quillin, M. L. & Matthews, B. W. (2000). Accurate calculation of the density of proteins. Acta Cryst. D56, 791–794. [DOI] [PubMed]
- Rupp, B. (2009). Biomolecular Crystallography: Principles, Practice, and Application to Structural Biology, 1st ed. New York: Garland Science.
- Wilson, W. W. (2003). Light scattering as a diagnostic for protein crystal growth – a practical approach. J. Struct. Biol. 142, 56–65. [DOI] [PubMed]
- Wilson, W. W. & DeLucas, L. J. (2014). Applications of the second virial coefficient: protein crystallization and solubility. Acta Cryst. F70, 543–554. [DOI] [PMC free article] [PubMed]