Abstract
The magnetohydrodynamic (MHD) stagnation point flow of a nanofluid over a permeable stretching/shrinking sheet is studied. Numerical results are obtained using boundary value problem solver bvp4c in MATLAB for several values of parameters. The numerical results show that dual solutions exist for the shrinking case, while for the stretching case, the solution is unique. A stability analysis is performed to determine the stability of the dual solutions. For the stable solution, the skin friction is higher in the presence of magnetic field and increases when the suction effect is increased. It is also found that increasing the Brownian motion parameter and the thermophoresis parameter reduces the heat transfer rate at the surface.
Introduction
Nanofluid refers to dispersion of nanoparticles in the base fluid. The inclusion of nanoparticles enhances thermal conductivity as reported by Masuda et al. [1]. Choi and Eastman [2] discovered that the addition of less than 1% of nanoparticles doubles the heat conductivity of the base fluid. We mention to this end that the paper by Wong and Leon [3] includes automotive, electronics, biomedical and heat transfer applications besides other applications such as nanofluid detergent. Saidur et al. [4] presented some applications of nanofluids in industrial, commercial, residential and transportation sectors based on available literatures. The capability of nanofluids to enhance thermal conductivity has attracted the interest of fluid dynamics community to conduct further studies.
Two models have been constantly used by researchers to study the behaviour of nanofluids, namely the Tiwari-Das model [5] and Buongiorno model [6]. While Tiwari-Das model highlights the volumetric fraction of nanoparticles which is used by Ul Haq et al. [7], Nadeem et al. [8] and Sheikholeslami et al. [9], Buongiorno model focuses on Brownian motion and thermophoresis effects. Many researchers then include the effect of Brownian motion and thermophoresis in their studies such as Nield and Kuznetsov [10], Kuznetsov and Nield [11–13], Khan and Pop [14], Bachok et al. [15, 16], Khan and Aziz [17], Ul Haq et al. [18], Haq et al. [19], Nadeem and Ul Haq [20, 21] and Nadeem et al. [22] among others. Sheikholeslami et al. [23, 24], Akbar et al. [25, 26] and Ellahi [27] study the flow of nanofluid with magnetic effects where different methods are used to solve the problems. Furthermore, Akbar et al. [28] also study the blood flow of a nanofluid by using homotopy perturbation method. Boundary layer flow of a nanofluid moving through several mediums such as cylinders, rectangular ducts and rotating plates are discussed by Zeeshan et al. [29] Ellahi et al. [30], Nadeem et al. [31] and Sheikholeslami et al. [32]. Notably, Ellahi et al. [33] produces series solutions of a non-Newtonian nanofluid where Reynold’s and Vogel’s model are used to represent variable viscosity.
The boundary layer flow over a stretching sheet is significant in applications such as extrusion, wire drawing, metal spinning, hot rolling etc. [34]. Wang [35, 36], Mandal and Mukhopadhyay [37], Gupta and Gupta [38], Andersson [39], Ishak et al. [40] and Makinde and Aziz [41] are among various names whose papers on stretching sheet are published. However, to complement the study of stretching sheet, Miklavčič and Wang [42] then begin the study of flow over a shrinking sheet in which they observed that the vorticity is not confined within a boundary layer and a steady flow cannot exist without exerting adequate suction at the boundary. However, according to Wang [43], a stagnation flow may also be considered so that the velocity of the shrinking sheet is confined in the boundary layer. As the studies of shrinking sheet garner considerable attention, these findings prove to be crucial to these researches. Numerous studies on these problems have been conducted by researchers such as Fang et al. [44], Bachok et al. [45], Bhattacharyya et al. [46], Lok et al. [47, 48], Zaimi et al. [49] and Roşca and Pop [50] among others.
Motivated by the above-mentioned researches, this paper aims at studying the magnetohydrodynamic (MHD) stagnation point flow of a nanofluid over a stretching/shrinking sheet with suction effect at the boundary which is the extension of a paper done by Ibrahim et al. [51]. MHD is the study of the dynamics of electrically conducting fluids such as plasmas, liquid metals and electrolytes The dependency of the skin friction coefficient and the local Nusselt number on five parameters, namely the stretching/shrinking, magnetic, velocity ratio, Brownian motion and thermophoresis parameters is the main focus of the present investigation. Numerical solutions are presented graphically and in tabular forms to show the effects of these parameters on the skin friction coefficient and the local Nusselt number. number.
Mathematical Formulation
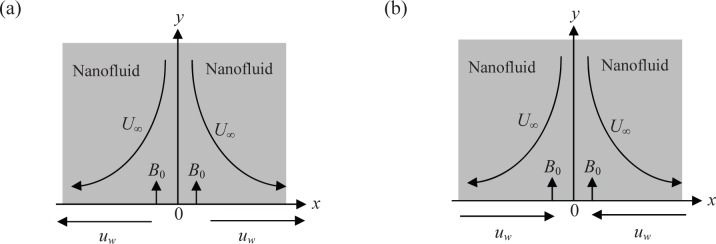
We examine the boundary layer flow of a nanofluid towards a stagnation point on a permeable stretching/shrinking surface, kept at a constant temperature T w and concentration C w, at y = 0 as shown in Fig. 1, where the x− and y− axes are taken along and normal to the stretching/shrinking surface. It is assumed that the free stream velocity is U ∞(x) = bx and the plate is stretched/shrunk with the velocity u w (x) = cx where b and c are positive constants. It is also assumed that the constant mass flux velocity is v 0 with v 0 < 0 for suction and v 0 > 0 for injection. The ambient values of the temperature and nanoparticle fraction are taken as T ∞ and C ∞, respectively. In view of thermal equilibrium, there is no slip between the base (or ordinary) fluid and suspended nanoparticles. Furthermore, the flow is subjected to a constant transverse magnetic field of strength B = B 0 which is assumed to be applied to the positive y-direction. Under these assumptions and the boundary layer approximations, the unsteady governing continuity, momentum and energy boundary layer equations are (see Ibrahim [51])
| (1) |
| (2) |
| (3) |
and
| (4) |
where u and v are the velocity components along the x- and y-axis respectively, U ∞ is the free stream velocity, t is time, T is the fluid temperature, α is the thermal diffusivity, ν is the kinematic viscosity, D B is the Brownian diffusion coefficient, D T is the thermophoresis diffusion coefficient and C is the nanoparticle volume fraction. Furthermore, σ = (ρc)p/(ρc)f is the ratio between the effective heat capacity of the fluid with ρ f and ρ p being the density of the fluid and the density of the particles respectively and c f and c p denote the specific heat of the fluid and the particle at constant pressure, respectively.
Fig 1. Geometry of the problem for (a) stretching sheet [49] and (b) shrinking sheet.
The equations are subjected to the boundary conditions
| (5) |
where λ is the stretching parameter with λ > 0 for stretching and λ < 0 for shrinking, and the subscript w denotes the values at the solid surface. We mention that we have followed in this paper the boundary conditions from the paper by Kuznetsov and Nield [11]. However, very recently Kuznetsov and Nield [13] have mentioned that the major limitation of the model in the paper [11] was active control of nanoparticle volume fraction at the boundary, while in the paper [13], the nanofluid particle fraction on the boundary is passively rather than actively controlled. It is a statement where, with thermophoresis taken into account, the normal flux of nanoparticles is zero at the boundary. This makes the model physically more realistic.
Steady-state flow
In order to solve the steady-state flow (∂/∂t = 0) of Eqs. (1) to (4) with the boundary conditions (5), we introduce the following similarity variable
| (6) |
where ψ is the stream function, which is defined as u = ∂ψ /∂y and v = −∂ψ/∂x. Thus, we have
| (7) |
where prime denotes differentiation with respect to η.
Substituting variables (5) into Eqs. (2) and (3) for the steady-state flow (∂/∂t = 0), we obtain the following ordinary differential (similarity) equations
| (8) |
| (9) |
and
| (10) |
subject to the boundary conditions (4), which become
| (11) |
Here, Pr is the Prandtl number, M is the magnetic parameter, S is the constant mass transfer parameter with S > 0 for suction and S < 0 for injection, A is the velocity ratio, Le is the Lewis number, Nb is the Brownian motion parameter and Nt is the thermophoresis parameter, which are defined as
| (12) |
The quantities of physical interest are the skin friction or shear stress coefficient C f, and the local Nusselt number Nu x, which are defined as
| (13) |
where τ w is the skin friction or shear stress along the plate and q w is the heat flux from the plate, which are defined as
| (14) |
Using (5), (10) and (11), we get
| (15) |
where Rex = uw(x)x/v is the local Reynolds number.
Flow stability
It has been shown in some papers (Weidman et al. [52], Roşca and Pop [50], Ishak [53] etc.) that dual (lower and upper branch) solutions exist. In order to determine which of these solutions are stable and physically realizable, a stability analysis to the solutions of Eqs. (1)–(5) needs to done. Thus, the new variables for the unsteady problem are
| (16) |
Therefore, Eqs. (2)–(4) can be written as
| (17) |
| (18) |
| (19) |
and are subjected to the boundary conditions
| (20) |
The following expressions are written to check the stability of the steady flow solution f(η) = f 0(η), θ(η) = θ 0(η) and ϕ(η) = ϕ 0(η) that satisfy the boundary-value problem (8)–(10) (see [50], [52], [53]),
| (21) |
where γ is an unknown eigenvalue parameter, and F(η,τ), G(η,τ) and H(η,τ) are small as compared to f 0(η), θ 0(η) and ϕ 0(η). By substituting (21) into Eqs. (17)–(19), the following linearized problems are obtained:
| (22) |
| (23) |
| (24) |
The boundary conditions are
| (25) |
We set τ = 0 to get the solution f(η) = f 0(η), θ(η) = θ 0(η) and ϕ(η) = ϕ 0(η) of the steady equations (8)–(10). Hence F = F 0(η), G = G 0(η) and H = H 0(η) in (22)–(24) identify initial growth or decay of the solution (21). Therefore, the following linear eigenvalue problems have to solved:
| (26) |
| (27) |
| (28) |
along with the boundary conditions
| (29) |
The smallest eigenvalue γ will determine the stability of the corresponding steady flow solution f 0(η), θ 0(η) and ϕ 0(η) for all parameters involved. Harris et al. [54] suggests relaxing a boundary condition on F 0(η) or G 0(η) to better find the range of possible eigenvalues. Hence, for the present problem, we relax the condition that as η → ∞ and for a fixed value of γ we solve the system (26, 27, 28) along with the new boundary condition.
Results and Discussions
The system of ordinary differential equations (8)–(10) subject to the boundary conditions (11) was solved numerically for different values of parameters: the stretching/shrinking parameter λ, suction parameter S, magnetic parameter M, velocity ratio parameter A, Brownian motion parameter Nb and thermophoresis parameter Nt. The Prandtl number Pr is set equal to 6.8 (water at 20°C) throughout the paper. The relative tolerance is set to 10–10. The boundary conditions (11) at η = ∞ are replaced by η = 10. This choice is adequate for the velocity and temperature profiles to reach the far field boundary conditions asymptotically. The function bvp4c in MATLAB is used to solve the equations due to its effectiveness in solving the boundary value problems which are much harder than initial value problems. However, the ordinary differential equations (8)–(10) need to be reduced to first order ordinary differential equations before solving them. These procedures are explained in detail by Shampine et al. [55, 56]. We note that for S = λ = M = 0 and A = 1, the skin friction coefficient (f″(0) = 1.232587) obtained is in excellent agreement with the result reported by Bejan [57] which gives rise to the confidence in the validity of our results.
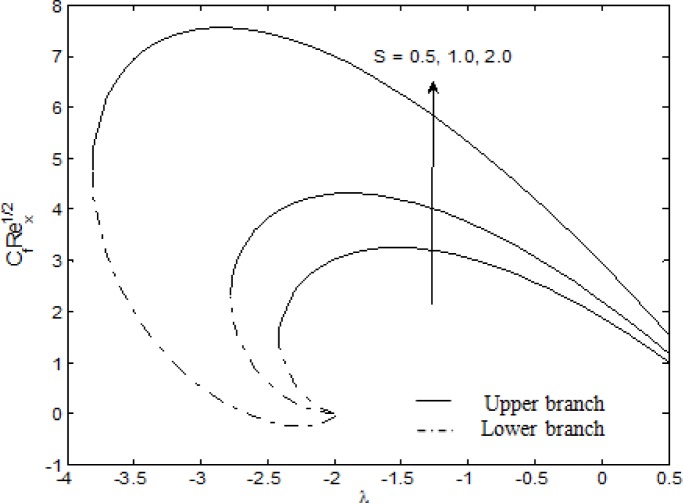
In this paper, we investigated the MHD stagnation point flow of a nanofluid over a stretching/shrinking sheet in the presence of suction effect at the boundary. Fig. 2 shows the skin friction coefficient for different suction parameter S where we can see that the range of solutions depend on S and the stretching/shrinking parameter λ. From Fig. 2, it is seen that for all values of S, unique solution exists for λ > ˗2 and λ = λ c where λ c is the critical values of λ when M = A = 1. Furthermore, it is noted that the range of λ, where solutions exist, increases as S increases as seen in Table 1. As suction increases, the vorticity will continue to be confined even for larger λ. As a result, the range of existence of solution increases [42, 58]. In addition, the range of solutions is also affected by the change in magnetic parameter M and velocity ratio parameter A. For future reference, we also include the values of λ c for different values of M and A in Table 1.
Fig 2. Variation of the skin friction coefficient with λ for different values of S when M = A = 1.
Table 1. Values of λ c.
| S | M | A | λ c |
|---|---|---|---|
| 0.5 | 1.0 | 1.0 | −2.4142 |
| 1.0 | −2.7755 | ||
| 2.0 | −3.8116 | ||
| 0.5 | 1.1 | −2.5060 | |
| 1.2 | −2.5508 | ||
| 1.0 | 1.1 | −2.5100 | |
| 1.2 | −2.6003 |
The effect of suction, magnetic, velocity ratio and stretching/shrinking parameters on the skin friction coefficient are displayed in Fig. 2 and Table 2. The skin friction coefficient decreases as λ increases. However, it increases with increasing S, M and A. From Fig. 2, it is observed that the differences between the skin friction coefficient grow as the sheet keeps shrinking. From the lower branch, the skin friction coefficient is seen to approach 0 as λ approaches-2.
Table 2. Variation of the skin friction coefficient for different values of M and A when S = 0.5 and λ = −1.
| M | A | f″(0) |
|---|---|---|
| 1.0 | 1.0 | 1.8285 |
| 1.1 | 2.4545 | |
| 1.2 | 2.8287 | |
| 1.0 | 1.1 | 2.7393 |
| 1.2 | 3.3264 |
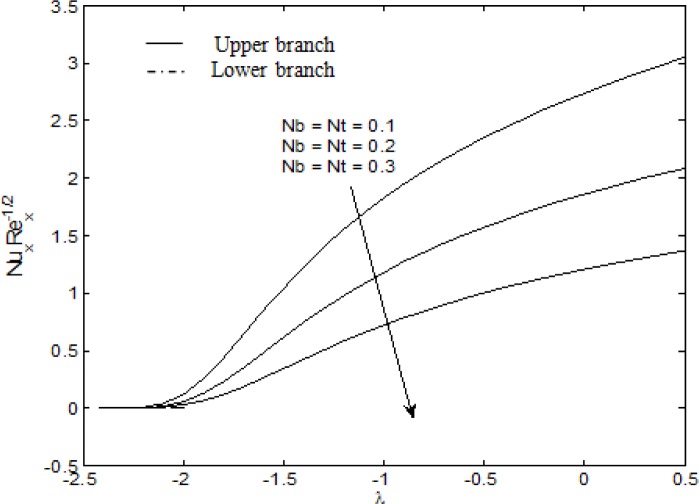
Fig. 3 shows the effects of Brownian motion and thermophoresis parameter on the surface heat transfer rate (local Nusselt number). The local Nusselt number increases with λ. However, as Nb and Nt increase, the local Nusselt number decreases. This is due to the fact that the thermal boundary layer thickness will increase once Nb and Nt are intensified. As the thermal boundary layer thickness grows larger, we can expect that the temperature gradient at the surface grows smaller [51]. Thus, the local Nusselt number decreases. It is interesting to note that the local Nusselt number for the three different values of Nb and Nt are shown to converge to approximately 0 at λ = λ c. Furthermore, similar to Fig. 2, from the lower branch, it is seen that the local Nusselt number approaches 0 as λ approaches-2.
Fig 3. Variation of the local Nusselt number with λ for different values of Nb and Nt when S = 0.5, M = A = 1, Pr = 6.8 and Le = 2.
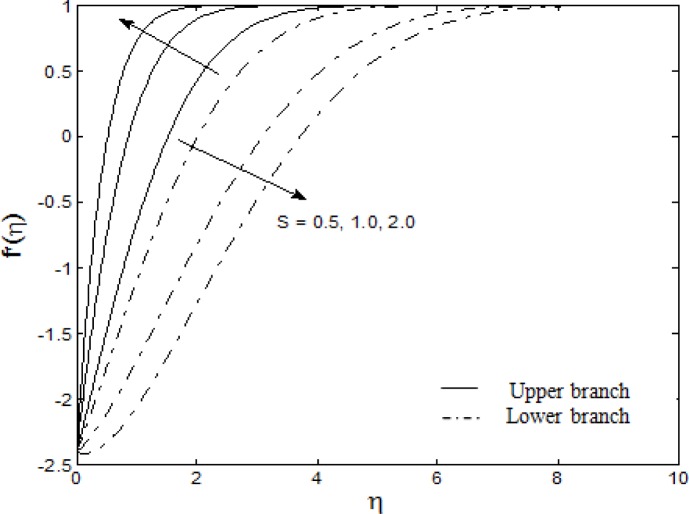
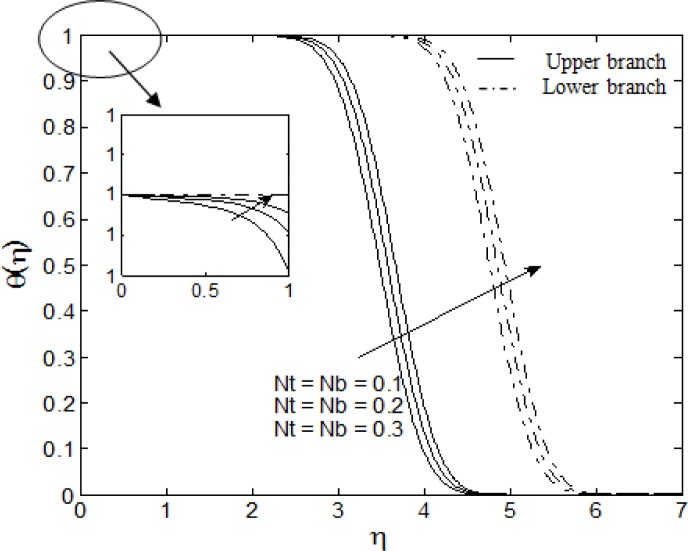
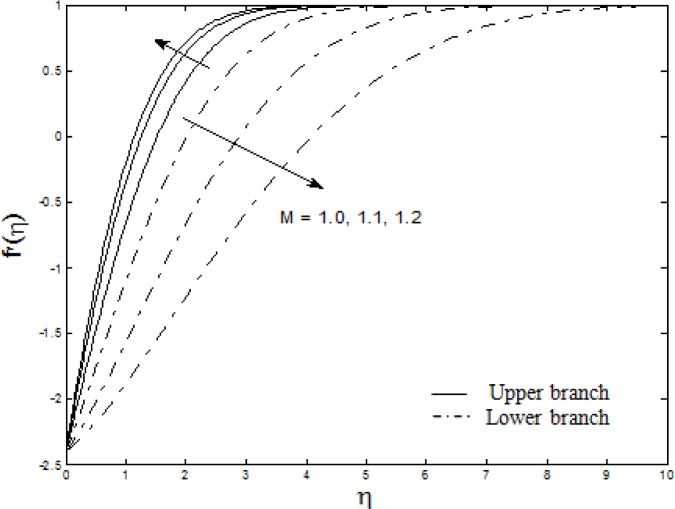
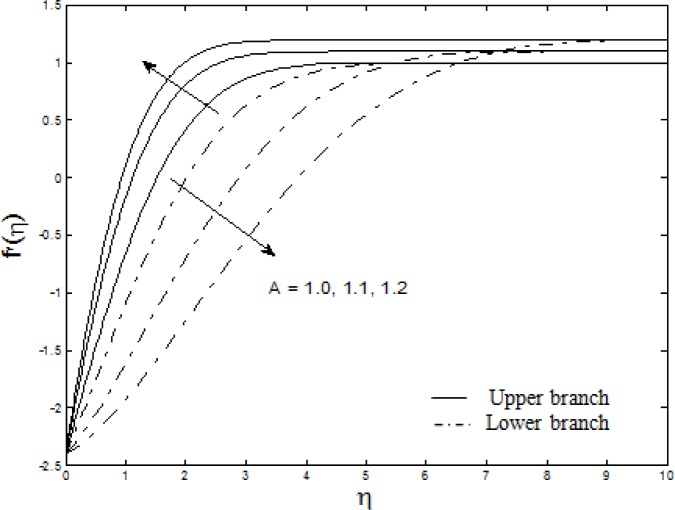
Figs. 4–7 depict the samples of velocity and temperature profiles for different values of S, M, A and Nt = Nb. These profiles satisfy the far field boundary conditions (11) asymptotically, which support the validity of the results obtained, as well as supporting the existence of dual solutions shown in Figs. 2 and 3. The velocity profiles in Fig. 4 show that as suction increases, the velocity increases for upper branch and decreases for lower branch. Furthermore, it is observed that with the increasing suction, the boundary layer thickness decreases for the upper branch while it increases for the lower branch. This phenomenon concurs with Fig. 2 (at λ = −2.4) where the skin friction coefficient increases for upper branch and decreases for lower branch as suction increases. Figs. 5 and 6 show the effects of magnetic parameter M and velocity ratio parameter A on the velocity for the shrinking sheet. It is seen that for the increasing M and A, the velocity also increases. The profiles generated are qualitatively similar to those of Ibrahim et al. [51]. Also, the boundary layer thicknesses decrease as both M and A increase. In Fig. 7, the temperature profiles generated show that the temperature increases as Nt and Nb increase. Furthermore, the profiles show that as the boundary layer thickness increases with the increasing Nt and Nb, the temperature gradient decreases and thus reducing the local Nusselt number shown in Fig. 3.
Fig 4. The velocity profiles for different values of S when M = A = 1 and λ = −2.4.
Fig 7. The temperature profiles for different values of Nb and Nt when S = 0.5, M = A = 1, Pr = 6.8, Le = 2 and λ = −2.4.
Fig 5. The velocity profiles for different values of M when S = 0.5, A = 1 and λ = −2.4.
Fig 6. The velocity profiles for different values of A when S = 0.5, M = 1 and λ = −2.4.
The numerical results show that dual solutions exist for Eqs. (8)–(10) with boundary conditions (11) when λ≤ −2. It is our intention to show that only the upper branch solutions are stable and physically realizable, while the lower branch solutions are not stable, and hence, not physically realizable. According to Weidman [52] and Merkin [59], as the eigenvalue γ = 0, Eqs. (26)–(28) yield the homogeneous problem which defines the critical value λ c, which is the turning point value that separates the stable and unstable branches. The sign of γ will change at the turning point. Therefore, we solved the eigenvalue problem (26)–(28) to determine the smallest eigenvalues γ on the upper and lower solution branches. These results are displayed in Table 3 for several values of λ when S = 0.5 and M = A = 1. The results show that positive values of γ are obtained at the upper branch while negative values of γ are found at the lower branch, showing that the values of γ change from positive (stable) to negative (unstable) at the turning points of the curves, which, as shown in Table 1, is λ c = −2.4142. It is also noted that for both upper and lower branches, |γ| decreases as λ approaches λ c which confirms the observation of Merkin [59] where γ = 0 at λ = λ c.
Table 3. The smallest eigenvalue γ when S = 0.5 and M = A = 1.
| Λ | γ | γ |
|---|---|---|
| (Upper branch) | (lower branch) | |
| −2.400 | 3.7393 | −2.7709 |
| −2.410 | 3.5737 | −2.6594 |
| −2.414 | 3.4331 | −2.5509 |
Conclusions
The magnetohydrodynamic (MHD) stagnation point flow of a nanofluid over a stretching/shrinking sheet with suction is studied. Numerical results were obtained using the function bvp4c in MATLAB for several range of parameters: suction parameter, magnetic parameter, velocity ratio parameter, stretching/shrinking parameter, and Brownian motion and thermophoresis parameters. The results show that dual solutions exist. The range of the solution domain increases with increasing the suction effect at the boundary as well as the presence of magnetic field. Furthermore, increasing suction as well as the magnetic effect causes the skin friction coefficient to increase. Increasing the Brownian motion and thermophoresis parameters lower the local Nusselt number.
Data Availability
All relevant data are within the paper.
Funding Statement
Funding was provided by Universiti Kebangsaan Malaysia (www.ukm.my); Grant number: DIP-2012-31. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Masuda H, Ebata A, Teramae K, Hishinuma N (1993) Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu. Bussei 7: 227–233. [Google Scholar]
- 2.Choi SUS, Eastman JA (1995) Enhancing thermal conductivities of fluids with nanoparticles. ASME International Mechanical Engineering Congress and Exposition. San Francisco, USA.
- 3. Wong KV, De Leon O (2010) Applications of nanofluids: Current and future. Advances in Mechanical Engineering 2010: Article ID 519659 (11 pages). [Google Scholar]
- 4. Saidur R, Leong KY, Mohammad HA (2011) A review on applications and challenges of nanofluids. Renewable and Sustainable Energy Reviews 15: 1646–1668. [Google Scholar]
- 5. Tiwari RK, Das MK (2007) Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of Heat and Mass Transfer 50: 2002–2018. [Google Scholar]
- 6. Buongiorno J (2006) Convective transport in nanofluids. Journal of Heat Transfer 128: 240–250. [Google Scholar]
- 7. Ul Haq R, Khan ZH, Khan WA (2014) Thermophysical effects of carbon nanotubes on MHD flow over a stretching surface. Physica E: Low-dimensional Systems and Nanostructures 63: 215–222. [Google Scholar]
- 8. Nadeem S, Ul Haq R, Khan ZH (2014) Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet. Alexandria Engineering Journal 53: 219–224. [Google Scholar]
- 9. Sheikholeslami M, Ellahi R, Ashorynejad HR, Domairry G, Hayat T (2014) Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium. Journal of Computational and Theoretical Nanoscience 11: 486–496. [Google Scholar]
- 10. Nield DA, Kuznetsov AV (2009) The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer 52: 5792–5795. [Google Scholar]
- 11. Kuznetsov AV, Nield DA (2010) Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences 49: 243–247. [Google Scholar]
- 12. Kuznetsov AV, Nield DA (2013) The Cheng–Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: A revised model. International Journal of Heat and Mass Transfer 65: 682–685. [Google Scholar]
- 13. Kuznetsov AV, Nield DA (2014) Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. International Journal of Thermal Sciences 77: 126–129. [Google Scholar]
- 14. Khan WA, Pop I (2010) Boundary-layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer 53: 2477–2483. [Google Scholar]
- 15. Bachok N, Ishak A, Pop I (2010) Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. International Journal of Thermal Sciences 49: 1663–1668. [Google Scholar]
- 16. Bachok N, Ishak A, Pop I (2012) Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinnking sheet. International Journal of Heat and Mass Transfer 55: 2102–2109. [Google Scholar]
- 17. Khan WA, Aziz A (2011) Natural convection flow of a nanofluid over a vertical plate with uniform surface heat flux. International Journal of Thermal Sciences 50: 1207–1214. [Google Scholar]
- 18. Ul Haq R, Nadeem S, Hayat Khan Z, Sher Akbar N (2015) Thermal radiation and slip effects on MHD stagnation point flow of nanofluid over a stretching sheet. Physica E: Low-dimensional Systems and Nanostructures 65: 17–23. [Google Scholar]
- 19. Haq R, Nadeem S, Khan Z, Okedayo T (2014) Convective heat transfer and MHD effects on Casson nanofluid flow over a shrinking sheet. Central European Journal of Physics 12: 862–871. [Google Scholar]
- 20.Nadeem S, Ul Haq R (2012) MHD boundary layer flow of a nanofluid passed through a porous shrinking sheet with thermal radiation. Journal of Aerospace Engineering doi: 10.1061/(ASCE)AS.1943–5525.0000299.
- 21. Nadeem S, Haq RU (2014) Effect of thermal radiation for magnetohydrodynamic boundary layer flow of a nanofluid past a stretching sheet with convective boundary conditions. Journal of Computational and Theoretical Nanoscience 11: 32–40. [Google Scholar]
- 22. Nadeem S, Haq RU, Khan ZH (2014) Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. Journal of the Taiwan Institute of Chemical Engineers 45: 121–126. [Google Scholar]
- 23. Sheikholeslami M, Bandpy MG, Ellahi R, Zeeshan A (2014) Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces. Journal of Magnetism and Magnetic Materials 369: 69–80. [Google Scholar]
- 24. Sheikholeslami M, Gorji Bandpy M, Ellahi R, Hassan M, Soleimani S (2014) Effects of MHD on Cu–water nanofluid flow and heat transfer by means of CVFEM. Journal of Magnetism and Magnetic Materials 349: 188–200. [Google Scholar]
- 25. Akbar N, Raza M, Ellahi R (2014) Interaction of nanoparticles for the peristaltic flow in an asymmetric channel with the induced magnetic field. The European Physical Journal Plus 129: Article ID 155 (12 pages). [Google Scholar]
- 26. Akbar N, Raza M, Ellahi R (2014) Influence of heat generation and heat flux on peristaltic flow with interacting nanoparticles. The European Physical Journal Plus 129: Article ID 185 (15 pages). [Google Scholar]
- 27. Ellahi R (2013) The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Applied Mathematical Modelling 37: 1451–1467. [Google Scholar]
- 28. Akbar NS, Rahman SU, Ellahi R, Nadeem S (2014) Nano fluid flow in tapering stenosed arteries with permeable walls. International Journal of Thermal Sciences 85: 54–61. [Google Scholar]
- 29. Zeeshan A, Baig M, Ellahi R, Hayat T (2014) Flow of viscous nanofluid between the concentric cylinders. Journal of Computational and Theoretical Nanoscience 11: 646–654. [Google Scholar]
- 30. Ellahi R, Aziz S, Zeeshan A (2013) Non-Newtonian nanofluid flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. Journal of Porous Media 16: 205–216. [Google Scholar]
- 31. Nadeem S, Riaz A, Ellahi R, Akbar NS (2014) Mathematical model for the peristaltic flow of Jeffrey fluid with nanoparticles phenomenon through a rectangular duct. Applied Nanoscience 4: 613–624. [Google Scholar]
- 32. Sheikholeslami M, Domiri Ganji D, Younus Javed M, Ellahi R (2015) Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. Journal of Magnetism and Magnetic Materials 374: 36–43. [Google Scholar]
- 33. Ellahi R, Raza M, Vafai K (2012) Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Mathematical and Computer Modelling 55: 1876–1891. [Google Scholar]
- 34. Fischer EG (1976) Extrusion of Plastics, New York: Wiley. [Google Scholar]
- 35. Wang CY (2002) Flow due to a stretching boundary with partial slip—an exact solution of the Navier–Stokes equations. chemical Engineering Science 57: 3745–3747. [Google Scholar]
- 36. Wang CY (2009) Analysis of viscous flow due to a stretching sheet with surface slip and suction. Nonlinear Analysis: Real World Applications 10: 375–380. [Google Scholar]
- 37. Mandal IC, Mukhopadhyay S (2013) Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium. Ain Shams Engineering Journal 4: 103–110. [Google Scholar]
- 38. Gupta PS, Gupta AS (1977) Heat and mass transfer on a stretching sheet with suction or blowing. The Canadian Journal of Chemical Engineering 55: 744–746. [Google Scholar]
- 39. Andersson HI (2002) Slip flow past a stretching surface. Acta Mechanica 158: 121–125. [Google Scholar]
- 40. Ishak A, Nazar R, Pop I (2009) Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature. Nonlinear Analysis: Real World Applications 10: 2909–2913. [Google Scholar]
- 41. Makinde OD, Aziz A (2011) Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. International Journal of Thermal Sciences 50: 1326–1332. [Google Scholar]
- 42. Miklavcic M, Wang CY (2006) Viscous flow due to a shrinking sheet. Quarterly of Applied Mathematics 64: 283–290. [Google Scholar]
- 43. Wang CY (2008) Stagnation flow towards a shrinking sheet. International Journal of Non-Linear Mechanics 43: 377–382. [Google Scholar]
- 44. Fang T, Yao S, Zhang J, Aziz A (2010) Viscous flow over a shrinking sheet with a second order slip flow model. Communications in Nonlinear Science and Numerical Simulation 15: 1831–1842. [Google Scholar]
- 45. Bachok N, Ishak A, Pop I (2011) Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Research Letters 6: Article ID 623 (10 pages). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Bhattacharyya K, Mukhopadhyay S, Layek GC (2011) Slip effects on boundary layer stagnation-point flow and heat transfer towards a shrinking sheet. International Journal of Heat and Mass Transfer 54: 308–313. [Google Scholar]
- 47. Lok YY, Ishak A, Pop I (2011) MHD stagnation point flow with suction towards a shrinking sheet. Sains Malaysiana 40: 1179–1186. [Google Scholar]
- 48. Lok YY, Ishak A, Pop I (2011) MHD stagnation-point flow towards a shrinking sheet. International Journal of Numerical Methods for Heat & Fluid Flow 21: 61–72. [Google Scholar]
- 49. Zaimi K, Ishak A, Pop I (2012) Boundary layer flow and heat transfer past a permeable shrinking sheet in a nanofluid with radiation effect. Advances in Mechanical Engineering 2012: Article ID 340354 (7 pages). [Google Scholar]
- 50. Roşca AV, Pop I (2013) Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. International Journal of Heat and Mass Transfer 60: 355–364. [Google Scholar]
- 51. Ibrahim W, Shankar B, Nandeppanavar MM (2013) MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. International Journal of Heat and Mass Transfer 56: 1–9. [Google Scholar]
- 52. Weidman PD, Kubitschek DG, Davis AMJ (2006) The effect of transpiration on self-similar boundary layer flow over moving surfaces. International Journal of Engineering Science 44: 730–737. [Google Scholar]
- 53. Ishak A (2014) Flow and heat transfer over a shrinking sheet: A stability Analysis. International Journal of Mechanical, Aerospace, Industrial and Mechatronics Engineering 8: 872–876. [Google Scholar]
- 54. Harris SD, Ingham DB, Pop I (2009) Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transport in Porous Media 77: 267–285. [Google Scholar]
- 55.Shampine LF, Reichelt MW, Kierzenka J (2000) Solving boundary value problems for ordinary differential equations in MATLAB using bvp4c. Available at <http://www.mathworks.com/bvp_tutorial>.
- 56. Shampine LF, Gladwell I, Thompson S (2003) Solving ODEs with MATLAB, Cambridge: Cambridge University Press. [Google Scholar]
- 57. Bejan A (2013) Laminar Boundary Layer Flow, in Convection Heat Transfer John Wiley & Sons, Inc. p. 30–95. [Google Scholar]
- 58. Bhattacharyya K, Layek GC (2011) Effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation. International Journal of Heat and Mass Transfer 54: 302–307. [Google Scholar]
- 59. Merkin JH (1985) On dual solutions occurring in mixed convection in a porous medium. Journal of Engineering Mathematics 20: 171–179. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.