Two Mechanisms of Killing of Pseudomonas aeruginosa by Tobramycin Assessed at Multiple Inocula via Mechanism-Based Modeling

Abstract

Bacterial resistance is among the most serious threats to human health globally, and many bacterial isolates have emerged that are resistant to all antibiotics in monotherapy. Aminoglycosides are often used in combination therapies against severe infections by multidrug-resistant bacteria. However, models quantifying different antibacterial effects of aminoglycosides are lacking. While the mode of aminoglycoside action on protein synthesis has often been studied, their disruptive action on the outer membrane of Gram-negative bacteria remains poorly characterized. Here, we developed a novel quantitative model for these two mechanisms of aminoglycoside action, phenotypic tolerance at high bacterial densities, and adaptive bacterial resistance in response to an aminoglycoside (tobramycin) against three Pseudomonas aeruginosa strains. At low-intermediate tobramycin concentrations (<4 mg/liter), bacterial killing due to the effect on protein synthesis was most important, whereas disruption of the outer membrane was the predominant killing mechanism at higher tobramycin concentrations (≥8 mg/liter). The extent of killing was comparable across all inocula; however, the rate of bacterial killing and growth was substantially lower at the 10^8.9 CFU/ml inoculum than that at the lower inocula. At 1 to 4 mg/liter tobramycin for strain PAO1-RH, there was a 0.5- to 6-h lag time of killing that was modeled via the time to synthesize hypothetical lethal protein(s). Disruption of the outer bacterial membrane by tobramycin may be critical to enhance the target site penetration of antibiotics used in synergistic combinations with aminoglycosides and thereby combat multidrug-resistant bacteria. The two mechanisms of aminoglycoside action and the new quantitative model hold great promise to rationally design novel, synergistic aminoglycoside combination dosage regimens.

INTRODUCTION

The rapid rise of multidrug-resistant (MDR) bacteria and a severe shortage of effective antibiotics are causing a global health crisis (1, 2). This situation is particularly daunting given the lack of new antibiotics in the pipeline for infections associated with Gram-negative bacteria that are resistant to all available monotherapies (3). The lack of effective monotherapies has forced physicians to use empirical antibiotic combinations for which a strong foundation on the mechanism(s) of synergy is not available (4, 5).

Aminoglycosides have been used since the 1970s, but their different mechanisms of action against Gram-negatives are not well understood at a quantitative level. While it is well known that aminoglycosides affect protein synthesis (6), their disruption of the outer membrane of Gram-negative bacteria has not been studied as often (7–10). Kadurugamuwa et al. (11, 12) covalently conjugated aminoglycosides to albumin and showed that these conjugated aminoglycosides can cause rapid and extensive killing of Pseudomonas aeruginosa (>3 log₁₀) without entering the bacterial cells and thus without inhibiting protein synthesis. The outer membrane of Gram-negatives is a major barrier for the target site penetration of many antibiotics (13–16). Thus, it is critical to thoroughly understand the effect of aminoglycosides on the outer membrane, but quantitative models are lacking.

Aminoglycosides bind to negatively charged lipopolysaccharides on the outer membrane of Gram-negatives, before they penetrate into the cytosol and exert their intracellular effect on protein synthesis (6). P. aeruginosa can modify the chemical composition of its outer membrane and thereby decrease the net negative charge on the outer membrane (17–20). This can confer aminoglycoside resistance. Additionally, adaptive resistance can be caused by aminoglycosides inducing overexpression of the MexY component of the MexXY-OprM efflux pump in P. aeruginosa (21–23). Such adaptive resistance to aminoglycosides has been previously reported (17, 18, 24–26). Overexpression of the MexXY-OprM efflux pump can also be caused by a mutation of mexZ which encodes a negative regulator of mexXY (27, 28). To combat P. aeruginosa exhibiting any of these resistance mechanisms, disruption of the outer membrane would be highly beneficial. This will likely enhance the intracellular penetration of aminoglycosides and potential combination antibiotics in wild-type and resistant P. aeruginosa.

Models on aminoglycoside pharmacodynamics often contained one bacterial population and one killing mechanism that was described by a Hill function (29–33). Two previous models for gentamicin against P. aeruginosa (34) or Escherichia coli (35) contained adaptive resistance. Quantitative time course models for aminoglycosides that describe multiple mechanisms of action at one or multiple inocula are lacking. Mechanism-based modeling is ideally suited to analyze the contributions of multiple mechanisms of action and of resistance (including phenotypic tolerance at high bacterial densities) to bacterial killing and regrowth (35–43). This approach allows one to predict the time course of bacterial killing and regrowth for traditional and front-loaded dosage regimens (44–46).

This study aimed to assess and quantify the time course of growth and killing of three P. aeruginosa strains at multiple inocula by tobramycin using a mechanism-based modeling approach. These models evaluated multiple mechanisms of killing and resistance of P. aeruginosa for tobramycin.

(Parts of the experimental data with a preliminary model were presented at the American Conference on Pharmacometrics [ACoP], 9 to 12 March 2008, Tucson, AZ.)

MATERIALS AND METHODS

Bacterial strains.

We used a genetically characterized clinical isolate of P. aeruginosa, PAO1 (PAO1-RH), from the REW Hancock Laboratory (Vancouver, Canada) (47). To assess a strain with lower intracellular tobramycin concentrations due to overexpression of the MexXY-OprM efflux pump, we studied an isogenic pair of a P. aeruginosa PAO1 wild type (PAO1-AO) and its mexZ mutant (PAO1-ΔmexZ) from the A. Oliver Laboratory (Palma de Mallorca, Spain) (48).

Susceptibility testing.

All static concentration time-kill studies for PAO1-RH were performed in cation-adjusted (12.5 mg/liter Mg²⁺ and 25 mg/liter Ca²⁺) Luria-Bertani broth (CA-LBB; Difco Laboratories, Detroit, MI), and all studies for PAO1-AO and its mutant were performed in cation-adjusted Mueller-Hinton broth (CA-MHB; BD, Sparks, MD). The MICs were determined at least in duplicate in CA-MHB and CA-LBB. Mutation frequencies of all strains were assessed on cation-adjusted Mueller-Hinton agar (CA-MHA) with tobramycin concentrations from 0.5 to 32 mg/liter. Tobramycin (Sigma-Aldrich, St. Louis, MO) was dissolved in sterile, distilled water. Viable counting was performed using Luria-Bertani agar (Difco Laboratories) for PAO1-RH and CA-MHA (Medium Preparation Unit, University of Melbourne, Australia) for the PAO1-AO and PAO1-ΔmexZ strains.

Time-kill experiments.

Static concentration time-kill studies were performed as previously described (41, 49, 50). Bacteria were incubated on agar for 19 h prior to each study. A bacterial suspension (10⁸ CFU/ml) was prepared spectrophotometrically in saline and diluted into fresh, prewarmed, sterile, drug-free broth. For the low (10^6.0 CFU/ml) and medium (10^7.5 CFU/ml) initial inocula with strain PAO1-RH, 20 ml of the diluted bacterial suspensions was grown for 70 min before the addition of tobramycin. For the high initial inoculum, the diluted bacterial suspension was grown for 9 h to reach a target inoculum of 10^8.9 CFU/ml. The low (10^5.1), medium (10^7.0), and high (10^7.7 CFU/ml) initial inocula of the PAO1-AO and PAO1-ΔmexZ strains were prepared via the same procedures.

A growth control and tobramycin concentrations between 0.125 and 64 mg/liter were studied in duplicate for PAO1-RH. Serial viable counts were determined over 2 days (41, 50). Antibiotic carryover was minimized by washing bacterial suspensions twice in sterile saline (for the PAO1-AO and PAO1-ΔmexZ strains) or by spiral plating of 50 μl of appropriately diluted (or undiluted) bacterial suspensions (for PAO1-RH). There was no indication of antibiotic carryover for any experiment. For PAO1-RH, sampling times were 0 (i.e., within <10 min of dosing), 0.25, 0.5, 1, 1.5, 2, 3, 4, 9.5, 13, 24, 36, and 52 h for the 10⁶ CFU/ml inoculum and 0, 0.125 (for 16 and 64 mg/liter and 10^7.5 CFU/ml only), 0.25, 0.5, 1, 2, 3, 4, 6 (10^7.5 CFU/ml only), 8, 12, 20, 24, 36, and 48 h for the 10^7.5 and 10^8.9 CFU/ml inocula. For the PAO1-AO and PAO1-ΔmexZ strains, sampling times were 0, 1, 3, 6, 24, 29, and 48 h.

Life cycle growth model.

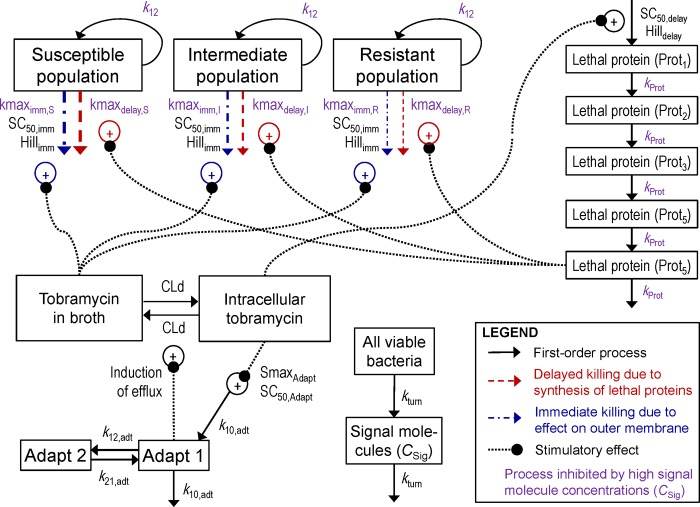
The proposed model contained a preexisting susceptible (S), intermediate (I), and resistant (R) bacterial population (Fig. 1). Bacterial replication for each population was described by a life cycle growth model, with bacteria preparing for replication (state 1) and bacteria immediately before the replication step (state 2) (41, 43, 45, 51). Each of these three populations contained bacteria in two states (e.g., CFU_S1 and CFU_S2 for the susceptible population), yielding six bacterial compartments in total. The viable count of all bacteria (CFU_all) was calculated with the following equation:

$${\text{CFU}}_{\text{all}}={\text{CFU}}_{\mathrm{S}1}+{\text{CFU}}_{\mathrm{S}2}+{\text{CFU}}_{\mathrm{I}1}+{\text{CFU}}_{\mathrm{I}2}+{\text{CFU}}_{\mathrm{R}1}+{\text{CFU}}_{\mathrm{R}2}$$ (1)

FIG 1.

Structure of the mechanism-based model describing the delayed killing due to the effect of tobramycin on protein synthesis and the immediate killing due to tobramycin disrupting the outer membrane of P. aeruginosa. The delay in killing was described by five transit compartments representing the synthesis of hypothetical lethal protein(s). Adaptive resistance was induced by the intracellular tobramycin concentration and was assumed to increase efflux of tobramycin. All viable bacteria were assumed to synthesize and excrete freely diffusible signal molecules. At high signal molecule concentrations (i.e., high bacterial densities), the rates of bacterial replication (k₁₂), immediate killing (kmax_imm,S/I/R), and delayed killing (kmax_delay,S/I/R) and the rates of synthesis and turnover of the lethal protein(s) (k_Prot) were attenuated.

Lower rates of growth and killing at high bacterial densities.

To describe the lower rates of bacterial growth and killing at high compared to low bacterial densities, we assumed that all viable bacteria synthesize and excrete freely diffusible signal molecules (41, 50). The latter represent one of several aspects of quorum sensing and phenotypic changes at high bacterial densities. These hypothetical signal molecules serve as a simplified model feature to capture the phenotypic bacterial changes over time. The differential equation for the signal molecule concentration (C_Sig) is

$$\frac{d(C_{\text{Sig}}\text{)}}{dt}=k_{\text{turn}}\cdot {\text{(CFU}}_{\text{all}}-C_{\text{Sig}}\text{) Initial condition (IC): }{C}_{\text{Sig},0}=\text{CFUo}$$ (2)

k_turn is the turnover rate constant for signal molecules (41, 50), and CFUo is the total initial inoculum. At steady state, the concentration of signal molecules equals CFU_all. The effect of signal molecules (Sig_Response) on various processes in the model was described by the signal molecule concentration (C_50,Sig) causing 50% of maximal response:

$${\text{Sig}}_{\text{Response}}=\frac{C_{\text{Sig}}}{C_{50,\text{Sig}}+C_{\text{Sig}}}$$ (3)

The Sig_Response approaches 0 at low signal molecule concentrations (i.e., low bacterial densities, C_Sig ≪ C_50,Sig) and 1 at high bacterial densities (C_Sig ≫ C_50,Sig). The bacterial growth rate constant (k₁₂) was calculated based on the fastest mean generation time at low bacterial densities (MGT_12,low = 1/k_12,low) and the longest mean generation time at high bacterial densities (MGT_12,high = 1/k_12,high):

$$k_{12}=k_{12,\text{low}}+(k_{12,\text{high}}-k_{12,\text{low}})\cdot {\text{Sig}}_{\text{Response}}$$ (4)

At low C_Sig, the k₁₂ approaches k_12,low, whereas k₁₂ becomes k_12,high at high C_Sig.

Intracellular penetration of tobramycin.

The penetration of tobramycin between broth and the intracellular target site was characterized by a first-order equilibration process (distribution clearance [CLd]). Overexpression of the MexXY-OprM efflux pump in response to aminoglycosides (21) caused an enhanced efflux of tobramycin from the intracellular space into broth. This adaptive resistance is described by the variable Adapt1 in equation 5 (see the next section). The volume of broth (V_broth) was 20 ml, and the intracellular volume of distribution (V_intra) was set to a negligibly small value (0.001 ml). While V_intra is expected to be smaller, this choice was sufficiently small to not affect the broth concentration and facilitated computation times. The differential equations for the amount of tobramycin in broth (A_broth) and the intracellular space (A_intra) were

$$\frac{d(A_{\text{broth}})}{dt}=-\text{CLd}\cdot C_{\text{broth}}+\text{CLd}\cdot (1+\text{Adapt}1)\cdot C_{\text{intra}}\text{IC}: A_{\text{broth},0}=C_{\text{Tobra}}\cdot V_{\text{broth}}$$ (5)

and

$$\frac{d(A_{\text{intra}})}{dt}=\text{CLd}\cdot C_{\text{broth}}-\text{CLd}\cdot (1+\text{Adapt}1)\cdot C_{\text{intra}}\text{IC}: A_{\text{intra},0}=0$$ (6)

The tobramycin concentration in broth (C_broth) is essentially not affected by the intracellular tobramycin concentration (C_intra = A_intra/V_intra), as V_broth is much larger than V_intra. Thus, the steady-state solution of equations 5 and 6 yields

$$C_{\text{intra},\text{SS}}=\frac{C_{\text{broth}}}{1+{\text{Adapt}1}_{\text{SS}}}$$ (7)

Adaptive resistance.

The variable Adapt1 describes the adaptive resistance to tobramycin and is zero in the absence of an aminoglycoside (except for the ΔmexZ mutant). Hocquet et al. (23) showed that adaptive resistance can be rapidly upregulated (within 2 h) and that it takes 6 to 24 h after removal of the aminoglycoside until adaptive resistance reverts back to baseline. A two-compartment model was suitable to describe the rapid onset and slow decline of adaptive resistance (Fig. 1). Stimulation of adaptive resistance (Stim_Adapt) was based on C_intra and was included in the differential equations for the central (Adapt1) and peripheral adaptation compartment (Adapt2):

$${\text{Stim}}_{\text{Adapt}}={\text{Smax}}_{\text{Adapt}}\cdot \frac{C_{\text{intra}}}{{\text{SC}}_{50,\text{Adapt}}+C_{\text{intra}}}$$ (8)

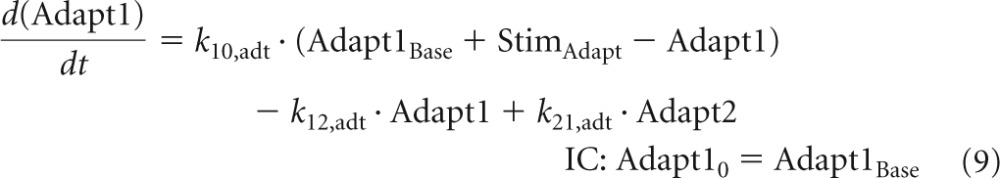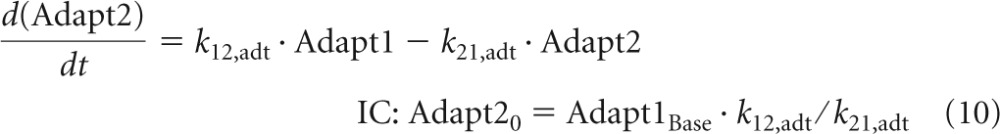The baseline of Adapt1 (Adapt1_Base) was zero for all strains except for the ΔmexZ mutant that expresses the MexXY-OprM efflux pump also in the absence of tobramycin. Equations 9 and 10 yield the steady-state solution (Adapt1_SS) for Adapt1:

$${\text{Adapt1}}_{\text{SS}}={\text{Adapt}1}_{\text{Base}}+{\text{Smax}}_{\text{Adapt}}\cdot \frac{C_{\text{intra,SS}}}{{\text{SC}}_{50,\text{Adapt}}+C_{\text{intra,SS}}}$$ (11)

Inserting Adapt1_SS into equation 7 yields the solution for the intracellular tobramycin concentration at steady state (C_intra,SS) as a function of C_broth for strains with an Adapt1_Base of 0:

$$C_{\text{intra},\text{ss}}={\left[2\cdot \left(1+\text{Sm}a{x}_{\text{Adapt}}\right)\right]}^{-1}\cdot \left[C_{\text{broth}}-\text{SC}{}_{50,\text{Adapt}}+\sqrt{{\left(C_{\text{broth}}-{\text{SC}}_{50,\text{Adapt}}\right)}^2+4\cdot \left(1+{\text{Smax}}_{\text{Adapt}}\right)\cdot C_{\text{broth}}\cdot {\text{SC}}_{50,\text{Adapt}}}\right]$$ (12)

Modeling of aminoglycoside-related bacterial killing.

Aminoglycosides interfere with protein synthesis and disrupt the outer membrane of Gram-negative bacteria (7–12). The effect on protein synthesis was modeled as a delayed killing process and disruption of the outer membrane as immediate killing.

Disruption of the outer membrane causing immediate killing.

We used C_broth to describe immediate killing (k_imm,S) of the susceptible (S) population via a Hill function:

$$k_{\text{imm},\text{S}}=\text{km}a{x}_{\text{imm},\text{S}}\cdot \left(1-{\text{Sig}}_{\text{Response}}\right)\cdot \frac{C_{\text{broth}}}{S{C}_{50,\text{imm}}+C_{\text{broth}}}$$ (13)

At low C_Sig (i.e., low bacterial densities), Sig_Response approaches zero and does not affect k_imm,S. When Sig_Response approaches 1 at high bacterial densities, immediate killing was attenuated. Similar equations were used for immediate killing of the intermediate (k_imm,I) and resistant (k_imm,R) populations by replacing kmax_imm,S with kmax_imm,I or kmax_imm,R.

Effect on protein synthesis causing delayed killing.

The detailed viable count profiles for PAO1-RH showed a (pronounced) lag time of bacterial killing at low tobramycin concentrations. This lag time was longer at the 10^7.5- than at the 10⁶-CFU/ml inoculum. We proposed to model this delayed killing by the time required to synthesize hypothetical lethal protein(s). The lower rate of protein synthesis at high bacterial densities therefore explained the longer lag time. The rate constant (k_Prot) for synthesis and turnover of lethal proteins at low bacterial densities (k_Prot,low) was faster than that at high bacterial density (k_Prot,high). The k_Prot was calculated as a function of Sig_Response:

$$k_{\text{Prot}}=k_{\text{Prot}+\text{low}}+\left(k_{\text{Prot},\text{high}}-k_{\text{Prot},\text{low}}\right)\cdot {\text{Sig}}_{\text{Response}}$$ (14)

We estimated the apparent mean turnover time of lethal proteins at low (MTT_Prot,low) and high (MTT_Prot,high) bacterial densities and calculated k_Prot,low as 5/MTT_Prot,low and k_Prot,high as 5/MTT_Prot,high. The value 5 reflects the mean turnover time associated with the 5 sequential transit compartments (Fig. 1). The C_intra was assumed to stimulate synthesis of the first step of the lethal proteins via a Hill function:

$${\text{Stim}}_{\text{Delayed\_killing}}=\frac{C_{\text{intra}}}{{\text{SC}}_{50,\text{delay}}+C_{\text{intra}}}$$ (15)

The differential equation for the first steps of the hypothetical lethal proteins (Prot₁) was

$$\frac{d\left({\text{Prot}}_1\right)}{dt}=k_{\text{Prot}}\cdot \left({\text{Stim}}_{\text{Delayed\_killing}}-{\text{Prot}}_1\right)\hspace{0.17em}\text{IC}:{\text{Prot}}_1=0$$ (16)

Differential equations for the second to fifth (i = 2 to 5) step of the lethal proteins were

$$\frac{d\left({\text{Prot}}_i\right)}{dt}=k_{\text{Prot}}\cdot ({\text{Prot}}_{\left(i-1\right)}-{\text{Prot}}_i$$ (17)

These five transit compartments empirically described a time delay (52) (similar to a lag phase) for the delayed killing mechanism. The fifth lethal protein compartment stimulated the delayed bacterial killing (k_delay,S) for the susceptible population (Fig. 1):

$$k_{\text{delay},\text{S}}={\text{kmax}}_{\text{delay},\text{S}}\cdot {\text{Prot}}_5$$ (18)

Similar equations were used for the killing of the intermediate and resistant populations by using kmax_delay,I or kmax_delay,R instead of kmax_delay,S. To describe an attenuated killing at high bacterial densities, the maximum rate constant for delayed killing (kmax_delay,S) was assumed to be smaller at high than at low signal molecule concentrations:

$${\text{kmax}}_{\text{delay},\mathrm{S}}={\text{kmax}}_{\text{delay},\mathrm{S},\text{low}}+({\text{kmax}}_{\text{delay},\mathrm{S},\text{high}}-{\text{kmax}}_{\text{delay},\mathrm{S},\text{low}})·{\text{Sig}}_{\text{Response}}$$ (19)

The same equations were implemented for the intermediate and resistant populations.

Differential equations for bacterial replication and killing.

Bacterial replication (i.e., doubling) was assumed to be 100% successful at low bacterial densities. At the maximum population size (CFU_max), the probability for successful bacterial replication (Prob_Succ) was 50%, yielding net stasis (41, 43, 45, 51):

$${\text{Prob}}_{\text{Succ}}=1-\frac{{\text{CFU}}_{\text{all}}}{\text{CFU}{}_{\text{max}}+\hspace{0.17em}{\text{CFU}}_{\text{all}}}$$ (20)

The replication factor (REPL) equals 2 × Prob_Succ. Implementing the delayed and immediate killing processes into this growth model yields the differential equations for the vegetative (CFU_S1) and replicating (CFU_S2) states of the susceptible population (initial conditions described below):

$$\frac{d\left({\text{CFU}}_{\text{S}1}\right)}{dt}=\text{REPL}\cdot k_{21}\cdot {\text{CFU}}_{\text{S}2}-k_{12}\cdot {\text{CFU}}_{\text{S}1}-\left(k_{\text{delay},\text{S}}+k_{\text{imm},\text{S}}\right)\cdot {\text{CFU}}_{\text{S}1}$$ (21)

$$\frac{d\left({\text{CFU}}_{\text{S2}}\right)}{dt}=-k_{21}\cdot {\text{CFU}}_{\text{S}2}-k_{12}\cdot {\text{CFU}}_{\text{S}1}-\left(k_{\text{delay},\text{S}}+k_{\text{imm},\text{S}}\right)\cdot {\text{CFU}}_{\text{S2}}$$ (22)

Similar equations were used for states 1 and 2 of the intermediate (CFU_I1 and CFU_I2) and resistant populations (CFU_R1 and CFU_R2). The respective differential equations were obtained by using k_delay,I or k_delay,R instead of k_delay,S and k_imm,I or k_imm,R instead of k_imm,S.

We estimated the log₁₀ fraction of bacteria in the intermediate (Log₁₀ Fr_I) and resistant (Log₁₀ Fr_R) populations relative to the total initial inoculum (CFUo). The initial condition for CFU_I1 was CFU_{I1,t = 0} = Fr_I × CFUo, and the initial condition for CFU_R1 was CFU_{R1,t = 0} = Fr_R × CFUo. If less than one bacterial cell of the resistant population was expected to be present in the entire broth volume, Fr_R was set to zero and this population was initialized at 0 (i.e., lacking). The initial condition for CFU_S1 was (1 – Fr_I – Fr_R) × CFUo. The initial conditions for CFU_S2, CFU_I2, and CFU_R2 were set to zero, as the numbers of bacteria in these compartments are substantially smaller than the number in state 1.

Estimation, parameter variability, and observation model.

The estimation, model diagnostics, parameter variability, and residual error models were the same as those described previously (43, 50, 53–57). We simultaneously fitted all data on strains PAO1-AO and PAO1-ΔmexZ. We assessed the significance of all relevant parameters/processes by leaving out one parameter or process at a time, reestimating the simplified model, and comparing it to the full model. Initial slopes were calculated in WinNonlin Pro (version 5.3).

Prospective validation.

The model was prospectively validated by studying a growth control and tobramycin concentrations of 1.5, 3, 8, 12, and 32 mg/liter that were not previously tested against two inocula (10^6.17 and 10^7.72 CFU/ml) of PAO1-RH in CA-LBB. We compared the population-predicted viable counts with the observed data.

Simulations.

Viable count profiles at an inoculum of 10^7.5 CFU/ml were predicted using the pharmacokinetics of tobramycin in critically ill patients (58). We simulated completely immunocompromised patients with normal renal function and bacteremia. A population mean of 3.40 liters/h was used for total clearance, 4.74 liters/h for intercompartmental clearance, 26.0 liters for central volume of distribution, and 40.0 liters for the peripheral volume of distribution. Tobramycin was simulated as a short-term (1-h) infusion at a daily dose of 5 mg/kg given every 24, 12, or 8 h. Additionally, we simulated a regimen with an 8 mg/kg loading dose on day 1 followed by 5 mg/kg as a 1-h infusion every 24 h.

RESULTS

Susceptibility and population.

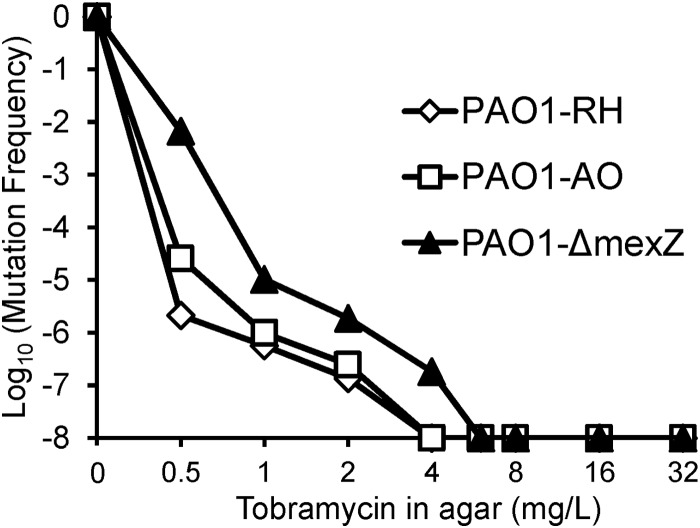
The MIC of PAO1-RH in CA-MHB broth was 0.5 mg/liter for tobramycin and meropenem, 1 mg/liter for gentamicin, ceftazidime, ciprofloxacin, and 2 mg/liter for amikacin, aztreonam, and piperacillin. The tobramycin MIC for PAO1-RH in CA-LBB was 1 mg/liter. The MIC was 0.25 mg/liter for PAO1-RH, 0.50 mg/liter for PAO1-AO, and 0.75 mg/liter for the PAO1-ΔmexZ mutant on CA-MHA. The targeted initial inocula of all strains were closely matched by the curve fits (Fig. 2 and Fig. 3). The observed mutation frequencies (Fig. 4) of the PAO1-ΔmexZ mutant were similar to those of the two PAO1 wild-type strains after accounting for the differences in MIC.

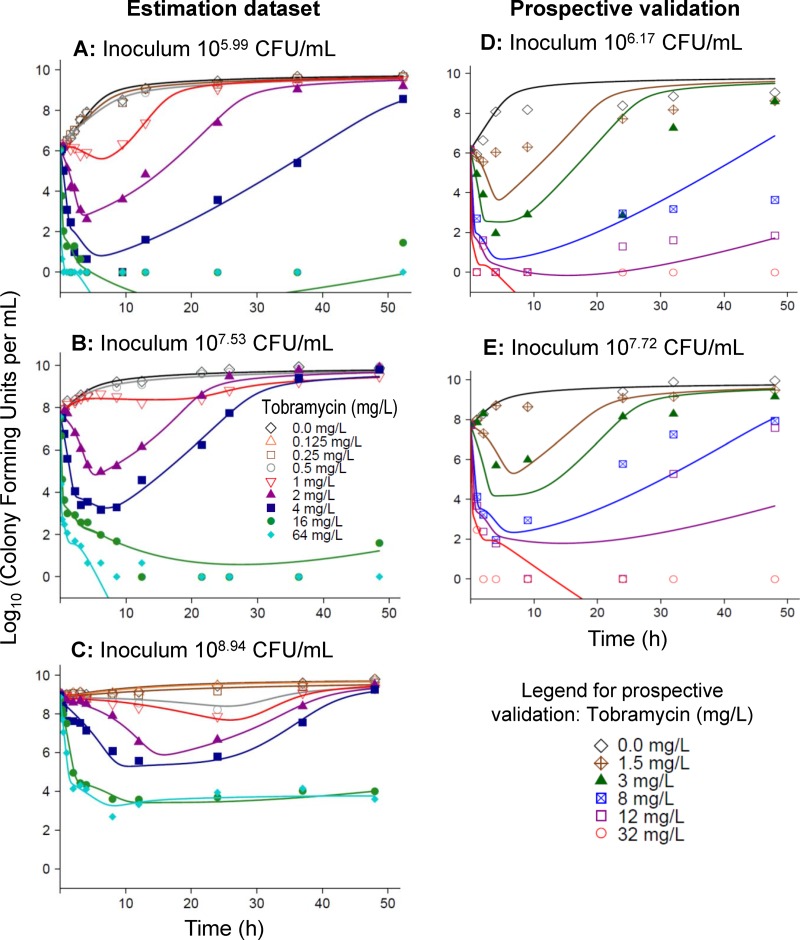
FIG 2.

Observed (markers) and fitted (lines) viable counts based on the final model for PAO1-RH. Observations plotted as 0 log₁₀ (CFU/ml) represent agar plates with no colonies. The left column shows the individual curve fits for the estimation data set at three initial inocula. The right column shows the population predictions for the prospective validation data set at two initial inocula. The validation data set was not used for model estimation.

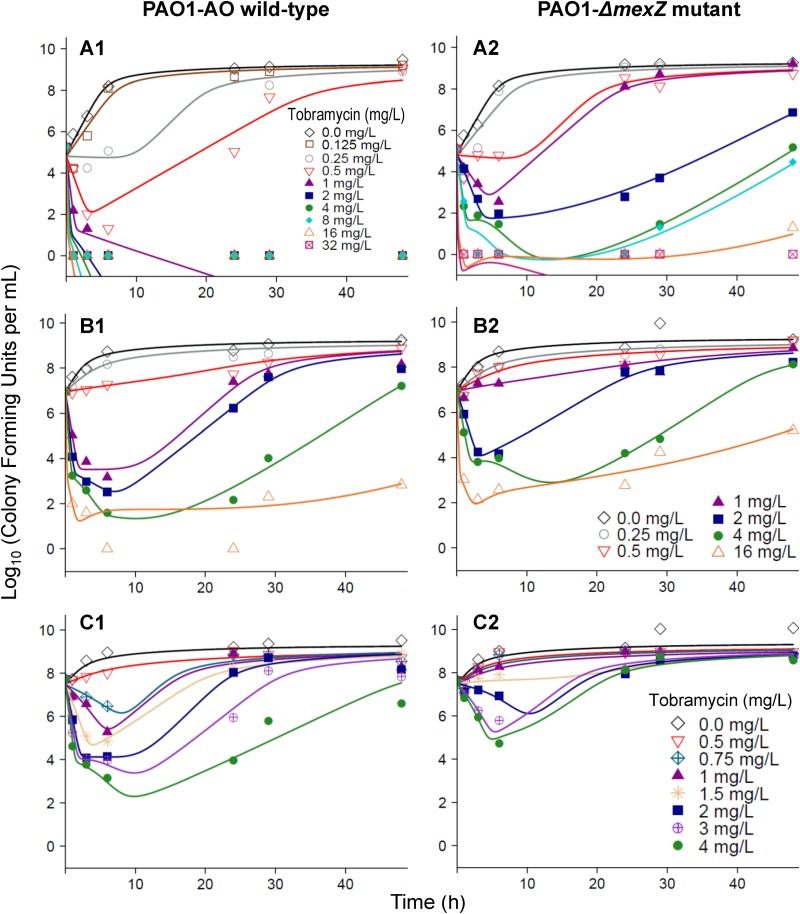
FIG 3.

Observed (markers) and individually fitted (lines) viable counts based on the final model for PAO1-AO (left) and the PAO1-ΔmexZ mutant (right) for initial inocula of 10^5.1 (A), 10^7.0 (B), and 10^7.7 (C) CFU/ml. Observations plotted as 0 log₁₀ (CFU/ml) represent agar plates with no colonies.

FIG 4.

Population analysis profile for tobramycin against three P. aeruginosa PAO1 strains. The agar MICs were 0.25 mg/liter for PAO1-RH, 0.5 mg/liter for PAO1-AO, and 0.75 mg/liter for the PAO1-ΔmexZ mutant. The plot shows the log₁₀ of the ratio of viable bacteria on agar plates containing the tobramycin concentration shown on the x axis divided by the total population. The initial inocula ranged between 10^7.8 and 10^8.0 CFU/ml. We plated at least 400 μl (on two separate plates) for each concentration. This yields a limit of counting of −7.5 log₁₀ (equivalent to, in total, 1 colony on two antibiotic-containing agar plates).

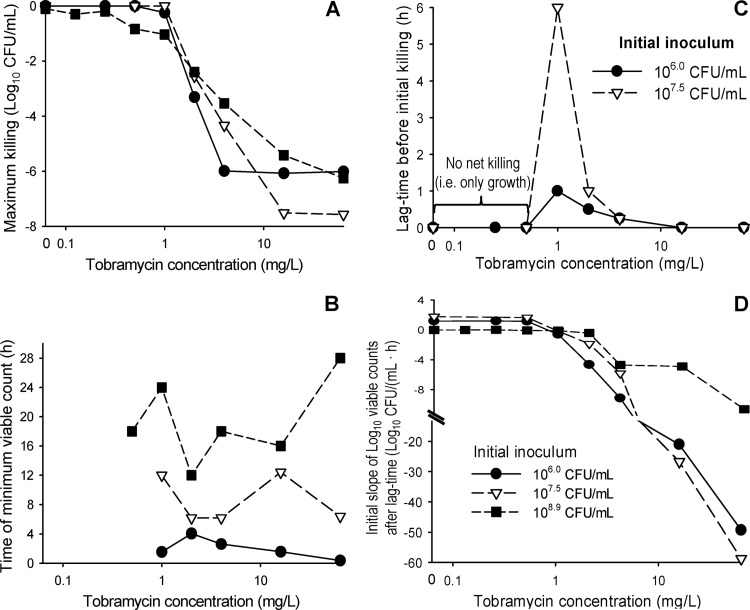
The maximum extent of killing (change in log₁₀ CFU/ml relative to the initial inoculum) was comparable across all three inocula for PAO1-RH (Fig. 5A). However, the minimum viable counts occurred several hours later at the high than at the lower inocula (Fig. 5B). At tobramycin concentrations of 0.5 to 4 mg/liter, there was a concentration-dependent lag time before viable counts declined for the 10⁶- and 10^7.5-CFU/ml inocula (Fig. 2). This lag time amounted to up to 6 h for the 10^7.5-CFU/ml inoculum (Fig. 5C). The initial slopes at each tobramycin concentration were comparable at the 10⁶- and 10^7.5-CFU/ml inocula (Fig. 5D), but killing was noticeably slower and no lag time was apparent at the 10^8.9 CFU/ml inoculum.

FIG 5.

Maximum extent of killing by tobramycin relative to the initial inoculum (A), time point of the minimum viable count (B), lag time of bacterial killing (C), and initial slope of the bacterial killing curves (D). Data represent arithmetic means for P. aeruginosa PAO1-RH studied at three initial inocula at the tobramycin concentrations shown in Fig. 2. Bacterial killing at the 10^8.9-CFU/ml inoculum was relatively slow, and a lag time before the initial killing phase was not clearly apparent. Therefore, this curve is not plotted in panel C. If the minimum viable count occurred multiple times due to nondetectable viable counts at the 10⁶ CFU/ml inoculum, the time of the first minimum viable count was reported in panel B.

The fitted viable counts described the observations at all three inocula excellently, with an r of 0.995 for PAO1-RH and 0.987 for the other strains for individual-fitted log₁₀ CFU/ml (Fig. 2 and 3) and an r of 0.928 for PAO1-RH and 0.907 for the other strains for the population-fitted log₁₀ CFU/ml. Both the individual and population fits of all three strains were unbiased. For the 64-mg/liter tobramycin curve at the 10^8.9-CFU/ml inoculum of PAO1-RH, the population fits described killing up to 12 h well, but the model predicted eradication instead of stasis between 12 and 48 h. Simplification of the final model by removal of one parameter or process resulted in significantly worse (P ≤ 0.003) model performance for all tested model parameters (Table 1), suggesting that inclusion of all model components was justified.

TABLE 1.

Parameter estimates of the mechanism-based population pharmacodynamic model for two wild-type P. aeruginosa strains (PAO1-RH and PAO1-AO) and a PAO1-mexZ mutant (isogenic to PAO1-AO)

Parameter	Symbol	Unit	Population mean (SE%), PAO1-RH	Performance of simplified models, Δ(−2× log likelihood)g	Population mean (SE%)
					PAO1-AO	PAO1-ΔmexZ mutant
Bacterial growth
Log10 for:
Low initial inoculum	Log10 CFUo		6.10 (1.2)d		4.85 (2.5)	4.85 (2.5)
Medium initial inoculum	Log10 CFUo		7.71 (0.8)		6.97 (2.0)	6.97 (2.0)
High initial inoculum	Log10 CFUo		8.84 (0.7)		7.50 (1.6)	7.50 (1.6)
Log10 (fraction of intermediate population at time zero)	Log10 FrI		−4.16 (1.7)		−3.47 (4.5)	−3.47 (4.5)
Log10 (fraction of resistant population at time zero)	Log10 FrR		−6.43 (1.9)	108 (P < 0.0001)h	−6.16 (2.9)	−5.83 (2.8)
Fastest mean generation time at low bacterial density
Susceptible population	MGT12,low,Sa	min	49.2 (5.5)		38.8 (18.9)	38.8 (18.9)
Intermediate population	MGT12,low,Ia	min	49.2 (5.5)		58.4 (44.1)	58.4 (44.1)
Resistant population	MGT12,low,Ra	min	49.2 (5.5)		99.9 (64.9)	99.9 (64.9)
Slowest mean generation time at high bacterial density	MGT12,higha	min	720 (fixed)	161 (P < 0.0001)i	720 (fixed)	720 (fixed)
Log10 (maximum population size)	Log10 CFUmax		9.78 (0.8)		9.23 (1.5)	9.23 (1.5)
Mean turnover time of hypothetical signal molecules	MTTSigb	h	11.4 (10.3)	154 (P < 0.0001)j	3.48 (29.6)	3.48 (29.6)
Log10 of signal molecule concn causing 50% of change from low to high bacterial density	Log10 C50,Sig		7.91 (1.1)	232 (P < 0.0001)k	7.55 (2.9)	7.55 (2.9)
Bacterial killing
Mean equilibration half-life between tobramycin in broth and in the intracellular space (t1/2eq was ln(2) · Vbroth/CLd)	t1/2eq	min	27.4 (11.3)		16.3 (23)	16.3 (23)
Maximum killing rate constant for immediate killing of the:
Susceptible population	kmaximm,S	1/h	134 (9.7)	110 (P < 0.0001)l	262 (9.4)	262 (9.4)
Intermediate population	kmaximm,I	1/h	10.6 (8.9)		33.4 (16.9)	33.4 (16.9)
Resistant population	kmaximm,R	1/h	0.255 (7.3)		0.410 (24.8)	0.410 (24.8)
Intracellular tobramycin concn causing 50% of kimm	SC50,imm	mg/liter	37.6 (7.9)		76.8 (24.8)	76.8 (24.8)
Hill coefficient for immediate killing	Hillimm		1.31 (4.6)	52.5 (P < 0.0001)	1.09 (6.1)	1.09 (6.1)
Maximum killing rate constant at low bacterial density for delayed killing of the:
Susceptible population	kmaxdelay,S,low	1/h	14.8 (8.7)e		5.54 (34.7)	5.54 (34.7)
Intermediate population	kmaxdelay,I,low	1/h	3.80 (8.2)e		1.19 (29.0)	1.19 (29.0)
Resistant population	kmaxdelay,R,low	1/h	2.12 (12.8)e		0.634 (13.7)	0.634 (13.7)
Maximum killing rate constant at high bacterial density for delayed killing of the:
Susceptible population	kmaxdelay,S,high	1/h	0.179 (18.4)e		0.162 (22.4)	0.162 (22.4)
Intermediate population	kmaxdelay,I,high	1/h	0.0461 (8.2)e		0.0350 (29.0)	0.0350 (29.0)
Resistant population	kmaxdelay,R,high	1/h	0.0257 (12.8)e		0.0186 (13.7)	0.0186 (13.7)
Intracellular tobramycin concn causing 50% of kdelay	SC50,delay	mg/liter	3.91 (11.7)		0.958 (20.1)	0.958 (20.1)
Hill coefficient for delayed killing	Hilldelay		1.86 (8.7)	14.5 (P = 0.0001)	5.61 (38.6)	5.61 (38.6)
Mean turnover time of lethal protein(s) at:
Low bacterial density	MTTProt,lowc	h	2.05 (9.0)	33.3 (P = 0.0001)m	4.29 (33.0)	4.29 (33.0)
High bacterial density	MTTProt,highc	h	24 (fixed)	8.73 (P = 0.003)n	24 (fixed)	24 (fixed)
Adaptive resistance
Baseline of adaptive resistance	Adapt1Base		0 (fixed)		0 (fixed)	0.981 (27.8)
Maximum extent of stimulation of adaptive resistance	SmaxAdapt		32.4 (6.5)	53.3 (P = 0.0001)o	58.3 (6.8)	44.1 (17.0)
Intracellular tobramycin concn causing 50% of SmaxAdapt	SC50,Adapt	mg/liter	36.5 (7.2)		1.38 (35.5)	1.38 (35.5)
Turnover rate constant for adaptive resistance	k10,adt	1/h	0.314 (9.7)		0.174 (18.3)	0.174 (18.3)
Intercompartmental transfer rate constant between the central and peripheral compartment for adaptive resistance	k12,adt	1/h	0.921 (21.1)	50.1 (P < 0.0001)p	1.99 (14.6)	1.99 (14.6)
Intercompartmental transfer rate constant between the peripheral and central compartment for adaptive resistance	k21,adt	1/h	0.167 (fixed)f		0.167 (fixed)	0.167 (fixed)
Residual variability
SD of additive residual error on log10 scale	σ		0.241 (4.0)		0.354 (5.3)	0.354 (5.3)

^aThe growth rate constant of the susceptible population (k_12,low,S) at low bacterial density was calculated as 1/MGT_12,low,S. The same equation was applied for the intermediate and resistant populations. The growth rate constant at high bacterial density (k_12,high) was calculated as 1/MGT_12,high. The k₂₁ was fixed to 50 1/h.

^bThe turnover rate constant (k_turn) of hypothetical signal molecules was calculated as 1/MTT_sig.

^cThe first-order rate constant k_Prot,low was calculated as 5/MTT_Prot,low and k_Prot,high as 5/MTT_Prot,high, reflecting the five transit compartments for the protein synthesis.

^dOwing to the small between-curve variability for in vitro static time-kill experiments, the between-curve variability was fixed to a small value (15% coefficient of variation for log-normally distributed parameters and a standard deviation of 0.1 for parameters estimated on a log₁₀ scale).

^eThe ratios of k_delay,S divided by k_delay,I and of k_delay,I divided by k_delay,R were estimated.

^fThis estimate was fixed to a mean transfer time (1/k_21,adt) of 6 h based on the data from Hocquet et al. (23).

^gDifference in the −2× log likelihood for a model which lacked the respective model parameter or model feature compared to the final model for strain PAO1-RH.

^hFor a model which lacked the resistant population. A model lacking both the intermediate and resistant population could not adequately describe the data.

ⁱFor this model, MGT_12,high was set to the value of MGT_12,low,S.

^jFor this model, MTT_Sig was fixed to a very small value (0.01 h), which results in an immediate (i.e., nondelayed) inoculum effect.

^kThis model lacked the inoculum effect.

^lThis model lacked the immediate killing effect.

^mFor this model, the delayed killing effect was delayed only by a very short time (i.e., MTT_Prot,low and MTT_Prot,high were fixed to 0.05 h).

ⁿFor this model, MTT_Prot,low was not inoculum dependent and MTT_Prot,high was not included in the model.

^oThis model lacked adaptive resistance (i.e., Smax_Adapt was fixed to zero).

^pFor this model, adaptive resistance was described by one instead of two compartments.

Killing of the PAO1-ΔmexZ mutant required approximately 2-fold-higher concentrations than that of PAO1-AO, and regrowth was more extensive for the PAO1-ΔmexZ mutant (Fig. 3), in particular for the low inoculum. The model estimated that the tobramycin-resistant population was lacking in the low initial inoculum for the PAO1-AO wild type but present for the PAO1-ΔmexZ mutant (Fig. 3).

High intracellular tobramycin concentrations (SC_50,Adapt) were estimated to yield half-maximal induction of adaptive resistance (Table 1) for strain PAO1-RH. Therefore, near-maximal induction required tobramycin concentrations (>100 mg/liter) considerably exceeding those seen in patients (58). At clinically relevant tobramycin concentrations ranging from 1 to 32 mg/liter, equation 12 predicted that adaptive resistance decreased the intracellular tobramycin concentration of PAO1-RH approximately 1.6- to 5.5-fold compared to the extracellular tobramycin concentration (i.e., C_broth).

Prospective experimental validation for PAO1-RH at two initial inocula using previously nonstudied tobramycin concentrations yielded highly adequate model predictions for all tobramycin concentrations except 1.5 mg/liter (Fig. 2). For the latter concentration, the extent of initial killing was overpredicted. Eradication and regrowth were overall excellently predicted at all studied concentrations.

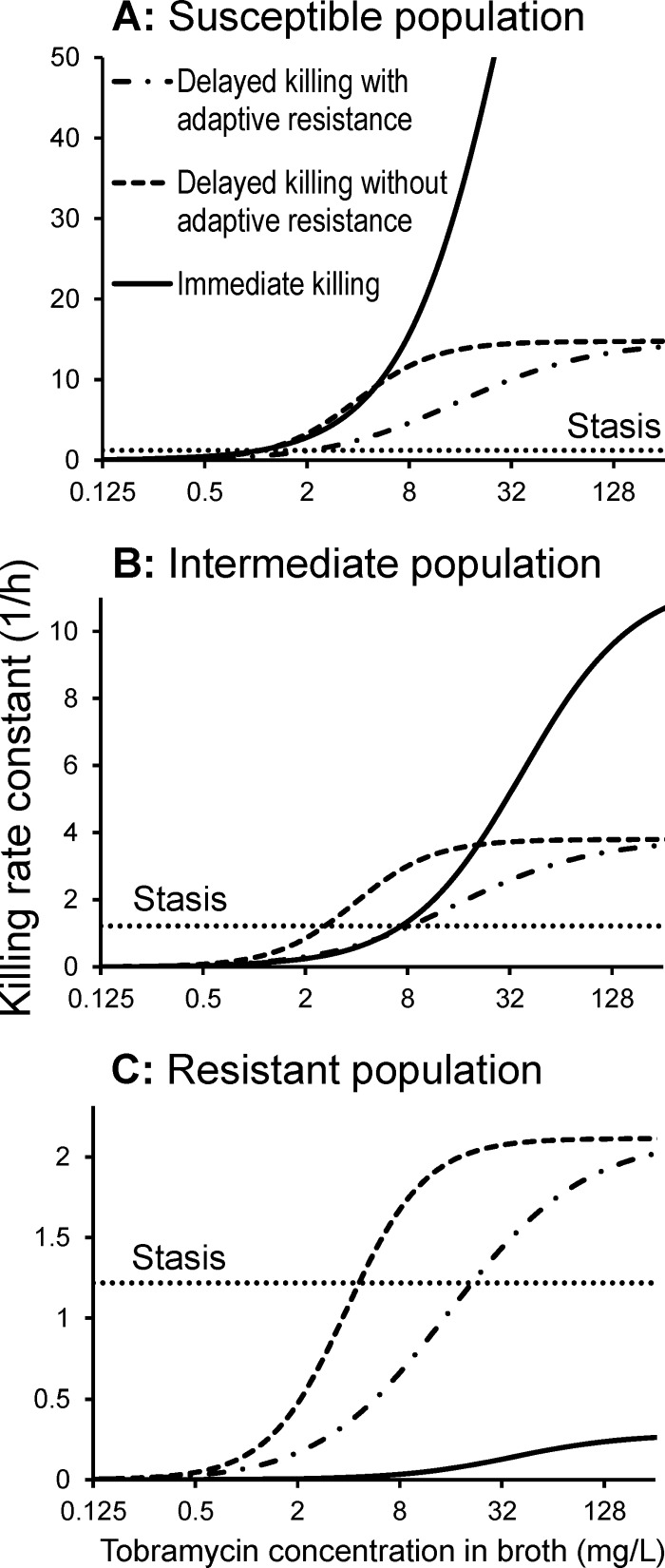
The calculated rate constants for immediate and delayed killing of PAO1-RH (Fig. 6) showed that immediate killing was a major component of total bacterial killing for the susceptible and intermediate populations. For the susceptible population, immediate killing was the predominant killing mechanism for tobramycin concentrations in broth above 4 mg/liter and was as important as delayed killing for tobramycin concentrations below 4 mg/liter (Fig. 6A). For the intermediate population, immediate killing contributed the predominant killing effect for tobramycin concentrations of at least 32 mg/liter, whereas delayed killing contributed the majority of killing for tobramycin concentrations up to 8 mg/liter (Fig. 6B). Against the resistant population, immediate killing was negligible, and approximately 4 to 16 mg/liter tobramycin in broth (Fig. 6C) was required to achieve stasis due to delayed killing.

FIG 6.

Killing rate constants for PAO1-RH at low bacterial densities for immediate killing and delayed killing (with or without adaptive resistance) for a range of extracellular tobramycin concentrations (i.e., tobramycin in broth). Adaptive resistance due to overexpression of the MexXY-OprM pump decreased the intracellular tobramycin concentration (C_intra) and therefore affected the delayed killing (due to the effect on protein synthesis) (Fig. 1) but not the immediate killing. In the absence of adaptive resistance, the intracellular tobramycin concentration (C_intra) was equal to the tobramycin concentration in broth (C_broth). The relationship between C_intra and C_broth at steady state is described in Materials and Methods. This figure illustrates the killing rate constants at low bacterial densities (i.e., Sig_Response = 0), and attenuated killing at high bacterial densities is not shown in this figure. Phenotypic tolerance at high bacterial densities attenuated both immediate and delayed killing. If the sum of the immediate and delayed killing rate constant equals the dotted, horizontal line, stasis of bacterial counts is achieved for the respective population. Stasis required approximately 0.7 mg/liter for the susceptible, 2 to 3.5 mg/liter for the intermediate, and 4 to 16 mg/liter for the resistant populations (ranges caused by adaptive resistance).

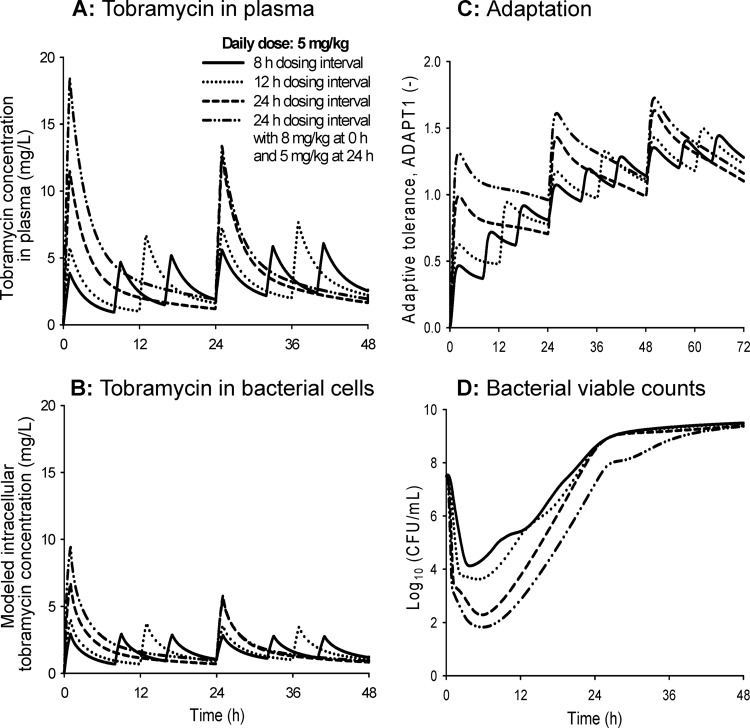
The highest tobramycin peak concentrations were predicted for regimens with a 24-h dosing interval, as expected (Fig. 7A and B). At clinically relevant tobramycin concentrations, the average extent of adaptation was relatively small (Adapt1, <2) (Fig. 7C). The area under the intracellular concentration-time curve (AUC_intra) divided by the area under the plasma concentration-time curve (AUC_plasma) represents a measure of the average extent of adaptation over time. The simulated AUC_intra/AUC_plasma values were comparable between the four evaluated dosage regimens. This ratio ranged between 48% and 61% on day 1 (i.e., when areas were integrated from 0 to 24 h), between 42% and 47% on day 2, and between 41% and 43% on day 3 for the four studied dosage regimens. The onset of adaptation was slower for regimens with an 8- and 12-h dosing interval than for regimens with a 24-h dosing interval (Fig. 7C). Despite their more rapid onset of adaptation, regimens with dosing every 24 h were predicted to achieve approximately 2 log₁₀ and 1.5 log₁₀ more killing than regimens with dosing every 8 h and 12 h, respectively, at the same daily dose (Fig. 7D).

FIG 7.

Predicted tobramycin concentrations in plasma (A) and in the intracellular space (B), extent of adaptive resistance (Adapt1) (C), and viable counts of the total population of PAO1-RH (D). The simulated dosage regimens used a daily dose of 5 mg/kg tobramycin given every 24 h (with or without a 3-mg/kg loading dose at 0 h), every 12 h, or every 8 h. The tobramycin MIC for PAO1-RH was 0.5 mg/liter in cation-adjusted Mueller-Hinton broth.

DISCUSSION

Aminoglycosides present an important part of our armamentarium of antibiotics (4, 59) and are known to have multiple mechanisms of action (6, 11, 12). Disruption of the outer membrane of Gram-negative bacteria by aminoglycosides may be particularly important to design synergistic combination regimens, as the outer membrane presents a major penetration barrier for many antibiotics (13, 14). This synergistic effect is most likely influenced by the extracellular tobramycin concentration at the outer membrane (11, 12), and as such is not affected by resistance mechanisms which act to decrease the intracellular tobramycin concentration. Only a small number of studies have assessed the effect of aminoglycosides on the outer membrane (7–12), and pharmacodynamic models with multiple mechanisms of aminoglycoside-related bacterial killing are lacking.

We propose the first pharmacodynamic model for aminoglycosides that accounts for two killing mechanisms as well as preexisting and adaptive resistance and described viable count profiles at multiple initial inocula. The proposed mechanism-based model for tobramycin against P. aeruginosa contains susceptible, intermediate, and resistant populations (Fig. 1). Delayed killing was attributed to the effect of tobramycin on protein synthesis and immediate killing to disruption of the outer membrane. Consistent across all three studied strains, delayed killing required lower intracellular tobramycin concentrations (SC_50,delay) (Table 1) than the immediate killing effect (SC_50,imm) due to disruption of the outer membrane. The estimated SC_50,imm was in agreement with the gentamicin concentration required to disrupt the outer membrane of P. aeruginosa in the presence of Mg²⁺ and Ca²⁺ (7) and to displace dansyl-labeled polymyxin B bound to P. aeruginosa lipopolysaccharide (8).

It was highly interesting to see lag times of up to 6 h before the viable count profiles of PAO1-RH declined (Fig. 2). These lag times consistently occurred in duplicate experiments at multiple tobramycin concentrations (Fig. 5C). It seems unlikely that such long lag times can be explained by the time required for tobramycin to penetrate to its intracellular target site (6). The proposed model explained these lag times by the presence of a delayed and an immediate killing mechanism (Fig. 1). The lag time associated with delayed killing can be explained by the time needed for the synthesis of hypothetical lethal protein(s), which required approximately 2 h at low bacterial densities (MTT_Prot,low) (Table 1) and longer at high densities. Aminoglycosides have been shown to cause misreading at the ribosome, and the incorporation of these misread proteins destabilizes the inner membrane and ultimately contributes to bacterial killing (6).

As high tobramycin concentrations yielded rapid killing without a lag time, the model assumed that immediate killing was caused by the disruptive effect of tobramycin on the outer membrane (11, 12). Immediate killing was most pronounced against the susceptible and intermediate populations but was essentially absent against the resistant population (Fig. 6), which is coincident with the reported phenotypic decrease of the net negative charge on the outer membrane of tobramycin-resistant Gram-negative bacteria (17–20, 60). Taken together, these results suggest that tobramycin might permeabilize the outer membrane of the susceptible and intermediate population but not of the tobramycin-resistant population. The latter population was relatively small and had a modeled log₁₀ mutation frequency between −5.83 and −6.43, depending on the strain (Table 1), which was in agreement with the observed population analysis profiles (Fig. 4). This population would need to be killed by the immune system or by a second antibiotic used in combination therapies.

We assessed two wild-type P. aeruginosa strains and a ΔmexZ mutant but did not study tobramycin-resistant isolates, which presents a potential limitation of this work. Future studies on different aminoglycoside-resistant strains are needed to quantify the relative contributions of immediate and delayed killing in resistant strains and to assess the extent and time course of synergy for aminoglycoside combination regimens. Previous hollow fiber and mouse pneumonia studies assessed the synergy of aminoglycoside plus β-lactam combinations in aminoglycoside-susceptible P. aeruginosa (59, 61, 62) and aminoglycoside-resistant Acinetobacter baumannii (63, 64). However, quantitative time course models that can predict the synergy of aminoglycoside-based combination dosage regimens are rare (65). Based on our results for the ΔmexZ mutant and its isogenic PAO1 wild type, delayed killing is expected to become less important for resistant strains with decreased intracellular aminoglycoside concentrations.

In addition to the genotypic resistance represented by three bacterial populations with different susceptibilities, the proposed model incorporated two phenotypic tolerance mechanisms, namely, the overexpression of the MexXY-OprM efflux pump and slower killing at high than at low bacterial densities (i.e., an inoculum effect) (Fig. 1). The rate of immediate killing could be completely inhibited, and the rate of delayed killing was up to 82-fold (for PAO1-RH) or up to 34-fold (for the other strains) slower at high (kmax_{delay,S/I/R,high}) than at low (kmax_{delay,S/I/R,low}) bacterial densities (Table 1). The rates of bacterial replication and of protein synthesis were also substantially slower at high than at low inocula. Therefore, the inoculum effect attenuated the rate but not the extent of killing by tobramycin at high bacterial densities (Fig. 2, 3, and 5). A previous model included a large (>50% of the total inoculum) population of E. coli at high bacterial densities that was resistant and could not be killed by gentamicin (35). Fortunately, for P. aeruginosa, our data showed that clinically achievable tobramycin concentrations of 4 and 16 mg/liter yielded 3.5 and 5.2 log₁₀ killing even against the highest tested inoculum of 10^8.9 CFU/ml (Fig. 2), demonstrating the absence of a large, resting, tobramycin-resistant population for P. aeruginosa.

Adaptive resistance (i.e., tolerance) of P. aeruginosa to aminoglycosides has been previously reported to be related to the overexpression of the MexY component of the MexXY-OprM efflux pump (21–23). In response to tobramycin, both the MIC and amounts of MexY protein isolated from P. aeruginosa cells were upregulated within less than approximately 2 h (23). After removal of tobramycin, it took approximately 6 to 24 h for this overexpression to revert back to baseline. This rapid onset and slow decline of adaptive resistance was best described by a two-compartment model (Fig. 1, Table 1). Our estimated rate constants for adaptive resistance resulted in half-lives of 0.5 h and 18 h for the two exponential phases of the adaptive resistance model for PAO1-RH. This time scale for the rapid onset and slow decline of adaptive resistance (Fig. 7C) was in agreement with the data from Hocquet et al. (23).

At clinically relevant tobramycin concentrations, adaptive resistance decreased the modeled intracellular tobramycin exposure (AUC_intra) to approximately half of the exposure in plasma (AUC_plasma) (Fig. 7). The onset of adaptive resistance was much more rapid for regimens with dosing every 24 h compared to dosing every 8 h (Fig. 7C). However, at the same daily dose, dosing every 24 h achieved 2 log₁₀ more killing than dosing every 8 h due to the greater drug exposure during the first 12 h, i.e., when most viable bacteria were from the susceptible or intermediate population (Fig. 7D).

The present work generated tobramycin time-kill profiles and determined the presence of a delayed and an immediate killing function via mechanism-based modeling. A limitation of this study is the lack of direct experimental data that demonstrate that the immediate killing is related to the effect of tobramycin on the outer membrane. Nevertheless, this is a minor consideration in view of a series of studies that demonstrated the effect of tobramycin on the outer membrane in P. aeruginosa (7–10) and that showed this extracellular effect resulted in >3 log₁₀ killing of P. aeruginosa (11, 12). Further, the tobramycin concentrations required for immediate killing in our model were in the same range as those reported for the effect of aminoglycosides on the outer membrane in P. aeruginosa (7, 8), suggesting that the proposed model is plausible.

In conclusion, this study showed that tobramycin kills P. aeruginosa by two mechanisms. The extracellular tobramycin concentration causes immediate and rapid killing at high tobramycin concentrations, whereas the intracellular tobramycin concentration was modeled to cause a delayed bacterial killing. The immediate killing mechanism is most likely not affected by the vast majority of resistance mechanisms that only reduce the intracellular tobramycin concentration. The rate of bacterial killing was substantially attenuated at high compared to low inocula. However, the extent of killing was comparable across all inocula. The proposed mechanism-based model is the first which contains two mechanisms of action as well as genotypic and phenotypic resistance to aminoglycosides. Future studies are warranted to evaluate the two killing mechanisms for aminoglycosides against strains with a variety of aminoglycoside-related resistance mechanisms. Overall, the two mechanisms of aminoglycoside action and our quantitative model hold great promise for the rational development and optimization of novel, synergistic aminoglycoside combination dosage regimens against multidrug-resistant Gram-negative bacteria.