Uncertainty analysis for absorption and first-derivative EPR spectra

Abstract

Electron paramagnetic resonance (EPR) experimental techniques produce absorption or first-derivative spectra. Uncertainty analysis provides the basis for comparison of spectra obtained by different methods. In this study it was used to derive analytical equations to relate uncertainties for integrated intensity and line widths obtained from absorption or first-derivative spectra to the signal-to-noise ratio (SNR), with the assumption of white noise. Predicted uncertainties for integrated intensities and line widths are in good agreement with Monte Carlo calculations for Lorentzian and Gaussian lineshapes. Conservative low-pass filtering changes the noise spectrum, which can be modeled in the Monte Carlo simulations. When noise is close to white, the analytical equations provide useful estimates of uncertainties. For example, for a Lorentzian line with white noise, the uncertainty in the number of spins obtained from the first-derivative spectrum is 2.6 times greater than from the absorption spectrum at the same SNR. Uncertainties in line widths obtained from absorption and first-derivative spectra are similar. The impact of integration or differentiation on SNR and on uncertainties in fitting parameters was analyzed. Although integration of the first-derivative spectrum improves the apparent smoothness of the spectrum, it also changes the frequency distribution of the noise. If the lineshape of the signal is known, the integrated intensity can be determined more accurately by fitting the first-derivative spectrum than by first integrating and then fitting the absorption spectrum. Uncertainties in integrated intensities and line widths are less when the parameters are determined from the original data than from spectra that have been either integrated or differentiated.

Introduction

In the early days of electron paramagnetic resonance (EPR), continuous wave (CW) data were obtained as absorption spectra, but quickly the use of magnetic field modulation and phase-sensitive detection made first-derivative spectra almost a defining characteristic of EPR (1,2). Other EPR detection methods such as pulse Fourier transform, field-swept echo-detected (3), and rapid scan EPR (4,5) generate absorption spectra. The signal-to-noise ratio (SNR) for a spectrum is a standard way to compare one first-derivative spectrum to another and to evaluate spectrometer performance. However, when evaluating methods that acquire data as absorption spectra with others that record the first-derivative, it is important to consider the uncertainties in derived parameters such as integrated intensity that are needed for quantitation of signal (2) and line widths, as well as SNR. In addition, automation of data analysis and improved capabilities of data fitting software mean that it is increasingly common to extract parameters by automated fitting, rather than by manual manipulation.

In the absence of noise, spectroscopic parameters can be found exactly. However, noise in the spectra introduces uncertainty into the derived parameters, which depends on the SNR. This paper addresses the question of how to quantitatively compare experimental absorption and first-derivative spectra including noise, and to estimate uncertainties in parameters derived from spectra with different SNR. Uncertainties are compared for parameters obtained: (i) by fitting the original absorption or first-derivative spectra, (ii) after differentiation of absorption spectra, and (iii) after integration of derivative spectra.

Sensitivity analysis is defined as the analysis of how the uncertainty in a final result is apportioned to different sources of uncertainty in the inputs (6). The related ‘uncertainty analysis’ focuses on how uncertainty in the inputs translates into uncertainty in calculated outputs (6). This article is an application of uncertainty analysis to the impact of noise in experimental data on the uncertainty in determination of the total number of spins (the integrated intensity of the absorption spectrum) and the line width for absorption and first-derivative EPR spectra. Stated differently, how good does the SNR for a first derivative spectrum need to be to give the same precision in the determination of the number of spins (or in measured line widths) as can be obtained from the absorption spectrum with a specified SNR. The focus is on cases with relatively low SNR. The analysis was performed by deriving analytical expressions and by Monte Carlo simulations. Noise was computer generated and added to the numerically generated spectra. Since integration and differentiation change the noise spectrum, these data manipulations also are discussed. If a spectroscopic model had a large number of parameters, Monte-Carlo analysis could be computationally expensive. The analytical method to estimate uncertainties has the advantage that it does not require extensive computations, but are only approximations when noise is not white.

Analytical Analysis

The following is a derivation of analytical equations for uncertainty analysis of an EPR lineshape model with two spectroscopic parameters and Gaussian white noise. One parameter always is the integrated signal intensity and the second parameter can be selected for a particular case, such as line width or hyperfine coupling. An absorption spectrum can be described by continuous function f Eq [1].

$$\mathrm{s}(H)={\mathrm{A}}_0\mathrm{f}({\mathrm{p}}_0,H)$$ [1]

where A₀ is the integrated intensity:

$${\mathrm{A}}_0=\underset{-\infty }{\overset{\infty }{\int }}\mathrm{s}(H)\mathrm{d}H$$ [2]

and p₀ is a spectroscopic parameter, such as line width. Since an experimental spectrum is a set of discrete values, s(H) for the uncertainty analysis is sampled at N discrete values of magnetic field:

$$s(H_i)={\mathrm{A}}_0\mathrm{f}({\mathrm{p}}_0,H_i)\mathrm{\delta }H+\mathrm{n}(H_{\mathrm{i}}),\mathrm{\delta }H=H_{\mathrm{i}+1}-H_{\mathrm{i}},\mathrm{i}=(1,\dots \mathrm{N})$$ [3]

The parameter δH is the field increment and is present in the equations to make the sum independent of N. The spectrum contains Gaussian white noise n with the standard deviation σ. It can be fitted to obtain A and p that differ from A₀ and p₀ because of noise:

$$\{\begin{array}{l}A={\mathrm{A}}_0+\mathrm{\delta }A\hfill \\ p={\mathrm{p}}_0+\mathrm{\delta }p\hfill \end{array}$$ [4]

The discrepancy between the fitting model with parameters in Eq. [4] and the spectrum, Eq.[3], is given by Eq. [5]:

$$\text{Err}(A,p),={\sum }_{\mathrm{i}=1}^{\mathrm{N}}{[\mathrm{s}(H_i)-A\mathrm{f}(p,H_i)\mathrm{\delta }H]}^2$$ [5]

It is assumed that δA ≪ A₀ and δp ≪ p₀, and that SNR is high enough that line fitting can obtain estimates of the parameters with acceptable uncertainties. Substitution of Eq.[4] into Eq.[5], Taylor expansion, and preservation only of linear terms gives

$$\text{Err}(\mathrm{\delta }A,\mathrm{\delta }p)\approx {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{[-\mathrm{\delta }A\mathrm{f}({\mathrm{p}}_0,H_i)\mathrm{\delta }H-\mathrm{\delta }p\mathrm{g}({\mathrm{p}}_0,H_i)\mathrm{\delta }H+{\mathrm{n}}_{\mathrm{i}}]}^2,\mathrm{g}(p,H_i)={\mathrm{A}}_0\frac{\partial }{\partial \mathrm{p}}\mathrm{f}(p,H_i)$$ [6]

The global minimum for Eq.[6] can be found by setting the partial derivatives of Err(δA,δp) with respect to δA and δp equal to zero. The result is a system of two algebraic equations:

$$\{\begin{array}{l}\mathrm{\delta }A(\mathbf{f},\mathbf{f})+\mathrm{\delta }p(\mathbf{f},\mathbf{g})=(\mathbf{n},\mathbf{f})/\mathrm{\delta }H\hfill \\ \mathrm{\delta }A(\mathbf{f},\mathbf{g})+\mathrm{\delta }p(\mathbf{g},\mathbf{g})=(\mathbf{n},\mathbf{g})/\mathrm{\delta }H\hfill \end{array}$$ [7]

where $(\mathbf{a},\mathbf{b})={\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{b}}_{\mathrm{i}}$ can be considered as the dot product of two sets of discrete values a and b. The solution of Eq.[7] is:

$$\begin{array}{l}\mathrm{\delta }A=\{(\mathbf{g},\mathbf{g})(\mathbf{n},\mathbf{f})-(\mathbf{f},\mathbf{g})(\mathbf{n},\mathbf{g})\}/(\mathrm{D}\mathrm{\delta }H)\hfill \\ \mathrm{\delta }p=\{(\mathbf{f},\mathbf{f})(\mathbf{n},\mathbf{g})-(\mathbf{f},\mathbf{g})(\mathbf{n},\mathbf{f})\}/(\mathrm{D}\mathrm{\delta }H)\hfill \end{array}$$ [8]

where

$$D=(\mathbf{f},\mathbf{f})(\mathbf{g},\mathbf{g})-{(\mathbf{f},\mathbf{g})}^2$$ [9]

A series of calculations with different values of n produces an ensemble of values for A and p. It follows from Eq.[8] that because the mean value of white noise (n) is equal to zero, the mean values of δA and δp are also zero. Thus, the mean values of A and p are A₀ and p₀, respectively. The uncertainties, σ_A and σ_p, are the standard deviations for A and p in the ensemble, and can be calculated using Eq. [8].

$$\begin{array}{l}{\mathrm{\sigma }}_A=\frac{1}{\mathrm{D}\mathrm{\delta }H}\sqrt{<{\{(\mathbf{g},\mathbf{g})(\mathbf{n},\mathbf{f})-(\mathbf{f},\mathbf{g})(\mathbf{n},\mathbf{g})\}}^2>}\hfill \\ {\mathrm{\sigma }}_A=\frac{1}{\mathrm{D}\mathrm{\delta }H}\sqrt{<{\{(\mathbf{f},\mathbf{f})(\mathbf{n},\mathbf{g})-(\mathbf{f},\mathbf{g})(\mathbf{n},\mathbf{f})\}}^2>}\hfill \end{array}$$ [10]

The notation < > denotes the average over the ensemble. Using the property of white Gaussian noise that two different values of the noise vector are not correlated, Eq. [11],

$$<{\mathrm{n}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{j}}>=\{\begin{array}{ll}0,\hfill & \mathrm{i}\ne \mathrm{j}\hfill \\ {\mathrm{\sigma }}^2,\hfill & \mathrm{i}=\mathrm{j}\hfill \end{array}$$ [11]

Eq.[10] can be reduced to:

$$\begin{array}{l}{\mathrm{\sigma }}_A=\frac{\mathrm{\sigma }}{\mathrm{\delta }H}\sqrt{(\mathbf{g},\mathbf{g})/D}\hfill \\ {\mathrm{\sigma }}_p=\frac{\mathrm{\sigma }}{\mathrm{\delta }H}\sqrt{(\mathbf{f},\mathbf{f})/D}\hfill \end{array}$$ [12]

For the square root to be real, the argument must be non-negative. It is shown below that D is a positive scalar. The dot product of two vectors f and g is equal to the product of their lengths times the cosine of the angle θ between them, so (f,g)² = (f,f)(g,g)cos²θ. Since cos²θ must be positive and less than 1, D must be ≥ 0. (f,f) and (g,g) also are positive. Since g is proportional to the derivative of f with respect to p, the two vectors will not be parallel, and therefore D cannot be 0. This equation provides a basis for uncertainty analysis for two spectroscopic parameters that define an EPR line shape. The uncertainties in σ_A and σ_p can be calculated from the experimental value of σ, the standard deviation of the noise.

Equation [12], which was derived for the absorption spectrum, can be modified to calculate uncertainties in spectroscopic parameters for the first derivative line. For that purpose, the function f(H) is replaced by its derivative with respect to H, as shown in Eq.[13]:

$$\text{df}(\mathrm{p},H)=\frac{\partial }{\partial \mathrm{H}}\mathrm{f}(\mathrm{p},H)$$ [13]

When Eq. [13] is expressed in the discrete form, multiplication by δH is required. In the equations for the first-derivative g, the normalization expression (Eq. [2]) is replaced by double integration. If two independent experiments are performed to measure an absorption and a first derivative spectrum (Eq.[12]) and the analogous equation for the first derivative, can be used to compare σ_A and σ_p for the two experiments.

The analytical approach described in this section can be extended for models with additional spectroscopic parameters.

Uncertainty Analysis Applied to Lorentzian or Gaussian Lineshapes

Lorentzian and Gaussian lineshapes are typical for EPR spectra. Two parameters of interest are integrated intensities (number of spins, A) and line widths. The general equations derived in the prior section are therefore applied to these specific lineshapes to compare uncertainties in parameters derived from absorption and first derivative spectra. The software package Mathematica^® was used to evaluate Eq. [12] and to simplify expressions.

Application to a Lorentzian lineshape

The function for a Lorentzian absorption lineshape (7) is:

$$\mathrm{s}(H_{\mathrm{i}})=\frac{A_0}{\pi }\frac{{\mathit{\text{Lw}}}_0}{H_{\mathrm{i}}^2+{{\mathit{\text{Lw}}}_0}^2}\mathrm{\delta }\mathrm{H},\mathrm{i}=1,\dots \mathrm{N}$$ [14]

where Lw₀ denotes half-width at half-height line width, A₀ is the integrated intensity with Σs(H_i)=A₀, and H_i = 0 at the center of the line. Uncertainties for A and Lw, relative to the mean values, can be calculated using Eq.[12] and the relationships

$$(\mathbf{x},\mathbf{y})=\frac{1}{\mathrm{\delta }\mathrm{H}}\underset{-\infty }{\overset{\infty }{\int }}\mathrm{x}(H)\mathrm{y}(H)\mathrm{d}H$$ [15]

where x, y are either f or g, resulting in

$$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}=\frac{{\mathrm{\sigma }}_{\mathrm{A}}}{{\mathrm{A}}_0}=\frac{2\mathrm{\sigma }}{{\mathrm{A}}_0}\sqrt{\frac{\pi \text{Lw}}{\mathrm{\delta }H}}\hfill \\ {\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}=\frac{{\mathrm{\sigma }}_{\mathrm{A}}}{{\text{Lw}}_0}=\frac{2\sqrt{2\mathrm{\sigma }}}{{\mathrm{A}}_0}\sqrt{\frac{\pi \text{Lw}}{\mathrm{\delta }H}}\hfill \end{array}$$ [16]

The maximum amplitude of the Lorentzian function (I_max) is given by ${\mathrm{I}}_{max}=\mathrm{s}(0)=\frac{{\mathrm{A}}_0\mathrm{\delta }\mathrm{H}}{\pi {\text{Lw}}_0}$. The signal-to-noise ratio for the absorption line is defined as SNR^abs = I_max/σ, so Eq. [16] can be rewritten as:

$$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}=\frac{2}{{\text{SNR}}^{\text{abs}}\sqrt{\pi \mathrm{k}}}\hfill \\ {\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}=\frac{2\sqrt{2}}{{\text{SNR}}^{\text{abs}}\sqrt{\pi \mathrm{k}}}\hfill \end{array}$$ [17]

where k = Lw₀/δH, is the number of data points per line width Lw₀.

Analogously, uncertainties in the parameters for the first derivative line:

$$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}=\frac{3\sqrt{3}}{{\text{SNR}}^{\text{der}}\sqrt{\pi \mathrm{k}}}\hfill \\ {\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}=\frac{3}{{\text{SNR}}^{\text{der}}\sqrt{\pi \mathrm{k}}}\hfill \end{array}$$ [18]

can be obtained by using Eq.[12] and [13] and defining SNR^der as the ratio of the peak-to-peak signal amplitude to σ. Eq. [17] and [18] can be used to compare uncertainties in A and Lw obtained from absorption and first-derivative spectra:

$$\begin{array}{l}\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}=\frac{3\sqrt{3}}{2}\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\approx 2.60\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\hfill \\ \frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}=\frac{3}{2\sqrt{2}}\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\approx 1.60\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\hfill \end{array}$$ [19]

It follows from Eq.[19] that if SNR^abs =SNR^der, the uncertainty in the measurement of A is 2.60 times larger for the derivative line than for the absorption, and uncertainties for the line width are about the same. Note that these ratios do not depend on the line width.

Application to Gaussian lineshape

Substitution of the equations for a Gaussian lineshape (7) into Eq. [12] and [13] gives the following results:

$$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}=\frac{\sqrt{3}{(ln(2)/2)}^{1/4}}{\sqrt[4]{\pi }{\text{SNR}}^{\text{abs}}\sqrt{\mathrm{k}}}\approx \frac{1}{{\text{SNR}}^{\text{abs}}\sqrt{\mathrm{k}}}\hfill \\ {\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}=\frac{\sqrt{3}{(ln(2)/2)}^{1/4}}{\sqrt[4]{\pi }{\text{SNR}}^{\text{abs}}\sqrt{\mathrm{k}}}\approx \frac{1.96}{{\text{SNR}}^{\text{abs}}\sqrt{\mathrm{k}}}\hfill \end{array}$$ [20]

Uncertainties for the first-derivative line:

$$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}=\frac{\sqrt[2]{5}\sqrt[4]{ln(4)}}{\sqrt[4]{\pi }\sqrt{\mathrm{e}}{\text{SNR}}^{\text{der}}\sqrt{\mathrm{k}}}\approx \frac{2.21}{{\text{SNR}}^{\text{der}}\sqrt{\mathrm{k}}}\hfill \\ {\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}=\frac{4\sqrt[0.75]{2}}{\sqrt[4]{\pi ln2}\sqrt{3\mathrm{e}}{\text{SNR}}^{\text{der}}\sqrt{\mathrm{k}}}\approx \frac{1.94}{{\text{SNR}}^{\text{der}}\sqrt{\mathrm{k}}}\hfill \end{array}$$ [21]

Eq. [20] and [21] can be used to compare uncertainties in A and Lw obtained from absorption and first-derivative spectra:

$$\begin{array}{l}\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}\approx 2.21\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\hfill \\ \frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}\approx 0.99\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}\hfill \end{array}$$ [22]

It follows from Eq.[22] that if SNR^abs =SNR^der, the uncertainty in the measurement for A is 2.21 times larger for the derivative than for the absorption spectrum, and uncertainties are about the same for the line widths. Note that these ratios are similar to what was obtained for Lorentzian lines, and so it is expected that similar results would be obtained for intermediate lineshapes.

Monte-Carlo analysis

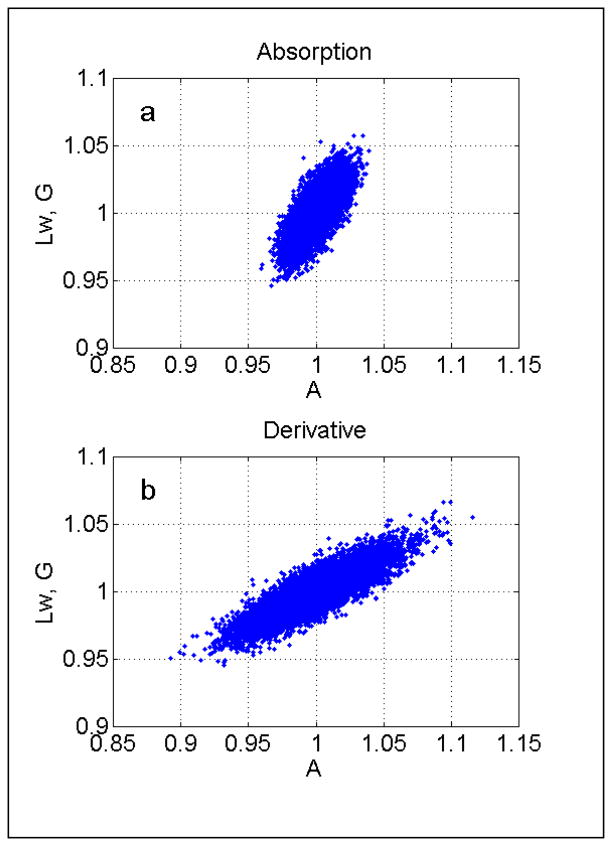
To test these analytical expressions, uncertainty analysis was carried out using numerical Monte-Carlo simulations in MatLab. Absorption and first-derivative Lorentzian lines with intensity A₀ and half width at half height Lw₀, were generated numerically. White Gaussian noise was added with the routine randn. The standard deviations of noise, σ, were selected to produce spectra with equal SNRs: SNR^abs = SNR^der. The spectra were fitted using the Matlab least-squares non-linear curve fitting routine lsqcurvefit to give A and Lw, for the absorption and derivative lines, respectively. The procedure of noise addition and line fitting was repeated 5,000 times to produce statistical ensembles for A and Lw. Scatter plots in Fig.1 show the values of A and Lw obtained with the input parameters A₀ = 1, Lw₀ = 1G and SNR = 5. σ_A and σ_Lw were computed as the standard deviations of A and Lw. The shapes of the plots reflect the behavior of the error functions (Eq. [5]). The greater elongation of the plot of observed errors for the first derivative than for the absorption reflects the greater uncertainty in A obtained from the first derivative. Similar numerical experiments performed with various SNR, A₀, and Lw₀ did not produce noticeable change in the uncertainties. Results for the Monte-Carlo analyses for A₀ = 1, Lw₀ = 1G and SNR = 5, 10, 15 are presented in Table 1, rows 2 - 4. Row 1 shows the predicted values based on Eq.[19]. The results of the Monte-Carlo simulations agree with the analytical analysis to within less than 2%. The agreement between the analytical expressions and Monte-Carlo analysis is not dependent on SNR.

Fig.1.

Scatter plots for A and Lw obtained for absorption (a) and first-derivative Lorentzian spectra (b). Each subplot has 5,000 points corresponding to the fitting results of 5,000 numerical experiments. In each experiment random noise was added to the absorption and derivative spectra with A₀ = 1, Lw₀ = 1G. The standard deviation of noise, σ, was selected to produce spectra with SNR=5.

Table 1.

Ratios of uncertainties in A and LW for absorption and derivative Lorentzian lines with the same SNR.

Row	Method	Filter	Broadening	SNR	$\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}$	$\frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}$
1	Eq. [19]	-		-	2.60	1.06
2	Monte-Carlo	None	-	5	2.64 (2%)a	1.06 (0%)a
3	Monte-Carlo	None	-	10	2.61 (0%)a	1.07 (1%)a
4	Monte-Carlo	None	-	15	2.62 (1%)a	1.07 (1%)a
5	Monte-Carlo	Butterworth	1%	5	2.58 (-1%)a	0.94 (-11%)a
6	Monte-Carlo	Butterworth	1%	10	2.13 (-18%)a	0.87 (-18%)a
7	Monte-Carlo	Butterworth	1%	15	2.12 (-18%)a	0.87 (-18%)a

^aDeviations from the values predicted by Eq. [19], row R1, are shown in parentheses.

Ratios of uncertainties obtained by the analogous method for a Gaussian lineshape are shown in Table 2. When there is no filtering, there is good agreement between the predictions from the analytical equations, and the results from Monte Carlo analysis, analogous to what was observed for the Lorentzian lineshape.

Table 2.

Ratios of uncertainties for A and LW for absorption and derivative Gaussian lines with the same SNR.

R	Method	Filter	Broadening	SNR	$\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}$	$\frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}$
1	Eq. [22]	-		-	2.21	0.99
2	Monte-Carlo	None	-	5	2.17 (2%)	0.98 (0%)
3	Monte-Carlo	None	-	10	2.20 (0%)	0.99 (1%)
4	Monte-Carlo	None	-	15	2.21 (1%)	0.99 (1%)
5	Monte-Carlo	Butterworth	1%	5	2.07 (-6%)	0.92 (-7%)
6	Monte-Carlo	Butterworth	1%	10	1.95 (-12%)	0.92 (-7%)
7	Monte-Carlo	Butterworth	1%	15	1.93 (-13%)	0.91 (-8%)

Impact of filtering on uncertainties

Experimental spectra usually are filtered, either in hardware or by post-processing, to reduce high-frequency noise. As a result, the white noise assumption, Eq.[11], that was used to derive Eq.[12] is violated, which can be demonstrated with a simple binomial filter:

$$\begin{array}{l}{\mathrm{n}}_{\mathrm{i}}^{\prime }=\frac{1}{4}({\mathrm{n}}_{\mathrm{i}-1}+2{\mathrm{n}}_{\mathrm{i}}+{\mathrm{n}}_{\mathrm{i}+1}),\mathrm{i}=(2,\dots ,\mathrm{N}-1)\hfill \\ {\mathrm{n}}_{\mathrm{i}+1}^{\prime }=\frac{1}{4}({\mathrm{n}}_{\mathrm{i}}+2{\mathrm{n}}_{\mathrm{i}+1}+{\mathrm{n}}_{\mathrm{i}+2})\hfill \end{array}$$ (23)

Each data point in the filtered array becomes a weighted sum of the neighboring points in the original array. As a result, two adjacent data points become correlated, $<{\mathrm{n}}_{\mathrm{i}}^{\prime }{\mathrm{n}}_{\mathrm{i}\pm 1}^{\prime }>\ne 0$. Introduction of a filter function into the analytical analysis would be cumbersome, but the impact of a filter can readily be evaluated using the Monte-Carlo analysis. A 4^th order low-pass Butterworth filter has been found to be useful with experimental data (8), so it was selected as the example to test. It was applied to the calculated absorption and first-derivative spectra. The cut-off frequencies of the filter were selected to produce 1% line broadening, which improves SNR without significantly compromising the spectral shape. The cut-off frequency that produces 1% broadening for the derivative line was about 50% larger than that for the absorption line. Filtering the spectra + noise reduced the ratios of uncertainties of A and Lw by as much as 18% for Lorentzian lines and 13% for Gaussian lines (Tables 1 and 2, rows 5-7).

The results shown in Tables 1 and 2 indicate that for spectra with equal SNR, fitting the absorption signal produces more precise values of the integrated signal intensity than fitting the first derivative. The derivative line is slightly more likely to give a more precise value of the line width. In addition, when comparing absorption and derivative spectra with different SNR, the inverse relationship between uncertainty and SNR (Eq. 17, 18, 20, 21) must be taken into account.

Changes in Uncertainties Caused by Differentiation or Integration

Change in noise caused by differentiation of absorption line

One way to compare absorption and first derivative spectra is by differentiation of the absorption line. In this section equations are derived to estimate the effect of differentiation on SNR and uncertainties in A and Lw. The impact of differentiation on the signal amplitude is known for a defined lineshape. To determine the change in SNR thus requires understanding of the change in noise. The change in σ depends on the type and cut-off frequencies of the filter that is used to reduce high-frequency noise. To analyze the impact of differentiation on white noise, the vector n is Fourier transformed to obtain

$$\mathrm{N}({\mathrm{v}}_{\mathrm{m}}),\text{where}{\mathrm{v}}_{\mathrm{m}}=\mathrm{m}\mathrm{\delta }\mathrm{v},\mathrm{m}=(-\frac{\mathrm{N}}{2},\dots ,\frac{\mathrm{N}}{2}-1)$$ [24]

In Eq.[24] δv is the frequency increment in units of 1/gauss. The rationale for expressing frequency in inverse magnetic field units lies in the nature of the discrete Fourier transformation, DFT. The Fourier transform of the spectrum is the sum of sinusoidal waves. The period of the longest wave is equal to the sweep width SW. The frequency that corresponds to this wave is |v₁| = δv = 1/SW. All other waves have frequencies that are integer multipliers of δv. Applying a filter in the frequency domain reduces the standard deviation of the noise σ in the magnetic field domain. The noise reduction due to the filter Z(v_m) can be quantitatively evaluated using Parsevals' theorem (9):

$$\sum _{\mathrm{i}=1}^{\mathrm{N}}{\left|{\mathrm{n}}_{\mathrm{i}}\right|}^2=\mathrm{N}{\mathrm{\sigma }}^2=\frac{1}{\mathrm{N}}\sum _{\mathrm{m}=-\frac{\mathrm{N}}{2}}^{\frac{\mathrm{N}}{2}-1}{\left|{\mathrm{Z}}_{\mathrm{m}}{\mathrm{N}}_{\mathrm{m}}\right|}^2$$ [25]

Where N_m is the Fourier transform of the noise, n, at point m. After averaging Eq.[25] over an ensemble of N_m, one can obtain an expression for σ:

$$\mathrm{\sigma }=\frac{{\mathrm{\sigma }}_{\mathrm{v}}}{N}\sqrt{\sum _{\mathrm{m}=-\frac{\mathrm{N}}{2}}^{\frac{\mathrm{N}}{2}-1}{\left|{\mathrm{Z}}_{\mathrm{m}}\right|}^2}$$ [26]

where σ_v is the standard deviation of the noise in the frequency domain, which does not depend on m if the noise is white. For a simple case when Z(v_m) is a sharp low-pass filter with a cut-off frequency v_cut, Eq.[26] can be approximated as

$$\mathrm{\sigma }\approx \frac{{\mathrm{\sigma }}_{\nu }}{N}\sqrt{\frac{2}{\mathrm{\delta }\mathrm{v}}\sqrt{{\mathrm{v}}_{\text{cut}}}}$$ [27]

Eq.[27] is consistent with the generalization that the SNR of the signal improves inversely proportional to the square root of the filter cutoff frequency.

A similar approach can be used to find the standard deviation σ^D of the noise in the differentiated spectrum. Differentiation in the magnetic field domain is equivalent to multiplication by j2πv_m in the frequency domain. This linear ramp amplifies the high frequency components and attenuates low frequency components of the noise. The resulting expression for the standard deviation is:

$${\mathrm{\sigma }}^D=\frac{{\mathrm{\sigma }}_v}{N}\sqrt{\sum _{\mathrm{m}=-\frac{\mathrm{N}}{2}}^{\frac{\mathrm{N}}{2}-1}{\left|2\pi v_{\mathrm{m}}{\mathrm{G}}_{\mathrm{m}}\right|}^2}$$ [28]

where G_m is the filter function. If a sharp low-pass filter with a cut-off frequency v_cut^D is used to reduce high frequency noise in the derivative spectrum, Eq.[28] becomes approximately

$${\mathrm{\sigma }}^{\mathrm{D}}\approx \frac{2\pi {\mathrm{\sigma }}_{\mathrm{v}}\mathrm{\delta }\mathrm{v}}{N}\sqrt{\sum _{\mathrm{m}=-\frac{\text{ncut}}{2}}^{\frac{\text{ncut}}{2}-1}{\mathrm{k}}^2}\approx 2\pi \frac{{\mathrm{\sigma }}_{\mathrm{v}}}{\mathrm{N}}\sqrt{\frac{2}{3\mathrm{\delta }\mathrm{v}}}\sqrt{{({\mathrm{v}}_{\text{cut}}^{\mathrm{D}})}^3},$$ [29]

where ncut = v_cut^D/δv. The standard deviation for noise in the first derivative (Eq.[29]) has a stronger dependence on the v_cut than for the absorption (Eq.[27]). In addition, multiplication by j2πv_m increases the signal bandwidth in the frequency domain, so to maintain the same broadening of the first-derivative and absorption lineshapes v_cut^D > v_cut, which increases noise.

Change in uncertainties caused by differentiation of absorption line

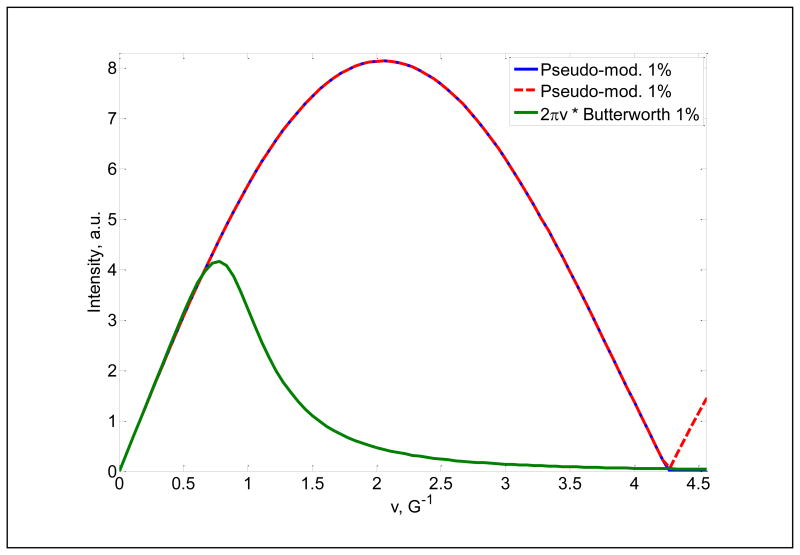
As noted by Posener (10) “resolution enhancement commonly associated with a derivative spectrum is purely subjective.” Although differentiation of the absorption signal is used to enhance resolution as perceived by the human eye (11), it does not add new spectroscopic information. The actual information content of the spectrum may be degraded by differentiation that devalues low-frequency components in the absorption signal. Monte-Carlo analysis was carried out to evaluate the change in σ_A and σ_LW due to differentiation. A Lorentzian absorption line was calculated and white Gaussian noise was added. Two methods were used to obtain the first derivative spectrum: (i) numerical differentiation followed by a 4^th order Butterworth low-pass filter, (ii) pseudo-modulation (12). The cut-off frequency of the Butterworth filter was adjusted to produce 1% broadening of the first-derivative line. The net effect of multiplication by j2πv_k to obtain the derivative, followed by the Butterworth filter is the filter function shown in Fig.2 (green trace). In the second method the modulation amplitude was also adjusted to broaden the line by 1%. Because of the oscillatory character of the Bessel function that is used as a filter for the pseudo-modulation method, an additional square filter in the frequency domain was used to delete high frequency noise starting from the first zero crossing of the Bessel function. Fig. 2 shows the original (red dashed) and square-filtered (blue) Bessel functions. For calculation of SNR and uncertainties, the absorption spectra also were filtered using a 4^th order Butterworth filter to produce 1% line broadening. The absorption and derivative spectra were fitted to determine A and Lw. The numerical experiment starting from noise addition to line fitting was repeated 5,000 times to produce statistical ensembles for A and Lw. The ensembles were analyzed and the results are presented in Table 3. Rows 1 and 5 show theoretical predictions based on the analytical analysis. Rows 2 - 4 and 6 - 8 show the results of Monte-Carlo analysis for the Butterworth filter and pseudo-modulation, respectively. Computations were done for values of SNR ≈ 5, 10 and 15 for the absorption line, where the approximation indicates that the SNR had random values with averages around 5, 10 and 15.

Fig.2.

Comparison of two methods to calculate the first derivative spectrum: (i) numerical differentiation followed by low-pass filtering with Butterworth filter (green), (ii) pseudo-modulation (blue). The parameters for both methods were selected to produce 1% line broadening. The pseudo-modulation filter is a Bessel function of the 1^st kind (dashed red). It was modified (blue) to reduce high frequency noise.

Table 3.

Comparison of SNR and ratios of uncertainties before and after differentiation of a Lorentzian absorption line.

Row	Method	Filter, 1% broadening		SNR (Abs)	$\frac{{\text{SNR}}^{\text{abs}}}{{\text{SNR}}^{\text{der}}}$	$\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}$	$\frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}$
		Absorption	Derivative
1	Eqs. [19,26,28]	Butterworth	Differentiation + Butterworth	-	3.2	8.3	3.4
2	Monte-Carlo	Butterworth	Differentiation + Butterworth	≈ 5	3.3	2.8	1.6
3	Monte-Carlo	Butterworth	Differentiation + Butterworth	≈ 10	3.3	3.4	2.1
4	Monte-Carlo	Butterworth	Differentiation + Butterworth	≈ 15	3.3	3.5	2.1
5	Eqs. (19,26,28)	Butterworth	pseudomodulation	-	11.6	30.2	12.3
6	Monte-Carlo	Butterworth	pseudomodulation	≈ 5	12.2	N/Ra	N/Ra
7	Monte-Carlo	Butterworth	pseudomodulation	≈ 10	12.1	4.1	2.5
8	Monte-Carlo	Butterworth	pseudomodulation	≈ 15	12.1	4.5	2.8

^aN/R indicates that the noise was too large to obtain reproducible results.

There is significant degradation of SNR after differentiation and filtering. Pseudo-modulation has greater impact than numerical differentiation and low-pass filtering. For both methods the theoretical predictions for SNR ratios are in good agreement with the computations. Degradation of the SNR results in an increase in the uncertainties σ_A and σ_LW. Substitution of SNR^der/SNR^abs = 3.2, calculated from Eq. [26] and [28], into Eq. [19] predicts the ratios of uncertainties shown in Table 3 row 1. The degradation in uncertainties of the parameters (rows 2 - 4) is not as great as predicted by Eq. [19] because differentiation and filtering substantially change the noise spectrum and the resulting noise is far from white. Eq. [19] predicts a greater increase in uncertainties (row 5) when pseudomodulation is used instead of the Butterworth filter, but the degradation of the uncertainties is less than predicted (rows 6 - 8). Reliable statistics were not obtained for the absorption line with SNR=5 and the pseudo-modulation method. Because of very high noise levels in the derivative spectra, line fitting did not give reliable results. Despite large differences in SNR^der obtained by (i) numerical differentiation together with a low-pass filter and (ii) pseudo-modulation, the impact on the uncertainties in A and Lw are smaller than predicted for white noise. This observation is a reminder that when noise is not white, precision of derived parameters is not a linear function of SNR.

Fig. 2 explains the differences in performance of the two differentiation methods. The Butterworth filter has a sharper drop-off than the Bessel function, so it filters out more high-frequency noise. However the uncertainties in the fitting parameters are more sensitive to low-frequency noise than to higher-frequency noise, so the degradation in uncertainties is not as great as predicted based on the degradation in SNR.

Change in noise caused by integration of first-derivative

An alternative approach to compare two experiments that measure an absorption spectrum and its first derivative is to integrate the derivative signal. Integration of a discrete signal by cumulative summation changes noise vector n to

$${\mathrm{n}\prime }_{\mathrm{m}}^{\text{cum}}=\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{n}}_{\mathrm{i}},\mathrm{i}=(1,\dots \mathrm{N}),\mathrm{m}=(1,\dots \mathrm{N})$$ [30]

The sum of m random numbers with standard deviation σ is a random number with a standard deviation given by Eq. (31)

$${\mathrm{\sigma }}_{\mathrm{m}}^{\text{cum}}=\mathrm{\sigma }\sqrt{\mathrm{m}}$$ [31]

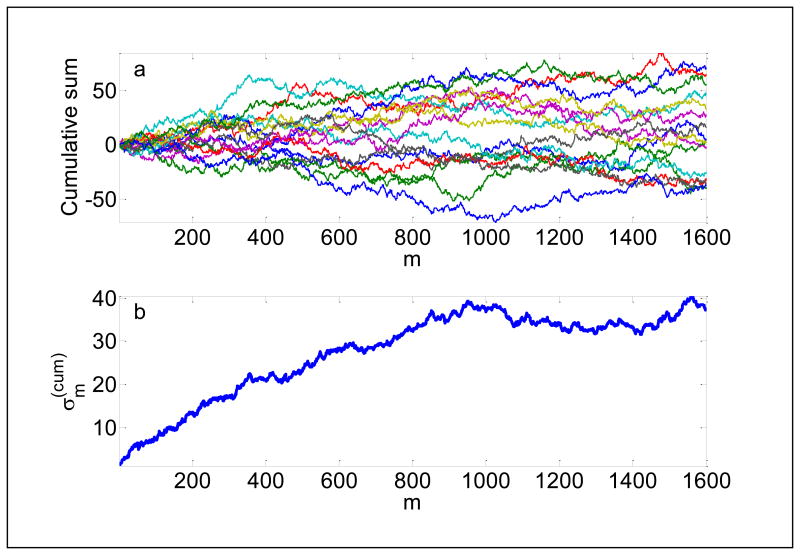
The standard deviation for the integrated noise becomes dependent on m. Eq.[31] explains the commonly observed fact that integration of the first-derivative line frequently gives a spectrum that requires an additional baseline correction. On average, the last point in the integration will have a deviation that is $\sqrt{\mathrm{N}}$ larger than that for the first point. Fig.3a demonstrates the results of cumulative integration of 16 computer-generated noise traces using the cumsum Matlab routine. Fig.3b shows the standard deviation of 16 traces computed at each point m. As expected from Eq.[31], ${\mathrm{\sigma }}_{\mathrm{m}}^{\text{cum}}$ grows proportional to $\sqrt{\mathrm{m}}$ The last point in the integrated noise, m=1600, is on average offset from the zero line by about $40=\sqrt{1600}$ Although integration is sometimes viewed as a filter, its impact on data is quite different.

Fig.3.

Cumulative integration of 16 computer-generated noise traces with zero mean value and standard deviation equal to 1 (a), and standard deviations for those 16 traces calculated at each point in the traces (b).

In integrations of experimental data, a polynomial baseline correction is often used to bring the end of the spectrum to the zero line. This does not eliminate the noise, but redistributes it across the spectrum.

Change in uncertainties caused by integration of first-derivative line

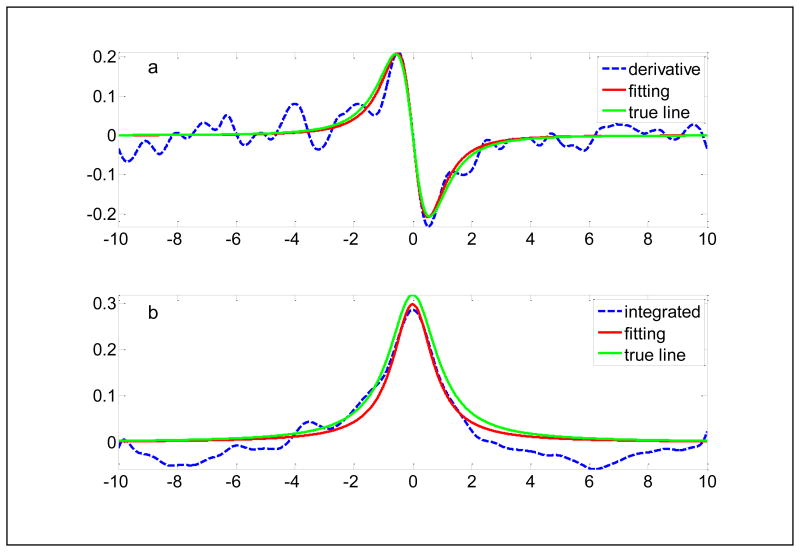
Integration of the first-derivative EPR line produces an absorption spectrum with visually improved smoothness. This is because integration in the magnetic field domain is equivalent to division by j2πv_m in the frequency domain. As a result, high-frequency components of the derivative line are attenuated and the low-frequency components are amplified. Monte-Carlo analysis was carried out to evaluate the change in σ_A and σ_Lw as a result of integration. A first-derivative Lorentzian line was generated (Fig.4a green line) and white Gaussian noise was added. The spectrum was filtered with a 4^th order low-pass Butterworth filter with v_cut^D adjusted to allow 1% of line broadening (Fig.4a dashed blue line). Since the bandwidth requirement of the first-derivative (Eq. [29]) is higher than for the absorption (Eq. [27]), filtering the first-derivative to 1% broadening does not introduce additional broadening of the absorption spectrum. The filtered line was integrated to produce an absorption spectrum. A first-order polynomial baseline correction was applied and the result was filtered by low-pass filter. The cut-off frequency of the filter was selected that produced 1% broadening of the noiseless computer-generated absorption spectrum (Fig.4b dashed blue line). The derivative and integrated lines were fitted to determine A and Lw. The fitting curves are shown in Fig. 4 (red curves). Numerical experiments starting from noise addition to line fitting were repeated 5,000 times to produce ensembles of A and Lw. Results of the uncertainty analysis for A₀ = 1, Lw₀ = 1G, SW = 20G, and SNR = 5, 10, 15 are presented in Table 4. They show that integration increases the uncertainties with which A and Lw for the Lorenzian line can be measured. This result may seem counterintuitive, because the integrated spectra look smoother and may have higher SNR. The downside is that integration amplifies the low-frequency noise and, as a result, distorts the baseline. Fig. 4 demonstrates that the accuracy of the line fitting procedure is more sensitive to the baseline distortion than to the standard deviation of the noise. As demonstrated in Table 4, integration increases σ_A and σ_Lw by factors of 3 and 4, respectively.

Fig.4.

Example of one of the 5000 trials for fitting the first-derivative (a) and its integral (b). The fitted lines (red) are compared to the noise-free (green) derivative and absorption Lorentzian lines.

Table 4.

Comparison of uncertainties for A and Lw before and after integration of the first derivative line.

Method	Filter	SNR (Deriv)	$\frac{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}}{{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}}$	$\frac{{\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}}{{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}}$
Monte-Carlo	1%	5	N/Ra	N/Ra
Monte-Carlo	1%	10	0.34	0.21
Monte-Carlo	1%	15	0.36	0.23

^aN/R indicates that the noise was too large to obtain reproducible results.

Results similar to those shown in Table 4 were obtained for the uncertainty analysis with different A₀ and Lw₀ when the sweep width SW was changed proportional to Lw₀, SW = 20 Lw₀. Changing the ratio of sweep width to line width produced minor changes in ${\mathrm{\sigma }}_{\mathrm{A}}^{\text{der}}/{\mathrm{\sigma }}_{\mathrm{A}}^{\text{abs}}$ and ${\mathrm{\sigma }}_{\text{Lw}}^{\text{der}}/{\mathrm{\sigma }}_{\text{Lw}}^{\text{abs}}$. In all cases integration of the derivative line resulted in increasing σ_A and σ_Lw.

Discussion

Quantitation of the number of spins in a sample has been a challenging goal of EPR spectroscopy from its earliest days (13). Methods developed before lab computers became common, including methods of weighing spectra cut out of chart paper, were reported in Poole's first edition (1) (page 591 and chapter 20) and in Alger (13) (pages 215-220). As computers became more readily available, integrating the area under the curve, and hence performing two successive integrations of a first-derivative curve, became an important technique (2). It has been recognized for many years that low frequency noise, including slow baseline drift, can dominate integrals of spectra, especially when the S/N is low (see for example Fig. 4.16 on p. 61 of (2). Alger also gives examples (13). Commonly, linear approximations to the baseline are used to correct each integration stage (see Appendix C of (2)), but low order polynomials are also used if enough points in the baseline can be identified. Spectra may be difficult to integrate accurately even when the baseline looks like “random noise” to the operator, as shown in (2) Figure C.1, page 133. The errors introduced by low frequency noise are demonstrated quantitatively by the analyses in this paper. We have shown that if the lineshape is known and spectra have the same SNR, simulations of the absorption spectra provide more accurate values for spin concentration than simulation of first-derivative spectra. Future developments in data analysis software development should depend more heavily on simulations of spectra to determine integrated intensities.

Measurements of line widths are key to the use of EPR for oximetry (14). The uncertainty analysis in this paper demonstrates that it is best to extract the line width parameter directly from the native data, whether absorption or first-derivative, rather than after integration or differentiation. For both absorption and first-derivative spectra the accuracy with which spectral parameters can be calculated increases proportional to SNR if noise is white, so SNR remains a key figure of merit for spectrometers and detection methods.

Conclusion

Comparison of different spectrometers and detection methods that give absorption and first-derivative data can be based on uncertainties in derived parameters. Uncertainty analysis was performed to determine how integration and differentiation impact uncertainties in A and Lw calculated from EPR spectra. Analytical expressions and Monte Carlo analysis of the uncertainties in A and Lw for Lorentzian or Gaussian lines were in good agreement if noise is white. The analytical expressions are simpler to use. When noise is not white, due either to spectrometer bandwidth or filtering, the Monte Carlo analysis gives more realistic results. Differentiation of the absorption line or integration of the first derivative reduces the precision with which integral intensity A or line width Lw can be extracted from noisy spectra. The most accurate approach to comparison of experimental methods that produce absorption and derivative spectra is line fitting of the experimental data. If SNR is the same for experimental data obtained as absorption and first-derivative spectra, the integrated intensity can be obtained about twice as precisely from the absorption as from the derivative. A conservative low-pass filter can be used to decrease the uncertainties in the line fitting results. Monte-Carlo simulations are more practical for extension to more complicated lineshapes. The analytical and Monte Carlo uncertainty analyses could be extended to a larger number of parameters, including the hyperfine splittings.