Finding Imaging Patterns of Structural Covariance via Non-Negative Matrix Factorization

Abstract

In this paper, we investigate the use of Non-Negative Matrix Factorization (NNMF) for the analysis of structural neuroimaging data. The goal is to identify the brain regions that co-vary across individuals in a consistent way, hence potentially being part of underlying brain networks or otherwise influenced by underlying common mechanisms such as genetics and pathologies. NNMF offers a directly data-driven way of extracting relatively localized co-varying structural regions, thereby transcending limitations of Principal Component Analysis (PCA), Independent Component Analysis (ICA) and other related methods that tend to produce dispersed components of positive and negative loadings. In particular, leveraging upon the well known ability of NNMF to produce parts-based representations of image data, we derive decompositions that partition the brain into regions that vary in consistent ways across individuals. Importantly, these decompositions achieve dimensionality reduction via highly interpretable ways and generalize well to new data as shown via split-sample experiments. We empirically validate NNMF in two data sets: i) a Diffusion Tensor (DT) mouse brain development study, and ii) a structural Magnetic Resonance (sMR) study of human brain aging. We demonstrate the ability of NNMF to produce sparse parts-based representations of the data at various resolutions. These representations seem to follow what we know about the underlying functional organization of the brain and also capture some pathological processes. Moreover, we show that these low dimensional representations favorably compare to descriptions obtained with more commonly used matrix factorization methods like PCA and ICA.

1. Introduction

The very high structural and functional complexity of the brain, captured at some macroscopic level by various structural and functional imaging methods, has prompted the development of various analytical tools aiming to extract representations of structure and function from complex imaging data, which can help us better understand brain organization. Conventional methods based on predefined partitioning of the brain into anatomical regions of interest, such as lobes, gyri, and fiber tracts have been complemented in the past 15 years by data-driven methods, which aim to tease out of the data anatomical and functional entities that describe brain structure and function in an unbiased, hypothesis-free way.

A widely-used family of methods that are free from regional hypotheses falls under the umbrella of Voxel-Based Analysis (VBA) (Goldszal et al., 1998; Ashburner et al., 1998; Ashburner and Friston, 2000; Ashburner, 2009; Thompson et al., 2000; Fox et al., 2001; Davatzikos et al., 2001; Shen and Davatzikos, 2003; Studholme et al., 2004; Bernasconi et al., 2004). These voxel-wise methods often lack statistical power because they repeat the same test at each voxel thus leading to multiple comparison problems. Moreover, they do not fully exploit the available data since they are myopic to the correlations between different brain regions, which often reflect characteristics of underlying brain networks.

Conversely, Multivariate Analysis (MVA) (Norman et al., 2006; Ashburner and Klöppel, 2011; McIntosh and Mišić, 2013) takes advantage of dependencies among image elements and thus, enjoys increased sensitivity. MVA methods can be separated into two sub-classes: i) confirmatory MVA techniques, such as structural equation modeling (McIntosh and Gonzalez-Lima, 1994) and dynamic causal modeling (Friston et al., 2003), that aim to assess the fitness of an explicitly formulated model of interactions between brain regions; and ii) exploratory techniques, such as Principal Component Analysis (PCA) (Friston et al., 1993; Strother et al., 1995; Hansen et al., 1999) and Independent Component Analysis (ICA) (McKeown et al., 1998; Calhoun et al., 2001; Beckmann and Smith, 2004), that aim to recover linear or non-linear relationships across brain regions and characterize patterns of common behavior. One may additionally aim to relate the extracted components to demographic, cognitive and/or clinical variables by either employing techniques like Partial Least Squares (McIntosh et al., 1996; McIntosh and Lobaugh, 2004; Krishnan et al., 2011) and Canonical Correlation Analysis (Hotelling, 1936; Friman et al., 2001; Witten et al., 2009; Avants et al., 2014), or by using the PCA and ICA components as features in supervised discriminative settings towards identifying abnormal brain regions (Duchesne et al., 2008), or patterns of brain activity (Mourão Miranda et al., 2005, 2007).

However, standard MVA methods suffer from limitations related to the interpretability of their results. PCA and ICA, which are commonly applied in neuroimaging studies, estimate components and expansion coefficients that take both negative and positive values, thus modeling the data through complex mutual cancelation between component regions of opposite sign. The complex modeling of the data along with the often global spatial support of the components, which tend to highly overlap, result in representations that lack specificity. While it may be possible to interpret opposite phenomena that are encoded by the same component through the use of opposite signs, it is difficult to associate a specific brain region to a specific effect. Finally, ICA, and particularly PCA, aim to fit the training data well, resulting in components that capture in detail the variability of the training set, but often do not generalize as well in unseen data sets.

Non-Negative Matrix Factorization (NNMF) (Paatero and Tapper, 1994; Lee and Seung, 2000) is an unsupervised MVA method that enjoys increased interpretability and specificity compared to standard MVA techniques. NNMF estimates a predefined number of components along with associated expansion coefficients under the constraint that the elements of the factorization take nonnegative values. This non-negativity constraint is the core difference between NNMF and standard MVA methods and the reason for its advantageous properties. It has been shown to lead to a parts-based representation of the data, where parts are combined in additive way to form a whole. Because of this advantageous data representation, NNMF has been applied in facial recognition (Zafeiriou et al., 2006), music transcription (Smaragdis and Brown, 2003), document clustering (Xu et al., 2003), machine learning (Hoyer, 2004; Cai et al., 2011), computer vision (Shashua and Hazan, 2005) and computational biology (Brunet et al., 2004; Devarajan, 2008).

However, the application of NNMF in medical imaging has been less investigated. In the case of structural imaging, a supervised approach for sparse non-negative decomposition was introduced by (Batmanghelich et al., 2009, 2012). This approach targets feature extraction in the context of a generative-discriminative framework for high-dimensional image classification. The derived overcomplete representation exploits supervised knowledge to preserve discriminative signal in a clinically interpretable way through the adoption of sparsity and non-negativity constraints. The use of NNMF for feature extraction was also briefly suggested by (Ashburner and Klöppel, 2011). Lastly, unsupervised matrix-factorization approaches have been tailored for connectivity analysis to take into account the nature of the data (Ghanbari et al., 2012) and (Eavani et al., 2013).

Contrary to previous approaches, we investigate in this paper the use of Non-Negative Matrix Factorization in an unsupervised setting as an analytical and interpretive tool in structural neuroimaging. The goal is to use NNMF to derive a distributed representation that will allow us to identify the brain regions that co-vary across individuals in a consistent way, hence potentially being part of underlying brain networks or otherwise influenced by underlying common mechanisms such as genetics and pathologies. We argue that NNMF is well-adapted for the analysis of neuroimaging data for four reasons: i) it provides a parts-based representation that facilitates the interpretability of the results in the context of brain networks; ii) it naturally produces sparse components that are localized and align well with anatomical structures; iii) it generalizes well to new data; and iv) it allows us to analyze the data at different resolutions by varying the number of estimated components. The second reason is of significant interest because in many scenarios, one expects co-varying networks to be formed by biologically related anatomical regions.

We apply the proposed approach to recover fractional anisotropy change relationships in mouse brain development, and to recover gray matter volume change relationships in human brain aging. Moreover, we contribute a useful and comprehensive comparison with PCA and ICA. We qualitatively and quantitatively evaluate the qualities of the respective representations and we demonstrate the superiority of the use of the proposed NNMF framework in detecting highly interpretable components that contain strongly co-varying regions. The high specificity of the obtained representation allows us to elucidate the distinct role of anatomical structures. As a consequence, we advocate the use of NNMF as an alternative tool for the study of structural co-variance (Seeley et al., 2009; Zielinski et al., 2010; Alexander-Bloch et al., 2013) that is now typically performed in a hypothesis-driven way assisted by Regions of Interest (ROI) or seed-based analysis.

2. Materials and methods

2.1. Methods

We consider a data set consisting of non-negative values that measure, through a medical image acquisition technique such as Magnetic Resonance Imaging, the expression of local biological properties of organ tissue for N samples. These samples typically represent different subjects, but they can also represent the same subject at different time points. For neuroimaging studies, the dimension D of the samples (i.e., images) is typically in the hundred of thousands, while the number of samples is typically in the hundreds. Thus, the data are represented by a tall matrix X that is organized by arraying each data sample per column (X = [x₁, …, x_N], x_i ∈ ℝ^D, and a data sample refers to a vectorized image).

Our aim is to extract a relatively small set of components that capture multivariate relations between the variables and reflect the inherent variability of the data. Moreover, we would like to extract these components in a purely data-driven (unsupervised) fashion without prior regional hypotheses.

Regularized matrix factorization is a broad framework encompassing diverse techniques that factorize the data matrix X into two matrices satisfying constraints related to modeling assumptions:

$$\mathbf{X}\approx \mathbf{C}\mathbf{L}$$ (1)

where C denotes the matrix that contains a component in each column (C = [c₁, …, c_K], K is the number of the estimated components, c_i ∈ ℝ^D and is assumed to be a unit vector ‖c_i‖² = 1). L contains the loading coefficients that, when used together with C, approximate the data matrix. Both C and L are necessary towards a comprehensive understanding of the data. C conveys information regarding the spatial properties of the variability effect, while the entries of L specify the strength of the effect in each data sample. Depending on the implemented modeling assumptions, C and L exhibit different properties. NNMF, PCA and ICA make different assumptions regarding the components whose linear combination generates the data.

In this section, we study the three methods in terms of the assumptions they employ, giving particular emphasis on the NNMF framework that is the main focus of this work.

2.1.1. Non-Negative Matrix Factorization

Non-Negative Matrix Factorization produces a factorization that constrains the elements of both the components and the expansion coefficients to be non-negative. This factorization is typically achieved by solving the following energy minimization problem:

$$\begin{array}{cc}\underset{\mathbf{C},\mathbf{L}}{\text{min}}\hfill & {\Vert \mathbf{X}-\mathbf{C}\mathbf{L}\Vert }_F^2\hfill \\ \text{subject to}\hfill & \mathbf{C}\ge 0,\mathbf{L}\ge 0.\hfill \end{array}$$ (2)

where ${\Vert ·\Vert }_F^2$ is the squared Frobenius norm (${\Vert \mathbf{X}\Vert }_F^2=\text{trace}({\mathbf{X}}^T\mathbf{X})$). In other words, the optimal non-negative matrices are the ones that best reconstruct the data matrix, while satisfying the non-negativity constraints.

The satisfaction of these constraints is what differentiates NNMF with respect to the rest of the methods and leads to components with unique properties. Two are the properties that are of significant interest in medical imaging. First, the non-negativity of the entries of the component matrix coincides with our intuition regarding the physical properties of the measured signal. By contrast, negative values are physically difficult to interpret. Second, and most importantly, the non-negative entries of the loading coefficient matrix result in a purely additive combination of the non-negative components. In other words, one may intuitively understand data approximation as the process of combining parts to form a whole. This is the principle behind the obtained parts-based representation.

The importance of parts-based representations as conceptualized by Lee and Seung (Lee and Seung, 1999) along with their algorithmic contributions (Lee and Seung, 2000), gave rise to an important body of work exploring diverse aspects of non-negative matrix factorization. Among this wealth of techniques, we adopt Projective Non-Negative Matrix Factorization (PNNMF) (Yang and Oja, 2010), and more specifically, its orthonormal extension (OPNNMF). Projective NNMF differs from the standard NNMF in the way that the loading coefficients are estimated, and as a consequence, in the nature of the obtained representation. Standard NNMF estimates separately the matrix L, which often gives rise to overcomplete representations. In other words, subsets of components are involved in the reconstruction of subsets of the data, as determined by the respective loading coefficients. Therefore, on the one hand, components may significantly overlap and, on the other hand, the loading coefficients can be used to provide a grouping of the data.

However, in PNNMF, the loading coefficients are estimated as the projection of the data matrix X to the estimated components C (L = C^TX). Thus, all components participate in the reconstruction of all data samples. The implications are twofold. First, the overlap between the estimated components is greatly decreased, leading to components exhibiting high sparsity.

This is a significant property in signal analysis and brain modeling (Daubechies et al., 2009) and has been associated with improved generalizability (Avants et al., 2014). Second, the components provide now a grouping of the data variables.

Apart from the previous difference, there are three additional reasons for choosing this variant. First, the number of parameters to be learned is lower (K × D for OPNNMF, as opposed to K × (D + N) for NNMF). Second, contrary to standard NNMF, it generalizes to unseen data without requiring retraining. Third, there is a connection between this approach and PCA. Given the equivalence between minimizing the reconstruction error and maximizing the variance (Bishop, 2006), one can note that the difference between this approach (see Eq. 3) and the conventional PCA (see Sec. 2.1.2) resides in the non-negativity of the entries of C (and, effectively, of the expansion coefficients C^TX).

OPNNMF factorizes the data matrix by minimizing the following energy:

$$\begin{array}{cc}\underset{\mathbf{C}}{\text{min}}\hfill & {\Vert \mathbf{X}-\mathbf{C}{\mathbf{C}}^T\mathbf{X}\Vert }_F^2\hfill \\ \text{subject to}\hfill & \mathbf{C}\ge 0,{\mathbf{C}}^T\mathbf{C}=\mathbf{I},\hfill \end{array}$$ (3)

where I denotes the identity matrix. In other words, OPNNMF positively weights variables of the data matrix that tend to co-vary, thus minimizing the reconstruction error and aggregating variance. Depending on the rank of the approximation, an adaptive exploration of the data variability is possible. By increasing the rank, it is possible to distinguish fine differences between covarying imaging variables by grouping them in different components. Let us note that the components are derived in a purely data-driven fashion without exploiting any prior knowledge. Moreover, the objective function comprises neither a smoothness term that will enforce spatial contiguity, nor a sparsity term. Nonetheless, sparsity is a key component of the physical model implemented by OPNNMF. The proposed analysis tool assumes that the observed signal admits a non-overlapping parts-based decomposition and, for each part, the observations mainly distribute along a line modeled by a scaled version of the corresponding component (Yang et al., 2007). This physical model is of particular interest in medical data, where one can expect anatomical networks to be characterized by different patterns of variability.

The solution to the previous non-convex problem can be estimated by iteratively applying the following multiplicative update rule (Yang and Oja, 2010):

$${\mathbf{C}}_{ij}^{\prime }={\mathbf{C}}_{ij}\frac{{(\mathbf{X}{\mathbf{X}}^T\mathbf{C})}_{ij}}{{(\mathbf{C}{\mathbf{C}}^T\mathbf{X}{\mathbf{X}}^T\mathbf{C})}_{ij}}$$ (4)

The multiplicative update can be interpreted as rescaled gradient descent. This update rule guarantees the positivity of the estimated components, while monotonically decreasing the energy towards attaining a local optimum (we refer the interested reader to (Yang and Oja, 2010) for a formal convergence analysis). Let us also note here that this update rule is simpler than the one of PNNMF, which further motivates our choice on computational grounds.

In order to apply the aforementioned scheme, an appropriate initialization scheme is necessary. Here, we employ the initialization strategy proposed by Boutsidis and Gallopoulos (2008)). This strategy is termed Non-Negative Double Singular Value Decomposition (NNSVD) and it basically consists of two SVD processes. The first process approximates the data matrix X, and its first K estimated factors are in turn approximated by their positive sections. The second process is used to approximate the resulting partial factors by their maximum singular triplets, which are then used to initialize matrix C.

This initialization scheme has been shown to allow NNMF algorithms to reduce the residual error faster than when random initialization is employed (Boutsidis and Gallopoulos, 2008). Moreover, it generates sparse initial components which promote the sparsity of the final non-negative decomposition. Lastly, being deterministic, it allows for consistent results across multiple runs. As a consequence, it is not possible to reach a more satisfying local minimum by simply rerunning the algorithm.

While multi-start optimization is typically adopted in similar non-convex problems, we believe that its effectiveness is not justified in this setting due to the high computational cost of the problem that renders the exploration of multiple initialization impractical. Last but not least, we have always been able to achieve a satisfactory solution by using this initialization scheme. On the contrary, random initialization has occasionally led to poor solutions.

2.1.2. Principal Component Analysis

Principal Component Analysis is one of the most widely used multivariate analysis methods. PCA maps the data to a lower dimensional space through an orthogonal linear transformation. PCA can be interpreted in two equivalent ways. It can be defined as the projection that either maximizes the variance of the projected data, or minimizes the reconstruction error calculated as the squared difference between the original data and their projections (Bishop, 2006).

In other words, PCA minimizes the following energy:

$$\begin{array}{cc}\underset{\mathbf{C},\mathbf{L}}{\min }\hfill & {\Vert \mathbf{X}-\mathbf{C}\mathbf{L}\Vert }_F^2\hfill \\ \text{subject to}\hfill & {\mathbf{C}}^T\mathbf{C}=\mathbf{I},\mathbf{L}={\mathbf{C}}^T\mathbf{X}.\hfill \end{array}$$ (5)

The solution to the previous problem is usually calculated by solving an eigenvalue problem through “economic” SVD, which exploits the typically low sample size of the data by calculating only the first relevant components. These components are typically ordered in descending order based on the magnitude of the variance they explain. Despite this important statistical interpretation, the derived components often lack visual interpretation. Moreover, the derived signed components have global support resulting in decreased specificity.

2.1.3. Independent Component Analysis

Independent Component Analysis (Hyvärinen et al., 2001; Hyvärinen and Oja, 2000) is another popular multivariate analysis technique whose aim is to identify latent factors that underlie sets of signals. These signals are typically given in the form of a data matrix 𝒳 that has as many rows as variables (or sensors) and as many columns as observations. Depending on how one defines sensors and observations in the context of images and voxel values, matrix 𝒳 may or may not be equal to X.

ICA assumes that the signals are generated through the mixture of a set of source signals:

$$𝒳=\mathbf{A}\mathbf{S},$$

where S denotes the matrix that comprises the source signals that build the data, and A denotes the invertible mixing matrix. The inverse mixing matrix is usually denoted as W and is referred to as unmixing matrix (S = W𝒳).

ICA aims to recover the unknown source signals by assuming that they have non-Gaussian distributions, and that they are statistically independent (or as independent as possible). Due to the latter assumption, the estimated source signals are called Independent Components (ICs).

In the context of image analysis, if one assigns images to variables, and voxel values provide observations for the variables (𝒳 = X^T), the case of spatial ICA arises. In this case, one assumes independence of pixels or functions of pixels. The estimated unmixing matrix W is of size N × N, and S is a matrix of size N × D containing the N spatially independent components in its rows. Thus, C = S^T, and L = (W⁻¹)^T. The spatial independent components, despite overlapping, are better localized than the principal components. Nonetheless, the mixed sign factorization and the resulting complex data modeling obstructs a comprehensive understanding of the role of distinct anatomical regions.

In this work, we employ the Joint Approximate Diagonalization of Eigenmatrices (JADE) method (Cardoso and Souloumiac, 1993; Cardoso, 1999) to perform spatial ICA. JADE is a nearly exact algebraic algorithm that uses the fourth-order cumulant tensor. This is a four-dimensional array whose entries are given by the fourth-order cross-cumulants of the data. This array can be considered as a generalization of the covariance matrix. JADE aims to transform the data so that the fourth-order cumulants are as small as possible. This can be understood as a generalization of the whitening procedure, which is a decorrelation transformation that transforms the data so that the variables have zero second-order correlations. Note that JADE also preprocesses the data by centering and whitening them in order to decrease the number of free parameters and increase its performance (Hyvärinen et al., 2001). Moreover, this step allows for controlling the number of estimated ICs.

2.2. Data sets

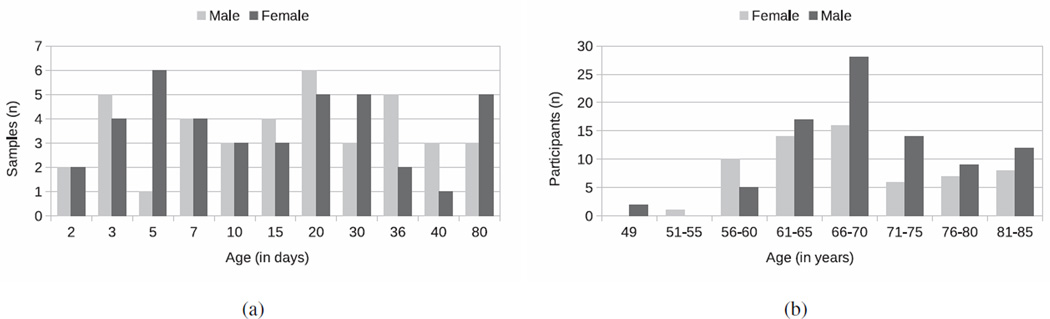
The first data set studies brain development and maturation in mouse brains. It consists of ex vivo acquired DT images of a population of 79 inbred mice of C57BL/6J strain (Fig. 1a). The imaged mice correspond to different postnatal stages, ranging from day 2 to day 80 (Verma et al., 2005). Early developmental stages were sampled more densely because development is more emphasized during that period. The images were deformably registered to a template image chosen from the age group of day 10 using DROID (Ingalhalikar et al., 2010). DTI-Studio (Jiang et al., 2006) was used to estimate tensors from which, the Fractional Anisotropy (FA) was calculated resulting in images with dimension 300 × 300 × 200 and a physical resolution of 0.0662 × 0.0664 × 0.0664.

Figure 1.

Information regarding the data sets: (a) sample composition by age (in days) for the DT mouse data set; (b) sample composition by age (in years) for the sMR human brain aging study.

The second data set consists of 158 sMR images (Fig. 1b) that were preprocessed based according to previously validated and published techniques (Goldszal et al., 1998). The preprocessing pipeline includes : (1) alignment to the Anterior and Posterior Commissures plane; (2) skull-striping; (3) removal of cerebellum; (4) N3 bias correction (Sled et al., 1998; Zheng et al., 2009); (5) tissue segmentation into gray matter (GM), white matter (WM), cerebrospinal fluid (CSF), and ventricles (Pham and Prince, 1999); (6) deformable mapping (Shen and Davatzikos, 2002) to a standardized template space (Kabani et al., 1998); (7) formation of regional volumetric maps, called RAVENS maps (Davatzikos et al., 2001; Shen and Davatzikos, 2003), generated to enable analyses of volume data rather than raw structural data; and (8) the RAVENS were normalized by individual intracranial volume (ICV) to adjust for global differences in intracranial size, down-sampled, and smoothed for incorporation of neighborhood information using an 8-mm Full Width at Half Maximum (FWHM) Gaussian filter. In this study, we utilized only the RAVENS maps that were derived from GM.

3. Results

3.1. Experimental Setting

We set off to test the hypothesis that NNMF is suitable for multivariate analysis of neuroimaging data due to its ability to capture and summarize the variability of the data into a few interpretable components. The interpretability of the results can be primarily evaluated through the visual inspection of the estimated components and loading coefficients matrix. Nonetheless, in order to assess the interpretability in a quantitative way, we measure: i) the component sparsity, and ii) the component incoherence.

Sparse descriptions have advantages of interpretability; descriptions involving fewer elements are easier to understand and interpret. Moreover, when these elements are well localized and exhibit high similarity, the description gains in specificity. Sparse and coherent components can be easily interpreted through their association to identifiable anatomical regions. Lastly, sparse representations often exhibit improved generalizability and agree with the hypothesis for an economic organization of the brain (Bullmore and Sporns, 2012).

The level of sparsity is measured using the definition proposed by Hoyer (Hoyer, 2004) that is based on the relationship between the L₁ and L₂ norms:

$$\text{sparsity}(\mathbf{c})=\frac{\sqrt{D}-({\sum }_{i=1}^D|\mathbf{c}(i)|)/\sqrt{{\sum }_{i=1}^D\mathbf{c}{(i)}^2}}{\sqrt{D}-1},$$

where c(i) denotes the i-th element of the vector c. This function takes values in the interval [0, 1]. If there is only one non-zero element in x, then the function evaluates to unity. On the contrary, if all elements have the same absolute value, then the function evaluates to zero. In other words, the higher values the function takes, the higher the sparsity of the component.

The second measure summarizes the dissimilarity of the elements within each component. By averaging this measure over all components, one can obtain a quantitative measure of the incoherence of the representation given by C. Mathematically, this translates to:

$$\text{incoherence}=\frac{1}{K}\sum _{k=1}^K\sum _{s=1}^N\sum _{i=1}^D{\mathrm{𝟙}}_{{\mathbf{c}}_k(i)\ne 0}{\Vert {\mathbf{x}}_s(i)-{\overline{\mathbf{x}}}_{ks}\Vert }^2,$$ (6)

where ${\overline{\mathbf{x}}}_{ks}={\sum }_{i=1}^D({\mathrm{𝟙}}_{{\mathbf{c}}_k(i)\ne 0}{\mathbf{x}}_s(i))/{\sum }_{i=1}^D{\mathrm{𝟙}}_{{\mathbf{c}}_k(i)\ne 0}$. 𝟙 denotes an indicator function; k, s, and i index the components, the samples and spatial positions, respectively. Ideally, this index should take values as low as possible signifying that the representation is compact and that the components comprise elements sharing similar appearance across the data collection.

To further quantitatively evaluate the investigated methods, we use them to extract features for a standard machine learning task. We chose age regression as an appropriate task because of the important age-related variability that is implied by the nature of the data sets and the increased interest it has raised in neuroimaging (Dosenbach et al., 2010; Franke et al., 2010, 2012; Erus et al., 2014). In the context of age regression, we assume the images to be spatially normalized to a common template. All images are given as an input to the respective matrix factorization technique. This strategy is equivalent to assuming that, whenever a new query image is given, one estimates each subspace anew. As all subspace projection techniques considered in this study are unsupervised, no age information is taken into account when estimating the subspace and no bias is introduced.

The loading coefficients L provide a low dimensional description of each data sample in the subspace spanned by the estimated components C.

This description greatly depends on the number of subspace dimensions. In order to account for that factor, the performance of the methods is investigated by varying the number of retained dimensions. A minimum number of 4 dimensions is used for all datasets, while the maximum number of dimensions is given by the number of the principal components that explain 85% of the variability in each dataset. Dimensions were more densely sampled in the range of principal components that account for an important amount of variance. The sampling rate reduces in the range of principal components that capture a small amount of variance.

Holding the number of dimensions constant, we performed 50 realizations of 10-fold cross validation. During each iteration, the data are partitioned into ten folds. Each fold is successively used as a test set, while the remaining folds are used to train a Support Vector Regression model (Drucker et al., 1997) using a Radial Basis Function (RBF) kernel (κ (α,β) = exp (−γ‖α − β‖²)). The implementation provided by LIBSVM (Chang and Lin, 2011) was used. The features produced by the different methods were normalized to the range of [0, 1], and the parameters of the RBF kernel were optimized by performing a grid-search on C (C > 0 is the penalty parameter of the error term) and the kernel parameter γ using an internal round of 5-fold Cross Validation. The accuracy of the regression is measured by the Mean Squared Error (MSE), that is the average squared difference between the predicted age and the true age. The MSE values are averaged over all fold experiments and all 50 realizations. The results are reported as a function of the estimated number of components.

In order to further quantify the quality of the low dimensional description of the data set, we examine how well it reflects age variability. Given the assumption that age is the dominant factor of data variability, we expect an important number of the estimated components to be relevant to age-related phenomena. The loading coefficients that represent the contribution of these components across the data samples should also comply with the aforementioned expectation and take values that change consistently with age, thus correlating highly with it. Therefore, we report the value of the coefficient of determination (R²) averaged over the derived components.

In order to deepen our understanding regarding the behavior of the different matrix factorization methods and give a comprehensive examination of their properties, we include two additional quality measures in our analysis. We examine the ability of each method to reconstruct the data as well as their ability to generalize to unseen data.

3.2. Qualitative Results

Let us now visually appraise the interpretability of the results. Our analysis will include the examination of the interpretability of both the estimated components (matrix C) and loading coefficients (matrix L). In order to ease the analysis, we examine the results that are obtained for a fixed number of components; 12 components for the mouse data set and 20 components for the human brain aging data set. Characteristic subsets of the derived components are reported.

3.2.1. Component Interpretability Mouse Data Set

During brain mouse development, there are two contrasting phenomena that can be observed through changes in FA values (Verma et al., 2005; Baloch et al., 2009): i) a decrease of FA values in Gray Matter (GM) cortical structures reflecting the transition of the cortex from a highly columnar organization, encoded by radially oriented tissue anisotropy, to an organization characterized by a decrease in anisotropy due to the development of cortical dendrites; and ii) an increase of FA values in White Matter (WM) structures reflecting progressive development and myelination of axons towards establishing more organized axonal pathways.

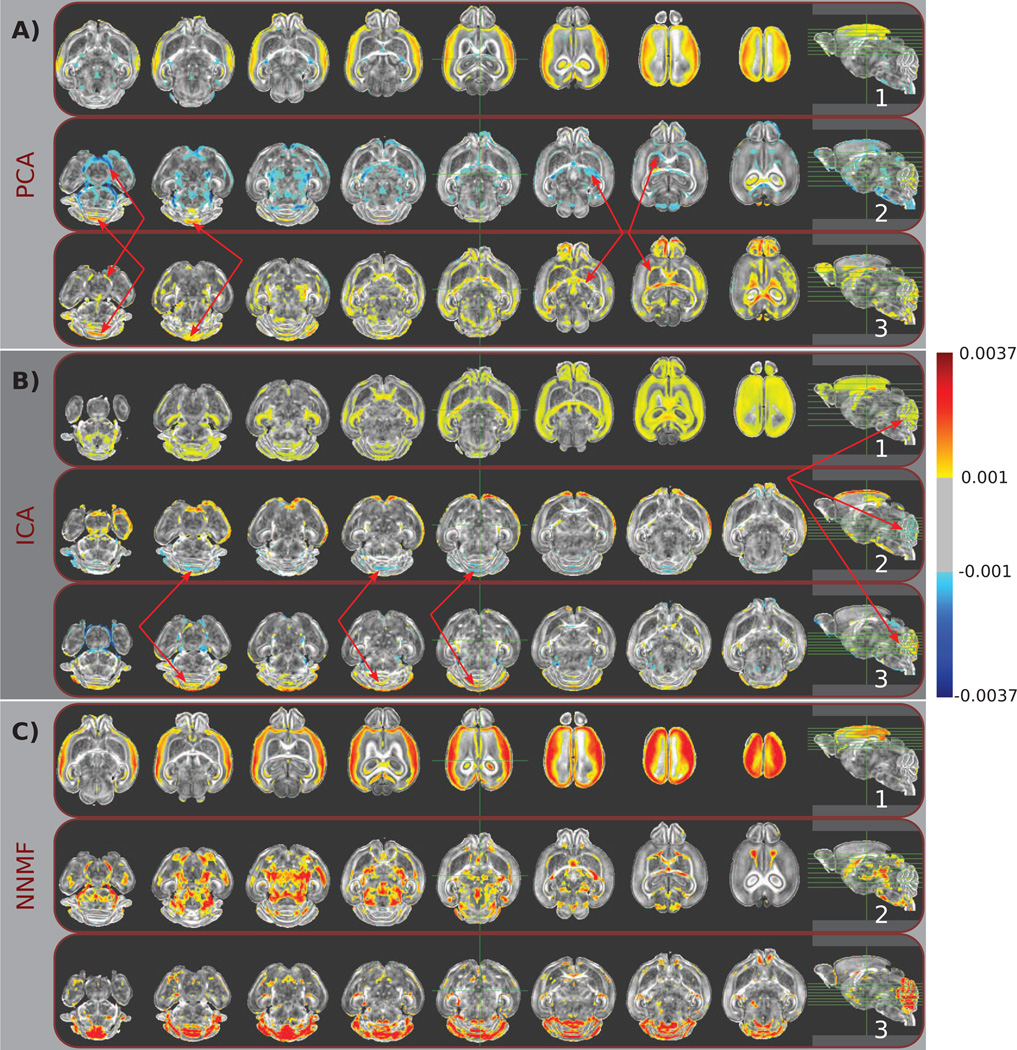
The first Principal Component (PC) that determines the direction of the most important variability seems to align with these two phenomena (Fig. 2A.1). One can verify by visual inspection that WM and GM structures are part of the first PC; GM structures take positive values, while WM structures take negative values. This difference of sign agrees with the two phenomena. ICA also groups together WM and GM structures along with the cerebellum (Fig. 2B.1). The corresponding IC mainly comprises elements with positive values. Moreover, the cerebellum is encoded by two additional components (Fig. 2B.2 and Fig. 2B.3) through the use of negative and positive values, respectively. As a consequence, it is challenging to associate cerebellum with a specific effect.

Figure 2.

Typical components estimated by A) PCA, B) ICA, and C) NNMF are color coded and overlaid over a template mouse brain. The same color-map (shown on the right) was used for all images for ease of comparison. Warmer colors correspond to higher positive values, while cooler colors correspond to lower negative values. Note the partially overlapping nature of the principal and independent components (indicated by red arrows), which limits the comprehensive understanding of the behavior of specific brain regions. Observe, for example, that the cerebellum is encoded by multiple PCs and ICs, often through the use of opposite signs and by being contrasted to different anatomical regions, resulting in a complex representation that limits our ability to readily comprehend its direction of variability. Conversely, non-negative components are well localized, allowing for analysis that enjoys specificity comparable to classical ROI approaches. Note, for example, that a single component signals the cerebellum, facilitating the characterization of its effect.

Fig. 2C shows three components estimated by NNMF. The depicted components are characteristic of the advantageous interpretability and specificity of the non-negative matrix factorizations. One can note that the first PC is separated into two non-negative components (see Fig. 2C.1 and Fig. 2C.2, respectively). The direction of the most important variability is decoupled; WM and GM structures are encoded by different components. Moreover, the cerebellum is part of a separate component (Fig. 2C.3).

The 3D rendering of the previously discussed components (see Fig. 3) allow us to further appraise the qualitative differences between the three representations. It is important to note that the same regions are signaled by all methods. Nonetheless, NNMF encodes them in separate components, leading to a representation characterized by high interpretability and specificity that facilitates further analysis.

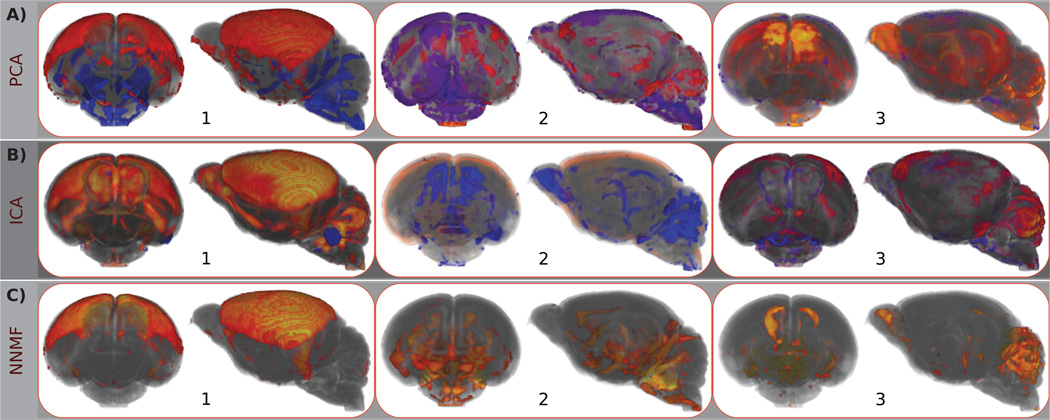
Figure 3.

Front and side views of 3D renderings of typical components estimated by A) PCA, B) ICA, and C) NNMF. The same components as the ones shown in the previous figure are depicted. Note that the color-map and opacity have been optimized to enhance visibility. Warm and cool colors correspond to positive and negative values, respectively. One may readily observe the global support of the estimated PCs that limits the specific of the derived representation. On the contrary, independent components are less dispersed. However, similar structures are encoded by multiple components, obstructing the characterization of specific anatomical regions. Non-negative components are parsimonious and highly non-overlapping, allowing for the characterization of specific brain areas.

Human Brain Aging Data Set

Aging is accompanied by loss of brain tissue and thinning of the cortex (Resnick et al., 2003; Salat et al., 2004; Fjell et al., 2009).

The holistic nature of the principal components is readily observed by visually inspecting the first, second, fifth and sixth PCs that are sequentially shown in Fig. 4A. One may also note that while the PCs may be individually interpretable (in the sense that one can interpret regions of opposite signs as phenomena with opposite directions of variance), it is difficult to associate a specific region with a specific effect due to the fact that the components highly overlap. For example, the first PC (Fig. 4A.1) comprises elements along most of the cortex that take negative values reflecting global thinning, along with positively weighted peri-ventricular structures reflecting increased ischemic tissue. Nonetheless, the partial overlap between the first and second PC (see arrows in Fig. 4A.1 and Fig. 4A.2) in the peri-ventricular area that is made possible through the use of opposite signs obstructs the comprehensive understanding of its role. This is also the case for deep GM structures that are assigned opposite sign values in the fifth and sixth PC (see arrows in Fig. 4A.3 and Fig. 4A.4).

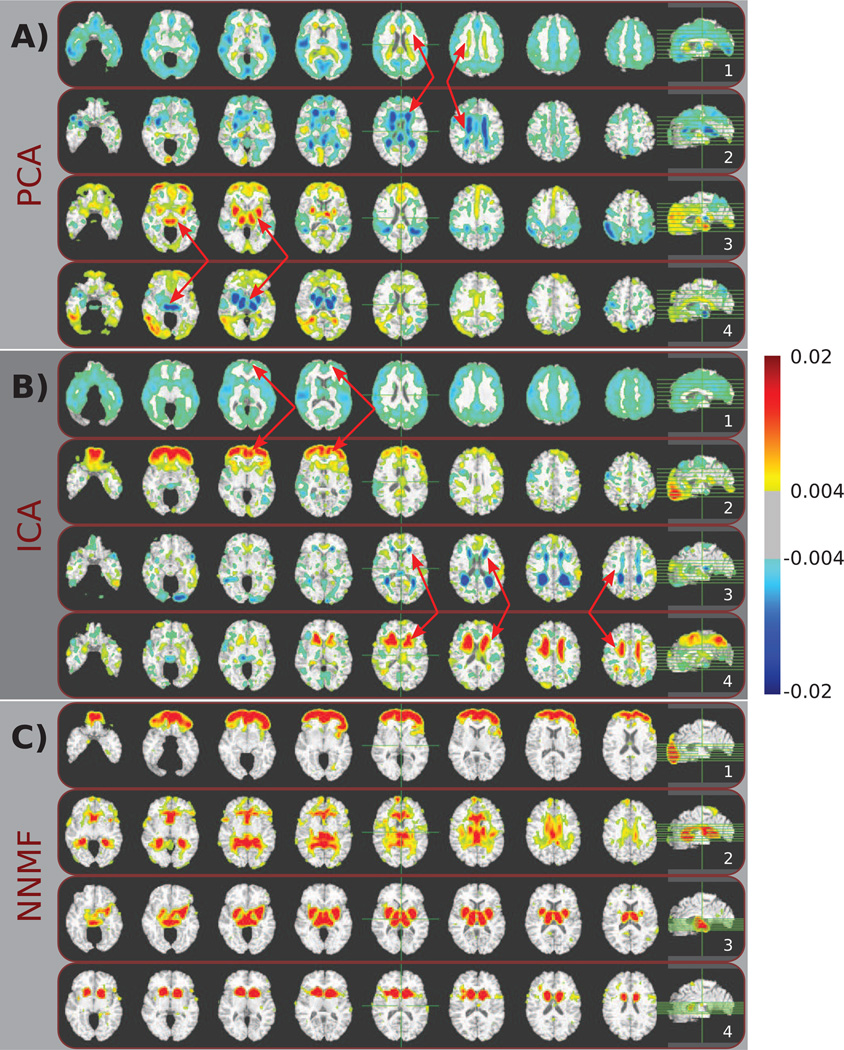
Figure 4.

Typical components estimated by A) PCA, B) ICA, and C) NNMF are color coded and overlaid over a template human brain. The same color-map (shown on the right) was used for all images for ease of comparison. Warmer colors correspond to higher positive values, while cooler colors correspond to lower negative values. Note how multiple principal and independent components highlight similar anatomical structures (indicated by red arrows). As a consequence, comprehensively understanding the behavior of specific brain regions is challenging. Conversely, non-negative components are well localized, aligning well with anatomical structures and allowing for analysis that enjoys specificity comparable to classical ROI approaches.

A typical subset of the components that were estimated by ICA is shown in Fig. 4B. Similar to PCA, a single IC encodes a direction of variability that reflects the global cortical thinning (Fig. 4B.1). Moreover, ICA also employs both negative and positive values resulting in mutually canceling overlapping regions. See, for example, the arrows in Fig. 4B.3 and 4B.4 that point to overlapping regions that have been assigned different signs. However, contrary to PCA, the ICs are sparser.

Fig. 4C reports four typical components estimated by NNMF. These components are significantly more sparse than the components estimated by the other two methods. Moreover, they are well localized and align with anatomical structures. Note, for example, that the component shown in Fig. 4C.1 highlights the prefrontal cortex, while peri-ventricular structures are encoded by the component depicted in Fig. 4C.2. Thalamus and putamen are part of the same component (Fig. 4C.3), while the head of caudate is encoded by a separate component (Fig. 4C.4). It is interesting to note that, despite some partial overlap, the estimated components constitute different parts that can be combined to form a brain, yet by construction, each part contains co-varying regions. In Sec. 4, we provide a more detailed discussion regarding these components.

Similar to the mouse data set case, we observe that all methods identify patterns of variability comprising similar brain regions. For example, thalamus and putamen can be seen in the PCs depicted in Fig. 4A.3 and Fig. 4A.4, respectively. The frontal lobe is encoded by the PC shown in Fig. 4A.3 and the IC depicted in Fig. 4B.2. PCA highlights peri-ventricular structures in the PCs shown in Fig. 4A.1 and Fig. 4A.2, while the ICs in Fig. 4B.3 and Fig. 4B.4 also capture peri-ventricular structures. However, contrary to PCA and ICA that mix these brain regions in the same components, or highlight them in multiple overlapping components; NNMF separates them in highly non-overlapping components that promote interpretability. NNMF components group brain regions that co-vary, while the loading coefficients summarize the contribution of these components across the population. Fig. 5

Figure 5.

Front and side views of 3D renderings of typical components estimated by A) PCA, B) ICA, and C) NNMF. The same components as the ones shown in the previous figure are depicted. Note that the color-map and opacity have been optimized to enhance visibility. Warm and cool colors correspond to positive and negative values, respectively. Principal components are holistic, highly-overlapping and comprise regions of opposite sign. Independent components are sparser than the PCs. However, they are spatially dispersed, hindering the interpretability of the results. Non-negative components exhibit high sparsity, are spatially contiguous and do not overlap, leading to a readily interpretable parts-based representation.

3.2.2. Loading Coefficients Interpretability

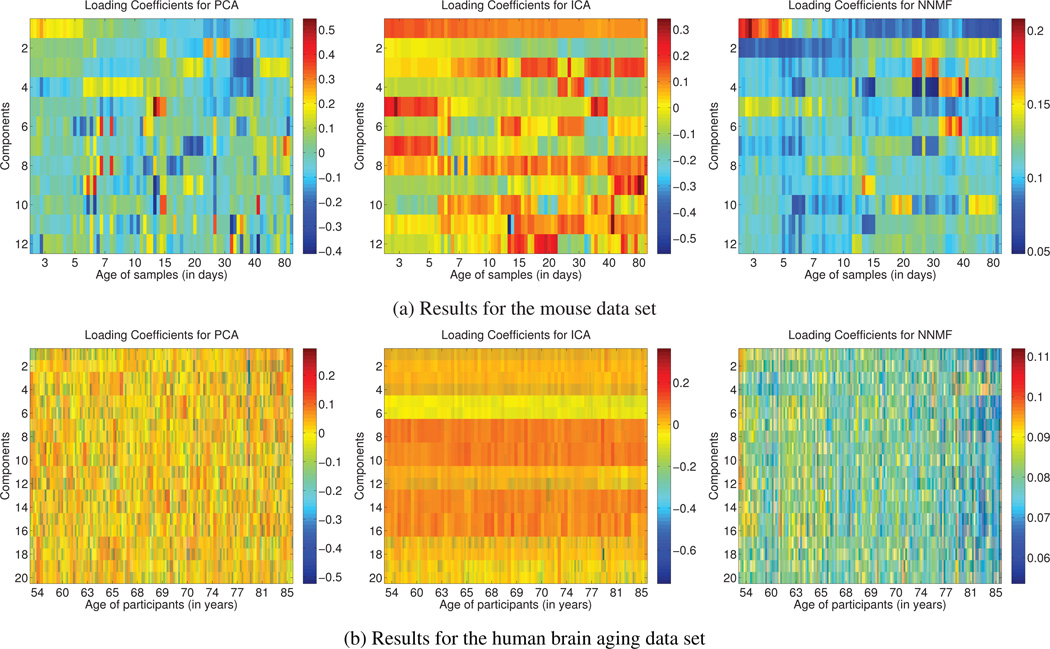
Being able to interpret the components is important because it allows us to identify covarying regions. However, being able to readily interpret the expansion coefficients (matrix L) is also important because it allows us to understand how the components contribute to the formation of the data, elucidating the captured directions of variability. In Fig. 6a and Fig. 6b, we show the loading coefficients for all subjects and components for the mouse and the human brain aging data set, respectively. Each element l_ij of the matrix L encodes the weight of the contribution of the i-th component to the reconstruction of the j-th data sample. In order to ease the presentation, the data samples are sorted in ascending age order and the age of the respective subjects is given on the horizontal axis. From left to right, the coefficients for PCA, ICA and NNMF are shown, respectively.

Figure 6.

Loading coefficients for every subject (matrix L) are color coded and shown in (a) for the mouse data set, and (b) for the human brain aging data set. From left to right, the results for PCA, ICA and NNMF are shown, respectively. In order to facilitate comparison the coefficients corresponding to each component are normalized to unit norm. The subjects have been sorted in ascending age order. The age of the subjects is given on the horizontal axis. Note that, in both cases, only the coefficients estimated by NNMF exhibit a consistent interpretable variation with age, suggesting that the captured components might reflect biological processes related to development and aging, respectively.

Before separately examining the obtained results, let us emphasize a common characteristic of all representations; their distributed nature. That is, all components are linearly combined to generate the data.

Mouse Data Set

The mouse data set consists of genetically engineered mice of different ages. The careful design of the data set eliminates most confounding variation emphasizing the effect of age. Thus, one would expect the estimated components to capture age-related factors of variance and the respective loading coefficients to change consistently with sample age. Given this assumption, let us now examine the loading coefficients that correspond to the components shown in Fig. 2.

The coefficients that correspond to the first PC are located in the first row of PCA result in Fig. 6a. We note a progressive decrease of the coefficients from positive values to negative ones that follows the age increase. This behavior coincides with the process that characterizes the development of GM and WM structures, which are high-lighted by the specific component. However, the coefficients that correspond to the rest of the components do not exhibit any consistent relationship with age. For example, the coefficients for the second, third and fourth component repeatedly change sign from positive to negative. This observation suggests that the derived components capture directions of variability that are possibly not of biological relevance.

As far as ICA is concerned, the coefficients in the first row of L shown in Fig. 6a correspond to the IC shown in Fig. 2. Similar to the PCA case, the value of the coefficients decreases for subjects of greater age. However, the coefficients remain strictly positive. As a consequence, this profile no longer agrees with the underlying biological phenomena since it characterizes GM and WM structures in the same way. Moreover, similar to PCA, many coefficients change sign arbitrarily.

Regarding NNMF, the coefficients shown in the two first rows of the matrix are of interest. We observe that they follow opposite trajectories; while the coefficients that correspond to the first component decrease, the coefficients that correspond to the second component increase. This behavior agrees well with the known developmental path of the anatomical structures identified by the respective components (cortical maturation causes reduced FA, and WM pathway formation causes increased FA). Regarding the rest of the coefficients, we note the gradual change of the values that follows the increase of age.

In conclusion, we observe that only the NNMF components contribute to each subject in a way that is consisted with its age. This observation suggests that the captured components might reflect biological processes related to development.

Human Brain Aging Data Set

This data set consists of healthy aging subjects coming from different age groups. Thus, many factors contribute to the inter-subject variability. Nonetheless, the wide spread of the subjects’ age range suggests that an important part of the data variance may be explained by age-related factors. Components, which effectively capture these factors, should be coupled with loading coefficients that are consistent with age.

However, both the results of PCA and ICA are not easily understood under the light of this observation. In the case of PCA, we observe random sign switches as well as important changes in the magnitude of the entries. In the case of ICA, we also observe sign switches. In both cases, one cannot readily interpret the results.

On the contrary, in the case of NNMF, one can note a gradual decrease of the values of the entries of the matrix L. The left hand side of the matrix is dominated by entries of yellow and red color, while the right hand side of the matrix is dominated by entries of blue color (warmer colors indicate higher values). It is also interesting to note that the loading coefficients that correspond to the fourth component gradually increase (entries of the fourth row of matrix). This component corresponds to the component in Fig. 4C.2 that emphasizes peri-ventricular structures, where ischemic tissue is known to increase with age.

In conclusion, we observe that only the NNMF components are associated with expansion coefficients that agree with age. Moreover, these components not only encode normal aging processes, but also pathophysiological aspects of aging. The good localization of the components along with the interpretability of the loading coefficients provides a comprehensive view of the data.

3.3. Quantitative Results

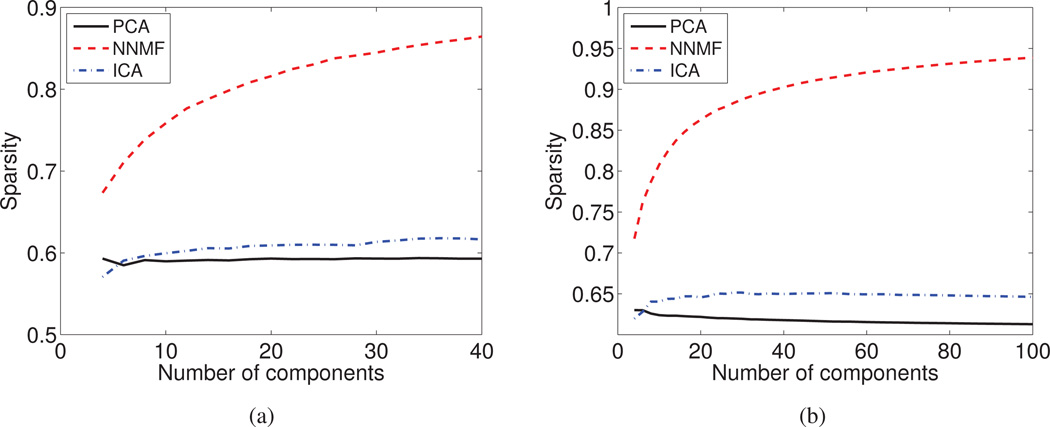
Sparsity

NNMF is undoubtedly the method that produces the sparsest components for both the mouse (Fig. 7a) and the human brain aging (Fig. 7b) data set. ICA produces components that are sparser than the ones given by PCA and whose level of sparsity tends to increase as the number of subspace dimensions increases. PCA produces components with global support and thus, it is the one that performs worse under this criterion.

Figure 7.

The average level of Sparsity is reported as a function of the derived components for (a) the DT mouse data set, and (b) the sMR human brain aging data set. NNMF is characterized by a relatively high level of sparsity, which monotonically increases with the number of derived components.

The success of NNMF lies in its ability to produce parts-based representations that are naturally sparse. NNMF does not opt to greedily model all data, but focuses instead on capturing and localizing the inherent variability. Distinct sources of variability are grouped into different parts. As the number of parts increases, we observe a hierarchical behavior leading to sparser components that provide a refined description of the captured variability and distinguish better between co-varying patterns.

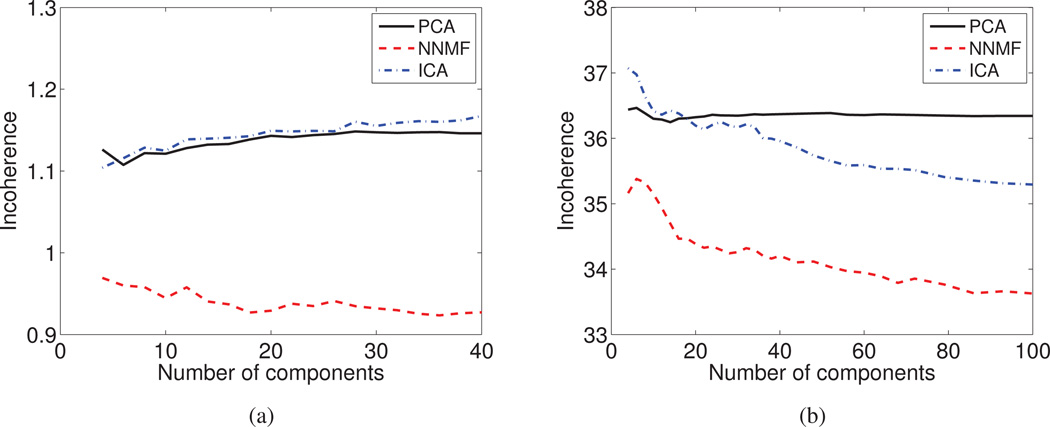
Incoherence

Among the three examined methods, NNMF yields by far the most coherent components (see Fig. 8a and Fig. 8b). PCA and ICA give components that are less coherent because: i) they mix effects by contrasting them in single components through the use of mixed-sign values; and ii) the components are characterized by extended spatial support.

Figure 8.

The Incoherence index is reported as a function of the derived components for (a) the DT mouse data set, and (b) the sMR human brain aging data set. NNMF provides increasingly coherent components by virtue of delivering sparse representations that group strongly co-varying regions.

NNMF produces components with low incoherence by virtue of its non-negativity principle that allows it to group elements that exhibit similar behavior throughout the population. NNMF is often seen as a relaxation of clustering and, similar to a clustering method, integrates similar elements while segregating dissimilar ones.

In order to deepen our understanding regarding the changes of the NNMF behavior as the number of components increases, we draw more the analogy between NNMF and clustering. The increase of the number of available components allows us to interrogate the data at multiple resolutions. Coarser resolutions allow us to examine general directions of variability, while finer resolutions allow us to examine data in higher detail. By increasing the number of degrees of freedom, regions that were encoded by the same component in coarser resolutions may be split into different components in finer resolutions, reflecting slight differences in co-varying patterns. At finer resolutions, NNMF components become sparser and group regions that co-vary more strongly. As a consequence, the derived components become more compact and their incoherence decreases.

Regression Accuracy

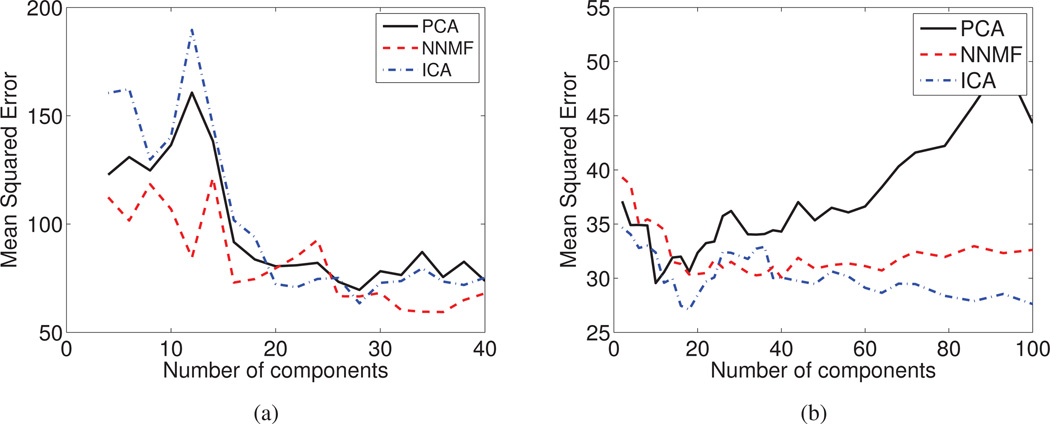
In Fig. 9a and Fig. 9b, we report the prediction accuracy that is obtained by training an SVM regression model with an RBF kernel on features extracted by using NNMF, PCA and ICA.

Figure 9.

The Mean Squared Error of the regression model for the Cross Validated data is reported as a function of the derived components for (a) the DT mouse data, and (b) sMR human brain aging data set. Note that, given an adequate number of features, the obtained prediction accuracy is similar for all three methods.

We observe that the regression accuracy depends greatly on the number of derived components. The results obtained with PCA features seem to be sensitive to the number of employed features (note how the accuracy deteriorates as the number of PCA features increases in Fig. 9b). However, given an adequate number of sub-space dimensions that can encode the relevant sources of variation, the prediction accuracy that we obtain is similar for all three cases.

We should emphasize that NNMF achieves similar prediction accuracy, while exhibiting high component (see Fig. 3 and Fig. 5) and coefficient interpretability (see Fig. 6). This may prove fundamental in better associating patterns that drive discriminative machine learning methods to anatomical or functional units.

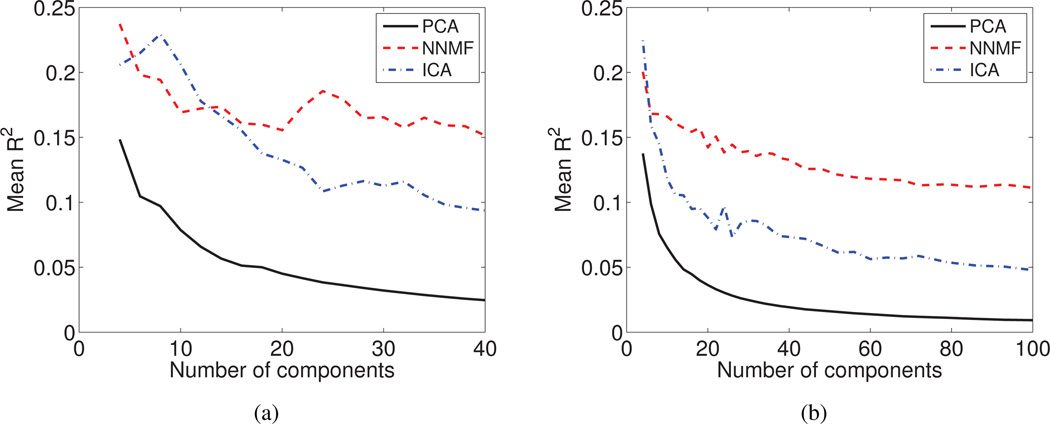
Low Dimensional Description Consistency with Age

PCA coefficients are the ones that are least consistent (Fig. 10a and Fig. 10b) demonstrating a performance that deteriorates with the addition of more components. This is because the additional components learn irrelevant variations in the data, aiming for a good reconstruction.

Figure 10.

The average value of the coefficient of determination (R²) is reported as a function of the derived components for (a) the DT mouse data, and (b) sMR human brain aging data set. The non-negative expansion coefficients estimated by NNMF capture age-related information, suggesting that the derived components might reflect biological processes related to development and aging, respectively.

ICA performs better than PCA for both data sets. However, NNMF outperforms ICA and PCA in both cases. It is important to note that while the other methods learn irrelevant variations with the increase of degrees of freedom, NNMF preserves relevant information.

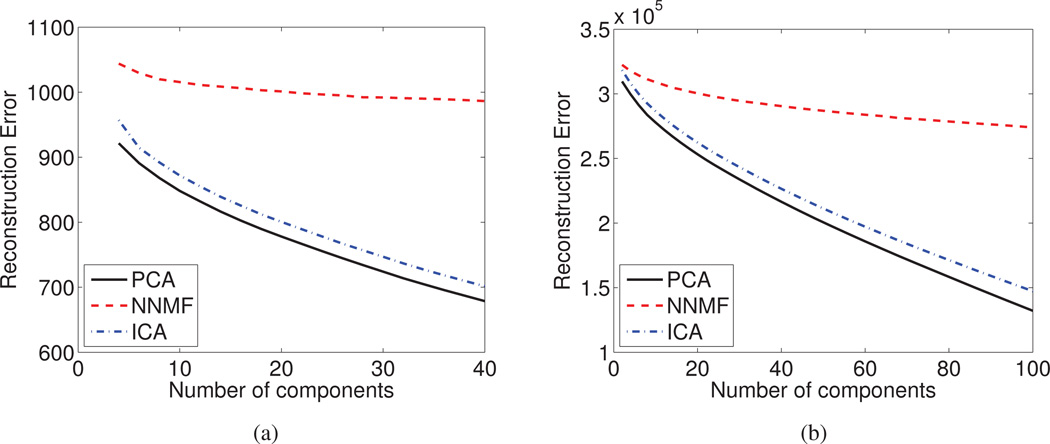
Reconstruction Error

The optimality of PCA in terms of capturing data information can be appreciated from Fig. 11a and Fig. 11b, where the reconstruction error is plotted as a function of the number of estimated components.

Figure 11.

The Reconstruction Error is reported as a function of the derived components for (a) the DT mouse data, and (b) sMR human brain aging data set. PCA and ICA faithfully model the data by exploiting all available degrees of freedom, hence, being potentially prone to over-learning.

We note that for both data sets, PCA and ICA are able to faithfully reconstruct the data, resulting in a decreased reconstruction error. The ability of both PCA and ICA to reconstruct the data monotonically increases with the increase of the available degrees of freedom. This is possible because of the overlapping nature of the components and the fact that these components are free to have both positive and negative values. PCA exploits every additional component in order to decrease the reconstruction error and eventually models the noise present in the data. This behavior makes PCA susceptible to over-learning and possibly limits its generalization to unseen data.

On the other hand, NNMF manifests a slower rate of reconstruction error diminution, which ultimately converges. NNMF discards an important amount of information, which is reflected by the increased, with respect to PCA and ICA, reconstruction error. Nonetheless, the comparable to PCA and ICA prediction accuracy implies that the discarded information is not pertinent. Therefore, NNMF is capable of retaining important information associated with the inherent data variability, while discarding irrelevant information, which may potentially lead to increased generalization ability.

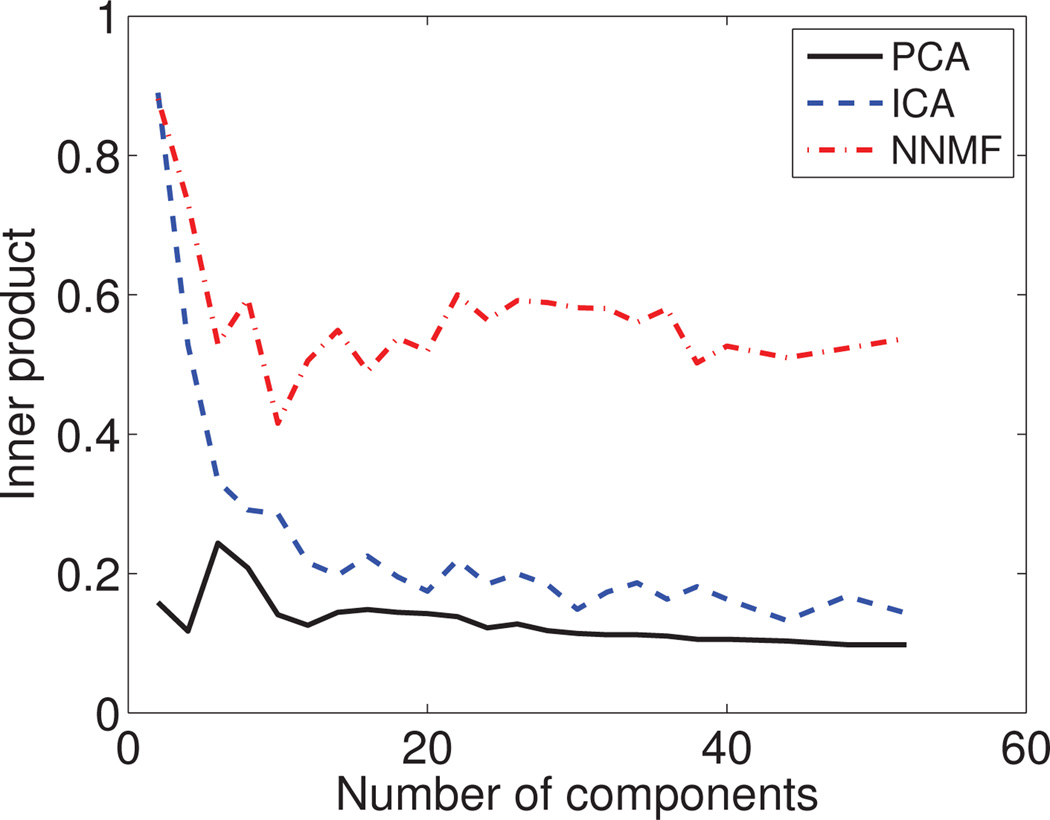
Reproducibility

To test the generalizability of our results, we split the human data set into two parts of 74 subjects each that have similar age and sex distributions. We run NNMF, PCA and ICA independently on each part at different resolutions by varying the number of derived components. The respective results were compared using inner-product; the median value of the inner-products is reported in Fig. 12.

Figure 12.

Reproducibility of results: The median value of the inner product between independently estimated corresponding components is reported. We present results by varying the number of derived components. NNMF demonstrates a better ability to generalize to unseen data.

We observe that the results obtained by NNMF exhibit correlation that is significantly stronger than the one of the PCA and ICA results, indicating much higher reproducibility. PCA can only consistently estimate the first principal component across the two splits. The rest of the PCs are not well reproduced. Similar to PCA, ICA estimates consistently few ICs, while the rest are poorly reproduced.

Conversely, NNMF robustly identifies similar components in both splits. This ability varies depending on the number of estimated components. The correlation between the results for the two splits drops initially with the increase of components and then increases till it reaches a plateau. Few larger components are estimated relatively more consistently. The correlation drops when analyzing the data at a medium resolution because, at that level, covarying regions can be attributed to different components with the same probability. As the number of components increases, the resolution at which structural covariance is examined, also increases. Hence, structurally co-varying regions are better and more reliably distinguished.

4. Discussion

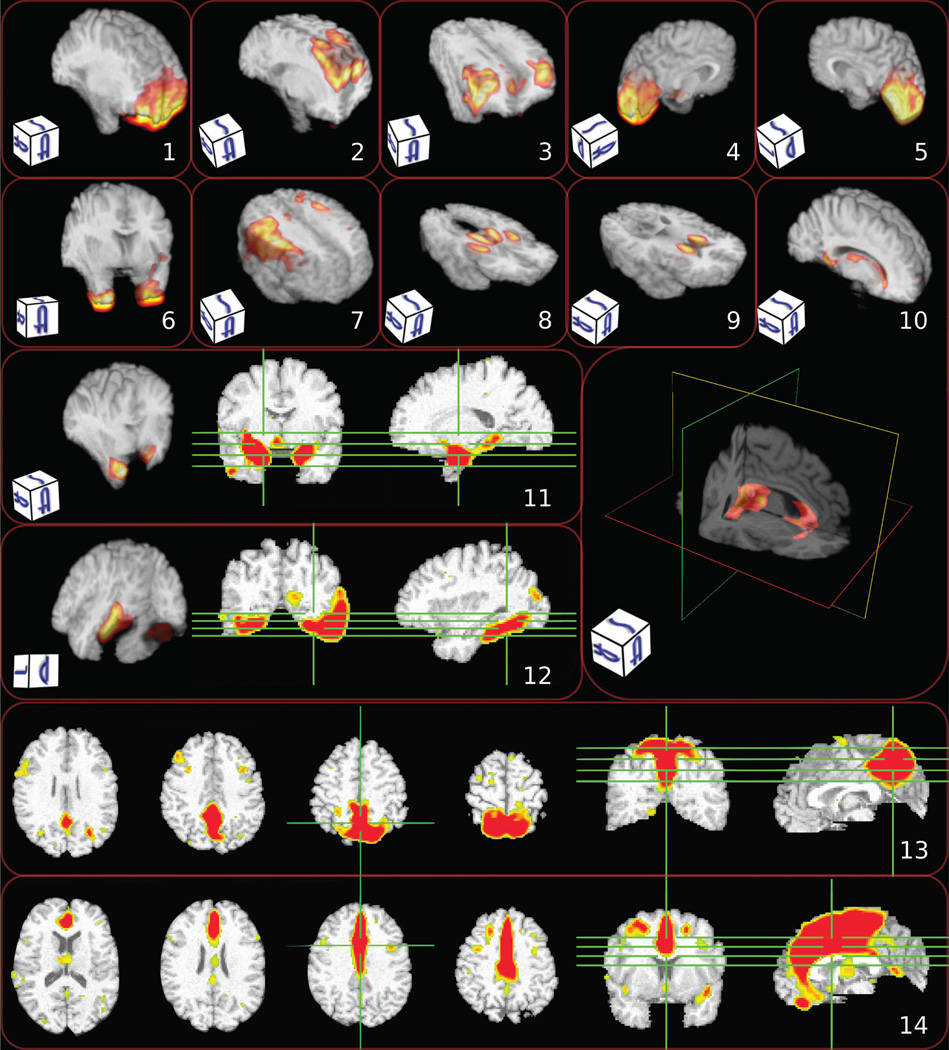
In this section, we first provide a brief synopsis of the paper, followed by a discussion of the properties of the non-negative matrix factorization. In order to facilitate the discussion, we present a broader selection of NNMF components (Fig. 13), which we use as visual examples of the discussed properties. Hereafter, we refer to components presented in Fig. 13. We conclude the section by exploring possible future directions of work.

Figure 13.

Characteristic components estimated by NNMF. Different visualization strategies were used in order to enhance the visual perception of the components (note that the 2D images use radiographic convention). Warmer colors correspond to higher values. Note the alignment with anatomical regions: 1) prefrontal cortex; 2) superior frontal cortex; 3) superior lateral cortex; 4) left occipital lobe; 5) right occipital lobe; 6) inferior anterior temporal; 7) motor cortex; 8) thalamus and putamen; 9) head of caudate; 10) peri-ventricular structures; 11) amygdala and hippocampus; 12) fusiform; 13) medial parietal including precuneus; and 14) anterior and middle cingulate.

Synopsis

In this paper, we investigated the use of a general multivariate analysis methodology based on unsupervised non-negative matrix factorization for extracting collections of brain regions that co-vary across individuals in consistent ways, thereby potentially being influenced by common underlying mechanisms such as genetics (Chen et al., 2013) and pathologies (Seeley et al., 2009).

Multivariate methods have been used in great extent for the analysis of neuroimaging data towards extracting patterns that explain variance in imaging data (Friston et al., 1993; McIntosh et al., 1996; McKeown et al., 1998; Calhoun et al., 2001; Mourão Miranda et al., 2005; Norman et al., 2006; Mourão Miranda et al., 2007; Caprihan et al., 2008; Duchesne et al., 2008; Ashburner and Klöppel, 2011; McIntosh and Mišić, 2013). Interpreting these patterns is essential in order to understand the biological phenomena and the regions that participate in them. Nonetheless, standard multivariate analyses are characterized by limited interpretability due to the lack of specificity stemming from the global support of the derived components and the complex modeling of the data that is achieved through complex mutual cancelations between component regions of opposite sign.

Conversely, NNMF enjoys advantageous interpretability and increased specificity by yielding non-negative factors. Non-negativity constraints tend to lead to sparse parts-based data representations. The derived components correspond to intuitive notions of the parts of the brain, which are combined in an additive fashion to form a whole. We found NNMF to decompose structural brain images into regions that tend to follow well-known functional units of the brain. Finally, NNMF compared favorably to the commonly applied PCA and ICA.

Model selection

An important feature of NNMF is that it produces a low dimensional description of the data set. The choice of subspace dimensions is important. The optimal dimension should be such that it allows the encoding of data variability while discarding noise. In this setting, the key idea is to investigate the variation of the residual error of the data approximation with the variation of the number of estimated components (Kim and Tidor, 2003; Frigyesi and Höglund, 2008; Hutchins et al., 2008). One may determine the optimal dimension by detecting the inflection point of the slope of the reconstruction error. In other words, one assumes that when the number of components is less than the intrinsic data dimension, there is excess information that is not encoded by NNMF. Thus, increasing the number of components leads to a significant additional decrease of the reconstruction error. On the contrary, when the number of components exceeds the optimal number, the additional components capture variance due to random noise resulting in a minor additional decrease of the reconstruction error.

Alternatively, the optimal rank may be estimated based on the Cophenetic Correlation Coefficient (CCC) (Brunet et al., 2004; Devarajan, 2008). This technique relies on the fact that the loading coefficient matrix L clusters the N data samples into K clusters and aims to determine the number of clusters that maximizes clustering stability as measured by CCC. However, it assumes an overcomplete representation and as a result, it cannot be directly applied to the case presented in this paper. Nonetheless, it can be easily adapted by taking into account the fact that the component matrix C clusters the D variables into K clusters and then calculating CCC with respect to this clustering. Finally, the classification and the regression accuracy that are obtrained by using the derived representations may be an interesting alternative in the cases that prior knowledge is available.

Structural parcellation

The obtained parts-based representation reveals structurally co-varying brain regions. This representation amounts to a soft clustering that parcellates structurally coherent units in a data-driven way that exploits group statistics. The orthogonality constraints emphasize the parcellation potential, leading to highly non-overlapping components that complement each other towards making up a whole.

The complementary nature of the representation can be easily noted by visual inspection of the components presented in Fig. 13.

Components 1, 2, and 3 decompose the frontal lobe to its prefrontal, superior and lateral parts, respectively. Note also how components 4 and 5 constitute the occipital lobe and components 8 and 9 complement each other to describe deep GM structures. Similarly, component 13 encodes the anterior and middle medial cortex, while component 14 captures the posterior cingulate gyrus and precuneus (a structure of particular interest in early Alzheimer’s Disease (AD)). Thus, we observe that the estimated structural co-varying regions are not just statistical constructs, but exhibit a high level of alignment with distinct anatomical structures.

Spatial smoothness

The estimated components exhibit high spatial connectedness despite the fact that no explicit regularization has been introduced in the objective function to enforce spatial smoothness. While it is true that local smoothing of the data during the pre-processing step implicitly influences the smoothness of the final result, we do not observe either a blob-like partition, or a partition driven by spatial proximity only (e.g., components 3, 6, 8 and 9 in Fig. 13).

Symmetry

Another important characteristic of the obtained representation is the symmetry of the estimated components. High symmetry is manifested, for example, in components 6, 8, 9 and 10. Various degrees of symmetry are manifested in most of the obtained components concurring with the strong symmetry the hemispheres exhibit.

This symmetry is completely data-driven and it breaks when not supported by the group statistics. Note, for example, that the symmetry of component 3 decreases in its inferior portion, while the symmetry of component 11 breaks in its superior part. We would also like to draw attention to components 4 and 5. We observe that the occipital lobe has been separated in two lateral components. This is in accordance with the known occipital asymmetry (Watkins et al., 2001; Good et al., 2001; Toga and Thompson, 2003) and the lateralization of visual processing.

Relation to pathophysiological mechanisms and functional networks

In conclusion, we observe a highly reproducible partition that is localized, exhibits high spatial continuity and allows for arbitrary component shapes that manifest various degrees of symmetry. The localization and component continuity agree with the local clustering aspect of an economic organization of the brain, while we hypothesize that the shape captures the mechanisms that drive development, aging or disease. The estimated units are not solely statistical constructs, but are consistent with brain regions that correspond to structural and functional networks, or in some cases reflect underlying pathological processes.

Pathophysiological mechanisms

The human brain is highly structurally and functionally specialized. As a consequence, one expects developmental or aging processes as well as disease processes to affect distinct regions in a specific way. We observe that such regions are part of estimated components.

Component 10 captures the increase with age of peri-ventricular ischemic tissue. Age-related or hypertension-related small vessel diseases (Pantoni, 2010) result to ischemic lesions that are prevalent in aging (Burns et al., 2005). These lesions are easily detected by neuroimaging and are classified during preprocessing as GM tissue, thus leading to the captured volumetric increase. Component 13 isolates a region of particular importance in early AD because of its early structural and functional change, and its dense projections to the hippocampus.

Last, different subregions of the frontal lobe are encoded by components 1–3, which suggests that they are characterized by distinct directions of variability. This is in accordance with previous studies that report that frontal cortical volumes decrease differentially in aging (Tisserand et al., 2002).

Functional networks

It is also interesting to remark that, while the components are estimated based on the group statistical properties of structural measures, they align well with reported functional entities. Components that break the brain to co-varying voxel groups, segregate units with distinct functional roles.

Component 9 highlights the head of caudate nucleus that has been associated to cognitive and emotional processes, in contrast to the body and tail that have been shown to participate to action-based processes (Robinson et al., 2012). Components 13 and 14 separate the cingulate cortex to its anterior and posterior parts. This separation is corroborated by the dichotomy between the functions of these parts (Vogt et al., 1992). Last, the division of the frontal pole to prefrontal, superior and lateral parts (components 1–3) concurs with the heterogeneity of frontal lobe function. Prefrontal cortex is associated to high-level cognitive tasks (Ramnani and Owen, 2004), superior frontal cortex is involved in self-awareness (Goldberg et al., 2006), while lateral frontal is associated to executive functions and working memory (MacPherson et al., 2002).

Future work

In this paper, we demonstrated the importance of non-negativity in the analysis of neuroimaging data. However, the advantageous interpretability of the results is accompanied by an important computational cost (computations were in the order of days for the reported experiments) that may hinder the wide use of these techniques. Therefore, devising techniques that can lower the computational burden without compromising the quality of the results is of extreme importance.

Future work also needs to address the extension of such non-negative matrix factorization frameworks to a supervised setting that will exploit available prior knowledge. Unsupervised methods aim to explain all sources of variability, thus introducing factors that may confound further analysis. Conversely, supervised methods can exploit prior knowledge to reveal patterns that solely explain relevant variability, leading to adaptive focus analysis.

Lastly, the application of this method for the analysis of structural co-varying networks in disease and health is a prominent direction for future exploration.

5. Conclusions

In this paper, we have proposed the use of NNMF for the analysis of neuroimaging data towards identifying brain regions that co-vary across individuals in a consistent way. We have contributed a comprehensive comparison between NNMF, PCA and ICA that demonstrates the potential of the proposed framework against standard multivariate analysis methods. We have qualitatively and quantitatively shown its ability to capture the inherent data variability in a way that allows for ease of interpretation. The derived components decompose structural brain images into regions that align well with anatomical structures and tend to follow well-known functional units of the brain.

Highlights.

• Non-Negative Matrix Factorization for the analysis of structural neuroimaging data.

• NNMF identifies regions that co-vary across individuals in a consistent way.

• NNMF components align well with anatomical structures and follow functional units.

• Comprehensive comparison between PCA, ICA and NNMF.

• NNMF enjoys increased specificity and generalizability compared to PCA and ICA.