Model-controlled hydrodynamic focusing to generate multiple overlapping gradients of surface-immobilized proteins in microfluidic devices

Abstract

Historically, it has been difficult to generate accurate and reproducible protein gradients for studies of interactions between cells and extracellular matrix. Here we demonstrate a method for rapid patterning of protein gradients using computer-driven hydrodynamic focusing in a simple microfluidic device. In contrast to published work, we are moving the complexity of gradient creation from the microfluidic hardware to dynamic computer control. Using our method, switching from one gradient profile to another requires only a few hours to devise a new control file, not days or weeks to design and build a new microfluidic device. Fitting existing protein deposition models to our data, we can extract key parameters needed for controlling protein deposition. Several protein deposition models were evaluated under microfluidic flow conditions. A mathematical model for our deposition method allows us to determine the parameters for a protein adsorption model and then predict the final shape of the surface density gradient. Simple and non-monotonic single and multi-protein gradient profiles were designed and deposited using the same device.

Introduction

Gradients in the concentration of surface-adsorbed proteins are thought to play central roles in tissue organization, axonal growth, and haptotaxis (cellular migration directed by concentrations of extracellular matrix macromolecules). Despite the importance of these phenomena to cancer, neuroscience, and developmental biology, there is at present a paucity of techniques to deposit protein gradients in a repeatable and accurate manner that would enable quantitative study of such phenomena.

Directed or biased cell migration (taxis) plays a major role in many biological processes, including cancer invasion. Without it, the ability of tumors to metastasize to other parts of the body would be largely eliminated.¹ There are various types of directed cell migration: chemotaxis, haptotaxis, durotaxis, etc. Both chemotaxis, i.e., migration in a gradient of soluble chemoattractants, and haptotaxis, i.e., migration in a gradient of extracellular matrix (ECM) macromolecules immobilized in a solid substrate, have been shown to play a role in cancer invasion.² Parameters obtained from chemotaxis and haptotaxis experiments can be used in models that attempt to predict how and when a tumor will spread,³ as well as how branched capillary structures form in models of angiogenesis.⁴ This information could help a physician decide what course of treatment to pursue.⁵

While chemotaxis data are readily available for different cell lines and there are a number of microfluidic devices that can produce chemical gradients within a microfluidic channel,^6–11 the same cannot be said for haptotaxis and methods to deposit gradients of surface-bound proteins. The main reason is that it is more challenging to create a predetermined gradient of molecules on a solid substrate than in a fluid. Generation of an immobilized gradient of proteins on a substrate depends crucially on the protein adsorption kinetics. The rate of adsorption of a protein to a surface depends on the specific protein being used, its concentration, and the amount of that protein already adsorbed, and can also be influenced by the presence of other proteins.

Methods exist for the generation of gradients on surfaces. One can generate a surface-bound gradient using self-assembled monolayers (SAMs) of alkanethiols.^12,13 Proteins will attach to methyl-terminated alkanethiols creating a protein gradient.¹⁴ A gradient of SAMs can also be created using electrochemical desorption¹⁵ or photoimmobilization.¹⁶ The advantage of SAMs is that proteins link covalently to them, and the resulting gradient is stable for a long period of time. The disadvantage is that these methods cannot provide gradient patterning on the micrometer scale, which is relevant for cell studies. Another issue is that there is no precise control over the shape of the gradient and complex gradient shapes cannot be generated. Photoimmobilization can generate complex patterns with the resolution needed for cell studies, but it has a high level of complexity, as it requires multiple processing steps in a clean room and organic synthesis. A number of studies employ microfluidic gradient generators. In this class of devices laminar flow is used to generate a gradient in the fluid by diffusion from parallel streams of different concentrations.⁶ Surface-bound gradients can be created on the surface by adsorption of the gradient from the fluid or polymerization of the fluid.^17,18 To prevent surface saturation the protein kinetics need to be known or competitive adsorption against another protein has to be used. These devices can generate gradients at the cell scale with precise control. However, the gradient profile flattens along the channel due to lateral diffusion, and patterning of a different profile requires a redesign of the mixing network. Another microfluidic method relies on stream depletion to generate a gradient along the channel.^19,20 This method can be combined with microfluidic generators to create two-dimensional gradients. Complex two-dimensional features can also be obtained by combining microfluidic gradient generators with SAMs²¹ or microfabricated stamps. These processes generally create binary patterns.

In this paper we present a new, accurate, simple and reproducible method for depositing a one-dimensional protein gradient using computer-controlled hydrodynamic focusing in a microfluidic device. We use software commands to adjust flow rates in three pumps connected to a microfluidic device. Since we can focus the protein stream dynamically at different locations, we can deposit any one-dimensional gradient shape using the same device. Because we do not use a mixing network, which requires a low flow rate,^7,22,23 we deposit proteins at much higher flow rates, thus reducing lateral diffusion and gradient deposition time. Such microfluidic devices can be fabricated on a clean bench instead of in a clean room because they contain no high resolution details, making our method accessible to a large number of users. Because of the simplicity of our device it can be built even by users with limited microfabrication experience. This approach can be used not only to deposit protein gradients within microfluidic channels, but also to obtain rapidly the surface binding characteristics for a wide range of proteins and flat surfaces.

Gradient generation

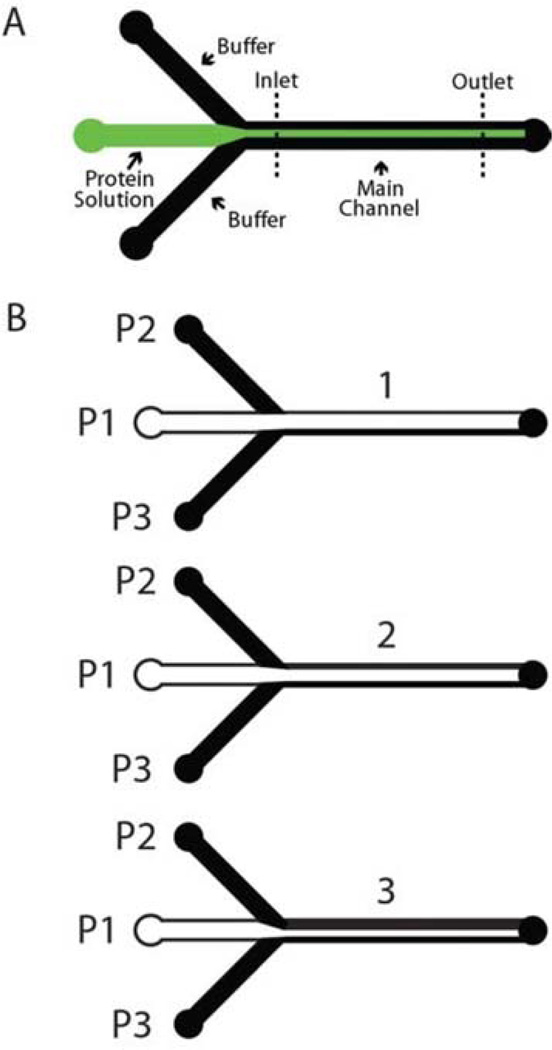
Our method can generate a protein concentration gradient in two different ways. Both approaches rely on the fact that mixing by lateral diffusion is limited in a laminar flow regime.²³ In order to maintain the gradient profile along the length of the channel, we use relatively high linear velocities. For a typical experiment, the total flow rate is 150 µL min⁻¹. The main channel is 900 µm wide and 90 µm high, which gives a linear velocity of 30 mm s⁻¹. This is an order of magnitude faster than in standard gradient mixers.^7,17 Three input channels connect to the main channel (Fig. 1A). The protein of interest flows through the middle channel, controlled by Pump 1 (P1), while the two side channels (P2 and P3) have buffer flowing through them to focus the center stream. In the “delta function” approach, we flow a narrow protein stream at a constant rate, and move it by sequentially increasing the flow on one of the side channels, while simultaneously decreasing the flow on the opposite side channel. By controlling the dwell time of the central stream over selected regions of the substrate, we can generate the desired gradient. In the “step function” approach we change the width of the protein stream by using one pump to increase or decrease the flow on the protein channel while using a second one to simultaneously decrease/increase the flow on one of the side channels by the same amount. By changing the amount of time we spend at each width step, different types of gradients can be generated. We generally use the second method, because it requires less time for gradient generation and is less sensitive to transient flows that might occur when switching flow rates. Once a gradient is created, the protein stream can be moved to another location in the channel, and another gradient can be created. This allows generation of non-monotonic gradient shapes.

Fig. 1.

(A) Mask layout for the microfluidic device used to deposit all the surface density gradients. Buffer channels are used to focus and steer the protein solution (shown in green), thus generating over time a surface density gradient in the main channel. (B) Creation of a three- step gradient. The middle stream contains protein (shown in white). To create the gradient the flow on buffer channel P2 is increased while simultaneously decreasing the flow on the protein channel P1 (see ESI for more on gradient creation, including pump rates).

Kinetics of Adsorption

Our approach allows us to determine de novo the adsorption kinetics for the desired protein, enabling us to control the amount of protein deposited at each step during gradient fabrication. We can readily use our data to specify parameters in any of several models for protein deposition^24–26 and this, in turn, helps us to understand the range of validity of the models. The kinetics of adsorption can vary depending on the protein being used and the bulk concentration of the protein in solution. We have obtained adsorption data for collagen and fibronectin and fitted it to several protein deposition models. The best fitting models are used to determine the deposition times needed for the gradient shape we wish to deposit. We have used four different models.

Random sequential adsorption (RSA)

The RSA model has been used extensively to model various processes from coal packing to protein adsorption.²⁷ In its simplest form, the RSA model consists of randomly placing objects into an n-dimensional volume, subject to the restrictions that the objects are placed sequentially, once placed each object is immovable, and two objects cannot overlap.

In modeling protein adsorption with the RSA model, it is assumed that proteins do not desorb once attached and that proteins do not stick to each other. The last assumption is only valid for low concentrations (<0.1 mg ml⁻¹ for laminin-1) of protein. However, the assumption is valid for our method since the protein solutions we use to deposit surface gradients have very low concentrations of protein (<20 µg ml⁻¹ for laminin-1). It is assumed that proteins adsorb to the surface until there is insufficient free space to accommodate additional proteins. This condition is called the jamming limit. With these restrictions in place, one can model the adsorption of proteins using two-dimensional RSA. Analytical models have been obtained for two-dimensional RSA. For intermediate-to-high coverage in two dimensions, Swendsen has shown that the RSA model approaches the jamming limit with t^−0.5.²⁶ The surface coverage for any two-dimensional uniformly distributed object can be expressed as Θ = j – yt^−0.5, where j is the jamming limit and y is a fitting coefficient. This assumption fails if one dimension is much smaller than the other dimension (needle-shaped objects).

Ilkovic equation

Hibbert et al.²⁴ compared several analytical adsorption models with experimental data. For diffusion-limited kinetics, the best fit for data at low-to-intermediate coverages was the Ilkovic model, which states that (∂c/∂x)_x=0 = c_b / (πDt)^0.5, where c is the concentration at the surface (x = 0), c_b is the bulk concentration, and D is the diffusion coefficient of the protein. We know that the surface coverage Γ is related to the concentration at the surface by (∂Γ/∂t) = D(∂c/∂x)_x=0. Substituting in the Ilkovic equation, and integrating with boundary condition Γ_t=0 = 0, we find that the surface coverage at time t is given by Γ = 2c_b(Dt/π)^0.5. This relation is only valid for low-to-intermediate coverages, since its prediction of continuous increase of coverage with the square root of time fails as the surface approaches a monolayer. We normalized the equation by dividing through by maximum surface coverage Γ_max, obtaining Θ =2c_b(Dt/π)^0.5/Γ_max (Table 1).

Table 1.

Summary of protein deposition models. Θ represents normalized surface coverage, c is the bulk concentration of protein in solution, D is the diffusion coefficient, Γ_max is maximum surface coverage, k=Γ_max/c, j is percentage maximum coverage, y is a fitting parameter and k_f is adsorption rate.

Deposition Model	Surface Coverage Eq.	Range	Reference
Ilkovic	Θ = 2cb(Dt/π)0.5 /Γmax	Low-to-intermediate	9
Langmuir	Θ = 1 − eDt/k2 erfc $\sqrt{Dt/k^2}$	All	14,15
RSA	Θ = j − yt0.5	Intermediate-to-high	11
Reaction Diffusion	Θ = 1 − e−kfct	All	12,13

Reaction-Diffusion Model

A mathematical model, developed by Vijayendran et al.,²⁸ has been adapted by Jiang et al.²⁹ to extract protein deposition kinetics in microfluidic devices. In the adapted model, desorption is considered to be negligible so that c_s(t)=c_s,sat(t)(1−e^−kfct), where c_s(t) is the protein surface density, c_s,sat(t) is the saturated protein surface density (jamming limit), k_f is the adsorption rate, and c is the bulk concentration of protein in solution. Dividing by c_s,sat(t) we obtain the normalized surface coverage Θ.

Langmuir isotherm

Langmuirian kinetics can be used to model deposition kinetics at low concentrations.³⁰ We used a linearized Langmuir isotherm solution of the diffusion equation³¹ Θ = 1 − e^{Dt / k2} erfc $\sqrt{Dt/k^2}$, where Θ is the normalized surface coverage, k=Γ_max/c, and Γ_max is the maximum surface coverage.

Data fit

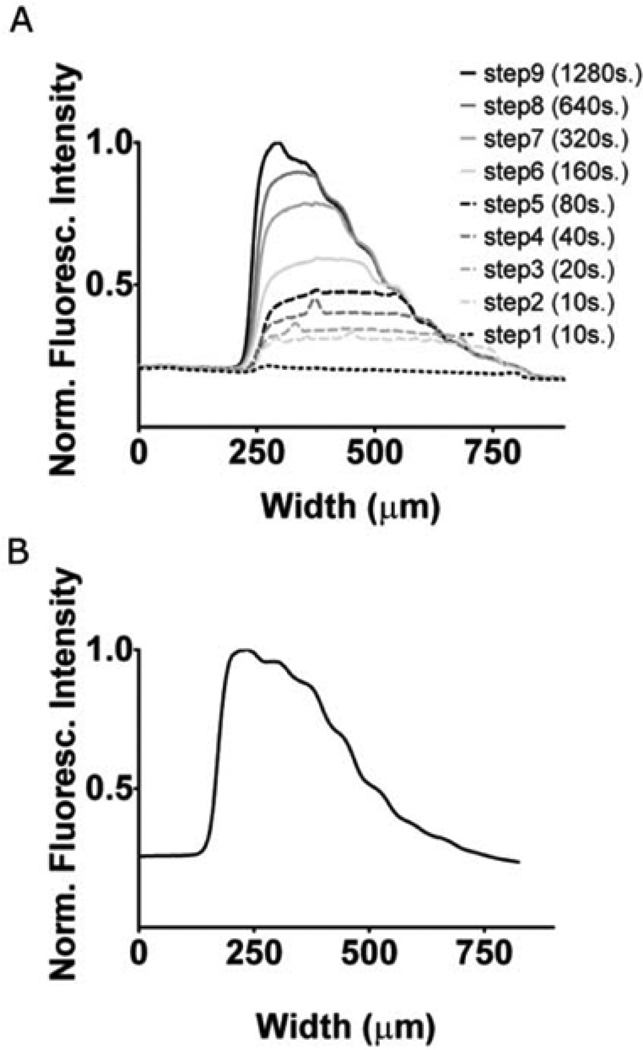
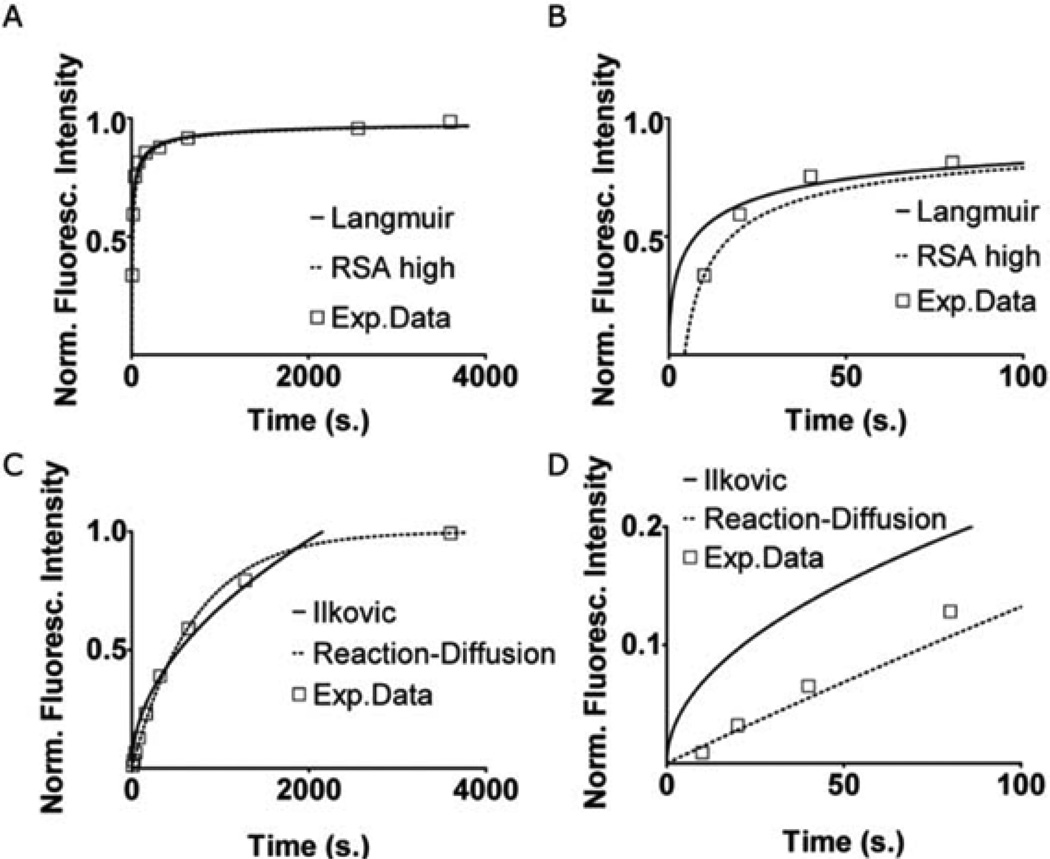
To extract the deposition kinetics required to control our gradient patterning, we begin with a simple nine-step gradient. The flow rates and time intervals for each time step are given in Table 1 in the ESI. Fig. 2A shows the fluorescence intensity profile at different time/width steps during gradient deposition. In practice, the deposition is performed in the dark to avoid photobleaching. The intensity values from each step were collected from three final intensity profiles for both fibronectin and type IV collagen. Fig. 3A and B show surface coverage values obtained from normalized intensity profiles for fibronectin. We fitted the adsorption data with the four kinetic models and plotted the ones for which we obtained a good fit. For fibronectin we obtained good fits using the linearized Langmuir isotherm and the RSA model. Fitting for K in the Langmuirian model we obtain a surface density of 1.33 × 10¹⁰ molecules cm⁻². This is similar to data obtained for the adsorption of fibronectin on polystyrene at low bulk concentrations of fibronectin in fluid.³² At high coverages the RSA model also provided a good fit.

Fig. 2.

(A) Gradient deposition for calibration. The protein used was type IV collagen. Each line shows the fluorescence intensity profile at that step number (step number is indicated in the legend, followed by the duration of the step in brackets). See Table 1 of the ESI for the full parameters. (B) Gradient intensity profile of type IV collagen on a slide containing aldehyde groups covalently bound to glass.

Fig. 3.

Fit to kinetic models for fibronectin (A, B) and type IV collagen (C, D). (B, D) represent the first 100 s from graphs A and C. “Exp.Data” shows combined surface density values extracted from three calibration gradients each. The parameter values are as follows: (A, B) RSA high j = 1, y = 2.1. Langmuir K = 1.1 × 10⁻³, D = 9 ×10⁻⁸ cm² s⁻¹. (C, D) Ilkovic D = 8 × 10⁻⁸ cm² s⁻¹, c = 9 × 10⁻⁹ M. Reaction–diffusion kf = 1.6 × 10⁵ M⁻¹s⁻¹, c = 9 × 10⁻⁹ M.

For type IV collagen we obtained good fits using the reaction–diffusion model and the Ilkovic equation (Fig. 3C and D). In the reaction–diffusion model we obtained a best fit adsorption rate k_f· = 1.6 × 10⁵ M⁻¹ s⁻¹. We used a diffusion coefficient for collagen in phosphate-buffered saline (PBS) of D = 8 × 10⁻⁸ cm² s⁻¹. In the Ilkovic equation we obtained a good fit for Γ_max =7.69 × 10¹⁰ molecules cm⁻².

Gradient deposition

Once we have determined the kinetics of adsorption for a particular protein, we can then generate almost any gradient shape. To parameterize the desired shape we used a digitization process. First, we generate in Matlab (The Mathworks Inc., Natick MA) a range of closely spaced values, in the protein concentration interval of interest, for the desired gradient shape. For simple gradients, this means calling the desired Matlab functions (exponential, cubic, etc.) on the interval. Complex gradients usually need to be broken down into multiple simple intervals. Once an interval of concentration values is generated, the data are binned according to the desired number of steps (resolution). For most of our experiments we use five steps, but we occasionally deposit gradients using as many as thirty steps. Each step is then assigned a concentration value, which is the mean of all the values in its bin. A kinetic model is then used to determine the time needed to deposit each concentration value. The time values, along with the desired flow rates, are entered into the pump control software. Since our approach does not require a mixing stage, we can deposit protein gradients with great speed: we have deposited linear and exponential gradients going from zero to 50–60% of the jamming limit in less than one minute.

This approach enables deposition of gradients using very small quantities of a rare or expensive protein. For a typical exponential gradient, the deposition process can last from several tens of seconds to several minutes, depending upon the range of concentrations desired. A typical five-step exponential gradient deposition would require only about 40 ng of protein (17 µl at a concentration of 2.5 µg ml⁻¹) if no dead space were present. The amount of protein required by the process is limited by how small a volume is required by the syringe and the delivery tubing, which we conservatively estimate to be on the order of 500 µl, i.e., approximately a microgram of protein. Hence the height of the device is not relevant to the amount of material required for the deposition. For particularly expen sive or rare proteins, we can paint a negative gradient using denatured BSA and add a small amount of the expensive protein solution on top of the BSA gradient.

Deposition modeling

Because we are “painting” our gradient using what in theory is a square “paintbrush,” the deposited gradient should resemble a series of clearly defined steps. In practice, however, the edges of the steps are blurred by at least three separate processes: (1) stream unsteadiness due to pump vibrations and tubing compliance, (2) transient flows generated when switching flow rates, and (3) diffusion at the protein–buffer interface. For the pumps and tubing used in this experiment, stream unsteadiness causes a constant blurring of about 10% of the narrowest protein stream. For the current device, the narrowest protein stream we used is 60 µm. Flow transients last for the order of a second, so they contribute to blurring mostly at short exposures required to produce a low protein surface density. Due to the high linear velocities we are using, diffusion is minimal and its effects can be ignored (see Fig. 4B). Blurring results in a stream cross-section that resembles the error function. If one can predict the resulting gradient shape, edge blurring can be used to generate a smooth gradient using a small number of steps. We model blurring by convolving the theoretical step function with a Gaussian function. Since the amount of blurring is inversely proportional with the surface concentration and dwell time, we used G = e^{−A2 / c2t1.5}, where A is a constant interval representing width and c is the protein surface density. We emphasize that the only free parameters in the model were specified by our earlier determination of protein binding kinetics. The close correspondence of the model and data in Figs. 5A and 5B reflects the accuracy with which we can produce, without parameter adjustment, the desired gradient.

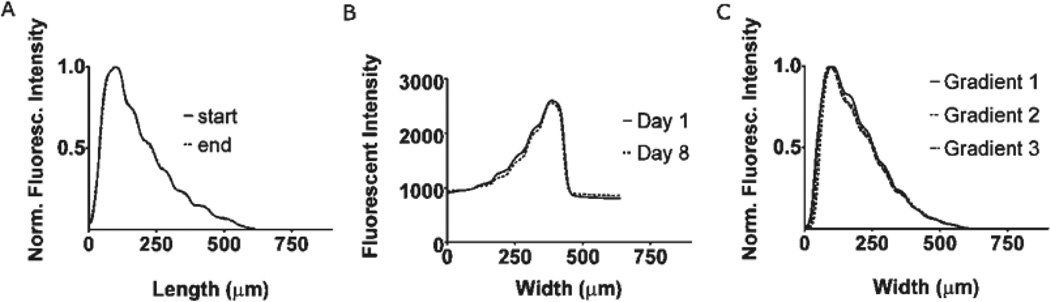
Fig. 4.

The protein used in all these experiments is type IV collagen. (A) Experimental determination of diffusion spreading between the inlet and outlet of the observation channel under a linear velocity of 30 mm s⁻¹. The fluorescence intensity profile remains virtually unchanged over a distance of 1 cm. (B) Experimental determination of gradient degradation over time. Represented are the profiles of a gradient taken one day and eight days after its creation at 4 °C. The y axis shows raw fluorescence intensity values. (C) Experimental determination of the repeatability of the control software used for gradient creation. The profiles represent three different gradients created using the same program.

Fig. 5.

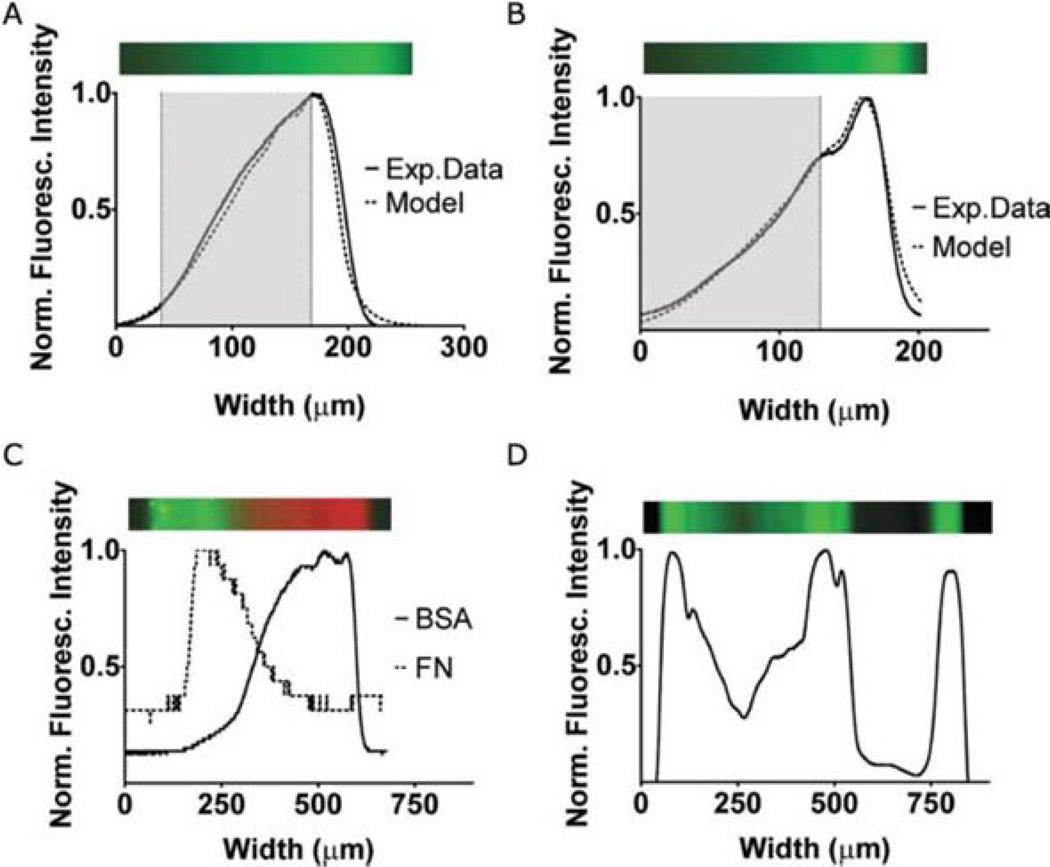
Demonstrations of gradients in surface-bound AlexaFluor488-Fibronectin. (A) Linear gradient surface coverage obtained from fluorescence intensity (solid line) compared to Gaussian model prediction (dashed line). (B) Exponential gradient surface coverage obtained from fluorescence intensity (solid line) compared to Gaussian model prediction (dashed line). Above the graphs are green pseudocolor images of the gradients. We fit grayed out areas of the graphs in A and B with linear and exponential function fits (see ESI). (C) Overlapping gradients of fibronectin (FN) and BSA. Parallel to the graph is featured a pseudocolor reconstruction of this double gradient, from two grayscale images. (D) Fluorescent intensity profile of complex gradient, spelling VU. Above the graph is a green pseudocolor reconstruction.

Linear gradient

To demonstrate our ability to produce a linear protein gradient, we diluted fluorescent fibronectin in PBS to a 2 × 10⁻⁸ M concentration. To deposit a linear gradient, we approximated the function y = ax + b. We used five deposition steps. The flow rates and time intervals are given in the ESO. Fig. 5A shows the predicted gradient shape and the fluorescence intensity profile. The total time for gradient generation was 37 s. Supplemental data show the closest linear fit for the range indicated by the gray area. The root mean square error between the linear fit and the gradient data over the target range is 0.009, indicating a good fit.

Exponential gradient

We have also demonstrated deposition of an exponential gradient of fluorescent fibronectin approximating the function y = ae^bx with five steps (Fig. 5B). Flow rates and time intervals are listed in the table in the ESI. The gradient was generated in 32 s. Supplemental data show the closest exponential fit for the range indicated by the gray area. The calculated root mean square error between the exponential fit and the deposited gradient is 0.005, which indicates an excellent fit.

Other gradients

Using hydrodynamic focusing, we can also generate multiple gradients using multiple proteins all in the same device (see Fig. 5C). This type of environment is closer to what a migrating cell is likely to encounter in vivo.^33–35 The gradient shape can be any arbitrary 1-D profile (Fig. 5D). Total deposition time for the gradient in Fig. 5D was 145 s.

Gradient stability

Because we are depositing our gradients on untreated glass, the stability of gradients over time becomes a concern. To investigate the stability of our gradients, we have placed a slide containing a gradient of type IV collagen in an incubator after filling the device with cell culture media. We have recorded fluorescent images over a 7 day interval and we observed a decrease in fluorescence intensity, but no change in gradient shape (ESI). We believe the decrease in intensity was due to the negative impact of the elevated temperature on the fluorophores. When we repeated the experiment with the device at 4 ° C, the recommended storage temperature for Oregon Green 488 fluorophores, we observed only a minimal change in fluorescence intensity (Fig. 4B).

To further address concerns over gradient stability we tested gradient deposition on slides containing primary aldehyde groups attached covalently to the glass. Proteins link covalently to the aldehyde groups forming a stable gradient. Fig. 2B shows a chemisorbed gradient of type IV collagen. The advantages of the aldehyde-coated slides are faster adsorption and more stable gradients (not shown), balanced by the high cost of the commercial slides or the additional steps of in-house coating.

Gradient consistency and repeatability

An issue with microfluidic gradient generators is that the gradient flattens as it travels along the channel due to diffusion across the laminar streams at the low flow rates imposed by the mixing network. In contrast, when using our device the gradient profile is maintained along the entire length of the channel (Fig. 4A) because of the high flow rate.

Another concern with microfluidic deposition of single protein surface-bound gradients is surface saturation. Unless the deposition is conducted for the same amount of time, the gradient profile will be different from device to device. To test the reproducibility of our method we used the same gradient program to deposit type IV collagen consecutively on three different devices (Fig. 4D). We observed good reproducibility with minimal differences between the gradients.

Materials and methods

Microfluidic devices

Devices (shown in Fig. 1) were made from polydimethylsiloxane (PDMS) using previously described rapid prototyping techniques.³⁶ Briefly, the device layout was designed in AutoCad (Autodesk, San Rafael CA), and printed to 35 mm film using a commercial film printer (Polaroid ProPallete 8000, Polaroid Corporation, Waltham MA). The remaining fabrication steps were carried out in our class 100 clean rooms. We used the film mask to generate a replica-casting master in SU-8-2050 (Microchem Corp., Newton MA). PDMS curing agent and pre-polymer (Sylgard 184, Dow Corning, Midland MI) were mixed together in a 1 : 10 ratio and poured over the master in a tissue culture dish. The dish was placed in a vacuum desiccator for at least one hour, and left overnight at 65 °C in a drying oven (Yamato DX400, Yamato Scientific America Inc., Santa Clara CA). The resulting mold was peeled from the master and cut to size, and access holes were punched for tubing using a blunt 16 gauge needle (Becton Dickinson, Franklin Lakes NJ) with a sharpened edge. The mold and a glass cover slip were exposed to air plasma (PDC-32G, Harrick Scientific, Pleasantville NY) for 30 s and then bonded together. The resulting bond is irreversible. For covalent gradient deposition we used SuperAldehyde2 (SA) glass slides (Telechem International, Sunnyvale CA). A clamp mechanism was used to attach the PDMS mold to the SA slide. Tygon tubing (Saint-Gobain, Akron OH), with internal diameter of 0.508 mm and external diameter of 1.524 mm, was inserted in the access holes and phosphate buffered saline (PBS, Fisher Scientific, Chicago IL) was injected into the device via the waste line. Air bubbles were removed after the input channels were connected by increasing the pressure on the waste line syringe, forcing the trapped gases to diffuse into the PDMS.

The outer input channels were connected to syringes containing PBS, while the middle channel was connected to a syringe containing a solution of the protein to be deposited. Flow rates on the syringes were controlled using Pico Plus syringe pumps (Harvard Apparatus, Holliston MA) connected to an Intel Pentium 4 computer (Dell, Round Rock TX) running Microsoft Windows XP (Microsoft, Redmond WA). For the devices used to test gradient stability the surface was blocked with 10% dry non-fat milk in PBS.

Custom pump control software

The necessary pump commands required to generate the gradient need to be simple, fast and reusable. Simplicity is achieved by restricting the choices available via the extensive use of drop-down boxes and point-and-click interfaces. To speed generation of the pump commands, we have implemented functionality that allows automatic generation of most of the required commands based on a set of initial conditions. We have implemented a hierarchy that maximizes reusability in which the simplest item is the hardware, namely the pump. Once a pump has been defined, it can be addressed by multiple actions in multiple gradient files. An action can send commands to one or multiple pumps, immediately or after a specified time delay. The types of commands that can be sent are start/stop, flow rate, flow direction, and volume to inject/withdraw. Each action can be used by multiple batch commands, which can play a series of actions in sequence once, several times, or in an infinite loop. A one-dimensional gradient of any complexity can be generated by a single batch command. The batch command is presented in the Graphical User Interface (GUI) as a push-button, part of our custom- developed software, which was written in C# (C-Sharp) using the SharpDevelop IDE (http://www.icsharpcode.net). The pump control code is provided in the ESI.

Gradient imaging

After deposition, we flushed the microfluidic device thoroughly with PBS and captured epifluorescent images of the gradients of proteins conjugated with a fluorophore using a monochrome, cooled CCD camera (CoolSNAP HQ, Roper Scientific, Trenton NJ), mounted on a Zeiss Axiovert 200 M inverted microscope (Zeiss, Thornwood NY). To correct for uneven stray and uneven excitation illumination, we used background subtraction and shading correction as described in the Metamorph documentation (Molecular Devices, Downingtown PA). The resulting picture was used to determine de novo the adsorption kinetics of the protein used to generate the gradient.

Reagents

ECM macromolecules were: Oregon green-conjugated collagen type IV (Molecular Probes, Invitrogen, Carlsbad CA), collagen type I (Sigma-Aldrich, St Louis MO), and fibronectin (Chemicon, Temecula CA). Except for the collagen type IV, all the matrix proteins were conjugated to AlexaFluor488 using a labelling kit from Molecular Probes. All washes were in PBS.

Conclusions

We have demonstrated a method for rapid patterning of protein gradients using computer-driven hydrodynamic focusing in a simple microfluidic device. Because we control the shape of the gradient dynamically, we can generate protein gradients that either require multiple complex fabrication steps or are impossible using other methods. Switching from one gradient profile to another requires only a couple of hours to devise a new control file, not days or weeks to design and build a new microfluidic device. This avoids experimental errors introduced by using multiple microfluidic devices to create different gradient patterns. At the same time, the precise control we have over the deposition time of each protein allows us to calculate the surface protein density of each protein across the channel. Therefore we do not lose precision as we increase gradient complexity. A variety of improvements to experimental apparatus, such as using non-compliant tubing, reducing tubing length, and even more precise syringe pumps, should further improve the precision with which we can deposit protein gradients.

Using our method, we already showed that we can easily extract valuable parameters such as deposition rate and surface density of the different ECM macromolecules and compare the validity of various models over a range of deposition parameters. We also demonstrated the capability to design and pattern simple and complex gradient profiles using the same device. Our preliminary cell migration data suggest that our method in generating gradients will be extremely valuable to study haptotaxis. Our research is being further developed in this scope, with one of the central goals being to calculate the haptotaxis coefficient for different cancer cell lines, surrounded by different types and shapes of extracellular matrices. These coefficients will be crucial in the accurate development of mathematical models of cancer growth and development, such as those by Anderson.³