Using Neural Data to Test A Theory of Investor Behavior: An Application to Realization Utility

Abstract

We use measures of neural activity provided by functional magnetic resonance imaging (fMRI) to test the “realization utility” theory of investor behavior, which posits that people derive utility directly from the act of realizing gains and losses. Subjects traded stocks in an experimental market while we measured their brain activity. We find that all subjects exhibit a strong disposition effect in their trading, even though it is suboptimal. Consistent with the realization utility explanation for this behavior, we find that activity in the ventromedial prefrontal cortex, an area known to encode the value of options during choices, correlates with the capital gains of potential trades; that the neural measures of realization utility correlate across subjects with their individual tendency to exhibit a disposition effect; and that activity in the ventral striatum, an area known to encode information about changes in the present value of experienced utility, exhibits a positive response when subjects realize capital gains. These results provide support for the realization utility model and, more generally, demonstrate how neural data can be helpful in testing models of investor behavior.

Over the past twenty years, economists have accumulated a large amount of evidence on how individual investors manage their financial portfolios over time. Some of this evidence is puzzling, in the sense that it is hard to reconcile with the simplest models of rational trading (Barberis and Thaler (2003); Campbell (2006)). Theorists have responded to this challenge by constructing new models of investor behavior. Empiricists, in turn, have started testing these newly-developed models.

Most of the empirical work that tests theories of investor behavior uses field data (Barber and Odean (2000); Barber and Odean (2001); Choi et al. (2009); Grinblatt and Keloharju (2009)). A smaller set of studies uses data from laboratory experiments. The advantage of experimental data is that it gives researchers a large degree of control over the trading and information environment, which can make it easier to tease theories apart (Plott and Sunder (1988); Camerer and Weigelt (1991); Camerer and Weigelt (1993); Weber and Camerer (1998); Bossaerts and Plott (2004); Bossaerts et al. (2007)).²

In this paper, we show how another kind of data, namely measures of neural activity taken using functional magnetic resonance imaging (fMRI) while subjects trade in an experimental stock market, can also be very useful in testing theories of investor behavior. In particular, we use neural data to test the validity of the “realization utility” theory of trading, a theory that has been used to address several facts about investor trading behavior, including the so-called disposition effect.

The disposition effect is the robust empirical fact that individual investors have a greater propensity to sell stocks trading at a gain relative to purchase price, rather than stocks trading at a loss³. This fact has attracted considerable attention because it has proven challenging to explain using simple rational models of trading behavior. This impasse has motivated the development of multiple competing alternative theories, both rational and behavioral (Shefrin and Statman (1985); Odean (1998); Barberis and Xiong (2009); Kaustia (2010)). The realization utility model (Shefrin and Statman (1985); Barberis and Xiong (2012)) is based on the assumption that, in addition to deriving utility from consumption, investors also derive utility directly from realizing gains and losses on the sale of risky assets that they own. For example, if an investor realizes a gain (e.g., by buying a stock at $20 and selling it at $40), he receives a positive burst of utility proportional to the capital gain. In contrast, if he realizes a loss (e.g., by buying a stock at $20 and selling it at $10), he receives a negative burst of utility proportional to the size of the realized loss. The presence of realization utility is important because, in combination with a sufficiently high time discount rate, it leads investors to exhibit a disposition effect (Barberis and Xiong (2012)).

Testing for the validity of a theory such as realization utility is difficult because it, and other theories of investor trading, often make similar predictions about behavior (see Weber and Camerer (1998) for an exception). Furthermore, it is extremely difficult, using data on behavior alone, to carry out direct tests of the computations driving behavior (e.g., tests of whether potentially realizable capital gains rather than net expected values are tracked when selling). On the other hand, a combination of neural measurement and careful experimental design allows for direct tests of the extent to which the computations made by the brain at the time of decision-making are consistent with the mechanisms posited by different models.

In this paper, we describe the results of an fMRI experiment designed to test the hypothesis that subjects experience realization utility while trading in an experimental stock market, and that this is associated with trading patterns consistent with the disposition effect. The experiment allows us to test several behavioral and neural predictions of the realization utility hypothesis.⁴

Behaviorally, we find that the average subject in our experiment exhibits a strong and significant disposition effect. This stands in sharp contrast to the prediction of a simple rational trading model in which subjects maximize the expected value of final earnings. The reason is that our experimental design induces positive autocorrelation in stock price changes, which, in turn, implies that a risk-neutral rational trader would sell losing stocks more often than winning stocks, thereby exhibiting the opposite of the disposition effect. The strong disposition effect displayed by our subjects is, however, consistent with the existence of realization utility effects.

When taken literally as a model of the decision-making process, the realization utility model makes several predictions about the neural computations that should be observed at different points in time. We describe these predictions in detail in the main body of the paper, but summarize them briefly here.

First, the realization utility model predicts that, at the moment when a subject is making a decision as to whether to sell a stock, neural activity in areas of the brain that are associated with encoding the value of potential actions at the time of a decision should be proportional to the capital gain that would be realized by the trade (i.e. to the difference between the sale price and the purchase price). In particular, the model implies that, at the time of decision, activity in the ventromedial prefrontal cortex (vmPFC), an area of the brain that has been reliably shown to be involved in the computation of the value of the different options⁵, should be positively correlated with the capital gain or loss associated with selling a stock.

Second, the realization utility model predicts that, across individuals, the strength of the disposition effect should be correlated with the strength of the realization utility signal in the area of the vmPFC that computes decision values. This follows from the fact that a subject who is strongly influenced by realization utility should exhibit both a strong disposition effect and neural activity in decision value areas that reflect the computation of the associated capital gain.

Third, the realization utility hypothesis states that realizing a capital gain generates a positive burst of utility, while realizing a capital loss generates a negative one. This predicts that, controlling for the size of the capital gain or loss, and regardless of the precise timing of the actual utility bursts, realizing a capital gain should increase activity in areas of the ventral striatum (vSt), while realizing a capital loss should decrease its activity. This is because the vSt is known to encode so-called reward prediction errors, which measure the change in the expected net present value of lifetime utility induced by new information or changes in the environment. Since selling a stock at a gain generates a utility burst, it also generates a change in the expected net present value of utility, one that should be reflected in the striatum at the moment of sale.⁶

Our fMRI measurements reveal patterns of neural activity that are largely consistent with the three neural predictions. This provides novel and strong support for the key mechanisms at work in the realization utility model. Furthermore, to our knowledge, this also provides the first example of how neural evidence can be used to test economic models of financial decision-making. We emphasize that the results do not imply that realization utility provides a complete description of the forces driving investor behavior, even in the context of our experiment. However, the fact that activity in the decision-making circuitry corresponds to some of the computations hypothesized by the realization utility model provides novel evidence in support of the model. It further suggests that mechanisms of this kind might also be at work in the real-world transactions of individual investors.

Using neural data to test an economic model is an unusual exercise in the field of economics because a common view in the profession is that models make as-if predictions about behavior, and are not to be taken as literal descriptions of how decisions are actually made (Gul and Pesendorfer (2008); Bernheim (2009)). In contrast to this view, we adopt a neuroeconomic approach which is based on the idea that knowledge about the computational processes that the brain uses to make decisions should be of central interest to economists because, since these processes describe the actual determinants of observed behavior, they provide valuable insights into the drivers of economic behavior (Camerer et al. (2005); Camerer (2007); Rustichini (2009); Glimcher (2010); Fehr and Rangel (2011)).

Our study contributes to the nascent field of neurofinance, which seeks to characterize the computations undertaken by the brain to make financial decisions, and to understand how these computations map to behavior. Several early contributions are worth highlighting. Lo and Repin (2002) investigate the extent to which professional experience affects the emotional arousal of traders in stressful situations, where arousal is measured using skin conductance responses and changes in blood pressure. Kuhnen and Knutson (2005) measure neural responses using fMRI during a simple investment task and find that activity in brain regions previously associated with emotional processing, such as the nucleus accumbens and the insula, predict subjects’ subsequent willingness to take risks. Knutson et al. (2008) take these ideas further by showing that exogenous emotional cues (e.g., erotic pictures) can be used to affect investment behavior, and that these cues increase activity in the same areas that they identified in their previous study. More recently, Bruguier et al. (2010) show that neural fMRI measurements of the extent to which subjects activate brain areas associated with concrete cognitive skills, such as the ability to predict another person’s state of mind, might be useful in identifying which subjects would be successful traders, and Wunderlich et al. (2011) discover how the brain tracks correlation in an attempt to optimally hedge two sources of risk. DeMartino et al. (2012) show that fMRI measures of activity in valuation and mentalizing (theory of mind) regions are associated with the propensity to buy during experimental price bubbles. Our paper contributes to this literature by showing that a combination of fMRI neural measurements and careful experimental design can be used to test the validity of specific economic theories of financial decision making. Our work also contributes more broadly to the rapidly growing field of neuroeconomics, which seeks to characterize the computations made by the brain in different types of decisions, ranging from simple choices to choices involving risk, self-control, and complex social interactions.⁷

The paper is organized as follows. Section I presents some background information about the disposition effect and realization utility. Section II describes the experimental design and the predictions of the realization utility hypothesis. Section III provides a detailed description of how the neural predictions can be tested using fMRI. Section IV describes the results. Section V briefly concludes.

I. Background: The Disposition Effect and the Realization Utility Model

Using an argument based on Kahneman and Tversky’s (1979) prospect theory, Shefrin and Statman (1985) predict that individual investors will have a greater propensity to sell stocks trading at a gain relative to purchase price, rather than stocks trading at a loss. They label this the “disposition effect” and provide some evidence for it using records of investor trading. More detailed evidence for the effect is presented by Odean (1998), who analyzes the trading activity, from 1987 to 1993, of 10,000 households with accounts at a large discount brokerage firm. The phenomenon has now been replicated in several other large databases of trading behavior.⁸

It is useful to explain Odean’s (1998) methodology in more detail because we will adopt a similar methodology in our own analysis. For any day on which an investor in Odean’s (1998) sample sells shares of a stock, each stock in his portfolio on that day is placed into one of four categories. A stock is counted as a “realized gain” (“realized loss”) if it is sold on that day at a price that is higher (lower) than the average price at which the investor purchased the shares. A stock is counted as a “paper gain” (“paper loss”) if its price is higher (lower) than its average purchase price, but it is not sold on that day. From the total number of realized gains and paper gains across all accounts over the entire sample, Odean (1998) computes the Proportion of Gains Realized (PGR):

$$\mathit{PGR}=\frac{\#\text{of}\text{realized}\text{gains}}{\#\text{of}\text{realized}\text{gains}+\#\text{of}\text{paper}\text{gains}}.$$

In words, PGR computes the number of gains that were realized as a fraction of the total number of gains that could have been realized. A similar ratio, PLR, is computed for losses:

$$\mathit{PLR}=\frac{\#\text{of}\text{realized}\text{losses}}{\#\text{of}\text{realized}\text{losses}+\#\text{of}\text{paper}\text{losses}}.$$

The disposition effect is the empirical fact that PGR is significantly greater than PLR. Odean (1998) reports PGR = 0.148 and PLR = 0.098.

While the disposition effect is a robust empirical phenomenon, its causes remain unclear. In particular, traditional rational models of trading have had trouble capturing important features of the data. Consider, for example, an information model in which investors sell stocks with paper gains because they have private information that these stocks will subsequently do poorly, and hold on to stocks with paper losses because they have private information that these stocks will rebound. This hypothesis is inconsistent with Odean’s finding that the average return of the prior winners that investors sell is 3.4% higher, over the next year, than the average return of the prior losers they hold on to. Another natural model involves taking into account the favorable treatment of losses by the tax code. However, this model also fails to explain the disposition effect because tax-loss selling predicts a greater propensity to sell stocks associated with paper losses. Another model attributes the disposition effect to portfolio rebalancing of the kind predicted by a standard framework with power utility preferences and i.i.d. returns. However, under this hypothesis, rebalancing is the “smart” thing to do, which implies that we should observe a stronger disposition effect for more sophisticated investors. In contrast to this prediction, the data show that it is less sophisticated investors who exhibit a stronger disposition effect (Dhar and Zhu (2006)).

Researchers have also proposed behavioral economics models of the disposition effect; these can potentially explain the stylized facts that the rational frameworks just described cannot explain. One popular model assumes that investors have an irrational belief in mean-reversion (Odean (1998); Weber and Camerer (1998); Kaustia (2010)). If investors believe that stocks that have recently done well will subsequently do poorly, and that stocks that have recently done poorly will subsequently do well, their optimal trading strategy would lead to a disposition effect. We label such beliefs “irrational” because they are at odds with Odean’s (1998) finding that the winner stocks investors sell subsequently do well, not poorly. While the mean-reversion hypothesis is appealing for its simplicity, and is consistent with some evidence from psychology on how people form beliefs⁹, some studies cast doubt on its empirical validity. For example, Weber and Camerer (1998) ask subjects to trade stocks in an experimental stock market, and find that they exhibit a disposition effect in their trading. In order to test the mean-reversion hypothesis, they add a condition in which subjects’ holdings are exogenously liquidated at full value at random times, after which subjects are asked to reinvest the proceeds across stocks in any way they like. Note that if subjects are holding on to stocks with paper losses because of a belief in mean-reversion, we would expect them to re-establish their positions in these stocks. But in fact, they do not.¹⁰

Another popular behavioral economics model posits that the disposition effect results from prospect theory preferences (Kahneman and Tversky (1979)). Prospect theory is a prominent theory of decision-making under risk which assumes that individuals make decisions by computing the utility of potential gains and losses. These gains and losses are measured relative to a reference point that is often assumed to be the status quo, and utility is concave over gains and convex over losses. At first sight, it appears that prospect theory preferences may be helpful for understanding the disposition effect. If an investor is holding a stock that has risen in value, he may think of it as trading at a gain. If, moreover, the concavity of the value function over gains induces risk aversion, this may lead him to sell the stock. Conversely, if the convexity of the value function over losses induces risk-seeking, the investor may be inclined to hold on to a stock that has dropped in value. Contrary to this intuition, Barberis and Xiong (2009) have recently shown that it is surprisingly difficult to derive behavior consistent with the disposition effect using this model. In fact, they show that an investor who derives prospect theory utility from the annual trading profit on each stock that he owns will often exhibit the opposite of the disposition effect. Further theoretical arguments against this model are provided by Kaustia (2010), who shows that it predicts that investors’ propensity to sell a stock depends on the magnitude of the embedded paper gain in a way that is inconsistent with the empirical evidence.

Another behavioral model of the disposition effect, and the one we focus on in this paper, is based on the realization utility hypothesis (Shefrin and Statman (1985); Barberis and Xiong (2012)). The central assumption of this model is that investors derive direct utility from realizing capital gains and losses on risky assets that they own: they experience a positive burst of utility when they sell an asset at a gain relative to purchase price, where the amount of utility depends on the size of the realized gain; and a negative burst when they sell an asset at a loss relative to purchase price, where the amount of disutility again depends on the size of the realized loss. Importantly, this hypothesis states that trades have a direct utility impact on investors, not just an indirect one through their effect on lifetime wealth and consumption.¹¹ Barberis and Xiong (2012) show that, when realization utility is linear and the time discount rate is sufficiently positive, a trader who maximizes the expected discounted sum of future realization utility bursts will exhibit a disposition effect. The intuition is simple. If an investor derives pleasure from realizing capital gains and, moreover, is impatient, he will be very keen to sell stocks at a gain. Conversely, if he finds it painful to sell stocks at a capital loss and also discounts future utility at a high rate, he will delay selling losing stocks for as long as possible.¹²

While the realization utility hypothesis makes predictions about behavior that are consistent with the disposition effect, as well as with other empirical patterns¹³, it is based on assumptions that depart significantly from those of traditional models. In particular, its predictions rely on the assumption that utility depends not only on consumption, but also on the act of realizing capital gains and losses. Given the unusual nature of this assumption, it seems especially important to carry out direct tests of the extent to which the hypothesized source of utility is actually computed by subjects and affects their decisions. In the rest of the paper, we show how this can be done using a combination of fMRI measures of neural activity and careful experimental design.

II. Experimental Design and Predictions

In this section, we first describe the experimental stock market that we set up to test the realization utility model, and then lay out the specific behavioral and neural predictions of the theory that we test.

A. Design

The design of the experimental stock market builds directly on an earlier non-neural experiment conducted by Weber and Camerer (1998).

Subjects are given the opportunity to trade three stocks – stock A, stock B, and stock C – in an experimental market. The experiment consists of two identical sessions separated by a one-minute break. Each session lasts approximately 16 minutes and consists of 108 trials. We use t to index the trials within a session.¹⁴

At the beginning of each session, each subject is given $350 in experimental currency and is required to buy one share of each stock. The initial share price for each stock is $100; after the initial purchase, each subject is therefore left with $50. Every trial t > 9 consists of two parts: a price update and a trading decision, each of which corresponds to a separate screen that the subject sees (Figure 1). In the price update part, one of the three stocks is chosen at random and the subject is shown a price change for this stock. Note that stock prices only evolve during the price update screens; as a result, subjects see the entire price path for each stock. In the trading part, one of the three stocks is again chosen at random and the subject is asked whether he wants to trade the stock. Note that no new information is revealed during this part.

Figure 1. Sample screens from a typical trial in the fMRI experiment.

For trials 10–108, subjects saw the price update screen for two seconds, followed by the trading screen for which they had up to three seconds to enter a decision (a blank screen was displayed in between in order to temporally separate neural activity associated with decision-making.) Because the blank screen is displayed for a random amount of time (uniformly distributed between 1 and 3 seconds), the average length of a trial, consisting of the three screens, is 7 seconds. The screens shown below are for a trial in which the subject owns a unit of both stocks A and B. If the subject had not owned stock A at the price update screen, the purchase price would not be displayed. If the subject had not owned stock B at the trading screen, he would have had the opportunity to buy stock B. The screens were displayed while subjects were inside the fMRI scanner, and decisions were entered with a handheld device. For trials 1–9, subjects only saw the price update screen and the blank screen, which allowed them to accumulate information about the price changes before they were asked to make a decision starting on trial 10.

We split each trial into two parts to temporally separate different computations associated with decision-making. At the price update screen, subjects are provided with information about a change in the price of one of the three stocks, but do not have to compute the value of buying or selling the stock, both because they are not allowed to make decisions at this stage, but also because they do not know which of the three assets will be selected for trading in the next screen. At the trading screen the opposite situation holds: subjects need to compute the value of buying or selling a stock, but do not need to update their beliefs about the price process since no new information about prices is provided.

Trials 1 through 9 consist only of a price update stage; i.e., subjects are not given the opportunity to buy or sell during these trials. This initial set of trials was added to allow subjects to accumulate information about the three stocks before having to make any trading decisions.

Each subject is allowed to hold a maximum of one share and a minimum of zero shares of each stock at any point in time. In particular, short-selling is not allowed. The trading decision is therefore reduced to deciding whether to sell a stock (conditional on holding it), or deciding whether to buy it (conditional on not holding it). The price at which a subject can buy or sell a stock is given by its current market price.

The price path of each stock is governed by a two-state Markov chain with a good state and a bad state. The Markov chain for each stock is independent of the Markov chains for the other two stocks. Suppose that, in trial t, there is a price update for stock i. If stock i is in the good state at that time, its price increases with probability 0.55 and decreases with probability 0.45. Conversely, if it is in the bad state at that time, its price increases with probability 0.45 and decreases with probability 0.55. The magnitude of the price change is drawn uniformly from {$5, $10, $15}, independently of the direction of the price change.

The state of each stock changes over time in the following way. Before trial 1, we randomly assign a state to each stock. If the price update in trial t >1 is not about stock i, then the state of stock i in trial t remains the same as its state in the previous trial, t−1. If the price update in trial t >1 is about stock i, then the state of stock i in this trial remains the same as in trial t−1 with probability 0.8, but switches with probability 0.2. In mathematical terms, if s_i,t ∈ {good, bad} is the state of stock i in trial t, then s_i,t = s_i,t−1 if the time t price update is not about stock i, whereas if the time t price update is about stock i, the state switches as follows:

	si,t+1=good	si,t+1=bad
si,t=good	0.8	0.2
si,t=bad	0.2	0.8

The states of the stocks are never revealed to the subjects: they have to infer them from the observed price paths. To ease comparison of trading performance across subjects, the same set of realized prices is used for all subjects.

A key aspect of our design is that, conditional on the information available to subjects, each of the stocks exhibits positive short-term autocorrelation in its price changes. If a stock performed well on the last price update, it was probably in a good state for that price update. Since it is highly likely (probability 0.8) to remain in the same state for its next price update, its next price change is likely to also be positive.

At the end of each session, we liquidate subjects’ holdings of the three stocks and record the cash value of their position. We give subjects a financial incentive to maximize the final value of their portfolio at the end of each session. Specifically, if the total value of a subject’s cash and risky asset holdings at the end of session 1 is $X, in experimental currency, and the total value of his cash and risky asset holdings at the end of session 2 is $Y, again in experimental currency, then his take-home pay in actual dollars is 15 + (X+Y)/24.¹⁵ Subjects’ earnings ranged from $43.05 to $57.33 with a mean of $52.57 and a standard deviation of $3.35.

In order to avoid liquidity constraints, we allow subjects to carry a negative cash balance in order to purchase a stock if they do not have sufficient cash to do so at the time of a decision. If a subject ends the experiment with a negative cash balance, this amount is subtracted from the terminal value of his portfolio. The large cash endowment, together with the constraint that subjects can hold at most one unit of each stock at any moment, was sufficient to guarantee that no one ended the experiment with a negative portfolio value, or was unable to buy a stock because of a shortage of cash during the experiment.

N=28 Caltech subjects participated in the experiment (22 male, age range 18 – 60, std. of age: 7.6).¹⁶ All subjects were right-handed and had no history of psychiatric illness, and none were taking medications that interfere with fMRI. The exact instructions given to subjects at the beginning of the experiment are included in the Appendix. The instructions carefully describe the stochastic structure of the price process, as well as all other details of the experiment. Subjects were not explicitly told that there was short-term positive autocorrelation in the stock price changes. However, they were given details regarding the Markov chain governing the stock price paths before the experiment, and so they had sufficient information to infer the positive autocorrelation. Before entering the scanner, the subjects underwent a practice session of 25 trials to ensure familiarity with the market software.

Note that there is a straightforward way to measure the extent to which a subject exhibits a disposition effect in his trading. We simply adapt Odean’s (1998) methodology, described in Section I, in the following way. Every time a subject faces a decision about selling a stock, we classify his eventual action as a paper gain (loss) if the stock’s current price is above (below) the purchase price and he chooses not to sell; and as a realized gain (loss) if the stock’s current price is above (below) the purchase price and he chooses to sell. We then count up the number of paper gains, paper losses, realized gains, and realized losses over all selling decisions faced by the subject and compute the PGR and PLR measures described earlier. We assign the subject a disposition effect measure of PGR-PLR. When this measure is positive (negative), the subject exhibits (the opposite of) a disposition effect.

B. Optimal trading strategy

We now characterize the optimal trading strategy for a risk-neutral Bayesian investor who is maximizing the expected value of his take-home earnings – from now on, we refer to this investor as an “expected value” investor. The optimal strategy for this investor is to sell (or not buy) a stock when he believes that it is more likely to be in the bad state than in the good state; and to buy (or hold) the stock when he believes that it is more likely to be in the good state. Formally, let p_i,t be the price of stock i in trial t, after any price update about the stock, and let q_i,t = Pr(s_i,t = good|p_i,t, p_i,t−1,…, p_i,1) be the probability that a Bayesian investor, after seeing the price update in trial t, would assign to stock i being in the good state in trial t. Also, let z_t take the value 1 if the price update in trial t indicates a price increase for the stock in question; and −1 if the price update indicates a price decrease. Then q_i,t = q_i,t−1 if the price update in trial t was not about stock i; but if the price update in trial t was about stock i, then:

$$\begin{array}{l}{q}_{i,t}(q_{i,t-1},z_t)=\frac{Pr(z_t\mid s_{i,t}=\mathit{good})\ast Pr(s_{i,t}=\mathit{good}\mid q_{i,t-1})}{q_{i,t-1}Pr(z_t\mid s_{i,t-1}=\mathit{good})+(1-q_{i,t-1})Pr(z_t\mid s_{i,t-1}=\mathit{bad})}\\ =\frac{(0.5+0.05z_t)\ast [0.8\ast q_{i,t-1}+0.2\ast (1-q_{i,t-1})]}{q_{i,t-1}[0.8\ast (0.5+0.05z_t)+0.2\ast (0.5-0.05z_t)]+(1-q_{i,t-1})[0.2\ast (0.5+0.05z_t)+0.8\ast (0.5-0.05z_t)]}\end{array}$$ (1)

The optimal strategy for an expected value investor is to sell (if holding) or not buy (if not holding) stock i in trial t when q_i,t < 0.5; and to hold or buy it otherwise.

Note that a trader who follows the optimal strategy described above will exhibit the opposite of the disposition effect. If a stock performed well on the last price update, it was probably in a good state for that price update. Since it is very likely to remain in the same state for its next price update, its next price change is likely to also be positive. The optimal strategy therefore involves selling winner stocks relatively rarely, and losing stocks more often, thereby generating the reverse of the disposition effect.

Of course, it is difficult for subjects to do the exact calculation in equation (1) in real time during the experiment. However, it is relatively straightforward for subjects to approximate the optimal strategy: they need simply keep track of each stock’s most recent price changes, and then hold on to stocks that have recently performed well while selling stocks that have recently performed poorly. The fact that a stock’s purchase price is reported on the trading screen makes it particularly easy to follow an approximate strategy of this kind: subjects can simply use the difference between the current market price and the purchase price as a proxy for the stock’s recent performance.¹⁷

C. Behavioral and neural predictions of the realization utility model

We now lay out the behavioral and neural predictions of the realization utility model, and contrast them with the predictions of the expected value model which assumes a risk-neutral optimal Bayesian decision-maker. The realization utility model we have in mind is one where, as in Barberis and Xiong (2012), realization utility has a linear functional form, the time discount rate is strongly positive, and the agent maximizes the discounted sum of current and future expected realization utility flows.

Consider the behavioral predictions first. During the instruction session, subjects were given the structure of the data generating process for stock prices. From this, it is straightforward to infer that price changes are positively autocorrelated. In such a market, an expected value investor will exhibit the opposite of the disposition effect: for the actual price process that our subjects see, the value of the PGR-PLR measure under the optimal trading strategy for an expected value investor is −0.76. In other words, this investor will have a much greater propensity to realize losses than to realize gains. By contrast, a trader who experiences bursts of realization utility and who discounts future utility at a high rate will sell winner stocks more often than the expected value trader and loser stocks less often. After all, he is keen to realize capital gains as soon as possible and to postpone realizing capital losses for as long as possible. Recall that the disposition effect is simply the statement that PGR-PLR>0; this statement is consistent with the realization utility hypothesis and not with the expected value model. Our first prediction is as follows.

Prediction 1 (Behavioral)

For an expected value investor, the value of the PGR-PLR measure is given by −0.76. On the other hand, for the realization utility investor, the value of PGR-PLR is greater than −0.76.

We now turn to the neural predictions of the expected value and realization utility models. As noted earlier, a key goal of the paper is not only to test the behavioral predictions of these models, but also to test if the models’ basic assumptions are consistent with the computations that subjects actually make during the choice process.

The neural predictions build on a basic finding from the field of decision neuroscience. A sizable number of studies have found evidence consistent with the idea that, in simple choice situations, the brain makes decisions by assigning values (often called “decision values”) to the options under consideration, and then comparing them to make a choice. These value signals are thought to reflect the relative value of getting the option under consideration versus staying with the status quo. In the context of our experiment, during selling decisions this variable would reflect the value of selling a stock versus keeping it, while during a buying decision it would reflect the value of getting the stock versus not buying it. A substantial body of work has shown that, in particular, activity in an area of the ventromedial prefrontal cortex (vmPFC) reliably encodes decision value computations at the time of choice.¹⁸

Since this finding is critical to our analysis, it is important to summarize the key lines of evidence that support it. First, activity in the vmPFC reliably correlates with behavioral measures of the value of the objects of choice, across a wide class of stimuli and choice paradigms, and regardless of whether the object is actually chosen or not.¹⁹ Second, additional studies have shown that the activity in these areas of the vmPFC is more likely to be associated with the computation of value than with alternative signals that are often correlated with values, but are distinct from them. For example, Plassmann et al. (2010) rule out that the vmPFC responses can be attributed to confounding anticipatory emotions or anticipatory emotion signals, and also show that these responses cannot be attributed to attentional, motor, or saliency signals. Litt et al. (2011) carry out an additional test that also rules out the interpretation of vmPFC activity as attentional, motor, or saliency signals, but show that activity in many other areas of the brain that has often been interpreted as a putative value signal (e.g., anterior insula activity) actually fits these alternative descriptions better.²⁰ Third, patients with lesions in their vmPFC exhibit impairments in decision-making (such as an increase in the the inconsistency of their choices, such as GARP violations) that has been widely interpreted as causal evidence for the role of vmPFC decision value signals in choice ((Fellows and Farah (2007); Camille et al. (2011); Camille et al. (2011)). Taken together, these findings provide strong support for the view, now widely held in neuroscience,²¹ that vmPFC responses at the time of choice encode valuation signals for the different stimuli for the purpose of guiding choice.²²

The first two neural predictions involve comparing the decision value signals that we observe in the vmPFC to the decision value signals that would be predicted by the realization utility model and by the expected value model. To see the restrictions implied by these two theories, consider the decision value signal that would be computed at the time of making a selling decision by an individual who makes choices according to the expected value model. In the context of our experiment, the decision value of selling a stock is given by the value of selling the stock minus the value of holding it. For the expected value investor, the value of selling the stock is zero: if he sells it, he will no longer own any shares of it, and so it can no longer generate any value for him. In contrast, the value of holding the stock can be approximated by the stock’s expected price change on its next price update:

$$E_t[\mathrm{\Delta }{p}_{i,t+1}\mid q_{i,t},\mathrm{\Delta }{p}_{i,t+1}\ne 0]=0.6(2q_{i,t}-1).$$

It follows that the decision value signal at the time of making a selling decision is given by 0–0.6(2q_i,t−1), or 0.6(1–2q_i,t); we will refer to this quantity throughout the paper as the net expected value of selling, or NEV. Note that this is only an approximation because the exact value of holding a stock is the stock’s expected cumulative price change until the subject decides to sell it. However, this approximation has little effect on our later results because the value of holding a stock until its next price change is highly correlated with the value of holding the stock until it is actually optimal to sell it (the latter quantity can be computed by simulation).

Now consider the decision value signal that would be computed at the time of making a selling decision by an individual who makes choices according to the realization utility model. In particular, consider a simple form of the model in which subjects maximize the sum of expected discounted realized capital gains and losses. For such a trader, the value of selling is linearly proportional to the capital gain or loss, given by p_i,t −c, where c is the purchase price, or cost basis. However, the expected impact of holding the stock on realization utility is approximately zero, as long as the discount rate is sufficiently high. Thus, for such an investor, the decision value of selling should be linearly related to p_i,t − c.²³ This, together with the fact that decision value signals have been found to be reliably encoded in the vmPFC, leads to the next prediction.

Prediction 2 (Neural)

For expected value traders, activity in the areas of the vmPFC associated with the computation of decision value should be linearly proportional to the NEV (given by 0.6(1–2q_i,t)) at the time of making selling decisions, and thus independent of the cost basis. In contrast, for subjects who experience realization utility proportional to realized capital gains and losses, activity in these areas of the vmPFC should be linearly related to the realizable gain or loss, p_i,t − c.

The previous arguments predict that subjects who place a larger weight on realization utility when making decisions should exhibit neural activity in the vmPFC that is more strongly correlated with the realizable capital gain or loss. At the same time, subjects with a larger weight on realization utility when making decisions should also exhibit a stronger disposition effect. It follows that the degree to which vmPFC activity correlates with the realizable capital gain should be correlated, across subjects, with the strength of the disposition effect that is observed in their trading.

Prediction 3 (Neural)

The degree to which vmPFC activity correlates with the realizable capital gain should be correlated, across subjects, with the strength of the disposition effect in their trading.

The final neural prediction is qualitatively different, in that it seeks to test directly if subjects experience bursts of realization utility that are proportional to the realized capital gains. One difficulty in testing this prediction is that, while the theory of realization utility says that the trader receives a utility burst at the moment of trade, it is hard to know, in practice, when exactly this burst occurs. For example, in our context, does it occur at the moment the subject presses a button to indicate his decision, or does it occur a little later when he reflects on the trade? Moreover, it is unclear what the duration of the burst is, in practice. In fact, the realization utility model leads to identical predictions under all of these variations of the utility burst, provided that the net present value of the utility burst is held constant. This makes it very difficult to test the model by looking for neural markers of the hedonic response, since we do not know when exactly to look for them.

Fortunately, however, an idea from computational neuroscience comes to the rescue. A sizable body of work has shown that an area of the brain called the ventral striatum (vSt) computes a quantity known as a prediction error in response to new information²⁴. The prediction errors measure the change in the net present value of lifetime utility before and after the news, taking into account all sources of utility. They are positive if the news indicates an improvement in the expected net present value of utility, and negative otherwise. Importantly, they reflect the change in discounted utility, but are insensitive to the precise timing of the hedonic impact of the news. This is useful because it means that we can test for hedonic effects associated with the realization of capital gains and losses by looking for a burst of activity in the vSt consistent with the change in utility that they generate. In short, when a trader sells a stock, this is associated with a utility burst; while we do not know the exact timing or duration of the burst, we do know that it generates a change in the expected net present value of utility, one that should be reflected at the moment of sale in the prediction error computed by the vSt.

Prediction 4 (Neural)

Under the realization utility hypothesis, neural responses in the area of the vSt known to encode prediction errors should increase at the precise moment that individuals decide to realize a capital gain, and decrease at the moment they decide to realize a capital loss.

III. fMRI data collection and analysis

In this section, we describe how the fMRI measures of neural activity were collected and analyzed. The section contains enough detail to serve as a brief primer on the subject to those unfamiliar with fMRI. For more details, see Huettel et al. (2004), Ashby (2011), and Poldrack et al. (2011).

A. fMRI data collection and measurement

We collected measures of neural activity over the entire brain using BOLD-fMRI, which stands for blood-oxygenated level dependent functional magnetic resonance imaging. BOLD-fMRI measures changes in local magnetic fields that result from the local inflows of oxygenated hemoglobin and outflows of de-oxygenated hemoglobin that occur when neurons fire. fMRI provides measures of the BOLD response of relatively small “neighborhoods” of brain tissue known as voxels, and is thought to measure the sum of the total amount of neural firing into that voxel as well as the amount of neuronal firing within the voxel. ²⁵

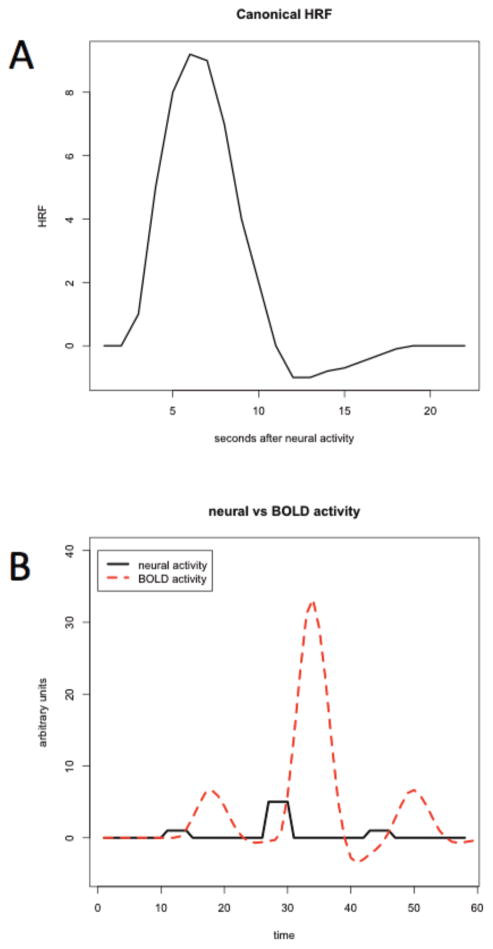
One important complication is that the hemoglobin responses measured by BOLD-fMRI are slower than the associated neuronal responses. Specifically, although the bulk of the neuronal response takes place quickly, BOLD measurements are affected for up to 24 seconds thereafter. Figure 2A provides a more detailed illustration of the nature of the BOLD response. The top panel depicts the path of the BOLD signal in response to one (arbitrary) unit of neural activity of infinitesimal duration at time zero. The function plotted here is called the canonical hemodynamic response function (HRF). It is denoted by h(τ), where τ is the amount of time elapsed since the neural activity impulse, and has been shown to approximate well the pattern of BOLD responses for most subjects, brain areas, and tasks.

Figure 2. BOLD measurements of neural activity.

(A) Because fMRI measures the blood oxygen level dependent (BOLD) response, and not neural activity directly, the mapping from neural activity to BOLD response is necessary in order to make inference about changes in neural activity. This mapping is widely known as the canonical hemodynamic response function, and is displayed here as a function of one arbitrary unit of instantaneous neural activity at time 0. (B) The BOLD response combines linearly across multiple sources of neural activity. This figure displays the BOLD response (dashed) as a function of three sequential sources of neural activity (solid).

Fortunately, there is a standard way of dealing with this complication. In particular, the BOLD response has been shown to combine linearly across multiple sources of neural activity (Boynton et al. (1996)). This property, along with knowledge of the specific functional form of the HRF, allows us to construct a mapping from predicted neural activity to predicted BOLD responses. Specifically, if the predicted level of neural activity at any particular time is given by a(t), then the level of BOLD activity at any instant t is well approximated by

$$b(t)={\int }_0^{\infty }h(u)a(t-u)du,$$

which is the convolution between the HRF and the neural inputs. The integral can be interpreted in a straightforward way: it is simply a lagged sum of all the BOLD responses triggered by previous neural activity. The properties of the BOLD response are illustrated in Figure 2B, which depicts a hypothetical path of neural activity (solid line), together with the associated BOLD response (dashed line).

During our experiment, we acquired two types of MRI data in a 3.0 Siemens Tesla Trio MRI scanner with an eight-channel phased array coil. First, we acquire BOLD-fMRI data while the subjects perform the experimental task with a voxel size of 3 mm³. We acquire this data for the entire brain (~ 100,000 voxels) every 2.75 seconds.²⁶ We also acquire high-resolution anatomical scans that we use mainly for realigning the brains across subjects and for localizing the brain activity identified by our analyses.²⁷

B. fMRI data pre-processing

Before the BOLD data can be analyzed to test our hypotheses, it has to be converted into a usable format. This requires the following steps, which are fairly standard – see Huettel et al. (2004), Ashby (2011), and Poldrack et al. (2011) – and which were implemented by way of a specialized but commonly-used software package called SPM5 (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK).

First, we correct for slice acquisition time within each voxel. This is necessary because the scanner does not collect data on all brain voxels simultaneously. This simple step, which involves a non-linear interpolation, temporally realigns the data across all voxels.

Second, we correct for head motion to ensure that the time series of BOLD measurements recorded at a specific spatial location within the scanner is always associated with the same brain location throughout the experiment.²⁸

Third, we realign the BOLD responses for each individual into a common neuroanatomical frame (the standard Montreal Neurological Institute EPI template). This step, called spatial normalization, is necessary because brains come in different shapes and sizes; as a result, a given spatial location maps to different brain regions in different subjects. Spatial normalization involves a nonlinear reshaping of the brain to maximize the match with a target template. Although the transformed data are not perfectly aligned across subjects due to remaining neuroanatomical heterogeneity, the process suffices for the purposes of most studies. Furthermore, any imperfections in the realignment process introduce noise that reduces our ability to detect neural activity of interest.

Fourth, we also spatially smooth the BOLD data for each subject by making BOLD responses for each voxel a weighted sum of the responses in neighboring voxels, with the weights decreasing with distance.²⁹ This step ensures that the error structure of the data conforms to the normality assumptions about the error structure of the regression models that we will later use to test our hypotheses (Huettel et al. (2004); Poldrack et al. (2011)).

Finally, we remove low-frequency signals that are unlikely to be associated with neuronal responses to individual trials.³⁰ An example of such a signal is the effect of a continuous head movement over the course of the experiment that is not fully removed by the second correction step described above.

C. fMRI main data analyses

The key goals of our analysis are to test if the region of the vmPFC that has been repeatedly shown to encode decision values at the time of choice exhibits activity consistent with Predictions 2 and 3; and if the area of the vSt known to encode prediction errors at the time of receiving utility-relevant news exhibits activity consistent with Prediction 4. To do this, we run statistical tests to see if there are areas within these regions of the brain, given by collections of spatially contiguous voxels called clusters, where the BOLD response reflects neural activity that implements the computations of interest (e.g., realization utility computations). This is complicated by the fact that, since every voxel contains thousands of neurons, the BOLD responses in a voxel can be driven by multiple signals. Fortunately, the linear properties of the BOLD signal allow for the identification of the neural signals of interest using standard linear regression methods.

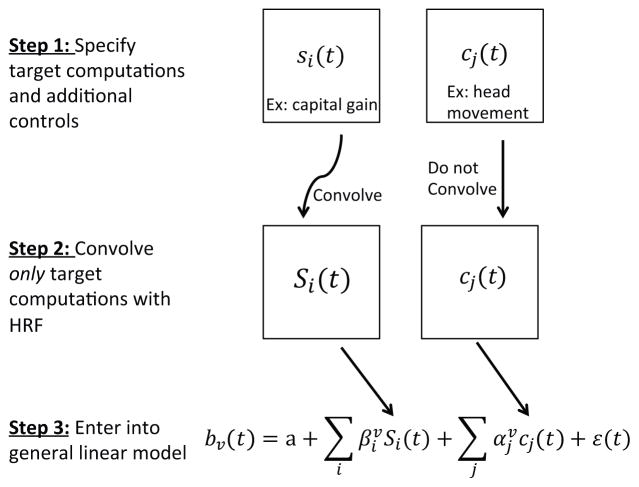
The general statistical procedure is straightforward, and will be familiar to most economists (see Figure 3 for a summary). The analysis begins by specifying two types of variables that might affect the BOLD response: target computations and additional controls. The target computations reflect the signals that we are looking for (e.g., a realization utility signal at the time of selling a stock). They are specified by a time series s_i(t) describing each signal of interest. For each of these signals, let S_i(t) denote the time series that results from convolving the signal s_i(t) with the HRF, as described above³¹. The additional controls, denoted by c_j(t), are other variables that might affect the BOLD time series (e.g., residual head movement or time trends). These are introduced to further clean up the noise inherent in the BOLD signal, but are not explicitly used in any of our tests. The control variables are not convolved with the HRF because they reflect parameters that affect the measured BOLD responses, and not neural activity that triggers a hemodynamic response.³²

Figure 3. Process of constructing a general linear model (GLM).

There are two sets of regressors: target computations and additional controls. Target computations reflect the signals of interest whereas additional controls are used to clean up noise that is inherent in the BOLD signal. Because target computations are induced by neural activity, we convolve these regressors, while we do not convolve additional controls because these variables do not trigger a hemodynamic response. Finally, we enter the two sets of variables, one of which is convolved, into a GLM with AR(1) noise.

The linearity of the BOLD signal implies that the level of BOLD activity b^v(t) in any voxel v at time t should be given by

$$b^v(t)=\text{constant}+{\mathrm{\sum }}_i{\beta }_i^v{S}_i(t)+{\mathrm{\sum }}_j{\alpha }_j^v{c}_j(t)+\epsilon (t),$$

where ε(t) denotes AR(1) noise. This model is estimated independently in each of the voxels that fall within the relevant region of interest (the vmPFC for Predictions 2 and 3, and the vSt for Prediction 4).

Our hypotheses can then be restated as tests about the coefficients of this regression model: signal i is said to be associated with activity in voxel v only if ${\beta }_i^v$ is significantly different from zero.

Two additional considerations apply to most fMRI studies, including this one. First, we are interested in testing hypotheses about the distribution of the signal coefficients in the population of subjects, not hypotheses about individual coefficients. This would normally require estimating a random effects version of the linear model specified above which, given the size of a typical fMRI dataset, is computationally intensive. Fortunately, it has been shown that there is a straightforward shortcut that provides a good approximation to the full mixed effects analysis (Penny et al. (2006)). It involves estimating the parameters separately for each individual subject, averaging them across subjects, and then performing t-tests. This is the approach we follow here.

Second, since our tests are carried out in each of the voxels in the relevant regions of interest (429 voxels for the vmPFC, and 68 for the vSt), there is a concern about false-positives. To address this problem, we correct for multiple comparisons within the relevant region of interest, a procedure known in the fMRI literature as a small volume correction (SVC). We report results as significant if they pass SVC correction at a level of p<0.05.³³

As noted earlier, we will conduct our tests in an area of the vmPFC that, in prior work, has been linked to the computation of decision values; and also in an area of the vSt that has been linked to the computation of prediction errors. Specifically, for the vmPFC region of interest, we construct a sphere with a 15 mm radius around the coordinates (MNI-space, x=3, y=36, z=−18) that were found to exhibit peak correlation with decision values at the time of choice in Plassmann et al. (2010), and then intersect this sphere with an anatomical mask of the vmPFC³⁴. For the vSt region of interest, we construct a sphere with a 15 mm radius around the coordinates (MNI-space, x = −15, y=6, z=−12) that were found to exhibit peak correlation with prediction errors in Lin et al. (2012), and then intersect this sphere with an anatomical mask of the vSt³⁵. As discussed in Section II, many studies have found very similar results; it is therefore not crucial which exact papers are used to define the regions of interest (so long as the radii of the spheres are sizable, as they are here).

IV. Results

A. Test of Behavioral Prediction 1

We begin our test of Prediction 1 by computing the strength of the disposition effect for each subject using the PGR-PLR measure described at the end of Section IIA. We find that the average PGR and PLR across subjects are 0.412 and 0.187, respectively. This implies an average PGR-PLR value of 0.225, which is significantly greater than 0 (p<0.001, in a two-tailed t-test against 0). In other words, not only is the average value of PGR-PLR significantly greater than the expected value benchmark of −0.76, but it is actually significantly positive. These results are inconsistent with the hypothesis that our subjects are all expected value investors, but are consistent with the hypothesis that some of them are influenced by realization utility.

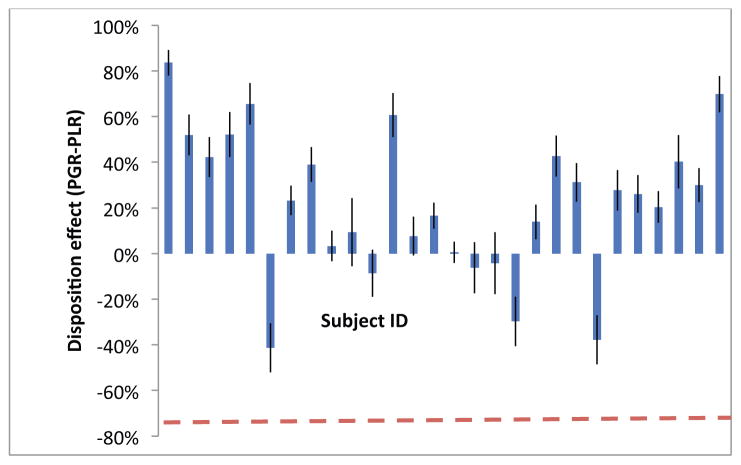
Figure 4 depicts tests of Prediction 1 at the individual level. Each vertical bar shows the value of PGR-PLR for a particular subject. The horizontal dashed line near the bottom of the figure marks the −0.76 value of PGR-PLR that corresponds to an expected value investor. The figure shows that every subject exhibits a disposition effect greater than −0.76. The hypothesis that the average disposition effect is not different from −0.76 is rejected with a t-statistic of 16.52.³⁶

Figure 4. Measures of the disposition effect (PGR-PLR) for each subject.

Standard error bars are computed as in Odean (1998) and the dotted line indicates the optimal level of the disposition effect that an expected value trader would exhibit, namely −0.76. All subjects exhibit a disposition effect greater than the optimal level and a majority of subjects have a disposition effect that is significantly positive. The figure indicates that there is significant heterogeneity in the size of the disposition effect across subjects (SD: 0.32).

The figure also shows that there is significant heterogeneity in the strength of the disposition effect across subjects: the value of PGR-PLR ranges from −0.41 to 0.83 and has a standard deviation of 0.32. This cross-individual variation is consistent with Dhar and Zhu (2006) who, using data on actual trading decisions, also find significant variation in the strength of the disposition effect across investors. Interestingly, while each of PGR and PLR varies a good deal across our subjects, the two variables have a correlation of only 0.03: subjects who are slow to sell losing stocks are not necessarily also quick to sell winning stocks.³⁷ This independence between selling behavior in the gain domain and in the loss domain is also consistent with the empirical findings of Dhar and Zhu (2006).

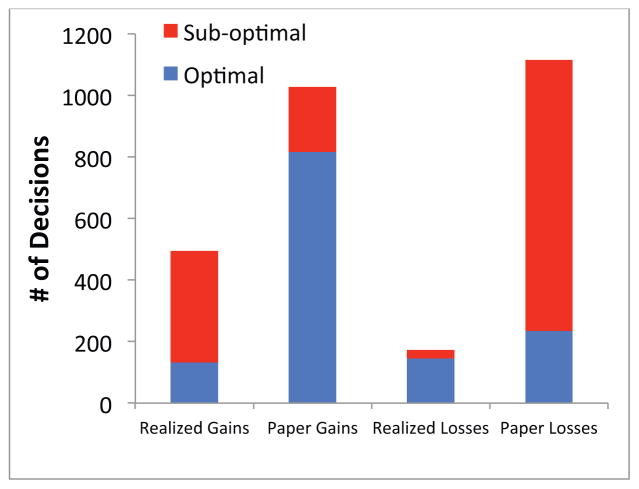
Figure 5 provides additional insight into our subjects’ selling behavior by showing, for each of the four types of decisions that a subject could make – decisions to realize a gain, decisions to realize a loss, decisions not to realize a gain, and decisions not to realize a loss -- the fraction of the decisions that are optimal, where “optimal” is defined by the expected value benchmark. For example, the figure shows that there were a total of 495 occasions in which our subjects realized gains, and that most of these decisions were suboptimal. Given that stocks exhibit short-term price momentum in the experiment, it is generally better to hold on to a stock that has been performing well. This explains why most (77.9%) of subjects’ decisions to hold on to winning stocks were optimal, and why most (67.5%) of subjects’ decisions to sell winning stocks were suboptimal. Similarly, in the experiment, it is generally better to sell a stock that has been performing poorly. This explains why most (79.2%) of subjects’ decisions to sell losing stocks were optimal, while most (80.3%) of their decisions to hold these stocks were suboptimal.

Figure 5. Total number of sell decisions by decision type and optimality.

Realized gains and losses refer to decisions where subjects sold a stock trading at a gain (loss.) Paper gains (losses) refer to decisions where subjects decided to hold a stock trading at a gain (loss). The optimality measures show an important aspect of our design: selling winners and holding losers, which leads to a disposition effect, are typically suboptimal decisions. Decisions are pooled across all subjects.

The disposition effect exhibited by our subjects is stronger than that found in empirical studies (Odean (1998); Frazzini (2006)). One possible reason for this is that the current price and the cost basis of a stock are both prominently displayed on the trading screen.³⁸ If, because of realization utility, a subject has a preference for realizing gains and for not realizing losses, the fact that we report the purchase price might make it particularly easy for him to cater to this preference, and hence to exhibit a disposition effect.³⁹

In summary, the behavioral results indicate that all of our subjects exhibit a strong disposition effect. This is inconsistent with the expected value model, but is consistent with the realization utility model.

B. Test of Neural Prediction 2

We now turn to Prediction 2. This states that, for subjects who experience realization utility, activity in an area of the vmPFC known to encode decision values at the time of making a decision should be correlated with the capital gain variable (p_t − c_t). By contrast, it states that, for expected value subjects, activity in this area should correlate with the NEV variable, but not with the capital gain.

The pre-specified region of the vmPFC in which we test for the decision value signals – a region we defined at the end of Section III -- is shown in Fig. 6 (light yellow). To carry out the main test of Prediction 2, we estimate the following general linear model (GLM) of BOLD activity for each individual:

$$b^v(t)=\text{constant}+{\beta }_1^v{I}_{\mathit{dec}}(t)(p_t-c_t)+{\beta }_2^v{I}_{\mathit{dec}}(t){\mathit{NEV}}_t+{\beta }_3^v\text{controls}+\mathrm{\epsilon }(\mathrm{t}).$$ (1)

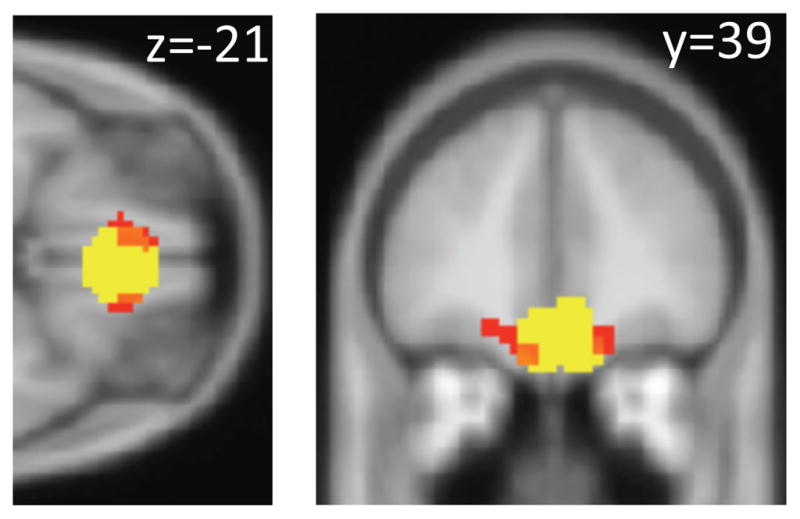
Figure 6. vmPFC activity reflects realization utility.

Estimation results from GLM 1,

$$b^v(t)=\text{constant}+{\beta }_1^v{I}_{\mathit{dec}}(t)(p_t-c_t)+{\beta }_2^v{I}_{\mathit{dec}}(t){\mathit{NEV}}_t+{\beta }_3^v\text{controls}+\epsilon (\mathrm{t})$$ (1)

The yellow area depicts our pre-specified region of interest of the vmPFC. Red voxels are those which exhibit activity at the time of trading screen onset that significantly correlate with the realizable capital gain. Orange voxels satisfy both features. For illustration purposes, the significance threshold for the image is p<0.001 with a 15 voxel extent threshold, but all statistics reported in the paper are also small volume corrected at p<0.05 using FWE. The z=−21 coordinate and the y=39 coordinate indicate which 2-dimensional plane is shown in each of the two brain maps.

As noted earlier, b^v(t) denotes the BOLD signal at time t in voxel v. I_dec(t) is an indicator function that equals one if, at time t, the subject is presented with an opportunity to sell a stock. (p_t − c_t) is the realizable capital gain, and NEV_t is the net expected value from selling the stock under consideration at time t, namely 0.6(1–2q_i,t).40 Finally, the controls vector includes the following variables: 1) an indicator function denoting the onset of a selling opportunity, 2) an indicator function denoting the onset of a buying opportunity, 3) an indicator function denoting the onset of a buying opportunity interacted with the NEV of buying the asset, 4) an indicator function denoting the onset of a price update screen when the subject owns the asset, 5) an indicator function denoting the onset of a price update screen when the subject owns the asset interacted with the price change, 6) an indicator function denoting the onset of a price update screen when the subject does not own the asset, 7) an indicator function denoting the onset of a price update screen when the subject does not own the asset interacted with the price change, 8) regressors controlling for physical movement inside the scanner, and 9) session indicator variables. Controls (1) - (7) are convolved with the HRF, whereas controls (8) and (9) are not.⁴¹ As described in Section III.A, these controls are necessary because the BOLD signal is affected up to 24 seconds after the initial neural impulse generated by the onset of a decision screen or price update screen⁴² (Figure 2). Therefore, a fraction of the variance in the BOLD signal we observe at the time subjects are computing their sell/hold decision can be attributed to the specific events we are controlling for. We will use this same vector of control variables in each GLM estimated in this paper. Finally, inferences about the extent to which the signals of interest are encoded in a given voxel are made by carrying out a one-sided t-test of the average of the individually estimated coefficients (i.e., ${\beta }_1^v$ and ${\beta }_2^v$) against zero, and by correcting for multiple comparisons within the pre-specified vmPFC region-of-interest.

As shown in Figure 6, the results from these tests are consistent with the predictions of the realization utility model, but not with those of the Bayesian expected value model. We find a cluster of 27 voxels where ${\beta }_1^v>0$ within the pre-specified vmPFC ROI associated with the computation of decision values in previous studies. Below, we refer to these 27 voxels as the vmPFC_ROI. In contrast to the significant results we find for the capital gain regressor, there are no clusters that significantly relate to the NEV variable at our statistical threshold.⁴³

The previous analysis identifies a region of the vmPFC in which responses at the time of choice are consistent with the computation of the decision value predicted by the realization utility model. We carried out two additional post-hoc region-of-interest (ROI) tests of the properties of the signals in this area. The first test investigates if the extent to which the capital gains variable is reflected in the vmPFC_ROI is different in trials involving capital gains and capital losses. To do this, we estimated the following GLM:

$$b^v(t)=\text{constant}+{\beta }_1^v{I}_{\mathit{dec}}(t)I_{\text{cap}.\text{gain}}(p_t-c_t)+{\beta }_2^v{I}_{\mathit{dec}}(t)I_{\text{cap}.\text{loss}}(p_t-c_t)+{\beta }_3^v\text{controls}+\mathrm{\epsilon }(\mathrm{t}),$$ (2)

where I_cap.gain and I_cap.loss are indicator variables for trials involving capital gains and capital losses, respectively. For each individual, we then compute both the mean ${\beta }_1^v$ and the mean ${\beta }_2^v$ across the voxels in the vmPFC_ROI,. We find that the mean values, across subjects, of ${\beta }_1^v=0.028$ and ${\beta }_2^v=0.029$ are not significantly different from each other (p=0.94), and thus we cannot reject a linear functional form of the net capital gain signal.

The second test checks whether, as predicted by the realization utility model, the signal in the vmPFC related to decision values is both positively correlated with p_t and negatively correlated with c_t. This test is important because it goes to the core of the “irrationality” implicit in the realization utility model, namely that people are influenced by the cost basis when deciding whether to sell an asset. The test is based on the following GLM:

$$b^v(t)=\text{constant}+{\beta }_1^v{I}_{\mathit{dec}}(t)p_t+{\beta }_2^v{I}_{\mathit{dec}}(t)c_t+{\beta }_3^v\text{controls}+\mathrm{\epsilon }(\mathrm{t}).$$ (3)

The key hypothesis of interest is that ${\beta }_2^v<0$. Importantly, we cannot carry out this test in vmPFC_ROI, because, since this region consists of voxels that correlate with p_t − c_t, the test will be biased in favor of the hypothesis. To avoid this bias, we first estimate model (3) for each of the 429 voxels in the independent vmPFC target region (taken from Plassmann et al. (2010) and an anatomical mask of vmPFC) and then identify voxels that exhibit significant correlation with p_t (p<.05, SVC). We define this set of voxels as vmPFC_p and then test whether voxels in this region significantly correlate with the cost basis. The effect size, averaged across voxels in vmPFC_p for each subject, and then across subjects, is given by β₂=−0.019 (p=0.03). This provides further evidence in support of the realization utility hypothesis.

C. Test of Neural Prediction 3

We now test Prediction 3. Specifically, we check whether, as predicted by the realization utility hypothesis, subjects whose neural activity in the vmPFC at the time of a sell decision is particularly sensitive to the realizable capital gain also exhibit a stronger disposition effect.

The test is carried out as follows. For each subject, we compute a neural measure of the degree to which a positive capital gain is represented in the vmPFC at the time of choice; and also a neural measure of the degree to which a negative capital gain – in other words, a capital loss – is represented in the vmPFC at the time of choice. These individual statistics are given by the maximum beta value across voxels in the vmPFC_ROI for the capital gain and capital loss regressors from model (2).⁴⁴

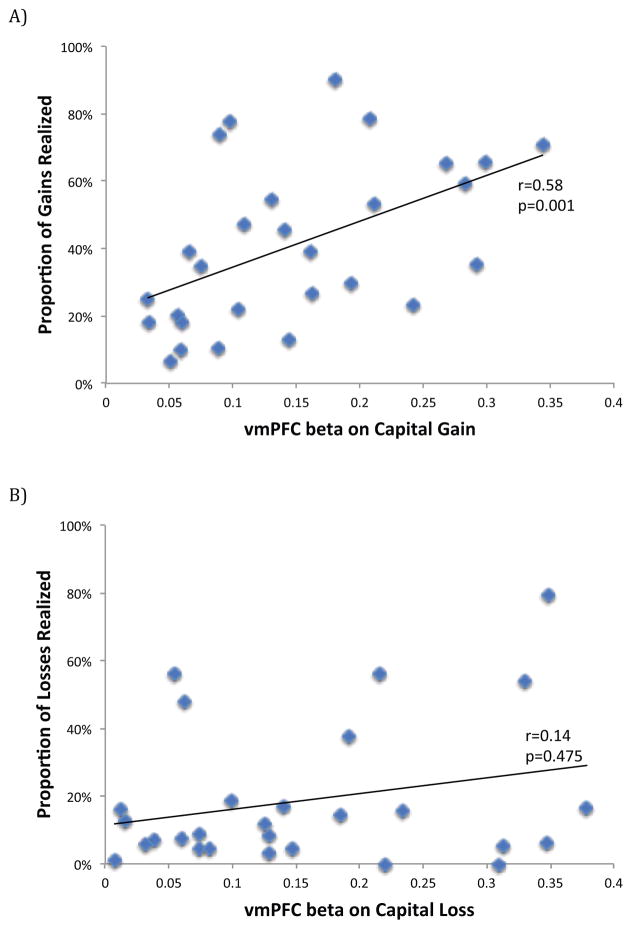
Consistent with Prediction 3, we find that the correlation between ${\beta }_1^v$ and PGR is 0.58 (p=0.001), indicating that subjects who exhibit stronger vmPFC activation in response to a capital gain do have a greater propensity to realize gains. In contrast, we do not find a significant correlation between ${\beta }_2^v$ and PLR (p=0.475). Figure 7 depicts this graphically.

Figure 7. Correlation between brain activity and measures of the disposition effect.

Each data point in the figure represents a single subject. (A) We find that activity in the vmPFC at the time subjects are offered the opportunity to sell a capital gain is highly correlated with their proportion of gains realized. (B) We do not find a similar correlation between vmPFC activity and the proportion of losses realized.

The results in this section are consistent with Prediction 3 for the case of selling decisions involving capital gains, but not for those involving capital losses. In Section V, we discuss in some detail why this might be the case.

D. Test of Neural Prediction 4

Prediction 4 tests another basic assumption of the realization utility model. The model posits that selling a stock at a gain should lead to a positive hedonic effect, and that selling a stock at a loss should lead to a negative hedonic effect, independently of the impact of the trade on lifetime consumption. As described in section II, while in theory this hedonic impact occurs at the moment of sale, in practice it is hard to know what its precise timing and duration are. However, we do know that the utility burst corresponds to a change in discounted lifetime utility; as such, it should generate a prediction error at the moment of sale. This leads to the following form of Prediction 4: controlling for the size of the capital gain, a decision to sell at a gain should lead to a positive response in the areas of the vSt known to correlate positively with prediction errors.

The yellow region in Figure 8 depicts the pre-specified region of the vSt that has been identified in previous studies as being involved in the computation of predictions errors, and over which we look for a positive effect of realizing capital gains.⁴⁵ The test of Prediction 4 is based on the following GLM:

$$b^v(t)=\text{constant}+{\beta }_1^v{I}_{\mathit{dec}}(t)I_{\text{cap}.\text{gain}}(t)(p_t-c_t)+{\beta }_2^v{I}_{\mathit{dec}}(t)I_{\text{cap}.\text{gain}}(t)I_{\mathit{sell}}(t)+{\beta }_3^v{I}_{\mathit{dec}}(t)I_{\text{cap}.\text{loss}}(t)+{\beta }_4^v\mathit{controls}+\mathrm{\epsilon }(\mathrm{t})$$ (4)

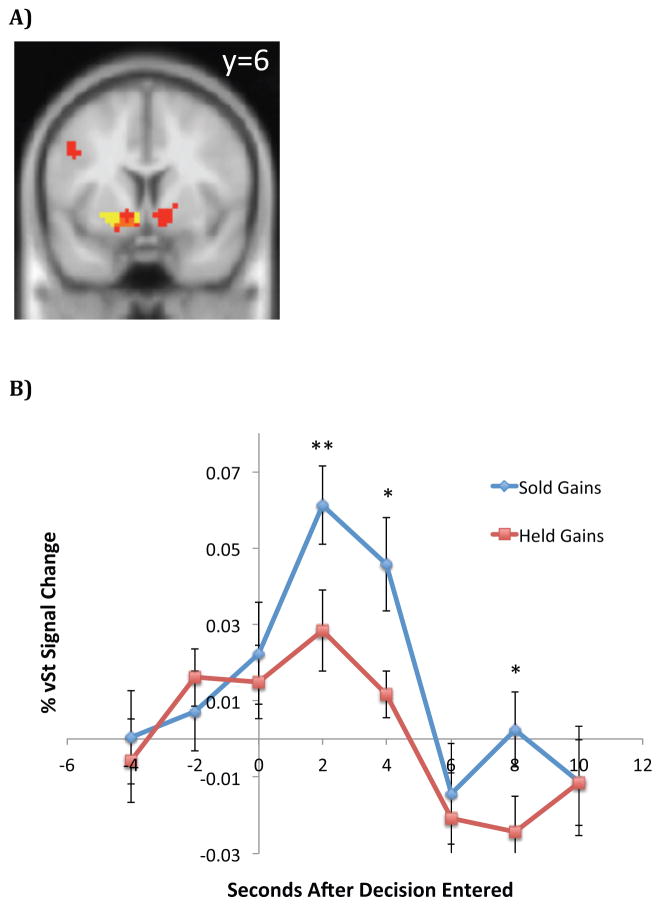
Figure 8. Direct tests of the realization utility hypothesis.

(A) Red voxels are those which exhibit greater activity when subjects realize capital gains compared to when they hold capital gains (shown at p<0.001 uncorrected with a 15 voxel extent threshold for illustrative purposes only). Yellow voxels indicate our a priori region of interest (ROI), which is based on peak voxels that correlate with prediction error in Lin et al. (2012) and an anatomical mask of vSt. Orange voxels indicate overlap between our a priori ROI and voxels which exhibit activity that correlates with realization of a capital gain. The y=6 coordinate indicates which 2-dimensional plane is shown in the brain map. (B) Activity in the vSt (averaged over a priori ROI) during trials when subjects were offered the opportunity to sell capital gains. The blue time series plots the average activity in trials where subjects realized capital gains, while the red time series plots the average activity in trials where subjects decided to hold capital gains. ** denotes p<0.01, * denotes p<0.05 (paired t-test). t=0 corresponds to the instant at which the subject enters his trading decision on a hand-held device.

As before, I_dec is an indicator function denoting an opportunity to sell a stock, I_cap.gain is an indicator function denoting that the subject has an opportunity to sell a capital gain, and I_cap.loss is an indicator function denoting that the subject has an opportunity to sell a capital loss. Finally, I_sell is an indicator function denoting that the subject sold the stock. Note that this model allows us to estimate the marginal effect that realizing a capital gain (the second non-constant regressor) has on neural activity in the vSt, after controlling for the size of the capital gain (the first non-constant regressor)⁴⁶. The key test of interest is whether there are voxels within the target vSt region for which ${\beta }_2^v>0$.

Consistent with Prediction 4, we find a region of the vSt in which activity correlates positively with the realization of capital gains (see Figure 8a, p<.05, SVC), while controlling for the magnitude of the capital gain. Figure 8b shows the timecourse of average BOLD response in the vSt when subjects issue a command to sell a capital gain (blue) compared to when they issue a command to hold a capital gain (red.) ⁴⁷

Ideally, we would also carry out a test for the case of capital losses; specifically, we would test for the presence of a negative impact in the same area of the vSt when a capital loss is realized. Unfortunately, there is an aspect of the data that does not allow us to do this. As predicted by the realization utility hypothesis, subjects realized very few losses over the course of the two fMRI sessions (the mean number of realized losses per subject scanning block is 3). We therefore do not have the necessary statistical power to look at the difference in neural responses in the conditions of realized vs. paper losses.

E. Tests of the mean-reversion theory of the disposition effect

As discussed in Section I, one prominent alternative behavioral theory of the disposition effect is that investors believe that stock prices mean-revert (Odean (1998); Weber and Camerer (1998); Kaustia (2010)). In our setting, such a belief would be irrational: stock prices in our experiment exhibit short-term positive autocorrelation. Nonetheless, if, for some reason, our subjects think that the stock prices in our experiment are mean-reverting, this could potentially explain why they tend to sell stocks that have recently gone up and hold on to stocks that have recently gone down. In this section, we test this alternative theory using both behavioral and neural data.

To investigate whether a belief in mean-reversion is driving our subjects’ behavior, we estimate the following mixed effects logistic model. The model tests whether, as predicted by the mean-reversion hypothesis, recent price changes can significantly predict subjects’ decisions to sell or hold a stock:

$${\mathit{sell}}_{t,s}=\alpha +{\beta }_1{\mathit{NEV}}_{t,s}+{\beta }_2(p_{t,s}-c_{t,s})+{\beta }_3{\mathrm{\Delta }}^1{p}_{t,s}+{\beta }_4{\mathrm{\Delta }}^2{p}_{t,s}+{\epsilon }_t$$ (5)

Here, sell_t,s =1 if subject i sold stock s at time t and 0 if he held it, and Δ^mp_t,s denotes the m^th most recent price change for stock s (these price changes may not have occurred in consecutive trials because price updates in the experiment take place at random times). We find that the capital gain has a coefficient of 0.017 and is a significant predictor of the propensity to sell, (t-stat=2.93), but that none of the other variables are. In particular, neither β₃ nor β₄ is significantly different from zero (p=0.569 and p=0.197, respectively). In other words, contrary to the mean-reversion hypothesis, recent price changes do not significantly predict the decision to sell.⁴⁸

We can also use the neural data to test the mean-reversion hypothesis. In particular, we test if neural activity in the target region of the vmPFC is correlated with recent price changes. This is done by estimating the following GLM:

$$b^v(t)=\text{constant}+I_{\mathit{dec}}(t)[{\beta }_1^v(p_t-c_t)+{\beta }_2^v{\mathrm{\Delta }}^1{p}_{t,s}+{\beta }_3^v{\mathrm{\Delta }}^2{p}_{t,s}]+{\beta }_4^v\text{controls}+\mathrm{\epsilon }(\mathrm{t})$$ (6)

Under the mean reversion hypothesis, the decision value of selling should be positively correlated with recent price changes: a recent price increase indicates a lower expected future return and hence a higher decision value of selling. Under this hypothesis, then, responses in the vmPFC (i.e., the area involved in the computation of decision values) should correlate positively with past price changes. Contrary to this hypothesis, we do not find any activity in the vmPFC that is significantly associated with the past price regressors at our omnibus threshold of p<.05 SVC.

In summary, then, both the behavioral and the neural analyses cast doubt on the mean-reversion hypothesis.⁴⁹

V. Discussion

In this paper we use neural data, obtained through fMRI while subjects traded stocks in an experimental market, to test the key assumptions of the “realization utility” theory of investor trading. We find broad (albeit not perfect) support for the neural predictions of the realization utility model. First, we find that activity in the vmPFC, an area known to encode decision values, is correlated with the capital gain (the decision value under realization utility), but not with a measure of the net expected value of future returns (the decision value under the expected value model). Second, we find that the strength with which the capital gain is reflected in the vmPFC decision value signal is correlated, across subjects, with the magnitude of proportion of gains realized; we do not, however, find the analogous correlation for capital losses. Finally, and perhaps most striking of all, we find that activity in the ventral striatum (an area known to encode information about changes in the expected value of lifetime experienced utility) exhibits a positive response when subjects realize capital gains, while controlling for the size of those gains. This finding is striking because it provides a direct test of the key mechanism at work in the realization utility model, and one that would have been very hard to carry out without neural data.

As noted in the previous paragraph, we do not find a correlation across individuals between the strength with which a capital loss is reflected in the vmPFC and the proportion of realized losses. Here we speculate as to why. One possibility is that the simple model of linear realization utility that we test is incomplete in important ways. For example, the model currently assumes that individuals react to capital gains and capital losses in symmetric and similar ways. But there are reasons to believe that this may not be fully correct. First, an asymmetry between the effect of capital gains and losses on the selling decision can be caused by the interaction of realization utility and myopic discounting, both of which are necessary to induce selling mistakes. Recall that individuals who experience realization utility at the time of selling, and who are sufficiently myopic, will accelerate the sale of assets involving capital gains and delay the sale of assets involving capital losses in order to maximize their present well-being, even though it is suboptimal under the expected value model. If the cross-individual variation in the discount rate for losses is sufficiently larger than that for gains (a hypothesis that has not yet been tested), then the decision value of selling a loss would be measured in our regression models with more noise than the decision value of selling a gain⁵⁰. If this is the case, then we would expect to see a behavioral--neural correlation for capital gains, but not for losses, even if subjects experience realization utility in both cases. Second, we find that the cross-subject correlation between the strength with which capital gains and capital losses are reflected in the vmPFC is only 0.01, and that the cross-subject correlation between their propensity to realize gains and their propensity to realize losses is 0.03. This suggests the possibility that individuals might exhibit a differential tendency to pay attention to capital gains and losses that is not captured by the theory (Karlsson et al. (2009); Kuhnen and Knutson (2011)).

These modifications of the benchmark realization utility model are inspired by the data, but are clearly also post-hoc and speculative. The good news, however, is that the same methodology developed here could be applied to test these alternative specifications directly.

We emphasize that the methods we present in this paper are not a substitute for traditional empirical methods in finance. On the contrary, brain imaging techniques are complementary tools that can be used to test assumptions about investor behavior that are difficult to evaluate using field data or experimental data alone. In particular, we see neural data as a valuable resource when studying the more psychological dimensions of investor behavior, precisely because these may derive from variables that are only observable at the neural level. For example, using the same data set as in this study, we are examining how neural measures of regret, which are very difficult to measure objectively in the field, can impact trading behavior in a systematic way (Frydman et al. (2012)). The identification of investors’ reference point – the reference rate of return that they use to determine whether an investment outcome is a “gain” or a “loss” – is another challenging question that neural data may help us answer.

Appendix: Experimental Instructions

Buying your stock

In this experiment you will be given 350 experimental dollars to invest in three different stocks. Your job is to choose when to buy and sell each stock, so that you earn the most money by the end of the experiment. Throughout the experiment, you will see the price of each stock changing (more detail below), and you will use this information to decide when to buy and sell. When you sell a stock, you receive an amount of cash equal to the price of the stock. When you buy a stock, you receive one unit of the stock, but you must give up an amount of cash equal to the current price of the stock.

The three stocks you can buy or sell are simply called Stock A, Stock B, and Stock C. To begin the experiment you MUST buy all three stocks, where each stock costs $100. Therefore, after you buy the three stocks, you will own one unit of each stock and have a total of $50 remaining. For the remainder of the experiment, you are only allowed to hold a maximum of 1 unit of each stock, and you cannot hold negative units (no short selling.) However, you can carry a negative cash balance by buying a stock for more money than you have, but any negative cash balances will be deducted from your final earnings.

Structure of the market

In the experiment, you will see two types of screens, a price update screen and an action screen. In the price update screen, one stock will be randomly selected and you will be told if the selected stock price has gone up or down, and by how much. Note that you will only see an update for one stock at a time. You will not be asked to do anything during this screen, you will simply see information about the change in price.

Following the price update screen, another stock will be randomly chosen (it may be the same one you just saw) and you will be asked to take an action. If you currently hold a unit of the stock, you will be asked if you would like to sell the stock at the current price. If you do not currently own a unit of the stock, you will be asked if you would like to buy a unit at the current price.

The experiment will start out with 9 consecutive price update screens, and then you will have the opportunity to buy or sell after each subsequent price update screen.

How the stock prices change

Each stock changes price according to the exact same rule. Each stock is either in a good state or in a bad state. In the good state, the stock goes up with 55% chance, and it goes down with 45% chance. In the bad state, the stock goes down with 55% chance and it goes up with 45% chance.

Once it is determined whether the price will go up or down, the size of the change is always random, and will either be $5, $10, or $15. For example, in the bad state, the stock will go down with 55% chance, and the amount it goes down by is $5, $10, or $15 with equal chance. Similarly, the good stock will go up with 55% chance, and the amount it goes up by will either be $5, $10, or $15.

The stocks will all randomly start in either the good state or bad state, and after each price update, there is a 20% chance the stock switches state.

Stock price changes
	Good state	Bad state
+	55%	45%
−	45%	55%

State changes
	Good state today	Bad state today
Good state tomorrow	80%	20%
Bad state tomorrow	20%	80%

Earnings and payout

You will play this market game TWO SEPARATE TIMES in the scanner. Each game will last approximately 15 minutes, and each game is independent from the previous one. This means when you start the second game, you will have to buy the three stocks at $100 again, and the stocks will start randomly in each state again.

Your earnings at the end of the experiment will be equal to the amount of cash you accrued over the two scanning sessions from buying and selling stocks, plus the current price of any stocks that you own.

$$\mathit{Earings}=\mathit{cash}+\mathit{price}{A}^{\ast }(\mathit{Hold}A)+\mathit{Price}{B}^{\ast }(\mathit{Hold}B)+\mathit{Price}{C}^{\ast }(\mathit{Hold}C)$$

Finally, your earnings will be converted using an exchange rate of 12:1. That means we divide your earnings by 12, and pay you this amount plus the $15 show up fee.

Button presses

During the Action screens, you will either be given the option to “Buy?” or “Sell?” depending on whether you hold the stock or not. The LEFT (blue) button indicates “YES”. And the RIGHT (yellow) button indicates “NO.” You have three seconds to enter your response, otherwise the computer will randomly select a response for you.