Global Genomic Arrangement of Bacterial Genes Is Closely Tied with the Total Transcriptional Efficiency

Abstract

The availability of a large number of sequenced bacterial genomes allows researchers not only to derive functional and regulation information about specific organisms but also to study the fundamental properties of the organization of a genome. Here we address an important and challenging question regarding the global arrangement of operons in a bacterial genome: why operons in a bacterial genome are arranged in the way they are. We have previously studied this question and found that operons of more frequently activated pathways tend to be more clustered together in a genome. Specifically, we have developed a simple sequential distance-based pseudo energy function and found that the arrangement of operons in a bacterial genome tend to minimize the clusteredness function (C value) in comparison with artificially-generated alternatives, for a variety of bacterial genomes. Here we extend our previous work, and report a number of new observations: (a) operons of the same pathways tend to group into a few clusters rather than one; and (b) the global arrangement of these operon clusters tend to minimize a new “energy” function (C⁺ value) that reflects the efficiency of the transcriptional activation of the encoded pathways. These observations provide insights into further study of the genomic organization of genes in bacteria.

Introduction

Up till very recently, our understanding about the global arrangement of operons in a bacterial genome has been very limited, mainly because of the lack of relevant data. The availability of both genomic and transcriptomic data for a large number of bacterial organisms (http://www.ncbi.nlm.nih.gov/genome/browse/) provides unprecedented opportunities for researchers to derive novel and deeper understanding about what determines the organization of the genomic information (such as operons and associated regulatory systems) in a genome. Understanding such an issue not only satisfies our scientific curiosity but also provides useful information that can guide the synthesis of artificially-designed chromosomes and organisms in the emerging field of synthetic biology [1–3]. A number of computational studies have been carried out aimed at understanding the genomic organization of genes. These include the studies of gene expression periodicities along a bacterial genome [4–8], transcriptional regulation [9–11], functional relatedness [5,12,13] and co-evolution relationship versus genomic co-locations [14]. While substantial efforts have been invested in studying the genome organization since early 90’s [15–18], our understanding about the factors and rules that may determine the global organization of a genome is still fragmented.

We have previously proposed the first model aimed to explain the organizational principle of a bacterial genome [19]. Our main finding was that the global arrangement of operons in a bacterial genome is tightly determined by the activation frequencies of the biological processes encoded in the genome, including metabolic and transcriptional regulation pathways [19,20]. This relationship can be captured to a large degree using a simple mathematical function, based on the sequential relationships among the relevant operons [19].

Here we extend our previous work to provide new and deeper understanding about the global arrangement of operons. Specifically we developed an improved scoring function which makes the current genomic arrangement of operons stand out more substantially against the alternative arrangements. This allows us to discover that operons in the same metabolic or transcriptional regulation pathway tend to group into a few, rather than one, sequentially nearby clusters, and the global arrangement of these operon clusters tends to make the transcriptional activation of the encoded pathways as efficient as possible.

Results

We have carried out our study on Escherichia coli K-12, which has 4144 protein-encoding genes [21] and 2462 predicted operons [22]. The 347 biological pathways encoded in E. coli K12 are retrieved from EcoCyc [23] and expression data for each gene under 466 growth conditions from the M3D database [24] are used to estimate the activation frequency of each pathway.

Operons encoding the same pathways tend to be clustered locally, but not globally, along the genome

We have previously used the following function to measure the global clusteredness of the component operons of the ith pathway, $c_i$ [19],

$$c_i={\displaystyle \sum _{j=1}^{M_i}}{d}_{\mathit{ij}}$$ (1)

where M_i represents the number of operons in the ith pathway and d_ij is the distance between the jth operon and $[M_i/2]\text{th}$ operon (i.e., median operon) in the ith pathway. Then the overall clusteredness of the operons encoding all the pathways, C, can be measured using the following function:

$$C={\displaystyle \sum _{i=1}^N}{c}_i$$ (2)

where N is the number of pathways under consideration (N = 347 in this study). A key discovery that we made was that the current genomic locations of all the operons in E. coli K12 tend to minimize this function in comparison with artificially-generated alternatives [19].

Our recent study indicates that while our initial one-cluster model per pathway provides an informative approximation, it is too crude. Our current analysis suggests that each pathway, particularly the one encoded by a large number of operons, tends to consist of a few operon clusters along the genome, as illustrated in Figure 1 (taking the four largest pathways in EcoCyc as examples). Based on this realization and analysis of the M3D gene expression data, we hypothesize that all the operons are arranged at specific genomic locations to facilitate the most efficient transcription of the operons encoding each pathway during the life cycle of the bacteria.

Figure 1.

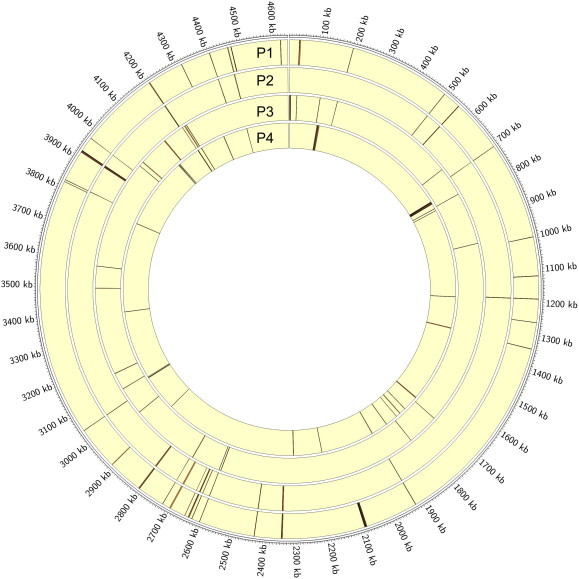
An illustration of the clustering property of operons in the same pathway The four rings from outside to inside, respectively, represent the genomic location of each operon in four metabolic pathways, namely phosphoribosyl pyrophosphate (PRPP) pathway (P1), de novo purine 2 pathway (P2), PWY0-781 pathway (P3) and glycolysis TCA glyox bypass pathway (P4), labeled by the black bars in the corresponding yellow rings.

We aim to use the following C⁺ function (to distinguish with previous C value, C⁺ was used here) to assess the validity of this hypothesis by identifying a partition of the genome into set of genomic segments such that the function is minimized:

$$C^{+}={\displaystyle \sum _{i=1}^N}{f}_i\times \left(t_i+\alpha {\displaystyle \sum _{j=1}^M}{\omega }_{\mathit{ij}}\right)$$ (3)

where N is the number of known pathways encoded in the target genome; M is the number of partitioned segments of the genome to be determined; f_i represents the activation frequency of the ith pathway estimated from the gene expression data in M3D following the method described previously [19] (with default value 1 for each pathway if such information is not available); t_i is the number of partitioned segments containing operons of the ith pathway; s_j is the number of operons in the jth partitioned segment ($j\in [1\text{,}M]$), and s_ij is the number of operons of the ith pathway covered in the jth partitioned segment; ${\omega }_{\mathit{ij}}$ is defined to be 0 if $s_{\mathit{ij}}=0$; otherwise ${\omega }_{\mathit{ij}}=(s_j-s_{\mathit{ij}})/s_j$; and α is a scaling factor whose default value is set as 1. Intuitively, this function measures the total number of partitioned segments that encode the operons of each pathway across all the pathways, along with a measurement of the density of such operons among all the operons encoded in each partitioned segment. A detailed dynamic programming procedure for calculating an optimal partition of a target genome, along with the associated M value, is given in Materials and methods section.

We have randomly reshuffled the genomic locations of X% (X = 10, 20,…,100) of all the E. coli K12 operons with the locations of the remaining operons fixed, and calculated the C⁺ value of each reshuffled genome. We reshuffled the genomic locations of selected operons 100,000 times for each X, as we did in our original study [19]. Figure 2A shows the C⁺ value distribution for all the selected Xs versus the current genome of E. coli K12. Clearly we see that the C⁺ value of the current genome tends to be smaller than the C⁺ values of the alternatives, i.e., the artificially-generated genomes. To compare the current scoring function with our previous scoring function C, we did the same calculation using the previous function C (shown in Figure 2B). We have estimated the tail probability of “X < the dash line” (dash line denotes the current genomic arrangement), i.e., a P-value, for each score distribution in Figure 2, which is summarized in Table 1.

Figure 2.

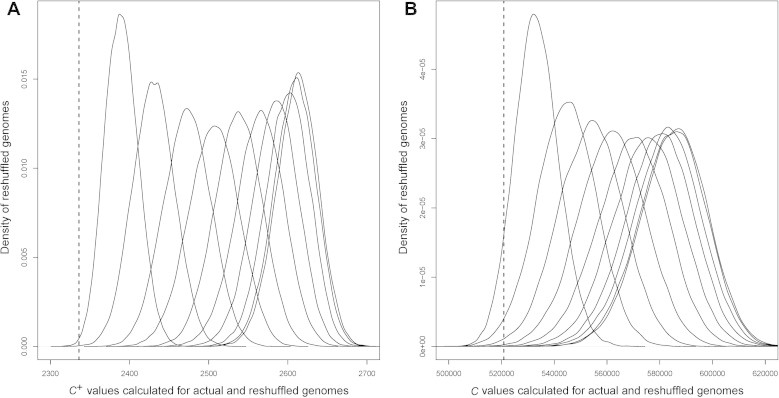
Comparison of the C and C⁺ value distributions for the actual and reshuffled genomes A. Distributions of C⁺-value for the E. coli K-12 genome. B. Distributions of C-value for the E. coli K-12 genome. In each panel, the x axis represents C or C⁺ value and the y axis represents the density of reshuffled genomes with a specific C or C⁺ value. For each distribution, X% (X = 10, 20,…,100) of all the operons were randomly reshuffled, arranged from left to right. The C or C⁺ value for the current arrangement of the operons in E. coli K-12 is represented by a vertical dash line.

Table 1.

Statistical tests of curves inFigure 2

% Of reshuffling	P (C value)	P (C+ value)	P (C value)/P (C+ value)
10	0.06947282	0.004927	14.09904
20	0.01698723	0.000201	84.51098
30	0.003641975	2.09E−06	1740.591
40	0.000705596	3.44E−08	20492.59
50	0.000120973	1.42E−11	8523197
60	1.75E−05	2.72E−14	6.43E+08
70	2.77E−06	4.31E−18	6.42E+11
80	7.47E−07	6.50E−22	1.15E+15
90	2.28E−07	1.01E−24	2.25E+17
100	1.45E−07	1.09E−25	1.33E+18

Note: P(X) is the tail probability (P-value) of “X < the dash line” (dash line denotes the current genomic arrangement) for each score distribution. The P-values are calculated based on the observations that all the score distributions follow a normal distribution by the skewness and kurtosis test [19].

Through the above analysis, we have demonstrated that the current genomic arrangement of operons in the genome of E. coli K12 tends to minimize the C⁺ value compared to those of the alternative genomic arrangements of operons; and the C⁺ function makes the actual genome stands out more significantly than previous C function against the alternatives. The effect of increasing the impact of ${\omega }_{\mathit{ij}}$ defined in Eq. (3) or estimating the actual pathway activation frequency based on M3D microarray data is presented in Figure S1 and Table S1.

Pathway-based analysis of the genomic partition

The above calculation also gives rise to an optimal partition of the E. coli K12 genome into 104 segments, which optimizes the C⁺ value (see details in Table S2). We have examined how the operons encoding the 347 biological pathways are located in the 104 partitioned segments of the E. coli genome. For each of the randomly-shuffled genomes and the original genome of the E. coli K12 shown in Figure 2, we retrieved the corresponding partitioned segments and calculated the total number of partitioned segments covered by each pathway across all the 347 pathways under consideration. From Figure 3, we can see that this total number of the current genome of E. coli K12 is clearly smaller than any of the randomly-reshuffled genomes.

Figure 3.

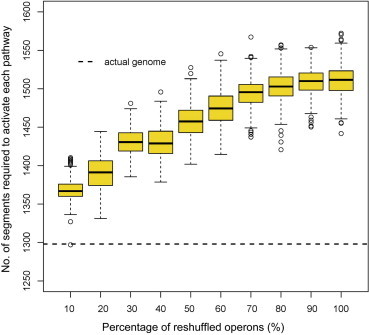
Comparison of the number of segments required to activate each pathway for the actual and the reshuffled genomes Ten boxplots for the E. coli K-12 genome, representing X% (X = 10, 20,…,100) of all the operons that were randomly reshuffled, are arranged from left to right. The number of partitioned segments for the actual genome is represented by a horizontal dash line.

In a separate study (Ma et al., unpublished data), we provided strong evidence that each of the partitioned segments corresponds to a supercoiled domain in the folded chromosome of E. coli K12 [25–28], each being independently foldable. Clearly when a pathway needs to be activated, the (folded) segments containing operons of the pathway need to unfold first to make all the relevant operons transcriptionally accessible, a process that consumes energy. The data shown in Figure 3 suggests that the organism has evolved to minimize the total number of segments that need to be unfolded in order to activate each pathway, hence making this part of the operating cost for the living bacteria as small as possible.

Concluding remarks

We have previously demonstrated that operons encoding more frequently activated pathways tend to be more clustered together in a genome [19]. We have also noted that what prevents such operons from forming one cluster is that many individual operons may each be involved in multiple pathways. Hence they form multi-operon clusters as we have demonstrated in this work that they tend to form a few operon clusters each contained in a folded genomic segment. To activate a pathway, energy is required to unfold the genomic segments that contain the operons encoding the pathway, so that the relevant operons are transcriptionally accessible. By putting all these results together, we speculate, with strong evidence, that operons encoding various pathways are specifically located in a given genome such there is a tendency to minimize the overall energy needed to have the relevant pathways transcribed, during the life cycle of the bacteria.

Materials and methods

A dynamic programming method for genomic partition

The optimization problem defined in Eq. (3) can be solved using a dynamic programming approach. The following recurrence equation gives rise to a simple dynamic programming algorithm for finding the optimal C⁺ (S, E) value, which generates a partition of a target genome and hence the number M of the partitioned segments, where S and E represent the first and the last inter-operonic regions of the genome, respectively.

$$C^{+}(S\text{,}i)={\displaystyle \underset{jϵ[i-U\text{,}i-L]}{\text{min}}}[C^{+}(S\text{,}j)+C^{+}(j\text{,}i)]$$ (4)

where L and U are set at 10 k bp and 100 k bp, defining the lower and the upper bounds of a partitioned segment [10–12].

Authors’ contributions

YX conceived the basic idea and planned the project. QM developed the algorithm, analyzed the data and carried out the computational experiments. Both authors edited the manuscript and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.

Appendix Supplementary. material

Supplementary Figure S1.

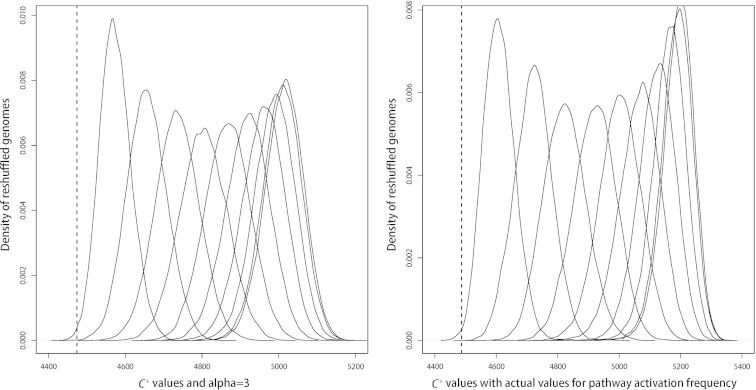
C⁺ value distributions for two special considerations. The distributions for actual and reshuffled genomes of C⁺ values, considering α = 3 (A) and actual values for pathway activation frequency (calculated by M3D microarray data) (B). In each panel, the x axis represents the C⁺ value, and the y axis represents the density of reshuffled genomes with a specific C⁺ value.

Supplementary Table S1

Statistical tests of curves in Figure S1

Supplementary Table S2.

The partitions of E. coli’s chromosome.