Debiasing the disposition effect by reducing the saliency of information about a stock’s purchase price

Abstract

The disposition effect refers to the empirical fact that investors have a higher propensity to sell risky assets with capital gains compared to risky assets with capital losses, and it has been associated with low trading performance. We use a stock trading laboratory experiment to investigate if it is possible to reduce subjects’ tendency to exhibit a disposition effect by making information about a stock’s purchase price, and thus about capital gains and losses, less salient. We compare two experimental conditions: a high-saliency condition in which the purchase price of a stock is prominently displayed by the trading software, and a low-saliency condition in which it is not displayed at all. We find that individuals exhibit a disposition effect in the high-saliency condition, and that the effect is 25% smaller in the low-saliency condition. This suggests that it is possible to debias the disposition effect by reducing the saliency with which information about a stock’s purchase price is displayed on financial statements and online trading platforms.

1. Introduction

A considerable effort in behavioral economics has been devoted to documenting systematic biases exhibited by investors and understanding the impact that these biases have on trading performance (Shleifer (2000); Barberis and Thaler (2003); Campbell (2006)). One of the most robust effects in this literature is the disposition effect, which refers to the empirical fact that investors have a higher propensity to sell risky assets with capital gains compared to risky assets with capital losses (Shefrin and Statman (1985); Odean (1998); Genesove and Mayer (2001); Grinblatt and Keloharju (2001); Feng and Seasholes (2005); Frazzini (2006); Kaustia (2010); Jin and Scherbina (2011)). This tendency has been associated with low trading performance.

One interesting aspect of the disposition effect is the possibility that financial accounting statements, and financial software platforms, may promote this behavior by prominently displaying the purchase price of stocks. For example, in a tax-free retirement account, this information should be irrelevant to an expected return maximizing investor, but for an investor who is prone to the disposition effect, easy access to purchase price information can potentially magnify its effect.³

There are several reasons why making information related to the purchase price of a stock salient might affect investor behavior. First, there is evidence that investors allocate attention to the most salient items on financial statements (Libby et al. (2002); Hirshleifer and Teoh (2003)). Second, a stock’s purchase price has been hypothesized to be an important driver of behavior in several influential models of the disposition effect. For example, in realization utility models of the disposition effect, investors receive a burst of positive utility when selling a risky asset that is trading at a gain relative to the purchase price, and receive a negative burst of utility when selling at a loss (Shefrin and Statman (1985); Barberis and Xiong (2012); Ingersoll and Jin (2013)). Importantly, these bursts of utility are independent of the direct impact of trading decisions on expected lifetime income, and these models explicitly assume that individuals will rely on purchase price information at the time of making selling decisions (Barberis and Xiong (2012); Ingersoll and Jin (2013)). Third, work in neuroeconomics suggests that manipulating the saliency of an attribute at the time of decision affects the weight that it receives in the decision. For example, studies in neuroeconomics (Busemeyer and Townsend (1993); Roe et al. (2001); Krajbich et al. (2010); Krajbich and Rangel (2011); Hare et al. (2011); Krajbich et al. (2012)) have shown that preferences are not fixed, but instead are modulated by attention. In particular, at the time of decision, individuals weight more heavily attributes, features, or items that are attended to more, at the expense of those that are attended to less. Together, these findings suggest that making purchase price information more salient can increase the weight that it receives at the time of decision, and thus, it can increase the size of the disposition effect.

A better understanding of how the display of information in trading software and on financial statements impacts the magnitude of the disposition effect is important, since there is a growing consensus that the disposition effect is an investment mistake that leads to underperformance (Odean (1998), Frazzini (2006)). However, despite the prevalence of this costly behavior among a wide variety of investor classes, there has been surprisingly little work done to rigorously understand how to “debias” this effect.

In this paper, we use a laboratory experiment to address this open question. We study if it is possible to reduce subjects’ tendency to exhibit a disposition effect by making information about a stock’s purchase price, and thus about capital gains and losses, less salient. In particular, we compare two experimental conditions: a high-saliency condition in which the purchase price of a stock is prominently displayed by the trading software, and a low-saliency condition in which it is not displayed at all. While there are a variety of attributes on financial statements that might affect investor behavior, we focus on manipulating the saliency of the purchase price, because this variable is a key input into several behavioral theories (described below) that have been proposed to explain the disposition effect.⁴

Consistent with previous experimental results (Weber and Camerer (1998); Weber and Welfens (2007); Frydman et al. (2014)), we find a disposition effect in the high-saliency condition, in which the purchase price information is displayed. The main contribution of this paper is to show that reducing the saliency of the purchase price information, by not displaying it at all, reduces the size of the disposition effect by 25%. This finding has two important implications. First, it shows that it is possible to reduce the costs associated with the disposition effect by reducing the saliency of purchase price information. Second, it highlights the limitations of such interventions, by showing that individuals exhibit strongly suboptimal trading behavior even when the purchase price is not saliently displayed.

2. Related Literature

Our study is related to several literatures in behavioral finance, which we discuss here.

First, our results are related to a growing body of literature that investigates the implications of limited attention on investor behavior and asset prices. In particular, several papers have studied the effect of inattention to news or earnings announcements on asset prices (Hong and Stein (1999); Peng and Xiong (2006); Cohen and Frazzini (2008); Dellavigna and Pollet (2009); Duffie (2010); Da et al. (2011)). Studies have also shown that seemingly irrelevant contextual environmental changes, that make some information relatively more salient without changing the actual amount of information available, can have profound effects on investor behavior (Bertrand and Morse (2011); Choi et al. (2012)). In contrast to this literature, we study how the saliency with which information is displayed at the time of making a financial decision affects how it is weighted in the decision.

Second, our study is related to a growing literature in behavioral finance that seeks to characterize the behavioral sources behind the disposition effect. One popular model of the disposition effect is based on prospect theory preferences (Kahneman and Tversky (1979)). In this model, gains and losses are measured relative to a reference point, which is often assumed to be the asset’s purchase price (Odean (1998), Weber and Camerer (1998)). Under this assumption, utility is concave over capital gains and convex over capital losses, and this induces the investor to become risk averse when the stock is trading at a gain, and risk-seeking when the stock is trading at a loss. While this argument is intuitively appealing, recent theoretical work has cast doubt on its validity (Barberis and Xiong (2009), Kaustia (2010)). In particular, models of trading in dynamic environments based on prospect theory preferences have a difficult time generating a disposition effect when the reference point is assumed to be the purchase price.⁵ Another popular model of the disposition effect is that investors have an irrational belief in mean-reversion (Odean (1998); Weber and Camerer (1998); Kaustia (2010)). If investors believe that stocks with strong (weak) recent performance will tend to subsequently do poorly (well), then this will lead investors to exhibit a disposition effect. However, field and laboratory evidence have also cast some doubt on this hypothesis (Odean (1998); Weber and Camerer (1998))⁶. More recently, the class of realization utility models described above has gained traction as a potential explanation for the disposition effect. For example, recent research has shown that neural data collected during an fMRI experiment is consistent with the key assumption of realization utility, namely, that investors get a burst of utility at the time of realizing a capital gain (Frydman et al. (2014)). Distinguishing among competing theories of the disposition effect is an important and open area of research, but it is not the focus of the current paper. Instead, here we investigate the extent to which it is possible to debias the disposition effect, regardless of the mechanism that generates it.

3. Experimental Design

3.1 Basic design

The basic experimental design follows closely Frydman et al. (2014), except for the manipulation of the salience of the purchase price variable.⁷ All subjects are given the opportunity to trade three stocks –A, B, and C – in an experimental stock market. The experiment consists of two sessions separated by a two-minute break. Each session lasts approximately 16 minutes and consists of 108 trials. In this section, we use t to index the trials. The first session consists of trials t =1 through t =108, and the second, of trials t =109 through 216. We describe the structure of the first session; the structure of the second session is identical to that of the first.

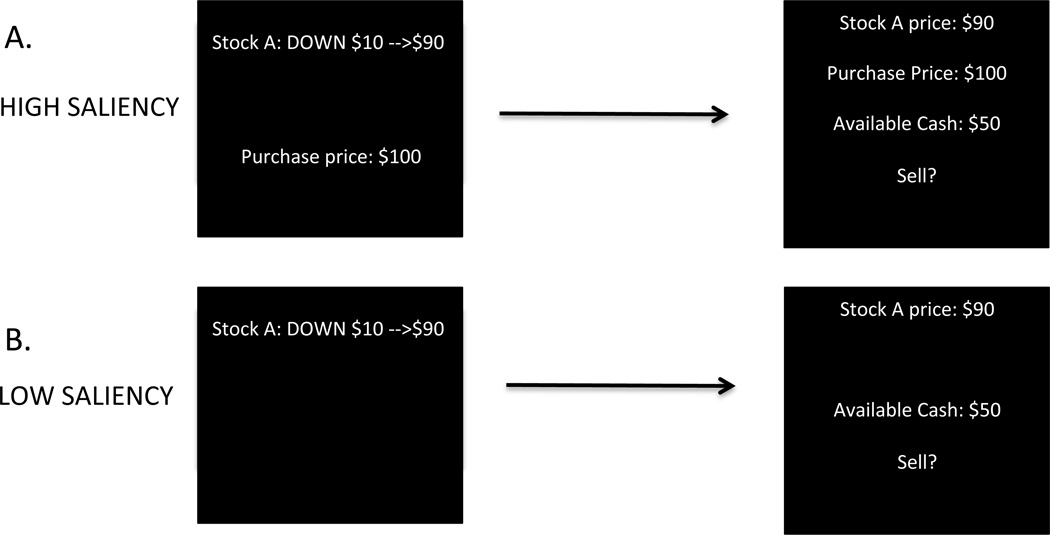
Before trial 1, each subject is given $350 in experimental currency, and is required to buy one share of each stock. The initial share price for each stock is $100; after this transaction, each subject is therefore left with $50. The majority of the trials (i.e., 10 through 108) are divided into two parts: a price update screen and a trading screen (Figure 1). During the price update screen, one of the three stocks is chosen at random and the subject is shown a price change for that stock only. Note that stock prices only evolve during the price update screens and, as a result, subjects see the entire price path for each stock. During the trading screen, one of the three stocks is again chosen at random and the subject is asked whether he wants to trade the stock. No new information is revealed during the trading screen.⁸

Figure 1. Sample screens from the two experimental conditions.

Each trial in every condition consists of a “price update” screen (2 seconds), followed by a 1 second inter-trial interval, then followed by a “trading” screen (3 seconds). A) HIGH-SALIENCY condition, during which current and purchase price information are displayed on both screens. B) LOW-SALIENCY condition, in which the purchase price is removed from both screens.

Trials 1 through 9 consist only of price updates; subjects are not given the opportunity to buy or sell during these trials. The idea behind this restriction is to let subjects accumulate some information about the price process for the stocks before having to make any trading decisions.

Each subject is allowed to hold a maximum of one share of each stock, and a minimum of zero shares of each stock, at any point in time. In particular, short-selling is not allowed. The trading decision is therefore reduced to deciding whether to sell a stock (conditional on holding it) or deciding whether to buy a stock (conditional on not holding it). The price at which a subject can buy or sell a stock is given by its current market price.

The price path of each stock is governed by a two-state Markov chain, with a good state and a bad state. The Markov chain for each stock is independent of the Markov chains for the other two stocks. In particular, suppose that, in trial t, there is a price update for stock i. If stock i is in the good state at that time, its price increases with probability 0.7 and decreases with probability 0.3. Conversely, if it is in the bad state at that time, its price increases with probability 0.3 and decreases with probability 0.7. The magnitude of the price change is drawn uniformly from {$5, $10, $15}, independently of the direction of the price change.

The state of each stock evolves independently as follows. Before trial 1, we randomly assign a state to each stock. States are then updated only after a stock receives a price update. More concretely, if the price update in trial t >1 is not about stock i, then the state of stock i remains the same as in the previous trial. In contrast, if the price update is about stock i, then the state of stock i in the trial remains the same as in trial t−1 with probability 0.8, but switches with probability 0.2. The states of the three stocks are not revealed to the subjects: they have to infer them from the observed price paths. In order to ease comparison of trading performance across subjects, the same set of realized prices was used for all subjects. From now on, we let s_i,t denote the state of stock i at the beginning of trial t.

A key aspect of our design is that, conditional on the information available to subjects, each of the stocks exhibits short-term price continuation. In particular, if a stock performed well on the last price update, it is likely that it was in the good state during the price update. Therefore, since it is highly likely (80%) to remain in the same state for its next price update, its next price change is also likely to be positive. This feature of the price process is useful, because it implies that the optimal strategy for a risk neutral Bayesian investor is to, on average, sell stocks that have recently performed poorly, and hold stocks that have recently performed well (see details below). This implies that a risk neutral Bayesian investor should exhibit the opposite of the disposition effect.

At the end of each of the two sessions, we liquidate subjects’ holdings of the three stocks and record the cash value of their position. We give subjects a financial incentive to maximize the final value of their portfolio at the end of each session. Specifically, if the total value of a subject’s cash and risky asset holdings at the end of session 1 is $X, in experimental currency, and the total value of his cash and risky asset holdings at the end of session 2 is $Y, again in experimental currency, then his take-home pay in actual dollars is 5 + (X+Y)/24. In other words, we average X and Y to get (X+Y)/2, convert the experimental currency to actual dollars using a 12:1 exchange rate, and add a $5 show-up fee. Average total earnings were $32.24. Earnings (not including the show-up fee) ranged from $19.14 to $33.15, and the standard deviation of earnings was $2.91.

In order to avoid liquidity constraints, we allow subjects to carry negative cash balances during a session, which makes it possible for them to purchase a stock even if they do not have sufficient cash at the time. If a subject ends the experiment with a negative cash balance, this amount is subtracted from the terminal value of his portfolio. The large cash endowment, together with the constraint that subjects can hold at most one unit of each stock at any moment, was sufficient to guarantee that no one ended the experiment with a negative portfolio value, or was unable to buy a stock because of a shortage of cash during the experiment.

The exact instructions given to subjects at the beginning of the experiment are included in the Appendix. The instructions carefully describe the stochastic structure of the price process, as well as all other details of the experiment. Before the first real trading session, subjects engaged in a practice session of 25 trials to familiarize themselves with the market software.

3.2 Experimental Conditions

Fifty-eight Caltech subjects participated in the experiment. Each subject was randomly assigned to one of two experimental conditions. Thirty-three subjects were assigned to the HIGH-SALIENCY condition, in which the current price and purchase price (if the asset was owned) were displayed on both the price update and trading screens (see Figure 1A). The purchase price denotes the price at which the stock was last purchased. Twenty-five subjects were assigned to the LOW-SALIENCY condition, in which only the current asset price is displayed during the price update and trading screens (Figure 1B).

Several aspects of the experimental design are worth highlighting. First, the only difference between the two conditions is the removal of the purchase price information. Second, the HIGH-SALIENCY condition is almost identical to the experiment in Frydman et al. (2014). We think of this condition as a control treatment because this previous study found that the average subject exhibited a sizable disposition effect, and because it resembles many real-world settings where purchase price information is prominently displayed on financial statements and trading software. Third, we think of the LOW-SALIENCY condition as a treatment intervention that allows us to test if the removal of the purchase price information reduces subjects’ tendency to exhibit a disposition effect.

3.3. Measuring the Disposition Effect

We now describe our method for calculating the disposition effect at the individual subject level, which follows a similar methodology to that of Odean (1998). Every time a subject is offered the opportunity to sell a stock, we classify his decision into one of four mutually exclusive categories: realized gains, realized losses, paper gains or paper losses. A decision is classified as a realized gain if the market price of the stock is above the purchase price, and the subject decides to sell the stock. A decision is classified as a realized loss if the market price of the stock is below the purchase price, and the subject decides to sell the stock. A decision is classified as a paper gain if the market price of the stock is above the purchase price, and the subject decides not to sell the stock. A decision is classified as a paper loss if the market price of the stock is below the purchase price, and the subject decides not to sell the stock.

For each subject, we count the number of realized gains, realized losses, paper gains, and paper losses over the course of both experimental sessions. We use them to compute the Proportion of Gains Realized (PGR) and the Proportion of Losses Realized (PLR) as follows:

$$\mathrm{P}\mathrm{G}\mathrm{R}=\frac{\mathit{\#}\mathit{\text{of realized gains}}}{\mathit{\#}\mathit{\text{of realized gains}}+\mathit{\#}\mathit{\text{of paper gains}}}$$ (1)

$$\mathrm{P}\mathrm{L}\mathrm{R}=\frac{\mathit{\#}\mathit{\text{of realized losses}}}{\mathit{\#}\mathit{\text{of realized losses}}+\mathit{\#}\mathit{\text{of paper losses}}}$$ (2)

Our individual measure of the disposition effect is then given by PGR-PLR. In particular, when PGR=PLR there is no disposition effect, the size of the disposition effect increases in PGR-PLR, and a subject with PGR < PLR exhibits the opposite of a disposition effect.

4. Theory and Hypotheses

In this section we present a simple model of selling decisions, and use it to derive hypotheses about the effect of making the purchase price less salient. We focus on selling decisions since the disposition effect refers to a particular form of decision mistakes at the time of the sell/hold decision.

4.1 Theory

Consider the problem of an individual who is deciding whether or not to sell stock i in trial t. The model assumes that individuals make selling decisions using a random utility model based on the following utility statistic:

$$U_{i,t}=\mathrm{\alpha }RE{V}_{i,t}+\mathrm{\beta }C{G}_{i,t}+{\mathrm{\eta }}_{i,t}$$ (3)

where REV_i,t denotes the relative expected value of selling the stock, CG_i,t denotes the capital gain, α and β are constants, and η_i,t are i.i.d. draws from the normal distribution. In every trial, the investor computes this statistic, and then sells if U_i,t >0, and holds if U_i,t <0.

The REV_i,t term is given by the difference between the current price for stock i, and the expected price immediately after the next price change for the stock. As we now show, REV_i,t is the key variable for an investor who trades to maximize expected final wealth. Let p_i,t be the price of stock i in trial t, after the price update, if any. Let q_i,t =Pr(s_i,t =good | p_i,t, p_i,t−1,…, p_i,1) be the Bayesian posterior that stock i is in the good state, given the price history. Since the state only evolves immediately after a price update, we have that q_i,t = q_i,t−1 if stock i was not updated in trial t. Now consider the case of a stock that received a price update. Let z_t take the value 1 if the price update in trial t indicated a price increase for the stock in question, and −1 if the price update indicated a price decrease. Given the Markovian structure of the price process, we can write q_i,t as follows:

$$q_{i,t}(q_{i,t-1},z_t)=\text{Pr}(s_{i,t}=\mathit{\text{good}}|q_{i,t-1},z_t)=\frac{\text{Pr}(z_t|s_{i,t}=\mathit{\text{good}})\text{Pr}(s_{i,t}=\mathit{\text{good}}|q_{i,t-1})}{\text{Pr}(z_t)}=\frac{\text{Pr}(z_t|s_{i,t}=\mathit{\text{good}})\text{Pr}(s_{i,t}=\mathit{\text{good}}|q_{i,t-1})}{\text{Pr}(z_t|s_{i,t}=\mathit{\text{good}})\text{Pr}(s_{i,t}=\mathit{\text{good}}|q_{i,t-1})+\text{Pr}(z_t|s_{i,t}=\mathit{\text{bad}})\text{Pr}(s_{i,t}=\mathit{\text{bad}}|q_{i,t-1})}=\frac{(0.5+0.2z_t)(0.8q_{i,t-1}+0.2(1-q_{i,t-1}))}{(0.5+0.2z_t)(0.8q_{i,t-1}+0.2(1-q_{i,t-1}))+(0.5-0.2z_t)(0.2q_{i,t-1}+0.8(1-q_{i,t-1}))}.$$ (4)

Furthermore, recall that subjects are told that there is an equal chance that each stock begins in the good or bad state. This implies that q_i,0 = 0.5 for each stock. Using this equation, we can then compute the relative expected value of selling the stock, which we denote by REV. Thus, we have that REV is given by:

$$RE{V}_{i,t}=p_{i,t}-E[p_{i,t+1}|q_{i,t},p_{i,t+1}\ne p_{i,t}]=-E[\mathrm{\Delta }{p}_{i,t+1}|q_{i,t},p_{i,t+1}\ne p_{i,t}]=\text{Pr}(s_{i,t+1}=\mathit{\text{good}}|q_{i,t})E[-\mathrm{\Delta }{p}_{i,t+1}|s_{i,t+1}=\mathit{\text{good}}]+\text{Pr}(s_{i,t+1}=\mathit{\text{bad}}|q_{i,t})E[-\mathrm{\Delta }{p}_{i,t+1}|s_{i,t+1}=\mathit{\text{bad}}]=-[(0.6q_{i,t}+0.2)[0.7(10)+0.3(-10)]+(0.8-0.6q_{i,t})[0.7(-10)+0.3(10)]]=2.4(1-2q_{i,t}).$$ (5)

Recall that the magnitude of a price change, regardless of its direction, is drawn uniformly from {$5, $10, $15}, and thus $10 is the average size of a price change. Note also that REV_i,t decreases with q_i,t, and that it is positive if and only if q_i,t <0.5. This is quite intuitive. Given the symmetry in the distribution of potential gains and losses, selling the asset increases expected income only when a price decrease is more likely than a price increase, which only happens when the asset is more likely to be in the bad state than in the good state⁹.

The CG term is computed as follows. Let c_i,t denote the last purchase price for stock i in trial t, and let p_i,t denote the price at which it currently trades. The capital gain variable is given by

$$C{G}_{i,t}=p_{i,t}-c_{i,t}.$$ (6)

This variable measures the increase in price of the stock since it was last purchased.

The motivation for including the REV term in the model is that it captures a motive based purely on maximizing expected wealth. For example, a risk-neutral Bayesian investor who seeks to maximize the expected value of his total trading profits is captured by a version of the model with β=0.

The motivation for including the CG term in the model is that several important explanations of the disposition effect predict that selling decisions are heavily influenced by this variable. As described in the introduction, these include models based on realization utility, prospect theory, and an irrational belief in the mean-reversion of stock prices. Consider how each of them relates to the CG statistic.

First, consider an individual who is driven solely by a realization utility motive. By assumption, the utility generated from selling a stock for such an individual is proportional to the realized capital gain at the time of selling. More formally, consider the problem of a pure realization utility trader with linear utility that discounts across experimental periods at a rate δ. If he sells at time t, his payoff is given by CG_i,t + δV(t+1,p_i,t, q_i,t), where the second term denotes the net present value of entering trial t+1 not owning asset i, given its current price and probability of being in the good state, and then trading optimally to maximize expected future realization utility flows in stock i. In contrast, if he keeps the asset until the next period he is allowed to trade, say at trial t + u, his payoff is given by

$${\mathrm{\delta }}^{u-1}(C{G}_{i,t}+\mathrm{E}[\mathrm{\Delta }{p}_{i,t+u}|q_{i,t},p_{i,t})])+{\mathrm{\delta }}^u\mathrm{E}[V(t+u,p_{i,t+u},q_{i,t+u})|p_{i,t},q_{\mathrm{i},\mathrm{t}}].$$ (7)

This implies that the relative value of selling for the trader is given by

$$C{G}_{i,t}(1-{\mathrm{\delta }}^{u-1})-{\mathrm{\delta }}^{u-1}\mathrm{E}[\mathrm{\Delta }{p}_{i,t+u}|q_{i,t},p_{i,t}]+\mathrm{\delta }V(t+1,p_{i,t},q_{\mathrm{i},\mathrm{t}})-{\mathrm{\delta }}^u\mathrm{E}(V(t+u,p_{i,t+u},q_{i,t+u}|p_{i,t},q_{\mathrm{i},\mathrm{t}}).$$ (8)

Previous studies have shown that this simple model can explain the disposition effect, as long as individuals also discount the future at a sufficiently high rate¹⁰; i.e., when δ is sufficiently small (Barberis and Xiong (2009); Barberis and Xiong (2012)). In this case of heavy discounting, we have that the relative value of selling the asset is approximately given by CG_i,t. In other words, the decision of a pure realization utility trader that has linear utility, and who discounts the future at a high rate, is approximately driven by the capital gains term¹¹.

Second, consider an individual who trades based on prospect theory preferences (Odean (1998); Weber and Camerer (1998)). In a simple version of this model, the individual has reference dependent utility defined over transactions for each stock separately, over-weights losses by a factor λ > 1, and uses the purchase price as the reference point. Furthermore, utility is concave in the gain domain and convex in the loss domain, inducing the S-shaped value function proposed by Kahneman and Tversky (1979). Much of the early literature examining the disposition effect through a prospect theory explanation uses a static setting, and for simplicity, we do the same here¹². Suppose an individual purchases a stock at price c, and the stock price increases to p_gain>c. The individual now finds himself in the gain domain, where he is risk averse because of the concave utility. This risk aversion will on average induce the individual to sell the stock because he no longer finds holding the stock attractive because of the increase in risk aversion. Similarly, if the stock decreases in price since purchase to p_loss<c, the investor finds himself in the convex region of the value function. Owing to the risk-seeking behavior that occurs in this domain, the individual finds it attractive to hold the stock since he has an increased appetite for risk. Because this is a static setting, the one period price change p_gain−c (for the gain case) and p_loss−c (for the loss case) are equivalent to the capital gain. In other words, individuals will on average, prefer to sell when CG_i,t > 0 and they prefer to hold when CG_i,t <0. This suggests that, in sufficiently simple and static trading settings, the behavior of traders with prospect theory preferences is approximately driven by the capital gain. We emphasize however, that recent studies have raised doubts about the generalizability of this result, particularly in complex dynamic settings (Barberis and Xiong (2009); Kaustia (2010); Hens and Vlcek (2011)).

Finally, consider a model based on an irrational belief in the mean reversion of stock prices, which has also been argued to provide an explanation for the disposition effect (Odean (1998); Weber and Camerer (1998)). In the simplest version of the model, individuals have linear utility and seek to maximize the expected value of total trading payoffs. However, unlike a Bayesian investor, and contrary to the true nature of the price process, they believe that prices exhibit mean reversion. More concretely, let π_i,t denote the mean of observed prices for stock i from period 1 through period t. The individuals then believes that E[Δp_i,t+u | p_i,t,, π_i,t] is decreasing in p_i,t − π_i,t., and that E[Δp_i,t+u | p_i,t,, π_i,t] > 0 if and only if p_i,t < π_i,t. Since the relative value of selling for these investors is given by −E[Δp_i,t+u | p_i,t,, π_i,t], it follows that their likelihood of selling the asset increases in p_i,t − π_i,t. But in our experiment p_i,t − π_i,t is highly correlated with CG_i,t (mean across subjects = 0.76, S.D. = 0.10), which implies that individuals with a belief in mean reversion trade on a signal that is highly correlated with the capital gains regressor.

The model described in (3) captures the idea that a subject’s decision can be affected by multiple motives, which can be classified into two types. First, there is the motive to maximize expected wealth from the experiment, which is captured by the REV variable. Second, there is the motive to trade based on the CG variable, which can be the result of realization utility preferences, simple prospect theoretic preferences, or an irrational belief in the mean reversion of stock prices.

Importantly, the goal of this paper is to investigate how a reduction in the saliency of the purchase price can decrease a subject’s tendency to make decisions based on the CG variable, and how it can decrease the disposition effect. However, our experimental design does not provide a clean test of which of the three mechanisms discussed here provides a better explanation for the disposition effect. This is an important question, but is beyond the scope of this paper.

4.2 Hypotheses

Using the procedure described in section 3.3, and the actual price path that the subjects see in the experiment, we can compute the PGR-PLR measure of the disposition effect for different types of traders. For a pure optimal Bayesian trader with linear utility, henceforth called an expected value trader, the PGR-PLR measure equals −0.55. To get an intuition for why, recall that expected value traders will sell stocks when the relative expected value of selling is positive, which occurs, on average, after a stock’s price has declined in the recent past. Therefore, this type of investor will tend to sell more capital losses than capital gains, which leads to a negative value of PGR-PLR. In contrast, for a trader that is driven solely by the realization of capital gains¹³, we have that PGR − PLR = 1. To see why, notice that this individual sells the stock only when CG_i,t > 0, which implies that he only realizes gains. It follows that PGR = 1 and PLR = 0. It is easy to see that a ‘hybrid’ trader that is influenced by both the REV and the CG variables will exhibit a measure of PGR-PLR that is between −0.55 and 1.

Based on the findings of our previous work (Frydman et al. (2014)), which used a design similar to the HIGH-SALIENCY condition, we hypothesized that in this control condition individuals’ selling decisions would be modulated by both motives, and that they would exhibit a sizable disposition effect.

Hypothesis 1

In the HIGH-SALIENCY condition individual selling decisions are responsive to both the REV and the CG variable. Furthermore, individuals sell capital gains and hold capital losses at a higher rate than an optimal trader (so that PGR − PLR> −0.55).

The central goal of the study is to investigate whether the disposition effect is modulated by the saliency with which the purchase price information is displayed. Although individuals can compute this information on their own, we hypothesized that making this information less salient, by removing it from the price update and trading screens, would decrease the magnitude of the disposition effect.

Hypothesis 2

The disposition effect is smaller in the LOW-SALIENCY than in the HIGHSALIENCY condition (i.e., PGR_LOW – PLR_LOW < PGR_HIGH – PLR_HIGH). Furthermore, individuals’ selling decisions are less responsive to the CG variables in the LOW-SALIENCY condition.

The second part of Hypothesis 2 is based on the fact that all of the simple models of the disposition effect described above predict that behavior is highly responsive to the CG variable. In particular, they predict that individuals are approximately indifferent between selling and keeping the asset when CG = 0, and that the likelihood of selling increases with CG.

One natural question is whether decreasing the saliency of the purchase price information also increases the impact of the REV variable on selling decisions. Although we test for this possibility below, we emphasize that it is hard to pin down an a priori hypothesis because it is not known if the effects of information saliency are direct (in which case only the CG mechanism should be affected by the treatment) or relative (in which case the impact of both CG and REV should be affected).

5. Results

5.1 Tests of Hypothesis 1

We begin the analysis by testing the two components of Hypothesis 1, which refer to selling behavior within the HIGH-SALIENCY control condition.

The average disposition effect in the HIGH-SALIENCY condition is 6.8%, as measured by the PGR-PLR statistic. This is well above the optimal value of −55% for an expected value trader (p<0.001), and below the value of 100% for a pure realization utility trader (p<0.001).

To test the predictions about the motives generating this behavior, we estimate the following logistic regression, separately for every subject, and only on trials in which the subject has an opportunity to sell a stock:

$$\text{Pr}({\mathit{\text{Sell}}}_t)=\mathit{\text{constant}}+{\beta }_{REV}RE{V}_t+{\beta }_{CG}C{G}_t+{\epsilon }_t$$ (9)

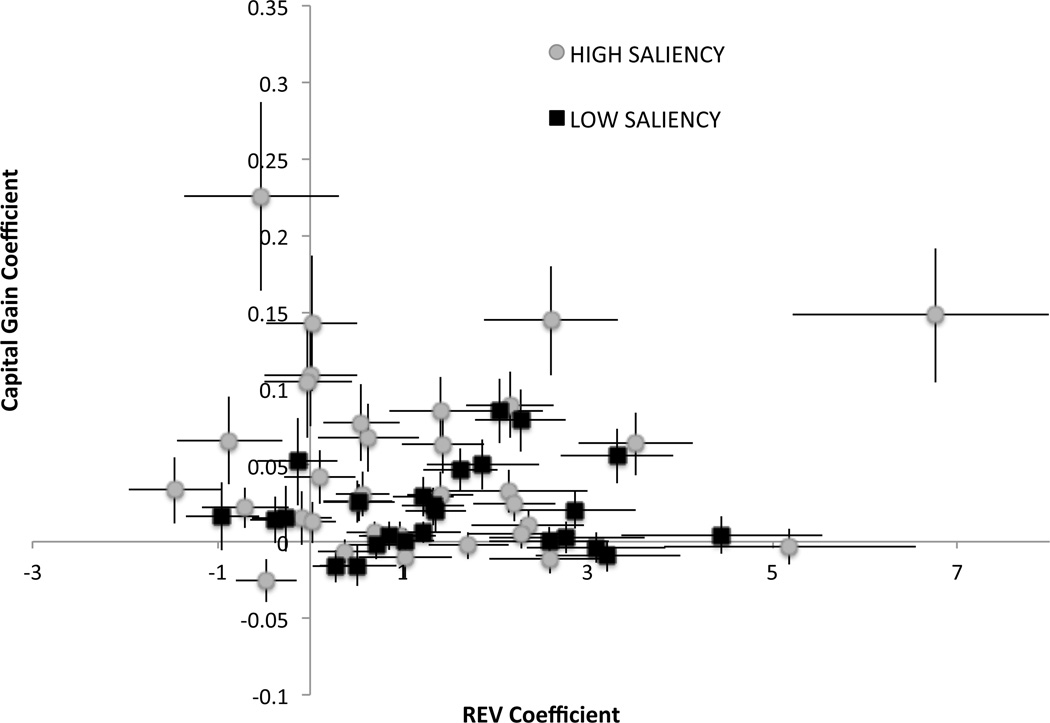
The model is estimated only using data from the HIGH-SALIENCY condition. The individual estimates provide a measure of the extent to which each subject’s selling decisions were responsive to the REV and the CG motives. Figure 2 plots the distribution of estimated coefficients β_REV and β_CG (circles), as well as their standard errors. As shown there, the majority of individuals had positive estimated coefficients for both variables, which provides support for the hybrid model proposed here.

Figure 2. Individual estimated coefficients from the hybrid model.

Each point refers to a subject’s estimated coefficients (β_REV, β_CG), estimated using the logistic model in (9) separately for each subject. Lines denote 95% confidence intervals of the estimates.

We then compute the average estimated coefficient across subjects, which has been shown to provide a good approximation to a mixed effects model with random coefficients (Friston et al. (2005); Penny et al. (2006)). The average β_REV is 1.18, and is significantly greater than zero (p<0.001). The average β_CG is 0.049, and is also significantly greater than zero (p<0.001).

Together, this provides evidence consistent with Hypothesis 1. In the control condition the population of subjects is sensitive to two motives when making selling decisions: the maximization of expected wealth and the realization of capital gains. The sensitivity of the decision to capital gains is important because it is consistent with the presence of a sizable disposition effect.

5.2 Tests of Hypothesis 2

Next, we compare the outcomes generated by the HIGH-SALIENCY and LOW-SALIENCY conditions, in order to measure the impact of reducing the saliency of the purchase price information.

First, as expected, the average disposition effect decreases from 6.8% to −9.0% (p=0.022). This shows that removing the purchase price information reduces the magnitude of the disposition effect by about 25%. Furthermore, because the PGR-PLR measure remains significantly above the optimal level of −0.55 in the LOW-SALIENCY condition, it also suggests that individuals take into account the capital gains variable when making selling decisions, even if this information is not shown in the price update and trading screens.

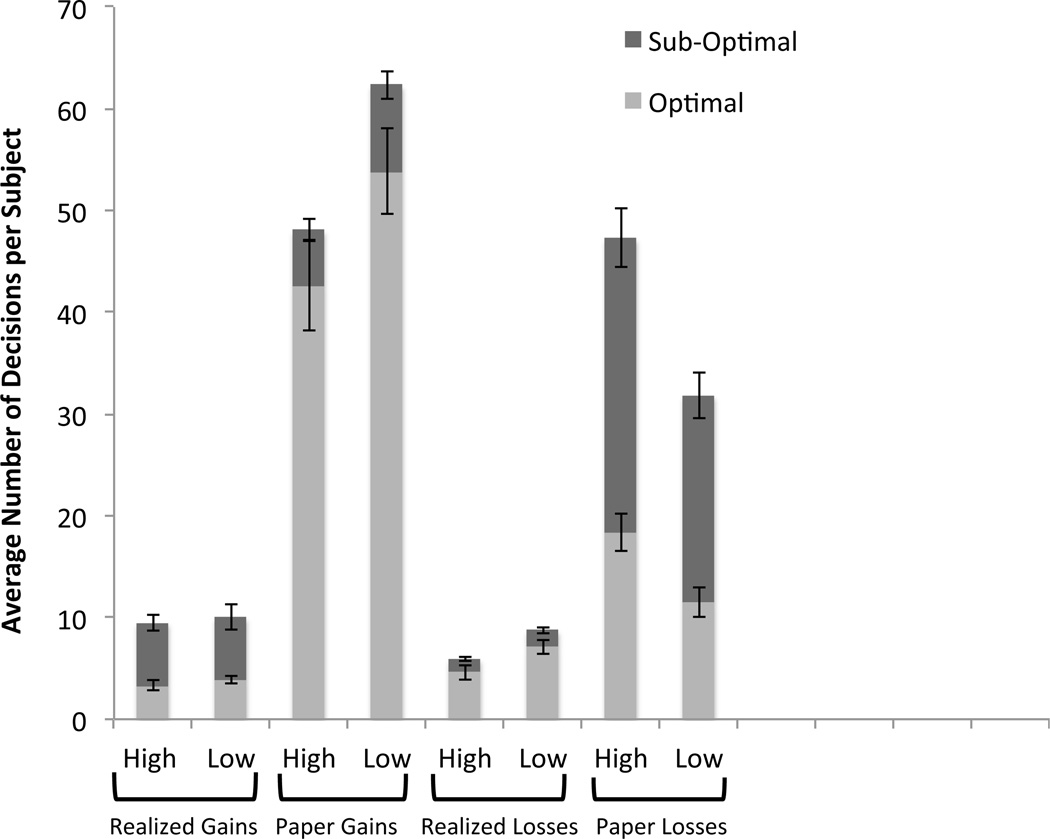
Second, Figure 3 depicts the percentage of decisions that are optimal, in the sense of being consistent with the maximization of expected wealth, by condition and decision type (realized gains, realized losses, paper gains, and paper losses). It shows that paper losses are, on average, suboptimal, and that reducing the saliency of the purchase price has a significant effect on the number of paper losses: they decrease from 47.3 to 31.8 (p=0.015).

Figure 3. Selling behavior disaggregated by decision type.

Data are binned according to whether the decision was optimal or sub-optimal, and whether it was generated from the HIGH-SALIENCY or LOW-SALIENCY condition. Realized gains and realized losses are optimal when the REV is positive, whereas paper gains and paper losses are optimal when the REV is negative. The chart shows that the LOW-SALIENCY treatment primarily affects behavior through the paper loss and paper gain channels; that is, the disposition effect is attenuated because of a reduction in paper losses and an increase in paper gains. Bars depict 95% confidence intervals of the sample mean across subjects, computed separately for each category.

Third, we repeat the logistic analysis described in (9), but this time using only data from the LOW-SALIENCY treatment condition. The individually estimated coefficients for β_REV and β_CG are plotted in Figure 2 (squares), along with their standard errors. As in the control condition, most subjects have positive estimates for both variables. We then compute the average estimated coefficient across subjects and find that the average β_REV is 1.49 and significantly greater than zero (p<0.001), and that the average β_CG is 0.02 and also significantly greater than zero (p<0.001).

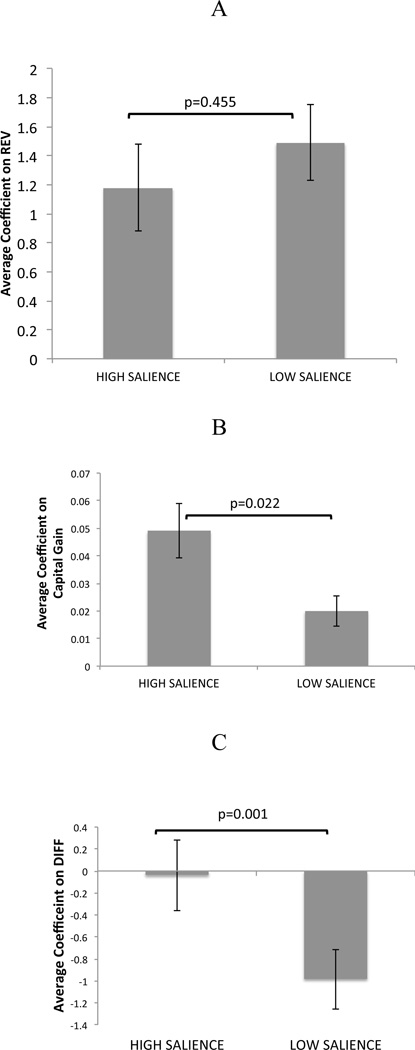
Fourth, as shown in Figure 4, we compare the distribution of estimated coefficients across the groups of subjects associated with each condition using unpaired two-tailed t-tests. This provides us with a measure of the treatment effect on the average subject’s β_CG and β_REV. The estimates of the β_CG coefficient exhibit a decrease from 0.049 in the HIGH-SALIENCY control condition to 0.020 in the LOW-SALIENCY treatment (p=0.022). In contrast, the changes in the estimates of the β_REV coefficient are not significant (HIGH-SALIENCY mean = 1.18, LOW-SALIENCY mean = 1.49, p=0.46).

Figure 4. Comparison of group estimates across conditions.

We estimate the logistic model in (9), separately for each individual. For each condition we then compute the average coefficient (across subjects), for both the REV and the CG regressors,. A) Average β_REV estimates. B) Average β_CG estimates. C) Average β_DIFF estimates (see text for details). Bars denote 95% confidence intervals of the sample group mean.

Fifth, as shown in Figure 4A, one limitation of the previous test is that there is significant heterogeneity across subjects in the extent to which they responded to the REV variable in both conditions. To address this concern, we construct a post hoc measure of the relative effect of the CG and the REV variables. This measure is computed in three steps: 1) z-score the CG and REV variables¹⁴ 2) re-estimate the logistic model in (9) at the subject level, and 3) compute the estimated difference β_DIFF = (β_CG − β_REV) at the subject level. The estimated coefficient β_DIFF provides an individual measure of the extent to which subjects are more influenced in their selling decisions by the CG variable as compared to the REV variable. As shown in Figure 4C, in the HIGH-SALIENCY condition the average coefficient is −0.03 and is not significantly different from zero (p=0.9). In contrast, the average coefficient decreases to −0.98 in the LOW-SALIENCY condition, and is significantly different than zero (p<0.001). A direct comparison between both conditions shows that the decrease associated with the treatment is significant (p<0.001).

Together, these results suggest that the removal of the purchase price information generates about a 25% decrease in the size of the disposition effect, and that this happens by decreasing the absolute and relative weight given to the capital gains variable in the selling decisions.

6. Discussion

In this study we use a laboratory experiment to investigate if it is possible to debias subjects’ tendency to exhibit a disposition effect, by decreasing the saliency with which the purchase price information of assets is displayed by the trading software. In particular, we compare the selling decisions of subjects in two experimental conditions. First, there is a HIGH-SALIENCY condition in which the purchase price of a stock is prominently displayed, and which is meant to resemble the information that is displayed on many financial statements and software trading platforms. Second, there is a LOW-SALIENCY condition that is identical except for the removal of explicit reminders of the purchase price.

Consistent with previous experimental results (Weber and Camerer (1998); Weber and Welfens (2007); Frydman et al. (2014)) we find a disposition effect in the control condition. We also find that the size of the disposition effect goes down by about 25% when the purchase price information is not displayed, and thus is less salient. To the best of our knowledge, this is the first demonstration that it is possible to debias the disposition effect by reducing the saliency of information related to the computation of capital gains. The result is also interesting because it suggests that there are limitations to this type of intervention, since individuals exhibit a measure of PGR-PLR that is significantly above the optimal level even when the purchase price information is not explicitly displayed.

Our results also show that subjects’ behavior is influenced by multiple motives, which include a desire to maximize expected wealth, and a desire to realize capital gains either directly (as in realization utility models of the disposition effect), or indirectly (as in prospect theoretic or mean reversion models of the disposition effect). Importantly, the results show that the relative weights given to these two motives are not fixed, and instead are modulated by contextual variables, such as what information is made salient at the time of decision. This result is interesting because it suggests that the saliency with which information is displayed during portfolio decisions has the potential to change preferences, and therefore impact investor behavior (Libby et al. (2002); Hirshleifer and Teoh (2003)). In particular, it suggests that preferences are not fixed or “hardwired”, but instead they are subject to systematic environmental influences. This motivates future analyses of investor behavior in which information saliency is incorporated explicitly.¹⁵

Although we find that reducing the saliency of the purchase price has a sizable effect on the disposition effect, our experimental setup does not allow us to identify the specific channel through which the change in behavior occurs. Based on recent theoretical discussions in the literature (Barberis and Xiong (2009); Barberis and Xiong (2012); Ingersoll and Jin (2013)), empirical data (Han and Kumar (2013)), and our recent fMRI work (Frydman et al. (2014)), we believe that realization utility is likely to be an important mechanism behind the disposition effect. However, as we emphasized above, this is not critical to our results, since they are consistent with any model of the disposition effect in which the capital gain variable is highly correlated with the utility of selling a risky asset. These alternative models include theories of the disposition effect based on a belief in the mean reversion of prices and static models based on prospect theoretic preferences (Odean (1998); Weber and Camerer (1998)). Distinguishing among the competing theories of the disposition effect is an important and open question, not least because it will contribute to our understanding of how to best mitigate its costly effects for investors.

Extrapolating from the lab, our results also provide a potential concrete recipe for debiasing the disposition effect in the field. In particular, since investors who are prone to the disposition effect will trade to realize capital gains, and hold stocks with capital losses, regulators can potentially debias this effect by stipulating that brokerage houses decrease the saliency of information related to capital gains. For example, they could mandate that purchase price information not be prominently displayed on financial statements or online trading platforms (as in our LOW-SALIENCY condition). We acknowledge that this intervention is not without complications for taxable accounts, since the purchase price carries useful information that allows the investor to compute the aftertax proceeds from realizing a capital gain. However, our proposed policy intervention is well-suited for tax-free accounts, such as a Roth IRA, where the purchase price should be irrelevant. More broadly, our results suggest that regulators can potentially use saliency and attention as a powerful tool to influence investor and consumer behavior, by requiring subtle changes to the layout of financial statements (Bertrand and Morse (2011); Choi et al. 2012)).

Interestingly, the US government recently enacted a new cost basis legislation in January 2011 which effectively makes the purchase price more salient and may have the unintended effect of shifting investors’ attention towards capital gains. Specifically, in order to increase compliance with paying capital gains tax, this legislation mandates that investors must decide, at the time of trading, which cost basis method they will use when reporting capital gains for tax purposes. Previously, investors decided this method after the trading decision, and so this legislation effectively increases the saliency of the cost basis during the decision phase. Our experimental results suggest that this may have a systematic and detrimental effect on the trading performance of some individual investors. If such an effect is present, this should work to increase government tax revenue even more, since an investor’s optimal tax policy is to realize losses immediately and defer realizing gains far into the future in order to minimize the present value of the capital gains tax burden (Constantinides (1983)). Future research should take advantage of the fact that this new legislation introduces a useful opportunity to test the effect of information saliency on trading behavior. In particular, a testable implication of our results is that the new cost basis legislation should induce investors to pay more attention to capital gains, and this should lead to a higher average disposition effect among individual investors starting in January 2011.