Coherent fluorescence emission by using hybrid photonic–plasmonic crystals

Abstract

The spatial and temporal coherence of the fluorescence emission controlled by a quasi-two-dimensional hybrid photonic–plasmonic crystal structure covered with a thin fluorescent-molecular-doped dielectric film is investigated experimentally. A simple theoretical model to describe how a confined quasi-two-dimensional optical mode may induce coherent fluorescence emission is also presented. Concerning the spatial coherence, it is experimentally observed that the coherence area in the plane of the light source is in excess of 49 μm², which results in enhanced directional fluorescence emission. Concerning temporal coherence, the obtained coherence time is 4 times longer than that of the normal fluorescence emission in vacuum. Moreover, a Young's double-slit interference experiment is performed to directly confirm the spatially coherent emission. This smoking gun proof of spatial coherence is reported here for the first time for the optical-mode-modified emission.

1. Introduction

The correlations of a radiation field between different temporal and spatial points, generally referred to as coherence ¹, vary strongly depending on the light source. The low correlations between spontaneous emission events from conventional incoherent light sources such as incandescent filaments or fluorescent tube lamps normally result in spatially isotropic and spectrally broad light with low intensity. Due to the high degree of coherence originating from a lasing emission process, however, lasers are able to produce highly directional and monochromatic light with well-defined phase and enormous intensities. Simple spatial (or frequency) filtering of the emitted light certainly increases the spatial (or temporal) coherence but at the drastic expense of intensity. It is of fundamental interest whether coherent light can be created from incoherent emission of many emitters by somehow directing the light into one (or a few) mode(s) without considerable loss in intensity. Such a mechanism for creation of light with high degree of coherence would be desirable in many respects. It could not only improve considerably the ability of the light beam steering ^2–4, such as the directionality ^5,6 and the spectrum ^7,8 of spontaneous emission, but also have important potential applications on imaging ^9,10, sensing ^11,12 and even new generation energy technologies ^13,14. In this paper, we propose and experimentally demonstrate a reliable concept for creating light with a high degree of coherence from fluorescence emission of molecules close to a nanostructured surface. Using leaky optical modes of a quasi-two-dimensional hybrid photonic–plasmonic crystal structure ^15–17, fluorescence spontaneous emission is transformed into light with a high degree of partial spatial as well as temporal coherence.

A quasi-two-dimensional photonic system (a flat metallic surface or a dielectric thin film with high refractive index) supports optical modes whose parallel wavevector is bigger than that of the free space (k = ω/c) as well as the wavevector perpendicular to the surface with a big imaginary part. This big imaginary part of the wavevector results in the optical field component normal to the surface being evanescent. Therefore, those quasi-two-dimensional photonic system support well defined quasi-two-dimensional optical modes (2D-OM) which can effectively trap light inside a very thin layer ^18,19. For the metallic surface case, the 2D-OM is well known as a surface plasmon mode, and for the dielectric thin film case, the 2D-OM is well known as a slab-guided mode. Because of their high photonic density of states inside a very thin layer, the 2D-OMs are widely applied to enhance the spontaneous emission rate ^20–23 and even lasing process ^24–26. Also, directional emission with the help of 2D-OM has been reported in ions ²⁴, polymers ^25,26, dyes ^23,27–32 and quantum dots ³³ doped photonic structures, and the connection between the directional emission and the coherence properties has been discussed on a qualitative level ^28,29. However, the observed effects have been mostly explained only by the interactions between a single spontaneous emitter and a photonic structure. To analyze the coherence properties of the emission by a large number of emitters that emit spontaneously, in other words, independently of each other, more thorough quantitative theoretical and experimental studies are required. Based on the macroscopic fluctuational electrodynamics ³⁴, it has been theoretically predicted that, a thermal light source could generate partially coherent field, both spatially and temporally, in the near-field region close to the surface, if it is modified due to the 2D-OMs, such as surface plasmon (or phonon) polariton modes ³⁴, dielectric slab-guided modes ³⁵ and even the modes on the surface of a topological insulator ³⁶. By using a designed structure, such as gratings, to scatter the near-field information to the far field area, this partially coherent field has been used to experimentally realize highly enhanced directional semimonochromatic thermal sources ^5,37–40. Furthermore, it is also predicted that the use of 2D-OMs could constitute a new paradigm to control the statistical and propagation properties of the light beam irradiated from a normal light source ^41,42. Although the idea of controlling the coherence properties of light by 2D-OMs has attracted a lot of interest, there are still several unsolved issues. First and foremost, the most direct experimental verification of the coherence of output light, namely Young's double-slit interference experiment, has not been performed yet. Secondly, despite numerous studies of modifying coherence properties of the thermal sources in the infrared region at ambient temperature, similar quantitative studies of fluorescence emission in the visible region are still rare. Importantly, and in contrast to the thermal sources whose active medium is a continuous solid material, in our study, the fluorescence emission is originated from a number of individual molecules.

Here, we investigate experimentally the spatial and temporal coherence of the fluorescence emission controlled by a quasi-two-dimensional hybrid photonic–plasmonic crystal structure covered with a thin fluoresence-molecular-doped dielectric film. Concerning the spatial coherence, we observe experimentally that the coherence area in the plane of the light source is in excess of 49 μm², which results in enhanced directional fluorescence emission. Concerning the temporal coherence, the obtained coherence time is around 4 times longer than that of the normal fluorescence emission in vacuum. Moreover, a Young's double-slit interference experiment is performed to directly confirm the 2D-OMs assisted partial spatial coherence emission. This smoking-gun proof of spatial coherence is reported here for the first time for the 2D-OMs modified emission.

2. Simple model

Prior to the experimental results, we present a toy model to show how the 2D-OMs could strongly modify the near-field spatial coherence properties of the field emitted by a large number of isolated point sources located inside a very thin layer (Fig.1a). A similar but more precise theory for the thermal radiation has been shown in Ref. 34. As mentioned in the introduction, the 2D-OMs refer to not only the suface plamon modes for metal cases, but also those slab-guided modes for the thin dielectric film cases. Here, for simplicity, the fluorescent molecules are simplified to be point-source emitters and the scalar approximation of the emission field 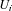at is assumed. The spectral degree of coherence of the near fields around the surface (for the surface-plasmon case) or inside a thin dielectric film (for the slab-guided mode case) is calculated by the relation 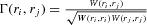. Here, 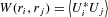is the cross-spectral density of these fields, where * denotes the complex conjugate and denotes the ensemble average over the spontaneous emission fluctuations. In the model, N point sources with a negligible dipole–dipole interaction located inside a very thin layer (the thickness approaches zero) are considered. It is supposed that there is no correlation between any two emitters. We consider the modes with the parallel wavevectors bigger than the wavevectors of the same frequency in the free space. This means that only the near-field components of the emitted field are taken into account.

Figure 1.

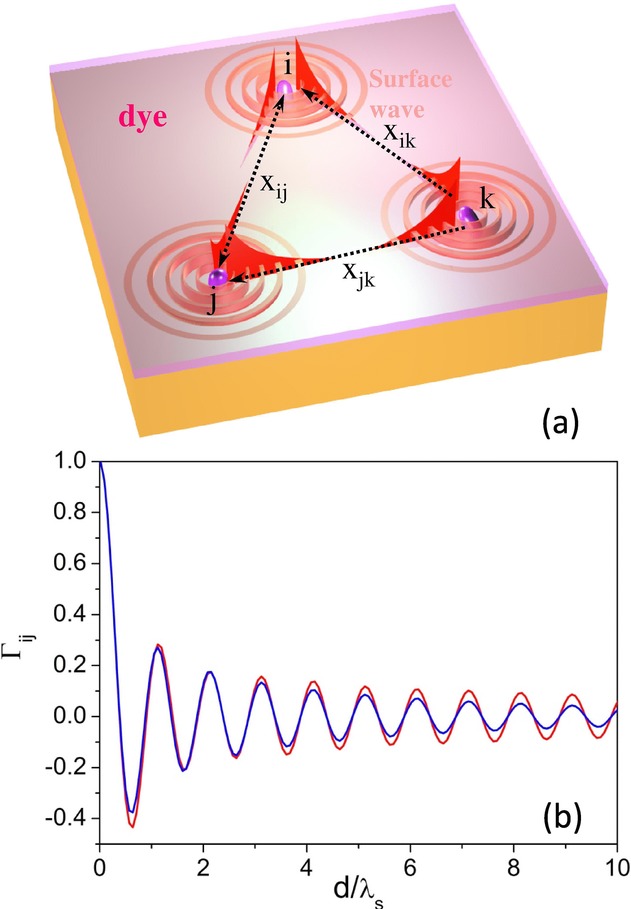
(a) The schematic view of the model of coherence properties of the fluorescence emission in the near field. (b) The calculated spectral degree of coherence in the near field as a function of distance, for the cases of an ideal OM without loss (red) and a realistic OM (blue) with 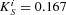μm⁻¹.

For the non-2D-OM case, because there is no propagation mode below the free-space light line, the field 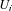is dominated by the evanescent field of the nearest emitter and the cross-spectral densities for any two different locations vanish. For the 2D-OM case, the result changes dramatically. Due to the 2D-OM, the parallel wavevector is not purely imaginary. Assuming a perfect coupling efficiency of the emitters to the 2D-OM, the field at any position of the system is contributed by all the emitters rather than the nearest one only (shown in Fig.1a and Eq. (1) in the Supporting informations). Due to the fact of this delocalization assissted by the 2D-OM, the spectral degree of coherence in general could be nonzero (detail discussions shown in the Supporting informations). Based on this toy model, it is helpful to discuss the effect of the 2D-OM on the degree of coherence in three cases, namely 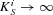, 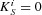and a finite value, e.g. 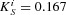μm⁻¹, where 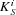is the imaginary part of the parallel wavevector. For the first case, the imaginary part of the wavevector is so large that the coupled 2D-OM is highly localized, which should yield a noncoherence result. For the second and the third cases, an ideal 2D-OM without loss and an realistic 2D-OM with finite propagation length are considered, respectively. In the last case, a finite propagation length can be due to either the absorption loss or the radiation loss caused by the defects or the structure scattering. Figure1b shows the results of the spectral degree of coherence as a function of the distance 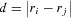obtained from the proposed toy model. In the calculation, 16 million emitters are uniformly dispersed in a 1600-μm² surface area, and the distance d is normalized by the wavelength of the 2D-OM. Clearly, because of the existence of the 2D-OM, in the near-field region, the partial spatial coherence properties of the emission field by a collection of isolated and uncorrelated emitters could be maintained over very long distances. From the discussions above, despite the approximations used, we can conclude that the fluorescence emission has strong partial spatial coherence properties in the near field, which are influenced by the propagation length of the 2D-OM.

It is worth mentioning that in this toy model, the correlation is zero for different emitters and has no contribution to the obtained coherence. It corresponds to the premise that each spontaneous emission event is independent. We do not consider strong coupling between the 2D-OM and the emitters as a possible origin of coherence ⁴³, since our system is in the weak-coupling regime and the observed coherence can be explained without strong coupling effects. However, the coherence effects mentioned above cannot be easily measured because they only appear in the near-field region. To realize a coherent fluorescence emission beam in the far field, the leaky 2D-OM ⁴⁴ existing in corrugated photonic structures will be used in our study. The propagating 2D-OM exchanges momentum with the periodic corrugated structures, resulting in photonic band structures ⁴⁵. The leaky modes corresponding to those above the free-space light line in the photonic band structures can radiate and display the coherent properties of the fluorescence emission in the far field.

3. Material and methods

In our experiments, well-defined leaky 2D-OM used to achieve high degree of coherent fluorescence emission are supported by the quasi-two-dimensional hybrid photonic–plasmonic crystal structure ¹⁵ shown in Figs.2a and b. A 200-nm thick Ag thin film was deposited onto a glass substrate by electron beam evaporation. An aqueous solution of monodisperse polystyrene (PS) spheres (8 wt%) of 500 nm diameter (size dispersion 1%) was injected into a channel that was formed from the Ag surface and the other parallel quartz slide separated by a U-shaped spacer ⁴⁶. By controlling the height of the channel, a large area (Fig.2a) monolayer array of PS spheres was then formed on the Ag surface by a self-assembly method. On top of the structure, a nominal 50-nm thick S101-doped polyvinyl alcohol (PVA) layer (10 mM) was spun cast. Based on SEM images, self-assembled PS spheres are arranged regularly in a hexagonal lattice (Fig.2b) and they maintain their arrangement after spin coating. From SEM it is difficult to determine how S101-doped PVA is distributed. A confocal fluoresence optical microscope (CFOM) was then used to observe a fluoresence image (see the inset of Fig.2a) from which the distribution of S101-doped PVA can be inferred. The PS spheres for CFOM observation are on a quartz substrate since our CFOM works in the transmission mode, and to obtain enough resolutions and eliminate the scattering of the PS spheres, an oil-immersed objective was used. Obviously, fluorescence from the sphere equator is more intense than that from the top. This implies that S101-doped PVA is not evenly distributed on PS spheres. Instead, it is much thicker on the sphere equator than on the top. Recently, these cost-efficient hybrid photonic–plasmonic crystal structures have been shown to exhibit high quality factors for both leaky slab-guided modes in a monolayer sphere array and leaky surface plasmon polariton modes on a flat metal surface ^{15–17,47,48}.

Figure 2.

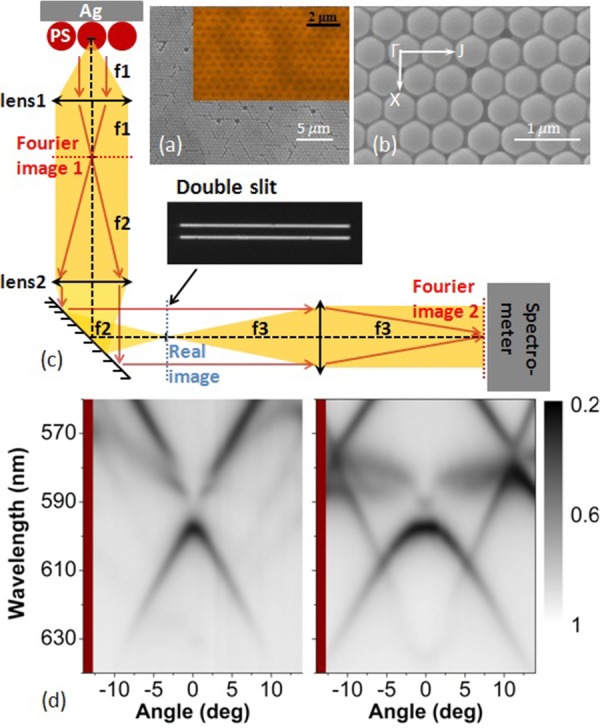
(a, b) The top-view SEM images of the photonic–plasmonic crystal structures in different magnifications. Inset of (a) corresponding to the fluorescence molecules distribution on top of the PS sphere array measured by an oil-immersed confocal fluorescence microscope. (c) The schematic view of the experimental setup, the used double-slit is shown in the inset. (d) Reflection spectra (without a double-slit) of the proposed structure as functions of the wavelength and the incident angle. The light is incident along the Γ–J direction. The left (right) panel is for p- (s-) polarized incident light.

To explore the 2D-OMs supported by the proposed structure as well as the coherence measurements, angular-resolved spectroscopy combined with Young's double-slit experiment was used (see Fig.2c). The back focal plane of the lens1, which is the Fourier image (momentum space) of the radiation field from the sample, carries the angular information. After lens2 and lens3, the spectrometer finally collects the Fourier image and gives us the results of the radiation intensity maps as functions of the radiation wavelength (or frequency) and the angles (or the inplane wavevector parallel to the sample). Also, a real image of the sample appears on the focal plane of the lens2 (blue dashed line). By using a double-slit (see inset of Fig.2c) on this real image plane, the radiation fields from two different places located on the sample are selected and intersect with each other on the Fourier image at the entrance of the spectrometer (for example, the red arrow lines shown in Fig.2c). This allows us to directly detect the spatial coherence properties on top of the sample surface in the far field. The numerical aperture of the setup is 0.25. As reference samples, an empty area without the structure and an monolayer spheres array with the same diameter on top of a glass substrate covered by the S101-doped PVA film are measured under the same experimental conditions. The double-slit is fabricated on a thick opaque Al film and mounted on the real image plane inside the setup. Two pairs of the double-slit are used in the experiment. In one double-slit, each slit has a 20 μm width, and the double-slit distance (center-to-center) is 70 μm. In the other, each slit has a 10 μm width, and the double-slit distance (center-to-center) is 40 μm. Because there are 10× magnifications on the real image, the actual slit width and the double-slit distance on the sample are equivalent to 2 μm and 7 μm, respectively, for the former, and 1 μm and 4 μm for the latter. In the measurement of the 2D-OM dispersions, a white-light source was used. In the fluorescence emission as well as coherence measurements, a continuous 532-nm laser was used to pump the molecules. The power intensity and spot size of the laser on the sample are around 0.01 mW/μm² and 300 μm², respectively.

4. Results and discussion

Figure2d shows the experimental reflection spectra (without a double-slit) as functions of the wavelength and the incident angle for both p- (left panel) and s- (right panel) polarized incident light along the Г–J direction (defined in Fig.2b). A flat Ag surface should be highly reflective in the visible regime. However, with the introduction of a monolayer array of PS spheres, the reflection of the Ag surface is considerably modified: reflection minima appear, in response to the emergence of the 2D-OMs. The loci of the reflection minima show well-defined dispersions of those modes. Similar to photonic crystals ⁴⁵, the 2D-OMs propagating along the PS sphere array undergo multiple Bragg scatterings due to the introduced periodicity. As a result, the 2D-OMs are characterized by complex band structures as shown in Fig.2d. For the dispersions of 2D-OMs along another direction (the Г–X direction), similar results are shown in the supporting information (Fig. S1).

To demonstrate the coherent fluorescence emission caused by the 2D-OMs as predicted by our simple model, the results of the S101 fluorescence emission and the Young's double-slit experiments are shown in Fig.3. Figure3a shows the enhancement of the fluorescence emission due to the structure as compared with the case of a flat film for both p (upper panel) and s (lower panel) polarizations along the Г–J direction (the case of the Г–X direction is shown in the supporting information Fig. S2). It is clear that the positions of the large emission enhancements observed in Fig.3a match the measured dispersion of the 2D-OMs shown in Fig.2d. This indicates that the molecular emission couples efficiently with the 2D-OMs. From the distribution of the fluoresence molecules (the inset of Fig.2a), because the molecules are far away from the metallic surface (∼250 nm), it has to be emphasized that the coupled 2D-OM mostly corresponds to the leaky guided modes of the PS spheres array (also called 2D photonic crystal slab modes) rather than the surface plasmon modes of the metallic surface ^15,32.

Figure 3.

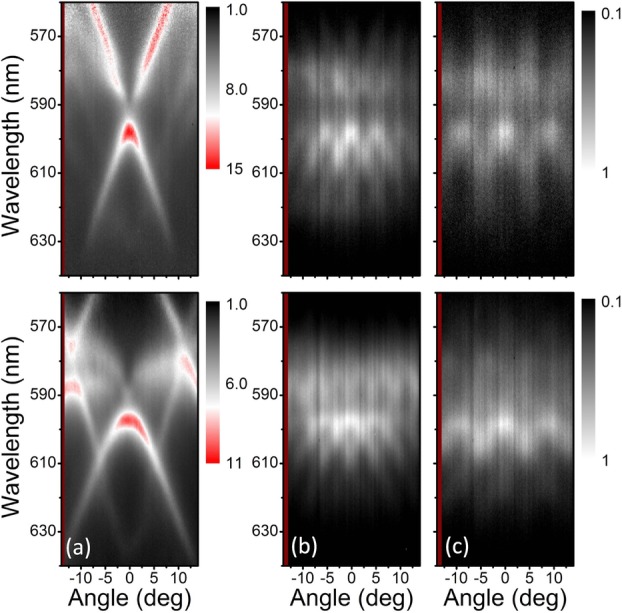
(a) The emission enhancement (without a double-slit) for S101 fluorescent molecules on top of the structure as a function of the wavelength and the emission angle. (b) The Young's double-slit experiment results for the case of a 7 μm double-slit distance on the sample. (c) The same as (b) but for the case of a 4-μm double-slit distance on the sample. The emitted light is detected along the Γ–J direction. The upper (lower) panel is for p- (s-) polarized emitted light.

When the double-slit is mounted on the real image plane inside the optical measurement setup, distinctive interference fringes for both p (upper panel) and s (lower panel) polarizations appear in a wide wavelength range nearly covering the whole S101 emission spectrum. The results of Young's double-slit experiments shown in Figs.3b and c correspond to the raw experimental data without any further data processing. For comparison, the results for the case of a flat film (Fig. S3) and the case of PS spheres array on top of a glass substrate (Fig. S4) are shown in the supporting information. It can be expected that no interference fringes are observed in the flat-film case since no leaky 2D-OM mode is supported. This means that the far-field emission of the fluoresence molecules on top of the metallic surface has no long-distance spatial coherence properties. For the case of monolayer PS spheres array on top of the glass substrate, very weak interference fringes are observed. Although the monolayer PS spheres array indeed supports 2D-OMs (guided modes), the resonance of the supported 2D-OMs is very weak (Fig. S4a) due to the fact that the refractive-index contrast between the PS (1.6) and glass (1.45) is very low. In this case, most of the fluorescense molecules do not couple to the guided mode. The emission shows in a broad angle range (shown in Fig. S4b), which greatly decreases the visibility of the interference fringe. The results shown in Fig. S4 also indicate that the metal surface, which gives high reflectivity of the interface between the PS sphere array and the metal, is also important for the guided modes of the PS spheres array. Furthermore, the results for the single-slit experiments are also shown in the supporting information (Fig. S5). Figs.3b (7-μm case) and c (4-μm case) with different double-slit distances show consistency with the fact that the separation between two fringes for a certain wavelength is inversely proportional to the double-slit distance. In addition, by comparing the results of emission (Fig.3a) and the corresponding double-slit interference pattern (Figs.3b and c), more important observations can be made. First, the interference results maintain the form of the dispersion of the 2D-OMs: the fringe pattern can be easily reproduced by replicating the original dispersion in the angle axis with intervals determined by the slit distance. This shows the strong connection between the 2D-OMs and the coherence. Considering the fact that the double-slit is located exactly on the plane of the real image, the clear visibility of the interference fringe observed in the momentum space can be interpreted as direct evidence of a long-range spatial coherence of the emission field on the sample plane. Secondly, it is worth emphasizing that the obtained high degree of spatial coherence emission is not obtained at the expense of the total emission intensity. On the contrary, due to the 2D-OMs, the maximum emission enhancement is around 10 times, which clearly shows that the approach proposed here is different from straightforward methods, such as using a pinhole to limit the numerical aperture of the system. Consequently, owing to the ability of constructive interference of the emission field, directional emission is observed (shown in the supporting information Fig. S6), which is an optical analog of the antenna array in the radio and microwave regimes.

In Fig.4, the emission for p and s polarizations emerging at the Г point, where the parallel wavevector, , is zero, are selected to study the relationship between the 2D-MOs and the degree of spatial coherence in more detail. From Fig.3a, it is clear that, for both p and s polarizations, the center wavelength of the 2D-MO around the Г point is 597 nm. In Figs.4a (p case) and b (s case), the emission intensity at 597 nm are shown as a function of the emission angle. Taking into account that 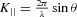, where θ is the angle, the plots shown here are actually equivalent to the mode distribution in the momentum space. According to the Fourier relation between momentum and position, wide distribution in the momentum space means that the mode is localized inside a small area in the real space. Obviously, the full width at half-maximum for the p case (Fig.4a) is smaller than that for the s case (Fig.4b), which indicates that the p-polarized emission has a larger mode volume in the real space. In other words, the propagation length of the p polarization is longer. The same conclusions can also be obtained by the fast Fourier transform (FFT) of the intensity as the function of the momentum, shown in Figs.4c (p case) and d (s case). We find that the intensity of the 2D-MOs near the Г point for the s polarization decreases to 0 after propagating 7 μm, however, the case for p polarization has not been totally dissipated even after 8 μm. As the coherence properties are directly related to the propagation length of the 2D-MOs, the results of the interference experiments for p- (Fig.4e) and s- (Fig.4f) polarized emission around 597 nm indeed behave differently. Clear interference fringes can be observed for the p-polarized emission both in the cases of 7 μm (upper panel in Fig.4e) and 4 μm (lower panel in Fig.4e) double-slit distances, which directly shows that the spectral coherence length and the area of coherence for the p-polarized emission on the sample plane is larger than 7 μm and 49 μm², respectively. Yet, interference fringes for the s-polarized emission can only be observed in the case of 4 μm (lower panel in Fig.4f) double-slit distance, which shows that the spectral coherence length for s-polarized emission is larger than 4 μm but less than 7 μm due to the small propagation length of the corresponding 2D-OM. Moreover, the above results obtained from the double-slit experiment are also well consistent with the spectral coherence length calculated from 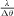, which is widely used in the optical coherence theory ¹. Here, 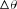is about 0.0628 and 0.0977 (3.6^o and 5.6^o in degree) for p and s polarizations, respectively, thus the calculated spectral coherence length are around 9.2 μm and 6.1 μm, which are around 15 and 10 times longer than the emission wavelength around the Г point, respectively. It is important to keep in mind that even higher degrees of coherence could be achieved by controlling the self-assembly process to reduce the defects ⁴⁹.

Figure 4.

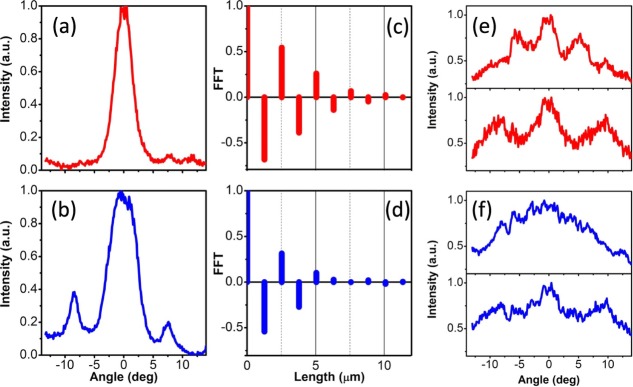
(a) The emission intensity around 597 nm of p-polarized light as a function of the emission angle. (b) The same as (a), but for s-polarized emission light. (c) The FFT results of the emission intensity distribution of p-polarized light in the momentum space obtained from (a). (d) The same as (c), but for s-polarized light. (e) The results of Young's double-slit experiment for p-polarized emission light around 597 nm wavelength by using 7 μm (upper) and 4 μm (lower) double-slit distances, respectively. (f) The same as (e), but for s-polarized emission light.

Since we have revealed the high degree of spatial coherence of the fluorescence emissions assisted by the leaky 2D-OMs, it is natural to also consider the temporal coherence properties of the system. Based on the coherence theory ¹, the degree of temporal coherence is related to the bandwidth of the emission light, which can be easily understood by the Fourier relation between time and frequency. A narrower bandwidth in the spectrum always corresponds to a longer coherence time of the emission. In Fig.5, the spectra of the fluorescence emission in the normal direction for both p (Fig.5a) and s (Fig.5b) polarizations are shown. The red and blue ones correspond to the emission from the structure, while the black ones correspond to the emission from the flat film as references. Without the structure, the fluorescence emission spectrum is broad and the bandwidth is around 37 nm. With the structure, for both p and s polarizations, narrow peaks with only 9 nm bandwidth appear. According to the definition of the coherence time, which is calculated by 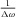¹, the coherence time of the emission increases by around 4 times due to the 2D-OMs. Note that the effect of the structure here to increase the coherence time of the emission is not the same as that of a normal narrow bandpass filter. In fact, due to the high local density of states close to the structure and the directional emission, the fluorescence emission is enhanced dramatically as shown in Fig.3a. As a final remark, in this work, we focused on spatial and temporal coherence properties of the emitted electromagnetic wave. The studies of photon statistics are beyond the scope of this article. We emphasize that when we talk about (partial) coherence, we do not mean a coherent state in the sense of Poissonian photon statistics. In addition, due to the fact that the photonic structure could trap light effectively, the emission photon could be amplified ⁵⁰ and the amplified spontenous emission can not be simply excluded. This part of the research should be studied in detail in future work.

Figure 5.

Fluorescence emission spectra at zero emission angle for a 50-nm thick S101-doped PVA layer on top of the photonic–plasmonic crystal structure (colored) and the flat film with the same thickness on top of the silver surface (black). (a) and (b) Data for p- and s-polarized emission, respectively.

5. Conclusion and outlook

In conclusion, we have investigated experimentally the coherence properties of the fluorescence emission assisted by the 2D-OMs. A simple toy model considering uncorrelated spontaneous emission from independent sources is used to illustrate how a 2D-OM can modify the degree of spatial coherence of the emission in the near-field regime. It is found that the propagation length of the 2D-OM essentially determines the final coherence properties. In the experiments, with the help of the leaky 2D-OMs supported by a quasi-two-dimensional photonic–plasmonic crystal structure, intense fluorescence emission with high spatial and temporal degree of coherence is achieved. The spectral coherence length, which turned out to be around 10 times longer than the emission wavelength, was directly measured by the classical Young's double-slit interference experiment. Last but not least, we also obtained experimentally temporal coherence with around 4 times longer coherence time than that of the normal fluorescence emission. Our findings have several important implications. First, the coherent emission reported here does not rely on a lasing process. This means that in contrast to a laser, no threshold power is required. Novel partially coherent fluorescene-based light sources with low energy consumption may be developed based on the concept presented here. Secondly, as we have shown, the coherence properties are directly related to the properties of the 2D-OMs. Utilizing the knowledge of the photonic band-structure engineering, one can thus control the degree of the coherence of the emission by controlling the band structure of the 2D-OMs, which include dielectric-guided mode and surface-plasmon mode. This provides a new degree of freedom in steering the light beam in applications, such as imaging and sensing.

Supporting Information

for this article is available free of charge under http://dx.doi.org/10.1002/lpor.201300196