Theoretical Investigation of the Electronic Structure of Fe(II) Complexes at Spin-State Transitions

Abstract

The electronic structure relevant to low spin (LS)↔high spin (HS) transitions in Fe(II) coordination compounds with a FeN₆ core are studied. The selected [Fe(tz)₆]²⁺ (1) (tz = 1H-tetrazole), [Fe(bipy)₃]²⁺ (2) (bipy = 2,2′-bipyridine), and [Fe(terpy)₂]²⁺ (3) (terpy = 2,2′:6′,2″-terpyridine) complexes have been actively studied experimentally, and with their respective mono-, bi-, and tridentate ligands, they constitute a comprehensive set for theoretical case studies. The methods in this work include density functional theory (DFT), time-dependent DFT (TD-DFT), and multiconfigurational second order perturbation theory (CASPT2). We determine the structural parameters as well as the energy splitting of the LS–HS states (ΔE_HL) applying the above methods and comparing their performance. We also determine the potential energy curves representing the ground and low-energy excited singlet, triplet, and quintet d⁶ states along the mode(s) that connect the LS and HS states. The results indicate that while DFT is well suited for the prediction of structural parameters, an accurate multiconfigurational approach is essential for the quantitative determination of ΔE_HL. In addition, a good qualitative agreement is found between the TD-DFT and CASPT2 potential energy curves. Although the TD-DFT results might differ in some respect (in our case, we found a discrepancy at the triplet states), our results suggest that this approach, with due care, is very promising as an alternative for the very expensive CASPT2 method. Finally, the two-dimensional (2D) potential energy surfaces above the plane spanned by the two relevant configuration coordinates in [Fe(terpy)₂]²⁺ were computed at both the DFT and CASPT2 levels. These 2D surfaces indicate that the singlet–triplet and triplet–quintet states are separated along different coordinates, i.e., different vibration modes. Our results confirm that in contrast to the case of complexes with mono- and bidentate ligands, the singlet–quintet transitions in [Fe(terpy)₂]²⁺ cannot be described using a single configuration coordinate.

1. Introduction

Switchable transition metal complexes are well-known candidates for high-density magnetic storage and other molecular devices.¹ Among them, Fe(II) complexes exhibiting spin-state transitions can have a large potential. The thermal spin-crossover (TSCO) in Fe(II) compounds has been extensively investigated with various experimental techniques including Mössbauer spectroscopy,² nuclear inelastic scattering (NIS),³ X-ray diffraction (XRD),^2d,4 magnetization measurements,^2d,4c,5 infrared (IR), Raman,^{3b,3d,5d,5e,6} optical,⁷ X-ray absorption⁸ (XAS), and emission (XES)⁹ spectroscopies; neutron scattering;¹⁰ and even more exotic techniques such as positron annihilation¹¹ or muon spin rotation.¹² During the TSCO in a (quasi)-octahedrally coordinated FeN₆ iron complex with 3d⁶ electron configuration, a low-spin (LS) ground state of the system is converted to a high-spin (HS) excited state, which involves a ΔS = 2 net change in the total electronic spin momentum of the iron(II) ion. The LS state is a singlet (closed subshell), while the HS state corresponds to a quintet state (Figure 1). The LS↔HS transition can be typically described as taking place along a single configuration coordinate: a stretching mode which corresponds to the symmetric elongation of the six Fe–N bonds (the so-called breathing mode). This mode is characterized by the Δr_HL = r_HS – r_LS parameter (where r_LS and r_HS are the equilibrium Fe–N bond lengths in the LS and HS state, respectively), which is typically ca. 0.2 Å for Fe(II) complexes. The elongation of Fe–N bond lengths is a consequence of the fact that two electrons are transferred from the nonbonding t_2g orbitals to the e_g* type antibonding orbitals, which leads to the expansion of the system (see Figure 1). Moreover, the spin-state transition is also characterized by the energy difference, ΔE_HL, between the minima of the lowest singlet and quintet potential wells (ΔE_HL = E_HS – E_LS), which is typically ca. 0–1000 cm^–1 for thermally induced spin-crossover (TSCO) systems. The spin-state transition temperature is known to be proportional to ΔE_HL.¹³

Figure 1.

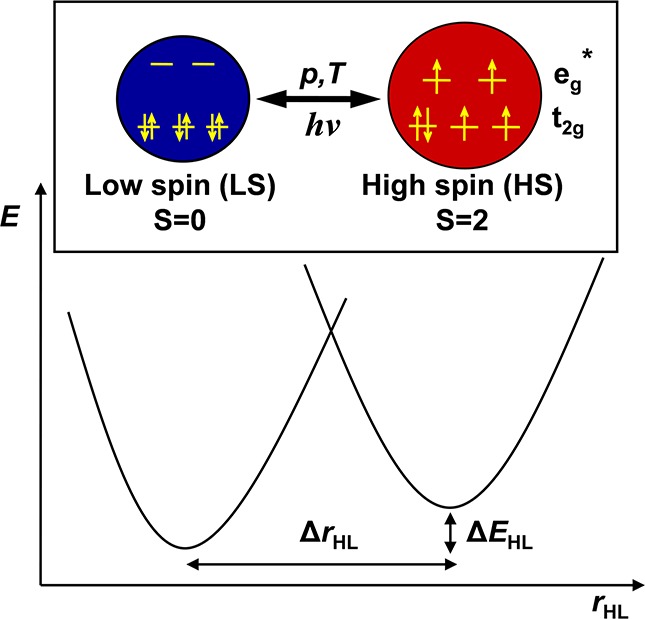
Schematic illustration of the LS↔HS transition in Fe(II) complexes with 3d⁶ electron configuration. The larger (red) circle represents the expansion of the system due to the occupation of two e_g* type antibonding orbitals. The potential energy curves corresponding to the LS and HS states, as well as Δr_HL and ΔE_HL, are also schematically represented.

The LS↔HS transition can be induced in a great number of Fe(II) complexes by varying the temperature or the pressure.^2−12,14 Moreover, it was found for several complexes that the spin-state transition can also occur when irradiating the LS system with light at low temperatures. It has been shown that the structural changes at low temperature photoexcitation were identical to the ones observed for TSCO complexes.¹⁶ The mechanism of this kind of switching was investigated in great detail; the name light-induced excited spin-state trapping (LIESST)^7a,7b coined for the phenomena describes the essence of it. In the LIESST phenomenon, the system is excited with light from the LS ground state to metal-centered (MC) d–d or to metal-to-ligand charge-transfer (MLCT) excited states, which decay to the quintet HS state via intersystem crossings through the participation of triplet states.¹⁷ The lifetime of the excited HS state is mainly determined by ΔE_HL and Δr_HL.^13,18 The mechanism of the switching can be investigated by pump–probe techniques: these are performed more conveniently on iron complexes with large ΔE_HL values (typically ca. 3500–6000 cm^–1), which decay rapidly back to the ground state. The light-switching of Fe complexes has recently been investigated with time-resolved techniques that include optical,¹⁹ IR,²⁰ Raman,¹⁹ XRD,²¹ X-ray absorption,^19c,22 and emission spectroscopies.^22e,23

One of the most studied spin-crossover Fe(II) complex is [Fe(ptz)₆](BF₄)₂ (ptz = 1-n-propyl-tetrazole),^{2c,4c,4d,6c,15} on which the LIESST effect was first observed. Recently, the bidentate iron complex [Fe(bipy)₃]²⁺ (bipy = 2,2′-bipyridine) also got into the focus of research, as the structure of its subnanosecond-lived HS state was characterized by ultrafast X-ray absorption^22b,22e and emission spectroscopies.^22e,23 With [Fe(terpy)₂]²⁺ (terpy = 2,2′:6′,2″-terpyridine), a most striking result was obtained when doped into the matrix of the analogous Mn compound [Mn(terpy)₂](ClO₄)₂: the lifetime of the light-induced excited HS state of this complex is more than 10 orders of magnitude larger than expected from the inverse gap rule.¹⁸ [Fe(terpy)₂]²⁺ is in a LS state at room temperature, which implies a large ΔE_HL, and hence a very fast decay of the light-induced HS state. The exact reason for this unexpected anomalous behavior is still to be revealed.^13b

Modern quantum chemical methods have also been extensively applied to iron complexes in order to investigate spin-state transitions. Such investigations address the accurate determination of structural changes as well as the description of the electronic excited states involved in the LIESST process. Usually, the relatively large size of spin-crossover complexes (at least 40 atoms) and the presence of the central iron atom with open d subshells limit the methods to density functional theory (DFT). Previously, the experimental value of the structural Δr_HL parameter in octahedral Fe(II) complexes was well reproduced with DFT methods.^13,24,25,26c On the other hand, extreme variations were observed for the DFT-calculated energy differences ΔE_HL for various density functionals.^{13,24a,25−30} Although some functionals gave an acceptable estimate to these spin-state energies, none of them showed a universal performance for all studied systems.

Beyond DFT, since high-level correlated methods such as coupled-cluster (CC) and multireference configuration interaction (MRCI) are computationally too demanding, the method of complete active space self-consistent field (CASSCF)/multiconfigurational second order perturbation theory (CASPT2) has been applied in a few cases for medium-sized (ca. 40–60 atoms) iron complexes.³¹⁻³⁵ In addition, the restricted active space self-consistent field (RASSCF)/RASPT2 method was also applied to transition metal complexes, which allows a larger active space suitable for the simultaneous computation of different types of excitations³⁶ (e.g., MC, MLCT and interligand excitations). It has been shown that the CASPT2 method gives reliable estimates for both Δr_HL and ΔE_HL,³¹⁻³⁵ albeit only a few Fe(II) complexes were considered so far. The overstabilization of the HS state by CASPT2 observed in a few cases seems to contradict the previous statement;³⁷ however, the combination of an appropriate active space and basis set can lead to an accurate estimate of spin-state splitting energies. In addition to ΔE_HL and Δr_HL, an accurate description of the excited states involved in the mechanism of the spin-state transitions and in the HS→LS relaxation would also be of high importance. Currently, the time-dependent density functional theory (TD-DFT) and CASPT2 methods are available for the calculation of such excited states. CASPT2 was found to give reliable results for transition metal complexes in several cases,^{17c,32,33,38,39} thus it can be used as a reference method for the estimation of excitation energies. On the other hand, an accurate CASPT2 method suffers from its high computational cost, and from the fact that a very large active space is required for the simultaneous description of MC and MLCT states. TD-DFT methods can be a solution for this problem, although it is well-known that no universal functional exists with the accuracy of the CASPT2 method. Hence, the selection of an appropriate functional for the accurate description of excited states in several Fe(II) compounds would be desirable. Therefore, in the present study we systematically investigate several DFT functionals, as well as the TD-DFT and the CASPT2 methods for the following Fe(II) complexes: [Fe(tz)₆]²⁺ (1) (tz = 1H-tetrazole), [Fe(bipy)₃]²⁺ (2) and [Fe(terpy)₂]²⁺ (3) shown in Figure 2. These compounds are reasonable model systems for the experimentally investigated switchable Fe(II) prototypes.

Figure 2.

3D representation of the studied iron complexes: [Fe(tz)₆]²⁺ (1), [Fe(bipy)₃]²⁺ (2), and [Fe(terpy)₂]²⁺ (3). For 2, we show the notation for N and N* on two neighboring bipy units, whereas for 3, we denote the axial and equatorial N positions of a ligand.

Besides the experimental achievements, computational efforts were also made for systems 1–3. Potential energy curves of 1 and 2 corresponding to the lower energy states were calculated at the CASPT2 level in order to investigate the LIESST mechanism.^17c,32,33 Additionally, the breakdown of the single configuration mode of the LIESST model in [Fe(terpy)₂]²⁺ has been suggested by a DFT study.^13b This means that the breathing mode alone is insufficient for the adequate description of the system: a second coordinate corresponding to a bending mode of the terpyridine rings is also required.

Although all these computational results are of high relevance, a systematic, density functional and multiconfigurational study on the same systems is necessary to gain new insights into the electronic structure as well as to better understand the performance of the available computational methods. Therefore, in this paper we present a comparative theoretical study on the applicability of DFT, TD-DFT, and CASPT2 methods to investigate the fundamental and excited electronic states relevant to spin-crossover. In addition, in the case of 3 we investigate the importance of the departure from the single configuration coordinate model.

In the following section, computational details for DFT, TD-DFT, and CASPT2 calculations are presented. In section 3.1, a brief report is presented on the calculation of structural parameters and spin-state splittings of the investigated complexes (the details are given in the Supporting Information). In section 3.2, the potential energy curves for the excited states of 1–3 are reported. Moreover, the DFT and CASPT2-calculated two-dimensional (2D) potential energy surfaces (PESs) and the ⁵E and ⁵B₂ quintet states of 3 are discussed in section 3.3. Finally, section 4 draws the most important conclusions.

2. Computational Details

2.1. DFT and TD-DFT Computations

DFT calculations were carried out with the ORCA2.8⁴⁰ and ADF2010.02⁴¹ program packages. In the case of ORCA calculations, geometries of the LS and HS states of the studied iron complexes were fully optimized with the gradient-corrected (GGA) exchange-correlation functionals RPBE,⁴² OPBE,⁴³ BP86,⁴⁴ and OLYP,^43b,45a the hybrid functionals B3LYP⁴⁵ and B3LYP*⁴⁶ (B3LYP* is a hybrid functional with 15% exact exchange contribution, while the standard B3LYP functional contains 20%), the meta-GGA functional TPSS,⁴⁷ and the meta-hybrid density functional TPSSh⁴⁷ in combination with the Gauss-type (GTO) TZVP basis set. These functionals have extensively been applied before to switchable Fe(II) complexes for the calculation of structural parameters and spin-state energy splittings.^{13,24a,25−30} ΔE_HL spin-state energies were calculated as E_HS–E_LS, where E_HS and E_LS are the electronic energies of the DFT-optimized structures. Since the computation of vibrational terms at the CASPT2 level of theory is too demanding and one of the main scopes of the present paper is to compare the performance of DFT and CASPT2, we did not consider zero-point energies in the present study. Two-electron integrals were approximated by the resolution of identity (RI) for GGA and by the method of chain of spheres (RIJCOSX) for hybrid exchange-correlation functionals.⁴⁸ Additionally, in all cases the second-order self-consistent field (SOSCF)⁴⁹ approach was followed. For ADF calculations, the BP86, RPBE, and OPBE GGA functionals were used in combination with the Slater-type (STO) TZP basis set. Values of ΔE_HL were calculated as differences of bonding energies with respect to spherical atoms.^27c In the cases of 2 and 3, fractional occupation numbers were applied for the calculation of the ⁵E quintet state. In contrast to ORCA calculations, where no molecular symmetry was applied, in ADF calculations the molecular symmetry groups C_i, D₃, and D_2d were respectively applied for the investigated complexes 1, 2, and 3. Moreover, the C₂ symmetry group was also applied for 2 and 3 in order to investigate the Jahn–Teller effect in the ⁵E HS state.

TD-DFT calculations were performed with the ORCA code. During the computational procedure, the approach of the Tamm-Dancoff approximation (TDA) was followed.⁵⁰ Thirty excited states were calculated with the B3LYP* functional in combination with the TZVP basis set. This functional provided reliable results for ΔE_HL for the studied complexes. In all cases, the lowest-lying MC excited states were selected by careful examination of the corresponding Kohn–Sham molecular orbitals and configurations. In the case of the calculation of the triplet states, two different methods were applied: (a) the TD-DFT procedure was invoked on a triplet reference or (b) on a singlet ground state. For 1 and 2, potential energy curves were evaluated by performing TD-DFT calculations at geometries generated from DFT-optimized structures by varying the Fe–N bond lengths, while for 3, curves were calculated along a combined coordinate of the axial Fe–N distance (r_Fe–Nax) and the NNN angle (φ_NNN), which connects the ¹A₁ and ⁵E minima.

In order to evaluate the 2D PESs of complex 3, geometries were generated from DFT-optimized structures of the ⁵E state reflecting the D_2d point group symmetry by simultaneously varying the r_Fe–Nax bond length and the φ_NNN bond angle, while the rest of the internal coordinates within the terpyridine rings were kept frozen. Then, constrained geometry optimizations were performed at the generated geometries for singlet, triplet, and quintet spin-states in order to include geometry relaxation. In these computations, all internal coordinates were optimized with the exception of r_Fe–Nax and φ_NNN. In all cases, the B3LYP*/TZVP method was applied. The separate computation of the nearly degenerate quintet surfaces could not be achieved, as point group symmetry is not readily available in ORCA. Therefore, both symmetry components of the quintet state were computed on the same relaxed surface.

2.2. CASPT2 Computations

[Fe(terpy)₂]²⁺ was also studied with the CASPT2 method using a reference wave function obtained by the state-averaged (SA) CASSCF method as implemented in the MOLCAS7.6 program package.^51,52 In these computations, the C₂ symmetry constraint was used with the Fe–N_ax bond being the symmetry axis. In the computations, the Douglas–Kroll Hamiltonian was applied to account for scalar relativistic effects.⁵³ In the CASSCF/CASPT2 computations, ANO-RCC basis sets⁵⁴ were used with the following contractions: (7s6p5d4f3g2h) for the Fe, (4s3p1d) for N, (3s2p) for C, and (2s) for H atoms. This basis set contraction was previously found to give accurate energetics for 1 and 2.^32,33 During the CASPT2 procedure, the deep core electrons (Fe [1s²...2p⁶]; C,N [1s²]) were not included in the treatment of electron correlation. Additionally, in the CASSCF calculation, the Fe-3p orbital along the Fe–N_ax bond had to be kept frozen in order to maintain the character of the active orbitals in the whole Fe–N_ax investigated range. In the CASPT2 calculations, the standard IPEA shift of 0.25 au in the zeroth-order Hamiltonian was applied.⁵⁵ In order to exclude possible intruder states, we applied the level shift technique⁵⁶ with a 0.2 au level shift in each CASPT2 computation for 3. Test computations with lower level shifts have shown that excitation energies were converged with respect to the level shift at this value.

The active space for all of the computations consisted of 10 electrons correlated in 12 orbitals. We followed Pierloot's³⁴ strategy by selecting the following active orbitals: the two e_g orbitals with Fe–N bonding character, the three 3d(t_2g) orbitals of Fe, the two e_g orbitals with the antibonding Fe–N character, and an additional set of five 4d orbitals on Fe (see Figure 3). These additional orbitals are required to properly describe the dynamical correlations of the 3d electrons.⁵⁷

Figure 3.

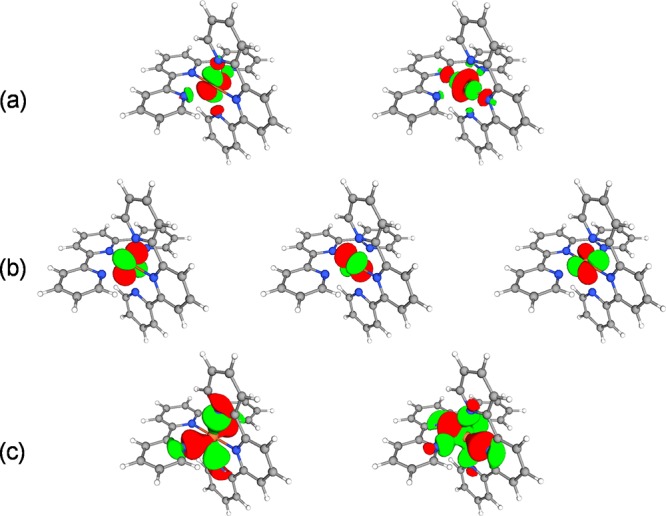
3D representation of the (a) Fe 3d-e_g antibonding, (b) Fe 3d-t_2g nonbonding, and (c) Fe–N 2p-e_g bonding active orbitals applied in the multiconfigurational treatment of [Fe(terpy)₂]²⁺. For simplicity, the additional set of 4d active orbitals (3 t_2g and 2 e_g) is not shown.

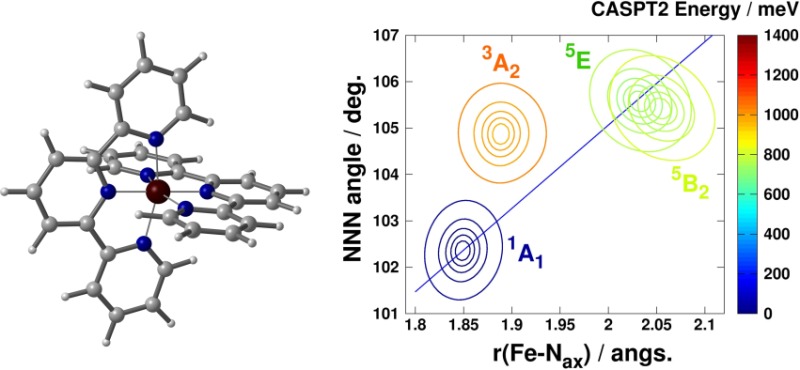
For [Fe(terpy)₂]²⁺, 2D potential energy surfaces were evaluated for the lowest singlet, triplet, and quintet states along the Fe–N_ax bond length and φ_NNN bond angle also by CASPT2. Since geometry optimization for this system at the CASPT2 level is too demanding, a nonrelaxed potential scan was performed using the structural parameters optimized for the ⁵E state by DFT. The value of ΔE_HL was determined by the calculation of CASPT2 energies at the minima of the singlet and quintet states. Potential energy curves were calculated along a combined coordinate of r_Fe–Nax and φ_NNN, similar to the one previously described for DFT calculations.

Energies obtained from separate CASSCF/CASPT2 calculations can only be compared when the active orbitals are indentical in the two separate calculations. The character of the orbitals as outlined above could perfectly be maintained in a state-specific CASSCF treatment of the quintet states of each irreducible representation at all the considered geometries. Unfortunately, this is not the case for the singlet and triplet states. For example, in case of the singlet ground state, the Fe-3d orbitals of quasi e_g character are unoccupied in the dominant electronic configuration of the wave function (a small nonzero occupation number arises by a small admixture of excited determinants to the main t_2g⁶ e_g⁰ determinant). Hence, the correlating orbitals for these e_g orbitals do not necessarily stay in the active space. To solve this issue, we rely on a state averaged CASSCF approach, in which the orbitals are optimized for an average of the four lowest roots in the case of singlet states and for an average of the two lowest roots in the case of triplet states when computing 2D surfaces. The electronic configuration of the excited singlet roots includes occupied t_2g⁵ and e_g¹ orbitals, and therefore the correlating Fe-3d orbitals of e_g character are now easily maintained in the active space. To ensure that the calculated singlet–quintet energy difference is not affected by the slight imbalance of the state-specific treatment of the quintet and the state-average treatment of the other two spin-states, we have generated a quasi state-specific energy at one geometry for the singlet. This was done by gradually increasing the weight of the ground state with respect to the excited states in a three-state average computation. 10:1:1 turned out to be the largest ratio of weights for the ground and the two excited states, respectively, for which the active orbitals still had the desired character. We took the resulting CASPT2 energy as an anchor point for the standard singlet state-average calculations to relate these to the quintet and triplet states. This can be justified by the observation for small model complexes that state average and quasi state specific energies evolve in a nearly parallel manner when the geometry of the complex changes.

For the calculation of excitation energies along the before mentioned combined coordinate, different numbers of roots were applied, corresponding to the states of interest. According to this principle, three, two, two, four, three, and two roots were applied for the singlet A, singlet B, triplet A, triplet B, quintet A, and quintet B states, respectively. We note that although we here use the A and B symmetries of the C₂ point group for the nomination of individual states of 3, the following sections will apply the notations of the D_2d point group. The correspondence between the two different notations is shown in the Supporting Information (SI).

Care had also to be taken in choosing the appropriate threshold for the Cholesky decomposition of the two-electron integrals.⁵⁸ Using the default threshold value (10^–4 E_h) resulted in small irregularities of 1–10 meV in the potentials which disappeared when the threshold was reduced to 10^–6 E_h. While these irregularities are rather small, they make it difficult to exactly locate the minimum of the potentials.

3. Results and Discussion

3.1. Investigation of the Structural Variations and Energetics of the Spin-State Transition in the Studied Fe(II) Complexes

The structural variations during the spin-state transition process often appear as a symmetrical change in the metal–ligand bond length and are usually characterized by the Δr_HL parameter. We investigated various DFT functionals and compared their performance on the estimation of Δr_HL with that of CASPT2 for complexes 1–3. Our results indicate that in general, both DFT and CASPT2 methods are suitable for the accurate estimation of Δr_HL (0.19–0.24 Å and ca. 0.2 Å calculated Δr_HL values were obtained for DFT and CASPT2, respectively, in agreement with experiments). BP86, TPSS, and TPSSh provide accurate results for all Δr_HL, r_LS, and r_HS structural parameters, while the OPBE functional systematically overestimates these parameters, with respect to the experimental value by ca. 0.04–0.09 Å. Moreover, while hybrid density functionals (B3LYP and B3LYP*) and the CASPT2 method give reliable estimates to Δr_HL, they respectively overestimate and underestimate both r_LS and r_HS, compared to the experimental values. The former effect is due to the fact that the inclusion of exact (Hartree–Fock) exchange slightly weakens the Fe–N bond, similarly to the HF method itself,^13a while the latter one is probably due to the presence of basis set superposition error (BSSE).^39,59 While our results show only minor structural differences apart from the elongation of Fe–N bonds in the LS and HS states of 1 and 2, this is not the case for 3. In fact, it has been suggested that the single configuration coordinate model is insufficient to describe the variations for 3, and the spin-state transition must involve also a bending mode of the terpyridine ligand.^13b This mode implies the in-plane displacement of the two side pyridine rings with respect to the middle one, which can be described by the apparent bending of the angle defined by the three N atoms of the ligand.

The spin-state splitting energy ΔE_HL determines the relative stability of the different spin states in transition metal compounds. Besides Δr_HL, ΔE_HL is the most decisive parameter that determines the lifetime of the HS states at low temperatures, where the HS→LS relaxation can only proceed through tunneling.¹³ For systems exhibiting TSCO, the splitting energy can be approximated as ΔE_HL ∼ k_BT_1/2. (T_1/2 is the temperature at which half of the complexes are converted to the HS state.) From this relation, for ΔE_HL we expect a few hundred cm^–1 for compounds exhibiting thermal spin-crossover, and a few thousand cm^–1 for the low-spin ones. The CASPT2-estimated values of ΔE_HL for the investigated complexes (220, 4617, and 5888 cm^–1 for complexes 1–3, respectively^32,33) are in excellent agreement with the experimental observations that derivatives of 1 undergo thermal spin-crossover at around 100–200 K, while 2 and 3 remain in the LS state at all temperatures and therefore can be only converted to the HS state by excitation with light. These results suggest that in principle, this multiconfigurational methodology could be widely applied to spin-crossover complexes, although it suffers from the laborious selection of the active space for every individual case and from its high computational cost. In fortunate cases, these problems can be avoided by the application of an appropriate density functional; therefore, we investigated the best-performing density functionals for the estimation of spin-state energy splittings in the studied systems. Our results indicate that the B3LYP* functional provides reasonable results for all of the studied Fe(II) complexes (189, 3076, and 3447 cm^–1 ΔE_HL values were obtained for complexes 1–3, respectively), which was also obtained previously for several transition metal complexes.^13,26b,60,61 However, we note that this method predicted the HS as a ground state for Fe(phen)₂(NCS)₂ (phen = 1,10-phenanthroline).^24a OPBE gives an excellent agreement with CASPT2 results for 2 and 3 but fails to predict the LS ground state for 1. Furthermore, while pure exchange-correlation functionals such as BP86 and TPSS give clearly too large ΔE_HL values, the meta-hybrid TPSSh method provides acceptable results. Therefore, it is clear from all these results that although DFT methods are readily available for the calculation of LS–HS state splittings, no universal functional exists with an accuracy comparable to the quantitative precision of the CASPT2 method. However, the overall performance of the B3LYP* method is rather good for 1–3; hence, we selected this functional for testing the TD-DFT approach in calculating the excited state spectra of these compounds.

Finally, we note that in the degenerate HS states of 2 and 3, the Jahn–Teller (JT) effect is operative; thus the DFT-computed structures are slightly distorted from the full D₃ and D_2d point group symmetries, respectively. These distortions imply changes of 0.01–0.02 Å in the Fe–N bond lengths and ca. 4° in the N–Fe–N* bending angle for complex 2 (where N and N* are the N atoms of two neighboring bipy units, see Figure 2) and 4° twisting of the planes of the terpyridine rings for complex 3. Moreover, these structural changes are accompanied by 0.08–0.11 eV energy lowering of the ⁵E state calculated at the DFT level of theory (for details, see section 3.3 and Table S5 in the SI). In the case of 2, this lowering has a considerable effect on ΔE_HL. On the other hand, for 3 the energy lowering of the ⁵E state does not imply a relevant reduction of the spin-splitting energy, since the JT effect shifts the ⁵E barely below the ⁵B₂; thus ΔE_HL remains almost the same, as discussed later in section 3.3. Note that the B3LYP* potentials and PESs presented in the following sections were calculated without the application of symmetry (with the ORCA code); therefore the JT effect was taken into account. We also estimated the JT lowering of the ⁵E energy by CASPT2, based on geometries optimized by DFT with higher (D₃ or D_2d) and lower (C₂) symmetries. For 2, in agreement with the DFT results, 0.10 eV lowering was obtained, while for 3, negligible energy differences were observed (see section 3.3). This is in agreement with the fact that the FeN₆ core in the corresponding DFT-optimized ⁵E HS structures is more distorted from the higher symmetries for 2 than for 3.

3.2. Potential Energy Curves Representing the Metal-Centered (MC) Excited States for 1–3

The detailed knowledge of MC excited states is essential for the understanding of spin-state transitions. At equilibrium positions, some of the d–d transitions can be measured by optical absorption spectroscopy, although in general they are suppressed by symmetry as expressed in the selection rules. Therefore, it is necessary to obtain accurate estimations for the d–d excitation energies, as the excited state potentials are supposed to play an important role in the mechanism of spin-state transitions. The spin-state transition process was recently investigated for a few Fe(II) complexes (including 1 and 2) by the calculation of potential energy curves connecting the different excited states at the CASPT2 level, which proved to be a suitable method for the description of MC excited states, despite its high computational cost.^32,33,39 The performance of TD-DFT in the prediction of PESs has not yet been reported; only vertical excitation energies were computed for the photoswitchable complexes 2 and 3, and also for [Fe(2-picolylamine)₃]²⁺.⁶² We made an effort to explore the energy of the excited states of the studied complexes, as a function of the coordinate(s) relevant to the spin-state transition with TD-DFT. For this, we have selected the B3LYP* functional, which gave reliable results for the energetics of 1–3. Below, we compare the performance of the TD-B3LYP* and CASPT2 methods for the studied Fe(II) complexes.

TD-B3LYP* potential energy curves for 1 and 2 calculated along the Fe–N breathing mode are presented in Figure 4. All TD-B3LYP* calculated curves are in good qualitative agreement with the previously published CASPT2 PESs.^32,33,63 Additionally, these TD-DFT potentials for 1 even show a good quantitative agreement compared to results obtained by the CASPT2 method,³² as seen in the comparison of B3LYP* and CASPT2-calculated values of ΔE_HL presented in section 3.1. The maximum deviations in the relative positions of crossing points and in the minimum energies from the corresponding CASPT2 values are 0.05 Å and 0.14 eV, respectively. We also note that the TD-B3LYP* calculated vertical excitation energies at equilibrium positions only show 0.1–0.2 eV deviations from experimental values^7b and also agree with CASPT2-calculated values³² (see Table 1). All TD-DFT curves are shifted by 0.08 Å toward larger Fe–N bond lengths, compared to the CASPT2 results. In the case of complex 2, the crossing points are reproduced up to 0.08 Å, while the energy values corresponding to the minima of the individual states are underestimated by 0.15–0.30 eV, compared to CASPT2 values (for details, see the SI). Thus, the performance of this hybrid TD-DFT method is acceptable also for 2, since it reproduces all crossing points of the individual states for both iron complexes with reasonable accuracy.

Figure 4.

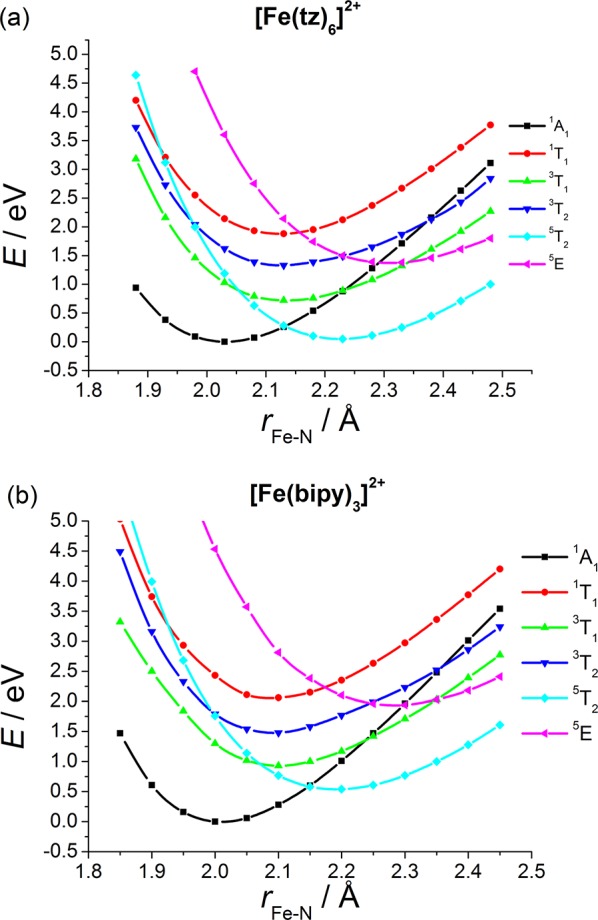
TD-B3LYP*/TZVP calculated potential energy curves for (a) [Fe(tz)₆]²⁺ (1) and (b) [Fe(bipy)₃]²⁺ (2). The zero value of the energy scale is set to the minimum of the ¹A₁ potential. The ³T₁ state was computed by a triplet SCF calculation, while the ³T₂ state was calculated with the TD-DFT method, using the ³T₁ reference state, as described in the text. This figure is to be compared with Figure 3 in ref (32) and Figure 3 in ref (33).

Table 1. Comparison of Experimental, CASPT2, and TD-B3LYP* Calculated Values of Vertical Excitation Energies at Equilibrium Positions for 1 (Values Are Given in eV).

transition	exptl.a	CASPT2b	TD-B3LYP*c
1A1→1T1	2.26	2.17	2.15
5T2→5E	1.51	1.57	1.45
1A1→3T1	1.28	1.19	1.05 (1.39)d
1A1→3T2	1.77	1.77	1.65 (1.65)d

^aFrom ref (7b).

^bFrom ref (32).

^cThis work.

^dFor the triplet transitions, the first TD-B3LYP* value was obtained with a triplet reference, while values given in parentheses were calculated applying a singlet reference state.

Despite the rather good description of most of the excited states, complications arose for the calculation of the triplet states with TD-DFT. The lowest-lying triplet states of 1 and 2 presented in Figure 4 were computed using a triplet reference state, as described in the Computational Details section. These TD-B3LYP* curves are in good agreement with the reported CASPT2 results for 1,³² although the ¹A₁→³T₁ excitation energy computed at the LS minimum shows a 0.23 eV deviation from the experimental value. Note that in TD-DFT calculations of optical spectra of transition metal compounds, triplet states are not computed from a triplet reference state but from a singlet reference determinant.⁶⁴ We compare the results obtained by these two TD-DFT methods applying a singlet or triplet reference for the calculation of triplet states for 1 in Figure 5. When employing a singlet reference, the excitation energies at the ¹A₁ minimum are well reproduced (see Table 1), but the positions of the ¹A₁/³T₁ and ¹A₁/³T₂ crossing points relative to the LS equilibrium position do not agree with the CASPT2 results (see the SI). On the other hand, with a triplet reference state the correct number of states is not reproduced (see Figure 5). While both CASPT2-calculated triplet states, ³T₁ and ³T₂, show the approximate 3-fold degeneracy,³² provided that at least six roots are included in the calculation, the TD-DFT procedure applying a triplet reference state describes the ³T₁ state only with a single determinant, so no more than four of the six states are accessible. This is obviously not the case for the calculation invoked on the singlet reference state, for which all the six triplet states are obtained. The above difficulties do not concern the singlet and quintet states. While all calculated singlet and quintet states can be generated with a single excitation from the corresponding ground states, this is not the case for the triplet states: certain triplet states could only be derived by a double excitation from the lowest-lying triplet state (note the two missing configurations in Figure 5b).

Figure 5.

TD-B3LYP*/TZVP calculated triplet states for 1 when invoking the corresponding excitations on a (a) singlet and (b) triplet reference state. The electron configurations corresponding to the individual triplet states are schematically represented in an octahedral ligand field (note that for the sake of simplicity in the case of b we do not show spin-polarized energy levels). For a better contrast, the ¹A₁ ground state potential is also shown. The zero value of the energy scale is set to the minimum of the ¹A₁ potential.

Finally, we discuss the results obtained for the MC excited states of [Fe(terpy)₂]²⁺. As previously shown, the structural variations at the spin-state transition in this iron complex cannot be described using the breathing mode alone; the inclusion of the bending mode of the terpyridine ligands—identified by the φ_NNN angle—is also necessary. As a consequence, PESs for 3 should be calculated above the plane spanned by the r_Fe–Nax and φ_NNN coordinates. Such surfaces for the lowest singlet, triplet, and quintet states will be presented in the next section. However, comparing the numerous sets of MC excited states along the single dimension that connects the LS and HS minima is particularly useful. Therefore, we evaluated the potential energies for 3 along this line, in order to get comparable results to those of 1 and 2. TD-DFT and CASPT2-calculated curves are presented in Figure 6. A reasonably good agreement is observed between TD-B3LYP* and CASPT2-computed curves, although—similarly to the case of 2—larger differences were found in the TD-DFT computed relative energies of the individual states compared to CASPT2 values, than for 1. Also, it is clear from Figure 6 that the calculated number of MC triplet states differs for the two methods, similarly to the case of 1. In fact, this effect is more apparent for 3 due to the strong axial distortion of the FeN₆ core. This results in a more relevant splitting of the triplet states, which could not be properly described by the applied TD-DFT approach. Nevertheless, the singlet, quintet, and even the lowest-lying ³A₂ triplet states for 3 are qualitatively well reproduced by the TD-B3LYP* method. Therefore, we conclude that with due care the TD-B3LYP* method is a promising and very economic alternative to multiconfigurational approaches for the calculation of the energetics of a spin-state transition system.

Figure 6.

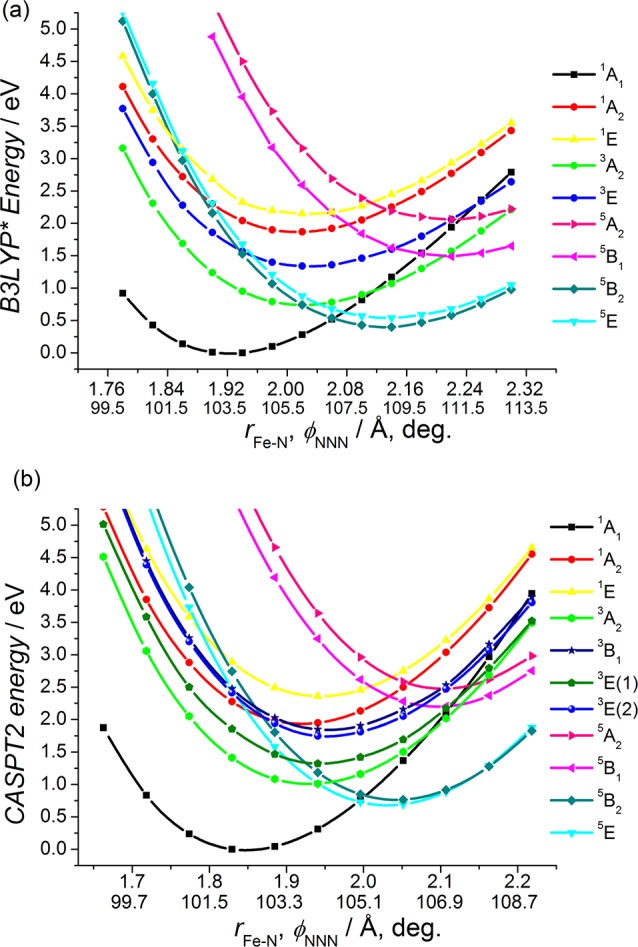
(a) TD-B3LYP* and (b) CASPT2-calculated PESs for [Fe(terpy)₂]²⁺ (3) along a combined coordinate, which connects the LS and HS minima. (In the case of a, the triplet states were computed using a triplet reference state.) The notation for each calculated state refers to the D_2d point group symmetry. The zero value of the energy scale is set to the minimum of the ¹A₁ potential.

3.3. 2D Potential Energy Surfaces for the Lowest Singlet, Triplet, and Quintet States of [Fe(terpy)₂]²⁺

As noted previously, the spin-state transition in 3 cannot be described along a single configuration coordinate based on the variation of the Fe–N bond lengths: the inclusion of the bending of the ligands is also required, i.e., the variation of the bite angle of the N donor atoms of the tridentate terpyridine ligand, which can be characterized by the NNN angle of the three pyridine rings (φ_NNN). Therefore, we computed the PESs above the plane spanned by r_Fe–Nax and φ_NNN for the lowest singlet, triplet, and quintet electronic states with the CASPT2 and B3LYP* methods, which are shown in Figure 7. For DFT, a relaxed surface, whereas for CASPT2, a nonrelaxed PES was computed, because geometry optimizations are computationally too demanding for this latter method. As seen in the figure, the description of the LS↔HS state transition indeed requires both the r_Fe–Nax and φ_NNN modes. It is interesting to note that reaching the triplet state takes place to a good approximation along only one of these modes: via opening the NNN angle when arriving from the singlet state, or via the bond length shortening from the quintet state. It holds for both the DFT and CASPT2 PESs that while the calculated values of the NNN angle for the triplet and quintet states are fairly similar, the axial Fe–N distances of the triplet state show resemblance to that of the singlet state. In contrast, DFT-optimized values of the Fe–N bond lengths for the triplet state of 1 and 2 show ca. 0.1 Å change from both the LS and HS states (for details, see SI). As triplet states are considered to be involved in the switching and relaxation processes, this effect could lead to a difference in the mechanism of the spin-state transition for 3, compared to 1 and 2, in addition to the breakdown of the single configuration coordinate model.

Figure 7.

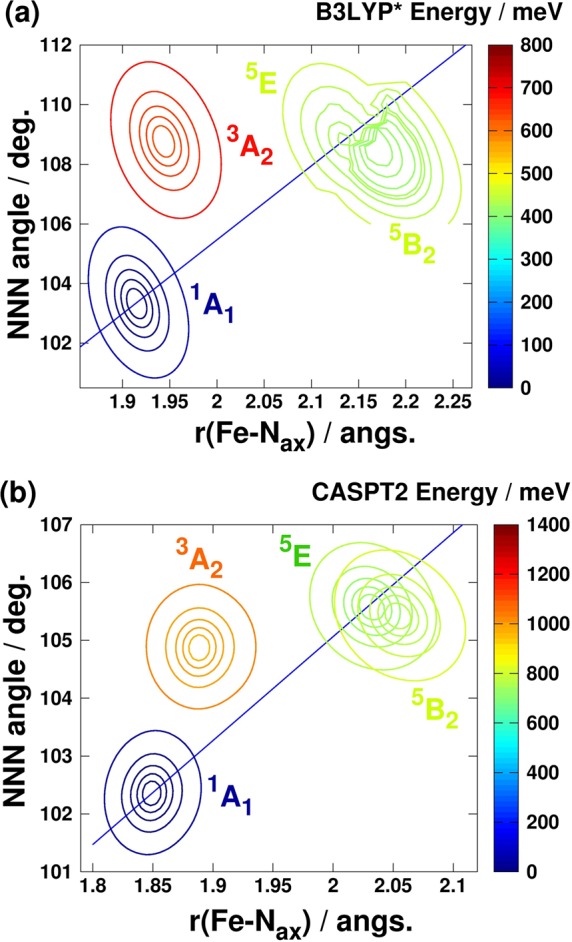
(a) B3LYP* and (b) CASPT2-calculated PESs for the lowest-lying singlet, triplet, and quintet states. The zero value of the energy scale is set to the minimum of the ¹A₁ surface. The blue lines represent the combined coordinates for the calculation of 1D potentials. CASPT2 and DFT-calculated energies were splined with a 2D cubic interpolation routine. Contour lines were drawn at the 2, 5, 10, 20, and 50 meV energy values from the minimum of the corresponding PES.

Finally, we focus on the lowest-lying quintet states of [Fe(terpy)₂]²⁺, whose properties are decisive for the most relevant characteristics of the molecular switching. Lowering the symmetry to D_2d splits the ⁵T₂ (O_h) state into the ⁵B₂ and ⁵E quintet states in 3. We investigated the structural and energy differences of these two states and found that both the DFT and the CASPT2 results indicate quite small differences in the r_Fe–Nax and φ_NNN values between the minima of the two quintet states: 0.04–0.05 Å and 0.02 Å difference in the axial Fe–N bond length for the B3LYP* and CASPT2 method, respectively. Moreover, while 0.5° of difference is seen in the B3LYP*-calculated φ_NNN value between the two quintet minima, only 0.2° of variation is predicted by the CASPT2 method. We have also evaluated the relative stability of the ⁵E and ⁵B₂ states by optimizing the corresponding HS structures with various density functionals and compared them to the CASPT2 result. As shown in Table 2, all methods suggest that these states are energetically quasi-degenerate, although the sign of the relative energies varies. While pure functionals and CASPT2 favors the ⁵E state, hybrid functionals stabilize the ⁵B₂ HS state. Moreover, GGA functionals combined with the STO-TZP basis set using the D_2d point group symmetry predict a higher energy difference, clearly overstabilizing the ⁵B₂ state compared to the CASPT2 result. This large stability of the ⁵B₂ state over the ⁵E one at D_2d symmetry has also been reported in a previous study.^13b However, GGA methods with C₂ or without a symmetry constraint lower the energy of the ⁵E state resulting in energy differences similar to those obtained with the GTO-TZVP basis set (see Table 2). It is important to note that this ca. 0.1 eV energy lowering is accompanied by a slight twisting (ca. 4 degrees) of the planes of the terpyridine rings, which is due to the Jahn–Teller effect. On the other hand, the twisting of the ligand planes by 0.4° lowers the CASPT2 energy of the ⁵E state only by 11 cm^–1 (larger distortions elevate the energy of the ⁵E state; e.g., ca. 6 and 550 cm^–1 energy differences are observed for 1 and 4° of twisting, respectively).

Table 2. DFT and CASPT2-Calculated ΔE = E_5B2 – E_5E Energy Differences for the HS States of 3.

method	ΔE/cm–1
ORCA (GTO basis)
RPBE/TZVP	47
OPBE/TZVP	140
OLYP/TZVP	14
BP86/TZVP	205
TPSS/TZVP	61
B3LYP/TZVP	–198
B3LYP*/TZVP	–110
TPSSh/TZVP	–80
ADFa (STO basis) with symmetry D2d; C2; –
RPBE/TZP	–964;b −55; −54
OPBE/TZP	–708; 59; 60
BP86/TZP	–677; 92; 99
MOLCAS (ANO-RCC basis)
CASPT2	329; 340c

^aIn the case of ADF results, the first two values were obtained using the D_2d and C₂ point group symmetries, respectively, while the last value was calculated without the application of symmetry.

^bFrom ref (13b).

^cThe CASPT2 values were calculated on a symmetric, D_2d geometry and on a slightly distorted structure (where the ligand planes were twisted by ca. 0.4 degrees), respectively. DFT values were computed by optimizing the quintet structures of 3, while CASPT2 values were determined from the corresponding PESs.

The CASPT2 results thus indicate the relative stability of the ⁵E state over the ⁵B₂ quintet state for 3. The lifetime of the quintet state is mainly determined by the Δr_HL and ΔE_HL values in most spin-transition complexes. In the case of the ⁵E state, the DFT-calculated Δr_HL(Fe–N_ax) value is 0.21–0.23 Å, which is close to 0.20 Å, the typical value for Fe(II) SCO compounds. On the other hand, the variation of this bond length for the ⁵B₂ state is 0.25–0.29 Å, thus showing a larger deviation from 0.20 Å. These larger structural variations could slow down the relaxation at low temperatures by increasing the barrier between the LS and HS states.^13b However, this alone is unlikely to account for the extremely high lifetimes of the HS state for [Fe(terpy)₂]²⁺ observed in loose matrices;^13b,18 moreover, we identified ⁵E as the lower-lying component of the HS state by CASPT2. In terms of the single configuration coordinate model, the energetics would indicate a shorter lifetime for 3 through the inverse energy gap law,^13b as all density functionals predict slightly larger values for the LS–HS state splitting energies for 3 than for 2. Furthermore, the comparison of the 4617 cm^–1 CASPT2 ΔE_HL value for 2 with the 5888 cm^–1 value for 3 also supports this statement. Therefore, this straightforward approach is not applicable for 3, as it was also proposed by Hauser et al.^13b A more appropriate configuration coordinate for 3 is made up by the combination of the breathing mode and the bending mode of the ligands. This two-mode model can account for the longer lifetime of the light-excited quintet states for 3 when compared to 2 in solution under ambient conditions. These results are in good agreement with experiments, which indicate the somewhat higher lifetime for the excited HS state of [Fe(terpy)₂]²⁺ (2.5 ns) than for that of [Fe(bipy)₃]²⁺ (665 ps) in aqueous solutions.^22b,65 It can be thus concluded that the light-induced spin-state transitions in 2 and 3 in solutions are relatively well-understood, but the reason for the extremely high lifetimes of the HS state of [Fe(terpy)₂]²⁺ observed in solid state measurements still remains unknown.

4. Conclusion

DFT, TD-DFT, and CASPT2 calculations were carried out to investigate the electronic structure of Fe(II) coordination compounds at LS↔HS state transitions. Our results indicate that the BP86, TPSS, and TPSSh functionals are the best suited for the description of the structural parameters that concern the coordinate bonds, although hybrid B3LYP and B3LYP* density functional methods give also accurate estimates for the relevant Δr_HL parameter. Hybrid functionals tend to slightly overestimate the Fe–N bond length, with respect to the experimental values, which is attributed to the exact exchange included in these density functional methods. In contrast, the CASPT2 method underestimates these bond lengths, probably due to the basis set superposition error; however, this technique also provides a good estimate for Δr_HL. The ΔE_HL spin-state splitting energy for all studied complexes was also computed with various density functionals and for [Fe(terpy)₂]²⁺ also with the CASPT2 method. The OPBE, B3LYP*, and TPSSh functionals provided reasonable results, even if the quantitative precision of the CASPT2 method could not be reached. Nevertheless, the B3LYP* functional gave rather reliable estimates for the spin-state splitting energies of all Fe(II) complexes investigated in this paper. We pointed out that the JT effect has to be taken into account for the ⁵E states of 2 and 3, since it lowers their energy by ca. 0.1 eV, as calculated at the DFT level of theory. A similar JT lowering value was obtained with the CASPT2 method for 2; however, for 3 only a very small effect was observed.

Potential energy surfaces corresponding to metal-centered states of 1–3 were investigated with the TD-DFT and CASPT2 methods, and it was found that the CASPT2-calculated potential energy curves could be well-reproduced by the TD-B3LYP* method for all complexes 1–3. In the case of 1, the agreement of TD-DFT and CASPT2 relative energies was particularly excellent. However, the TD-DFT procedure using the triplet reference state could not reproduce the correct number of triplet states. We reported that this problem can be avoided by starting the triplet TD-DFT calculation from a singlet reference determinant; however, the calculation for certain triplet states is less accurate, in such cases. The results suggest that the TD-B3LYP* method can be an acceptable and economic alternative to multiconfigurational approaches for the calculation of MC excited states in Fe(II) complexes, although care should be taken to verify the results for all spin-states. Furthermore, efforts will be made to assess the performance of this approach concerning the relevant MLCT states.

Finally, the two-dimensional PESs for the lowest-lying singlet, triplet, and quintet states of 3 were evaluated along the r_Fe–Nax and φ_NNN configuration coordinates with both DFT and CASPT2 methods to contribute to the better understanding of the spin-state transition and relaxation processes. DFT and CASPT2-calculated energy surfaces of 3 revealed that the minimum of the ³A₂ state lies far out from the line connecting the LS and HS states: only φ_NNN shows significant changes when going from the lowest-lying singlet to the triplet state. In contrast, a transition between the triplet and quintet states does not change this angle, but it requires a large variation of r_Fe–Nax. Mapping out the arrangement of these PESs can be a valuable contribution for a detailed discussion of the mechanism of the transitions in [Fe(terpy)₂]²⁺. Furthermore, our CASPT2 results indicate that the ⁵E HS state is energetically more favorable than the ⁵B₂ one by 340 cm^–1. Both experimental and computational results suggest that while the longer lifetime of the HS state of 3, compared to that of 2 under ambient conditions, can be attributed to the breakdown of the single configuration mode model, its anomalous behavior at low temperatures requires a more elaborate explanation.

Supporting Information Available

The details of the calculation of structural and energetic parameters for the studied complexes, the correspondence between the notations of the C₂ and D_2d point group for the different electronic states of 3, DFT-optimized values of the Fe–N bond length for the ³T₁ state of 1 and 2, and the comparison of TD-B3LYP* and CASPT2-calculated crossing points and minimum energies for the lowest-lying singlet, triplet, and quintet d⁶ states of 1 and 2. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.