On Predicting Mössbauer Parameters of Iron-Containing Molecules with Density-Functional Theory

Abstract

The performance of six frequently used density functional theory (DFT) methods (RPBE, OLYP, TPSS, B3LYP, B3LYP*, and TPSSh) in the prediction of Mössbauer isomer shifts(δ) and quadrupole splittings (ΔE_Q) is studied for an extended and diverse set of Fe complexes. In addition to the influence of the applied density functional and the type of the basis set, the effect of the environment of the molecule, approximated with the conducting-like screening solvation model (COSMO) on the computed Mössbauer parameters, is also investigated. For the isomer shifts the COSMO-B3LYP method is found to provide accurate δ values for all 66 investigated complexes, with a mean absolute error (MAE) of 0.05 mm s^–1 and a maximum deviation of 0.12 mm s^–1. Obtaining accurate ΔE_Q values presents a bigger challenge; however, with the selection of an appropriate DFT method, a reasonable agreement can be achieved between experiment and theory. Identifying the various chemical classes of compounds that need different treatment allowed us to construct a recipe for ΔE_Q calculations; the application of this approach yields a MAE of 0.12 mm s^–1 (7% error) and a maximum deviation of 0.55 mm s^–1 (17% error). This accuracy should be sufficient for most chemical problems that concern Fe complexes. Furthermore, the reliability of the DFT approach is verified by extending the investigation to chemically relevant case studies which include geometric isomerism, phase transitions induced by variations of the electronic structure (e.g., spin crossover and inversion of the orbital ground state), and the description of electronically degenerate triplet and quintet states. Finally, the immense and often unexploited potential of utilizing the sign of the ΔE_Q in characterizing distortions or in identifying the appropriate electronic state at the assignment of the spectral lines is also shown.

1. Introduction

Mössbauer spectroscopy¹⁻⁴ (MS, and its synchrotron derivatives^5,6) is a very powerful experimental tool in different fields of chemistry, material science, and physics, as this technique can obtain invaluable information on the local electronic structure, symmetry, and magnetic properties. Although it can be applied to more than 40 kinds of nuclide, the properties of ⁵⁷Fe are by far the best suited for MS. Therefore, most experiments focus on the measurement of iron, which is an element that has a special importance due to its wide occurrence and utilization. Since the demonstration of the Mössbauer-effect,¹ thousands of iron-bearing systems have been investigated including simple inorganic salts,^2,7,8 complexes with chelating ligands,^2−4,7,9 organoiron^2,3,7 and intermetallic^2,7 compounds, alloys,^2,7 magnetic thin films,¹⁰ multilayers,¹¹ biologically important heme- and metalloproteins,^2,7,9 and so on.

The interpretation of Mössbauer spectra is not straightforward, and the support of theory is essential for extracting all the relevant physical/chemical information from the measured data. A good agreement between experiment and theory can lead to a suitable method to understand and predict spectroscopic properties. State-of-the-art quantum chemical methods have been applied to calculate spectroscopic parameters for decades. The highest-level wave function-based correlated methods, such as coupled-cluster (CC) theory, can give a very accurate description of the electronic structure.¹² However, present computational resources strongly limit these methods to molecules made up of 10–20 atoms; hence they are hardly applicable to iron complexes. Density functional theory (DFT) can provide acceptable results at less cost; however, it utilizes approximate exchange-correlation functionals which can lead to contradictory results. A careful exploration of the application of the functionals to the studied problem is, therefore, crucial to the successful application of DFT. Nevertheless, this approach has been successfully used for the calculation of ⁵⁷Fe Mössbauer parameters by several research groups.

The literature of these calculations is substantial; in what follows we list a few relevant works from the last 15 years. First of all, band structure DFT calculations has been successful to compute the ⁵⁷Fe Mössbauer parameters in solids;¹³ however, the main scope of the present study is to describe molecular systems. E. Oldfield et al. calculated the isomer shifts and quadrupole splittings of numerous iron-containing compounds including organometallic molecules,¹⁴ protein model systems,¹⁴⁻¹⁷ and two- and three-coordinated¹⁸ Fe(II) and spin-crossover complexes.¹⁹ Several researchers including L. Noodleman and co-workers applied DFT to compute the Mössbauer properties of the active and intermediate sites of biologically important proteins.²⁰⁻²² The Mössbauer spectral properties of high-valent Fe complexes were also computed with DFT.²³⁻²⁷ In all these previous efforts a good overall performance of DFT methods was achieved in the estimation of the Mössbauer parameters, even when different selected classes of iron complexes were considered.^21c,28−32 In particular, important achievements were reported by R. Friesner et al., who investigated the influence of the applied density functionals and geometries on the computed Mössbauer parameters for a large set of Fe complexes.³¹ However, in this and also in several other works, DFT failed for certain systems, leading to large deviations from the experimental values, particularly for the quadrupole splitting parameter.^{18,28a,30b,31,33,34} Furthermore, it is not yet clear which computational method (i.e., density functional, basis set, inclusion of solvent effects, etc.) is to be applied in case of an arbitrarily selected Fe complex. With the present work, we aim to address these issues by investigating the applicability of various density functional techniques to a very extended and diverse set of iron complexes. We also test the performance of the DFT approach in some chemically relevant issues (isomerism, transformations, etc.). Our motivation is to provide benchmarks, as well as a recipe for predictive calculations, and show how problematic cases can be recognized and treated.

The present paper is organized as follows. Section 2 describes the details of the applied DFT calculations. In section 3.1, we present the studied set of Fe complexes, as well as their main electronic structure-related and experimental Mössbauer parameters. Section 3.2 describes the origin of the isomer shift (δ) and quadrupole splitting (ΔE_Q) parameters. Sections 3.3 and 3.4 report the results obtained for δ and ΔE_Q, respectively. In section 3.5 we present the case studies of geometric (cis-trans) isomerism, phase transitions (spin-crossover and inversion of the orbital ground state), and the prediction of the sign of quadrupole splittings of Fe complexes. Also, we discuss the problematic cases of electronically degenerate triplet and quintet states. Finally, the most important conclusions are summarized in section 4. The tabulated computational results and further details of the work are given in the Supporting Information (SI).

2. Computational Details

The ORCA2.8 program package³⁵ is a suitable software for the geometry optimizations and the calculation of isomer shifts and quadrupole splittings of the investigated iron compounds. The program uses Gauss-type atomic orbitals (GTOs) for the construction of molecular orbitals. In order to study the influence of the type of the primitive basis set (GTOs or Slater-type orbitals, STOs) on the computed Mössbauer parameters as well as to treat the electronically degenerate states of certain special Fe(II) complexes, we also utilized the ADF2012.01 code.³⁶

2.1. ORCA Calculations

The geometries of all investigated Fe complexes were fully optimized at the BP86³⁷/TZVP level of theory. This method provided reliable structures for previously studied transition metal compounds.³⁸ The electron density and the electric field gradient (EFG) tensor at the ⁵⁷Fe nucleus were computed with the gradient-corrected (GGA) exchange-correlation functionals RPBE³⁹ and OLYP,⁴⁰ the hybrid functionals B3LYP^40b,41 and B3LYP*⁴² (with 15% amount of exact exchange), the meta-GGA functional TPSS,⁴³ and the meta-hybrid density functional TPSSh⁴³ at the BP86-optimized geometries. These functionals have been frequently used before to calculate Mössbauer parameters¹⁴⁻³⁴ and/or other important properties (e.g., spin-state energy splittings^38d,44) of iron complexes. Note that DFT-optimized geometries, which are good approximations to the experimental structure, have been successfully applied previously in the accurate computation of Mössbauer parameters using different density functionals.^{14,29,30b,30c,31} The computed electron densities and EFGs were used to evaluate the isomers shifts and quadrupole splittings, as described in sections 3.3 and 3.4, respectively. We also mention that counterions and solvent molecules were not included in the calculations, as previous results suggest that they have only a minor effect on these quantities.^18,31 Since calculations utilizing regular GTO basis functions for Fe would surely fail,^30c for the accurate description of the electron density and the EFG at the ⁵⁷Fe nucleus we used the core-polarized CP(PPP)³⁰ basis function for the iron atom. For the other atoms the TZVP basis set was used; nevertheless for the sake of simplicity, this combined basis will be referred to as CP(PPP). Relativistic effects were not included in the computations, since it was shown that they do not improve the quality of the computed Mössbauer parameters.^30b The integral accuracy parameter was increased to 7.0 at the Fe center in order to provide more accurate core properties. Two-electron integrals were approximated by the resolution of identity (RI) for GGA and by the method of chain of spheres (RIJCOSX) for hybrid exchange-correlation functionals.⁴⁵ Since the calculation of Mössbauer properties in gas phase might be far from realistic, the geometry optimizations and the calculation of Mössbauer parameters were repeated by approximating the solid-state effects of the molecular environment with the conducting-like screening model⁴⁶ (COSMO) with a dielectric constant for methanol (ε = 32.7). This is of course arbitrary, but – probably due to the intermediate dielectric constant of methanol – it is a frequent choice for modeling the effect of the molecular environment in the condensed phase.^21c,28

2.2. ADF Calculations

The electron densities and EFGs were also computed with the functionals introduced above in combination with the Slater-type (STO) TZP all-electron basis set at the BP86-optimized geometries. The calculations were also repeated with the application of the COSMO model. We note that while ORCA computes the electron density directly at the ⁵⁷Fe nucleus, ADF evaluates this property on a small sphere; however, this barely affects the calculated isomer shifts, as was shown in ref (28b). For the case studies described in section 3.5 we retain the best-performing functionals only: the COSMO-TPSSh method for the investigation of low-spin octahedral Fe(II) cis-trans isomers and the B3LYP functional for the study of electronically degenerate triplet/quintet states, spin-crossover complexes, and orbital singlet and doublet states of Fe(II) compounds. We mention that in the case of these B3LYP computations, we assessed the triplet states of Fe(TPP) and the quintet states of [Fe(DTSQ)₂]^2–, [Fe(H₂O)₆]²⁺, and [Fe(DCTU)₆]²⁺ (for the abbreviations, see Table 1) by imposing the corresponding occupations of the Fe-3d orbitals within the D_2h, D_2d, and D_3d point group symmetries, respectively. Additionally, for [Fe(DCTU)₆]²⁺ we substituted the large cyclohexyl groups with methyls, in order to reduce computational cost. For the evaluation of the sign of the EFG we selected the COSMO-TPSSh method, which was identified as one of the best-performing methods for the calculation of quadrupole splittings over the whole investigated data set. All these computations were also carried out at the BP86-optimized geometries, with the application of the STO-TZP basis set.

Table 1. Iron Complexes Investigated in the Present Study.

entry	system	symm.a	Fe ox.b	Sc	T/K	δ/mm s–1d	δ4.2K/mm s–1d	ΔEQ/mm s–1e	ref
1	Fe(phen)2(NCS)2 (LS)	C2	2	0	77	0.34	0.37	0.34	(48)
2	Fe(LN4)(NCS)2 (LS)	C1	2	0	80	0.44	0.47	0.77	(49)
3	{Fe[HC(3,5-Me2pz)3]2}I2 (LS)	C1	2	0	4.2	0.46	0.46	0.21	(50)
4	Fe(OEP)(CO)	C4v	2	0	4.2	0.27	0.27	1.84	(51)
5	Na2[Fe(CN)5(NO)]	C4v	2	0	77	–0.18	–0.15	+1.72	(52)
6	Na2[Fe(CN)5(ON)]	C4v	2	0	77	0.00	0.03	2.75	(52)
7	Na2[Fe(CN)5(η2-NO)]	C1	2	0	77	0.01	0.04	2.86	(52)
8	Cp2Fe	D5d	2	0	80	0.53	0.56	+2.38	(53)
9	[CpFe(CO)3]PF6	C1	2	0	78	0.05	0.08	1.88	(53)
10	[CpFe(CO)2]Cl	C1	2	0	4.2	0.27	0.27	1.82	(14)
11	[CpFe(CO)2]Br	C1	2	0	78	0.25	0.28	1.87	(54)
12	[CpFe(CO)2]Me	C1	2	0	78	0.08	0.11	1.76	(55)
13	Fe(CO)3(butadiene)	C1	0	0	77	0.03	0.06	–1.46	(53)
14	Fe(CO)3(cyclo-butadiene)	C1	0	0	78	0.02	0.05	1.52	(55)
15	Fe(CO)5	D3h	0	0	143	–0.18	–0.12	+2.52	(56)
16	Et4N[Fe(CO)4H]	C3v	0	0	77	–0.17	–0.14	1.36	(57)
17	[Fe(bipy)3](ClO4)2	D3	2	0	77	0.33	0.36	0.39	(58)
18	[Fe(phen)3](ClO4)2	D3	2	0	77	0.34	0.37	0.23	(58)
19	[Fe(terpy)2]Cl2	D2d	2	0	80	0.27	0.30	–1.00	(59)
20	Fe(phen)2(NCS)2 (HS)	C2	2	2	77	1.01	1.04	2.82	48
21	Fe(LN4)(NCS)2 (HS)	C1	2	2	80	1.10	1.13	2.51	(49)
22	{Fe[HC(3,5-Me2pz)3]2}I2 (HS)	C1	2	2	190	1.02	1.09	3.86	(50)
23	(PPh4)2[Fe(DTSQ)2]	D2d	2	2	4.2	0.67	0.67	–4.01	(60)
24	(PPh4)2[Fe(SPh)]4]	C2	2	2	4.2	0.66	0.66	–3.24	(60)
25	Fe(phen)2Cl2	C2	2	2	77	1.07	1.10	3.27	(55)
26	FePy4Cl2	D4	2	2	4.2	1.10	1.10	–3.14	(55)
27	Na[Fe(TPpivP)(OAc)]f	C1	2	2	4.2	1.05	1.05	+4.25	(61)
28	Na[(DBC)(THF)2][Fe(TPP)(OPh)]	C1	2	2	4.2	1.03	1.03	+4.01	(62)
29	Fe(TMP)2(NCS)2	C2	2	2	90	1.07	1.11	3.27	(63)
30	Fe(LN4′)(NCS)2	C1	2	2	80	1.16	1.19	2.14	(64)
31	[Fe(H2O)6]SO4	D2h	2	2	5	1.39	1.39	3.38	(65)
32	(Et4N)2[FeCl4]	Td	2	2	4.2	1.00	1.00	3.30	(66)
33	(Et4N)2[FeBr4]	Td	2	2	4.2	0.97	0.97	3.23	(67)
34	Fe(OEP)	Ci	2	1	4.2	0.59	0.59	+1.60	(68)
35	Fe(TPP)	D2h	2	1	4.2	0.52	0.52	+1.51	(68)
36	Fe(thpu)(Hthpu) (LS)	C1	3	1/2	80	0.28	0.31	3.09	(69)
37	[Fe(acpa)2]PF6 (LS)	C2	3	1/2	78	0.25	0.28	2.24	(70)
38	[Fe(bipy)3](ClO4)3	D3	3	1/2	80	0.06	0.09	1.90	(71, 72)
39	[Fe(phen)3](ClO4)3	D3	3	1/2	80	0.10	0.13	1.84	(71, 72)
40	[Fe(terpy)2](ClO4)3	D2d	3	1/2	77	0.07	0.10	–3.43	(72)
41	[Fe-trans-(cyclam)(N3)2]PF6	Ci	3	1/2	80	0.28	0.31	–2.24	(73)
42	Fe(OEP)(PyMe2)2	D2h	3	1/2	4.2	0.26	0.26	2.15	(74)
43	Fe(thpu)(Hthpu) (HS)	C1	3	5/2	241	0.47	0.57	0.81	(69)
44	[Fe(acpa)2PF6 (HS)	C2	3	5/2	320	0.33	0.46	0.53	(70)
45	(n-Pr)4N[Fe(SEt)4]	S4	3	5/2	4.2	0.25	0.25	0.62	(75)
46	FeCl(MBTHx)2	C1	3	5/2	4.2	0.43	0.43	0.98	(76)
47	K[Fe(EDTA)(H2O)]	C2	3	5/2	4.2	0.60	0.60	0.76	(77)
48	Fe(acac)3	C3	3	5/2	78	0.53	0.56	0.64	(78)
49	Fe(tfa)3	C3	3	5/2	78	0.53	0.56	0.67	(78)
50	[Fe(H2O)6]Cl3	D2h	3	5/2	78	0.50	0.53	0.00	(79)
51	Et4N[FeCl4]	Td	3	5/2	77	0.30	0.33	0.00	(80)
52	Et4N[FeBr4]	Td	3	5/2	77	0.36	0.39	0.00	(80)
53	FeCl3	Oh	3	5/2	78	0.53	0.56	0.00	(81)
54	KFeF4	Oh	3	5/2	4.2	0.69	0.69	0.00	(55)
55	Fe(dtc-Et2)2Cl	Cs	3	3/2	4.2	0.50	0.50	2.70	(82)
56	(Et4N)2[Fe(η4-MAC*)Cl]	C1	3	3/2	4.2	0.25	0.25	+3.60	(83)
57	Fe(mnt)2(idzm)	C2	3	3/2	77	0.36	0.39	2.64	(84)
58	trans-[Fe(TMC)(O)(NCCH3)](OTf)2	C1	4	1	4.2	0.17	0.17	1.24	(85)
59	[Fe(N4Py)(O)](ClO4)2	Cs	4	1	4.2	–0.04	–0.04	+0.93	(86)
60	Et4N[Fe(η4-MAC*)Cl]	C1	4	2	4.2	–0.04	–0.04	–0.89	(83)
61	Fe(PPh3)2(″S2″)2	C2v	4	1	4.2	0.16	0.16	1.52	(87)
62	Fe(PPh3)(″S2″)2	Cs	4	1	4.2	0.12	0.12	3.03	(87)
63	PPh4[Fe(B*)(O)]	C1	5	1/2	4.2	–0.42	–0.42	+4.25	(88)
64	[Fe(cyclam-acetate)(N)]PF6	C1	5	1/2	4.2	–0.02	–0.02	–1.60	(26, 89)
65	[Fe(Me3cyclam-acetate)(N)](PF6)2	C1	6	0	4.2	–0.29	–0.29	+1.53	(27)
66	K2FeO4	Td	6	1	78	–0.85	–0.82	0.00	(90)

^aApproximate point group symmetry of the molecular structure.

^bFe oxidation state.

^cFe spin state.

^dReferred to α-iron at room temperature.

^eIf available, the experimental sign of ΔE_Q (+ or −) is given; in all other cases, we show the absolute value of quadrupole splittings.

^fIn the computation, the large TPpivP ligand was substituted with porphine. The following abbreviations are used in the table: LS = low spin state, HS = high spin state, phen = 1,10-phenanthroline, LN₄ = N-[(1-H-imidazol-4-yl)methylene]-N′-(1-pyridin-2-yl-ethylidene)-2,2-dimethyl-propane-1,3-diamine, pz = pyrazolyl ring, OEP = dianion of octaethylporphyrin, bipy =2,2′-bipyridine, terpy = 2,2′:6′2″-terpyridine, DTSQ = bis(dithiosquarato-S,S′) dianion, TPpivP = ″pivalamide-picket-fence″ porphyrin, DBC = dibenzo-18-crown-6), TPP = tetraphenylporphyrinate, TMP = 3,4,7,8-tetramethyl-1,10-phenanthroline), LN₄′ = N,N′-bis[(1H-imidazol-4-yl)methylene]-2,2-dimetyl-propane-1,3-diamine, cyclam = 1,4,8,11-tetraazacyclotetradecane, thpu = dianion of pyruvic acid thiosemicarbazone, acpa = anion of N-(1-acetyl-2-porpylidene)(2-piridylmethyl)amine), MBTHx = bis(N-methylbenzothiohydroxamato) anion, EDTA = tetra-anion of ethylenediaminetetraacetic acid, acac = acetylacetonate, tfa = trifluoroacetylacetonate, dtc-Et₂ = diethyldithiocarbamate, MAC* = tetra-anion of 1,4,8,11-tetraaza-13,13-diethyl-2,2,5,5,7,7,10,10-octamethyl-3,6,9,12,14-pentaoxocyclotetradecane, mnt = cis-1,2-dicyano-1,2-ethylenedithiolato, idzm =2-(p-pyridyl)-4,4,5,5-tetramethylimidazolinium, TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane, ″S2″ = 1,2-benzenedithiolato-S,S′ dianion, B* = tetra-anion of 3,3,6,6,9,9-hexamethyl-3,4,8,9-tetrahydro-1H-1,4,8,11-benzotetraazacyclotridecine-2,5,7,10(6H,11H)-tetraone. Note that counterions were not included in the computations.

3. Results and Discussion

3.1. The Studied Iron Complexes

The data set describing the studied Fe complexes and their experimental Mössbauer parameters is given in detail in Table 1. Although many of the investigated compounds have been studied in previous computations focusing on the Mössbauer properties, several complexes included in our data set are new in this respect. The diversity of the studied systems was set by choosing from inorganic salts, covalent compounds and complexes with chelating ligands various systems with different local symmetries, oxidation and spin states of the Fe center. The selected set provides wide, (−0.82) – (+1.38) and (−4.01) – (+4.25) mm s^–1, ranges for the isomer shift and quadrupole splitting parameters, respectively. To the best of our knowledge, this is the largest and the most diverse data set investigated in Mössbauer spectral studies. Note that the conception for constructing this set for such a study is rather complementary to the one applied in the recent work of R. Friesner et al.³¹ While the authors of that work restricted their investigation to compounds with available crystallography and low-temperature (measured at 4.2 K) Mössbauer data, we wish to address a chemically very diverse set of Fe complexes, and for many systems only higher temperature experimental data is available. To overcome this drawback, for the isomer shifts we corrected all measured values to 4.2 K by an approximation of the shift due to the second-order Doppler effect.² The correction was approximated by a shift of 0.12 mm s^–1 for δ_4.2K – δ_300K, which was reported to be linear with the temperature.^21a,47 For the quadrupole splittings, the temperature dependence cannot be expressed in an explicit general form; therefore, we can only keep in mind that the calculated value corresponds to the low-temperature measurement. Also, we did not follow the approach of only choosing systems with known X-ray structures, partly because the applicability of using these geometries for the predictive calculation of Mössbauer parameters is limited, and more importantly, because a combined spectroscopy-theory approach should be sufficient and successful in itself and is also more easily available for a larger community. Finally, we did not consider antiferromagnetically coupled systems (such as nitrosyls and polynuclear Fe complexes), since the calculation of their Mössbauer properties with a broken-symmetry approach has already been discussed in several previous works.^21,28,31 On the other hand, we included three Fe(II) and two Fe(III) spin-crossover systems, which were not considered in the above-mentioned study.³¹

3.2. The Origin of the Isomer Shift and Quadrupole Splitting

The isomer shift and quadrupole splitting parameters are a result of the electric hyperfine interaction between the nuclear charge density ρ_n(r) and the electric potential Φ(r) of the surrounding charges:

1

We can expand Φ(r) in a Taylor series around the ⁵⁷Fe nucleus at r = 0 and substitute it into eq 1;^9,91 after applying the algebra described in the SI (eqs S1–S7), we realize that for nuclear transitions the relevant interactions stem from the second derivative of the potential:

2

Here

3

is the electric field gradient (EFG) tensor, which is made traceless. It can be shown that the first term of eq 2 describes an electric monopole interaction (E_M), which depends on the electron density at the nucleus (ρ_e(0)) and can be expressed as

4

where R² is the mean square radius of the nucleus (regarded as a homogeneous sphere), and ε₀ is the permittivity of the vacuum. (Note that here we applied the first Maxwell Equation:

5

thus second derivatives of the Φ(r) potential are replaced by the more easily calculable electron density).

The isomer shift is a consequence of the fact that the nucleus has a finite size (which changes during the Mössbauer-transition) and is determined by the difference of two E_M terms, evaluated for the absorber (A) and the source (S):

6

The second term of eq 2 describes the electric quadrupole interaction (E_Q) between the nonspherical nucleus (i.e., a nucleus with a quadrupole moment) and the asymmetry of the electron distribution represented by the EFG at the ⁵⁷Fe nucleus

7

where Q_αα is the quadrupole moment tensor of the nucleus. The diagonalized traceless EFG matrix V_αα (which can be obtained by the transformation to a principal axis system with z on the axis of the largest distortion of the electron distribution) can be characterized by two independent parameters: the main tensor component V_zz and the asymmetry parameter η = (V_xx – V_yy)/V_zz (with |V_zz| ≥ |V_yy| ≥ |V_xx|). The correct negative sign in the definition of V_αα is usually omitted in the Mössbauer literature; therefore, from this point on we shall adapt to this convention, and thus we do not consider it for V_zz (and also for V_xx and V_yy). Note that in many cases it suffices to take into account the V_zz term only, since the contribution of η is small and thus can be neglected. The quadrupole interaction splits the I = 3/2 excited state of ⁵⁷Fe into two sublevels, with m_I = ±3/2 and ±1/2, while the I = 1/2 ground state remains unsplit. The quadrupole splitting (ΔE_Q) is defined as the energy separation of the two I = 3/2 substates.

3.3. Calculated Isomer Shifts Results: Correlation with Experiment

In a typical Mössbauer experiment, the spectrum is recorded by moving a single-line (i.e., unsplit) source with respect to a ⁵⁷Fe-containing absorber with different velocities and recording the transmitted intensity. When the differences in the nuclear transition energies in the source and the absorber are compensated by the Doppler-effect, the transmission decreases (this is why in the Mössbauer literature the nuclear energy is measured in the mm s^–1 unit of Doppler velocity). The detected resonance absorption is characterized by the isomer shift (δ), which arises due to the different electron densities at the ⁵⁷Fe nuclei in the absorber and the source (eq 6). Since ρ_e(0)_S can be taken as a constant (as the same source can be used for taking all Mössbauer spectra), the isomer shift can be expressed as

8

where ρ(0) is the electron density at the absorbing Fe nucleus and α, β are calibration constants. As ρ(0) can be readily determined with DFT calculations, α and β can be evaluated by the linear fit to the experimental isomer shifts versus the computed electron densities. This technique has been widely applied for the calculation of isomer shifts of various iron compounds.¹⁴⁻³⁴ An alternative approach was suggested by R. Kurian and M. Filatov, who calculated ⁵⁷Fe isomer shifts by the differentiation of electronic energy with respect to the nuclear radius; however, in several cases the results showed large deviations from the experimental values.⁹²

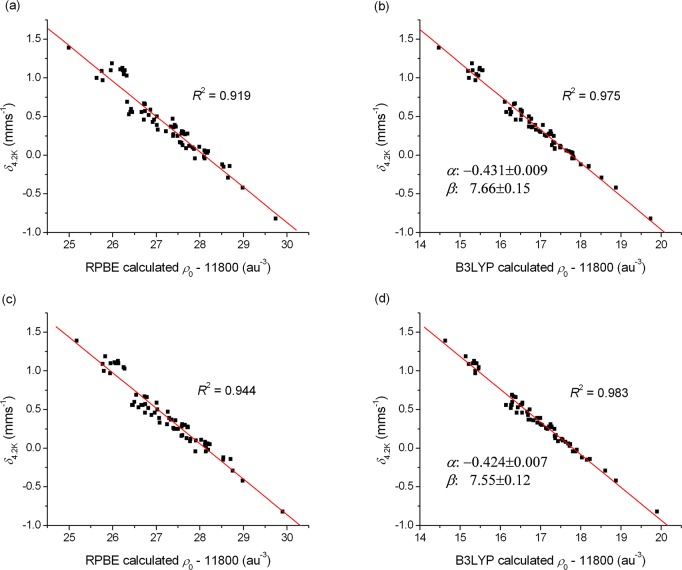
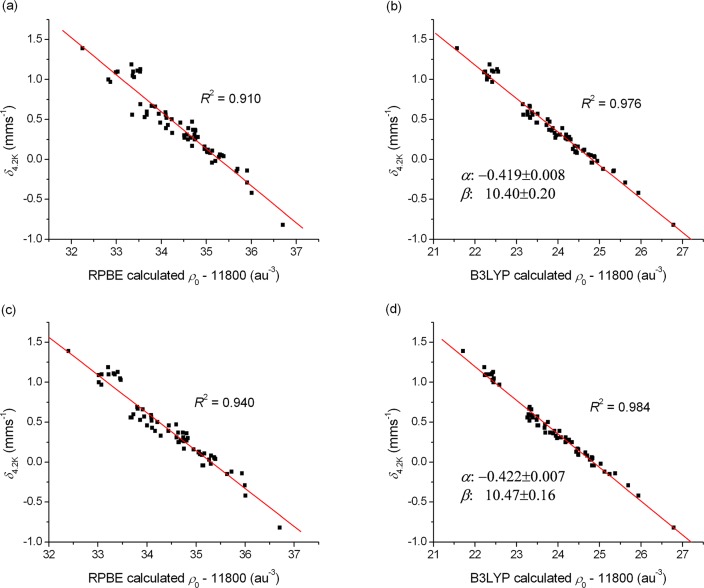
We have fit the above eq 8 to the electron density determined with the different DFT theories using 6 functionals and 2 type of basis sets for all the 66 investigated molecules. The large set of ρ(0) and δ values are presented in Tables S4–S7 and Figures S2–S5 in the SI, while the fits are described in Table 2. All results were obtained by fitting the full data set with a single line; therefore, in contrast to certain previous fits,^21c,28,31 our parametrization does not depend on the Fe oxidation state or other parameters. The linear fits obtained for the RPBE and B3LYP density functionals are presented in Figures 1 and 2 (these two functionals are representatives of the pure (GGA) and hybrid DFT methods, respectively). The results presented in these figures and Table 2 indicate that the hybrids (B3LYP, B3LYP*, and TPSSh) provide better linear fits than the GGA functionals, in agreement with previous studies.^{30b,30c,31,93} This is due to the fact that while the potential generated by GGA functionals is in most cases unsatisfactory in the vicinity of the ⁵⁷Fe nucleus, the inclusion of the nonlocal corrections in global hybrid functionals results in a more accurate potential and electron density.^92b Although the very popular B3LYP functional is often inadequate for many properties of transition metal complexes (e.g., for the calculation of spin-state splitting energies, see refs (38d) and (44)), in this case it gives excellent results, somewhat outperforming B3LYP* and TPSSh. Comparing the results obtained with the three GGA functionals, we found only small differences in their performance indicating that the Hartree–Fock exchange (HFx) included in hybrid density functionals has a vital role for the correct description of the electron density around the Fe nucleus.

Table 2. R², MAE, and Maximum Deviation Parameters Obtained for the Calculation of Isomer Shifts^d.

method	R2a	MAEb (mm s–1)	max. dev.c (mm s–1)
		GTO-CP(PPP) Basis
RPBE	0.919; 0.944	0.10; 0.08	0.30; 0.21
OLYP	0.900 ;0.940	0.11; 0.09	0.28; 0.22
B3LYP	0.975; 0.983	0.06; 0.05	0.15; 0.14
B3LYP*	0.964; 0.979	0.07; 0.05	0.20; 0.15
TPSS	0.937; 0.958	0.09; 0.07	0.25; 0.19
TPSSh	0.965; 0.979	0.06; 0.05	0.21; 0.15
		STO-TZP Basis
RPBE	0.910; 0.940	0.10; 0.08	0.33; 0.24
OLYP	0.840; 0.881	0.14; 0.13	0.37; 0.28
B3LYP	0.976; 0.984	0.05; 0.05	0.17; 0.12
B3LYP*	0.967; 0.979	0.06; 0.05	0.21; 0.15
TPSS	0.932; 0.945	0.09; 0.08	0.30; 0.25
TPSSh	0.954; 0.966	0.07; 0.06	0.25; 0.17

^aSquare of the correlation coefficient obtained for the linear fits.

^bMean absolute error.

^cMaximum deviation from the corrected experimental values. The corresponding α, β fit parameters are presented in the SI.

^dThe values given after the semicolon correspond to results obtained with the COSMO solvation model.

Figure 1.

Linear correlations between the (a) RPBE, (b) B3LYP, (c) COSMO-RPBE, (d) COSMO-B3LYP (in combination with the GTO-CP(PPP) basis set) calculated electron density (ρ₀) at the ⁵⁷Fe nucleus and the corrected experimental isomer shift (δ_4.2K). The fitting parameters are indicated for the B3LYP method; for all other applied DFT methods the results are shown in the SI.

Figure 2.

Linear correlations between the (a) RPBE, (b) B3LYP, (c) COSMO-RPBE, (d) COSMO-B3LYP (in combination with the STO–TZP basis set) calculated electron density (ρ₀) at the ⁵⁷Fe nucleus and the corrected experimental isomer shift (δ_4.2K). The fitting parameters are indicated for the B3LYP method; for all other applied DFT methods the results are shown in the SI.

We have also tested whether the results can be improved by employing an approximation for the effects of the host solid matrix. The application of the COSMO solvation model improves the mean absolute errors (MAE) obtained for the isomer shifts by 0.01–0.02 mm s^–1 for all density functionals; it also reduces the maximum deviation values in several cases by up to 0.09 mm s^–1. In particular, the COSMO-B3LYP method gives a value of R² = 0.984, similar to the one reported by F. Neese et al.;^30c however, our results were obtained on a much larger and more diverse test set. Note that previous results^30c,32 suggest that similarly accurate isomer shifts can be obtained with the double hybrid B2PLYP⁹⁴ method; however, the computational cost of this functional is higher than the one of B3LYP due to the included correction of second-order perturbation theory.

Furthermore, we also compared the performance of the STO and the GTO basis sets. It is well-known that the electron density shows a cusp at the nucleus, which is better reproduced by STO basis functions, than GTOs.⁹⁵ This drawback can be overcome by using a core-polarized basis set for Fe (e.g., Partridge⁹⁶ or Watchers⁹⁷ basis functions, or the CP(PPP) basis developed by F. Neese,³⁰ which we used in our calculations); without this, GTO-based calculations could not compete with those using STOs. Our results show that the application of the STO-TZP basis set barely improves the quality of the computed isomer shifts for the B3LYP and B3LYP* methods. For the other four functionals, the performance of the GTO-CP(PPP) basis set is even superior when compared to the one of the STO-TZP basis (Table 2). To conclude this section we claim that the COSMO-B3LYP is a very reliable method for the calculation of Mössbauer isomer shifts for the different types of Fe compounds covered in the present work. COSMO-B3LYP provides accurate results (with a MAE of 0.05 mm s^–1 and a maximum deviation of 0.12 mm s^–1); therefore, it can become a first choice for predictions.

3.4. Calculated Quadrupole Splittings Results: Correlation with Experiment

As was discussed in section 3.2, the quadrupole splitting (ΔE_Q) observed in the Mössbauer experiment originates from the electric quadrupole interaction between the nuclear quadrupole moment and the electric field gradient. Rewriting eq 7 for the case of ⁵⁷Fe, the expression that describes the energy splitting for the case of the ⁵⁷Fe nucleus is

9

Since Q, the nuclear quadrupole moment can be taken as a constant (0.16 barn for ⁵⁷Fe),^30b the EFG uniquely determines ΔE_Q. The EFG describes the asymmetry of the charge distribution around the Fe center, which is influenced by both the local electronic structure and the coordination of the ligands. The values of V_xx, V_yy, and V_zz are obtained by the diagonalization of the traceless EFG matrix (see section 3.2). The EFG is determined as a second derivative of the potential arising from the charge distribution around the nucleus in a full ab initio manner using

10

The task of the DFT calculations is thus to provide a rather accurate charge distribution.

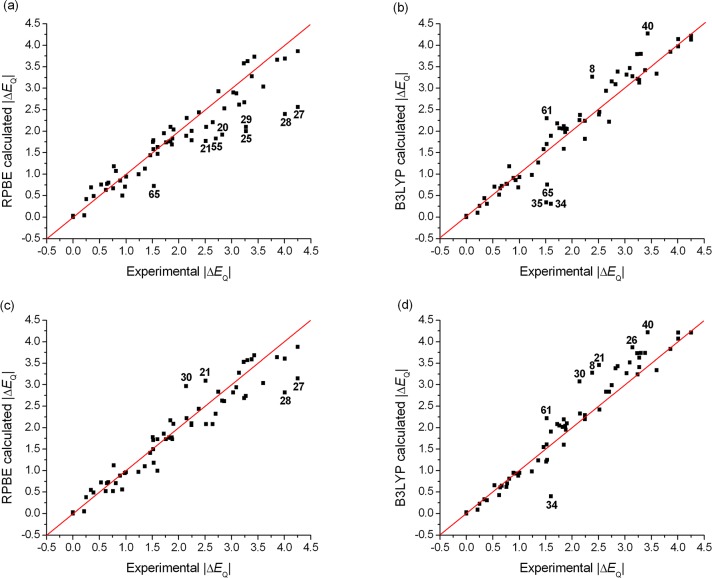
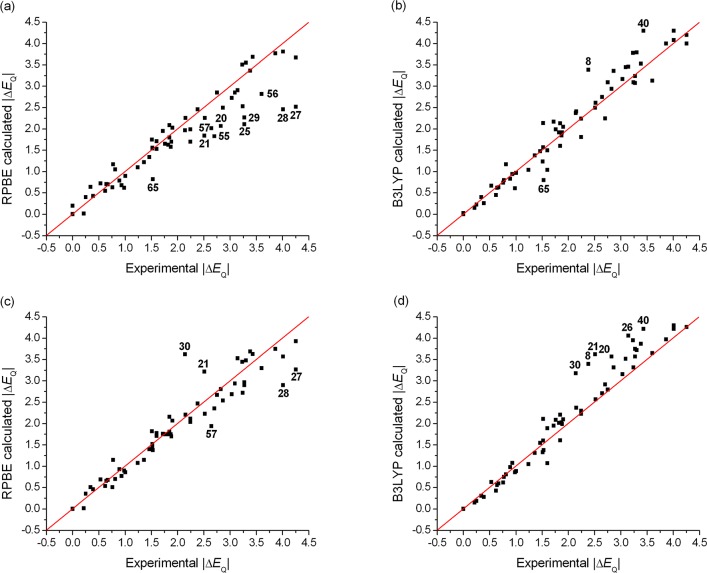
We have performed the ΔE_Q calculation for the same set of Fe compounds with the same conditions as before. (Note that in this section we only consider the magnitude of ΔE_Q, since experimentally its sign has only been determined for a limited number of Fe compounds. The results obtained for those cases with a known sign will be presented at the end of section 3.5.) The calculated ΔE_Q and η values are presented in Tables S8–S14 in the SI, and the comparison between calculations and experiments for a GGA (RPBE) and a hybrid (B3LYP) method is shown in Figures 3 and 4. The results exhibit a good overall agreement with the experiment. However, the deviations from the experimental values are larger than those of the isomer shifts: the observed MAE values are between 0.20 and 0.35 mm s^–1 for the different functionals, which correspond to 10–18% absolute error. This has several contributing factors, which include the experimental error in the determination of ΔE_Q, its possible dependence on the temperature and the molecular structure, and the fact that it is a second derivative and its calculated value is determined fully ab initio, while experimental δ values are used for the calibration of isomer shifts. Furthermore, while with the isomer shifts the best-performing methods provide accurate δ values over the whole investigated data set, this is not the case for ΔE_Q. In fact, even the best-performing functionals can produce maximum deviations up to 0.7–1.1 mm s^–1 (corresponding to 48–66% absolute error) between the experimental and calculated values of ΔE_Q (Table 3).

Figure 3.

Comparison of experimental and (a) RPBE, (b) B3LYP, (c) COSMO-RPBE, (d) COSMO-B3LYP (in combination with the GTO-CP(PPP) basis set) calculated quadrupole splittings (ΔE_Q). The red line connects the ΔE_Q(exp.) = ΔE_Q(calc.) points. The largest outliers can be identified by the numbers defined in Table 1. Correlations for all the other applied DFT methods are shown in the SI.

Figure 4.

Comparison of experimental and (a) RPBE, (b) B3LYP, (c) COSMO-RPBE, (d) COSMO-B3LYP (in combination with the STO-TZP basis set) calculated quadrupole splittings (ΔE_Q). The red line was drawn at ΔE_Q(exp.) = ΔE_Q(calc.). The largest outliers can be identified by the numbers defined in Table 1. Correlations for all the other applied DFT methods are shown in the SI.

Table 3. R², MAE, and Maximum Deviation Parameters Obtained for the Calculation of Quadrupole Splittings^d.

method	R2a	MAEb (mm s–1)	max. dev.c (mm s–1)
		GTO-CP(PPP) Basis
RPBE	0.875; 0.926	0.31; 0.24	1.69; 1.19
OLYP	0.852; 0.918	0.32; 0.24	1.89; 1.40
B3LYP	0.926; 0.947	0.24; 0.25	1.29; 1.20
B3LYP*	0.925; 0.948	0.24; 0.22	1.20; 1.11
TPSS	0.906; 0.936	0.28; 0.23	1.42; 0.87
TPSSh	0.942; 0.942	0.21; 0.19	0.82; 1.05
		STO-TZP Basis
RPBE	0.887; 0.919	0.30; 0.23	1.73; 1.48
OLYP	0.870; 0.906	0.31; 0.24	1.94; 1.54
B3LYP	0.949; 0.958	0.21; 0.25	1.01; 1.11
B3LYP*	0.949; 0.960	0.21; 0.21	0.80; 1.09
TPSS	0.914; 0.923	0.27; 0.22	1.49; 1.66
TPSSh	0.948; 0.955	0.21; 0.18	0.73; 1.12

^aSquare of the correlation coefficient of the linear fit obtained for experimental and calculated values of quadrupole splittings.

^bMean absolute error.

^cMaximum deviation from the experimental values.

^dThe values given after the semicolon correspond to results obtained with the COSMO model.

Concerning the effect of the type of the basis set, we recall that the application of the CP(PPP) basis set on the Fe atom is essential for the reproduction of the cusp at the nucleus; without this the performance of the GTOs would be inferior, compared to those of the STO basis functions. For the prediction of quadrupole splittings, the general performance of the STO-TZP basis set is slightly better than that of the GTO-CP(PPP) basis (Table 3), but in several cases, CP(PPP) provides more accurate results (e.g., for complexes 56 and 57, see Figures 3a,c and 4a,c). Therefore, in agreement with previous computational Mössbauer spectral results,^18,28b we did not observe the clear preference for the use of the STO basis over the core-polarized GTO basis set.

In order to assess the applicability of different exchange-correlation functionals, we investigated their influence on the calculated quadrupole splittings. In general, the application of hybrid functionals results in more accurate ΔE_Q values, thus the inclusion of the HFx improves the theoretical description. Moreover, we found systematic variations in the comparison of results obtained with GGA- and hybrid-type functionals. For instance, B3LYP provides significantly larger ΔE_Q values (up to 1.7 mm s^–1) than RPBE, for the high-spin (S = 2) Fe(II) and intermediate-spin (S = 3/2) Fe(III) complexes, and also slightly larger ΔE_Q values than the other two hybrid functionals, B3LYP* and TPSSh. On the other hand, for low-spin (S = 0) Fe(II) compounds, only small differences are seen between the ΔE_Q values calculated with GGA and hybrid functionals. As is well-known, the exchange interaction increases with the value of the spin angular momentum.^44c Hence the above effect is obviously due to the fact that the influence of the HFx to the EFG is more dominant for intermediate- and high-spin complexes than for the low-spin ones.

Our results give evidence that pure functionals substantially underestimate ΔE_Q for the S = 2 Fe(II) and S = 3/2 Fe(III) complexes (see Figures 3a and 4a), which may stem from the inadequate description of the exchange interaction. These cases are better described with the hybrid methods due to the inclusion of HFx. Furthermore, we point out that the 20% amount of HFx included in the B3LYP functional is required to better reproduce the quadrupole splittings of the high-spin Fe(II) and intermediate-spin Fe(III) compounds: the corresponding experimental ΔE_Q values are underestimated with the other two hybrids, B3LYP* and TPSSh, by 0.3–0.6 mm s^–1. On the other hand, the TPSSh method reproduces better the experimental ΔE_Q values of the S = 0 Fe(II), S = 1/2 Fe(III), Fe(IV), Fe(V), and Fe(VI) compounds. All applied density functionals yield accurate quadrupole splittings for the S = 0 Fe(II) and S = 5/2 Fe(III) complexes (except for complex 8, see below), which is explained by the reliable description of the symmetrically occupied Fe-3d subshell by DFT.

In order to test the role of the environment of the molecule, we also investigated the effect of the COSMO solvation model on the calculated quadrupole splittings. We found that the inclusion of the molecular environment improves the general performance of most methods (except for B3LYP, where R² increases, but also MAE increases, see Table 3), which is in agreement with a previous study.^21c However, the results indicate that in the case of the hybrid functionals, it results in the dramatic increase of ΔE_Q for the high-spin (S = 2) Fe(II) complexes. Since the effect is only pronounced for these systems, it must be related to the enhanced exchange interaction. While COSMO partially corrects the mentioned deficiencies of the GGA methods for several S = 2 Fe(II) and S = 3/2 Fe(III) complexes, it induces the overestimation of quadrupole splittings provided by the hybrid functionals up to 1.12 mm s^–1 (52% error). On the other hand, COSMO turned out to be beneficial for all other Fe complexes with various oxidation and spin states. In particular, in the case of complex 65, while the gas phase DFT computations underestimate the experimental ΔE_Q value by ca. 0.8 mm s^–1, COSMO reduces this error by 0.3–0.4 mm s^–1.

The largest differences observed between the measured and DFT-calculated values of ΔE_Q are worth a careful examination. In principle, several possible sources of errors can contribute to the mismatch observed between the experimental and calculated quadrupole splittings, which include the effect of temperature, the poor approximation of the solid-state effects, and unsatisfactory molecular geometry used in the calculations; we briefly address these issues here, focusing on the outliers (8, 21, 26, 30, 34, and 40) of one of the best-performing exchange-correlation functional, COSMO-TPSSh. With the temperature, it is unlikely that the largest discrepancies stem from temperature effects, since the corresponding experimental ΔE_Q values were taken from Mössbauer measurements carried out at liquid He (4.2 K) or liquid N₂ (77 K) temperatures and relevant thermal variations of the quadrupole splitting typically take place at higher temperatures. Furthermore, calculations made on X-ray structures do not produce better overall performance, and results also in numerous outliers, as it has been seen in ref (31); these suggest that solid-state effects do not alter the EFG of the complexes significantly. Finally, in order to investigate the possibility of inadequacy of the structures obtained in the molecular optimization with the pure BP86 functional, we carried out further test computations for the problematic complexes. We performed both geometry optimizations and the calculation of the quadrupole splitting with a hybrid functional at the COSMO-TPSSh level, and we found that the large errors of the outliers cannot be amended this way (see Table S12).

As the consideration of the possible sources of errors has not provided a satisfying explanation of the outliers, we shall consider whether the treatment of the electronic structure is appropriate in all cases. For GGAs, the discrepancies in most cases can be assigned to the incorrect treatment of the exchange interaction, as stated above. Although hybrid functionals give more accurate results, even for these methods large deviations from the corresponding experimental values are observed in a few cases. For instance, in the case of ferrocene (Cp₂Fe, complex 8), the experimental quadrupole splitting is systematically overestimated by all hybrid functionals, while GGAs provide results in good agreement with this value, as also reported in ref (29). This effect originates from the fact that GGA functionals reproduce better the energetics of π-type charge-transfer (Fe-3d→Cp-π* donation and Cp-π→Fe-3d* backdonation) and the experimental HOMO–LUMO energy gap than hybrid methods,^29,98 which quantities are decisive for the bonding and the increased EFG in Cp₂Fe. Large deviations are observed also for the experimental and hybrid DFT ΔE_Q values for the square planar S = 1 Fe^II(OEP) (34) and Fe^II(TPP) (35) complexes; however, the GGA-type RPBE method yields accurate results. As will be addressed in section 3.5, the key to this effect stems from the treatment of electronically degenerate states by DFT. Furthermore, for the hybrids, we also identified two main outliers: [Fe(terpy)₂]³⁺ (40) and Fe(PPh₃)₂(″S2″) (61). In contrast to our results presented above, we found that in these distorted open-shell hexacoordinate complexes, the inclusion of the exact exchange results in the overestimation of ΔE_Q. This effect is surprising, since hybrid methods provide reliable results for other quasi-octahedral systems possessing the same S = 1/2 3d⁵, and S = 1 3d⁴, electron configurations. Also, our results indicate that the hybrid methods give accurate estimates to the ligand-only contributions of quadrupole splittings for hexacoordinate complexes (e.g., deviations up to only 0.1 mm s^–1 were observed for 19, which is the S = 0 Fe(II) analogue of 40). Therefore, these discrepancies for 40 and 61 most likely stem from the incorrect description of the partially occupied and split t_2g-like orbitals. For systems with such electron structure (including a relevant distortion), we propose the application of GGA functionals, which provide accurate ΔE_Q values.

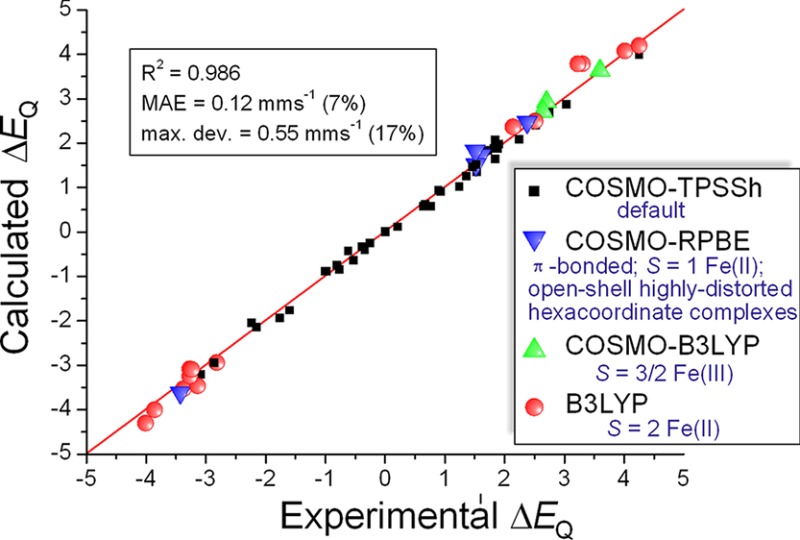
Based on the results presented above, we conclude that although none of the applied density functionals show a good universal performance over the whole investigated data set, with the careful selection of an appropriate DFT method, this technique is very promising for the accurate prediction of quadrupole splittings. The hybrid TPSSh functional combined with COSMO gives satisfactory results for most cases. However, for the S = 2 Fe(II) and S = 3/2 Fe(III) complexes, the B3LYP (for the latter compounds in combination with the COSMO model) method provides more accurate ΔE_Q values. Furthermore, in the special cases of π-bonded compounds, square-planar arrangements with S = 1 and largely distorted open-shell hexacoordinate systems we suggest using the GGA-type COSMO-RPBE method. The application of the carefully selected DFT methodology described above in this paragraph yields a MAE value of 0.12 mm s^–1 (7% error) and a maximum deviation of 0.55 mm s^–1 (17% error) on the investigated set of 66 complexes. These results are shown in Figure 5a. Therefore, we conclude that the suggested approach provides accurate ΔE_Q values over the variety of the investigated complexes, which enables the reliable prediction of ⁵⁷Fe quadrupole splittings.

Figure 5.

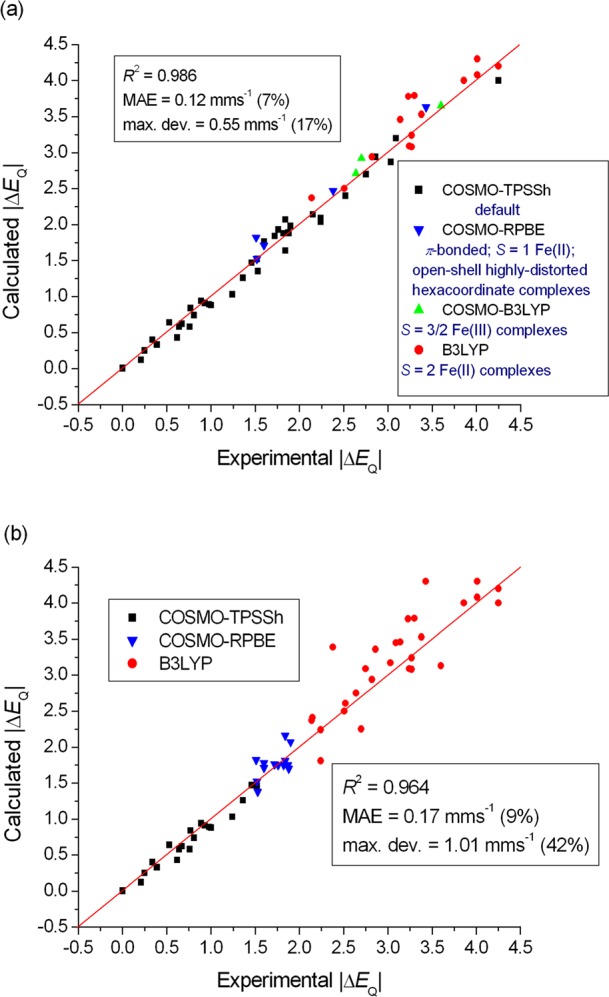
Comparison of experimental and DFT-calculated quadrupole splittings (ΔE_Q), applying exchange-correlation functionals for different (a) chemical classes of Fe complexes and (b) ranges of experimental ΔE_Q (in combination with the STO-TZP basis set). The red line was drawn at ΔE_Q(exp.) = ΔE_Q(calc.).

It is apparent from Figure 5a that the classes of compounds treated separately in the above recipe fall into different regions. This interesting observation hints that a strategy can also be proposed, where the selection of the applied density functional is solely guided by the experimentally observed ΔE_Q values. A good correlation with the experiment over the whole investigated ΔE_Q range may provide a basis for the development of stronger model-independent techniques for the accurate prediction of quadrupole splittings. Encouraged by this, we test the applicability of an alternative approach utilizing the above idea, with the use of three arbitrarily selected regions: ΔE_Q ≤ 1.5, 1.5 < ΔE_Q ≤ 2.0, ΔE_Q > 2.0. These results are shown in Figure 5b. The obtained MAE value of 0.17 mm s^–1 (9% error) and the maximum deviation of 1.01 mm s^–1 (42% error) and also the outliers observed in the ΔE_Q > 2.0 region clearly indicate the lower efficiency of the method, compared to the above one based on the chemical classification of Fe complexes. However, the approach produces deviations only up to 0.32 mm s^–1 (17% error) in the ΔE_Q < 2.0 region. Therefore, the success and applicability of this technique is limited by the discrepancies detected in the ΔE_Q > 2.0 region. We have tried to apply different region limits and DFT methods but could not significantly improve the performance, which is barely better than that of the best hybrid functional. Consequently, due to the problematic cases leading to the outliers, a robust model-independent description does not seem to be attainable.

3.5. Case Studies for the Quadrupole Splitting in Mössbauer Spectroscopy

In this section we check the reliability of the DFT approach by testing its performance in the prediction of quadrupole splittings in a few chemically relevant applications of MS. Also, we examine the apparent difficulties introduced by the electronically degenerate states of open-shell Fe(II) complexes and propose a method to overcome them.

a. Electronically Degenerate States of S = 1 Fe(II) Complexes

An intriguing class of compounds possesses open-shell electronically degenerate states in solids. As noted previously in section 3.4, the incorrect treatment of these states induces large variations in the experimental and calculated ΔE_Q values. For instance, the experimental quadrupole splittings of the planar S = 1 Fe(OEP) (34) and Fe(TPP) (35) porphyrin-derivative complexes are underestimated with the B3LYP/CP(PPP) method by 1.2–1.3 mm s^–1. On the other hand, the serious overestimation of ΔE_Q (by 1.4–2.3 mm s^–1) for these complexes was also experienced in earlier works, when hybrid exchange-correlation functionals were applied with no symmetry constraints,³¹ or when the EFG was computed with the GGA-type BPW91 functional on a D_4h structure of complex 35.^16b However, a quite acceptable ΔE_Q value of 1.75 mm s^–1 was obtained with the same functional, when the D_2d symmetry of the system (obtained from its crystal structure⁹⁹) was employed.^16b We made efforts to understand the reasons behind these discrepancies by a detailed investigation.

The lowest-lying electronic states of Fe(TPP), applying the D_4h point group symmetry, are the triplet ³A_2g and ³E_g states. The DFT calculations deliver quadrupole splitting values of ΔE_Q(³A_2g) = 0.40 mm s^–1 and ΔE_Q(³E_g) = 3.08 mm s^–1. This large difference suggests that the origin of the above-mentioned discrepancy between theory and experiment requires a close and careful inspection of the electronic structure. We have discussed in the SI that the five Fe-3d orbitals make different contributions to the EFG (eq S15, Table S1); therefore, their occupation has a major influence on the quadrupole splitting. In Figure 6, we show that the small ΔE_Q obtained for the ³A_2g state is due to the symmetric occupation of the degenerate d_xz and d_yz orbitals and the double occupation of the d_z² orbital, whereas the large quadrupole splitting in ³E_g can be attributed to the asymmetric occupation of these orbitals. Since the energy separation of these states is small (∼0.12 eV), DFT calculations can converge to either of these states. Lowering the symmetry removes the degeneracy. D_2h was found to be the highest symmetry for which we observed a mixing of the d_xy and d_z² orbitals in the ground state (mediated by the ligands), which resulted in the accurate quadrupole splitting value of 1.25 mm s^–1. We mention that the mixing was also observed when utilizing the RPBE/CP(PPP) method, without the application of any symmetry constraints, which also provided accurate results.

Figure 6.

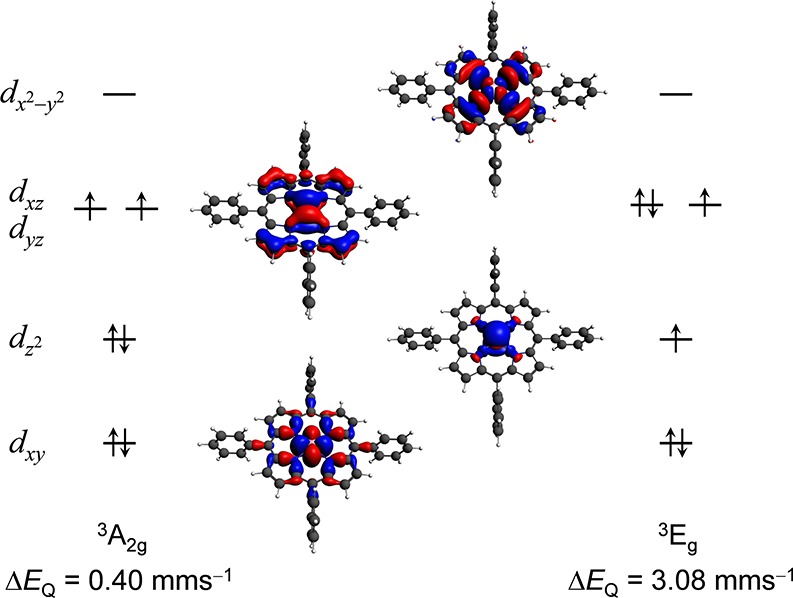
Schematic representation of the electronic configurations and the 3D illustration of the DFT Fe-3d orbitals of the triplet ³A_2g and ³E_g (D_4h) states of Fe(TPP) (35). Note that for the sake of simplicity we do not show spin-polarized energy levels and we only show one component of the degenerate d_xz, d_yz orbitals and ³E_g states. The given ΔE_Q values were computed at the B3LYP/STO-TZP level of theory and are to be compared with the experimental value of 1.51 mm s^–1.

b. Electronically Degenerate States of a S = 2 Fe(II) Complex

The DFT-calculated ΔE_Q values of a S = 2 Fe(II) quasi-tetragonal complex, [Fe(DTSQ)₂]^2– (23), reported in previous studies^28a,31 also showed very large deviations (0.71–1.65 mm s^–1) from the experimental value of 4.01 mm s^–1. When investigating the electronic structure of this complex in the D_2d symmetry, we found that its two lowest-lying states, ⁵A₂ and ⁵B₂, are degenerate. The calculated quadrupole splittings for these states show a large difference due to the different occupation of the d_z² and d_x²–y² orbitals. While the ΔE_Q(⁵A₂) = 4.30 mm s^–1 value is in good agreement with the experiment, the 2.92 mm s^–1 value obtained for the ⁵B₂ state is as far from the experimental one as those reported in refs (28a) and (31) (Figure 7). Therefore, the comparison between the calculation and the experiment permits us to identify the true ground state, and the problematic ⁵B₂ electronic configuration can be avoided by the application of symmetry. Note that 23 does not appear as an outlier in Figures 3 and 4, since in every case for our calculations it converged to the ⁵A₂ state, which yielded quadrupole splittings in agreement with the magnitude of the experimental ΔE_Q. Furthermore, the sign of the experimental ΔE_Q has also been determined for this compound: it is negative. This is in very good agreement with our calculations, where ΔE_Q(⁵A₂) < 0 and ΔE_Q(⁵B₂) > 0, which allows the unambiguous identification of the true ground state for this system: it is the ⁵A₂. Without imposing the Fe-3d electronic configuration corresponding to this state, DFT calculations (with both GGA and hybrid functionals) can converge either to the ⁵A₂ or to the ⁵B₂ state depending on the starting geometry and the applied exchange-correlation functional. The above results suggest that the largest differences observed between the experimental and DFT-calculated ΔE_Q values in previous studies^28a,31,33,34 can be also attributed to the selection of the inappropriate ground state from the electronic quasi-degenerate states.

Figure 7.

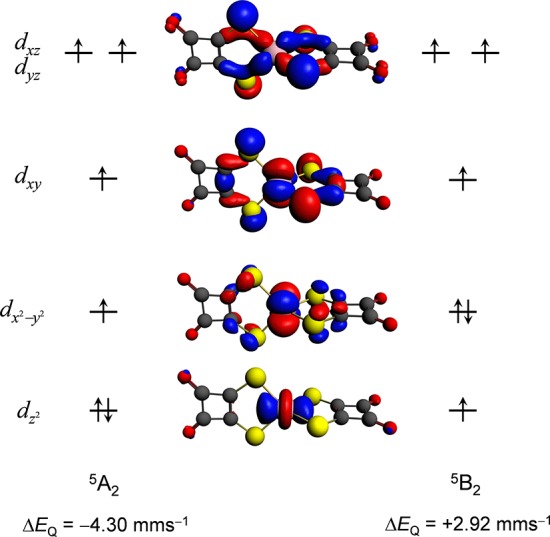
Schematic representation of the electronic configurations and the 3D illustration of the DFT Fe-3d orbitals of the quintet ⁵A₂ and ⁵B₂ states of [Fe(DTSQ)₂]^2– (23). Note that for the sake of simplicity we do not show spin-polarized energy levels and that we only show one component of the degenerate d_xz, d_yz orbitals. The given ΔE_Q values were computed at the B3LYP/STO-TZP level of theory and are to be compared with the experimental value of −4.01 mm s^–1.

c. Geometric Isomerism of Octahedral Low-Spin Fe(II) Complexes

In addition to the valence electrons, the ligands also contribute to the electric potential and the V_zz at the ⁵⁷Fe nucleus, and this can also be a rich source of chemical information. Compounds where the V_zz induced by the electrons cancels provide an ideal testing ground to study how DFT reproduces the ligand contribution. In this section we investigate how geometric isomerism can affect the V_zz. In octahedral geometry, complexes with a composition of FeA₂B₄ can have two different isomers with the two A ligands in trans or cis positions. For a potential Φ = q/r generated by a point charge q of the monatomic ligand, its contribution to the main component of the EFG can be expressed as

11

where r,ϑ are polar coordinates. Representing the A and B ligands by the q_A and q_B point charges, and applying the algebra described in detail in the SI (eqs S12–S14), the −2(q_A – q_B) and 4(q_A – q_B) expressions can be derived for the V_zz of the cis and trans isomers, respectively (note that the constant r^–3 term is omitted and η = 0, due to the axial symmetry) (Figure 8). In the case of the S = 0 Fe(II) electronic configuration, no unpaired electron contributes to the EFG, thus the ligand contribution determines the EFG and ΔE_Q, and the above point charge approximation should give acceptable results. Therefore, a −1: 2 ratio is expected for the quadrupole splittings of cis and trans isomers of low-spin FeA₂B₄ complexes. Also, for the FeAB₅ system a V_zz of 2(q_A – q_B), thus a 1:2 ratio to the trans case is expected. We utilized one of the best-performing DFT methods and found that the hybrid functional, COSMO-TPSSh, reproduces the above derived −1:2:1 ratio of the corresponding quadrupole splittings reasonably well, in the case of octahedral Fe(II) model compounds (for more details, see Table S15 in the SI). For the cis-trans isomers of FeX₂(RNC)₄ and FeX(RNC)₅⁺ (X = CN, R = Et or X = Cl, R = Ph) experimental data is also available, and the DFT-predicted ΔE_Q values not only show the approximate −1:2:1 ratio but are also in a fair agreement with the measured values, as seen in Table 4.

Figure 8.

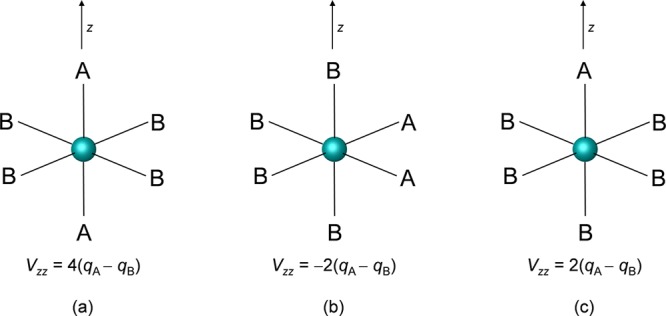
3D representation of the structures of the octahedral (a) trans-FeA₂B₄, (b) cis-FeA₂B₄, and (c) FeAB₅ complexes. Parametric V_zz values expected from the point charge model are also shown. The orientation of the z axis was chosen to be the principal axis.

Table 4. Comparison of Experimental and DFT-Calculated ΔE_Q Values of Octahedral Fe(II) Complexes^c.

compound	temp/K	exptla	COSMO-TPSShb
trans-Fe(CN)2(EtNC)4	300	0.59	–0.43
cis-Fe(CN)2(EtNC)4	300	0.29	+0.18
Fe(CN)(EtNC)5+	300	0.17	–0.24
trans-FeCl2(PhNC)4	295	1.55	+1.70
cis-FeCl2(PhNC)4	295	0.78	–0.88
FeCl(PhNC)5+	295	0.73	+0.77

^aExperimental ΔE_Q values were taken from ref (9).

^bIn combination with the STO-TZP basis set.

^cValues are given in mm s^–1.

d. Phase Transitions

MS is also a powerful tool to study phase transitions.^3,9,100,101 Here we focus on those where the microscopic origin is either spin crossover^{48–50,69,70} or a change in the orbital degeneracy^102−104 in Fe complexes. The ΔE_Q is very sensitive to the variations in the electronic structure induced by both processes. The quadrupole splitting is typically small for octahedral low-spin (S = 0) Fe(II) and high-spin (S = 5/2) Fe(III) complexes, where the distribution of the 3d electrons is symmetric: (t_2g)⁶(e_g)⁰ or (t_2g)³(e_g)², therefore the electronic contribution to the V_zz is zero. On the other hand, it is large in their counter-pairs in the spin crossover process, the high-spin (S = 2) Fe(II) and low-spin (S = 1/2) Fe(III) compounds. With their respective configurations (t_2g)⁴(e_g)² and (t_2g)⁵(e_g)⁰, the filling of the 3d (in fact, the t_2g) subshell is uneven, thus the d-electron contribution to the V_zz is large, according to its population dependence discussed in the SI (see Table S1 and Figure S1). Consequently, these values reflect the variations in the occupation of the corresponding Fe-3d orbitals. As can be seen in Table 5, DFT provides reliable ΔE_Q results for Fe(II) and Fe(III) spin-crossover compounds, thus it gives a strong support for the prediction or interpretation of the Mössbauer spectra at spin-state transitions.

Table 5. Comparison of Experimental and DFT-Calculated ΔE_Q Values of Fe(II) and Fe(III) Spin-Crossover Complexes^c.

compound	temp/K	exptla	B3LYPb
Fe(phen)2(NCS)2 (LS) (1)	77	0.34	0.40
Fe(phen)2(NCS)2 (HS) (20)	77	2.82	2.94
Fe(LN4)(NCS)2 (LS) (2)	80	0.77	0.80
Fe(LN4)(NCS)2 (HS) (21)	80	2.51	2.50
{Fe[HC(3,5-Me2pz)3]2}I2 (LS) (3)	4.2	0.21	0.15
{Fe[HC(3,5-Me2pz)3]2}I2 (HS) (22)	180	3.86	4.00
Fe(thpu)(Hthpu) (LS) (36)	80	3.09	3.45
Fe(thpu)(Hthpu) (HS) (43)	241	0.81	1.17
[Fe(acpa)2]PF6 (LS) (37)	78	2.24	2.24
[Fe(acpa)2]PF6 (HS) (44)	320	0.53	0.67

^aExperimental values were taken from references given in Table 1.

^bIn combination with the STO-TZP basis set. For the abbreviations, also see Table 1.

^cValues are given in mm s^–1.

A different type of phase transition triggered by the redistribution of the 3d electrons is the inversion of the orbital ground state. This phenomenon was intensively studied in the high-spin (S = 2) [Fe(H₂O)₆]²⁺ and [Fe(DCTU)₆]²⁺ (DCTU = N,N′-dicyclohexylthiourea) complexes, frequently with MS.^102,103 The symmetry of the system is D_3d, which corresponds to a trigonally distorted octahedron. Being a high-spin complex, five of the six d electrons are equally distributed on the five 3d orbitals, hence it is the sixth one which will contribute to the V_zz. The lowest-lying orbitals are a 2-fold-degenerate e_g (d_xz, d_yz) and the a_1g (d_xy). Depending on the distortion, either of them can be lowest, and thus populated by the sixth electron, giving rise to the orbitally degenerate doublet (D) or singlet (S) state. (In solids, the crystal symmetry may stabilize the D state.) The corresponding term is ⁵E_g for the D and ⁵A_1g for the S state. Note that the electron-only contribution to the V_zz for the S and D states is ±2: ∓1, according to Table S1 presented in the SI. The experiments revealed that at low temperatures the system is in the orbital singlet ground state, which undergoes a phase transition around 200 K, and at higher temperature the doublet becomes the ground state. Mössbauer measurements yield smaller ΔE_Q values for the D (⁵E_g) state than for the S (⁵A_1g) one, by ca. 2 mm s^–1, which is attributed to the population variations associated with the singlet-doublet transition. As shown in Table 6, this phenomenon is also reflected well by the DFT results, for which a good agreement was observed with the experimental quadrupole splittings.

Table 6. Comparison of Experimental and DFT-Calculated ΔE_Q Values of Orbital Singlet (S) and Doublet (D) States of Fe(II) Complexes^c.

compound	state	temp./K	exptl.a	B3LYPb
[Fe(H2O)6]2+	S	107	–3.36	–3.66
[Fe(H2O)6]2+	D	295	+1.40	+1.25
[Fe(DCTU)6]2+	S	77	–3.31	–3.27
[Fe(DCTU)6]2+	D	300	+1.32	+0.94

^aExperimental values were taken from refs (102) and (103).

^bIn combination with the STO-TZP basis set. Note that for [Fe(DCTU)₆]²⁺, we performed the calculations on the [Fe(DMTU)₆]²⁺ (DMTU = N, N′-dimethylthiourea) model compound in order to reduce computational cost.

^cValues are given in mm s^–1.

e. Determination of the Sign of Quadrupole Splittings

In most of the foregoing, we did not consider the sign of ΔE_Q, only its magnitude, because the sign is usually not reported in the experimental literature. However, the sign of the quadrupole splitting gives information on the charge distribution that is very relevant to structural or coordination chemistry, as became obvious in the previous case studies too. It is determined by the sign of the V_zz, the largest component of the diagonalized traceless EFG tensor. For instance, in the case of an axially distorted octahedral complex with six identical ligands, the sign of the V_zz reveals whether the system is compressed or stretched along the principal z axis (Figure 9). Different ligands can also change the sign of the EFG, according to the electron density on their donor atoms. The effect of a negative V_zz is that it inverts the energy ordering of the quadrupole-split m_I = ±3/2 and ±1/2 nuclear energy levels for the I = 3/2 excited state, thus, it flips the lines of the quadrupole doublet. The detection of this flipping, in fact the detection of the sign of the V_zz, is therefore very difficult experimentally because it requires either the application of an external magnetic field or the orientation-dependent measurement of the line intensities on a single crystal.

Figure 9.

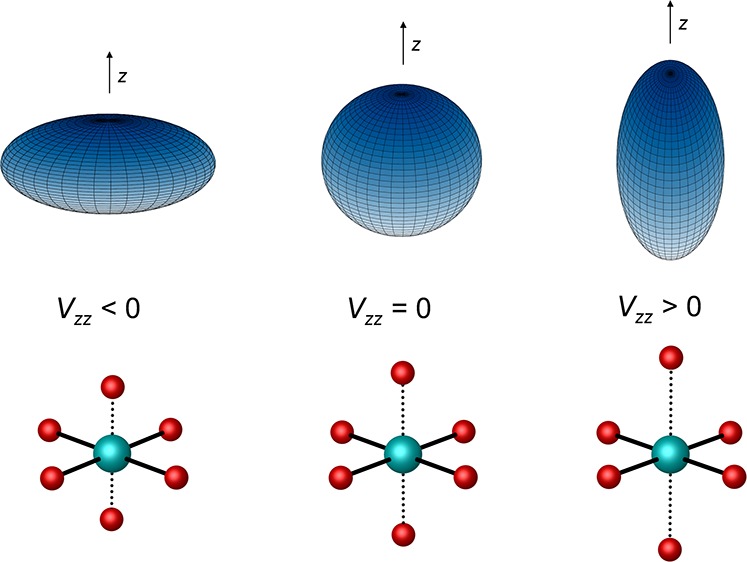
Illustration of the sign of the EFG for a distorted spherical charge distribution (top) and for Fe complexes with O_h symmetry (bottom). In case of a negative (respectively positive) V_zz, the charge distribution around the Fe nucleus is represented as an oblate (respectively prolate) spheroid, while the complex undergoes a tetragonal distortion by being compressed (respectively stretched) along the principal z axis. Note that a zero V_zz corresponds to a fully symmetric system with an undistorted charge distribution, represented by a sphere, or equal bond lengths for the O_h case.

We evaluated and compared the DFT-calculated and measured signs of ΔE_Q and found an excellent agreement in correctly reproducing the sign for all compounds for which it has been determined experimentally (Table S16). In particular, the calculations predict the correct negative sign for the ⁵A₂ state of complex 23, while the opposite sign is predicted for ⁵B₂; which also supports the results presented in section 3.4b. Also, the correct relative signs were obtained for the cis/trans-FeA₂B₄ and FeAB₅ complexes. The computations also provide the correct signs for the orbital singlet and doublet states of the [Fe(H₂O)₆]²⁺ and [Fe(DCTU)₆]²⁺ complexes (Table 6), which signs were also obtained from the interpretation of an axial, trigonal crystal field.¹⁰³ These results suggest that the computational approach is highly effective for the determination of the sign of quadrupole splittings, which should be considered as a very powerful tool in the investigation of the electron structure and local symmetry.

We have also re-evaluated the data obtained with combination of the four different techniques using a chemical classification (presented before in Figure 5a), this time using the sign of ΔE_Q, when available from the experiment, and assuming the calculated one, when it is not. The plot and the fitted line along with the parameters describing the fit and its goodness is shown in Figure 10. The agreement is very good, and the parameters indicate that exploiting the sign of the quadrupole splitting can make MS a more powerful technique in structural research.

Figure 10.

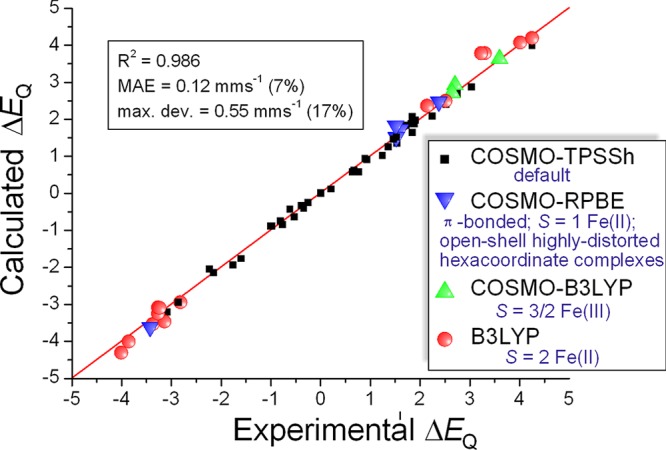
Comparison of experimental and DFT-calculated quadrupole splittings (ΔE_Q), applying exchange-correlation functionals for different chemical classes of Fe complexes and using the sign of ΔE_Q as described in the text above.

4. Conclusion

We carried out DFT calculations on a large and diverse data set of Fe complexes, to investigate the applicability of various computational methods in the prediction of Mössbauer parameters. For the isomer shifts, we found that the performance of hybrid functionals is superior, compared to those of the pure DFT methods, due to the inclusion of nonlocal corrections. Moreover, the approximation of the environment of the molecule by the application of the COSMO model makes the calculations more reliable in predicting isomer shifts. Our results do not indicate the clear preference for Slater-type orbitals, as the enhanced core-polarized Gaussian basis set showed a similar performance. The best agreement between experiment and theory was obtained for the COSMO-B3LYP method, which provided accurate ⁵⁷Fe isomer shifts for all the 66 investigated compounds.

Our results for the prediction of quadrupole splittings also indicate an improved general performance of the hybrid methods over those of the GGAs. While in general TPSSh provided the most accurate results, the also well-performing B3LYP method turned out to be the optimal for high-spin (S = 2) Fe(II) and intermediate-spin (S = 3/2) Fe(III) complexes. However, large deviations from experiment were observed for the ΔE_Q values obtained with hybrid density functionals for molecules with π-type charge-transfer, for square planar S = 1 compounds, or for highly distorted hexacoordinate open-shell Fe complexes (including the systems 8, 40, 34, 35, and 61). For these systems GGA functionals are found to give a correct description of the EFG. On the other hand, while hybrid functionals gave reliable results for intermediate- and high-spin complexes, GGA methods seriously underestimated the corresponding, relatively large quadrupole splittings of these systems, most probably due to the inappropriate description of the exchange interaction in GGAs, which is better handled in hybrid functionals by the inclusion of Hartree–Fock exchange. The application of the COSMO solvation model to approximate the role of the molecular environment improves the DFT-calculated quadrupole splittings for the majority of the studied Fe complexes. However, COSMO led to the serious overestimation of the quadrupole splittings of high-spin Fe(II) complexes when used in combination with hybrid functionals. Similar to the isomer shift results, we also did not observe the clear preference of the Slater-type basis set over the core-polarized Gaussian one for the prediction of quadrupole splittings.

Although no single universal method can be proposed for the calculation of ⁵⁷Fe quadrupole splittings, in most cases hybrid exchange-correlation functionals in combination with the COSMO model yield sufficiently accurate results. However, in the special cases mentioned above, the omission of COSMO and/or the application of a suitable GGA functional are essential to avoid the failures described in the present study. We have provided a recipe for choosing the proper DFT technique based on a chemical classification of the compounds. This combined DFT approach delivers an excellent agreement between experimental and calculated quadrupole splittings for all investigated Fe complexes. An alternative method is also tested, where the density functional is chosen according to the magnitude of the experimental ΔE_Q, which could pave the way to a model-independent approach in assigning the Mössbauer spectra. However, the performance of this approach is barely better to that of the best hybrid, because it cannot remedy the problem of outliers.

The reliability of the DFT approach was also investigated by verifying its performance for a few case studies related to problems of high chemical relevance. We found that the largest differences between the experimental and DFT-calculated quadrupole splittings in our work and in the literature can be mainly attributed to the difficulties introduced by the description of the proper ground state. We observed this effect for the 23 and 35 complexes, and by the investigation of their electronic structure we concluded that these failures can be avoided by the careful treatment of the symmetry of these molecules to select the appropriate one from among their (quasi)-degenerate states. Our results indicate that the DFT-calculated quadrupole splittings of low-spin cis/trans-Fe^IIA₂B₄ and Fe^IIAB₅ compounds follow the ratio −1:2:1 estimated in a point charge model and agree with the experimental values. The computational method was also tested for the prediction of quadrupole splittings at phase transitions, such as spin crossover and the inversion of the orbital ground state. DFT provided good results, confirming that a combined theory and MS approach is a powerful tool to study such transitions. Finally, we found a perfect agreement for the experimental and DFT-determined signs of quadrupole splittings, which suggests the wide applicability of DFT calculations in the prediction and interpretation of this property, which is invaluable for the description of the electronic structure and local symmetry.

Supporting Information Available

The detailed derivation of the equations corresponding to the electric monopole and quadrupole interactions and the ligand contributions to V_zz for the FeA₂B₄ and FeA₅B complexes, the contributions of the Fe-3d electrons to V_zz, the electronic configurations relevant to spin crossover and the inversion of the orbital ground state, the tabulated DFT-calculated δ, ΔE_Q, η values, fit parameters and the figures representing the correlation between calculated and experimental Mössbauer parameters for all applied density functionals, the comparison of experimental and COSMO-TPSSh ΔE_Q values for selected Fe complexes computed at different geometries, the results obtained for the quadrupole splittings of cis/trans-Fe^IIA₂B₄ and Fe^IIA₅B model compounds, and the comparison of experimental and DFT-calculated signs of quadrupole splittings. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Dedication

We dedicate this paper to the memory of the late Professor Attila Vértes, author of over 500 original scientific papers related to Mössbauer spectroscopy. Attila Vértes would turn 80 years old in 2014. He introduced us to this experimental technique, and we dare to believe he would enjoy reading this work.