Quantifying inter-species differences in contractile function through biophysical modelling

Abstract

Animal models and measurements are frequently used to guide and evaluate clinical interventions. In this context, knowledge of inter-species differences in physiology is crucial for understanding the limitations and relevance of animal experimental assays for informing clinical applications. Extensive effort has been put into studying the structure and function of cardiac contractile proteins and how differences in these translate into the functional properties of muscles. However, integrating this knowledge into a quantitative description, formalising and highlighting inter-species differences both in the kinetics and in the regulation of physiological mechanisms, remains challenging. In this study we propose and apply a novel approach for the quantification of inter-species differences between mouse, rat and human. Assuming conservation of the fundamental physiological mechanisms underpinning contraction, biophysically based computational models are fitted to simulate experimentally recorded phenotypes from multiple species. The phenotypic differences between species are then succinctly quantified as differences in the biophysical model parameter values. This provides the potential of quantitatively establishing the human relevance of both animal-based experimental and computational models for application in a clinical context. Our results indicate that the parameters related to the sensitivity and cooperativity of calcium binding to troponin C and the activation and relaxation rates of tropomyosin/crossbridge binding kinetics differ most significantly between mouse, rat and human, while for example the reference tension, as expected, shows only minor differences between the species. Hence, while confirming expected inter-species differences in calcium sensitivity due to large differences in the observed calcium transients, our results also indicate more unexpected differences in the cooperativity mechanism. Specifically, the decrease in the unbinding rate of calcium to troponin C with increasing active tension was much lower for mouse than for rat and human. Our results also predicted crossbridge binding to be slowest in human and fastest in mouse.

Key points

• To facilitate translation of data from animal models into clinical applications, it is important to analyse and quantify the differences and relevance of specific physiological mechanisms between species.

• We propose a novel approach for the quantification of inter-species differences in terms of biophysical model parameters and apply this to elucidate the differences in cardiac contraction mechanisms between mouse, rat and human.

• Our results indicate that the parameters related to the sensitivity and cooperativity of calcium binding to troponin C and the activation and relaxation rates of tropomyosin/crossbridge binding kinetics differ most significantly between mouse, rat and human.

• Our results predict crossbridge binding to be slowest in human and fastest in mouse.

Introduction

Computational models of cardiac myocyte physiology provide a biophysical and quantitative framework for integrating and simultaneously interpreting multiple experimental data sets. This capacity to integrate data allows consistency of different data sources to be tested within a single mechanistically based framework, with the potential to provide greater insight into the complex and often multi-scale regulation that is crucial to physiological systems. However, this ability to integrate data also exposes models to the risk of including irrelevant or inappropriate information, which can significantly distort model predictions. To provide a specific set of examples of particular relevance to this study, in models of cardiac myocyte electrophysiology and contraction, the majority of integrated data have been recorded from small mammals, namely mouse, rat, guinea pig and rabbit. The increase in both quality and quantity of this experimental data is now supporting a transition from more generic mammalian-based models (Luo & Rudy, 1994) to increasingly species-specific models parameterised mainly from data collected from a given species under consistent conditions (Smith et al. 2007; Niederer et al. 2009; Li et al. 2010). However, in the majority of cases this transition remains incomplete due to reuse of model components because of lack of experimental data, slowing the transition to species-specific understandings.

To facilitate translation of data from animal models into clinical applications, it is important to analyse and quantify the differences and relevance of specific physiological mechanisms between species. Quantitative descriptions of this system have the capacity to formalise and highlight such inter-species differences both in kinetics and in regulation. However, such a formalisation is not trivial due to the complexity of the system and the many factors involved. To address this issue, in this study we propose a novel method for characterising inter-species differences using biophysical modelling. The biophysical models consist of sets of mathematical equations, representing the time-dependent dynamics of various components of the modelled system (‘model outputs’), which are controlled by a number of input parameters. The underlying assumption of the approach applied in this study is that the fundamental physiological mechanisms are conserved between species, meaning a single set of mathematical model equations can be used to represent multiple species by tuning the model parameters to enable the biophysical models to replicate experimentally measured data for each species. Inter-species differences can then be represented entirely by differences in values of the model input parameters. Analysing these resulting parameter sets then enables both quantification and qualitative insight into the mechanistically based differences in physiological function between species. This information can also be used to determine the relevance of experimental results obtained in one species for another. This approach, in turn, ultimately provides the potential of quantitatively establishing the human relevance of both animal-based experimental and computational models for application in a clinical context.

However, even in mature models it is important to acknowledge that obtaining meaningful results from computational models is challenging. In addition to the substantial variation observed in measured values from experiments, the structure of the biophysical models is such that a variety of different combinations of parameter values can generate approximately the same model output (Gutenkunst et al. 2007). It was therefore crucial in this study for us to also take measurement error into account when parameterising models, and to evaluate the robustness of the parameter estimates.

We recently presented a generalised framework for combined model parameterisation and analysis of model mechanisms (Tøndel et al. 2014) (see Figs 1 and 2), based on systematic exploration of the effects of varying the values of the input parameters. Using this framework requires two sets of data, one containing the input parameter values and one containing the model outputs resulting from the simulations. These two datasets are used to generate a metamodel (Tøndel et al. 2012, 2013) – a statistical regression-based approximation of the relationships between input parameters and model output metrics. The metamodel can then be used to analyse the impact of variations/noise in the model inputs on the simulation results. This procedure is repeated iteratively, gradually focusing on the most relevant ranges for the parameters by identifying sets of simulations that give output metrics close to the measured data. Analysis of the resulting parameter estimates with principal component analysis (PCA) (Jolliffe, 2002) provides a route for evaluation of the variation in parameter values replicating a set of measured data, and to define the degree to which different parameters can be constrained by available measurements. Combined, this constitutes a powerful approach to identify robust parameter estimates, which can be applied to generate new hypotheses about the investigated biological system.

Figure 1.

Illustration of classical and inverse metamodelling for sensitivity analysis and parameter estimation

Classical metamodelling was used for sensitivity analysis of the Land model (Land et al. 2012a) and the Niederer model (Niederer et al. 2006), using the regression coefficients as sensitivity measures (Tøndel et al. 2014). The inverse metamodelling was included in the parameter fitting pipeline shown in Fig. 2. The figure is reproduced from Tøndel et al. (2014) with permission from BioMed Central.

Figure 2.

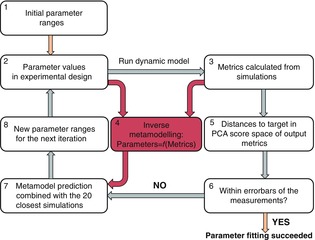
Schematic representation of the parameter fitting pipeline

Steps 2–8 were repeated in each iteration (Tøndel et al. 2014). The figure is reproduced from Tøndel et al. (2014) with permission from BioMed Central.

In this study, we apply this approach to fit the parameters of two models of cardiac contraction to replicate the physiology of multiple species (mouse, rat and human). The models are fitted to replicate routine experimental measurements and metrics that quantitatively describe measurable cellular transients. Cardiac contraction is largely controlled by changes in the cytosolic calcium (Ca²⁺) concentration measured as Ca transients (time series) that vary substantially between species, and are prone to measurement noise. Hence, it is important to determine the sensitivity of the parameter estimates to noise in the measured Ca transients, and thereby to analyse the robustness of the parameter estimates. Accounting for these sensitivities, the resulting sets of species-specific parameter values then form the basis for a quantification of inter-species differences in terms of physiological parameters.

Methods

Ethical approval

All direct data used in this study relate to model parameters that were fitted to measured data in the referenced studies, each of which complied with national ethical requirements where the experiments were performed.

Biophysical models of cardiac contraction

Cardiac muscle fibres generate tension during the action of actin and myosin crossbridge cycling (Gordon et al. 2000; Land, 2013). The muscle cells consist of many contractile sub-units, called sarcomeres, each organised into thin and thick filaments. The thick filaments contain myosin crossbridges that bind to the thin actin filament, generating force. This process is initiated by electrical activation, which results in an increase in cytosolic calcium. Binding of calcium to the regulatory calcium binding site on troponin C (TnC) within the sarcomeres initiates a cascade of conformational changes in the associated tropomyosin complex that makes the thin filament actin sites available for binding to the thick filament myosin crossbridges. A crossbridge cycle consists of a binding of the myosin crossbridge to actin followed by a force-generating power stroke and a subsequent detachment using ATP. The functional properties of TnC, including its ability to be activated by Ca²⁺, therefore have significant regulatory influence on the contractile reaction of the myocyte. Myocyte contractility is also influenced by the strength of interaction between actin and myosin, the rate of crossbridge cycling and the rate of ATP hydrolysis by myosin ATPase (Gordon et al. 2000).

Contractile protein isoforms differ in amino acid sequence between species. This translates into functional differences in the sarcomere and gives rise to inter-species differences in the resulting function (Gillis et al. 2007). While there is relatively high conservation of the amino acid sequences of TnC homologues between species and tissue types, there is wide variation in the functional properties of these proteins (Gillis et al. 2007). Moreover, regulatory proteins in the heart are potential targets for phosphorylation (Scruggs et al. 2009). Such post-translational modification results in changes in the calcium sensitivity and kinetics of force development and leads to changes in the rate and strength of cardiac contraction (Weisberg & Winegrad, 1996; Stelzer et al. 2007). This may differ between species.

To study inter-species differences, we fitted the parameters of two biophysically based models of cardiac cell contraction, the model developed by Niederer et al. (2006) (the ‘Niederer model’) and the model developed by Land et al. (2012a) (the ‘Land model’), both consisting of differential equations describing length dependence and velocity dependence of the contractile force, using experimental data for mouse, rat and human Ca transients and tension dynamics. The Land model was originally parameterised for mouse at 37°C in a whole-organ context, while the Niederer model was originally parameterised for rat at 25°C, and, as such, is unable to capture the fast relaxation kinetics of mouse cardiac muscle at higher pacing frequencies with the default parameter values.

Both models applied here have a relatively low level of detail compared to many other contraction models, making them suitable for use with organ-scale simulations, but they include enough biophysical mechanisms to enable the direct coupling of parameters to biological data and exploration of different hypotheses. The two models represent two different frameworks for simulating the generation of contractile force in cardiac cells as a consequence of calcium binding, and were originally parameterised for different species and temperatures, using un-physiological data sets that provided the necessary data to constrain the parameters. These data are not readily available for humans at physiological temperatures, so we aimed to fit the models to other measurements describing more physiological responses.

The rationale behind utilising two different models was to have the opportunity to evaluate whether our results were consistent between the two models, even though they were based on two different model frameworks and originally developed for different species and temperatures. Consistency in the results for the two models provides confidence in the conclusions drawn from the study. A description of the two contraction models including the differential equations is given in Appendix 1.

In the Land model, the calcium/TnC dynamics are represented by a standard cooperative binding equation having a Hill curve where the binding sensitivity is length-dependent and assumed to approximate the steady state solution. The Niederer model, on the other hand, uses a simple molecular binding model for troponin binding. Tropomyosin/crossbridge dynamics are represented in the Land model by a modified version of the four-state Markov model crossbridge dynamics component from Rice et al. (2008), using only the so-called non-permissive and permissive (crossbridge cycling) states. In the Niederer model, tropomyosin/crossbridge dynamics are represented by a model of the transient changes in the proportion of available actin sites, which each have a length-dependent sensitivity for binding myosin crossbridges. Both models utilise the fading memory model (FMM) (Hunter et al. 1998) for the velocity dependence. The FMM represents the velocity response as several strain rate-dependent variables that all decay with time. An advantage of this model is that it is independent of the contraction model, and can be added after modelling isometric tension and length dependence. The velocity dependence parts of the two models were not considered in this study (the velocity was set to zero for all simulations), due to lack of available data for human and rat at 37°C.

Fitting of the model parameters

The model parameters of the two contraction models described above were fitted to experimental data for mouse, rat and human found in the literature, and differences in the obtained parameter values were used to quantify inter-species differences. The generation of simulated data for mouse, rat and human, as well as the parameter fitting methodology are described in detail in Appendix 2.

Output metrics used to fit the model parameters

Given an input Ca transient, the model simulations result in output tension transients, with characteristics depending on the input parameter values and initial conditions for the model (see Appendix 1 for the model equations). The following output metrics were calculated from the tension transients resulting from simulations with different model parameter values (and input Ca transients (see Fig. 3)), and matched to measured data: time to 50 and 90% relaxation (RT₅₀ and RT₉₀), time to peak tension (TTP) and peak tension values (Peak). For human, data for 95% relaxation (RT₉₅) were used instead of RT₉₀.

Figure 3.

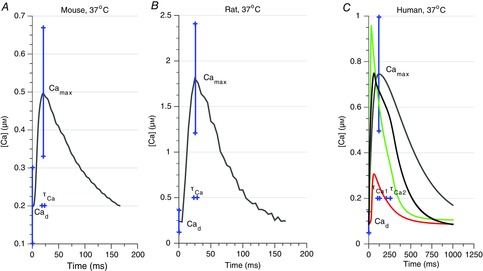
Measured Ca transients at 37°C and alternative, modelled human Ca transients

A, measured mouse Ca transient; B, measured rat Ca transient; and C, modelled human Ca transients. The human Ca transient in grey was modelled using eqn (A2.1) with measured data from Beuckelmann et al. (1992) and used to represent a ‘measured’ Ca transient for human, while the Ca transient in red was modelled using the Grandi–Pasqualini–Bers (2010) model (Grandi et al. 2010), the Ca transient in green using the Ten Tusscher (2006) model (Ten Tusscher & Panfilov, 2006) and the Ca transient in black was modelled using the O'Hara–Rudy (2011) model (O'Hara et al. 2011). The error bars used on the Ca transient parameters in the sensitivity analysis and subsequent parameter fitting are illustrated in blue.

For mouse, additional output metrics calculated from the relationship between individual Ca²⁺ concentrations and the resulting force (described in more detail in Appendix 2) were included in the parameter fitting. As the Land model had been parameterised for mouse at 37°C, the force–pCa relationship resulting from simulations with this model using the default parameter values was used as reference data for these metrics in addition to measured tension transient metrics. In the mouse parameterisation, simulations were run with both the Land and the Niederer model using sarcomere lengths of 90, 100 and 110% of resting sarcomere length (i.e. extension ratio, λ, equal to 0.9, 1 and 1.1). In the rat and human parameterisations, only the tension transient metrics at resting sarcomere length were included, due to lack of data on these additional metrics.

Parameter fitting procedure

The parameter fitting procedure is illustrated in Fig. 2, and is based on varying the input parameters in an experimental design (here consisting of 5000 different combinations of parameter values sampled using latin hypercube design (LHD) (McKay et al. 1979)), running the model to generate corresponding output metrics, and using the resulting input–output data to generate a metamodel approximation of the relationships between parameters and output metrics. This procedure is repeated iteratively, the simulations generating output metrics closest to the measured data are identified in each iteration, and new experimental designs in the parameters are generated based on the parameter values of these close simulations (Tøndel et al. 2014). Thus, a zooming into the most biologically relevant ranges for the parameters is achieved.

The initial ranges (i.e. the ranges within which the parameter values were varied in the first experimental design of the parameter fitting pipeline) for the Land and Niederer model parameters used in the parameter fitting to data for mouse, rat and human are given in Tables1 and 2, while the constraints used on some of the Niederer model parameters during the parameter fitting are given in Table3. The measured data used to fit the model parameters are given in Table4.

Table 1.

Initial ranges for the Land model parameters used in the model parameterisation

			Fitting to mouse data		Fitting to rat and human data
		Parameter set
		from original	Minimum	Maximum	Minimum	Maximum
Parameter	Description	publication	value	value	value	value
Tref	Reference tension (kPa)	120	100	140	90	140
Ca50ref	Calcium sensitivity at resting sarcomere length (μm)	0.6–0.8	0.5	0.8	0.5	2
TRPN50	Troponin C sensitivity	0.35	0.25	0.5	0.3	0.5
nTRPN	Hill coefficient for cooperative binding of Ca2+ to TnC	2	1	2.5	1	2
kTRPN	Unbinding rate of Ca2+ from TnC (ms−1)	0.1	0	0.5	0.05	0.4
nxb	Hill coefficient for cooperative crossbridge action	5	3	7	2	7
kxb	Scaling factor for the rate of crossbridge binding (ms−1)	0.1	0	0.6	0	0.1
β1	Magnitude of length-dependent activation effects	−1.5	−2	−1	−1.5*	−1.5*
β0	Magnitude of filament overlap effects	1.65	1	5	1.65*	1.65*

^*β₁ and β₀ were not varied in the model parameterisation to rat and human data, as only resting sarcomere length was used.

Table 2.

Initial ranges for the Niederer model parameters used in the model parameterisation

			Fitting to mouse data		Fitting to rat and human data
		Parameter set
		from original	Minimum	Maximum	Minimum	Maximum
Parameter	Description	publication	value	value	value	value
Ca50ref	Calcium sensitivity at resting sarcomere length (mm)	0.3×10–3	0.27×10–3	0.41×10–4	0.5×10–3	2×10–3
krefoff	Unbinding rate of Ca2+ from TnC in the absence of tension (ms−1)	0.2	0.07	0.15	0.05	0.4
kon	Binding rate of Ca2+ to TnC (μm−1 s−1)	100	140.1	317.0	50	500
nr	Relaxation parameter	3	1.17	2.30	—*	—*
β0	Magnitude of filament overlap effects	4.9	0.02	0.96	−1.5†	−1.5†
β1	Magnitude of length-dependent activation effects	−4	−1.60	−1.01	1.65†	1.65†
γ	Effect of tension on the unbinding rate of Ca2+ from TnC	2	3.29	5.00	1	5
nH	Hill coefficient in the steady-state force–pCa curve	5	9.0	15.0	4	15
Tref	Reference tension (kPa)	100	91.9	140.0	90	140
α0	Monoexponential activation rate seen in caged Ca2+ experiments (ms−1)	0.008	0.02	0.06	0.01	0.5
αr1	Slow relaxation rate (ms−1)	0.002	0.24	0.52	0.01	0.5
αr2	Fast relaxation rate (ms−1)	0.00175	0	0.02	0*	0*
Kz	Relaxation parameter	0.15	0.04	0.12	—*	—*

^†β₁ and β₀ were not varied in the model parameterisation to rat and human data, since only resting sarcomere length was used.

^*As α_r2 was set to zero, the parameters n_r and K_z became redundant.

Table 3.

Constraints used on some of the Niederer model parameters during the parameter fitting

Parameter	Minimum value	Maximum value
krefoff	0.05	0.4
kon	50	500
γ	1	5
nH	—	15
Tref	90	140

Table 4.

Description of the output metrics used to describe the tension transients, together with measured data for mouse, rat and human at 37°C, used to fit the contraction model parameters

Metric	Description	Mouse data*	Rat data†	Human data‡
RT50	Time to 50% relaxation (ms)	16–30	27–37	109–125
RT90	Time to 90% relaxation (ms)	41–59	40–68	—
RT95	Time to 95% relaxation (ms)	—	—	291–377
TTP	Time to peak tension (ms)	26–41	34–58	147–172
Peak	Peak tension (kPa)	32–52	36–48	20–50

^*Measured data for mouse at 37°C from Land et al. (2012a).

^†Measured data for rat at 37°C, based on data from Janssen et al. (2002), Hiranandani et al. (2006), Monasky et al. (2008) and Monasky & Janssen (2009).

^‡Measured data for human at 37°C (Land et al. 2012b) used to fit the contraction model parameters, based on data from Land (2013).

When fitting the Land and Niederer model parameters to the measured data in Table4, the mean values of the measurements were used as the target values; however, all resulting simulations generating output metrics values within the error bars for the measurements (i.e. the span of the values given in Table4) were considered successful in replicating measured data. This was assessed in a look-up of simulations within the ranges given in Table4.

The possibility of a reduction of the Niederer model complexity by setting the fast relaxation rate parameter α_r2 = 0 (omitting the second relaxation term of eqn (A1.11) in Appendix 1) while keeping the replication of measured data was tested for rat and human, as this was found to be possible for mouse by Tøndel et al. (2014). This makes the relaxation parameters n_r and K_z redundant, so these were not varied during the parameter fitting.

Evaluation of the sensitivity to the Ca transient

To evaluate the importance of the Ca transient characteristics (and possible noise in measured Ca transients used in the simulations) for the results, simulations were run with three different types of Ca transients: (1) experimentally measured Ca transients (Fig. 3), (2) synthetic Ca transients where the Ca transient characteristics were varied within a range around the measured Ca transient parameters and (3) Ca transients modelled using previously published biophysical models of the ventricular myocyte paced at room temperature (Ten Tusscher & Panfilov, 2006; Grandi et al. 2010; O'Hara et al. 2011) (Fig. 3C). The Ca transients modelled using the Grandi–Pasqualini–Bers, Ten Tusscher and O'Hara–Rudy models were used only in the parameter fitting to human data, and were included as supplementary analyses due to lack of a complete measured Ca transient time series. The ‘measured’ Ca transient for human was based on eqn (A2.1) in Appendix 2 using measured Ca transient parameters from Beuckelmann et al. (1992), while the measured Ca transients used for mouse and rat were measured time series data (Ca traces).

The synthetic Ca transients were generated by varying the following parameters in an experimental design consisting of 5000 different combinations of parameter values sampled using LHD within the ranges given in Table5: diastolic Ca²⁺ (Ca_d), peak Ca²⁺ concentration (Ca_max) and the time constants τ_Ca1 (time to peak Ca²⁺ concentration) and τ_Ca2 (time constant for Ca²⁺ decline), and formed the basis for a systematic analysis of the sensitivity of the model outputs to variations in the Ca transient characteristics compared to the sensitivity to the varied model parameters. A regression-based sensitivity analysis (from a classical metamodel (see Fig. 1)) was carried out to identify the Ca transient parameters and model input parameters most important for the model outputs. The regression coefficients from the metamodel are direct measures of the impact of variations in the various inputs on the simulation results. The generation of the synthetic Ca transients and the sensitivity analysis are described in more detail in Appendix 2.

Table 5.

Ranges for the Ca transient parameters used to generate the synthetic Ca transients

		Mouse simulations			Rat simulations			Human simulations
				Fitted			Fitted			Measured/fitted
Parameter	Description	Min.	Max.	value*	Min.	Max.	value*	Min.	Max.	value†
Cad	Diastolic Ca2+ (μm)	0.1	0.3	0.2	0.12	0.36	0.24	0.048	0.142	0.095
Camax	Peak Ca2+ concentration (μm)	0.33	0.67	0.50	1.21	2.41	1.81	0.497	0.995	0.746
τCa1	Time to peak Ca2+ concentration (ms)	18.9	23.1	21.0	23.4	28.6	26.0	108	132	120
τCa2	Time constant for Ca2+ decline (ms)	18.9	23.1	21.0	23.4	28.6	26.0	213.3	260.7	237

^*Values fitted from the measured Ca traces.

^†Measured values from Beuckelmann et al. (1992) were used for Ca_d and Ca_max, while the values for τ_Ca1 and τ_Ca2 were fitted from the measured Ca trace given in Beuckelmann et al. (1992).

Analysis of inter-species differences in contraction model parameter spaces

For each of the two contraction models, maps of the parameter spaces illustrating the distribution of the parameter sets giving output metrics within the error bars for measured data for the three different species, as well as the inter-species differences were generated using PCA (Jolliffe, 2002) of all parameter sets resulting from fitting the parameters to data for mouse, rat and human (when using the measured Ca traces). More details of the PCA are given in Appendix 2: ‘Principal component analysis’ and ‘Data used to analyse inter-species differences in contraction model parameter spaces’. These maps show which ranges of parameter values that correspond to specific species, and illustrate the separation of the results for the three different species as clusters/regions in the parameter spaces. These regions correspond to different combinations of ranges of values for the various parameters, giving simulations that replicate measured data for the different species, and can be related back to the underlying physiology through the parts of the mathematical models controlled by the various parameters.

The PCA score vectors represent the directions of highest variance in the data, as described in Appendix 2. In our analysis, plots of the PCA score vectors consequently show the separation of parameter values replicating measured data for the different species, while the corresponding loading vectors represent the contribution of the individual model parameters to the species differences. The size of the clusters of parameter values representing each species provides a quantitative indication of how constrained the system is given the utilised set of output metrics. Similarly, a PCA of the output metrics for the different species can indicate which metrics differ the most between species.

Results

We have analysed the sensitivity of the model results to variability in the input Ca transients, and investigated how this affects the parameter estimates. Building on these results, we have fitted the model parameters for two contraction models to data for mouse, rat and human, respectively, using a previously published parameter fitting method. The parameter fitting resulted in several alternative parameter sets for each of the three species, replicating the parameterising data. Analysis of these parameter sets with PCA showed the value ranges for the different input parameters within which measured data for the different species could be replicated, i.e. the degree of identifiability of the parameters. Comparison of the results obtained for the different species, taking the span within the species into account, indicated inter-species differences in parameters directly linked to physiological cell mechanisms.

Analysis of the sensitivity to the Ca transient

Figure 4 shows the regression coefficients from the metamodels made for the Land model and the Niederer model, using synthetic Ca transients with varying characteristics. Parameters having high absolute values for the regression coefficients had high impact on the model outputs. This allows us to elucidate the sensitivity of the simulation results to variations in the Ca transient given as input. Figure 4 shows that both models were quite sensitive to the Ca transient parameters, as the regression coefficients for the Ca transient parameters had comparable absolute values to those for the contraction model parameters. This indicates that variations in the Ca transient can have a large impact on the simulation outputs and consequently also on the parameter fitting results. This is notable due to the significant variation in Ca transients recorded experimentally, and the common use of a single representative trace in contraction model fitting. To achieve robust parameter estimates and indications of the uncertainty in the parameter values, it is therefore important to take possible variations in the Ca transients into account. Only the sensitivity analysis of the output metrics from the mouse data obtained at 110% of resting sarcomere length is shown (taking length dependence into account), but the sensitivity patterns for 90 and 100% of resting sarcomere length were very similar for both models.

Figure 4.

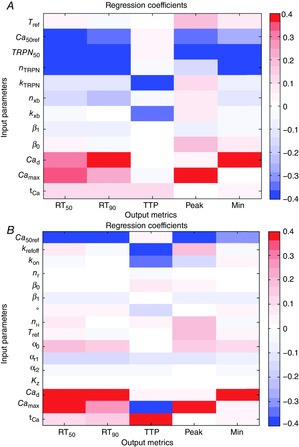
Sensitivity analysis results

Sensitivity patterns for the Land model (A) and the Niederer model (B), represented by the regression coefficients from a classical metamodel, made using the output metrics calculated at 110% of resting sarcomere length.

Fitting of the model parameters to measured data

As described in the previous section, we have shown that Ca transients can play a significant role in parameter estimation. To account for these effects in our parameter fitting for the two contraction models, we introduced three different sets of Ca transient data:

1. for mouse and rat, we fitted the model parameters using representative experimentally measured Ca traces,

2. for all three species, we used synthetically generated Ca transients based on measured phenotypic data, where the Ca transient characteristics were allowed to vary within a certain range of the measured values (see Table5), and

3. for human we used Ca transients generated by three different biophysical models of the human ventricular myocyte paced at room temperature (the Grandi–Pasqualini–Bers, Ten Tusscher and O'Hara–Rudy models).

Tables6 and 7 show the mean and standard deviations (SD) of the Land and Niederer model parameter values producing simulated tension transients replicating measured data for the three different species, using the three different sets of Ca transients described above. The resulting tension transients from the simulations with both models at resting sarcomere length, using measured and synthetic Ca transients, are shown in Figs 7, for mouse, rat and human, respectively. Figure 8 shows the resulting human tension transients obtained using Ca transients modelled with the Grandi–Pasqualini–Bers, Ten Tusscher and O'Hara–Rudy models. The span for the TTP and Peak values for mouse, rat and human – which were used together with RT₅₀ and RT₉₀/RT₉₅ to fit the model parameters – are illustrated in Figs 8 together with the tension transients from simulations replicating the measured data.

Table 6.

Mean ± SD for the Land model parameters giving mouse, rat and human output metric values

	Mouse data	Rat data		Human data
	Using the	Using the	Using	Using the
	measured	measured Ca	synthetic Ca	Beuckelmann	Using synthetic	Using the Grandi–
	Ca transient	transient	transients	Ca transient	Ca transients	Pasqualini–Bers Ca
Parameter	(n = 11*)	(n = 72)	(n = 67)	(n = 15)	(n = 13)	transient (n = 12)
Tref	118.4 ± 11.2	109.91 ± 13.12	112.8 ± 13.8	132.5 ± 5.8	128.2 ± 6.1	117.1 ± 14.8
Ca50ref	0.63 ± 0.06	1.92 ± 0.24	1.78 ± 0.23	1.19 ± 0.05	0.95 ± 0.17	0.52 ± 0.09
TRPN50	0.39 ± 0.04	0.40 ± 0.04	0.45 ± 0.04	0.34 ± 0.02	0.35 ± 0.04	0.37 ± 0.05
nTRPN	2.07 ± 0.24	1.55 ± 0.34	1.53 ± 0.34	2.91 ± 0.32	2.63 ± 0.38	1.54 ± 0.32
kTRPN	0.16 ± 0.09	0.21 ± 0.09	0.21 ± 0.10	0.23 ± 0.08	0.16 ± 0.06	0.14 ± 0.09
nxb	5.25 ± 0.86	3.6 ± 1.0	3.97 ± 1.18	3.25 ± 0.44	3.66 ± 0.69	3.38 ± 0.84
kxb	0.21 ± 0.17	0.03 ± 0.02	0.04 ± 0.03	0.02 ± 1.17×10–3	0.02 ± 4.11×10–3	4.9×10–3 ± 8.2×10–4
β1	−1.49 ± 0.27	—	—	—	—	—
β0	2.45 ± 0.81	—	—	—	—	—
Cad	—†	—	0.24 ± 0.07	—	102.4 ± 24.2	—
Camax	—	—	1.53 ± 0.23	—	594.6 ± 140.6	—
τCa1	—	—	26.15 ± 1.43	—	121.6 ± 7.5	—
τCa2	—	—	26.15 ± 1.43	—	224.1 ± 5.8	—

^*n denotes the number of succeeding parameter sets.

^†The parameters for which no results are given were not varied in the respective parameter fittings. The parameters β₀ and β₁ were not varied for rat and human, as only resting sarcomere length was used. Ca transient parameters are not given where the measured Ca transients were used.

Table 7.

Mean ± SD for the Niederer model parameters giving mouse, rat and human output metric values

	Mouse data		Rat data		Human data
							Using the
					Using the		Grandi–
	Using the	Using	Using the	Using	Beuckel-	Using	Pasqualini–	Using the	Using the
	measured	synthetic Ca	measured Ca	synthetic	mann Ca	synthetic	Bers Ca	Ten Tusscher	O'Hara–Rudy
	Ca transient	transients	transient	Ca transients	transient	Ca transients	transient	Ca transient	Ca transient
Parameter	(n = 7*)	(n = 3)	(n = 63)	(n = 46)	(n = 52)	(n = 31)	(n = 6)	(n = 99)	(n = 122)
Ca50ref	0.34×10–3 ±	0.34×10–3 ±	1.89×10–3 ±	1.78×10–3 ±	1.11×10–3 ±	1.60×10–3 ±	1.1×10–3 ±	2.0×10–3 ±	0.93×10–3 ±
	2.03×10–5	2.4×10–5	3.4×10–4	3.79×10–4	1.57×10–4	2.53×10–4	4.0×10–4	6.4×10–5	6.2×10–5
krefoff	0.11 ± 0.03	0.07 ± 0.01	0.13 ± 0.05	0.17 ± 0.09	0.28 ± 0.08	0.21 ± 0.03	0.17 ± 0.07	0.11 ± 3.2×10–3	0.29 ± 0.04
kon	230.10 ± 44.80	234.20 ± 34.90	194.6 ± 95.4	188.0 ± 91.9	271.1 ± 130.6	330.1 ± 113.2	299.9 ± 79.3	212.0 ± 6.20	240.9 ± 73.5
nr	1.78 ± 0.33	1.64 ± 0.81	—	—	—	—	—	—	—
β0	0.40 ± 0.36	0.60 ± 0.52	—	—	—	—	—	—	—
β1	−1.30 ± 0.10	−1.50 ± 0.26	—	—	—	—	—	—	—
γ	4.39 ± 0.40	3.82 ± 0.98	2.14 ± 0.40	2.75 ± 1.29	2.46 ± 0.82	1.68 ± 0.52	1.08 ± 0.05	1.02 ± 0.01	1.74 ± 0.26
nH	12.22 ± 1.34	14.05 ± 0.92	7.74 ± 2.18	8.27 ± 3.35	10.08 ± 2.07	11.22 ± 2.21	6.17 ± 1.60	7.32 ± 0.21	13.66 ± 0.80
Tref	122.00 ± 11.20	115.30 ± 13.00	111.7 ± 14.2	112.0 ± 15.2	118.9 ± 12.8	119.2 ± 13.2	107.0 ± 17.0	92.2 ± 1.79	104.2 ± 7.98
α0	0.04 ± 0.01	0.04 ± 0.02	0.08 ± 0.04	0.12 ± 0.09	0.26 ± 0.11	0.31 ± 0.06	0.41 ± 0.12	0.08 ± 2.4×10–3	0.28 ± 0.03
αr1	0.38 ± 0.08	0.37 ± 0.11	0.11 ± 0.04	0.16 ± 0.09	0.05 ± 0.01	0.07 ± 0.02	0.01 ± 2.2×10–3	0.01 ± 3.6×10–4	0.01 ± 9.0×10–4
αr2	0.01 ± 0.01	4.3×10–3 ± 6.0×10–3	—	—	—	—	—	—	—
Kz	0.07 ± 0.03	0.09 ± 0.04	—	—	—	—	—	—	—
Cad	—†	0.22 ± 0.03	—	0.24 ± 0.07	—	103.2 ± 24.4	—	—	—
Camax	—	0.51 ± 0.03	—	1.73 ± 0.32	—	869.0 ± 92.2	—	—	—
τCa1	—	21.15 ± 0.81	—	26.45 ± 1.46	—	120.2 ± 7.4	—	—	—
τCa2	—	21.15 ± 0.81	—	26.45 ± 1.46	—	232.7 ± 13.3	—	—	—

^*n denotes the number of succeeding parameter sets. ^†The parameters for which no results are given were not varied in the respective parameter fittings. The parameters β₀ and β₁ were not varied for rat and human, as only resting sarcomere length was used. Ca transient parameters are not given where the measured or fixed Ca transients were used.

Figure 7.

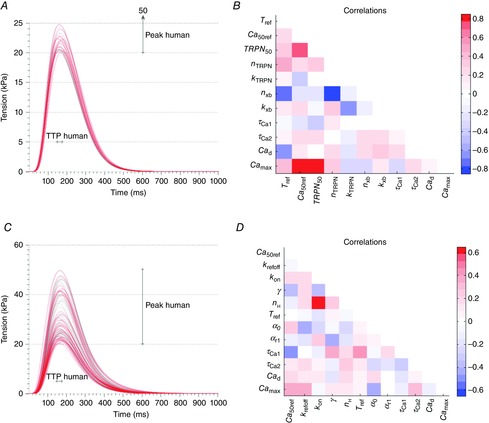
Results from parameter fitting to data for human

A and B, tension transients (A) and parameter correlation patterns (B) for the Land model simulations giving human output metric values. C and D, tension transients (C) and parameter correlation patterns (D) for the Niederer model simulations giving human output metric values. The grey lines represent the parameter sets found using the Beuckelmann Ca transient shown in Fig. 3C, while the red lines represent the parameter sets found when the Ca transient parameters were varied according to the ranges in Table5.

Similar to what has previously been found for mouse (Tøndel et al. 2014), our results show that reduction of the Niederer model by setting the fast relaxation rate parameter α_r2 to zero was possible while maintaining the fit to measured data also for both rat and human. This parameter was very poorly constrained both when using measured Ca traces and when including variations in the Ca transients (seen from the results of the mouse parameterisation). Hence, for all three species applied here, the equation system of the Niederer model could be simplified. The results for rat and human reported here are therefore produced using this reduced Niederer model version. More details of the results of the parameter fitting are given in Appendix 3.

For the Land model, the mouse data could only be replicated when using the measured Ca transient; no succeeding parameter sets were found using the synthetic Ca transients. Similarly, using the Ca transients modelled with the Ten Tusscher and O'Hara–Rudy models did not result in any simulations replicating the human data with the Land model, but the human data could be replicated using the Grandi–Pasqualini–Bers Ca transient. However, for the Niederer model, parameter sets replicating measured data for all three species could be found using all three types of Ca transients. Hence, our results indicate that the Land model cannot be fitted to replicate human contraction behaviour using these modelled Ca transients within physiologically feasible parameter ranges. This can be attributed to either deficiencies of the Land model equations or the Ca transients generated by the Ten Tusscher and O'Hara–Rudy models. Note that the time to peak values for these Ca transients are relatively low compared to experimental data.

The results in Tables6 and 7 show that, as expected due to the results from the regression-based sensitivity analysis (Fig. 4), the parameter estimates were quite sensitive to introduction of variations to the Ca transients around the measured Ca traces. However, for most of the parameter estimates, the mean value obtained using synthetic Ca transients was within the error bars (standard deviations) of the estimates obtained using the measured Ca traces. Hence, the results were relatively consistent between these two types of Ca transients.

However, the human model parameter estimates found using the Grandi–Pasqualini–Bers, Ten Tusscher and O'Hara–Rudy Ca transients showed relatively large differences in most model parameters compared to the values obtained using the Beuckelmann transient. This was expected due to the large difference in, for example, the peak values for the Ca transients and the sensitivity of the model outputs to the Ca transients used, as seen in the sensitivity analysis. The maximum difference between the mean Land model parameter estimates obtained with the Beuckelmann transient and those obtained when Ca transient variation was included was found in the k_TRPN parameter (30%), while the maximum difference between the results obtained with the Beuckelmann transient and those obtained with the Grandi–Pasqualini–Bers Ca transient was seen for the k_xb parameter (76%). For the Niederer model, the maximum difference between the mean parameter estimates obtained with the Beuckelmann transient and those obtained when Ca transient variation was included was found in the Ca_50ref parameter (44%), while the maximum difference between the Beuckelmann transient results and the results obtained with the modelled Ca transients were seen for the α_r1 parameter (80% for all three modelled Ca transients).

Correlations between model parameters and Ca transient characteristics

Using synthetic Ca transients with varying characteristics allows us to identify possible correlations between the obtained model parameter estimates and the Ca transient parameter values giving simulations that replicate measured data. For the Land model, this analysis was not possible for mouse, as only the measured Ca transient gave simulations that replicated the mouse data. Moreover, the high correlations between many of the Niederer model parameters and the Ca transient parameters, indicated in Fig. 5C, may be partly caused by the low number of parameter sets (only three) included in this analysis. For the rat and human parameterisations, however, more parameter sets replicating the measured data were obtained, providing more reliable indications of parameter correlations.

Figure 5.

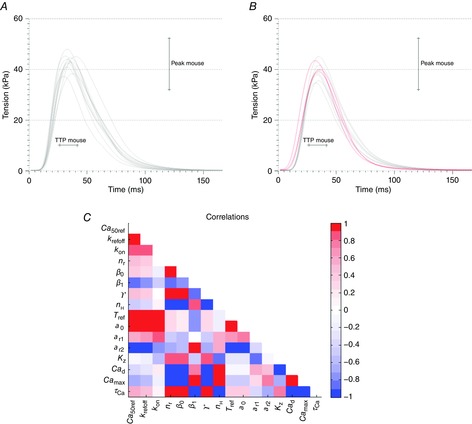
Results from parameter fitting to data for mouse

A and B, tension transients for the Land model simulations (A) and the Niederer model simulations (B) giving mouse output metric values. The grey lines represent the parameter sets found using the measured Ca transient shown in Fig. 3A, while the red lines represent the parameter sets found when the Ca transient parameters were varied according to the ranges in Table5. C, parameter correlation patterns for the Niederer model simulations giving mouse output metric values.

The correlation patterns between the Land and Niederer model parameters and the Ca transient parameters giving rat model outputs are shown in Fig. 6B and D, respectively, while the correlation patterns for the human parameters are shown in Fig. 7B and D, respectively. The results are described in more detail in Appendix 3. In summary, the main correlation patterns for both the Land and the Niederer models were the same for the rat and human results. Moreover, for both models, the correlation patterns observed between the model parameters when using one representative Ca trace (measured for rat and based on the Beuckelmann Ca transient parameters for human) showed the same main correlation patterns (results not shown).

Figure 6.

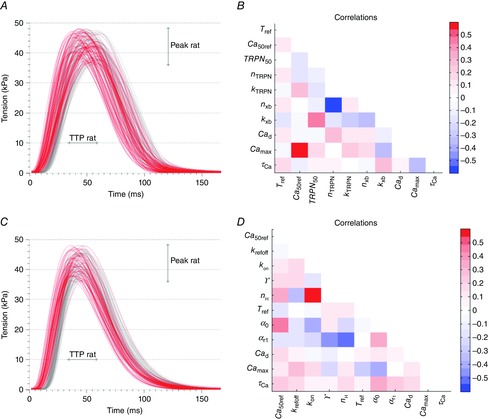
Results from parameter fitting to data for rat

A and B, tension transients (A) and parameter correlation patterns (B) for the Land model simulations giving rat output metric values. C and D, tension transients (C) and parameter correlation patterns (D) for the Niederer model simulations giving rat output metric values. The grey lines represent the parameter sets found using the measured Ca transient shown in Fig. 3B, while the red lines represent the parameter sets found when the Ca transient parameters were varied according to the ranges in Table5.

For the Land model, the main correlation patterns were a negative correlation between the parameters n_xb and n_TRPN (the Hill coefficients for cooperative crossbridge action and cooperative binding of Ca²⁺ to TnC, respectively), and a positive correlation between Ca_50ref (the calcium sensitivity at resting sarcomere length) and Ca_max (the peak value of the Ca transient).

For the Niederer model, the strongest correlations observed were a positive correlation between the parameters k_on (the binding rate of Ca²⁺ to TnC) and n_H (the Hill coefficient in the steady-state force–pCa curve), a negative correlation between α_r1 (the slow relaxation rate) and γ (the effect of tension on the unbinding rate of Ca²⁺ from TnC), and a positive correlation between α₀ (the monoexponential activation rate) and Ca_50ref. Moreover, the peak value of the Ca transient had a high positive correlation with k_refoff (the unbinding rate of Ca²⁺ from TnC in the absence of tension) and a negative correlation with α₀. As seen for the Land model, Ca_50ref and Ca_max were positively correlated.

Analysis of inter-species differences in contraction model parameter spaces

PCA was carried out for the two models separately, on all parameter sets able to replicate the mouse, rat and human measurements (using measured Ca transients). The scores from the PCA represent the spread in the parameter values, and are plotted in Fig. 9A for the Land model and Fig. 9B for the Niederer model. Our results showed that the fitting procedure resulted in distinct clusters of parameter values representing each of the three species in the first three principal components (PCs). Figure 9 shows that the spread of Land model parameter values giving mouse output metrics is smaller for human than for rat or mouse, while for the Niederer model the spread is smallest for the mouse data. The sparse data for mouse compared to rat and human was probably caused by application of output metrics describing the force–pCa relationship in addition to tension transient metrics to constrain the model parameters for this species (the force–pCa metrics were not available for rat and human). Using additional metrics to constrain parameters gives the system fewer degrees of freedom, and generally lowers the uncertainty in the parameter estimates, which was the motivation for including these additional metrics for mouse. Hence, inclusion of these additional metrics also for rat and human might decrease the sizes of these clusters. The fact that fewer data points represent mouse in the PCA model implies that the ‘model centre’, i.e. the mean parameter values, are closer to rat and human values than to mouse values. However, Fig. 9 shows that the PCA model is still capable of separating the data for the three species into clearly defined clusters, and thereby illustrate the inter-species differences and the relative contributions of the various model parameters to these differences.

The three species were mostly separated along PC1 and PC2, which combined explained about 60% of the variance in the data for both models. The PCA loadings shown in Fig. 10 indicate the relative contribution from each of the model parameters to the inter-species differences, while the mean parameter estimates are shown together with the minimum and maximum values obtained for each parameter for the three species in Fig. 11. As PCA accounts for the entire variation in the dataset, not only between the different species, the span in parameter values within a single species seen in Fig. 11 has to be taken into account when making conclusions about the inter-species differences. Figure 11 shows that for the Land model, the parameters k_TRPN, n_xb and k_xb were those having the largest spans in the parameter estimates within the results for the individual species (k_xb was badly constrained only for mouse). For the Niederer model, k_refoff, k_on, n_H and α₀ had the largest spans. The other parameters were relatively well constrained by the measured data used to fit the parameters.

Our results indicated that the parameter Ca_50ref, the calcium concentration needed for 50% bound TnC in steady state, differs most significantly between mouse, rat and human in both the Land and the Niederer model. This parameter was among the highest ranked contributors to the first three PCs for both models (Fig. 10), and shows relatively high variability in mean value and span (Fig. 11). The value of this parameter is highest for rat and lowest for mouse. A high calcium concentration in the Ca transients is linked to a lower calcium sensitivity, i.e. a high value of Ca_50ref, a pattern that was confirmed by the parameter correlation analysis above. This is consistent with the measured Ca transients, where the highest value for Ca_max was observed for rat and the lowest for mouse.

Furthermore, the parameter n_TRPN, which participates in controlling the dynamics of the fraction of regulatory TnC sites with bound Ca²⁺ in the Land model, differed significantly between species; much higher values of n_TRPN were obtained for human than for rat and mouse (Fig. 11). This parameter determines the cooperativity of calcium binding to TnC. Figure 10 shows that this parameter has a relatively large contribution to the first PC. There is presently not sufficient data available to fully characterise this effect at physiological temperatures, but the proposed mechanism involves changes in the unbinding rate of calcium to TnC when the thin filament is unblocked. A similar effect was represented in the Niederer model as a decrease in this off-rate with increasing active tension, linked to the parameter γ, which was also among the most widely changing parameters and had a large contribution to PC2 in the PCA for the Niederer model (Fig. 10B). The values of γ were much higher for mouse than for rat and human, meaning that for mouse, the unbinding rate of Ca²⁺ from TnC decreases to a lower degree with increasing active tension. An explanation of this result might be that a lower effect of tension on Ca²⁺ unbinding is required for mouse, as a high effect of tension leads to a slower relaxation. The unbinding rate of Ca²⁺ from TnC in the absence of tension (k_refoff) showed slightly higher values for human than for rat and mouse, and had a large contribution to PC1 in Fig. 10B.

In the Land model, the TnC sensitivity, TRPN₅₀, and the unbinding rate of Ca²⁺ from TnC, k_TRPN, showed only minor differences taking the span of the parameter value estimates (shown in Fig. 11) into account. The small changes in k_TRPN are consistent with the hypothesis that calcium binding is fast and diffusion limited, and the similarities in TRPN₅₀ are also expected physiologically, considering the tight coupling between TnC binding, thin filament activation and crossbridge cycling.

The identifiability of the Land model parameter k_xb (scaling factor for the rate of crossbridge binding, which participates in controlling the dynamics of the fraction of available crossbridges cycling) was very low for mouse (causing a high contribution to PC2 in Fig. 10A), probably caused by the fast mouse kinetics giving this parameter an undefined upper limit (as was seen also in Tøndel et al. 2014). The identifiability of this parameter was much higher for rat and human, which have slower kinetics (see Fig.11). Our results thus demonstrated the importance of differences in crossbridge binding and predicted that this is slowest in human and fastest in mouse. This was also confirmed by the results from the Niederer model, where the tropomyosin/crossbridge parameters α₀ and α_r1 were among those that showed the largest differences between the species (and relatively large loading values in Fig. 10B). The results for human showed the highest activation rate and the lowest relaxation rate, while the lowest activation rate and the highest relaxation rate were observed for mouse.

For both models and all species, the reference tension T_ref had approximately the same value, which is consistent with the conservation of systolic pressure seen across mammals. Also n_H, the Hill coefficient in the steady-state force–pCa curve, had values within the same range for all three species. The mean values of k_on, the binding rate of Ca²⁺ to TnC in the Niederer model, differed only slightly between the species, but the identifiability of this parameter was relatively low for rat and human.

Discussion

Models are increasingly moving from generic repre-sentations, with parameters fitted to data from a wide variety of species, to focusing on representing specific species and using correspondingly focused data. In parallel, these models have developed to a point where they can provide a framework for simulating human physiology with a stronger link to clinical data (Ten Tusscher et al. 2009; Iyer et al. 2010; Niederer et al. 2011; Smith et al.2011; O'Hara & Rudy, 2012). However, due to the inherent practical and ethical limitations on access to human tissue, the data for fitting the parameters for human models are routinely augmented using animal measurements. To effectively inform our interpretation of these models it is thus important for us to distinguish and quantify differences between human cells and other species at the level of model parameters.

Assuming conservation of the underlying physiological mechanisms, parameter fitting can be exploited to provide a method for quantifying differences in physiology between species identified by distinct regions of the model parameter space corresponding to measurements from different species. We show in this study that the same model frameworks can be used to represent physiological function for three different species by adjusting the parameter values. Hence, a single set of model equations can represent multiple species by tuning the model parameters to the experimental data set from each species. This provides the opportunity to gain a deeper understanding of the differences in, for example, ion conductivities, kinetics and binding affinities. Understanding such differences is important for the use of animal models to guide clinical interventions.

Specifically, in our study, we have tuned the parameters of the Land and Niederer models of contraction to represent differences between mouse, rat and human, and presented maps of the parameter spaces of the two models generated with PCA. Our results showed distinct clusters in both parameter spaces corresponding to the three different species-specific models. These results indicate that the parameters related to calcium sensitivity, the cooperativity of Ca²⁺ binding to TnC and the activation and relaxation rates of tropomyosin/crossbridge binding kinetics differ most significantly between mouse, rat and human, while, for example, the Hill coefficient in the steady-state force–pCa curve and the reference tension show only minor differences between the species. The latter was not unexpected due to the similarities in the systolic pressure observed across these species.

Our results also identify that the sensitivity of calcium binding to TnC is highest for mouse and lowest for rat. This was potentially due to the large differences in the calcium transients seen in Fig. 3, with a higher calcium concentration in the transients being linked to a lower calcium sensitivity. The relatively small inter-species differences in the unbinding rate of Ca²⁺ from TnC (represented by the parameter k_TRPN in the Land model) seen here support the hypothesis that calcium binding is fast and diffusion limited. However, on the other hand, tension-dependent feedback on the Ca²⁺ unbinding rate from TnC seems to be species dependent. In the Niederer model, active tension has a lower effect on the unbinding rate for mouse than for rat or human (seen from the differences in the parameter γ). Furthermore, the dynamics of the fraction of actin sites available for crossbridge binding showed large differences between the species, with the highest activation rate and the lowest relaxation rate observed for human, and the lowest activation rate and the highest relaxation rate for mouse. The large inter-species differences in crossbridge binding are consistent with the results of Palmer & Kentish (1998), who estimated crossbridge cycling rate differences between rat and guinea pig to be six times faster in rat. Also Harding et al. (1990) showed that myocytes from larger animals tend to contract and relax more slowly than those from smaller animals.

Rice et al. (2008) published species-specific values for the rate constants for unbinding of calcium to TnC, as well as crossbridge cycling rates, according to differences between rat and rabbit. In their study, the largest modification to adjust the model from rat to rabbit was a factor of 5 decrease in the transition rates in the crossbridge cycle, to simulate the differences in myosin isoforms. Additionally, a 10% lower unbinding rate of Ca from TnC and a slightly higher Ca²⁺ sensitivity were used for rabbit compared to rat. These modifications are consistent with our findings with respect to differences between smaller and larger animals. Our results have also demonstrated the importance of differences in crossbridge binding, and predicted this to be slowest in human and fastest in mouse. Moreover, expected inter-species differences in the sensitivity of calcium binding to TnC – caused by large differences in the calcium transients – have been confirmed in our analysis.

By fitting contraction models to measured tension transient characteristics (time to peak tension, peak tension and relaxation time), we have identified unexpected inter-species differences in the cooperativity mechanism of Ca²⁺ binding to TnC. This is represented by the decrease in the unbinding rate of calcium to TnC with increasing active tension, which was much lower for mouse than for rat and human. This result was unexpected, as TnC sequences are known to be relatively consistent between species (Gillis et al. 2007). This discrepancy between conserved TnC sequence and differences in kinetics may be explained by differences in troponin I (TnI) properties or phosphorylation level between species. Differences in TnI phosphorylation have previously been shown to be important for contractile performance in myocytes (Westfall & Borton, 2003; Wijnker et al. 2014). Takimoto et al. (2004) showed that TnI phosphorylation plays an important role in the rate dependence of cardiac muscle. Thus, such differences in phosphorylation may also play an important role in differences between species depending on their heart rate (HR).

The smaller decrease in the unbinding rate of calcium from TnC with increasing active tension observed here for mouse, compared to rat and human, may be due to the higher HR in mice. Additionally, with the smaller ventricular cavity within which flow is viscous rather than inertia dominated, the need to maintain pressure for a longer period following the initial development of tension will be smaller. This increased cooperativity may be because the need for the mouse to sustain tension over this period is less than for rat and human. Specifically, a rapid spike in tension that decays quickly will have a lower effect in human due to a higher inertia. However, note that a larger difference is here predicted between mouse and rat than between rat and human. This may be caused by the larger representative Ca transient recorded in the rat in contrast to the smaller transient in the mouse. This allows the rat model to accommodate a decrease in unbinding of TnC without producing a long tension transient.

As discussed by Tøndel et al. (2014), there is no guarantee that all possible clusters of parameter values producing feasible model outputs have been found. However, a set of 5000 different parameter value combinations in each iteration of the parameter fitting pipeline is quite substantial, ensuring a dense sampling. Moreover, LHD (McKay et al. 1979), which was used here, is a sampling method that has been developed especially for generating even sampling in high-dimensional spaces. It is therefore likely that all feasible regions of the parameter space are identified during the fitting procedure. Moreover, the results of Tøndel et al. (2014) indicated that the fitting procedure used in this study is relatively robust, as two independent parameter fittings (one with the full Niederer model version and one with the reduced equation system) identified the same region of the Niederer model parameter space replicating mouse data.

In the present study, independent parameter identifications were run using first a single Ca transient, and subsequently with variations mimicking measurement error introduced in the Ca transients. The resulting parameter estimates from these independent fittings were relatively consistent for most of the parameters, and for both models. However, the results obtained in the human parameterisation showed that the differences in the obtained parameter estimates due to differences between the modelled Ca transients were larger than those caused by introducing variations in the Ca transient parameters around measured data. This result highlights the importance of using replicated measurements of Ca transients when parameterising models and careful consideration of the model to use if modelled Ca transients are applied.

Moreover, the resulting values of parameters for the two models representing the same mechanisms are relatively consistent between the models, giving additional confidence in the uniqueness of the reported parameter estimates. The lack of Land model simulations replicating mouse data when using synthetic Ca transients was unexpected, especially given the dense sampling used here, but indicates that the model was unable to replicate the tension transient with nominal noise in the Ca transient. This could reflect the fact that contraction parameters or proteins are tuned to the Ca transient given the need to generate similar tension in all cells. Another explanation might be that some bias was introduced due to fitting the model parameters to the force–pCa relationship of the default Land model in addition to the tension transients for mouse.

In this study our combined parameter fitting and multivariate data analysis approach was used to quantify species differences, but other interesting applications would be analysis of temperature differences or differences between patients, something that is highly relevant for the application of models for both understanding basic physiology and ultimately clinical application. Additionally, this type of analysis could also be used to guide the identification of the value of specific experimentally based assays for both understanding given physiological systems or subsystems, to delineate mechanisms and/or to develop more models capable of providing increasingly relevant physiological understandings in experimental contexts.

Glossary

Abbreviations

Ca_d

diastolic Ca²⁺

Ca_max

peak Ca²⁺ concentration

FMM

fading memory model

HC-PLSR

hierarchical cluster-based partial least squares regression

HR

heart rate

LHD

latin hypercube design

OLS

ordinary least squares

PC

principal component

PCA

principal component analysis

Peak

peak tension

PLSR

partial least squares regression

RT₅₀

time to 50% relaxation

RT₉₀

time to 90% relaxation

RT₉₅

time to 95% relaxation

SL

sarcomere length

TnC

troponin C

TnI

troponin I

TTP

time to peak tension

τ_Ca1

time to peak Ca²⁺ concentration

τ_Ca2

time constant for Ca²⁺ decline

Appendix 1 Description of the biophysical models

Length dependence equations of the Land model

In the Land model (Land et al. 2012a), the calcium sensitivity is given by

A1.1

where Ca_50ref is the calcium sensitivity at resting sarcomere length, λ is the extension ratio, i.e. the sarcomere length (SL) relative to the resting SL, and β₁ is the magnitude of the length-dependent activation effects.

The dynamics of the fraction of regulatory TnC sites with bound calcium (represented by TRPN) is given by

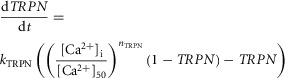A1.2

where k_TRPN is the unbinding rate of Ca²⁺ from TnC, [Ca⁺²]_i is the concentration of free Ca²⁺ and n_TRPN is the Hill coefficient for cooperative binding of Ca²⁺ to TnC.

The dynamics of the fraction of available crossbridges cycling (XB) is given by

A1.3

A1.4

where k_xb is the scaling factor for the rate of crossbridge binding, n_xb is the Hill coefficient for cooperative crossbridge action and TRPN₅₀ is the TnC sensitivity.

The influence of filament overlap on tension h(λ) is given by

A1.5

and

A1.6

where β₀ is the magnitude of the filament overlap effects.

When the velocity dependence is not taken into account (the velocity is set to zero), the normalised force F_n then becomes

A1.7

and the active tension T_a is given by

A1.8

Length dependence equations of the Niederer model

Also in the Niederer model (Niederer et al. 2006), the Ca sensitivity, [Ca^{2 +} ]₅₀, is given by eqn (A1.1). The dy-namics of the concentration of Ca²⁺ bound to TnC site II, 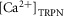, is given by

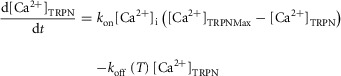A1.9

where k_on is the binding rate of Ca²⁺ to TnC, 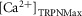is the maximum concentration of ions that can bind to TnC site II, [Ca²⁺]_i is the concentration of free Ca²⁺, T is the tension and

A1.10

k_refoff is the unbinding rate of Ca²⁺ from TnC in the absence of tension, γ is the effect of tension on the unbinding rate of Ca²⁺ from TnC and T_ref is the reference tension.

The dynamics of the fraction of actin sites available for crossbridge binding (z) is given by

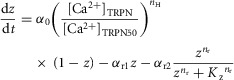A1.11

where α₀ is the monoexponential activation rate seen in caged Ca²⁺ experiments, [Ca²⁺]_TRPN50 is the concentration of Ca²⁺ bound to TnC at half activation, n_H is the Hill coefficient in the steady-state force–pCa curve, α_r1 is the slow relaxation rate, α_r2 is the fast relaxation rate, and n_r and K_z are relaxation parameters.

In this model it is assumed that crossbridges bind rapidly relative to thin filament kinetics and that not all actin sites are available at full activation. Thus, tension is proportional to z and the ratio of z to the fraction of actin sites available at full activation, z_Max, for a given SL (z/z_Max) is equal to the ratio of the isometric tension at a given [Ca²⁺]_i and SL, T₀, to the maximum tension at full activation for the same SL (T₀/T_0Max):

A1.12

with half activation [Ca²⁺]_50.

The fraction of actin sites available at full activation (z_Max) is defined by solving dz/dt = 0 with [Ca²⁺]_TRPN = [Ca²⁺]_TRPNMax (full activation) from eqn (A1.11), giving

A1.13

where

A1.14

A1.15

The maximum tension at full activation for a given SL, T_0Max, is defined by

A1.16

where T_ref is the reference tension (the maximum tension at resting SL), β₀ is the magnitude of the filament overlap effects and λ is the extension ratio (relative to resting SL).

Combining eqn (A1.9) with eqn (A1.16) gives

A1.17

Combining eqn (A1.16) with T₀/T_0Max = z/z_max gives isometric tension defined as

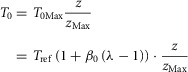A1.18

Appendix 2 Supplementary descriptions of the methods

Generation of simulated mouse data

Versions of the Land and Niederer models functioning for mouse at 37°C have already been published (Land et al. 2012a; Tøndel et al. 2014). However, as shown in Tøndel et al. (2014), intrinsically coupled parameters exist, meaning that many combinations of parameter values can generate the same model output, as long as a specific relationship between the values of the coupled parameters is maintained. The original models may have been fully constrained by detailed un-physiological measurements, but here we fitted the parameters to a set of functional, ensemble, physiological data. Hence, the published parameter sets may not represent unique sets for replicating the observed metrics. This was shown to be the case for the Niederer model by Tøndel et al. (2014), resulting in several different alternative parameterisations capable of reproducing measured data. To evaluate whether this is the case also for the Land model and to analyse the span of different parameter values replicating mouse experimental data, a set of simulations was run with the Land model, using 5000 different length dependence parameter value combinations varied in an LHD (McKay et al. 1979). The ranges used for the Land model parameters are given in Table1 and the Ca transient (Land et al. 2013) used in the simulations is shown in Fig. 3A. The outputs from the simulations were compared to those obtained with the default parameter set using the procedure described by Tøndel et al. (2014).

For mouse, the default output from the Land model (which had already been fitted to data for mouse at 37°C) was used as the target values in fitting of the Niederer model to mouse at 37°C, and in searching for additional Land model parameter values replicating measured data. In addition to the output metrics in Table4 calculated from the tension transients resulting from the simulations, we also matched the force–pCa (F–pCa) relationships of the two models to the Land model default output, using metrics from simulations run with fixed Ca²⁺ concentrations. The Ca²⁺ concentrations used were a logarithmically spaced series of 82 different concentrations from 0.15 to 1 μM together with the concentration 10 μM. The resulting steady-state tensions were normalised by the maximal simulated tension value.

Model and experimental steady state force–calcium curves are routinely approximated by a Hill curve that can be logarithmically transformed to be linear. The relationship between pCa and log(F/(1 – F)) was therefore fitted to a straight line using ordinary least squares (OLS) regression (values of (1 – F)<10⁻³ were removed to avoid numerical errors), and the following metrics were calculated to represent the properties of the force–pCa relationship (see also Tøndel et al. 2014):

• slope and intercept of the fitted line

• root mean square error of prediction from fitting to a straight line (representing the deviation from a straight line)

• correlation coefficient between the fitted line and the simulated force–pCa data (representing the deviation from a straight line)

• maximum tension

• root mean square deviation between the simulated force values and the target Land model force (in standardised variables)

The F–pCa curves were simulated for 90, 100 and 110% of resting sarcomere length, and the resulting F–pCa metrics were used as additional output constraints (together with the tension transient characteristics in Table4) to fit the model parameters.

To analyse the sensitivity of the Land model and the Niederer model to the input Ca transient, and provide an indication of the spread in possible Ca transients and parameter values that would generate output metrics within the error bars for the measured metrics – thereby taking into account that the measured Ca transients can be noisy – we also carried out an analysis where the input Ca transient was varied using an extended version of the equation from Hunter et al. (1998). Equation (A2.1) was used to calculate the Ca transients based on four new metrics: diastolic Ca²⁺ (Ca_d), peak Ca²⁺ concentration (Ca_max) and the time constants τ_Ca1 (time to peak Ca²⁺ concentration) and τ_Ca2 (time constant for Ca²⁺ decline). For mouse, we used τ_Ca1 = τ_Ca2 = τ_Ca, which was equal to the time to peak Ca²⁺ concentration. As described below, for human, the values of τ_Ca1 and τ_Ca2 were not set equal, which was the reason for separating the equation into two parts.

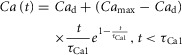A2.1

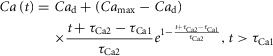Simultaneously, the model parameters of the two models were varied in an LHD of 5000 parameter value combinations, to evaluate the sensitivity of the modelling results to the Ca transient, while varying the parameter values within a specific distance from the mouse parameter values found in Land et al. (2012a) and Tøndel et al. (2014). Thereby the sensitivity of the model outputs to variations in the model parameters and the Ca transient could be analysed simultaneously, and possible coupling between Ca transient parameters and model parameters identified. The ranges used for the model parameters of the Land model and the Niederer model are given in Tables1 and 2, respectively. The ranges for the Niederer model parameters were found using the mean of the parameter sets found in Tøndel et al. (2014) ± the mean divided by 10, keeping the parameter values in the proximity of those previously determined (Tøndel et al. 2014).

The following values for the three Ca transient parameters correspond to the measured Ca transient (shown in Fig. 3A) used in Tøndel et al. (2014): Ca_d = 0.2, Ca_max = 0.5 and τ_Ca = 21. Here, Ca_d, Ca_max and τ_Ca were varied in an LHD of 5000 combinations of values, using ranges according to the precision levels for Ca_d and Ca_max reported by Beuckelmann et al. (1992), i.e. 50 and 33%, respectively. In addition, a 10% error was applied to the time constant τ_Ca. This gave the ranges shown in Table5 for the Ca transient parameters in eqn (A2.1). These are illustrated as error bars in Fig. 3A. The same ranges for Ca_d, Ca_max and τ_Ca were used in both the Land model and the Niederer model simulations. Simulations were run with both models from the resulting Ca transients calculated using eqn (A2.1), and for 90, 100 and 110% of resting sarcomere length. Based on the simulation results, the output metrics in Table4 were calculated, used in the sensitivity analysis described below and compared to the experimentally measured data. The resulting dataset formed the first iteration of the parameter fitting pipeline illustrated in Fig. 2, which was used to identify additional parameter sets replicating mouse data.

Generation of simulated rat data

The Land and Niederer models were fitted to rat data, first using a measured Ca transient (shown in Fig. 3B), and subsequently using Ca transients generated from eqn (A2.1) with Ca transient parameters varied in an experimental design, to take measurement error into account. As for the mouse parameterisation, τ_Ca1 = τ_Ca2 = τ_Ca, and the error bars used on the Ca transient parameters were calculated to match the precision level reported by Beuckelmann et al. (1992). Also for rat, 10% error was applied to τ_Ca. This produced the ranges in Table5 for the Ca transient parameters in eqn (A2.1), as illustrated in Fig. 3B.

For the Land model, the parameter ranges given in Table1 were used in the initial experimental design in the parameter fitting procedure (see Fig. 2), with β₁ and β₀ at default values, as only resting sarcomere length was used. These initial ranges were based on prior knowledge about biologically feasible values for the different parameters. The parameters T_ref, TRPN₅₀, n_TRPN, k_TRPN and n_xb were only allowed to vary within the ranges given in Table1, with the exception of n_TRPN, which was given an upper bound of 5. The other parameters were allowed to vary outside the initial ranges during the parameter fitting.

For the Niederer model, the initial parameter ranges given in Table2 were used in the parameter fitting. For all simulations, only resting sarcomere length was used. In addition, we set α_r2 = 0, causing the model component involving n_r and K_z to be zero, and the values of n_r and K_z consequently redundant, to test whether we could make a reduced model version for rat, as was found to be the case for mouse in Tøndel et al. (2014). During the fitting procedure, the constraints shown in Table3 were used on the Niederer model parameter values.

For both models, the experimental designs contained 5000 simulations based on LHD (McKay et al. 1979) in each iteration of the parameter fitting pipeline, and the output metrics in Table4 were calculated from the resulting tension transients (for rat, only the metrics representing the tension transient characteristics were included due to lack of data for the force–pCa relationship). The experimentally measured data in Table4 were used to fit the parameters for both contraction models.

Generation of simulated human data

As for the rat parameterisation, the initial ranges for the model parameters submitted to the fitting pipeline (see Fig. 2) when fitting to human data were according to Tables1 and 2 for the Land model and the Niederer model, respectively. Only resting sarcomere length was used. According to Beuckelmann et al. (1992), Ca_d was 95 ± 47 nM and Ca_max 746 ± 249 nM in normal cells. The time constants τ_Ca1 and τ_Ca2 were fitted from a measured Ca transient from Beuckelmann et al. (1992), giving τ_Ca1 = 120 ms and τ_Ca2 = 237 ms. The human Ca transient data were generated using eqn (A2.1), resulting in the Ca transient shown in Fig. 3C.

The models were first fitted using the Ca transient in Fig. 3C, and subsequently fitted using Ca transient parameters varied in an experimental design using ranges according to the error bars given above and illustrated in Fig. 3C. A 10% error was put on the fitted time constants τ_Ca1 and τ_Ca2. The ranges used for the Ca transient parameters are shown in Table5. For both contraction models, the experimental designs contained 5000 simulations based on LHD (McKay et al. 1979) in each fitting iteration, and the output metrics and measured data in Table4 were used to fit the model parameters (only the metrics representing the tension transient characteristics were included due to lack of data for the force–pCa relationship). The same constraints were used for these parameter values as in the rat parameterisation. In the same way as for the parameter fitting procedures for mouse and rat, the feasibility of a reduced version of the Niederer model was analysed by setting the Niederer model parameter α_r2 = 0.

As the human Ca transient used above was not based on measured time series data, but based only on measurements for Ca transient parameters (and the Ca transient calculated using eqn (A2.1)), for comparison, the same procedure was repeated using Ca transients calculated using the following three models: Grandi–Pasqualini–Bers (2010) (Grandi et al. 2010), Ten Tusscher (2006) (Ten Tusscher & Panfilov, 2006) and O'Hara–Rudy (2011) (O'Hara et al. 2011). These Ca transients are shown together with the Beuckelmann transient in Fig. 3C.

Sensitivity analysis methodology

To evaluate the sensitivity of the modelling results to the Ca transient, the output metrics from the simulations were related to the Ca transient parameters using metamodelling, an approach that has been shown to be useful for sensitivity analysis, as well as analysis of interactions between input parameters and covariance patterns between model outputs (Tøndel et al. 2013).

Here so-called classical metamodelling (see Fig. 1) was applied for the sensitivity analysis, predicting the model outputs as functions of the input parameters using regression methodology (Kleijnen, 2007; Tøndel et al. 2010, 2011, 2012, 2013; Vik et al. 2011; Isaeva et al. 2012a, 2012b, 2012c; Martens et al. 2013) (when the input parameters are predicted as functions of the model outputs, the approach is referred to as inverse metamodelling (Tøndel et al. 2012; Isaeva et al. 2012b)). The regression coefficients can then be used as measures of the sensitivity of the model outputs to variations in the input parameters and the Ca transient. High absolute values for the regression coefficients indicate high sensitivity. The approach described by Tøndel et al. (2014), based on partial least squares regression (PLSR) (Wold et al. 1983; Martens & Martens, 1986, 2001; Martens & Næs, 1989; Tøndel et al. 2010; Vik et al. 2011), was used for the sensitivity analysis.

The sensitivity analysis was done on the results from the mouse simulations (with the parameter value ranges given in Tables1 and 2), as feasible parameter ranges were already known for this species (Land et al. 2012a; Tøndel et al. 2014).

Parameter fitting methodology

The approach presented by Tøndel et al. (2014), and there applied to re-parameterise the Niederer model to match the output from the Land model, was applied to fit the model parameters of both models to measured data for rat and human at 37°C. As described in Tøndel et al. (2014), the fitting of model parameters to measured metrics was based on a combination of inverse metamodelling (illustrated in Fig. 1) using the locally linear regression method hierarchical cluster-based partial least squares regression (HC-PLSR) (Tøndel et al. 2011, 2012, 2013) and an iterative zooming into regions of the parameter space that produced feasible model outputs using repeated experimental designs in the parameter values. The same HC-PLSR settings as in Tøndel et al. (2014) were used. The parameter fitting pipeline is illustrated in Fig. 2. Steps 2–8 were repeated iteratively until parameter values generating output metric values within the error bars for the measured data from the literature were found.

Principal component analysis

PCA (Jolliffe, 2002) decomposes the data into latent variables (linear combinations of the original variables) represented by so-called scores and loadings, where the scores represent the coordinates of each data point in the new coordinate system spanned by the PCs from PCA and the loadings are the coefficients in the linear combinations of the original parameters making up the new coordinate system. The PCA score vectors therefore represent the spread of the simulations, while the corresponding PCA loading vectors are the weights in the linear combination, and in our case represent the contribution of each of the model parameters to the PCA scores. Equation (A2.2) shows the PCA decomposition of the data (X) into scores (T) and loadings (P).

A2.2

Using A PCs, this becomes

A2.3

where E_A represents the error caused by excluding (A_max – A) PCs. In the present study, the number of included PCs was chosen so that they together explained 99% of the total variance in X.

Data used to analyse inter-species differences in contraction model parameter spaces

Only the results achieved using the measured Ca transients were used for mouse and rat, while for human, only the results achieved using the Ca transient from Beuckelmann et al. (1992) in Fig. 3C were included in the PCA. For the Niederer model, the parameter sets given by Tøndel et al. (2014) were used for mouse. For the Land model, all parameter sets from the simulations with the measured mouse Ca transient (as described in ‘Generation of simulated mouse data’) that were found to replicate the output metrics from the default Land model parameter set were used. The parameter values were scaled by subtracting the mean and dividing by the standard deviation over the values for each parameter prior to the PCA, to make the analysis independent of the absolute value ranges for the different parameters.

Appendix 3 Details of the results from the parameter fitting

Fitting of the model parameters to mouse measurements

Fitting of the Land model parameters to measured data for mouse

To characterise the uncertainty in the parameter value estimates, 5000 simulations were run with the Land model, first using the measured mouse Ca transient and subsequently using varying Ca transient parameters. For mouse, both the tension transients for 90, 100 and 110% of resting sarcomere length, and the resulting force–pCa relationships were matched to the result obtained with the default parameter set as described by Tøndel et al. (2014). This resulted in 11 distinct parameters sets for the Land model that were capable of replicating the experimental data when the measured mouse Ca transient was used in the simulations. The tension transients from these 11 simulations at resting sarcomere length are shown in Fig. 5A and the mean and standard deviations for the mouse parameter values are given in Table6. When we used the measured mouse Ca trace, the maximum variation was found in the parameter k_xb (±81%). No additional parameter sets replicating the measured data were identified when Ca transient variation was included in the parameter fitting.

Fitting of the Niederer model parameters to measured data for mouse

In Tøndel et al. (2014), seven Niederer model parameter sets were found to replicate measured data for mouse using the measured Ca transient. When taking Ca transient variations into account, three additional parameter sets were identified that gave tension transients for 90, 100 and 110% of resting sarcomere length and force–pCa relationships matching the results from the default Land model. The tension transients at resting sarcomere length from the Niederer model simulations that gave mouse output metrics are shown in Fig. 5B and the mean and standard deviations over the set of parameter value combinations are given in Table7.

Table7 shows that most of the parameter estimates are sensitive to variations in the input Ca transient, but that a few parameters, for example the Ca²⁺ sensitivity, Ca_50ref, the monoexponential activation rate, α₀, and the slow relaxation rate, α_r1, showed good stability against variations in the Ca transients. When we used the measured mouse Ca trace, the maximum variation was found in the α_r2 (±100%) parameter for the Niederer model. When Ca transient variation was included in the fitting, the variation in the α_r2 parameter changed to ±140%. Hence, the conclusion made by Tøndel et al. (2014) that the α_r2 parameter was redundant was confirmed here. The second largest variation was found in the parameter β₀ for the Niederer model (±90% when using the measured Ca transient, and ±87% when Ca transient variation was included).

Fitting of the model parameters to rat measurements

Fitting of the Land model parameters to measured data for rat

Fitting of the Land model parameters to measured data for rat using only the measured Ca transient resulted in 72 parameter sets producing output metric values within the reported ranges of the measured data. When a varying Ca transient was used in the parameter fitting, 67 additional parameter sets produced output metrics replicating the measurements. The mean and standard deviations for the rat parameter values are given in Table6, while the tension transients from simulations at resting sarcomere length are shown in Fig. 6A. When we used the measured rat Ca trace, the maximum variation was found in the parameter k_xb (±67%) (the same parameter as for the mouse results). When Ca transient variation was included in the fitting, the variation in the k_xb parameter changed to ±75%.

Fitting of the Niederer model parameters to measured data for rat

For the Niederer model, 63 simulations gave output metrics within the measured ranges for the rat data when using only the measured Ca transient. When a varying Ca transient was used in the parameter fitting, 46 additional parameter sets produced output metrics replicating the measurements. The tension transients from simulations at resting sarcomere length with all rat parameter sets are shown in Fig. 6C, and the mean and standard deviations for the parameter values are given in Table7.

When we used the measured rat Ca trace, the maximum variation was found in the α₀ (±50%) parameter for the Niederer model. When Ca transient variation was included in the fitting, the variation in the α₀ parameter changed to ±75%.

Similar to what was found for mouse in Tøndel et al. (2014), our results show that reduction of the Niederer model by setting the fast relaxation rate parameter α_r2 to zero was possible while maintaining the fit to measured data also for rat.

Fitting of the model parameters to human measurements

Fitting of the Land model parameters to measured data for human

When the Ca transient from Beuckelmann et al. (1992) was used, 15 parameter sets produced metrics within the error bars for the human measurements. Varying the Ca transient parameters within the error bars reported in Beuckelmann et al. (1992) resulted in 13 additional parameter value combinations replicating measured data for human. The mean and standard deviations over these human parameter values are given in Table6 and the tension transients resulting from all simulations at resting sarcomere length replicating human data are shown in Fig. 7A.

Fitting of the Land model to the Grandi–Pasqualini–Bers Ca transient resulted in 12 parameter sets (the mean and standard deviations are given in Table6), giving the tension transients at resting sarcomere length shown in Fig. 8A. The results obtained using the Grandi–Pasqualini–Bers Ca transient showed large deviations from the results obtained with the Beuckelmann transient, something that was expected due to the large difference in, for example, the peak value for the two Ca transients. In particular, the following parameters showed large differences from the results obtained with the Beuckelmann transient: T_ref, Ca_50ref, n_TRPN and k_xb.

Figure 8.

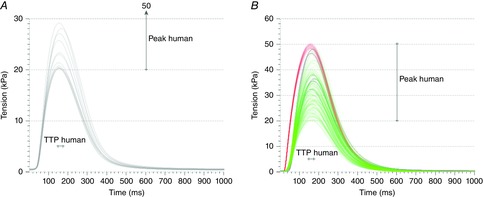
Results from model parameter fitting using the alternative, modelled Ca transients for human

A, tension transients for the Land model simulations giving human output metric values when using the Grandi–Pasqualini–Bers Ca transient. B, tension transients for the Niederer model simulations giving human output metric values when using the Grandi–Pasqualini–Bers Ca transient (grey), the Ten Tusscher Ca transient (red) and the O'Hara–Rudy Ca transient (green).

Figure 9.

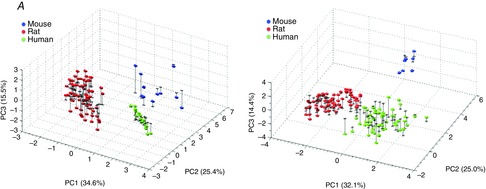
Maps of inter-species differences in the model parameter spaces

PCA-based maps of the parameter spaces of the Land model (A) and the Niederer model (B). The three first PCs from a PCA of the parameter sets found to replicate measured data for mouse, rat and human, respectively, are shown. The percentage explained variance by each PC is shown in parentheses. The lines illustrate the distance from the different points to the plane spanned by PC1 and PC2.

Figure 10.

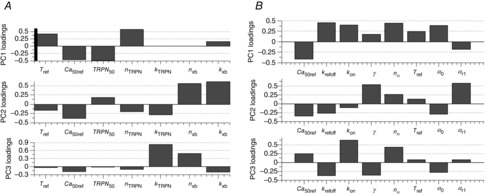
Contribution of the different parameters to the inter-species differences

PCA loadings for the first three PCs from the analysis of the succeeding parameter sets for the Land model (A) and the Niederer model (B).

Figure 11.

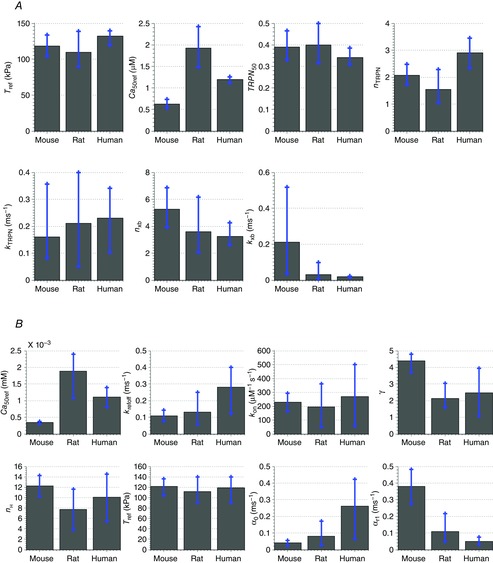
Land model and Niederer model parameter values for mouse, rat and human

Mean parameter estimates obtained for the Land model (A) and the Niederer model (B) from parameter fittings using the measured Ca transients for mouse and rat, and the Beuckelmann Ca transient (Beuckelmann et al. 1992) for human. The error bars indicate the maximum and minimum values obtained for each parameter.

When we used the Beuckelmann Ca transient for human, maximum variation was found in the parameter k_TRPN (±35%). When Ca transient variation around the Beuckelmann transient was included in the fitting, the variation in the k_TRPN parameter changed to ±38%. However, when the Grandi–Pasqualini–Bers Ca transient was used, the variation in the Land model parameter k_TRPN changed to ±64%.

Fitting of the Niederer model parameters to measured data for human

Fitting of the Niederer model parameters to measured data for human resulted in 52 parameter sets replicating the measured data when the Ca transient from Beuckelmann et al. (1992) was applied, and 31 additional parameter sets when the Ca transient parameters were varied. The mean and standard deviations for these parameter sets are given in Table7, and the tension transients resulting from simulations at resting sarcomere length are shown in Fig. 7C. Our results showed that reduction of the Niederer model by setting α_r2 = 0 is possible while keeping the replication of measured data also for human. Hence, for all three species applied here, the equation system of the Niederer model could be simplified.

Fitting of the Niederer model to the Grandi–Pasqualini–Bers, Ten Tusscher and O'Hara–Rudy Ca transients resulted in 6, 99 and 122 parameter sets, respectively (the mean and standard deviations are given in Table7), giving the tension transients at resting sarcomere length shown in Fig. 8B. The relatively large differences in the parameter estimates reflect the large differences in the Ca transients and the sensitivity of the model outputs to the Ca transients used. The following parameters showed large differences in estimated values according to the Ca transient applied: Ca_50ref, k_on, γ, n_H, α₀ and α_r1.

When we used the Beuckelmann Ca transient for human, maximum variation was found in the parameter k_on (±48%). When Ca transient variation around the Beuckelmann transient was included in the fitting, the variation in k_on changed to ±34%. Applying the modelled Ca transients, maximum variation was found in the k_refoff (±41%) parameter when using the Grandi–Pasqualini–Bers Ca transient, in the α_r1 (±3.6%) parameter when using the Ten Tusscher Ca transient and in the k_on (±30%) parameter when using the O'Hara–Rudy Ca transient.

Correlations between model parameters and Ca transient characteristics

Parameter correlation patterns for the Land model

The correlation patterns between the Land model parameters and the Ca transient parameters giving rat model outputs are shown in Fig. 6B, and indicate that the Hill coefficients for cooperative crossbridge action and cooperative binding of Ca²⁺ to TnC (the parameters n_xb and n_TRPN) are highly negatively correlated, the rate of crossbridge binding (represented by the scaling factor k_xb) is positively correlated to TnC sensitivity (TRPN₅₀), and the calcium sensitivity at resting sarcomere length (Ca_50ref) has a high positive correlation with the peak value of the Ca transient (Ca_max). Several of the other parameters were also correlated, but to a lower degree.

The correlation patterns between the Land model parameters and the Ca transient parameters giving human model outputs shown in Fig. 7B show that the strong negative correlation between n_xb and n_TRPN seen for rat was confirmed here, but here n_xb was in addition negatively correlated to the reference tension T_ref. The parameters k_xb (scaling factor for the rate of crossbridge binding) and k_TRPN (unbinding rate of Ca²⁺ from TnC) were also negatively correlated, while Ca_50ref had a high positive correlation with the TnC sensitivity (TRPN₅₀) and the peak value of the Ca transient. The latter two parameters were also positively correlated. Diastolic Ca²⁺ (Ca_d) was negatively correlated with T_ref.

Parameter correlation patterns for the Niederer model

The correlation patterns between the Niederer model parameters and the Ca transient parameters giving rat model outputs are shown in Fig. 6D, indicating that several of the parameters of the Niederer model are correlated, for example k_on (the binding rate of Ca²⁺ to TnC) and n_H (the Hill coefficient in the steady-state force–pCa curve), which were positively correlated. n_H was also negatively correlated to the slow relaxation rate, α_r1, which was again negatively correlated to the effect of tension on the unbinding rate of Ca²⁺ from TnC (represented by the parameter γ). The monoexponential activation rate, α₀, was positively correlated with the Ca²⁺ sensitivity, Ca_50ref. The peak value of the Ca transient had a positive correlation with k_refoff (the unbinding rate of Ca²⁺ from TnC in the absence of tension), and a negative correlation with the activation rate α₀. The Ca transient metric τ_Ca was positively correlated to Ca_50ref and α₀.

The correlation patterns between the Niederer model parameters and the Ca transient parameters giving human model outputs shown in Fig. 7D show that the strong positive correlation between k_on and n_H seen for rat was confirmed here, as was the negative coupling between α_r1 and γ. Likewise, the activation rate parameter α₀ was positively correlated with Ca_50ref, and the peak value of the Ca transient had also for human a high positive correlation with k_refoff and a negative correlation with α₀. The Ca transient metric τ_Ca1 was negatively correlated with Ca_50ref and positively correlated with γ and T_ref. As seen for the Land model, Ca_50ref and Ca_max were positively correlated. Hence, also for the Niederer model, the correlation patterns for rat and human were relatively similar.

Summary

The parameter sets provided here for the Land and Niederer models enable the spatial coupling of common cellular models for use in human electromechanics simulations. Moreover, we previously found that for mouse at 37°C, a reduced version of the Niederer model was sufficient to reproduce the isometric twitch and steady state force–calcium experimental data (Tøndel et al. 2014), and in this study we have shown that this reduced version applies for all three species. This reduced complexity of the Niederer model, achieved for all three species by identifying redundant model components, makes this model more suitable for integration with large-scale whole organ simulations. All parameter sets were successfully tested for model stability.

Additional Information

Competing interests

The authors declare that they have no competing interests.

Author contributions

K.T. contributed to conception of the study and design of the computer experiments, performed the computer simulations, analysed the data and wrote the paper. S.L. participated in designing the computer experiments, collecting the experimental data from the literature and writing of the paper. S.A.N. contributed to conception of the study and to writing of the paper. N.P.S. contributed to conception and coordination of the study and to writing of the paper. All authors read and approved the final manuscript.

Funding

The research leading to these results received funding from the Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 611823; FP7 Marie Curie Actions Intra-European Fellowship for Career Development (IEF) no. 298494; the Department of Health via the National Institute for Health Research (NIHR) comprehensive Biomedical Research Centre award to Guy's & St Thomas’ NHS Foundation Trust in partnership with King's College London and King's College Hospital NHS Foundation Trust; the United Kingdom EPSRC (EP/G007527/2, EP/H02025X/1), Welcome Trust (WT 088641/Z/09/Z) and Biotechnology and Biological Sciences Research Council BBSRC (BB/J017272/1).