Inward rectifier potassium currents in mammalian skeletal muscle fibres

Abstract

Inward rectifying potassium (Kir) channels play a central role in maintaining the resting membrane potential of skeletal muscle fibres. Nevertheless their role has been poorly studied in mammalian muscles. Immunohistochemical and transgenic expression were used to assess the molecular identity and subcellular localization of Kir channel isoforms. We found that Kir2.1 and Kir2.2 channels were targeted to both the surface andthe transverse tubular system membrane (TTS) compartments and that both isoforms can be overexpressed up to 3-fold 2 weeks after transfection. Inward rectifying currents (IKir) had the canonical features of quasi-instantaneous activation, strong inward rectification, depended on the external [K⁺], and could be blocked by Ba²⁺ or Rb⁺. In addition, IKir records show notable decays during large 100 ms hyperpolarizing pulses. Most of these properties were recapitulated by model simulations of the electrical properties of the muscle fibre as long as Kir channels were assumed to be present in the TTS. The model also simultaneously predicted the characteristics of membrane potential changes of the TTS, as reported optically by a fluorescent potentiometric dye. The activation of IKir by large hyperpolarizations resulted in significant attenuation of the optical signals with respect to the expectation for equal magnitude depolarizations; blocking IKir with Ba²⁺ (or Rb⁺) eliminated this attenuation. The experimental data, including the kinetic properties of IKir and TTS voltage records, and the voltage dependence of peak IKir, while measured at widely dissimilar bulk [K⁺] (96 and 24 mm), were closely predicted by assuming Kir permeability (PKir) values of ∼5.5 × 10⁻⁶ cm s⁻¹ and equal distribution of Kir channels at the surface and TTS membranes. The decay of IKir records and the simultaneous increase in TTS voltage changes were mostly explained by K⁺ depletion from the TTS lumen. Most importantly, aside from allowing an accurate estimation of most of the properties of IKir in skeletal muscle fibres, the model demonstrates that a substantial proportion of IKir (>70%) arises from the TTS. Overall, our work emphasizes that measured intrinsic properties (inward rectification and external [K] dependence) and localization of Kir channels in the TTS membranes are ideally suited for re-capturing potassium ions from the TTS lumen during, and immediately after, repetitive stimulation under physiological conditions.

Key points

• This paper provides a comprehensive electrophysiological characterization of the external [K⁺] dependence and inward rectifying properties of Kir channels in fast skeletal muscle fibres of adult mice.

• Two isoforms of inward rectifier K channels (IKir2.1 and IKir2.2) are expressed in both the surface and the transverse tubular system (TTS) membranes of these fibres.

• Optical measurements demonstrate that Kir currents (IKir) affect the membrane potential changes in the TTS membranes, and result in a reduction in luminal [K⁺].

• A model of the muscle fibre assuming that functional Kir channels are equally distributed between the surface and TTS membranes accounts for both the electrophysiological and the optical data.

• Model simulations demonstrate that the more than 70% of IKir arises from the TTS membranes.

• [K⁺] increases in the lumen of the TTS resulting from the activation of K delayed rectifier channels (Kv) lead to drastic enhancements of IKir, and to right-shifts in their reversal potential. These changes are predicted by the model.

Introduction

Inward rectifier potassium (Kir) channels are known to play a crucial role in skeletal muscle physiology as, together with chloride channels (ClC-1; Bretag, 1987), they are responsible for the characteristic negative resting membrane potentials that result from potassium and chloride concentration gradients (Katz, 1948; Hodgkin & Horowicz, 1957, 1959b; Stanfield et al. 2002). The properties of Kir currents (IKir) were extensively investigated in amphibian muscle fibres (Hodgkin & Horowicz, 1959b, 1960; Standen & Stanfield, 1978b; Leech & Stanfield, 1981; Stanfield et al. 2002) where they have been shown to originate at the surface and transverse tubular system (TTS) membranes (Almers, 1972b; Standen & Stanfield, 1979; Ashcroft et al. 1985). In contrast, IKir measurements in mammalian skeletal muscle fibres are scarce (Duval & Leoty, 1980; Beam & Donaldson, 1983; Barrett-Jolley et al. 1999) and have yielded an incomplete characterization of the functional properties of Kir channels in their natural environment.

It has been reported, by immunohistochemistry (IH) and molecular biological methods, that mammalian skeletal muscles express several types of Kir channels, including Kir1.1, Kir2.1, Kir2.2, Kir2.6 and Kir6.2 (KATP) channels (Kubo et al. 1993; Raab-Graham et al. 1994; Takahashi et al. 1994; Doupnik et al. 1995; Inagaki et al. 1995; Kondo et al. 1996; Kristensen et al. 2006; Dassau et al. 2011). Nevertheless, it is generally accepted that Kir channels in skeletal muscle belong to the Kir2.x family, and that Kir2.1 and Kir2.2 may be the most prevalent isoforms (Doupnik et al. 1995; Stanfield et al. 2002; Hibino et al. 2010; Dassau et al. 2011); yet, the evidence about their location in the surface and TTS membrane is less conclusive (Kristensen et al. 2006; Dassau et al. 2011). Also, heterologously expressed Kir2.1 and Kir2.2 channels display strong inward rectification, are constitutively active and are able to form heterotetramers (Doupnik et al. 1995; Stanfield et al. 2002; Hibino et al. 2010). However, their functional characterization in the naïve environment of skeletal muscle fibres, together with a quantitative balance of the respective IKir contributions from the surface and TTS membranes, as estimated for amphibian muscle, is missing.

This paper reports results from experiments that have been carefully designed to characterize IKir in murine fast muscle fibres and to ultimately define the distribution of Kir channels between the surface and TTS membrane compartments. To this end, we have combined electrophysiological and optical methods and model simulations to quantitatively assess not only the physiological properties of ion channels in the context of adult mammalian skeletal muscle fibres, but also their relative distribution between surface and TTS membranes (S/TTS ratio). This approach has been used previously to perform similar studies of the ClC-1 currents (DiFranco et al. 2011a), sodium (NaV1.4; DiFranco & Vergara, 2011) and potassium delayed rectifier channels (KV1.4 and KV3.4; DiFranco et al. 2012) of adult murine fibres. We also performed IH and transient expression experiments to study the targeting of native and transgenic IKir2.1 and 2.2 channels.

The present work extends previous studies from our laboratory characterizing other ion conductances present in the sarcolemma and TTS membranes that are responsible for the electrical properties of mammalian skeletal muscle fibres. The knowledge gained here is vital to understand the homeostasis of potassium ions during sustained activity, and how it may affect the fibres’ excitability.

Methods

Biological preparations

Animals were handled according to guidelines laid down by the Animal Care Committee of the University of California. Mice were killed by deep isoflurane anaesthesia, followed by quick neck dislocation. Flexor digitorum brevis (FDB) and interossei (IO) muscles were dissected from 4- to 6-month-old male mice (C57BL) obtained from Jackson Laboratory (Bar Harbor, ME, USA). Muscle fibres were isolated by enzymatic dissociation as previously described (Woods et al. 2004; DiFranco et al. 2007, 2011a,b, 2013).

Although most of the experiments were performed in untreated isolated fibres from naïve (control) animals, some were isolated from animals transfected with recombinant DNA of Kir2 channels. Once dissociated, the fibres were usually stained with the potentiometric dye di-8-ANEPPS following previously described procedures (DiFranco et al. 2005, 2011a, 2012). Only fibres displaying sharp sarcomere banding patterns were used for the experiments.

Transfection of FDB and IO muscles with plasmids (pEGFPC1, Clontech, Palo Alto, CA, USA) coding for inward rectifier channels was attained by in vivo electroporation (DiFranco et al. 2006, 2009). Plasmids for two Kir2x channels, from different species, were used: a mouse Kir2.1 tagged with enhanced green fluorescent protein (EGFP) at the N terminus (EGFP-mKir2.1) and a rat Kir2.2 tagged with EGFP at the N terminus (EGFP-rKir2.2); both were kindly donated by Dr C. Vandenberg (University of California, Santa Barbara).

Electrophysiological and optical methods

Dissociated fibres were placed on coverslip-bottomed Petri dishes that were mounted on the stage of an inverted microscope. The microscope was equipped with a standard epifluorescence illuminator, a CCD camera and a custom-made low noise photo-detector based on the use of a PIN photodiode and a patch-clamp amplifier (DiFranco et al. 2011a, 2012). Brightfield and fluorescence images of dissociated fibres were acquired with the CCD camera, and the voltage-dependent fluorescence changes of di-8-ANEPPS were recorded with the photodetector as described elsewhere (DiFranco et al. 2011a, 2012). The surface area of the fibres was calculated using a proprietary finite path integration algorithm as applied to the contour of the fibres in brightfield image projections taken with a 10× objective. This method takes into account the irregular geometry of isolated FDB fibres. The algorithm also provides the effective length of the fibres (i.e. the length of the integration path). To match the experimental data with the predictions of the model, which is based on a cylindrical approximation, we back-calculated, from the surface area and the effective length, an equivalent diameter.

A two microelectrode amplifier (Dagan, Minneapolis, MN, USA) was used to record and control the membrane potential of the fibres (DiFranco et al. 2011a, 2012; DiFranco & Vergara, 2011). Most experiments were performed under voltage-clamp conditions. The holding potential (HP) was set at the calculated potassium equilibrium potential (see below). Both microelectrodes were filled with the internal solution (see below), and had resistances of 8–10 MΩ. Under these conditions, we verified that potential distortion in the voltage records is not observed even when currents as large as 1.5 mA cm⁻² are activated.

Western blot analysis of Kir2.1 and Kir2.2 expression

FDB and IO muscles were collected together and homogenized as described elsewhere (DiFranco et al. 2011a,b, 2012; DiFranco & Vergara, 2011). The proteins in the microsomal fraction (50 μg) were separated by SDS-PAGE. After transfer to PVDF membranes, proteins were immunoblotted with two mouse monoclonal antibodies: anti-Kir2.1 (NeuroMab, Davis, CA, USA, 75-210/ clone N112B/14) or anti-Kir2.2 (NeuroMab 75-203/ clone N124B/38). Both antibodies were diluted at 1:500. The secondary antibody used was an HRP-conjugated goat anti-mouse (MP Biomedicals, Santa Ana, CA, USA) diluted at 1:2000. The dihydropyridine receptor (DHPR), detected with anti-DHPRa1s antibody (Thermo Scientific MA3-920, Waltham, MA, USA; 1:500), was used as a membrane marker of the TTS membranes (DiFranco et al. 2011b). Blot images were collected using a CCD camera attached to a ChemiDoc chemiluminescent detection system and analysed using Quantity One software (BioRad Laboratories, Hercules, CA, USA).

Immunohistochemistry

Immunohistochemistry was performed using the same antibodies as for Western blotting. FDB and IO muscles were dissected out and cleaned from connective tissue. Muscles were stretched to ∼20% their slack length, pinned down to Silgard bottomed Petri dishes and fixed in 2% formaldehyde (in PBS, pH 7.4) for 30 min. After three washes with PBS, tissue was permeabilized with Triton X-100 (0.2% in PBS added with 5% normal goat serum, NGS) for 90 min, and then washed three times (10 min each) with PBS plus 5% NGS. Incubation with primary antibodies (either anti-Kir2.1 or Kir2.2, 1:100 dilution) was performed overnight at 4°C, followed with three washes with PBS added with 5% NGS (10 min each). Incubation with secondary antibody (goat anti-mouse linked to Alexa Fluor 488, dilution 1:1000; Life Technologies, Carlsbad, CA, USA) was performed overnight at 4 °C, and then washed three times before imaging. Muscles were imaged using a two-photon laser scanning microscope (TPLSM; Radiance 2100, BioRad), using a 20 × 0.75 NA objective (Olympus). Excitation was set at 880 nm and emission was collected with a cube composed of 424–44/488/540–80 nm (excitation/dichroic/emission). The location of the maximum intensity of bands in second harmonic generation images (410–490 nm) of the fibres was used as a marker of the M-line position.

Solutions

Fibers were enzymatically dissociated in Tyrode solution (in mm: 150 NaCl, 4 KCl, 2CaCl₂, 1MgCl₂, 20 Mops, 10 glucose). Fixation, permeabilization and antibody incubation were done in PBS. Kir currents were measured in the presence of various extracellular [K⁺] concentrations (12, 24, 48 and 96 mm). To this end, appropriate volumes of two solutions, one devoid of potassium (0-K⁺ External, in mm: 154 NaCl, 2CaCl₂, 1 MgCl₂, 20 Mops, 10 glucose) and one containing 96 mm K⁺ (96-K⁺ External, in mm: 96 KCl, 48 NaCl, 2 CaCl₂, 1 MgCl₂, 20 Mops, 10 glucose) were mixed. The internal solution contained (mm): 150 KOH, 110 aspartic acid, 5 MgCl₂, 5 reduced glutathione, 5 ATP di-Na, 5 creatine phosphate di-Na and 10 EGTA. The calculated potassium equilibrium potential (E_K) for solutions containing 96, 48, 24 and 12 mm [K⁺] was −11, −29, −46 and −64 mV, respectively. E_Cl in all solutions was constant (−70 mV). TTX (200 nm), 9-anthracene carboxilic acid (200 μm) and nifedipine (20 μm) were used to block Na⁺, Cl⁻ and Ca²⁺ currents, respectively. IKir was blocked with Ba²⁺ (1 mm), or by bathing the fibres in TEA-Cl External solution in which K⁺ was replaced by TEA⁺: 154 TEA-Cl, 2 CaCl₂, 1 MgCl₂ and 20 Mops.

Radial cable model simulations

The properties of IKir, and the impact that they have on membrane potential changes in the TTS, were simulated using a simplified model for Kir channels and by including them in the radial cable model of the muscle fibre (Adrian et al. 1969b; Adrian & Peachey, 1973; Ashcroft et al. 1985; DiFranco et al. 2011a, 2012; DiFranco & Vergara, 2011). Details of model equations and integration methods are described in the Appendix.

Data acquisition and analysis

Data acquisition and conditioning was as previously described (DiFranco et al. 2011a,b; DiFranco & Vergara, 2011). Unless indicated otherwise, data are presented as means ± SEM. Means were compared using Student's t test; significance was set at P < 0.05.

Results

Kir currents from FDB fibres

Inward K⁺ currents were first recorded in the presence of 96 mm external potassium concentration in fibres voltage-clamped at a holding membrane potential (HP) close to the theoretical E_K (−10 mV). Note that under these conditions, the delayed rectifier K⁺ conductance (K_V) is mostly inactivated (DiFranco et al. 2012). Figure 1A shows that low amplitude hyperpolarizing pulses (e.g. to −40 mV, trace c) elicit robust inward currents while equal magnitude depolarizing pulses (e.g. to +20 mV, trace b) result in negligible outward currents. Although the inward currents in response to small hyperpolarizations do not apparently decay in time during the 100 ms pulses, they visibly decay in response to larger hyperpolarizations (e.g. to −80, −120 and −160 mV, traces d, e and f, respectively). Simultaneous recordings of the membrane potential are shown in Fig. 1E. Note that these records do not show obvious distortions even in the presence of currents as large as ∼1.2 mA cm⁻². Furthermore, Fig. 1B shows that inward currents are virtually eliminated by the addition of 1 mm Ba²⁺ to the external solution; an equivalent blockage was attained by 5 mm Rb⁺ (data not shown). By subtracting currents before and after Ba²⁺ addition, a Ba²⁺-sensitive current component is obtained at each pulse magnitude (Fig. 1C). Hereafter, we refer to this net current as the inward rectifier K⁺ current (IKir). Peak IKir values of ∼1.2 mA cm⁻² are measured in response to 150 mV hyperpolarizing pulses (Fig. 1A, trace f). Voltage records in Fig. 1D, measured in the presence of Ba²⁺, are almost identical to those in Fig. 1E, reinforcing the fact that the voltage clamp control is well maintained regardless of the magnitude of the currents. The strong inward rectification of IKir is clearly appreciated in the peak I–V plot of Fig. 1F. The asymptotic slope of the I–V plot, i.e. the maximal conductance (gKir_max) at the prevailing conditions was, for this particular fibre, 8.2 mS cm⁻²; also, as expected, the reversal potential of IKir is ∼−10 mV.

Figure 1.

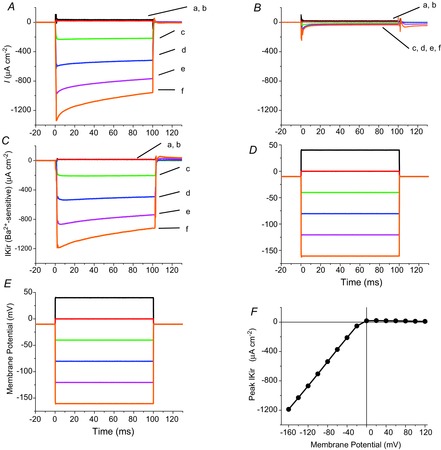
Potassium inward rectifying currents in adult FDB fibres

A, membrane currents in response to 100 ms voltage-clamp pulses recorded from an FDB fibre in the presence of 96 mm [K⁺]. Pulses were to +40, +20, −40, −80, −120 and −160 mV in traces a–f, respectively. B, membrane currents recorded after adding 1 mm Ba²⁺ to the external solution. Note that most currents seen in control conditions are blocked. C, Ba²⁺-sensitive currents (IKir) obtained by subtracting equivalent traces in A and B. D and E, membrane potential traces, as recorded by the voltage electrode simultaneously with the traces in A and C, respectively. F, voltage dependence of the peak (onset) IKir in C.

Dependence of IKir on the extracellular K⁺ concentration ([K⁺]_o)

Ever since the classical work of Hodgkin & Horowicz (1959a), it has been well documented in a variety of biological preparations that gKir depends on [K⁺]_o, but not on [K⁺]_i (Almers, 1972b; Hagiwara & Takahashi, 1974; Hagiwara & Yoshii, 1979; Leech & Stanfield, 1981). Curiously, this property has been only indirectly suggested for rat muscle fibres (Beam & Donaldson, 1983), but not directly proved in mammalian muscle preparations (e.g. mouse). For reasons that will become obvious later in the paper, we needed to quantitatively establish the [K⁺]_o dependence of IKir while maintaining [K⁺]_i constant. Consequently, as shown in Fig. 2, we performed experiments like those illustrated in Fig. 1 for several fibre populations in the presence of 12 mm (7 fibres, open squares), 24 mm (11 fibres, filled squares), 48 mm (8 fibres, open circles) and 96 mm (10 fibres, filled circles) extracellular [K⁺], while keeping the intracellular concentration constant (150 mm). For all concentrations tested, although inward rectification is a common feature, the asymptotic slopes of the I–V plots progressively decrease from large to small extracellular [K⁺]. From these plots we obtained gKir_max values of 1.0, 1.85, 4.43 and 7.53 mS cm⁻² for 12, 24, 48 and 96 mm K⁺, respectively. In addition, as [K⁺]_o was reduced, the reversal potentials for IKir extrapolated from the plots were −10, −29, −46 and −64 mV (filled circles, open circles, filled squares and open squares, respectively) for 96, 48, 24 and 12 mm [K⁺]_o, respectively; these values are quite close to the theoretical equilibrium values of −11, −29, −46 and −64 mV.

Figure 2.

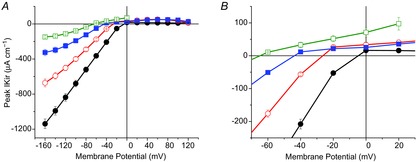
Effects of the extracellular K+ concentration on the slope and reversal potential of IKir

A, voltage dependence of the peak IKir recorded in fibres bathed with external solutions containing 96 mm (filled circles), 48 mm (open circles), 24 mm (filled squares) and 12 mm (open squares) [K⁺]_o. The symbols are connec-ted with lines of the same colour, and the bars represent SEM. B, enlarged section of the plot in A to show the leftward shift of reversal potential of the currents in response to reduced [K⁺]_o. The reversal potentials for 96, 48, 24 and 12 mm were −4.5, −26, −43 and −64 mV, respectively. The corresponding theoretical E_K values were (in mV): −11 (filled circles), −24 (open circles), −46 (filled squares) and −64 (open squares).

Two Kir isoforms are expressed in adult FDB fibres

To determine which Kir isoform(s) may be responsible for the IKir records in Fig. 1 and the I–V plots in Fig. 2, we performed Western blot and IH analysis of FDB muscles (Fig. 3). Using antibodies specific for Kir2.2, we identified a single band of ∼50 kDa, demonstrating the presence of this isoform in FDB microsomal fractions (Fig. 3A). Our results concur with previous data demonstrating that this isoform appears as a single band with a similar molecular weight (Leonoudakis et al. 2004; Fang et al. 2005). We used the same antibody to determine the subcellular localization of Kir2.2 in permeabilized muscle fibres (Fig.3B) using fluorescence TPLSM imaging. As shown in panel 1 of Fig. 3B, Kir2.2 appears to be distributed in double bands of fluorescence which are transversally orientated with respect to the long axis of the muscle fibres (TTS membranes), and seems to be lacking at the periphery. The overlay in panel 3 illustrates that every pair of Kir2.2 bands is flanked by consecutive M lines, in turn demonstrated in the second harmonic generation (SHG) images in panel 2. Altogether, this pattern of fluorescence distribution reveals that Kir2.2 channels are typically expressed mostly in the TTS membranes, as illustrated previously for ClC-1 and K_V channels (DiFranco et al. 2009, 2012). The same results as those shown in Fig. 3A and B were obtained in FDB muscles of three other animals.

Figure 3.

Expression and subcellular localization of native Kir channel in FDB muscles

A and C, Western blot analysis of Kir2.2 and Kir2.1 expression, respectively. The dihydropyridine receptor was used as a loading control. B and D, TPLSM analysis of the targeting of Kir2.2 and Kir2.1, respectively. For both sets of data, panels 1 and 2 are the images of the fluorescence of the secondary antibodies and the corresponding backscattered second harmonic generation signal, respectively. The overlay of equivalent images is shown in the corresponding panel 3. Arrows indicate surface expression of Kir2.1.

For the same microsomal fractions, we assessed the expression of Kir2.1 channels. In contrast to the case of Kir2.2, Western blot analysis demonstrates the existence of two bands (Fig. 3C); one band has a molecular weight of ∼50 kDa (the same as Kir2.2) and the other is heavier, ∼55 kDa. The ∼50 kDa band for Kir2.1 has been reported in other tissues and is in agreement with the molecular mass predicted from the primary structure of this protein (Karkanis et al. 2003; Tao et al. 2007). Although larger than predicted from the primary structure, a 55–60 kDa band has also been reported in skeletal and cardiac muscle by other investigators using anti-Kir2.1 antibodies (Melnyk et al. 2002; Kristensen et al. 2006). The subcellular distribution of Kir2.1 seems to be also slightly different from that of Kir2.2 (Fig. 3B). TPLSM image analysis illustrates that the Kir2.1isoform is expressed not only in the TTS membranes, but also quite prominently at the surface membrane (Fig. 3D, arrows). Consistent results were obtained in FDB muscles of three other mice.

Functional Kir channels in the TTS membranes

As there are no channel blockers available that can specifically distinguish between Kir2.1 and Kir2.2, the relative proportion of each isoform's contribution to IKir records cannot be readily assessed. Nevertheless, we will focus the rest of this paper in answering another all-important question, namely what is the relative distribution of Kir channels (both Kir2.1 and Kir2.2) between the TTS and surface membranes? This is an important issue physiologically because, during typical repetitive action potential (AP) activation (e.g. tetanic trains of APs), Kir channels in the TTS membranes both regulate and are regulated by the luminal [K⁺], which is in turn increased by the efflux of K⁺ ions through K_V channels (DiFranco et al. 2012). Our strategy to answer this question is based on the combination of optical and electrophysiological approaches applied to fibres stained with di-8-ANEPPS with model simulations, as already described for currents carried by ClC-1, NaV1.4 and K_V channels (DiFranco et al. 2011a, 2012; DiFranco & Vergara, 2011).

Figure 4 shows, for a fibre in 96 mm [K⁺]_o, the voltage-dependent di-8-ANEPPS fluorescence changes (measuring voltage changes in the TTS) in the absence (Fig. 4A) and in the presence of 1 mm Ba²⁺ (Fig. 4B). These optical records, elicited by pulses to +40, +20, −40, −80, −120 and −160 mV (traces a–f, respectively), were measured simultaneously with the IKir records (Fig. 4C and D, respectively). The comparison between optical records obtained under control conditions (Fig. 4A) and those in 1 mm [Ba²⁺] demonstrates the effects of the presence (Fig. 4C) and absence (Fig. 4D) of IKir in the TTS voltage changes. Whereas Ba²⁺ did not have significant effects on IKir and optical records elicited by depolarizing pulses (traces a and b in Fig. 4A and B), it significantly altered those in response to hyperpolarizing pulses (compare traces d–f in Fig. 4A and B). Thus, blockage of IKir by Ba²⁺ resulted in a marked increase in the amplitude of the optical signals, an effect that was particularly prominent for large hyperpolarizations (compare traces f in Fig. 4A and B), and progressively less notorious for smaller hyperpolarizations (traces c–e). Note that the effects of Ba²⁺ on the optical records are paralleled by the proportionally more significant reduction of IKir in response to large hyperpolarizations than to small hyperpolarizations (compare the effects of Ba²⁺ on traces f and c in Fig. 4C and D). It is also interesting to note the large discrepancy between the step-like time courses of the optical signals in the presence of Ba²⁺ (both for hyperpolarizing and for hyperpolarizing pulses) and their asymmetrical properties under control conditions. Although depolarizing pulses result in step-like optical responses, they steadily increase in magnitude during hyperpolarizing pulses; this property is more notorious for large hyperpolarizations (i.e. traces e and f, Fig. 4A), still visible for smaller pulses (trace d, Fig. 4A) and inconspicuous for the smallest hyperpolarizations (trace c, Fig. 4A). Importantly, the magnitude increases observed during large hyperpolari-zing pulses approximately correlate with the decays seen in IKir records (e.g. compare the decay kinetics of the IKir trace f of Fig. 4C, with the corresponding magnitude increase in ΔF/F of Fig. 4A).

Figure 4.

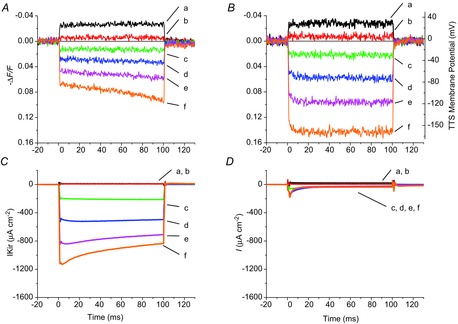
Effect of IKir activation on voltage-dependent di-8-ANEPPS transients

A and B, di-8-ANEPPS transients elicited by step voltage clamp pulses (to +40,+20, −40, −80, −120 and −160 mV) are represented by traces a–f, respectively, efore (A) and after (B) blocking IKir. C and D, corresponding currents for A and B, respectively. Fibre diameter, 59 μm; length, 556 μm; capacitance, 5.9 μF cm⁻².

The results described in the previous paragraph are illustrated in better detail in Fig. 5A, where the optical signals in response to pulses of +50, −30 and −150 mV amplitudes were recorded before (traces a, b and c) and after the addition of Ba²⁺ (traces d, e and f) and shown superimposed for comparison. Ba²⁺ blockage of IKir does not affect the properties of optical traces in response to depolarizing pulses, mildly alters those in response to small hyperpolarizations, but significantly modifies those in response to large hyperpolarizations. A tentative conclusion from these observations and those of Fig. 4 is that voltage changes in the TTS, monitored by di-8-ANEPPS in response to voltage clamp pulses, are significantly attenuated due to the shunting effect of local IKir currents. Further evidence in support of this generalization is shown in Fig. 5B, where the voltage dependence of the di-8-ANEPPS transients at the onset of voltage pulses is plotted (for the same fibre) under control conditions (closed circles) and in the presence of Ba²⁺ (open squares) or TEA⁺ (filled squares). Under the three conditions, the maximal ΔF/F (amplitude) of optical signals in response to depolarizing pulses are superimposable; this is expected because in all cases outward currents are quite mall. In contrast, the amplitude of di-8-ANEPPS signals is significantly lower (i.e. attenuated) under control conditions than those observed in the presence of Ba²⁺ and TEA⁺. The voltage dependence of average ΔF/F signals under control conditions (filled squares) and in the presence of 1 mm Ba²⁺ (filled circles) obtained in eight fibres is shown in Fig. 5C. Values for hyperpolarizations larger than −20 mV are significantly different (P < 0.05). To obtain a quantitative descriptor of the effects of IKir on TTS voltage changes, plots like those shown in Fig. 5B were subtracted (point-by-point) for every fibre; this difference, normalized by the maximal ΔF/F at the largest depolarization, is hereafter termed ‘TTS voltage attenuation’, or simply ‘attenuation’. The average attenuation, calculated from the same fibres as in Fig. 5C, is shown in Fig. 5D. The attenuation is very small in the depolarizing direction, but increases almost linearly with the amplitude of the hyperpolarization, reaching values up to ∼45% for hyperpolarizations to −160 mV. Note that the voltage dependence of the TTS attenuation (Fig. 5D) is remarkably similar to that of IKir, as shown in Figs 1D and 2A. As suggested previously, and as will become clear later in the paper, this is not a coincidence but a manifestation of the notion that attenuation is due to IKir itself as a significant proportion of the current arises from the TTS membranes. This concurs with the biochemical data indicating the presence of both Kir2.1 and Kir2.2 in this membrane compartment (Fig. 3B and D).

Figure 5.

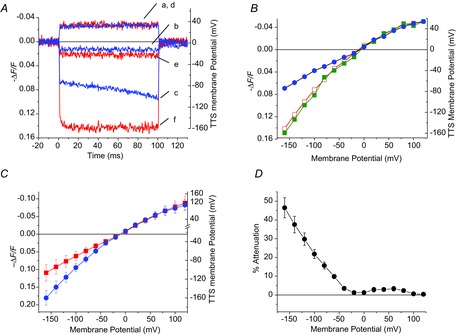
Voltage dependence of di-8-ANEPPS transient attenuation

A, comparison of di-8-ANEPPS transients elicited by voltage pulses (to +40, −40 and −160 mV), before (traces a, b and c, respectively) and after blocking IKir (traces d, e and f, respectively). B, peak (at the onset of traces) ΔF/F as a function of membrane potential calculated from records obtained in the same fibre as in A. The data were obtained in the presence of 96 mm [K⁺] before and after adding 1 mm [Ba²⁺] (filled circles and open squares, respectively), and after exchanging the K⁺-based external solution with a TEA⁺-based solution (filled squares). C, average peak (at the onset of traces) ΔF/F as a function of membrane potential, calculated from data obtained from eight fibres. D, voltage dependence of the attenuation of di-8-ANEPPS transients by activation of IKir. The symbols and bars in C and D represents the mean and SD.

Radial cable model predictions of TTS and surface membrane contributions to IKir

To further determine the contribution of functional Kir channels in the TTS and surface membranes to IKir, we compared the properties of experimental records with those predicted by radial cable model simulations (Fig. 6 and Appendix). Figure 6A and C displays optical and IKir records, obtained from a fibre in 96 mm [K⁺], in response to depolarizing (to +40 and +20 mV, traces a and b, respectively) and hyperpolarizing pulses (to −40, −80, −120 and −160 mV, traces c–f, respectively), respectively. Figure 6B and D displays model predictions of average TTS voltage changes and IKir, in response to identical pulses as those in Fig. 6A and C. The model geometrical parameters matched the fibre's parameters; the rest were those in the Appendix. The Kir permeability (PKir) for both the surface and the TTS membranes was set at an identical value (7.5 × 10⁻⁶ cm s^–1; PKir S/TTS = 1). A summary comparison of the properties of experimental records (Fig. 6A and C) with model predictions (Fig. 6B and D) reveals that most features of IKir (rectification, amplitude, decay) are accurately accounted for by the model. Nonetheless, for parameters that yield the best predictions of the IKir records, the model predicts TTS voltage changes that differ in two aspects with respect to the experimental optical records: (1) the predicted TTS hyperpolarizations at the onset of the pulses are proportionally smaller (more attenuated) than in the experimental records, and (2) the predicted traces display a more pronounced increase during the pulses. Although we cannot fully explain these discrepancies (discussed later), it is notable that the presence of Kir channels in the TTS (PKir > 0) is essential to account for the decay in the IKir records (which is due to K⁺ depletion in the TTS lumen, as shown below) and the corresponding increase in TTS voltage during the pulses. Alternatively, simulations incorporating Kir channels solely at the surface membrane predict IKir records without any decay and regularly spaced step-like TTS voltage changes (see below and Fig. 10D).

Figure 6.

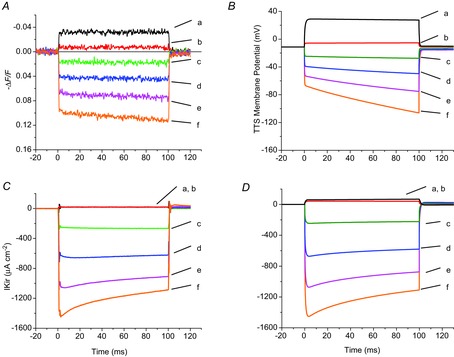
Model simulation of TTS membrane potential and IKir in response to voltage clamp pulses

A and C, experimental di-8-ANEPPS transients (A) and total IKir (C) recorded in a fibre bathed in 96 mm extracellular [K⁺]. B and D, model predictions of the average (along the radius) TTS membrane potential and total IKir. For all panels, the responses to pulses to +40, +20, −40, −80, −120 and −160 mV are represented by traces a–f, respectively. Fibre diameter, 56 μm; length, 497 μm; capacitance, 6.5 μF cm⁻². See text for details.

Figure 10.

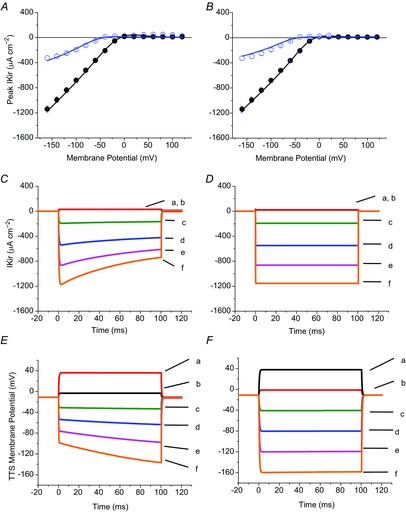
Comparative model simulations of IKir and TTS membrane potential changes using two PKir distributions

A, model predictions (continuous lines) of peak IKir recorded in 24 mm (open circles and error bars) and 96 mm extracellular [K⁺] (filled circles with bars). PKir = 5.5 × 10⁻⁶ cm s⁻¹; S/TTS = 1. B, model predictions of the same data as in A, but assuming that Kir channels are exclusively located at the surface membrane. PKir = 2 × 10⁻⁵ cm s⁻¹; S/TTS = 0. C and D, simulated IKir traces assuming the conditions in A and B, respectively. The traces are calculated in response to voltage clamp pulses to +40, +20, −40, −80, −120 and −160 mV (traces a–f, respectively). E and F, time course of average TTS membrane potential changes calculated in response to the same pulses as in C and D.

Another set of supporting evidence for the concept that the non-linear properties of di-8-ANEPPS fluorescence records result from the presence of Kir channels in the TTS is shown in Fig. 7. Figure 7A and C shows di-8-ANEPPS records and model predictions of TTS voltage changes, respectively, from the same fibre as in Fig. 6 at the experimental condition ([K⁺]_o = 96 mm). Interestingly, in agreement with the results shown in Figs 4 and 5, blocking of IKir with 1 mm Ba²⁺ results in a marked increase in the amplitude of the TTS optical signals elicited by hyperpolarizing pulses (traces c–f, Fig. 7C), an effect that is strongly matched by the model in the simulated TTS voltage records when PKir was set to zero (traces c–f, Fig. 7D). Whenever IKir currents are blocked by 1 mm Ba²⁺ (as illustrated above) or 5 mm Rb⁺ (data not shown), the model correctly predicts step-like linear responses comparable to those recorded experimentally.

Figure 7.

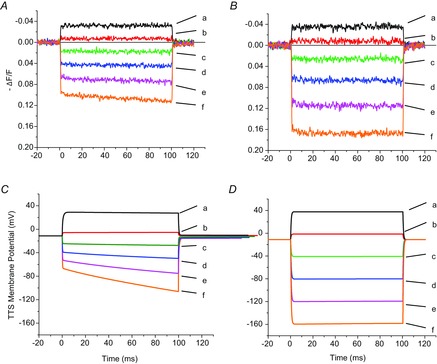
Model prediction of the effect of blocking IKir on the di-8-ANEPPS recorded in the presence of 96 mm extracellular [K⁺]

A and B, di-8-ANEPPS transients recorded in response to voltage pulses (to +40, +20, −40, −80, −120 and −160 mV) represented by traces a–f, respectively, before (A) and after (B) blocking IKir with 1 mm [Ba²⁺]. C and D, predicted average TTS membrane potential in response to the same pulses as in A and B, respectively. PKir = 7.5 × 10⁻⁶ cm s⁻¹; S/TTS = 1.

We also tested the accuracy of the model in predicting the voltage-dependent peak IKir and attenuation at different [K⁺]_o. The filled and open circles in Fig. 8A correspond to average experimental peak IKir data obtained at 96 and 24 mm [K⁺], respectively. The continuous lines illustrate the ability of model simulations to quantitatively predict the voltage dependence of the data when Kir channels are assumed to be at the same density in the surface and TTS membranes (S/TTS = 1). What is remarkable about these predicted currents is that the close overlap between data and model simulations was obtained with the same PKir value (5.5 × 10⁻⁶ cm s⁻¹) and only changing [K⁺]_o in the model (as in the experiments) from 96 mm (black) to 24 mm (blue). Equally as important, the model predictions of the attenuation in the optical data (continuous lines in Fig. 8B) fit remarkably well the experimental data at each of the conditions tested.

Figure 8.

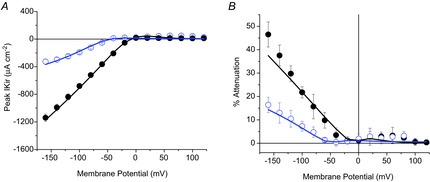
Simultaneous model prediction of peak IKir and optical attenuation for two extracellular [K⁺]

A, model predictions (continuous lines) of the experimental peak IKir (symbols) recorded in a fibre exposed to 96 mm (filled circles) and 24 mm (open circles) [K⁺]_o. B, model predictions (continuous lines) of the percentage peak attenuation, calculated from the same fibres as in A (symbols and error bars). PKir = 5.5 × 10⁻⁶ cm s⁻¹; S/TTS = 1.

The TTS membranes contribute the largest fraction of IKir

The accurate correlation between model predictions and experimental data described above has the advantage that it allows us to calculate the fraction of IKir contributed by Kir channels in the TTS (responsible for the attenuation in optical records) and surface membranes, the sum of which accounts for the total IKir. Model predictions to average IKir data at [K⁺]_o of 96 and 24 mm (filled circles and error bars) are shown in Fig. 9A and B, respectively. The simulations used identical values of PKir for both the TTS and the surface membranes (5.5 × 10⁻⁶ cm s⁻¹; PKir S/TTS = 1). Both the TTS (dash-dot lines) and the surface (dashed lines) current contributions to the total IKir show similar voltage dependence (inward rectification) to the currents measured experimentally (filled circles). From the model predictions at [K⁺]_o = 96 mm (Fig. 9A), we estimate that ∼71% of the total IKir arises from the TTS membranes, and only a small fraction (∼29%) is contributed by Kir channels in the sarcolemma. Similar (but not identical) results were obtained for experiments and simulations at [K⁺]_o = 24 mm (Fig. 9B); in this case, the contribution of the current arising from the TTS membranes accounts for ∼76% of the total IKir, a predominant percentage with respect to that of the sarcolemma. Although these results may not be surprising, given the preponderance of TTS versus surface membrane in skeletal muscle fibres (∼5-fold in these data and simulations), they are based on unprecedented simultaneous measurements of IKir and average TTS voltage changes (optical data). Furthermore, it must be highlighted that although the bulk [K⁺]_o in the experiments and model simulations is constant, the [K⁺] in the lumen of the TTS changes drastically during the pulses, depending on time and radial position, but is iteratively calculated in the model simulation (see below). Consequently, the agreement between model simulations and experimental data for a channel that has a demonstrated dependence on [K⁺]_o (see Fig. 2) is a remarkable achievement with important physiological consequences.

Figure 9.

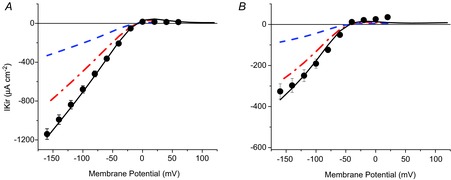
Model simulation of the IKir arising from the surface and TTS membranes

A, model predictions (continuous lines) of the total peak IKir (symbols and error bars) of fibres exposed to 96 mm [K⁺]_o. The predicted IKir contributions from the TTS and surface membranes are represented by the dash-dot and dashed lines, respectively. B, as for A, but for 24 mm [K⁺]_o. PKir = 7.5 × 10⁻⁶ cm s⁻¹; S/TTS = 1.

A final demonstration that the non-linear properties of the experimental data can only be accounted for if and when Kir channels are functionally expressed in the TTS membranes is provided in Fig. 10. One set of model predictions for peak I–V of IKir versus time, and optical data (TTS membrane potential vs. time), made while assuming PKir = 5.5 × 10⁻⁶ and S/TTS = 1, is shown in Fig. 10A, C and E, respectively. The simulated results are quite comparable to those shown in Figs 6B and D, 7C or Fig. 8A and B, respectively. In Fig. 10B, D and F, a contrasting set of simulations were made assuming that Kir channels are only at the surface membrane (S/TTS = infinity). As expected, PKir had to be increased to 2 × 10⁻⁵ cm s⁻¹ to predict approximately the same total IKir of this set of simulations. It is interesting to note in Fig. 10A and B that, regardless of the relative distribution of Kir channels, the model is able predict the peak I–V data (symbols) with reasonable accuracy (continuous lines) both in 96 mm (filled circles) and 24 mm [K⁺] (open circles). However, the kinetics of predicted IKir records are extremely different between TTS/S = 1 (Fig. 10C) and TTS/S = 0 (Fig. 10D) simulations. Clearly, when all the channels are placed at the surface membrane, the model fails to predict the experimentally observed decay of the currents (i.e. the currents are step-like). This suggests strongly that the decay of experimental currents is due to K⁺ depletion of the lumen of the TTS, and may explain why the decay is more pronounced at larger than smaller hyperpolarizations. In a similar fashion, simulations lacking Kir channels in the TTS fail to reproduce the optical data (compare traces d to f in Fig. 10E and F). Under these conditions, the model predicts step-like optical responses similar to those obtained when Kir channels were blocked by adding Ba²⁺ (Fig. 7B and D). Together, these latter results can be readily explained by considering that if the ionic currents arise only from the surface membrane the TTS will ideally reach the command voltage level with no attenuation.

The extreme alternative to the above situation, assuming that all PKir is placed in the TTS membranes, results in model predictions for the attenuation in the TTS voltage changes that overly exceed those observed experimentally (data not shown). This indicates that the functional expression of Kir channels in the surface membrane is an actual requirement for the compatibility between electrical and optical data.

Prediction of K⁺ depletion in the TTS during long hyperpolarizations

As stated previously, the radial model dynamically calculates the changes in the luminal [K⁺] (at each radial position of the TTS) that result from the flux of K⁺ ions through Kir channels (see Appendix). Typical predictions of the time-dependent changes in luminal [K⁺] at the middle point of the fibre radius (r = a/2; a = fibre radius) when [K⁺]_o is 96, 24 and 4 mm are shown in Fig. 11A, B and C, respectively. The [K⁺] traces were calculated in response to 100 ms depolarizations or hyperpolarizations to +20, 0, −40, −80, −120 and −160 mV (traces a–f, respectively). Note that the depletion of K⁺ in the lumen of the T-tubules starts at the onset of the pulses and that [K⁺] progressively diminishes during the pulses to values which, depending on the magnitude of IKir, can be surprisingly lower than the initial [K⁺]. For example, when [K⁺]_o is 96 mm, the luminal [K⁺] reaches ∼17 mm at the end of 100 ms hyperpolarizations to −160 mV, ∼3 mm when [K⁺]_o is 24 mm and ∼0.6 mm when [K⁺]_o is 4 mm (bottom traces in Fig. 11A, B and inset in C, respectively). To illustrate how E_K varies during the time-dependent K⁺ depletion at the centre of the fibre, we included approximate values in a logarithmic scale at the right ordinate axes of Fig. 11A and at the inset of Fig. 11C. At the end of 100 ms hyperpolarizations, E_K shifts by ∼43 mV (from −10 to −55 mV), ∼56 mV (from −46 to −102 mV) and ∼48 mV (from −90 to −144 mV), for [K⁺]_o = 96, 24 and 4 mm, respectively. These large changes in luminal [K⁺] and E_K, resulting from the voltage-dependent activation of IKir, are exacerbated at the centre of the fibre (r = 0; data not shown). In contrast, at radial positions closer to the periphery of the fibre, the changes are much smaller and follow much faster kinetics (data not shown).

Figure 11.

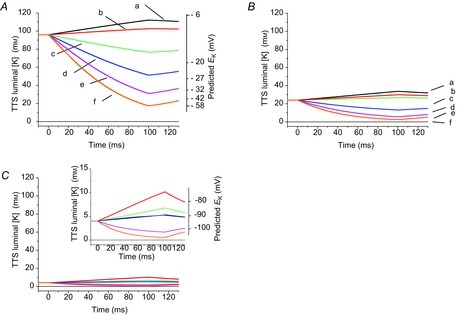
IKir activation leads to reductions in the TTS luminal [K⁺]

A, model predictions of TTS luminal [K⁺] changes (left ordinate axis) in response to pulses to +20, 0, −40, −80, −120 and −160 mV (traces a–f, respectively) in a fibre exposed to a bulk [K⁺]_o = 96 mm. The right ordinate axis shows the predicted E_K from the TTS luminal [K⁺]. B, luminal [K⁺] changes for the same fibre in 24 mm [K⁺]_o. Pulses to the same values as in A were used. C, luminal [K⁺] changes in response to the same values as in A, but predicted for a fibre exposed to 4 mm [K⁺]_o. The traces are shown in a narrower [K⁺] scale in the inset, which also includes the predicted values for E_K. PKir = 5.5 × 10⁻⁶ cm s⁻¹; S/TTS = 1. In all panels the solid horizontal lines indicate the luminal [K⁺] prior to pulse application (equal to bulk [K⁺]_o).

As expected, the interplay between the properties (kinetics, voltage dependence, radial dependence) of the changes in luminal [K⁺], and the [K⁺] dependence of IKir at every radial segment of the TTS, simultaneously explain the overall decay of the TTS contribution to the total IKir, and time- and voltage-dependent attenuation of TTS signals. In addition, as noted in Fig. 11, the replenishment of K⁺ in the lumen of the T-tubules when IKir is terminated, as exemplified by the restoration of the luminal [K⁺] immediately after the pulses, follows a much slower time course than the depletion during the pulses. This phenomenon, which probably has important physiological implications for myotonia, ultimately results from limitations imposed by the relatively slow replenishment of K⁺ ions through the tortuous path of TTS, even when the diffusion coefficient for these calculations was assumed to be that of an ideal solution (see Appendix).

Interplay between IK_V and IKir currents

To investigate the dynamic dependence of Kir channels on luminal [K⁺], and the ability of radial cable model simulations to predict these effects, we took advantage of the possibility to activate the prominent K_V channels in the TTS (Beam & Donaldson, 1983; DiFranco et al. 2012) and measure the effects of the resulting increase in luminal [K⁺] on IKir. The typical two-pulse protocol for this type of experiment was used, for a fibre equilibrated in [K⁺]_o = 24 mm (E_K = −46 mV). As illustrated in the inset in Fig. 12A a fixed depolarizing pre-pulse (+120 mV, 100 ms) was followed by a hyperpolarizing test pulse (5 ms) to −160 mV (red trace), or the test pulse was applied in the absence of a pre-pulse (blue trace). The large conditioning pre-pulse was used to activate a prominent IK_V (outward current in red trace of Fig. 12A). The hyperpolarizing test pulse elicited a large IKir (inward current in red trace of Fig. 12A, and also shown in an expanded scale in Fig. 12B). Notably, the IKir recorded in the absence of the conditioning pulse (inward current; blue trace, Fig. 12A and B) is significantly smaller than in its presence. In other words, the presence of IK_V significantly influenced the magnitude of IKir. The obvious conclusion of this result is that the activation of IK_V resulted, at the end of the 100 ms conditioning pulse, in a large increase in luminal [K⁺], which enhanced IKir to substantially exceed its magnitude at 24 mm [K⁺]_o. Significantly, this explanation is accurately confirmed by the model simulations for each of the experimental conditions (green and cyan traces, Fig. 12A and B), which simultaneously (and closely) predict the results obtained both in the absence (cyan trace) and in the presence (green trace) of IK_V. The voltage dependence of peak IKir elicited by test pulses (ranging from −160 to +40 mV) in both experimental situations is shown in Fig. 12C. In the absence of conditioning pulses (blue symbols and line), an I–V plot with properties similar to those shown in Fig. 12 was obtained; the estimated reversal potential in this case was −44 mV, almost exactly E_K. In addition, as illustrated in Fig. 12C, application of the conditioning pulse produced three significant changes in the I–V plot (red symbols and line): (1) the magnitude of peak IKir increased significantly at all test hyperpolarizations; (2) consequently, the limiting slope of the I–V plot became steeper (larger gKir_max); and (3) there was a prominent rightward shift of the reversal potential of IKir to ∼24 mV. All these changes are readily predicted as resulting from K⁺ accumulation effects in the lumen of the TTS, by the radial cable model simulations; this includes the shift in reversal potential, which results from a predicted average increase of ∼40 mm in the luminal [K⁺]. Important implications of these observations, aside of providing further validation of the model and the parameters used therein (see Appendix), are that they provide quantitative support for observations made previously in rat muscle fibres (Beam & Donaldson, 1983) and for understanding what happens when fibres are physiologically activated by high frequency trains of APs, giving origin to the so-called late after-potential (Freygang et al. 1964a,b; Kirsch et al. 1977; Wallinga et al. 1999; Fraser et al. 2011).

Figure 12.

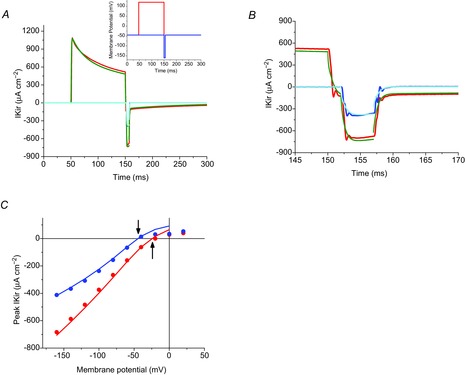
Model predictions of K⁺ accumulation in the TTS

A, inset: a two-pulse experiment used to activate both the delayed and the inward K⁺ rectifier currents in a fibre bathed in 24 mm extracellular [K⁺]. A conditioning pulse to 120 mV (red trace, 100 ms) was followed by a short (5 ms) test pulse to −160 mV (blue trace). The test pulse was applied in the absence of conditioning pulse. The main plot shows: (1) the experimental (red trace) and model predicted currents (green trace) in response to the overall pulse paradigm; and (2) the experimental (blue trace) and model predicted currents (cyan trace) in response to the test pulse alone. B, a portion of the same traces as in A, but displayed at an expanded scale. C, Voltage dependence of the tail currents (IKir) in response to test pulses ranging from −160 to 40 mV (every 20 mV) recorded in the presence (blue symbols) and in the absence (red symbols and lines) of a 120 mV conditioning pulse. The blue and red lines correspond to the model predictions of the tail currents calculated with and without conditioning pulse, respectively. The arrows indicate estimated reversal potentials. Model predictions: PKir = 6.8 × 10⁻⁶ cm s⁻¹; S/TTS = 1. Fibre diameter, 57 μm; length, 429 μm; capacitance, 4.6 μF cm⁻².

IKir can be increased by specific isoform overexpression

The final question that we investigated was whether EGFP-tagged Kir isoforms can be functionally expressed by adult FDB fibres, and to what extent the total IKir was incremented by this transgenic overexpression. Using TPLSM imaging we first assessed the subcellular membrane targeting of EGFP-tagged Kir2.1 and Kir2.2 channels. The fluorescence image in the left panel of Fig. 13A demonstrates that the pattern of expression of EGFP-Kir2.1 channels in skeletal muscle fibres is at both the surface and the TTS membranes, and identical to that shown in Fig. 12 for endogenous Kir2.1 channels. The overlay of the SHG and EGFP fluorescence images (right panel, Fig. 13A) corroborates this conclusion. Similar results were obtained from the TPLSM analysis of the Kir2.2 channel (data not shown). Knowing that tagged transgenic versions for both Kir isoforms are readily expressed in muscle fibres, we investigated whether they were functionally active and if their properties were distinguishable in electrophysiological measurements of IKir. Figure 13B shows a summary of our results. The black symbols and lines show typical results of sham transfected control fibres in 96 mm [K⁺]_o, illustrating the functional properties of naïve Kir channels, supposedly a mixture Kir2.1 and Kir2.2 channels. The voltage dependences of peak IKir values obtained from transfected fibres overexpressing EGFP-Kir2.1 and EGFP-Kir2.2 are shown in blue and red (symbols and lines), respectively. The significant increase (P < 0.05) in average peak IKir in transfected fibres, compared to naïve fibres, demonstrates that both isoforms are functionally overexpressed. In addition, IKir recorded from fibres transfected with either transgenic Kir2.1 or Kir2.2 share the strong inward rectification properties as the native fibres. Interestingly, in spite of the fact that we used comparable amounts of DNA (60 μg per foot), that the genes were subcloned to the same backbone plasmid (i.e. they share the same promoter and plasmid size) and that IKir values were measured at comparable post-transfection periods (14 days), the peak IKir values were significantly different for each isoform. Namely, transgenic expressions of Kir2.1 channels nearly tripled the naïve IKir (gKir_max increased from 7.8 to 22.2 mS cm⁻²), whereas those of Kir2.2 increased gKir_max only to 12.3 mS cm⁻² (∼60% increase).

Figure 13.

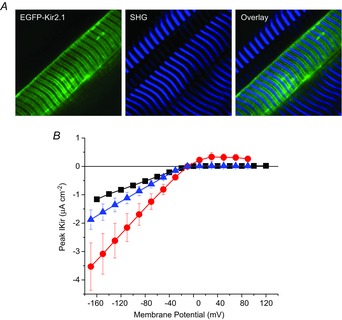
Transgenic Kir2.1 and Kir2.2 are functionally expressed in adult FDB fibres

A, subcellular localization of transgenic EGFP-Kir2.1. Left and centre panels are TPLSM images of the EGFP fluorescence and the backscattered SHG signal from the myosin, respectively. The left panel is the overlay of the right and centre panels. Images were taken from a live muscle 12 days after transfection. B, voltage dependence of peak IKir from naïve fibres (black symbols, n = 12), and fibres expressing either EGFP-Kir2.1 (red symbols, n = 3) or EGFP-Kir2.2 (blue symbols, n = 4). The symbols and bars represent the mean ± SEM.

Discussion

In this paper, we present a comprehensive study of the inward potassium conductance in adult mammalian skeletal muscle fibres. The work reported here represents our laboratory's ultimate installment of a long term project aiming to characterize the functional properties of the principal ion channels of mammalian muscle fibres. In a series of recent papers we have previously described sodium, chloride, calcium and potassium delayed rectifier currents, carried by Nav1.4, ClC-1, Cav1.1, and Kv1.4 and Kv3.4 channels, respectively. Our studies typically include a combination of electrophysiological, optical and computational approaches, as well as biochemical, histochemical and molecular biology techniques. In the current studies, in addition to confirming the presence of at least two isoforms of Kir channels in the surface and TTS membranes, we were able to determine, for the first time, the relative distribution of Kir channels in the surface and TTS membrane compartments while simultaneously providing a realistic model for the changes in K⁺ concentration in the lumen of the TTS that result from, and modulate, the electrical activity of the fibres as a whole.

Subcellular localization of Kir isoforms

The immunoblotting data demonstrate the presence of Kir2.1 and Kir2.2 in microsomal fractions of the same muscle used for the electrophysiological studies. As found previously in other preparations (Stonehouse et al. 1999; Leonoudakis et al. 2004; Fang et al. 2005), Kir2.2 monomers were identified as a single band of ∼50 kDa (Fig. 3A). Instead, two bands of ∼55 and ∼50 kDa were identified by anti-Kir2.1 antibodies (Fig. 3C); these bands span the range of molecular weights found for this isoform in tissues as diverse as the hippocampus, smooth muscle, mesenchymal stem cells and corneal endothelium (Stonehouse et al. 1999; Karkanis et al. 2003; Yang et al. 2003; Tao et al. 2007). As no cross-reactivity occurs with the specific antibody against either Kir2.1, when challenged with Kir2.2/2.3 (Fang et al. 2005), the larger molecular weight band recognized by anti-Kir2.1 may represent a post-translational modification of the protein, such as glycosylation and phosphorylation (Yang et al. 2003). In fact, several putative glycosylation and phosphorylation sites (for protein kinases A and C and tyrosine kinase) have been identified in Kir2.1 (Yang et al. 2003). Our observation of a double band for Kir2.1 is in agreement with reports of small and large molecular weight bands in CHO and COS cells transfected with IKir2.1 (NeuroMab and Fang et al. (2005), respectively), and with the same observation in a preparation from murine macrophages tested with an antibody comparable to ours (Moreno et al. 2013).

In this report, the immunoblotting data were corroborated by the immunohistochemical assessment of the membrane targeting of native Kir isoforms. The antibodies demonstrate the presence of the Kir2.1 and Kir2.2 isoforms at the surface and TTS membranes, but the fluorescence revealing the surface membrane location of Kir2.2 is not apparent, unlike that for Kir2.1; this may suggest preferential targeting of Kir2.2 to the TTS membranes. Nevertheless, neither TPLSM imaging nor Western blot analysis of membrane fractions, based on the use of different antibodies for each channel isoform, would allow for a conclusive assessment of individual channel density and/or membrane targeting. Thus, it is reasonable to assume that, as a first approximation, similar densities of Kir2.1 and Kir2.2 are expressed in both the surface and the TTS membranes. In addition, due to the promiscuity of Kir tetramer formation, any attempt to ascribe functional properties of IKir records to either Kir isoform would be premature and baseless.

Although not a definitive proof of native channel targeting, our transfection experiments demonstrate that transgenic Kir2.1 and Kir2.2 channels (from mice and rat DNA, respectively) are delivered to the surface and TTS membranes. Furthermore, the functional evaluation of transgenic Kir channel expression suggests that both isoforms are significantly overexpressed above the normal level of naïve channels as, as demonstrated in Fig. 3, the peak IKir is more than tripled by transgenic expression. Interestingly, the apparent absence of limited regulation in the expression of transgenic ion channels is similar to what happens with ClC-1 channels, which can also be overexpressed in adult skeletal muscle fibres (DiFranco et al. 2009). However, the situation is in sharp contrast to what happens with the dihydropyridine receptor calcium channel (Cav1.1; DiFranco et al. 2011b) and the sodium channel (Nav1.4; Capote et al. 2008) in which the expression of transgenic channels is made at the expense of a reduction of the native isoforms. Although many factors may be responsible for the differential regulation of the expression of ion channels in skeletal muscle fibres, it is worth noting that multimeric channels (i.e. ClC-1 and Kir) are readily overexpressed, whereas the expression of single polypeptide channels (i.e. Nav1.4 and Cav1.1) is tightly regulated.

The significant increase of peak IKir afforded by the overexpression of Kir2.1 and Kir2.2 may compromise the accuracy of the voltage control of the fibres by the voltage clamp amplifier. This problem may explain, at least in part, why the error bars (SEM) are more prominent for large peak IKir values, associated with large hyperpolarizations, as shown in Fig. 3 (solid triangles and circles). Note, however, that these type of errors in the data are not present in naïve fibres (in this case the error bars in Fig. 3 are contained within the symbols). Furthermore, peak IKir data with values larger than 1.5 mA cm⁻² were not included in the analysis of the rest of the paper in order to eliminate the possibility that voltage control errors affect any of the conclusions and model analysis of the paper.

Properties of IKir

The IKir records reported here display the signature features of Kir channels recorded from other skeletal muscle preparations and cell expression systems: (1) large inward and negligible outward currents elicited by hyperpolarizing and depolarizing pulses of the same amplitude, respectively, when applied from holding potentials close to E_K (Standen & Stanfield, 1978b; Leech & Stanfield, 1981; Stanfield et al. 1994; Bradley et al. 1999); (2) currents are readily blocked by external Ba²⁺ and/or Rb⁺ (Hagiwara & Takahashi, 1974; Beam & Donaldson, 1983; Stanfield et al. 2002; DiFranco et al. 2013); and (3) gKir_max depends on the bulk [K⁺]_o (Almers, 1972b; Hagiwara & Takahashi, 1974; Hagiwara & Yoshii, 1979; Leech & Stanfield, 1981; Stanfield et al. 2002). As described in the Appendix, our model incorporates equations to calculate inward rectifier current contributions at the surface membrane and at each of the radial elements of the TTS. These are straightforward model equations taken from the literature (Goldman, 1943; Hodgkin & Katz, 1949; Standen & Stanfield, 1978a) to describe the key features of Kir channels: i.e. gKir is modulated by extracellular K⁺ and blocked by intracellular cations (Vandenberg, 1987; Lopatin et al. 1994; Lopatin & Nichols, 1996). What is interesting is that this theoretical framework for Kir channels, while originally applied to explain the properties of IKir in amphibian muscle fibres without explicitly taking into consideration that the majority of the currents arise from the TTS membranes (Standen & Stanfield, 1978b), when incorporated into our model describing the electrical properties of the TTS and surface membranes, is capable of providing an accurate description of the inward rectification and [K⁺] dependence of gKir in the fibre as a whole. An obvious corollary is that realistically the characteristics of the channels are still manifested, even when they are expressed in a membrane compartment that, as a whole, is not voltage clamped and in which ion depletion occurs dynamically.

However, if IKir was arising solely from the well-clamped surface membrane compartment, the current records would have shown instantaneous activation and no decay with time. In contrast, the experimental data clearly demonstrate that IKir records are not instantaneous and decay during 100 ms pulses; furthermore, the extent of the decay increases with the amplitude of the hyperpolarizing pulses. Interestingly, the model simulations demonstrate that this decay can be faithfully accounted for by the depletion of K⁺ ions in the TTS; to accomplish this, depletion was calculated by the simultaneous integration of the diffusion equation for K⁺ ions in the TTS lumen, and the results are shown in Fig. 1. In this way, the larger the hyperpolarization, the larger the depletion, and thus the larger the decay of the currents. Our assumptions also imply that, in isolated fibres, no decay is expected in the currents originating at the surface membrane, and the decay of the currents in the tubules is expected to be a function of the radius, as depletion is expected to be more pronounced in the centre of the fibre, as shown in Fig. 1.

One small disagreement can be observed between the experimental and simulated data: the simulated TTS membrane potential (Figs 6 and 7) showd a larger increase during the pulse than that reported by di-8-ANEPPS. Although we do not have a definite explanation for this result apparently implying more significant K⁺ depletion than that actually occurring in the fibres, we are currently investigating the two not mutually exclusive options that K⁺ ion transport through the TTS walls might by associated with significant water flow, and/or that there is a some implicit inactivation (arising from multiple potential modulators) of Kir channels that has not yet being included in our model.

Relative distribution of gKir between the surface and TTS membranes

In contrast to the case of ClC-1 channels, which have not be unanimously established to be endogenously expressed in the TTS (Lueck et al. 2010; DiFranco et al. 2011a; Lamb et al. 2011), it is generally accepted from work in amphibian muscle fibres that a significant fraction of gKir is located in the TTS (Hodgkin & Horowicz, 1959a, 1960; Almers, 1972a,b; Standen & Stanfield, 1979; Almers, 1980; Heiny et al. 1983; Ashcroft et al. 1985). A typical problem with the subcellular location of ClC-1 channels is that antibodies for ClC-1 may not be reliable (Aromataris & Rychkov, 2006), but as discussed above, available antibodies for Kir2.1 and Kir2.2 are reliable for both Western blot analysis and IH and demonstrate the presence of both channels in the TTS. Nevertheless, although the rationale for using optical recordings of TTS voltage changes as an independent variable that puts boundaries for the respective contributions to IKir from the TTS and surface membranes has been utilized in amphibian muscle fibres (Heiny et al. 1983; Ashcroft et al. 1985), the functional account for the distribution of Kir channels in mammalian muscle fibres, as presented in this paper, does not have a precedent in the literature. The presence of a strong component of IKir arising from the TTS membranes is uniquely revealed in optical measurements of TTS voltage (Figs 4 and 5) as current-dependent attenuations can only arise from a membrane compartment that is not under voltage-clamp control; namely, the surface membrane potential is time- and amplitude-independent, regardless of the sign of the voltage command pulses. In contrast, the features of the optical signals (representing a spatial average of the membrane potential changes in the TTS membranes) depend on the sign and amplitude of the command pulses; in fact, the time course of signals recorded in response to large hyperpolarizations resembles the negative mirror image of current records.

Previous studies from our laboratory have demonstrated that the deviations of the TTS membrane potential changes from the command pulses typically depend on the properties of the ionic currents activated (DiFranco et al. 2011a, 2012; DiFranco & Vergara, 2011). For example, attenuation of the optical signals is produced upon activation of large inward ClC-1 currents (DiFranco et al. 2011a) and of outward K⁺ currents across delayed rectifier (K_V) channels (DiFranco et al. 2012). In contrast, the activation of Na currents (thorough NaV1.4 channels) results in an overshoot in the optical signals (DiFranco & Vergara, 2011). Interestingly, deactivation of ClC-1 currents (DiFranco et al. 2011a) has similar effects on the optical records as the depletion-dependent decay of IKir presented here. Overall, the point of this discussion is to emphasize that in all cases, the deviation from linearity in the voltage dependence (either attenuation or overshoot) of the optical signals can be, and has been, used as an independent measurement to assess, through the comparison between model predictions and data, the TTS contribution to the total currents.

The radial model incorporating Kir channels reproduces simultaneously the main features of both the TTS signals and the total IKir in fibres exposed to higher than physiological bulk [K⁺] (Figs 6–10). We found that the best predictions of the experimental data were obtained when the density distribution of Kir channels is approximately equal between the sarcolemma and TTS membranes (PKir S/TTS = 1). Extreme cases of PKir distribution were incompatible with the experimental data. Thus, modelling the absence of Kir channels in the TTS while maintaining the amplitude of total IKir approximately the same as in the experiments (Fig. 10D) resulted in voltage changes in the TTS (Fig. 10F) akin to optical signals and model predictions in the presence of Ba²⁺ with amplitudes that depend linearly on the command voltages (Fig. 7B and D, respectively). In addition, when Kir channels are excluded from the TTS, IKir records generated by the model do not decay during the pulses and become step-like currents (Fig. 10D). On the other hand, if all PKir is placed in the TTS, the predictions for the attenuation in the TTS voltage are incompatible with those observed experimentally.

The main consequence of the even distribution of PKir in surface and TTS membranes is that most of the total IKir arises from the TTS. We demonstrated that this is the case, regardless of [K⁺]. Using exactly the same model parameters, the simulations in Fig. 9 demonstrate that 71–76% of the total IKir arises from the TTS. It must also be stressed that the simulation predicting the current distribution in Fig. 9 also accurately predicted the attenuation seen in these experiments.

Shared role of potassium channels on the dynamics of TTS luminal [K⁺]

We demonstrated, using model simulations, that the decay of IKir in response to large hyperpolarizing currents is mostly due to luminal depletion of K⁺ ions. This implies that as long as a non-zero driving force exists, Kir channels should be able to help recover the K⁺ ions translocated into the TTS during the repolarization phase of APs.

Our double pulse experiments demonstrate this. For a given test potential (i.e. the hyperpolarization reached during the brief test pulse), IKir increases when a conditioning pulse is applied (Fig. 2). The reason for this is that K⁺ ions carried outwardly by Kv channels accumulate in the TTS lumen and this in turn increases IKir. Thus, if instead of using a hyperpolarizing pulse as a test, the membrane potential was returned to the holding potential (E_K), a significant inward current would persist until the luminal [K⁺] returned to baseline. The consequence of this is that a significant fraction of the K⁺ ions translocated by the activation of K_V channels are recovered through the TTS walls and are not lost to the extracellular space. A similar situation is expected during repetitive stimulation of the muscle fibres. Namely, accumulation of K⁺ ions in the TTS during sustained trains of APs will increase gKir, and as long as the membrane potential returns (after each action potential) to values that are negative with respect to local E_K values at the T-tubules, K⁺ ions will be recovered back to the fibre interior. This condition occurs physiologically due to the presence of ClC-1 channels in the TTS, as we demonstrated previously (DiFranco et al. 2011a). Furthermore, the sustained increase in luminal [K⁺] expected from the K⁺ translocation during each AP progressively leads to both an enhancement in gKir and a shift in E_K, comparable (but less remarkably) to what we demonstrated, with model support, in Fig. 2. These effects have been previously suggested, although not directly proved, to be responsible for the late after-potential in skeletal muscle fibres (Freygang et al. 1964a,b; Kirsch et al. 1977; Wallinga et al. 1999; Fraser et al. 2011).

The present report on the characteristics of inward rectifier currents arising from the surface and TTS membranes of mammalian muscle fibres represents a substantial advance with respect to previous studies from our laboratory addressing the same problem in amphibian muscle fibres (Heiny et al. 1983; Ashcroft et al. 1985). Not only is this a more meaningful biological preparation, potentially translatable to the human case, but these studies involve several technical and conceptual improvements over the previous work. (1) We have adopted a more user-friendly potentiometric dye (di-8-ANEPPS) that allows for the use of conventional epifluorescence microscopy, with the advantage of providing an excellent efficiency (∼14%/100 mV) and afford signals with very fast response time and high signal-to-noise ratio (DiFranco et al. 2005, 2007, 2011a, 2012; DiFranco & Vergara, 2011). (2) The radial cable model has been refined with that presented previously for inward rectification (Ashcroft et al. 1985). In addition to the use of intrinsic equations that better represent Kir channels’ rectification and dependence on external [K⁺] properties (Standen & Stanfield, 1978a), the current model includes the integration of a radial diffusion equation for K⁺ ions, which accounts for luminal [K⁺] changes (intracellular and bulk are assumed constant). The model also permits the analysis of the dynamic interactivity between Kir and K_V channels using realistic values for both conductances. A foreseeable further improvement will be the addition of an equation to account for water movements. (3) A remarkable achievement is the ability to simultaneously predict IKir and TTS membrane potential changes at different bulk [K⁺] without any change in model parameters.

Summary

Using combined optical and electrophysiological approaches, we demonstrate that functional Kir channels (mostly Kir2.1 and Kir2.2) are approximately equally distributed between surface and TTS membranes. Under these conditions, radial cable model simulations account for most of the experimental observations and suggest that >70% of IKir is generated in the TTS membranes. The model also predicts significant radial-dependent depletion of luminal K (and concomitant changes in E_K) associated with inward IKir, and accumulation of K associated with the activation of large outward IKv. Both predictions are in agreement with experimental observations. Altogether, our work provides solid supporting evidence for understanding the role of Kir channels in mammalian skeletal muscle, particularly in response to repetitive stimulation and fatiguing conditions.

Glossary

Abbreviations

AP

action potential

DHPR

dihydropyridine receptor

EGFP

enhanced green fluorescent protein

FDB

flexor digitorum brevis

IH

immunohistochemistry

IO

interossei

TPLSM

two-photon laser scanning microscope

TTS

transverse tubular system

Appendix

Radial cable model equations for the TTS of mammalian skeletal muscle fibres including potassium inward rectifier permeability and ion diffusion

The radial cable model equations are essentially the same as those described in detail previously (DiFranco et al. 2011, 2012; DiFranco & Vergara, 2011), which in turn followed the nomenclature published elsewhere (Adrian et al. 1969a; Adrian & Peachey, 1973; Ashcroft et al. 1985; Kim & Vergara, 1998; DiFranco et al. 2007) and the assumption (Adrian & Peachey, 1973) that the lumen of the TTS is separated from the extracellular fluid by an access resistance (R_s, in Ω cm²). The partial differential equation that governs the radial (r) and time (t) dependent changes in T-tubule membrane potential (u(r,t)) in response to voltage changes at the external boundary is (Adrian et al. 1969b):

A1

where a is the radius of the muscle fibre, R = r/a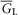, T = t/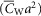 and ν = a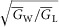. In these equations, the parameters 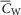and 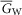are the capacitance (in μF cm⁻³) and conductance (in S cm⁻³) of the tubular membrane per unit volume of muscle fibre, respectively 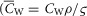and 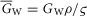). Also, 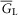is the effective radial conductivity 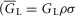, in S cm⁻¹). Equation 1 must be numerically integrated to predict the voltage of TTS cable elements when non-linear conductances, in parallel with capacitive elements (Adrian & Peachey, 1973; Ashcroft et al. 1985; DiFranco et al. 2011, DiFranco 2012; DiFranco & Vergara, 2011) being present. To this end, we replace the term 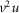in eqn 1 with the more general term: 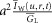, where 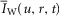is a generalized current normalized per volume of fibre. Keeping the same definitions for R and T, eqn. 1 is transformed into:

A2

Inward rectifier K⁺ (Kir) channels

For the simulations in this paper we assumed that 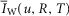is contributed by the flow of K⁺ ions across the TTS walls and the sarcolemma through inward rectifier (Kir) channels, as diagrammatically illustrated in Fig. 14. As originally proposed by Standen & Stanfield (1978a), the overall rectification properties of Kir channels can be described by a Goldman–Hodgkin–Katz constant-field approximation (Goldman, 1943; Hodgkin & Katz, 1949) modified to include a dual-valence external K⁺ binding site (K) and a dual-valence internal cation blocking site (S) located at an electric distance δ from the cell's interior (Standen & Stanfield, 1978a). The reasoning for the dual-valance sites is based on the blocking effects of external Ba²⁺ (Standen & Stanfield, 1978a) and that internal blocking ions have been demonstrated to be Mg²⁺ (Vandenberg, 1987) or various polyamines (Lopatin et al. 1994). According to this model, the magnitude of IKir can be calculated from the following formula (Standen & Stanfield, 1978b):

A3

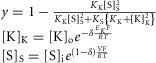A3a

Figure 14.

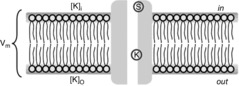
Modified GHK model of Kir channel

 

Note that R, T, and F in these equations correspond to the traditional constants and should not be confused with the normalized variables in the cable equations. The description and values of the parameters in these equations are given in Table1. By replacing eqns 3 and 4 in eqn 2, we can calculate the current across the TTS membranes:

A4

where 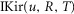and 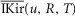are dimensionally scaled per cm² of TTS membrane and per cm³ of fibre, respectively.

Table A1.

Parameter definitions and values for muscle Kir channels

Parameter	Symbol	Value	Units
Dissociation constant for K of the K-binding site	KK	300	[mm]2
Dissociation constant for K of the S-blocking site	KS	0.015	[mm]2
Concentration of intracellular blocking particle S	[S]i	0.8	mm
Fraction of the electrical field sensed by S	δ	0.3
K permeability	PKir	0.5–2 ×10−5	cm s−1
Temperature	T	293	K
Faraday constant	F	96,485	J V eq.−1
Thermodynamic gas constant	R	8.3145	J K mol−1

Numerical integration of model equations

TTS voltage

The TTS cable is assumed to be made of n = 60 radial shells, sealed at the centre of the muscle fibre. As described elsewhere (Kim & Vergara, 1998; DiFranco et al. 2007, 2011, 2012; DiFranco & Vergara, 2011), at a given time j, the finite differences approximation of the partial differential equation for the T-tubular voltage (eqn. 2), while using an implicit Crank–Nicolson algorithm (Crank, 1975; Gerald, 1978), yields the following equation for an arbitrary annulus i:

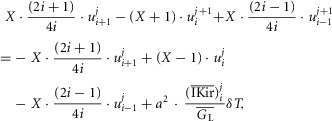A5

where 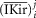is the current per unit volume (calculated from eqn 5) flowing through the T-tubular element at shell i and at the time interval j during the numerical integration process. Equation 6 is a recursive formula allowing the calculation of 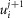at a time interval 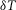, while knowing . The system of tridiagonal coefficient matrices was solved using an LU decomposition algorithm (Gerald, 1978). The integration of eqn 5, updating the value of IKir for every cable element and for the surface membrane, was performed with a fourth order Runge–Kutta algorithm at every time step. The values of the general cable parameters utilized for the simulations shown in the paper are summarized in Table2. Specific parameters are given in the figure legends.

Table A2.

Specific muscle fibre and radial cable model parameters

	Symbol	Value	Units
Radius	a	20–30	μm
Specific capacitance TTS wall	CW	0.9	μF cm−2
TTS lumen conductivity	GL	9.5	mS cm−1
TTS access resistance	Rs	20–40	Ω cm2
Fraction of fibre volume occupied by the TTS	ρ	0.00424
Volume to surface ratio of the TTS	ς	1.2 × 10−6	cm
Tortuosity factor on the TTS	σ	0.21
K diffusion coefficient	DK	1-1.5 × 10−5	cm2 s−1

Potassium diffusion in the TTS lumen

Changes in luminal potassium concentration in the TTS ([K]_o) occurring in response to the current flow across the T-tubule walls were calculated from simultaneous integration of the diffusion equation (Barry & Adrian, 1973; Friedrich et al. 2001):

A6

where D_K is the diffusion coefficient of potassium ions in the lumen of the TTS (in cm² s⁻¹), F is the Faraday constant, IKir is the total potassium current per cm³ of fibre and ρ is the fractional volume of the TTS. Using the dimensionless variables R = r/a and τ = σD_Kt/a², this equation becomes:

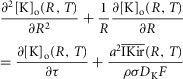A7

Potassium concentration changes in the lumen of the TTS

The finite difference approximation and Crank–Nicolson algorithm used for the integration of eqn 8 to calculate the luminal K concentration () at every shell i and at time interval j follows an analogous procedure to that described for the TTS voltage calculations. For simplicity, let us denote [K] = : c. Thus, at a given time j, the finite differences approximation of the partial differential equation for [K]_o in the TTS (eqn 8) is:

where 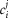is the finite difference representation of the luminal K concentration at radial position i at time j, and 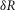is the normalized distance between shells.

Also:

Then:

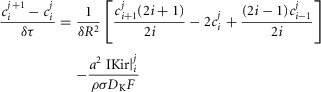A8

where is the current per unit fibre volume (calculated through the T-tubular element at shell i and at time interval j during the numerical integration process). Equation 11 allows us to establish recurrence using the Crank–Nicolson algorithm. If we denote 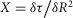, then:

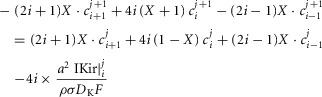A9

At the outside boundary (i = n) we apply Fick's law to the T-tubules’ opening:

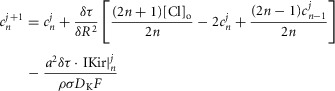From Crank (1975), for the inside (closed) boundary (i = 0):

Equation 12 is a recursive formula allowing, together with the respective equations of the boundary conditions, for the calculation of 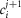at a time interval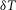, while knowing 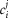. The system of tridiagonal coefficient matrices was solved using an LU decomposition algorithm as described for the TTS voltage.

The values of the general cable and K diffusion parameters utilized for the simulations shown in this paper are summarized in Table2. Specific Kir channel parameters are given in Table1. Electroneutrality in the TTS lumen was ascertained by balancing the anion (Cl⁻) and cation (Na⁺ and K⁺) concentrations at every TTS radial element. For simplicity, we assumed the diffusion coefficients of Na⁺ and Cl⁻ to be the same as that for K⁺ (D_K) and their values approximated to those in aqueous solutions. In the absence of firm data demonstrating otherwise, the model predictions were calculated assuming a constant TTS/fibre volume ratio (ρ) for the duration of the pulses. Thus, perturbations associated with potential volume changes in the TTS were excluded.

Total current and optical signals

The total ionic currents calculated from integration of the radial cable equations at each radial cable element of the TTS were the sum of two contributions: (1) a surface membrane component, calculated from the direct numerical integration of eqn 3 in response to V_COM; and (2) a TTS component, which encompasses the effective sum of currents originated in this membrane compartment; this was calculated from the application of Kirchhoff laws at the external opening of the TTS (Ashcroft et al. 1985; Kim and Vergara, 1998), as:

where 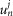is the voltage across the outermost segment of the TTS at time interval j.

Under the assumption that di-8-ANEPPS optical signals occur homogenously at superficial and deep regions of the TTS, and that changes in its optical properties with the transmembrane voltage occur identically at every submicroscopic region of the TTS, then the optical signal obtained within our illumination disc is expected to represent an ensemble average of the voltage contributed by every cable element in the TTS (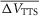) weighted by the radius of each annulus. This is calculated, for each successive time step, using a numerical trapezoidal integration algorithm based on Simpson's rule (Gerald, 1978) from the formula:

However, as described in detail elsewhere (Kim and Vergara, 1998; DiFranco et al. 2012), the actual contributions of different radial elements to the overall fluorescence transients were corrected by the optical properties of the objective used both to illuminate the preparation and to collect the fluorescence.

Additional information

Competing interests

None declared.

Author contributions

Conception and design of the experiments: M.Di.F. and J.L.V. Collection, analysis and interpretation of data: C.Y., M.Q., M.Di.F. and J.L.V. Drafting the article and revising it critically for intellectual content: M.Di.F. and J.L.V. The experiments were performed at the Department of Physiology, David Geffen School of Medicine, University of California Los Angeles (UCLA), USA.

Funding

The current work was supported by NIH/NIAMS grants AR047664 and AR54816 (J.L.V.), a multi-PI grant AR041802 (PI, Susan Hamilton, Baylor College of Medicine, Houston, TX), and a grant in aid (J.L.V.) from the Muscular Dystrophy Association of America (MDA). The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the MDA.