Abstract
The goal of this study was to determine quantitative relationships between electrophysiologic parameters and the propensity of cardiac tissue to undergo atrial fibrillation. We used a computational model to simulate episodes of fibrillation, which we then characterized in terms of both their duration and the population dynamics of the electrical waves which drove them. Monte Carlo sampling revealed that episode durations followed an exponential decay distribution and wave population sizes followed a normal distribution. Half-lives of reentrant episodes increased exponentially with either increasing tissue area to boundary length ratio (A/BL) or decreasing action potential duration (APD), resistance (R) or capacitance (C). We found that the qualitative form of fibrillatory activity (e.g., multi-wavelet reentry (MWR) vs. rotors) was dependent on the ratio of resistance and capacitance to APD; MWR was reliably produced below a ratio of 0.18. We found that a composite of these electrophysiologic parameters, which we term the fibrillogenicity index (Fb = A/(BL*APD*R*C)), reliably predicted the duration of MWR episodes (r2 = 0.93). Given that some of the quantities comprising Fb are amenable to manipulation (via either pharmacologic treatment or catheter ablation), these findings provide a theoretical basis for the development of titrated therapies of atrial fibrillation.
Introduction
Atrial fibrillation (AF) is the most prevalent cardiac arrhythmia in the United States, affecting an estimated 2.66 million adults as of 2010 [1],[2]. Unfortunately, despite the magnitude of its impact on the healthcare system [3], current treatments have proven inadequate, particularly in patients with longer lasting AF [4],[5],[6]. At least in part, this is due to our inability to tailor therapies to the specific electrical abnormalities of individual patients’ hearts. Instead, the severity of AF is categorized in a binary fashion based upon whether episodes of AF last less than or greater than 7 days [7], and ablation strategy is selected based upon this classification (i.e. pulmonary vein encircling alone vs. encircling plus additional atrial ablation) [4],[8]. Because the duration of AF episodes reflects the degree of electrical derangement in the heart, and this property exists along a continuum [9], it is therefore not surprising that basing therapy on a binary system often leads to unsatisfactory results.
It seems reasonable to suppose that better outcomes could be achieved by basing therapy on a more comprehensive assessment of atrial electrophysiology which accounts for the unique characteristics of individual patients’ hearts. Indeed, the relationship between atrial properties and the propensity to fibrillate has long been a subject of intense investigation. As early as 1912, investigators recognized that a “critical mass” of tissue is required to support fibrillation [10],[11],[12]. In addition, it has long been appreciated that shortened refractory period and slowed conduction velocity are pro-fibrillatory [13],[14],[15]. Nevertheless, the precise manner in which these factors determine the atria’s propensity to fibrillate remains poorly understood, and thus the degree to which they should be manipulated in the treatment of AF is unclear.
Accordingly, the purpose of this study was to quantify how electrophysiologic parameters determine the propensity of atrial tissue to support fibrillation. We pursued this goal with the aid of a previously described computational model which allowed us to study the behavior of multi-wavelet reentry (MWR), a chaotic propagation pattern which has long been considered one of the key mechanisms of AF [16],[17],[18]. In a previous paper, we introduced the idea of viewing MWR from a population dynamics perspective [19]. The wave population varies as a function of wave births and deaths and MWR terminates when the population reaches zero. We hypothesized that while the destinies of individual waves cannot be easily anticipated, the effect of parameter changes (e.g., changes in area, boundary length and wavelength) on average wave behavior (i.e. AF duration) can be quantitatively predicted. Further, we propose that changes to these parameters are pro- or anti-fibrillatory based upon their relative impact on the probabilities of wave births and deaths.
Methods
We performed a series of numerical experiments with a previously described computational model of cardiac electrical propagation [12],[19],[20]. Model code was written in C++ and simulations were run on the Vermont Advanced Computing Core (see www.uvm.edu/∼vacc/ for specifications). The model consists of a rectangular grid of excitable “cells” (each representing a roughly 1 mm2 group of cells) having a combined area of A and an outside boundary length of BL. The cells are connected to each other by electrically conducting pathways of resistance R via von Neumann neighborhoods (up, down, right and left). Because relative rather than absolute voltages guide the model’s behavior, each cell had a voltage which varied on a continuous scale between a minimum, V min = 0, representing the resting or polarized state, and a maximum, V max = 1, representing the fully depolarized state. Pairs of connected cells exchange charge at a rate determined by their voltage differences and R. The accumulated charge in a cell determines its voltage in inverse proportion to its capacitance C. When the voltage of a cell reaches a set threshold V min<V thresh<V max that cell’s voltage ascends rapidly to V max, and is then refractory for the duration of the action potential, APD. In this way, the depolarization of one cell spreads to its neighbors to generate a propagating action potential. The model time step was scaled relative to the length of typical action potentials such that it represented approximately 1ms. A degree of heterogeneity was also introduced by randomizing cellular APDs around mean values using a uniform distribution of +/−10ms.
Reentrant activity was initiated in the model via high-frequency burst pacing (100Hz for 1s) from a virtual electrode placed over a randomly chosen cell. Due to the chaotic nature of MWR, even small changes in the position from which reentry was induced could result in large differences in the state of the model’s activity at a given time step; thus, induction from each electrode location produced a unique episode of MWR. The qualitative nature of reentry depended on the values of the model parameters. Reentrant patterns were visually categorized by an observer blinded to the model parameters into four distinct groups: pure MWR, MWR with occasional rotor formation, rotors with occasional bouts of MWR, or rotors only (see S1 Video for representative examples of these reentrant phenotypes).
At each time step, we located all those cells which had become depolarized within the previous 10ms and defined the individual waves existing at that point in time to be the distinct groups of contiguous depolarized cells (Fig. 1); this allowed us to track the wave population through time. Fig. 2 shows two representative examples of wave population versus time.
Fig 1. Wave Identification Algorithm.
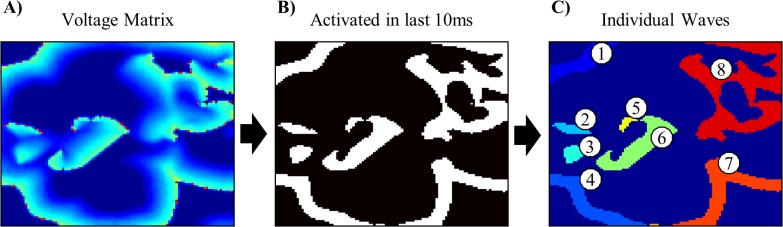
A) – an example of MWR in the computational model, B)—the cells that became depolarized within the previous 10ms (shown in white), C) – the eight distinct groups of contiguous depolarized cells which constitute the individual waves.
Fig 2. Wave Population Time Series.
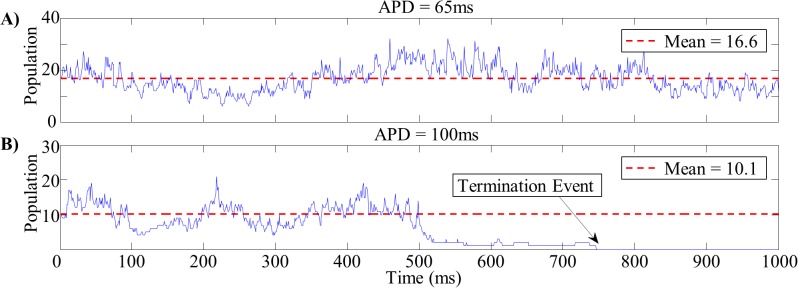
Examples of wave population time series for short (A) and long (B) wavelength tissues. The mean wave population for the short wavelength tissue (16.6 waves) was substantially lower than that of the long wavelength tissue (10.1 waves). At approximately 750ms, the wave population in the long wavelength tissue drops to zero and reentry terminates.
We generated three series of rectangular virtual tissues in each of which a single parameter was varied (A/BL, APD and RC as shown in Table 1). Tissue sizes in our model typically ranged between 2,500 and 10,000 cells. This range allows for between 5 and 50 waves to coexist on a tissue depending on that tissue’s properties. This range of wave to chamber size ratios encompasses that found in mapping studies of multi-wavelet reentry in humans [21],[22].
Table 1. Tissue Parameter Ranges.
| Tissue Series | A/BL | APD | RC |
|---|---|---|---|
| #1 (Varying A/BL) | 12.5 to 25mm | 80ms | 10ms |
| #2 (Varying APD) | 20mm | 50 to 100ms | 10ms |
| #3 (Varying RC) | 20mm | 80ms | 8 to 16ms |
| #4 (Randomized) | 12.5 to 25mm | 30ms to 150ms | 8 to 16ms |
Ranges of model parameter values used in the virtual tissue experiments.
We used a Monte-Carlo approach to determine how both the duration and population dynamics of MWR were affected by the values of these key parameters. In each tissue, we initiated 500 unique episodes of MWR and recorded the durations of each episode up to a maximum of 10,000s or until spontaneous termination occurred. We generated histograms by binning episodes according to their duration to produce probability distributions of episode length. Runs which failed to initiate reentry or lasted the maximum duration were excluded. In those same tissues, we initiated an additional 10 episodes of reentry in which we recorded the activation patterns of each cell for up to a maximum of 10s or until spontaneous termination occurred; these activation patterns were used to calculate the wave population at each time step. Since approximately 2s worth of model time could be produced in 1s of real computing time, individual simulation durations ranged between 1s and 1.5hrs depending on the tissue’s propensity to fibrillate. We generated histograms by binning time steps according to their population level.
We also tested the interaction between multiple simultaneous parameter changes. We generated one hundred additional virtual tissues with randomized properties (Table 1). In each of these tissues we initiated 500 unique episodes of MWR, and recorded the duration of each episode for up to 10,000s or until spontaneous termination occurred.
Results
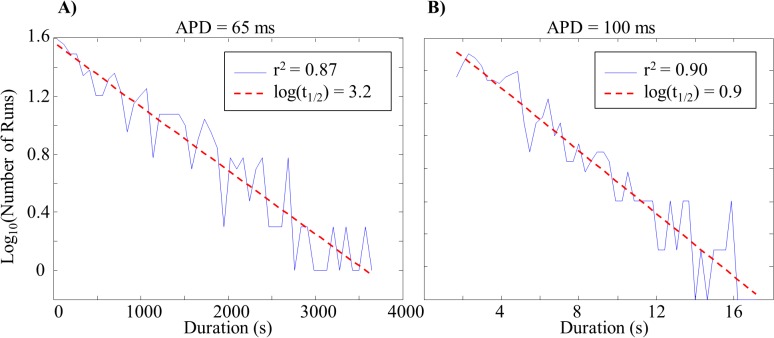
Semi-logarithmic histograms of the number of MWR episodes as a function of duration were well fit by linear regression (Fig. 3), indicating that the number of episodes to last a given duration followed an exponentially decaying distribution. It was therefore possible to calculate the half-life of reentry (t 1/2, the amount of time required for half of initiated episodes to terminate) from the slope of these regressions, λ, (Equation 1).
Fig 3. Episode Duration Distributions.
Example semi-logarithmic plots demonstrating the exponentially decaying number of MWR episodes to last a given duration. Short wavelength tissue (A) had a shallow slope and resulted in a longer half-life (approximately 26 minutes). Long wavelength tissue (B) had a steep slope and resulted in a shorter half-life (approximately 7 seconds).
| (1) |
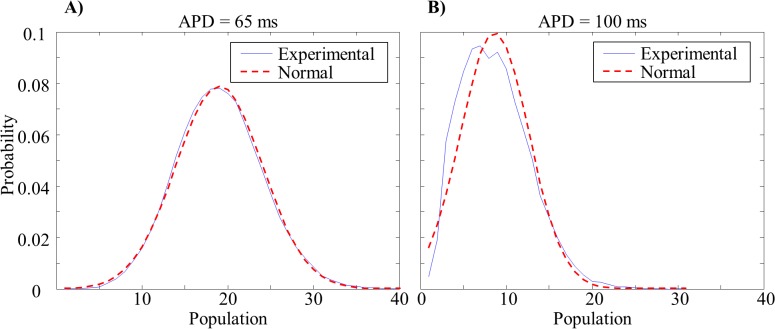
Normalized histograms of the amount of time spent at a given population level (expressed as relative probability) revealed that the probability of a given number of waves was normally distributed around the mean wave population (mean r 2 = 0.94 over ±2σ from the mean population—Fig. 4).
Fig 4. Wave Population Distributions.
Probability distributions of the percentage of time spent at each individual wave population for short (A) and long (B) wavelength tissues (red line—normal distribution).
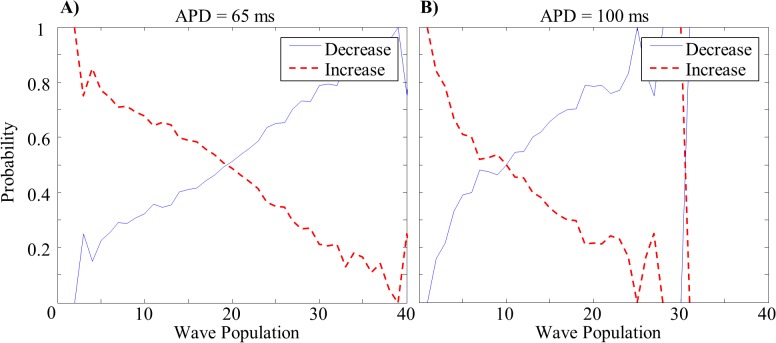
The probability that a population of waves will increase (red) or decrease (blue) in number at the next time step is a function of population size (Fig. 5). When the current population number falls below the mean, the probability that the number of waves will increase at the next time step is increased, and visa-versa. When the population number equals the mean there is an equal probability of having an increase and a decrease in the number of waves at the next time step. The population variance is inversely related to the rate at which these probabilities diverge from one another. The jaggedness of the plots near the highest and lowest populations is due to smaller sample sizes at the population extremes (i.e. fewer naturally occurring instances of these numbers of waves).
Fig 5. Population Dynamics Probabilities.
Representative examples: probabilities of increases or decreases in population as a function of current number of waves. (A) short and (B) long wavelength tissues.
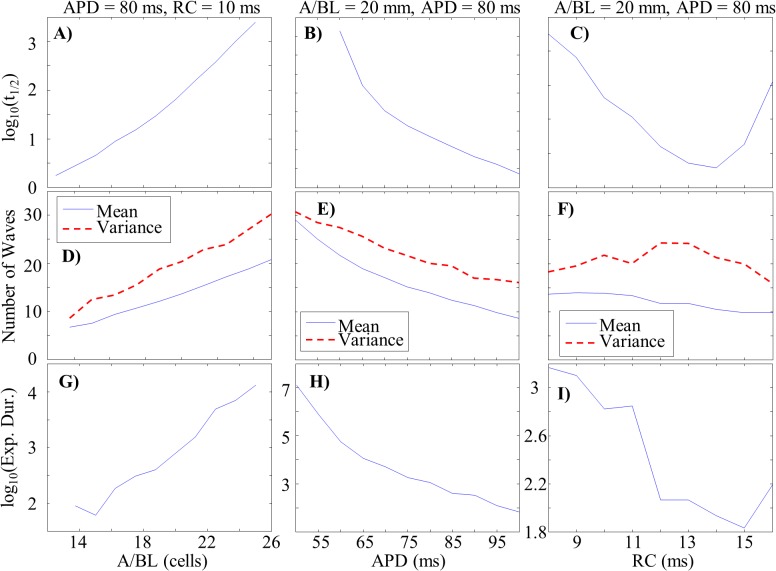
Half-life increased exponentially with either increasing A/BL or decreasing APD or RC (Fig. 6, A-C). These exponential relationships broke down when the ratio of RC/APD reached approximately 0.15–0.20. We were unable to generate values of t 1/2 for APD values below 60ms due to computational limitations (all episodes lasted until the maximum allowed time, 10,000s).
Fig 6. Parameter Dependencies of MWR Behavior.
A-C: Semi-log plots of MWR half-life as a function of A/BL (A), APD (B), and RC (C). D-F: The mean number of waves per time step (shown in blue) and population variance (shown in red) as functions of A/BL (D), APD (E), and RC (F). G-I: Semi-log plots of the expected duration of reentry (calculated from the population mean and variance) as a function of A/BL (G), APD (H), and RC (I). Note the similar parameter dependencies of MWR half-life and expected duration.
Mean wave population increased linearly with increasing A/BL and decreased linearly with increasing APD and RC (Fig. 6, D-F). Changes in variance ran largely parallel to changes in population mean for both A/BL and APD but had a positive dependence on RC, increasing until RC/APD reached approximately 0.15–0.2 and decreasing at higher values. We were unable to generate meaningful data for A/BL values below 13.75 due to the short durations of MWR. We calculated the probability of reaching a zero wave population according to Equation 2 (the cumulative probability below zero of a normal distribution function).
| (2) |
Here, μ is the population mean and σ is the standard deviation of the population’s variability. We approximated the expected duration of reentry as the inverse of these cumulative probabilities. For example, if there is a twenty percent chance of termination per second, on average we expect reentry to last 5 seconds. Just as with the dependency of t 1/2 on these parameters, increases in expected duration were found with increasing A/BL, decreasing APD, and decreasing RC (Fig. 6, G-I). Similar breakdowns in the linearity of these dependencies were seen at ratios of RC/APD of 0.15–0.20.
We composed a metric for a tissue’s propensity to fibrillate that incorporates the effects of what we considered to be the three most relevant parameters (A/BL, APD, and RC) on MWR episode duration. We term this metric the fibrillogenicity index and define it as
| (3) |
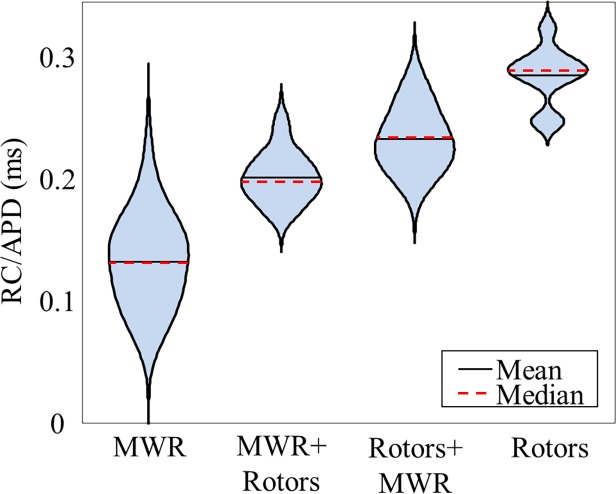
There was a clear exponential relationship between t 1/2 and Fb, but an r 2 correlation value of only 0.42 (Fig. 7A). We noticed that the majority of outlying points were exhibiting non-MWR type of behavior. After limiting our plot to tissues displaying only MWR the correlation between log(t 1/2) and Fb was much greater (r 2 = 0.82, Fig. 7B). We calculated the ratio of RC/APD for tissues in each of the four behavior categories (Fig. 8). An analysis-of-variance revealed a statistically significant (p<<0.001) difference in this value between groups, suggesting a method for predicting the behavior-type of a tissue based solely on the ratio of RC/APD. A receiver-operator curve analysis showed that a RC/APD cutoff of 0.18 resulted in a sensitivity of 91.4% with a false positive rate of only 5.7%. Using this cutoff value, we re-plotted log(t 1/2) as a function of Fb and found that the r 2 correlation coefficient improved to 0.93 (Fig. 7C).
Fig 7. Utility of the Fibrillogenicity Index.
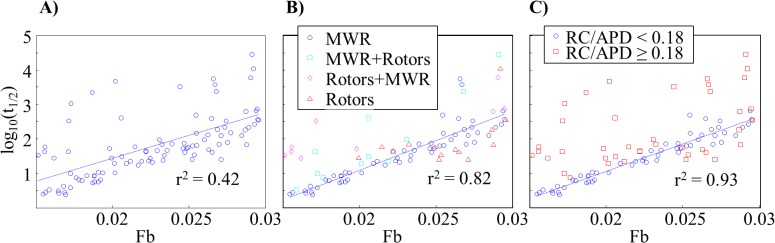
The logarithm of the MWR half-lives as a function of the fibrillogenicity index. For all randomly generated tissues, the fit is poor (A). Limiting the analysis to tissues displaying only MWR results in a substantially improved correlation coefficient (B). Using an RC/APD cutoff of 0.18 to identify likely MWR episodes further improves correlation coefficient (C).
Fig 8. Parameter Dependency of Reentrant Behavior.
Violin plot showing the distribution of RC/APD ratios for the four different categories of reentrant behavior. Violin width corresponds to relative sample density.
Discussion
Multi-wavelet reentry can at times appear to be an incomprehensible writhing mass of waves that fuse, divide, and annihilate across the atria in an apparently random fashion. Due to the complex, non-linear dynamics of propagation, it is extremely difficult to predict the long-term destiny of individual waves. However, by analyzing the system’s bulk characteristics rather than the evolving states of each specific wave, we have demonstrated that the ensemble behavior (i.e. MWR duration) can be predicted with a remarkable degree of accuracy. Knowledge of the statistics of wave population dynamics provides the link between atrial properties (size, shape and wavelength) and the duration of MWR episodes. By understanding how and why changes in parameters affect statistical metrics such as population mean and variance, we can predict how those same changes will ultimately alter episode duration.
Population Dynamics
Changes in wave population result from transient imbalances between wave formation events such as division, and wave reduction events such as fusion or annihilation. These life cycle events are the consequence of specific interactions between waves and their environment: division results from wave-front/wave-tail interactions, fusion results from wave-front/wave-front interactions, and annihilation results from wave-front/boundary interactions. The balance of these processes determines the population mean. The extent to which deviations in the number of waves alter this balance determines how avidly the population returns to the mean. While a reduction in the wave population increases the probability of wave division there is a non-zero probability that the population will continue to decrease and ultimately result in a zero wave population (MWR termination). Lower mean number of waves (which requires fewer sequential reduction events) and higher variance (which reduces the tendency to return to the mean) both result in a higher probability of reaching zero population and termination.
Tissue Properties, Wave Population and MWR Duration
By influencing the relative probabilities of wave division, fusion and annihilation, tissue properties determine the duration of MWR episodes. Increasing the ratio of tissue area to boundary length (A/BL) decreases the rate of wave annihilation relative to wave fusion and division and thus increases both mean number of waves and MWR duration. Increasing APD increases wavelength and therefore the area encompassed by individual waves. This preferentially increases the likelihood of annihilation and fusion and leads to a decrease in both the mean number of waves and MWR duration. As RC increases wavelength decreases but there is a concomitant increase in the excitable gap between waves. The combined effect is to gradually decrease mean number of waves and increase population variance, and ultimately leads to a decrease in MWR duration. Sufficient increase in the excitable gap reduces wave-wave interactions and allows for the formation of stable rotors.
The qualitative relationship between a tissue’s properties (area, boundary length and wavelength) and its capacity to maintain fibrillation has been studied in both animal models and humans. Garrey was the first to formulate the ‘mass hypothesis’, demonstrating that the duration of fibrillation correlated with tissue area and width (no measurements of wavelength or refractoriness were performed) [11]. Subsequently the role of wavelength (as well as tissue size) was shown to correlate with AF duration in animal models [23],[24] and in humans [25]. While it has long been recognized that increases in A/BL or decreases in APD will result in increased duration of multi-wavelet reentry [17],[25],[24], this study presents the first quantitative analysis of these dependencies (e.g., linear vs. exponential, etc.).
The fibrillogenicity index captures the balance between the two major forces which affect wave population dynamics: the size and shape of the tissue in which MWR exists (as determined by A/BL), and the size and shape of the waves themselves (as determined by APD and RC). So long as these opposing forces are scaled together, the absolute values of individual parameters are inconsequential. As an important caveat, our probabilistic formulation for predicting the duration of MWR is dependent upon individual waves having a non-zero probability of interacting with other waves or with tissue boundaries. Accordingly, we found that as pure MWR transitions to include spatially stable rotors, the fibrillogenicity index becomes less predictive of episode duration.
Application of the Fibrillogenicity index to Therapy
Perhaps the most promising aspect of the fibrillogenicity index is its potential application in treatment strategies. A common approach in deciding which lesion set to apply is to classify patients as having either paroxysmal (< 7 days) or persistent (≥7 days) AF [7]. Ablation is typically limited to pulmonary vein encirclement and isolation in paroxysmal AF, whereas patients with persistent AF are felt to require further atrial substrate modification (such as roof and isthmus lines or ablation of complex fractionated atrial electrograms (CFAE) [4],[8]). While this binary approach can be effective in patients whose AF durations are less than a few months, cure rates are 50% or lower in patients with longer lasting AF [6]. Obviously, standard treatment protocols are inadequate within this population. Regardless of which strategy one chooses for deciding where to ablate, a method is required for determining how much to ablate. In other words, if more extensive ablation is called for, by what degree should it be increased? Optimization of any approach to targeted ablation will require a titration method for determining the extent of lesions necessary at driver sites. The fibrillogenicity index has been designed to provide just such guidance, and thus offers a potentially useful compliment to any map-guided ablation strategy.
Limitations
As in any purely in silico experiment, the generalizability of our results remains limited and these findings will require validation in a biologic system, ultimately humans. None the less, computational modeling does offer some unique and powerful advantages over biologic experimental preparations. Only through the use of a computational model was it possible to explicitly isolate and manipulate each variable independently. Furthermore, the Monte-Carlo approach we made use of in characterizing probability distributions of MWR episode durations relied on collecting data from a large number of reentrant episodes. This type of high volume data collection is not possible in the clinical arena. Even within the computational arena however, we restricted our analysis to highly idealized instances of atrial substrate (two dimensional rectangular tissues with homogeneously distributed cell properties). Future extension of the fibrillogenicity index must account for the complex geometries, regional heterogeneities and anisotropy found in human hearts.
Our probabilistic formulation of wave population dynamics applies only to situations in which the positions of reentrant circuits change chaotically. However, as intercellular resistance and action potential duration are altered to produce a shortened propagation wavelength and a smaller radius of curvature, multi-wavelet reentry resolves gradually into a more spatially stable, rotor-driven, form of reentry. The phenotype of reentrant behavior is dependent on the ratio of RC/APD. As with the magnitudes of other parameters presented in this study, a direct mapping to the biological realm would be inappropriate. Instead, it is the way in which a relative change in these parameters affects the ultimate behavior of the tissue which is of interest. For example, any decrease in APD increases not only the duration of reentry, but also the likelihood of rotor-driven reentrant forms.
We have not explicitly addressed the impact of remodeling in our simulations. It has been demonstrated that progressive changes to ion channel expression and development of interstitial fibrosis can increase AF burden [26]. For example, coupling between myocytes and fibroblasts/myofibroblasts has been shown to alter APD, resting membrane potential, and conduction velocity [27],[28], and can ultimately lead to an increase in tissue’s propensity to fibrillate [29]. Remodeling effectively describes the movement through parameter space that results from feedback between behaviors (AF itself) and parameters (e.g. resistance, capacitance, APD). By focusing only on the steady state situation we have defined the mapping between model parameters and behavior (i.e. Fb). Thus with the fibrillogenicity index we can predict the impact, though not the dynamics, of remodeling.
The fibrillogenicity index is calculated from parameters that we have complete knowledge of in the computational environment but which are difficult to measure in the clinical setting. Though it is relatively straightforward to gather information regarding the size and shape of a patient’s atria (e.g. via CT scan or electro-anatomic mapping), measurements of APD, resistance and capacitance cannot easily be obtained. We have previously demonstrated that electrogram frequency (when acquired using electrodes with high spatial resolution) correlates well with tissue wavelength and may therefore offer a practical, measurable alternative for calculating the fibrillogenicity index.
Conclusions
We report a mechanistic, population dynamics based framework for understanding multi-wavelet reentry using a computational model of propagation. During MWR, the number of waves which coexist on a given tissue follows a normal distribution, the mean and variance of which can be used to calculate the probability of spontaneous termination. Three key parameters influence the duration of reentrant episodes: tissue size and shape, action potential duration, and resistance and capacitance. Increases in the tissue-area to boundary-length ratio, or decreases in APD or RC resulted in exponential increases in the duration of MWR episodes. We demonstrated that the phenotype of reentrant behavior (MWR vs. spatially stable rotors) is dependent upon the ratio of RC/APD; below a ratio of 0.18 reentry reliably fits into the category of pure MWR. Finally, we have defined a metric for quantifying a tissue’s propensity to fibrillate. The fibrillogenicity index is derived from a tissue’s properties and accurately predicted MWR half-life over a wide range or durations (1s to 6hrs, r 2 = 0.93). We believe that the fibrillogenicity index provides a foundation upon which patient-specific treatment protocols for AF can be built.
Supporting Information
In this video, we present examples from four different positions along the spectrum of reentrant behavior: 1) pure MWR, 2) MWR with occasional rotor formation, 3) rotors with occasional bouts of MWR, and 4) stable rotors.
(MP4)
(XLSX)
Data Availability
All relevant data will be made publicly available at the time of acceptance at www.dryad.com
Funding Statement
The Peter Spector laboratory at the University of Vermont received funding from the Evslin Family Foundation, Inc., a non-profit angel donor group. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of manuscript.
References
- 1. Go AS, Hylek EM, Phillips KA, Chang Y, Henault LE, Selby JV, et al. Prevalence of Diagnosed Atrial Fibrillation in Adults. J Am Med Assoc. 2014;285: 2370–2375. [DOI] [PubMed] [Google Scholar]
- 2. Lloyd-Jones DM, Wang TJ, Leip EP, Larson MG, Levy D, Vasan RS, et al. Lifetime risk for development of atrial fibrillation: the Framingham Heart Study. Circulation. 2004;110: 1042–1046. [DOI] [PubMed] [Google Scholar]
- 3. Sanoski CA. Clinical, economic, and quality of life impact of atrial fibrillation. J Manag Care Pharm. 2009;15: S4–S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Calkins H, Reynolds MR, Spector P, Sondhi M, Xu Y, Martin A, et al. Treatment of atrial fibrillation with antiarrhythmic drugs or radiofrequency ablation: two systematic literature reviews and meta-analyses. Circ Arrhythm Electrophysiol. 2009;2: 349–361. 10.1161/CIRCEP.108.824789 [DOI] [PubMed] [Google Scholar]
- 5. Oral H, Knight BP, Tada H, Ozaydin M, Chugh A, Hassan S, et al. Pulmonary Vein Isolation for Paroxysmal and Persistent Atrial Fibrillation. Circulation. 2002;105: 1077–1081. [DOI] [PubMed] [Google Scholar]
- 6. Tilz RR, Rillig A, Thum A-M, Arya A, Wohlmuth P, Metzner A, et al. Catheter ablation of long-standing persistent atrial fibrillation: 5-year outcomes of the Hamburg Sequential Ablation Strategy. J Am Coll Cardiol. 2012;60: 1921–1929. 10.1016/j.jacc.2012.04.060 [DOI] [PubMed] [Google Scholar]
- 7. January CT, Wann LS, Alpert JS, Calkins H, Cigarroa JE, Cleveland JC, et al. 2014 AHA/ACC/HRS Guideline for the Management of Patients With Atrial Fibrillation: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines and the Heart Rhythm Society. J Am Coll Cardiol. 2014; 64(21): 2246–2280. [DOI] [PubMed] [Google Scholar]
- 8. Wright M, Haïssaguerre M, Knecht S, Matsuo S, O’Neill MD, Nault I, et al. State of the art: catheter ablation of atrial fibrillation. J Cardiovasc Electrophysiol. 2008;19: 583–592. 10.1111/j.1540-8167.2008.01187.x [DOI] [PubMed] [Google Scholar]
- 9. Charitos EI, Pürerfellner H, Glotzer TV, Ziegler PD. Clinical Classifications of Atrial Fibrillation Poorly Reflect its Temporal Persistence: Insights From 1195 Patients Continuously Monitored with Implantable Devices. J Am Coll Cardiol. 2014;63: 2840–2848 10.1016/j.jacc.2014.04.019 [DOI] [PubMed] [Google Scholar]
- 10. Cox JL. The Surgical Treatment of Atrial Fibrillation. J Thorac Cardiovasc Surg. 1991;101: 584–592. [PubMed] [Google Scholar]
- 11. Garrey WE. The nature of fibrillary contraction of the heart—its relation to tissue mass and form. Am J Physiol. 1914;33: 397–414. [Google Scholar]
- 12. Spector PS, Correa de Sa DD, Tischler ES, Thompson NC, Habel N, Stinnett-Donnelly J, et al. Ablation of multi-wavelet re-entry: general principles and in silico analyses. Europace. 2012;14(5): v106–v111. 10.1093/europace/eus278 [DOI] [PubMed] [Google Scholar]
- 13. Jacquemet V, Virag N, Kappenberger L. Wavelength and vulnerability to atrial fibrillation: Insights from a computer model of human atria. Europace. 2005;7(2): 83–92. [DOI] [PubMed] [Google Scholar]
- 14. Rensma PL, Allessie MA., Lammers WJ, Bonke FI, Schalij MJ. Length of excitation wave and susceptibility to reentrant atrial arrhythmias in normal conscious dogs. Circ Res. 1988;62: 395–410. [DOI] [PubMed] [Google Scholar]
- 15. Wang J, Bourne GW, Wang Z, Villemaire C, Talajic M, Nattel S. Comparative mechanisms of antiarrhythmic drug action in experimental atrial fibrillation. Importance of use-dependent effects on refractoriness. Circulation. 1993;88: 1030–1044. [DOI] [PubMed] [Google Scholar]
- 16. De Groot MS, Houben RPM, Smeets JL, Boersma E, Schotten U, Schalij MJ, et al. Electropathological Substrate of Longstanding Persistent Atrial Fibrillation in Patients With Structural Heart Disease Epicardial Breakthrough. Circulation. 2010;3: 1674–1682. [DOI] [PubMed] [Google Scholar]
- 17. Moe GK, Rheinboldt WC, Abildskov JA. A computer model of atrial fibrillation. Am Heart J. 1964;67: 200–220. [DOI] [PubMed] [Google Scholar]
- 18. Moe GK. On the multiple wavelet hypothesis of atrial fibrillation. Arch Int Pharmacodyn Ther. 1962;140: 183–188. [Google Scholar]
- 19. Carrick RT, Benson B, Habel N, Bates ORJ, Bates JHT, Spector PS. Ablation of multiwavelet re-entry guided by circuit-density and distribution: maximizing the probability of circuit annihilation. Circ Arrhythm Electrophysiol. 2013;6: 1229–1235. 10.1161/CIRCEP.113.000759 [DOI] [PubMed] [Google Scholar]
- 20. Spector PS, Habel N, Sobel BE, Bates JHT. Emergence of complex behavior: an interactive model of cardiac excitation provides a powerful tool for understanding electric propagation. Circ Arrhythm Electrophysiol. 2011;4: 586–591. 10.1161/CIRCEP.110.961524 [DOI] [PubMed] [Google Scholar]
- 21. Allessie M, Lammers W, Bonke F, Hollen J. Experimental evaluation of Moe’s multiple wavelet hypothesis of atrial fibrillation In: Zipes DP, Jalife J. Cardiac Arrhythmias. Grune & Stratton; Orlando, FL: 1985. pp. 265–276. [Google Scholar]
- 22. Allessie MA, de Groot NMS, Houben RPM, Schotten U, Boersma E, Smeets JL, et al. Electropathological substrate of long-standing persistent atrial fibrillation in patients with structural heart disease: longitudinal dissociation. Circ Arrhythm Electrophysiol. 2010;3: 606–615. 10.1161/CIRCEP.109.910125 [DOI] [PubMed] [Google Scholar]
- 23. Byrd GD, Prasad SM, Ripplinger CM, Cassilly TR, Schuessler RB, Boineau JP, et al. Importance of geometry and refractory period in sustaining atrial fibrillation: testing the critical mass hypothesis. Circulation. 2005;112: I7–I13. [DOI] [PubMed] [Google Scholar]
- 24. Lee AM, Aziz A, Didesch J, Clark KL, Schuessler RB, Damiano RJ Jr. Importance of atrial surface area and refractory period in sustaining atrial fibrillation: testing the critical mass hypothesis. J Thorac Cardiovasc Surg. 2013;146: 593–598. 10.1016/j.jtcvs.2012.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kojodjojo P, Peters NS, Davies DW, Kanagaratnam P. Characterization of the Electroanatomical Substrate in Human Atrial Fibrillation: The Relationship between Changes in Atrial Volume, Refractoriness, Wavefront Propagation Velocities, and AF Burden. J Cardiovasc Electrophysiol. 2007;18: 269–275. [DOI] [PubMed] [Google Scholar]
- 26. Wijffels MCEF, Kirchhof CJ, Dorland R, Allessie MA. Atrial fibrillation begets atrial fibrillation: a study in awake chronically instrumented goats. Circulation. 1995;92: 1954–1968. [DOI] [PubMed] [Google Scholar]
- 27. Jacquemet V, Henriquez CS. Modelling cardiac fibroblasts: interactions with myocytes and their impact on impulse propagation. Europace. 2007;9(6): vi29–vi37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Jacquemet V, Henriquez CS. Loading effect of fibroblast-myocyte coupling on resting potential, impulse propagation, and repolarization: insights from a microstructure model. Am J Physiol Heart Circ Physiol. 2008;294: H2040–H2052. 10.1152/ajpheart.01298.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. McDowell KS, Arevalo HJ, Maleckar MM, Trayanova N. Susceptibility to arrhythmia in the infarcted heart depends on myofibroblast density. Biophys J. 2011;101: 1307–1315. 10.1016/j.bpj.2011.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
In this video, we present examples from four different positions along the spectrum of reentrant behavior: 1) pure MWR, 2) MWR with occasional rotor formation, 3) rotors with occasional bouts of MWR, and 4) stable rotors.
(MP4)
(XLSX)
Data Availability Statement
All relevant data will be made publicly available at the time of acceptance at www.dryad.com