Bayesian dose-finding designs for combination of molecularly targeted agents assuming partial stochastic ordering

Abstract

Molecularly targeted agent (MTA) combination therapy is in the early stages of development. When using a fixed dose of one agent in combinations of MTAs, toxicity and efficacy do not necessarily increase with an increasing dose of the other agent. Thus, in dose-finding trials for combinations of MTAs, interest may lie in identifying the optimal biological dose combinations (OBDCs), defined as the lowest dose combinations (in a certain sense) that are safe and have the highest efficacy level meeting a prespecified target. The limited existing designs for these trials use parametric dose–efficacy and dose–toxicity models. Motivated by a phase I/II clinical trial of a combination of two MTAs in patients with pancreatic, endometrial, or colorectal cancer, we propose Bayesian dose-finding designs to identify the OBDCs without parametric model assumptions. The proposed approach is based only on partial stochastic ordering assumptions for the effects of the combined MTAs and uses isotonic regression to estimate partially stochastically ordered marginal posterior distributions of the efficacy and toxicity probabilities. We demonstrate that our proposed method appropriately accounts for the partial ordering constraints, including potential plateaus on the dose–response surfaces, and is computationally efficient. We develop a dose-combination-finding algorithm to identify the OBDCs. We use simulations to compare the proposed designs with an alternative design based on Bayesian isotonic regression transformation and a design based on parametric change-point dose–toxicity and dose–efficacy models and demonstrate desirable operating characteristics of the proposed designs. © 2014 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

Cancer treatment development is in the era of molecularly targeted agents (MTAs) [1,2], which are drugs or other substances that interfere with specific molecules necessary for tumor growth and progression. MTA combination therapy, however, is still in its early stages of development [3]. In principle, the use of combinations of MTAs is attractive for a variety of reasons. Specifically, a combination of treatment agents may achieve a greater blockade of cancer cell growth by inhibiting sequential signal transduction sites in one transduction pathway, by simultaneously impacting the extracellular targets and the intracellular tyrosine kinase that regulates a pathway, by simultaneously impacting a transduction pathway and its bypassing mechanism, or by targeting different transduction pathways in a potentially additive strategy [2]. Thus, it is imperative that we develop robust and efficient statistical designs for dose-finding clinical trials for combinations of MTAs.

The designs proposed in this paper are motivated by a phase I/II clinical trial that uses a combination of two MTAs to treat patients with pancreatic, endometrial, or colorectal cancer. One agent being investigated in the trial inhibits AKT (protein kinase B, which plays vital roles in multiple cellular processes). The second agent inhibits MEK (a mitogen-activated protein kinase/extracellular signal-regulated kinase, which is an enzymatic activator of protein kinase family that regulates several processes in support of cellular proliferation). The investigators assume that at a fixed dose of either agent, neither efficacy nor toxicity of the combined agents decreases with an increasing dose of the other agent, on the basis of their understanding of the mechanism of the effects of the combination agents. As with many MTA combinations, the investigators also believe that both efficacy and toxicity may plateau within the tested dose range. Thus, the primary objective of the trial is to determine the lowest dose combinations (to be formally defined in Section 2.1) that are safe and have the highest efficacy level meeting a prespecified target, which we term the optimal biological dose combinations (OBDCs).

Numerous methods have been proposed for designing phase I dose-finding clinical trials for combinations of cytotoxic agents [4–7]. A common assumption underlying these methods is that the dose–toxicity and dose–efficacy relationships are characterized by a monotonic increase in the outcome probability as the dose of one drug increases when the dose of the other drug is held fixed. Thus, the goal of these trials is to identify the maximum tolerated dose combination. A recent trend in drug development in oncology favors integrating phase I and phase II trials so that the drug development process may be expedited while potentially reducing costs [8]. Huang et al., [9] proposed a parallel phase I/II design for combination of chemotherapies in which the first stage uses a modified ‘3+3’ algorithm, the limitations of which have been extensively discussed in the literature ([10–12], among others). Yuan and Yin [13] proposed a phase I/II design using a copula-type parametric model for the toxicity probabilities across dose combinations in the phase I portion. Neither of these designs explicitly incorporates partial ordering constraints in assessing efficacy in their phase II portion of the trial. Recently, Wages and Conaway [14] proposed a phase I/II design for chemotherapy combination trials, assuming partial ordering constraints for both toxicity and efficacy using parametric models. While their methods may be efficient in situations where certain ordering (rather than partial ordering) constraints are known a priori, the computational burden of their methods may increase considerably when such information is not available.

For MTAs, the hypothesized dose–efficacy and dose–toxicity relationships are different. Specifically, there may be a plateau in the dose–efficacy curve such that higher doses of MTAs may not necessarily improve clinical benefit [15–19]. In addition, toxicity does not necessarily increase with an increasing dose of MTAs [16,18–21]. For example, if toxicity is incurred by unintended target inhibition, this effect may also reach a plateau in the tested dose range as the dose increases, on the basis of a mechanism similar to that of the efficacy of the agents.

Very limited literature exists on phase I/II dose-finding designs for combinations of MTAs. Mandrekar et al., [20] proposed a dose-finding design for trials evaluating combinations of biological agents based on a continuation ratio model that allows for a potential drop in the probability of efficacy and no toxicity with an increasing dose of either agent when the dose of the other agent is fixed. Hirakawa [22] developed a dose-finding design for combinations of two drugs where the dose–efficacy curve may plateau beyond certain dose levels. Recently, Cai et al., [21] have proposed a dose-finding design for MTA combination trials using a change-point model for the dose–toxicity surface and a quadratic model for the dose–efficacy surface to account for a potential plateau in the dose–toxicity surface and a potential decreasing trend in the dose–efficacy surface. All these designs use parametric models for dose–toxicity and dose–efficacy relationships, which may be sensitive to the strong parametric model assumptions.

While some authors have considered models that allow for decreased efficacy with an increased dose [20,21], in this paper we focus on a more likely scenario in which the dose–efficacy curve for each agent may either increase or increase and then plateau in the tested dose range given a fixed dose of the other agent [15–19,22]. We assume that the dose–toxicity relationships may follow the same pattern. That is, we assume matrix-ordering constraints for both dose–toxicity and dose–efficacy relationships while allowing for temporary or continuous plateaus in the tested dose range. We aim to develop novel dose-finding designs for combinations of MTAs that are based only on the partial ordering assumptions [23,24], targeting particularly at potential plateaus in the dose–efficacy and/or dose–toxicity surfaces, with the ultimate goal of identifying the OBDCs.

To achieve the preceding goal, we consider computationally feasible approaches to Bayesian inference under partial order constraints without parametric model assumptions. The first is a Bayesian isotonic regression transformation (BIT) approach [25–27]. We show that, however, this approach has a limitation of potentially overcorrecting the order when used to model non-decreasing dose–response surfaces where a plateau may be present. This motivates us to propose a second approach that is also based on postprocessing of the unconstrained posterior distributions (thus maintaining computational efficiency), yet which appropriately accounts for not only the non-decreasing trend but also potential plateaus in the dose–response surfaces. This second approach uses partial stochastic ordering (PSO) assumptions, for which we demonstrate that computation can be carried out efficiently as no posterior samples need to be drawn for posterior inferences. We develop a dose-combination-finding algorithm to identify the OBDCs.

The organization of the article is as follows. In Section 2.1, we describe PSO assumptions for predicted patient binary outcomes as the motivation and basis of our proposed methods. In Section 2.2, we consider a BIT approach to account for the partial ordering constraints and illustrate a limitation of this approach to modeling dose–response relationships that may plateau in the tested dose range. We then propose a second approach based only on PSO assumptions to address the limitation of the BIT approach in Section 2.3. In Section 3, we propose a dose-combination-finding algorithm. In Section 4, we apply the proposed designs to the motivating clinical trial for pancreatic, endometrial, or colorectal cancer, examine the operating characteristics of the designs and compare them with a design based on parametric change-point models through simulations. We provide concluding remarks in Section 5.

2. Method

2.1. Notation and partial stochastic ordering assumptions on predicted toxicity and efficacy outcomes

Following Hunsberger et al., [16], we assume that each patient has a binary response for toxicity and efficacy, respectively, after treatment with the MTA combination. Toxicity can be defined as having or not having predefined dose-limiting toxicities. Efficacy can be a pharmacodynamic response assessed by the change in relevant biomarker measurements that are considered to confer clinical benefit to the patients. Alternatively, efficacy can be assessed by tumor response, such as complete or partial remission. We assume that the toxicity and efficacy outcomes can be observed in a short period of time, such as after one cycle of treatment.

Suppose each MTA (A or B) has J or K dose levels being tested, respectively, resulting in a J × K dose-combination matrix. Let (j,k) denote a combination with dose level j of agent A and k of agent B, j = 1,…,J, k = 1,…,K, 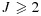, 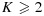. Let D={(j,k):j = 1,…,J,k = 1,…,K} be the set of all dose combinations. We define a partial order ≼ on D as follows:

and in which we say that combination (j₁,k₁) is lower than (j₂,k₂) or combination (j₂,k₂) is higher than (j₁,k₁). We further define a combination (j,k) to be one of the lowest combinations in a subset C⊂D (for use only in the decision rules in our proposed dose-combination-finding methods), if for all (j^′,k^′)∈C, 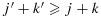. Therefore, there can be multiple ‘lowest’ combinations in C. For example, if C={(j,k):j > 1 or k > 1}, then the lowest combinations in C are (1,2) and (2,1) (Figure 1). Alternatively, if C={(1,2),(3,1)}, then the lowest combination in C is (1,2). We note that alternative definitions for the lowest combinations are possible, depending on the physicians' interest. For example, a plausible alternative definition that is not the focus of this paper is a combination (j,k)∈C such that for all (j^′,k^′)∈C, eithe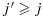r or .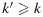

Figure 1.

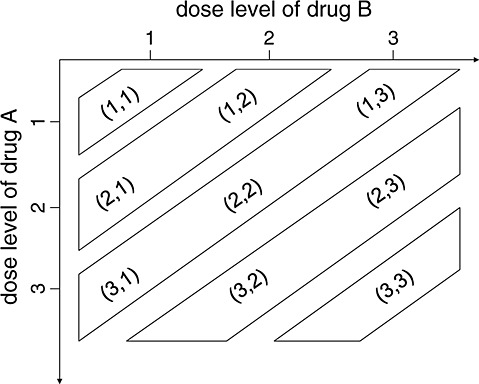
An illustration of dose combinations.

We now define a stochastic order between two random variables. For two random variables, X and Y, with corresponding cumulative distribution functions, F and G, X is said to be stochastically smaller than Y if 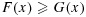for all x. Furthermore, X is said to be stochastically strictly smaller than Y if 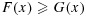for all x, and F(x) > G(x) for at least one x [28]. Also, two random variables X and Y are said to be stochastically equal if X is stochastically smaller than Y and Y is stochastically smaller than X.

We consider it reasonable to make the following PSO assumption on the predicted toxicity and efficacy outcomes of patients across dose combinations.

Assumption A₁. Given any observed data, the toxicity and efficacy outcomes of a patient to be treated at (j₁,k₁) are stochastically smaller than those of a patient to be treated at (j₂,k₂) where (j₁,k₁)≼(j₂,k₂).

Note that Assumption A₁ allows for cases where the outcomes of the two future patients treated at (j₁,k₁) and (j₂,k₂) are stochastically equal. This is important for dose-finding trials of MTA combinations as a plateau may be present in the dose–efficacy and/or dose–toxicity surface.

Denote p_jk and q_jk as the toxicity and efficacy probabilities of a patient treated at dose combination (j,k). One can easily show that the subsequent Condition C₁ is a sufficient condition for Assumption A₁. See Appendix 1 in the Supporting information.

Condition C₁. Given any observed data, 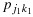and 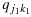are each stochastically smaller than 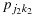and 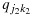, respectively, as long as (j₁,k₁)≼(j₂,k₂).

In the following sections, we will consider two postprocessing inference approaches, both of which ensure that Condition C₁ is satisfied, so that Assumption A₁ is met.

2.2. Bayesian isotonic regression transformation

In the Bayesian paradigm, there have been two general approaches to inference on order-constrained model parameters. The first is a fully Bayesian approach in which priors for the relevant parameters are specified in an order-constrained parameter space. While this may be a desirable approach, difficulties may arise in both specification of the prior and computation of the posterior in the presence of complex ordering constraints. For example, the matrix-ordering constraints we consider in this paper allow for the presence of potential plateaus across unspecified sets of dose combinations, making it tedious to specify priors that satisfy these constraints while ensuring that the specified prior and chosen hyperparameters are intuitive or easily interpretable. In addition, posterior computation for these models can be expensive. The second is a postprocessing approach that is typically based on transformation and may involve two steps. In the first step, one obtains the posterior distribution based on a model that ignores the order constraints. In the second step, the order constraints are incorporated by postprocessing the unconstrained posterior distribution of the model parameters via transformations. For example, BIT uses isotonic regression to directly transform the posterior samples of the unconstrained model parameters into order-constrained samples. Thus, posterior inference based on these order-constrained samples automatically accounts for the ordering constraints [25–27]. Note that in this approach only the model parameters that are assumed to follow certain ordering or partial ordering constraints need to be transformed. For example, in Li et al., [27] the toxicity probability is assumed to follow the matrix order while the efficacy probability is assumed to be unordered. Thus, the BIT is only applied on the toxicity probabilities across dose–schedule combinations [27]. As the isotonic regression is a minimal distance mapping (see its following definition), and the prior distribution implicitly defined by the ratio of the transformed posterior distribution and the likelihood is data dependent, such an approach has been considered an empirical Bayes-type procedure [26]. Generally speaking, the primary motivation and utility of this type of approach is computational [25–27]. This is because computation in the first step, which does not involve ordering constraints, is typically quite efficient, and general algorithms for isotonic regression are well developed, including, for example, the minimum lower sets algorithm (MLSA) for a partially ordered set [29]. Such algorithms have been implemented in the design of dose-finding and dose–schedule-finding trials [27,30]. Compared with certain fully Bayesian prior specification approaches based on truncation for order-constrained parameters, the BIT approach respects the data in an intuitive way [25].

Therefore, we first propose a BIT approach to modeling the posterior toxicity and efficacy probabilities while assuming matrix-ordering constraints across dose combinations with potential plateaus. We start by assuming independent Beta(a₁,b₁) and Beta(a₂,b₂) prior distributions for toxicity and efficacy, respectively, at each dose combination, where a₁, b₁, a₂ and b₂ are constants that often do not depend on (j,k). Let n_jk denote the number of patients that have been treated at combination (j,k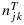), and and 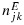denote the number of patients that experienced toxicity and showed efficacy, respectively. Given the binomial likelihood and beta prior distributions, the posterior distributions of toxicity and efficacy at combination (j,k), without accounting for the partial ordering constraints, are

(1)

(2)

In the second step, following Li et al., [27], we use isotonic regression to transform each sample from the unconstrained posterior distribution for the toxicity probabilities into an order-constrained sample. Specifically, hereafter we denote C as the set of dose combinations at which at least one cohort of patients has been treated and ≼ as the partial order defined on C⊂D in Section 2.1. Let p={p_j,k} and q={q_j,k}. A draw 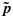of p from its unconstrained posterior distribution 2 can be regarded as a real-valued function on C, and the isotonic regression 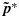of 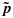is defined as an isotonic function on C that minimizes the weighted sum of squares

subject to the constraints 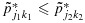whenever (j₁,k₁)≼(j₂,k₂). The weights {w_jk} are taken to be the posterior precisions of p_jk [25–27]. By the preceding definition, the partial ordering constraints are satisfied for the transformed posterior samples 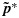. A similar transformation is applied on the unconstrained posterior samples of the efficacy probabilities 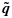to obtain order-constrained posterior samples 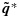. Thus, the partial ordering constraints are automatically accounted for in the corresponding posterior inference based on these transformed posterior samples for toxicity and efficacy probabilities in a dose-finding study. In addition, this isotonic regression transformation of p or q is a minimal distance mapping from the unconstrained to the constrained parameter space. We use the MLSA to calculate the isotonic regression under the matrix-ordering constraints [29]. As the application of BIT on posterior samples of p_jk and q_jk ensures almost sure partial ordering, the PSO Condition C₁ is clearly met. We propose a dose-combination-finding algorithm in Section 3.

2.3. Isotonic regression of the posterior distribution functions

While the BIT approach has the attractive feature of reduced computational burden while accounting for the partial ordering constraints, it faces a challenge in modeling the dose–toxicity and dose–efficacy surfaces where plateaus may be present. In fact, the BIT approach results in posterior distributions that are always strictly partially ordered across dose combinations, thus making it less sensitive in identifying plateaus in the tested dose range and therefore undesirable for determining the OBDCs. To demonstrate this limitation, let us look at two simplistic examples.

Suppose three patients are treated at each of dose combinations (1,1) and (1,2), with two and one responses being observed, respectively. Under independent Beta(a₂,b₂) priors, the corresponding posterior distributions for q_1,1 and q_1,2 are Beta(2 + a₂,1 + b₂) and Beta(1 + a₂,2 + b₂), respectively. Let us assume for now that a₂=b₂=0.5. It is straightforward to show that q_1,1 is stochastically strictly larger than q_1,2. A proof of this is given in Appendix 2 in the Supporting information. Thus, on the basis of the non-decreasing assumption for efficacy with respect to dose that allows for the possibility of a plateau, and to respect the observed data, it may be desirable to estimate the two posterior distributions to be equal (i.e., as close to the unconstrained posterior distributions as possible while adhering to the ordering constraint). Using the BIT approach, however, as the unconstrained posterior draws for q_1,1 and q_1,2 are made independently (under the independent priors and independent binomial likelihood across dose combinations), there will be a positive probability of the transformed posterior draws 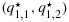satisfying 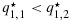. In fact, 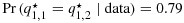and ! The posterior means are similarly strictly ordered (despite that the sample means are 0.67 and 0.33, respectively; see Figure 2). If the response outcomes are instead one and two out of three patients at combinations (1,1) and (1,2), respectively, that is, the outcomes are reversed, then it is clear that q_1,1 is already stochastically strictly smaller than q_1,2. Presumably no correction of the posterior distributions is necessary in this case. However, BIT would estimate the posterior distributions for q_1,2 to be even larger and q_1,1 to be even smaller than the corresponding unconstrained posterior distributions. We argue that in both of the preceding cases the BIT approach has made more adjustments than necessary to account for the ordering constraint or, in other words, has ‘overcorrected’ for the order. See Figure 2 for a graphical illustration.

Figure 2.

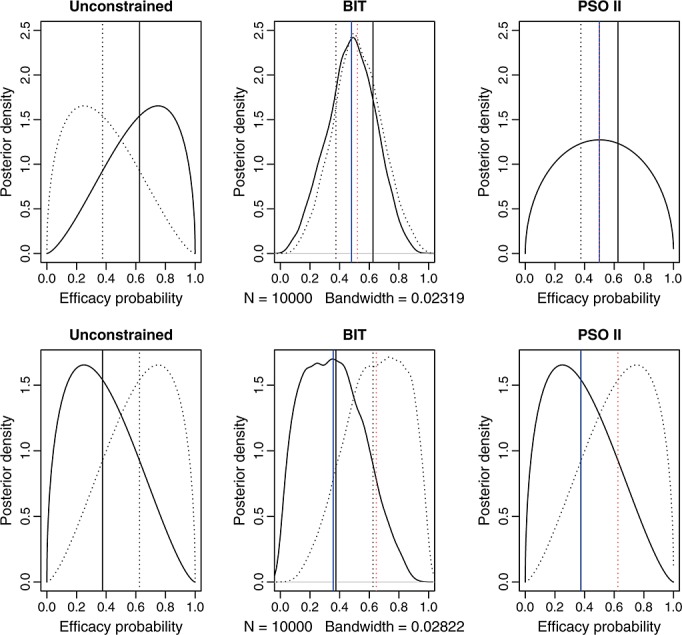
The top three panels are posterior densities of the efficacy probability when two out of three and one out of three responses are observed at combinations (1,1) and (1,2), respectively. The bottom three panels are the corresponding posterior densities when one out of three and two out of three responses are observed at combinations (1,1) and (1,2), respectively. The solid and dotted curves are the density curves at combinations (1,1) and (1,2), respectively. The vertical lines indicate the posterior means, with black representing unconstrained and blue and red representing constrained posterior means, and the solid and dotted lines correspond to combinations (1,1) and (1,2), respectively. The blue solid and red dotted lines overlap on the top right panel; the black and blue solid lines overlap and the black and red dotted lines overlap on the bottom right panel. BIT, Bayesian isotonic regression transformation; PSO II, partial stochastic ordering using sample sizes as weights.

Although overly simplified, the preceding examples demonstrate the general trend for this approach, even for more complex situations that involve multiple combinations. Intuitively, correction of the order occurs with a high probability if two underlying distributions are close to each other. It is possible that the extent of overcorrection is also higher under those situations. While such ‘overcorrection’ effects of the BIT approach would not be a concern were the sample size large, the sample size at each dose combination in a typical phase I/II dose-finding trial for combination therapy is small. Understanding these effects of the BIT approach may help us interpret the operating characteristics of the BIT-based design presented in Section 4.

To address the preceding ‘overcorrection’ issue of the BIT approach, we propose an intuitive and novel transformation approach that applies isotonic regression directly on the marginal posterior distribution functions. Under this approach, Condition C₁ is clearly met. Let F_jk(x) and G_jk(x) be the cumulative distribution functions of p_jk and q_jk, respectively, at combination (j,k), conditional on observed data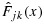, and and 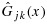be the corresponding unconstrained cumulative distribution functions. For simplicity, when 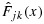and 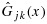are not directly calculable, we use the same notation to denote the empirical distribution functions of p_jk and q_jk, on the basis of their unconstrained posterior samples. For a fixed x, let 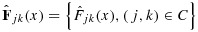. An order-restricted estimate 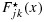of F_jk(x) is obtained by applying isotonic regression on 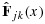with respect to the reversed partial order ≼^r on C, where ≼^r is defined as (j₁,k₁)≼^r(j₂,k₂) if 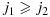and 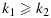. We consider two different weights in the isotonic regression on the cumulative distribution functions: the precisions of the posterior beta distributions (as also used in the BIT approach) and the numbers of patients treated at the combinations (recommended for estimates of ordered proportions in the frequentist context by Robertson et al., [29]), to be denoted as PSO I and PSO II, respectively, in Section 4. One can easily show that 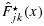is indeed a distribution function. In fact, using the notation from Robertson et al., [29], 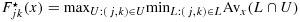, where L and U are lower and upper sets in C, and Av_x(L ∩ U) is the weighted average of 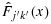for all (j^′,k^′)∈C (see the definitions of lower and upper sets in, e.g., [27]). Because for any (j,k), 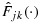is a distribution function, implying that 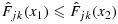for all x₁<x₂, we have 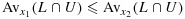for any L and U; thus, .

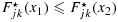Using the preceding approach to inference, the posterior distributions will be equal when two out of three and one out of three responses are observed at combinations (1,1) and (1,2), respectively. The posterior means will also be equal. If the responses are reversed at the two combinations, then the resulting posterior distributions will be unchanged as Beta(1 + a₂,2 + a₂) and Beta(2 + a₂,1 + a₂), because they are already stochastically strictly ordered. These can be seen in Figure 2. The preceding examples thus demonstrate that the proposed approach based only on PSO appropriately accounts for the order and corrects it as needed. Intuitively, the proposed isotonic regression of the distribution functions is appropriate in the sense that it ensures that the stochastic partial ordering condition C₁ is directly met while keeping the estimated posterior distributions as close to the unconstrained posterior distributions as possible (i.e., to respect the observed data), by minimizing the weighted sum-of-square distance between the unconstrained and constrained marginal posterior distribution functions. This is particularly important and useful given the small sample sizes of dose-finding trials, where correction of the ordering constraints may be frequently needed because of high variability of the observed outcomes.

2.4. Theoretical framework and justification of the proposed partial stochastic ordering-based approach

In this section, we describe the theoretical framework and summarize the justification of the PSO-based approach proposed in Section 2.3.

First, for computational convenience, we choose to model the toxicity and efficacy outcomes separately across dose combinations (without the need to assume their independence within patients) and base our dose-finding algorithm on only the marginal posterior distributions of the toxicity and efficacy probabilities. As our goal is to make inferences on the marginal probabilities of the toxicity and efficacy outcomes, we rely on the correct specification of the marginal binomial likelihood with each of the toxicity and efficacy outcomes (as is the case). Furthermore, this strategy allows us to use existing algorithms, such as the MLSA, for performing isotonic regression of the unconstrained marginal posterior distribution functions of the toxicity and efficacy probabilities across dose combinations under the matrix-ordering constraints. Cunanan and Koopmeiners [31] conducted an extensive simulation study to compare two common phase I/II design methods that model the correlation structure between the toxicity and efficacy outcomes [32,33], with the corresponding versions of these methods that assume independence, when the correlation is present. Their paper concludes that, in general, modeling the correlation structure does not enhance the performances of these dose-finding methods. In fact, surprisingly, the models that assume independence can perform even better than the models that correctly specify the correlation structure in some cases while performing similarly in other cases. According to the authors, the potential reasons behind these results may include the following: (1) The likelihood contains very little information about the correlation parameter, and any benefit of modeling the correlation is negated by the need to estimate an additional correlation parameter; (2) phase I/II clinical trials with small sample sizes do not provide sufficient information for selecting the correct copula model; (3) properly modeling the correlation between the two endpoints is necessary to complete proper inference (hypothesis tests, credible intervals, etc.), but it may be that modeling this correlation is not necessary in a phase I/II clinical trial where the goal is to select a dose at study completion regardless of the error associated with the estimates of the toxicity and efficacy probabilities. In a related study, Cai et al., [21] also proposed to model the toxicity and efficacy outcomes independently in order to identify the OBDC and showed through simulations that correctly modeling the correlation structure resulted in negligible improvements in the performance of their design. On the basis of these considerations, we elect to focus on separately modeling the dose–toxicity and dose–efficacy relationships in the current paper. Furthermore, our simulation study in Section 4 shows satisfactory performance of the proposed designs compared with both the BIT-based design and a design based on parametric change-point models for the dose–toxicity and dose–efficacy surfaces.

Second, like the BIT approach, the PSO-based approach is also a postprocessing approach, falling in the category of a transformation-based two-step approach to order-constrained posterior inference. Specifically, in the PSO-based approach, the matrix-ordering constraints on the toxicity and efficacy probabilities across dose combinations are incorporated by separately isotonically transforming the unconstrained marginal posterior distribution functions of the toxicity and efficacy probabilities across dose combinations. By Theorem 1 of Hoff [34], there exists a joint posterior distribution of the toxicity probabilities across dose combinations that is almost surely matrix-ordered and that has the marginal cumulative distribution functions of the toxicity probabilities across dose combinations that are identical to those obtained through isotonic regression of the unconstrained posterior distribution functions of the toxicity probabilities. Note that isotonic regression of the marginal distribution functions is a minimal distance mapping. In addition, a joint prior distribution implicitly defined by the ratio between a joint order-constrained posterior distribution with the isotonically transformed marginals and the likelihood is also almost surely matrix-ordered and data dependent. This suggests that the PSO-based approach can be similarly considered as an empirical Bayes-type procedure [26]. The preceding statements also hold for the efficacy probabilities.

The proposed PSO-based approach has some additional features: (1) Being nonparametric, it is potentially more robust than a parametric approach (as shown in our simulation study); (2) the PSO-based approach respects the data in a more intuitive way than the BIT approach (i.e., by not overcorrecting for order), as explained in Section 2.3 and also illustrated in Figure 2; and (3) the proposed PSO-based approach is an extension of a frequentist nonparametric approach to the estimation of stochastically ordered survival functions [35] while applied in a Bayesian context. We detail such a connection subsequently.

Let X₁,…,X_m and Y₁,…,Y_n be independent random samples from two distributions, F and G, respectively, and let F_m and G_n be the corresponding empirical distribution functions. Suppose 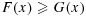for all x. Define P(x) = 1−F(x), Q(x) = 1−G(x), P_m(x) = 1−F_m(x), and Q_n(x) = 1−G_n(x). Let

Rojo [35] proposed estimators

(3)

and

(4)

for F(x) and G(x), and showed the following: (1) 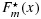and 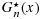satisfy the stochastic order constraint; (2) 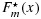is strongly uniformly consistent for F(x) when m goes to infinity, and similarly, 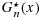is strongly uniformly consistent for G(x) when n goes to infinity, each without the need of both m and n going to infinity; and (3) for censored data, under suitable conditions, the processes 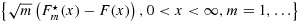and 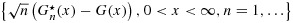are weakly convergent, so that asymptotic confidence bands for the distribution functions can be constructed.

We note that Equations 6 and 7 suggest that the estimators 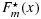and 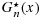are isotonic regressions of F_m(x) and G_n(x), with the sample sizes m and n being the weights. While Rojo's [35] method is applicable only in the two-sample stochastic ordering case, our proposed approach is applicable to PSO cases such as matrix stochastic ordering for the toxicity and efficacy probabilities across dose combinations. Consequently, our approach is an extension of the Rojo [35] method to the partial ordering case while being applied in a Bayesian context.

3. Dose-combination-finding algorithm

Let 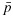and 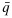be the physician-specified upper limit for toxicity and lower limit for efficacy, respectively. We define admissible dose combinations as those with toxicity probabilities less than or equal to 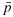and efficacy probabilities larger than or equal to 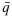. The admissible plateau is defined as the combinations with the largest efficacy probability among the admissible combinations. We define the OBDCs, or target combinations, as the lowest combinations in the admissible plateau. We propose an algorithm to sequentially allocate patients to dose combinations that are both safe and efficacious. Suppose we treat patients in cohorts of size c. Let n and n_jk be the current total sample size and the sample size at dose combination (j,k), respectively. We categorize a combination as safe, having acceptable toxicity, or excessively toxic as follows:

1. (j,k)is safe if .

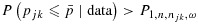2. (j,k)has acceptable toxicity if .

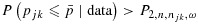3. (j,k)is excessively toxic if .

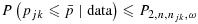Here, 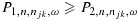are cutoffs that depend on a weighted average of n_jk and n:

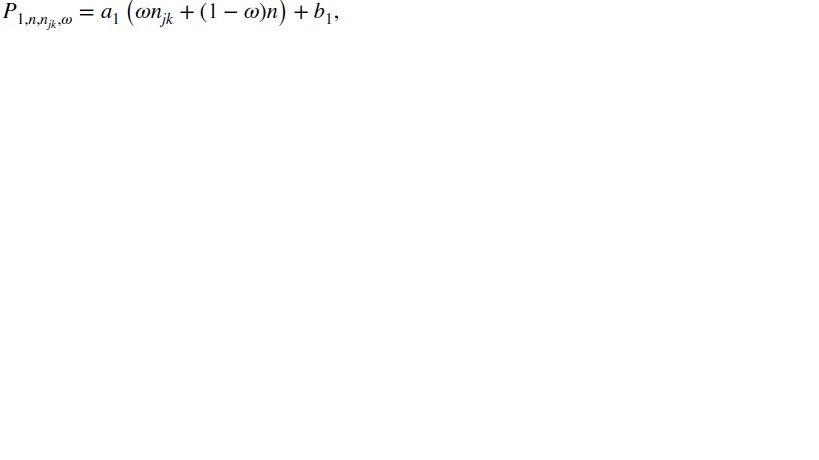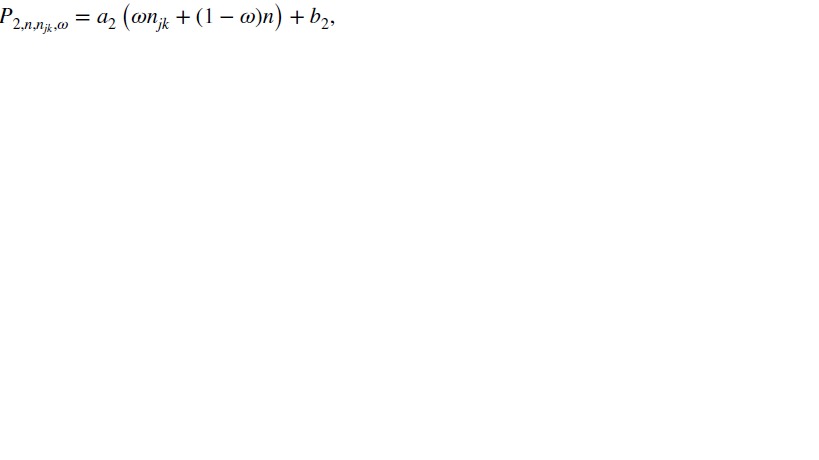with 0≤ω≤1 being the weight given to n_jk, which reflects the relative importance of the two sample sizes, and a₁, b₁, a₂, and b₂ being tuning parameters. Suppose P₁>P₂ at the smallest sample size (n = n₁₁=c). As one may expect P₁ and P₂ to converge as the sample size becomes large, reasonable tuning parameters should satisfy a₁<a₂ and b₁>b₂+(a₂−a₁)c. These conditions, however, imply that when ω·n_jk+(1 − ω)·n is sufficiently large, P₁ may become less than P₂. In that case, we will define P₁=P₂=a₂(ωn_jk+(1 − ω)n) + b₂ to ensure .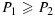

We define a dose combination as having acceptable efficacy if 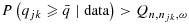, where

In the preceding definitions, we let the cutoff probabilities depend on both the sample size at (j,k) and the total sample size. When the total sample size increases, the posterior probability estimates are more reliable because they have borrowed strength across combinations. Similarly, if n_jk is large, the probability estimates at this combination are more reliable. Thus, our criteria for declaring a dose combination as safe, excessively toxic, or having acceptable efficacy are in general liberal at the beginning of the trial and more stringent at a later stage of the trial. We evaluate the sensitivity of the operating characteristics of the design to different values of ω in simulation studies.

We say a dose combination is acceptable if it has acceptable levels of both toxicity and efficacy. Let 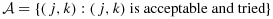. For each dose combination (j,k), we define its lower neighbors as (j − 1,k) and (j,k − 1), as applicable. Some combinations may have only one or zero lower neighbor. For example, combination (1,1) has zero lower neighbor, and each of combinations (1,2) and (2,1) has only one lower neighbor.

Because of the randomness of the data, we proposed a practical rule that resulted in increased probability of selecting the target combinations in our simulations. Specifically, at any point during the trial, let the efficacy probability point estimates be the isotonic regression of the observed efficacy probabilities with respect to the partial order among all tried combinations. Denote q_max as the largest efficacy point estimate among all acceptable combinations. Define the best combination in 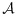as the one with the largest 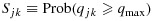, with the largest S_jk denoted as S_max. The acceptable plateau is defined as combinations (j,k) in 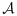that satisfy 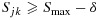, with δ > 0 to be tuned through simulations to achieve desirable operating characteristics of the design. Similar to 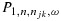, 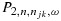and 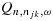, to adequately explore the admissible plateau early in the trial and become more focused and stringent when more data are accruing toward the end of the trial, we let δ decrease with the total sample size, as follows:

where a_δ<0 and b_δ are tuning parameters. It is important to point out that all the preceding posterior probabilities can be calculated without drawing posterior samples, as the values of the beta cumulative distribution functions are directly calculable in any common computer software such as R.

We propose a dose-combination-finding algorithm, as follows:

1. Patients in the first cohort are treated with (1,1). If at any evaluation point, (1,1)is deemed to be excessively toxic or the maximum sample size is reached, we terminate the trial.

2. If there is at least one dose combination that has both safe lower neighbors and has not been used to treat patients, we allocate the next cohort of patients at the lowest such combination. When there are multiple such lowest combinations, we randomly select one with equal probability. If no untried combination has both safe lower neighbors, then the next cohort of patients is assigned to the lowest combination in the acceptable plateau in 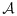, or the trial is terminated if 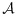is empty. When there are two or more lowest combinations in the acceptable plateau, we randomly pick one with equal probability.

3. At the end of the trial, we select the lowest dose combinations in the acceptable plateau as the recommended combinations. There can be more than one recommended combination.

4. Application and simulation

Our trial design was motivated by a phase I/II clinical trial of a combination of an AKT inhibitor and a MEK inhibitor in patients with pancreatic, endometrial, or colorectal cancer. For each agent evaluated in the study, three doses are selected for testing, starting from 60% of the single-agent maximum tolerated dose and resulting in a total of nine dose combinations. Toxicity is defined as having one or more of the dose-limiting toxicities, such as grade 4 neutropenia lasting 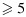days or febrile neutropenia. Efficacy is defined as complete or partial remission, according to the Response Evaluation Criteria in Solid tumors (RECIST) 1.1. As the investigators hypothesize that plateaus may exist in the dose–efficacy (and dose–toxicity) surfaces in the tested dose range, the primary objective of the study is to determine the OBDCs, that is, the lowest dose combinations that are safe and have the highest efficacy level meeting a prespecified target. Specifically, the physician-specified toxicity upper limit and efficacy lower limit are 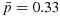and .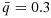

On the basis of this trial, we constructed 12 scenarios with different true probabilities of toxicity and efficacy to assess the performance of our proposed designs, in comparison with a design that uses a parametric change-point model from Cai et al., [21] for both the dose-toxicity and dose-efficacy surfaces (hereafter referred to as the Cai design) (Table I). Both efficacy and toxicity were assumed to either increase with dose or first increase and then plateau. We designed the target combinations at different locations on the dose-combination matrix and used different plateau shapes for efficacy and toxicity, in order to cover a wide array of practical scenarios. Specifically, Scenarios 1–7 describe situations in which there is only one target combination (with a varying location) and the efficacy probability plateaus in the tested dose range. Scenarios 8–10 represent situations in which there is more than one target combination. In Scenarios 11–12, the efficacy probability strictly increases with an increasing dose, that is, without a plateau in the dose–efficacy surface. The toxicity and efficacy outcomes were assumed to be independent.

Table I.

True toxicity and efficacy probabilities of each dose combination for the 12 scenarios. The combinations in bold are the OBDCs.

	True pr(toxicity)				True pr(efficacy)				True pr(toxicity)				True pr(efficacy)
Dose	1	2	3		1	2	3		1	2	3		1	2	3
	Scenario 1								Scenario 2
1	0.05	0.10	0.10		0.10	0.40	0.40		0.05	0.05	0.05		0.05	0.05	0.05
2	0.10	0.15	0.15		0.15	0.40	0.40		0.10	0.10	0.10		0.30	0.30	0.30
3	0.40	0.45	0.45		0.20	0.40	0.40		0.45	0.50	0.50		0.35	0.50	0.50
	Scenario 3								Scenario 4
1	0.05	0.45	0.45		0.35	0.35	0.35		0.05	0.08	0.50		0.30	0.30	0.30
2	0.08	0.45	0.45		0.35	0.45	0.45		0.08	0.50	0.50		0.30	0.30	0.30
3	0.08	0.45	0.45		0.35	0.45	0.45		0.50	0.50	0.50		0.30	0.30	0.30
	Scenario 5								Scenario 6
1	0.02	0.04	0.45		0.05	0.10	0.30		0.02	0.04	0.06		0.10	0.10	0.10
2	0.04	0.06	0.50		0.10	0.30	0.40		0.04	0.06	0.10		0.10	0.15	0.40
3	0.06	0.10	0.50		0.10	0.50	0.50		0.06	0.10	0.15		0.10	0.15	0.40
	Scenario 7								Scenario 8
1	0.05	0.45	0.50		0.05	0.40	0.40		0.05	0.08	0.10		0.05	0.10	0.32
2	0.10	0.50	0.50		0.35	0.50	0.50		0.08	0.10	0.15		0.10	0.32	0.32
3	0.10	0.50	0.50		0.35	0.50	0.50		0.10	0.15	0.45		0.32	0.32	0.32
	Scenario 9								Scenario 10
1	0.05	0.08	0.10		0.05	0.10	0.10		0.05	0.08	0.10		0.02	0.30	0.30
2	0.08	0.10	0.12		0.10	0.12	0.35		0.08	0.50	0.50		0.30	0.35	0.35
3	0.10	0.12	0.15		0.10	0.35	0.35		0.10	0.50	0.50		0.30	0.35	0.35
	Scenario 11								Scenario 12
1	0.02	0.03	0.05		0.05	0.10	0.15		0.05	0.10	0.15		0.05	0.20	0.30
2	0.03	0.05	0.06		0.10	0.15	0.25		0.10	0.45	0.50		0.20	0.35	0.40
3	0.05	0.06	0.10		0.15	0.25	0.55		0.15	0.50	0.50		0.45	0.50	0.60

The maximum sample size was chosen to be 54, and patients were treated in cohorts of size 3. We assigned independent Beta(0.5,0.5) priors for the toxicity/efficacy probabilities at each dose combination, to reflect prior ignorance. The chosen tuning parameters were a₁=0.015, b₁=0.3, a₂=0.026, b₂=0.03, a₃=0.009, b₃=0.02, a_δ=−0.0015, b_δ=0.4515, and ω = 0.3 under the proposed designs based only on PSO, a₁=0.01, b₁=0.25, a₂=0.02, b₂=0.015, a₃=0.005, b₃=0.014, a_δ=−0.001, b_δ=0.551, and ω = 0.3 under the BIT approach, and a₁=0.015, b₁=0.3, a₂=0.035, b₂=0.02, a₃=0.002, b₃=0.001, and ω = 0.5 under the Cai design. We note that because the Cai design uses change-point models that are designed specifically to identify the plateau, we set δ = 0, and consequently, we do not need to specify parameters a_δ and b_δ. P₁ was defined as equal to P₂ when ω·n_jk+(1 − ω)·n is greater than 24.5, 23.5, and 14.0, for the PSO, BIT, and Cai designs, respectively. Each set of parameters was tuned via simulations to achieve overall desirable operating characteristics. One may notice that these tuning parameters reflected looser cutoff probabilities P₁, P₂, Q, and δ in the BIT design than in the PSO-based designs. As the BIT approach tended to either underestimate or overestimate the toxicity and efficacy probabilities, looser cutoff probabilities were required in order to control the percentage of inconclusive trials to be low when there was at least one target combination.

Under each scenario, we simulated 1000 trials. We present the selection percentages of the dose combinations, the average number of patients treated at each dose combination, and the observed toxicity and efficacy percentages in Table II. ‘PSO I’ and ‘PSO II’ refer to the proposed designs based only on PSO and using posterior precisions and sample sizes as weights for isotonic regression, respectively. ‘BIT’ refers to the design based on Bayesian isotonic regression transformation. ‘Cai’ refers to the Cai design. We retain the same decision rules used in our approach for the Cai design and use appropriately tuned design parameters for a fair comparison. We use our decision rules because the definition of the OBDC and thus the goal of the trial design as well as the assumption made on the dose–efficacy relationship in Cai et al., [21] are different from those of our design.

Table II.

Selection percentage and number of patients treated (in parentheses) at each dose combination under the proposed designs assuming partial stochastic ordering (PSO I and PSO II), the design using Bayesian isotonic regression transformation (BIT), and a design based on parametric change-point models (Cai). The combinations in bold are the OBDCs.

	Dose	1	2	3				1	2	3
		Selection percent (number patients)			Tox	Eff		Selection percent (number patients)			Tox	Eff
		Scenario 1						Scenario 2
	1	0.5 (5.3)	52.4 (16.9)	24.5 (7.7)				0.3 (4.9)	0.9 (4.8)	2.7 (3.5)
PSO I	2	6.6 (5.5)	18.8 (6.8)	8.9 (2.5)	15.1	32.9		46.2 (16.5)	25.4 (8.3)	15.4 (3)	15.1	25.1
	3	3 (3.9)	1.5 (3.9)	0.5 (1.1)				8.2 (5.6)	2.1 (5.7)	0.2 (1)
	1	0.1 (5.1)	52.5 (16.8)	23.9 (7.3)				0.5 (4.9)	1.6 (4.8)	2 (3.7)
PSO II	2	8 (5.9)	21.7 (6.9)	8.2 (2.7)	14.7	33.0		47.0 (16.5)	26.2 (8.3)	15.5 (3.4)	14.7	25.2
	3	4 (3.9)	1.7 (3.8)	0.5 (1.2)				7 (5.3)	1.5 (5.2)	0.2 (1.1)
	1	0.1 (3.8)	46.4 (15.7)	30 (9.2)				0 (3.1)	0.5 (3.6)	2.5 (4.2)
BIT	2	5.9 (5.2)	29.4 (9)	6.1 (2.7)	14.9	34.1		35.6 (14.8)	35 (10.9)	18.5 (3.4)	15.3	26.4
	3	4.8 (3.9)	1.4 (3.7)	0.1 (0.6)				12.4 (7)	1.5 (5.8)	0.1 (0.5)
	1	22 (16.5)	55.2 (10.4)	16.1 (5.3)				4.8 (8.8)	8.5 (4.4)	5.2 (3.6)
Cai	2	22.5 (5.1)	9.8 (3.9)	3.2 (3.3)	14.7	27.1		47.4 (12.7)	20 (5.7)	9.9 (4.1)	18.7	25.4
	3	4.7 (3.5)	0.6 (3.1)	0.4 (2.7)				16.9 (7.7)	3.6 (3.8)	1.2 (2.7)
		Scenario 3						Scenario 4
	1	55.0 (23.2)	4.9 (5.5)	3.3 (2.4)				52.8 (23.7)	27 (8.6)	1.9 (3.5)
PSO I	2	22.4 (10.6)	4.5 (2.7)	0.1 (0.7)	15.4	35.7		26.6 (8.8)	1.9 (3.7)	0.1 (0.4)	16.6	30.2
	3	15.5 (7.3)	0.7 (1.4)	0.4 (0.2)				1.4 (3.7)	0.2 (1.2)	0 (0.1)
	1	53.1 (23.0)	6.6 (5.6)	1.6 (2.2)				50.5 (23.0)	28.1 (8.9)	1.5 (3.8)
PSO II	2	24 (10.8)	3.2 (2.5)	0.2 (0.6)	15.4	35.5		28.7 (8.9)	1.4 (3.7)	0.1 (0.4)	16.9	29.5
	3	16.7 (7.8)	0.3 (1.2)	0 (0.2)				1.8 (3.7)	0.2 (1.2)	0 (0.1)
	1	35.1 (16.3)	11.5 (7.5)	1.1 (2.4)				23.8 (12.1)	39.8 (12.9)	2.9 (4.3)
BIT	2	40.9 (15.6)	4.1 (3.1)	0.2 (0.7)	17.4	35.9		38.7 (12.7)	3.2 (4.4)	0.1 (0.4)	19.4	29.7
	3	14.6 (6.9)	0.5 (1.3)	0 (0.1)				2.1 (4.4)	0.1 (1.2)	0 (0)
	1	93.5 (31.0)	2 (3.5)	0.2 (3.1)				90.7 (30.9)	4.1 (3.7)	1.5 (3.3)
Cai	2	3.8 (3.6)	0.6 (3.2)	0 (2.3)	17.6	36.7		3.8 (3.7)	0.9 (3.1)	0.1 (2.3)	18.4	29.5
	3	1.3 (3.3)	0.3 (2.6)	0 (1.5)				0.8 (3.3)	0.2 (2.5)	0 (1.1)
		Scenario 5						Scenario 6
	1	0.1 (4.1)	2.5 (5.3)	8 (5.6)				0.7 (5.3)	2 (5.1)	7.9 (4.8)
PSO I	2	2.4 (5.1)	34.6 (11.3)	3 (2.4)	13.2	28.5		2.4 (5.1)	12.4 (5.8)	49.6 (11.1)	7.7	21.0
	3	5.4 (4.7)	52.0 (14.2)	0.4 (1)				8 (4.8)	11.9 (4.9)	18.9 (6.8)
	1	0.4 (4)	1.2 (5.3)	8.7 (5.5)				0.8 (5.5)	3.2 (5.1)	5.8 (4.7)
PSO II	2	1.5 (4.7)	35.9 (11.6)	2.1 (2.3)	13.1	28.9		3.2 (5.3)	9.9 (5.6)	49.8 (11.2)	7.6	21.0
	3	4.7 (4.8)	52.4 (14.7)	0.6 (1)				6.8 (4.7)	12 (5)	19.3 (6.7)
	1	0 (3.1)	1 (5)	13.5 (6.4)				0 (3)	0.3 (3.5)	5 (5.7)
BIT	2	0.6 (4.1)	47.7 (14.6)	2.3 (2.2)	13.3	28.4		0.4 (3.5)	8 (5.8)	67.8 (15.1)	8.0	22.9
	3	8.1 (5.8)	43.1 (12.1)	0 (0.6)				3.7 (4.9)	17.2 (6.4)	13.6 (5.6)
	1	3 (8)	15.9 (7.3)	26.1 (7.9)				4.6 (8.3)	5.6 (4.8)	24.6 (7.5)
Cai	2	9.3 (5.2)	30.3 (6.8)	4.9 (4.1)	16.8	23.9		7.6 (4.7)	9.6 (4.2)	20.7 (6.6)	6.9	17.4
	3	18.6 (5.4)	28.5 (6.2)	2.8 (2.9)				17.9 (6)	14.7 (4.6)	23.8 (5.9)
		Scenario 7						Scenario 8
	1	0.5 (5.1)	10.2 (8.7)	2.4 (2.3)				0.2 (4.3)	2.2 (5.6)	51.8 (9.0)
PSO I	2	62.7 (22.3)	2.9 (2.7)	0.3 (0.5)	20.4	34.1		2.1 (5.7)	48.0 (8.9)	8.1 (3.6)	11.7	25.0
	3	25.1 (10.3)	0.5 (1)	0 (0.1)				52.0 (9.7)	8.4 (4.2)	0.7 (2.7)
	1	0.3 (5.1)	10.1 (8.7)	1.7 (2.3)				0.3 (4.3)	2.1 (5.4)	53.6 (9.4)
PSO II	2	61.3 (22.6)	1.3 (2.5)	0.1 (0.4)	20.2	34.0		1.5 (5.6)	47.1 (9.3)	8 (3.7)	11.9	25.1
	3	26.4 (10.5)	0.4 (1)	0 (0.1)				51.1 (9.2)	7.2 (3.9)	1.2 (2.9)
	1	0 (4.5)	19.4 (10.9)	2.1 (2.8)				0 (3.1)	1.2 (4.5)	49.1 (10.0)
BIT	2	69.1 (23.1)	2.5 (3)	0.1 (0.5)	22.2	34.9		0.9 (4.6)	42.8 (8.9)	11.4 (4.6)	11.9	26.7
	3	20.2 (7.9)	0.2 (0.9)	0 (0)				48.7 (10.4)	12.5 (5.1)	0.7 (2.6)
	1	11.5 (15.4)	25.2 (8.4)	2.2 (3.6)				3.4 (10.3)	17.2 (6.7)	38.6 (7.2)
Cai	2	51.0 (11.6)	5.7 (3.8)	0.2 (2)	24.0	30.0		17.3 (6.4)	30.8 (5.2)	6.5 (3.8)	11.6	21.2
	3	22.6 (5.5)	0.7 (2.4)	0.2 (1.2)				40.3 (7.1)	6.6 (3.8)	1.7 (3.2)
		Scenario 9						Scenario 10
	1	0.1 (4.7)	1.4 (5.6)	5.7 (4.9)				0 (4)	46.7 (14.8)	17.3 (6.4)
PSO I	2	2 (5.5)	9.2 (5.5)	41.1 (8.0)	10.4	19.6		44.4 (13.5)	5 (4.3)	0.7 (1.7)	14.5	28.6
	3	6.5 (5.1)	41.8 (9.0)	11.3 (4.7)				20.3 (7.2)	0.9 (1.7)	0 (0.3)
	1	0.1 (4.7)	2 (5.8)	7.9 (5.1)				0.2 (4)	46.3 (14.2)	18.9 (6.5)
PSO II	2	1.9 (5.7)	11.1 (5.6)	40.8 (8.0)	10.4	19.4		47.1 (14.8)	4.2 (4.2)	0.4 (1.6)	14.2	28.6
	3	7.5 (5.1)	40.1 (8.4)	8.9 (4.5)				18.6 (6.6)	0.6 (1.7)	0.2 (0.4)
	1	0 (3)	0.4 (3.5)	3.5 (5.4)				0 (3.3)	40.7 (13.6)	23.2 (7.5)
BIT	2	0.5 (3.7)	5.7 (5.6)	52.8 (10.5)	10.9	21.7		41.1 (14.0)	7.1 (4.6)	0.4 (1.6)	14.6	29.1
	3	5.1 (5.9)	54.2 (11.3)	7.5 (4)				22.7 (7.3)	0.6 (1.8)	0 (0.2)
	1	1.4 (7)	5.6 (5.1)	25.4 (7)				9.8 (14.1)	47.8 (9.0)	14 (4.7)
Cai	2	6.1 (5)	13.2 (4.5)	19.8 (5.7)	10.1	17.1		48.1 (8.7)	13.9 (4.1)	1.1 (3.1)	17.4	23.7
	3	25.7 (7.1)	19.6 (5.7)	17.4 (5.4)				16.5 (4.6)	1.2 (3.3)	0.4 (2.4)
		Scenario 11						Scenario 12
	1	0.1 (3.7)	0.7 (4.3)	8 (5.5)				0.2 (4.3)	15.6 (8.8)	25.6 (7.3)
PSO I	2	1.2 (4.4)	6.2 (4.7)	17.4 (6.2)	6.0	25.7		15.7 (9)	11 (5.6)	0.7 (1.8)	18.2	30.4
	3	6.3 (5.3)	17.3 (6.6)	52.6 (13.2)				57.6 (14.1)	1.4 (2.3)	0.4 (0.5)
	1	0.2 (3.8)	90.9 (4.4)	9.1 (5.3)				0.3 (4.4)	13.1 (8.9)	29.1 (7.7)
PSO II	2	1.4 (4.6)	9.4 (5.3)	16.4 (6.1)	6.0	24.9		14.4 (8.8)	9.7 (5.2)	0.5 (1.7)	18.1	30.5
	3	6.6 (5)	17 (6.7)	51.2 (12.5)				57.5 (14.3)	1.5 (2.2)	0.2 (0.5)
	1	0 (3)	0.1 (3.6)	10.5 (5.8)				0 (3.5)	15.8 (9.2)	32.1 (8.1)
BIT	2	0.3 (3.6)	8 (5.1)	30.7 (8.4)	5.8	24.1		19.9 (10.7)	14.8 (5.5)	0.6 (1.7)	18.2	30.0
	3	9.8 (5.9)	27.7 (8.7)	36.9 (9.5)				57.9 (12.8)	1.4 (2.1)	0 (0.2)
	1	1.4 (7)	7.6 (4.9)	28.1 (7.5)				7.1 (10.5)	22.7 (6.6)	20.9 (5.3)
Cai	2	7.6 (4.9)	14.3 (4.6)	14.8 (5.3)	5.1	19.7		25.8 (8)	22.8 (5.2)	2.8 (3.5)	21.0	28.6
	3	25.1 (7.2)	16.6 (5.7)	24.8 (6.4)				38.5 (8.6)	6.4 (3.8)	1 (2.4)

In all scenarios, PSO I and II performed comparably, and the target combinations had the highest selection percentages and were used to treat the largest number of patients among all combinations under the two PSO designs. This was not the case for the BIT or Cai design. For example, the highest selection percentage and number of patients treated were not at the target combinations in Scenarios 3, 4, and 5 under the BIT design nor in Scenarios 5, 6, 9, and 11 under the Cai design. The percentages of toxicity and efficacy were comparable under PSO and BIT, although the latter yielded overall slightly higher percentages of both. The Cai design yielded overall lower efficacy percentages and more chances of higher toxicity percentages. Out of the 12 scenarios, the PSO I and II designs performed consistently or almost consistently better than the BIT design in Scenarios 1–5, 10, and 11 and better than the Cai design in Scenarios 5–9, 11, and 12 in terms of the selection percentage of the target dose combination(s) and the number of patients treated at the target combination(s). These results reflect the ‘overcorrection’ of the partial ordering constraints by the BIT approach, as well as the sensitivity of the performance of the Cai design to potential violation of the parametric model assumptions. In Scenario 2, the admissible plateau included dose combinations (2,1), (2,2), and (2,3). With identical true efficacy probabilities of 0.3 at these combinations, the BIT method tended to underestimate the efficacy probability at the lowest combination in the plateau, that is, (2,1), thus with a higher probability excluding it from the acceptable plateau and declaring combination (2,2) as the OBDC, while the true OBDC was (2,1). A similar interpretation applies to the results in Scenarios 1, 3, 4, and 10. In particular, in Scenario 1, the true equal efficacy probabilities among combinations (1,2), (1,3), and (2,2) imply that the efficacy probability at (1,2) may be considerably underestimated in the BIT design. The toxicity probability at combination (2,2) may also be considerably underestimated. As a result, the selection percentage (and number of patients treated) at the target combination (1,2) may be reduced and the corresponding percentage and number of patients treated at combination (2,2) may be increased (compared with the PSO designs). In Scenario 5, the reason combination (2,2) was selected more than the true OBDC (3,2) in the BIT design may be seen as a result of both the potential overestimation of the toxicity probability at combination (3,2) and the corresponding increased chances for it to fall out of the acceptable plateau, and the larger δ value chosen in the BIT design in order to achieve overall desirable operating characteristics. The results in Scenario 11 is a reflection of the combined effects of the overestimation of the toxicity probability at combination (3,3), overestimation of the efficacy probabilities at combinations (2,3) and (3,2), and the larger δ value chosen by the BIT method. Similar to the argument made in Section 2.3, as the multiple combinations that are lower than combinations (2,3) and (3,2) have only moderately lower efficacy probabilities, the chances for overestimation of the efficacy probabilities at combinations (2,3) and (3,2) are higher. This may have contributed to the larger selection percentages of the combinations (2,3) and (3,2) as the target combinations in the BIT design than in the PSO designs. The BIT design performed better than the PSO I and II designs in Scenarios 6, 7, and 9, where ‘overcorrection’ of the partial ordering constraints actually helped the selection of the target combination(s). For example, in Scenario 6, the admissible plateau includes combinations (2,3) and (3,3). Overestimation of the toxicity probability at combination (3,3) may increase the chances of excluding it from the acceptable plateau and consequently declaring combination (2,3) as the target combination. The PSO I and II designs overall performed slightly better in Scenario 8, and the BIT design performed slightly better in Scenario 12. The comparison in these scenarios may be seen as the results of overcorrection of partial ordering in combined toxicity and efficacy probabilities by the BIT approach. For example, in Scenario 8 the slightly worse selection percentages of and the slightly better allocations of patients to the target combinations by the BIT design may be a combined result of the underestimation of the efficacy probabilities at the target combinations and the overestimation of the toxicity probabilities at combinations (2,3) and (3,2). While it appears that the chosen larger δ value in the BIT design decreased its performance in some scenarios, we note that, were a smaller δ chosen, results for the BIT design will become considerably worse in Scenarios 2, 3, 4, and others. The chosen δ has achieved overall the best operating characteristics of the BIT design. In summary, the results across all scenarios supported the pattern of ‘overcorrection’ of the partial ordering constraints by the BIT approach, and the PSO I and II designs performed overall better than the BIT design.

The Cai design performs extremely well in Scenarios 3 and 4, with considerably higher target combination selection percentages and greater numbers of patients treated at the target combination compared with the PSO and BIT designs. In Scenarios 1, 2, and 10, it yielded slightly higher target combination selection percentages but had lower numbers of patients treated at the target combinations compared with the PSO and BIT designs. These results again reflect the sensitivity of the Cai design to a correct specification of the dose–toxicity and dose–efficacy curves. That is, when the true scenarios are close to the assumed parametric models, the performance of the Cai design may be dramatically enhanced. However, overall the Cai design does not perform as well as either the PSO or BIT designs. We further carried out sensitivity analyses to evaluate the performance of the designs with varying weights ω in the cutoff probabilities. The weights examined were 0, 0.1, 0.3, 0.7, 0.9, and 1 besides 0.5. We summarize the selection percentage of and the average number of patients treated at each OBDC with each weight for the PSO I, PSO II, BIT, and Cai designs, respectively, in Tables S1–S4 in the Supporting information. On the basis of the selection probabilities of the target combinations, we found that 0.3 is the overall best weight for the PSO I design. This is determined using the following criteria. For example, for PSO I, we first picked the best four ω^′s in each scenario and counted the frequency of each ω falling in the best four among the 12 scenarios. The frequencies of the seven weights 0, 0.1, 0.3, 0.5, 0.7, 0.9, and 1 were 7, 5, 12, 8, 8, 4, and 3, respectively. Next, we selected the weights in each scenario that resulted in selection probabilities of the target combinations within 94% of the best selection. The corresponding frequencies were 7, 3, 10, 8, 7, 4, and 6, respectively. Both criteria suggested that ω = 0.3 yielded the best overall operating characteristics of the design. Using similar criteria, ω = 0.3 was also found to be the best weight for the PSO II and BIT designs, and ω = 0.5 was the best for the Cai design.

As the performances of the two PSO-based designs are very similar, to numerically illustrate the proposed methods, we present the following information only based on the PSO I design in Table III: (1) hypothetical data of a trial simulated under Scenario 1 of Table I; (2) calculated posterior probabilities based on isotonically transformed marginal posterior distributions of the toxicity and/or efficacy probabilities, and related parameters; and (3) the corresponding dose-combination assignment decisions. Because of space limitations, we show these results for only a few cohorts rather than for all cohorts in the trial.

Table III.

Illustration of a simulated trial using the PSO I design.

Data			Estimates										Dose
													combo
													assignment
Combo	Tox	Eff	P1		P2		qmax	Sjk	Smax	δ	Accpt	Lowest
			Unc	C	Unc	C					plateau	accpt
												plateau
(1,1)	0/3	0/3	0.89	0.89									(1,2), (2,1)
(1,1)	0/3	0/3	0.89	0.89									(3,1), (2,2), (1,3)
(2,1)	0/3	0/3	0.89	0.89
(1,2)	1/3	1/3	0.46	0.46
(1,1)	0/3	0/3	0.89	0.89									(3,2), (2,3)
(2,1)	0/3	0/3	0.89	0.89
(1,2)	1/3	1/3	0.46	0.81
(3,1)	1/3	1/3	0.46	0.46
(2,2)	0/3	2/3	0.89	0.81
(1,3)	0/3	3/3	0.89	0.81
(1,1)	0/3	0/3	0.89	0.89	0.13	0.13	0.5	0.03	0.5	0.42			(1,2)
(2,1)	0/3	0/3	0.89	0.89	0.13	0.13		0.03
(1,2)	1/3	1/3	0.46	0.84	0.58	0.46		0.29			X	X
(3,1)	1/3	1/3	0.46	0.46	0.58	0.46		0.29			X
(2,2)	0/3	2/3	0.89	0.84	0.911	0.46		0.37			X
(1,3)	0/3	3/3	0.89	0.84	0.995	0.56		0.5			X
(3,2)	2/3	0/3	0.11	0.11	0.13	0.46		0.37
(2,3)	0/3	0/3	0.89	0.84	0.13	0.56		0.5			X
(1,1)	0/3	0/3	0.89	0.89	0.13	0.13	0.5	0.03	0.5	0.41			(3,1)
(2,1)	0/3	0/3	0.89	0.89	0.13	0.13		0.03
(1,2)	1/6	1/6	0.80	0.87	0.25	0.25		0.047
(3,1)	1/3	1/3	0.46	0.46	0.58	0.43		0.29			X	X
(2,2)	0/3	2/3	0.89	0.87	0.911	0.43		0.37			X	X
(1,3)	0/3	3/3	0.89	0.87	0.995	0.56		0.5			X	X
(3,2)	2/3	0/3	0.11	0.11	0.13	0.43		0.37
(2,3)	0/3	0/3	0.89	0.87	0.13	0.56		0.5			X
(1,1)	0/3	0/3	0.89	0.89	0.13	0.13	0.5	0.03	0.5	0.4065			(2,2)
(2,1)	0/3	0/3	0.89	0.89	0.13	0.13		0.03
(1,2)	1/6	1/6	0.80	0.87	0.25	0.25		0.047
(3,1)	2/6	1/6	0.47	0.47	0.25	0.25		0.047
(2,2)	0/3	2/3	0.89	0.87	0.911	0.38		0.37			X	X
(1,3)	0/3	3/3	0.89	0.87	0.995	0.56		0.5			X	X
(3,2)	2/3	0/3	0.11	0.11	0.13	0.38		0.37
(2,3)	0/3	0/3	0.89	0.87	0.13	0.56		0.5			X

Notes: (1) 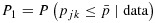, , 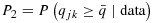where 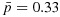, 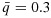. (2) The dose combinations in bold are used to treat the current cohort of patients. When multiple combinations are in bold, they are used to treat cohorts of patients in an order randomly chosen, essentially on the basis of our proposed dose-combination-finding algorithm. The same statement is true when the dose-combination assignment for the next cohort of patients (last column) includes multiple combinations. (3) The underlined combinations are found to be excessively toxic. (4) Combo: combination; Tox: toxicity; Eff: efficacy; Unc: unconstrained; C: constrained; accpt: acceptable.

5. Discussion

We have proposed Bayesian designs to select OBDCs in phase I/II clinical trials. The proposed approach does not assume a parametric dose–efficacy or dose–toxicity model and is based only on PSO assumptions. The dose–efficacy and dose–toxicity surfaces allow for potential plateaus in the tested dose range, as may be expected for MTAs. The performances of the proposed designs are compared with those of a design based on BIT and a design based on parametric change-point models for the dose–toxicity and dose–efficacy surfaces. Our simulation studies show that although both the PSO- and BIT-based designs perform reasonably well and better than the design based on parametric models, the PSO-based design performs the best in terms of correctly selecting the target combinations and assigning more patients to the target combinations.

The proposed designs can be applied without changes when the definition of the OBDCs is replaced by the lowest dose combinations that are safe and have an efficacy probability at most δ₀ less than or 100p% of the highest probability, with δ > 0 or 0 < p < 1 being a prespecified value. The only difference is that we may need to choose a larger δ in our proposed designs. Slight modifications of our designs can be sufficient if an alternative definition of the lowest dose combinations is used.

The proposed PSO-based inference approach has a number of attractive features: (1) It has a general and simple framework. The method does not need to change if the plateau appears in the middle or at the end of the tested dose range, whereas a parametric approach might. The proposed method can be easily extended to account for different types of ordering constraints, for example, umbrella ordering that allows for a plateau at the peak. The proposed method can also be easily extended to different outcome types, with changes needed in only the estimation of or sampling from the posterior distributions based on the unconstrained models. For example, if the efficacy and/or toxicity outcomes are not observed immediately, then we can model corresponding time-to-event outcomes on the basis of similar PSO assumptions. (2) The proposed approach makes minimal acceptable assumptions and thus potentially serves as a ‘reference’ approach. For example, when efficiency is a priority, one can compare alternatively proposed (such as model-based) designs with our proposed designs to evaluate potential efficiency gained and robustness lost before deciding which design to choose, possibly taking into account the likelihood of hypothesized scenarios in the trial. (3) The proposed approach is computationally efficient. In our proposed design with binary endpoints, posterior inference does not require posterior simulation of the toxicity or efficacy probabilities. With the R code we provide, upon request, for performing isotonic regression of the unconstrained posterior distribution functions under the matrix-ordering constraints, the design will be relatively straightforward to implement in practice. The computational efficiency remains the same for other outcomes, including continuous outcomes such as tumor size.

Supporting Information

Additional supporting information may be found in the online version of this article at the publisher's web site.