Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Apr 7.
Published in final edited form as: J Theor Biol. 2015 Jan 20;370:39–44. doi: 10.1016/j.jtbi.2015.01.010

Axonal transport cargo motor count versus average transport velocity: Is fast versus slow transport really single versus multiple motor transport?

Robert H Lee 1, Cassie S Mitchell 1
PMCID: PMC4359950  NIHMSID: NIHMS657296  PMID: 25615423

Abstract

Cargos have been observed exhibiting a “stop-and-go” behavior (i.e. cargo “pause”), and it has generally been assumed that these multi-second pauses can be attributed to equally long pauses of cargo-bound motors during motor procession. We contend that a careful examination of the isolated microtubule experimental record does not support motor pauses. Rather, we believe that the data suggests that motor cargo complexes encounter an obstruction that prevents procession, eventually detach and reattach, with this obstructed-detach-reattach sequence being observed in axon as a “pause.” Based on this, along with our quantitative evidence-based contention that slow and fast axonal transport are actually single and multi-motor transport, we have developed a cargo level motor model capable of exhibiting the full range of slow to fast transport solely by changing the number of motors involved. This computational model derived using first-order kinetics is suitable for both kinesin and dynein and includes load-dependence as well as provision for motors encountering obstacles to procession. The model makes the following specific predictions: average distance from binding to obstruction is about 10 μm; average motor maximum velocity is at least 6 μm/s in axon; a minimum of 10 motors is required for the fastest fast transport while only one motor is required for slow transport; individual in-vivo cargo-attached motors may spend as little as 5% of their time processing along a microtubule with the remainder being spent either obstructed or unbound to a microtubule; and at least in the case of neurofilament transport, kinesin and dynein are largely not being in a “tug-of-war” competition.

Keywords: kinesin, dynein, stop-and-go hypothesis, neurofilament, microtubule

1. Introduction

What lies behind “fast” versus “slow” axonal transport? While in-axon data abounds for the existence of for these two modes of transport, there is no isolated microtubule data to support two separate modes. Of course, it is possible that one or more as of yet unknown assistive proteins play a role. But, what if there are not two modes but instead, one very long range of transport speeds. We recently showed quantitative evidence that slow axonal transport might be equated to single motor axonal transport based solely on an analysis of cargo loading forces and single motor stall forces(Mitchell and Lee, 2009). This suggestion begs the question, “Is fast axonal transport simply multi-motor transport?” That is, is the only difference between slow and fast transport the number of motors involved?

In the work presented here, we quantitatively examine what it would theoretically take to make this proposition true. That is, what assumptions must we make to transform slow and fast transport into a single/multi motor transport theory? Many of the presented assumptions have strong experimental support, some are controversial, and the remainder are presented here as model predictions, as they go beyond the current experimental record.

The most contentious assumption that we examine in this theoretical study is also one for which we believe there is strong experimental support: there is no motor equivalent to “stop and go” cargo transport. That is, the experimental evidence supports a cargo-level multi-second “pause” in axon, but not a motor-level multi-second pause in otherwise nominal procession. Instead, we suggest that, at the motor level, cargo pause events are really stop, detach, and reattach events. It is interesting to note that this concept is in line with the original model developed by Brown and colleagues(Brown et al., 2005), which simply had “on track” and “off track.” However, subsequent models (Craciun et al., 2005), introduced the “pause” as a means to explain the longer time constants observed in the original data (Wang and Brown, 2001).

Furthermore, we contend that the experimental evidence supports the notion that the stop in cargo movement (i.e. cargo “pause”) is due to obstruction. Thus, nominal motor procession is halted because further stepping is physically impeded (e.g. the motor has either reached the end of the microtubule or another complex is blocking further microtubule access). Eventually, this motor detaches and subsequently binds to a microtubule again in a different location. For example, while motor events in isolated microtubule experiments are often characterized as “pause” (e.g. (Dixit et al., 2008; Ross et al., 2008)), examination of the supplemental data shows that these events are terminated, not by the motor starting to process after not moving for an extended period, but by the end of the experimental recording. In short, observed motor “pauses” are classified as such because they were not observed detaching before recording time ran out.

The product of our theoretical examination of the experimental literature is a unified computational model capable of producing the entire spectrum of axonal transport velocities. Utilizing this model, we make specific predictions regarding the specifications of the transport infrastructure required for the model and its theoretical assertions to be true in axon.

2. Methods

As a basis for the presented computational models, we conducted an extensive review of in vitro mechano-chemical procession of kinesin and dynein, as well as what is known about cargo level transport in vivo. This review is summarized in the Supplementary Information. The key findings of this review, which subsequently become the basis for the models presented, are:

  • 1)

    There is no evidence for motor-level “pausing.” It is true that motor procession is step-wise and therefore there is a time lag between steps. However, these time lags are substantially shorter in duration than the multi second pausing of cargos observed in vivo.

  • 2)

    There is no evidence of a delay between binding to microtubule and procession.

  • 3)

    Motor encounters with potential obstructions result in immediate pass, immediate reversal or a halt that ultimately resolves with detachment (Dixit et al., 2008; Ross et al., 2008).

  • 4)

    In addition to typical obstructions, there is support for motors becoming more severely entangled in a manner that results in prolonged unbinding delays (Brown et al., 2005; Dixit et al., 2008; Ross et al., 2008).

  • 5)

    In vitro (isolated microtubule) binding rates and in vivo binding rates are the result of very different constraints and are therefore not meaningfully comparable (Craciun et al., 2005; Dixit et al., 2008).

  • 6)

    In vitro (isolated microtubule) maximum procession velocities are possibly as much as an order of magnitude slower than in vivo maximum procession velocities (Dixit et al., 2008; Kural et al., 2005). We suggest that this may be due to unavoidable bulk flow disturbances in vitro.

  • 7)

    Unbinding and procession rates are load-dependent in a roughly linear manner (Coppin et al., 1997; Mallik et al., 2004).

  • 8)

    Cargo load on processing motors is velocity dependent (Mitchell and Lee, 2009)

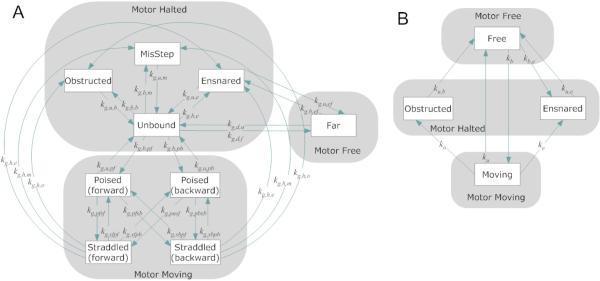
Based on these key findings, as well as other experimental observations, we developed a generalized kinetic model of single motor movement along a microtubule intended to encapsulate all possible scenarios (Figure 1a). This generalized kinetic model was subsequently reduced into an in-axon cargo level motor model (Figure 1b; See supplement for development details).

Figure 1.

Figure 1

Open in a new tab

Development of motor model. A: Generalized model with all possible transitions included. B: simplified model generated by merging states.

The model consists of four states: moving, obstructed, free and ensnared. Moving represents nominal procession along the microtubule and as such actually represents two of the generalized model states (anterograde poised and straddled). Note that the rate of procession is load dependent. Obstructed represents all conditions that result in an otherwise functioning motor being prevented from stepping (except cargo obstructions). Thus obstructions due to end-of-microtubule, MAP (such as tau), other microtubules would be included. Free represents a cargo-attached motor that is not bound to a microtubule. In vivo, this is regarded as being “close” to a potential microtubule such that the motor only needs to rotate into position, but not necessarily translationally diffuse a distance. Finally, Ensnared represents all conditions wherein the motor is inappropriately adhered to the microtubule and is incapable of procession. It assumed that these conditions take longer to resolve than obstructions (i.e. would have lower rates of unbinding).

The transitions between the states are considered to be independent, first order (i.e. Poisson-like) random events described by a single rate constant. The exceptions are the rates of transition from Moving to Obstruction and Ensnared, which are procession velocity dependent (i.e. the faster a motor processes, the quicker it will reach an Obstruction). Note that there are no transitions back from Obstructed or Ensnared to Moving, as we contend that the experimental evidence does not support these transitions. There is also no transition directly from Free to Obstructed as the probability of binding exactly in front of an obstruction is sufficiently low to be ignored.

The net result is roughly two parallel loops wherein motors go from Free to Moving to either Obstructed or Ensnared and then return to Free. (The effect of the direct Free to Ensnared transition is to create a longer time constant component of non-movement.)

Simulation

To quantify the ramifications of the assumptions/predictions the model was numerically solved for steady state transport based on load, number of motors and values for the kinetic rate constants. This was accomplished by simulating all motor events for a single cargo. Since the goal of this work was “proof of concept” regarding whether single versus multi-motor could possibly explain slow versus fast axonal transport, we intentionally kept the multi-motor simulations simplistic. Thus, all attached processing motors equally shared the load and moved at the same speed. A motor becoming Obstructed/Ensnared instantly stopped the cargo and also instantly shifted all force from processing motors into a negative load on the obstructed/ensnared motor. Cargoes were modeled as linear viscous drag loads based on our prior work (Mitchell and Lee, 2009). Thus a “neurofilament” was nominally a 1.25 pN load at 600 nm/s and 12.5 pN load at 6000 nm/s. Likewise a “1 mm diameter vesicle” was a 5.7 pN load at 1000 nm/s and a 34.2 pN load at 6000 nm/s. “Steady state” transport was simulated as the average of 16000 individual motor events for each cargo.

2.1 Prediction Generation

The goal with our approach to prediction generation was to develop “clean and clear” predictions versus, for example complex quantitative relationships. Thus, the concepts behind the predictions were qualitatively developed by logical inference on the ramifications of the proposed model given what is experimentally known. The final numerical values associated with the predictions were generated by partial parameter sensitivity analyses wherein key parameters were determined and varied over a reasonable range.

3. Results and Discussion

We begin by comparing and contrasting our developed model to the current gold standard cargo model developed by Brown and colleagues(Brown et al., 2005). We then present a general evaluation of the developed model followed by a detailed examination and discussion of the model's predictions.

3.1 Comparison to Brown cargo model

The gold standard model for axonal transport has, for some time, been from the Brown lab. The comprehensive examination of neurofilament transport in axon (Brown et al., 2005) was the basis of some of the presented model's parameters (average velocities as well as data on cargo pausing time constants). Moreover, the Brown model has been the basis of both our prior work (Mitchell and Lee, 2009; Mitchell and Lee, 2012) as well as the work of many others e.g. (Craciun et al., 2005; Gazzola et al., 2009; Kam et al., 2009; Kuznetsov, 2011; Kuznetsov, 2013; Peter and Mofrad, 2012; Zadeh and Shah, 2010), which have included motor-level pausing. However, the Brown model was developed as a cargo model rather than a motor model attached to a cargo. Nearly, a decade on, with a wealth of isolated microtubule preparation data, we are now in a position to reexamine the central premises of the Brown model (Brown et al., 2005; Li et al., 2012), namely “Stop and go” and motor switching.

As stated in the introduction, the original Brown model simply described cargo transport as being either “on track” or “off track” and anterograde or retrograde. This aligns with our Moving and Free states. To handle the long time constants observed in the experimental data, the Brown model (Brown et al., 2005) was expanded to include a second state in each direction (Craciun et al., 2005). It is here that the concept of an “on track pause” (i.e. a motor-level pause) was introduced (Craciun model states u1 and u1). This corresponds to our Obstructed and Ensnared states. However, we contend subsequent experimental data support transition to Free only, with no transition back to Moving. This change eliminates motor “pause” in favor of “stop-detach-reattach.” This is more than semantics as it also eliminates the need to pause after binding before moving. It also, however eliminates the longer time constants. We introduce the Obstructed versus Ensnared difference to return to two time constants. In short, and viewed at the highest level, our proposed model is two three-stage loops in parallel, each with a different loop time constant, versus two two-stage loops in series.

3.2 Basic evaluation of the developed model

A cursory examination of the parameter value solution space clearly indicated that a model of the proposed form could readily achieve the stated goal. Thus, we conclude that, yes, a single model with no motor level pause can exhibit the full range of axonal transport velocities solely by varying the number of motors. (See Table 1 below for an example parameter value solution set.)

Table 1.

Developed model simulation parameters. (See supplement for full parameter derivations and definitions.)

Rate Constant Kinesin Dynein Description
kb(s−1) 1 2 Free to Moving
ku(s−1) 0.15+0.4/pN .21+0.4/pN Moving to Free
Vmax(μm/s) 6 6 Maximum procession velocity with no load
do(μm) 10 15 Average distance from binding to Obstructed
ku,o(s−1) 0.15+0.4/pN .21+0.4/pN Obstructed to Free
de(μm) 300 450 Average distance from binding to Ensnared
ku,e(s−1) 0.01+0.4/pN 0.01+0.4/pN Ensnared to Free
kb,e(s−1) 0.03 0.03 Free to Ensnared
Open in a new tab

With this conclusion in hand, we turn our focus to two tasks. 1) determining the limits of the above conclusion, (presented here as predictions), and 2) determining a reasonable or “base” set of parameter values from which future work, beyond the conceptual work presented here, could proceed.

The predictions are as follows:

3.3 Predictions

3.3.1 Prediction 1: no competition between kinesin and dynein for neurofilament transport

Brown experimental data suggests simultaneously that the ratio of anterograde to retrograde transport is 2:1 while direction reversals were “rare.” With a motor level “pause” removed in our model, this observation is only achievable if competition between kinesin and dynein is also rare, thus permitting a motor to unbind and reattach without the other motor type taking over. Note that this is also consistent with the modeling work of Kunwar et al. (Kunwar et al., 2011) in that they also had a cargo model with no pause, but also no obstructions, wherein cargo “pausing” was the result of tug-of-war. Ultimately, they concluded that this approach did not reproduce the experimental data to their satisfaction.

3.2.2 Prediction 2: average distance between obstructions is at least 4 μm and likely about 20 μm

The idea of multi-motor transport equating to fast transport imposes an average minimum velocity. Taken to the extreme (i.e. infinite motors), minimum velocity becomes a battle between the fraction of motors obstructed (preventing movement) and the fraction of motors trying to process. That is, increasing the number of motors also increases the frequency of obstruction. From the isolated microtubule preparation (see Supplement), the unbinding rate under high load appears to be roughly linear at about 0.4 s−1N−1. Taken to an extreme in maximum procession velocity (12 μm/s) and doubling the unbinding change with load, we reach a fundamental limit on the average distance from binding to obstructions of about 2 μm. With maximum procession velocities reduced closer to what could be considered reasonable (say 6 μm/s), and the observed change in unbinding rate with load, average distance from binding to obstruction increases to 10 μm. Further reductions in maximum velocity dramatically increase the average distance to obstruction. Assuming binding occurs, on average, in the middle of obstructions, then the distance between obstructions would be twice the distance from binding to obstruction. Thus we predict a value in the vicinity of 20 μm. This in turn, suggests average MT lengths greater than 20 μm.

Note that these predictions are longer than expected based on previous measures of average MT length (Yu and Baas, 1994). However, the Yu study included even very short lengths; it may be that very short MT fragments are not operational but rather are, themselves, being transported(Kuznetsov and Kuznetsov, 2014). Based on the move-to-move probability from Brown, it is evident that continuing at the same speed or nearly the same speed was the most common transition. This suggests runs frequently lasting longer than 10 seconds, which in turn suggests average distance between binding and obstruction on the order of 10 μm or greater.

3.3.3 Prediction 3: The minimum number of motors for fastest “fast” transport is about 10

Based on a broad examination of model parameter values that could still achieve Brown data average velocities, we predict that the fastest “fast” transport velocities observed experimentally would require a substantial number of motors (at least 10). This prediction is largely independent of parameter values with the exception of directly binding to Ensnared. Eliminating direct binding to ensnared forces the binding rate to procession to be much lower to meet the slow transport criterion. This, in turn, dramatically increases the number of motors needed to about 30. Since eliminating the direct binding-to-ensnared also alters the cargo pause-to-pause probability in a manner that is inconsistent with Brown, we concluded with Brown that the long cargo pauses are a significant aspect of slow transport. Thus, the criteria for single motor slow (i.e. 0.18 μm/s) and multi-motor fast (i.e. 4.7 μm/s) along, with the Brown pause-to-pause probability, effectively specify this minimum. Note that not so fast “fast” transport (say 2.3 μm/s) was possible with the presented model with as few as 4 motors. This prediction is consistent with findings about the effect of motor count on transport (Elluru et al., 1995).

3.3.4 Prediction 4: Single motor, slow transport is both drag force and unbinding rate limited

With the longer run lengths predicted (#2 above), it is very likely that we would experimentally observe maximum procession velocity with cargo in tow in the data of Brown and colleagues. Examining both the velocity transitions as well as the example runs in Wang (Wang and Brown, 2001), it appears that that velocity is 3 μm/s or less. In contrast, the fastest fast transport requires maximum unloaded procession velocities to be at least 5 μm/s. This strongly suggests that cargo load is reducing procession velocity in the slow transport case. However a single motor pulling a cargo that is halted due to obstructed or ensnared is under essentially zero load and so its unbinding rate is quite low. Thus, in single motor transport case, unbinding rate is high while processing and low while halted.

3.3.5 Prediction 5: Dynein takes bigger steps during fastest fast retrograde transport

The available data for specifying dynein transport is more limited than that for kinesin. Consequently, this prediction is more speculative than the others. Nonetheless, dynein are known to be able to take longer steps under low load and sufficient ATP (Mallik et al., 2004). This long stepping, which could quadruple dynein's procession velocity partially counteracts the overall effect of its lower force generating ability in producing the fastest fast transport. That is, dynein tend to get hung up on obstacles for longer durations because their ability to pull one another off is lower due to their lower force (1.25 pN vs 5.7 pN for kinesin (Coppin et al., 1997; Gao, 2006)). However, while processing with enough dynein pulling a cargo, the individual load on a given dynein is sufficiently small that they can take longer steps, thus canceling the obstacle issue. Secondarily, dynein's ability to back up and go around may also assists in this speed-up during fast transport.

3.3.6 Prediction 6: Dynein binding rate to microtubule is as much as three times greater than kinesin

Examination of parameter value restrictions in the presented model indicates that to match Brown slow retrograde transport velocities (of presumably the same neurofilaments being anterogradely transported by kinesin), requires a dynein binding rate that is 2-3 times higher than that used for kinesin. Our binding rate is defined as binding from “close” to the microtubule. One possible explanation for dynein having a higher binding rate in this definition is that it appears to have a longer operational length than kinesin. That is, kinesin has been shown to hold a cargo approximately 17 nm from the microtubule (Kerssemakers et al., 2006), while dynein holds cargo 28 nm in the same tests (Mizuno et al., 2007). Thus, dynein are potentially sweeping a much larger volume when unbound (about 4.5 times as much, all else being equal). Interestingly, the needed factor between binding rates corresponds better with swept area rather than volume, suggesting that the distance swept is more or less fixed.

3.4 Final Model Parameters

Based on the above analysis, we have chosen a middle-ground set of parameter values (Table 1) for the developed model. This set reasonably reproduces the original Brown velocity averages as well as velocity transitions and examples of processing that are qualitatively similar to Brown. They are not, however, intended to be the last word on these kinetic parameters. That is, they are not predictions in and of themselves because these parameters remain too experimentally underspecified. Nonetheless, we offer them as a reasonable starting point for future work.

As an overview of model performance we present a “Brown like” velocity transition summary for a single kinesin pulling a neurofilament (Table 2). Time was segmented into 4.7 second for which an average velocity was calculated and binned in 500 nm/s increments. Thus V0 represents zero velocity, V1 0-500 nm/s, V2 500-1000 nm/s etc. The probabilities shown are for consecutive time segments. Thus, there is a 90.5% chance that a “paused” neurofilament will remain paused in the next 4.7 s segment. Comparison to Brown reveals that we are quite similar but off by about one velocity segment at the high end. Given the simplicities of our simulation, we consider this to be quite good as doing something as simple as using a modest range of cargo sizes, rather than a single cargo size, readily resolves the difference.

Table 2.

Velocity transition table comparable to Brown (Brown et al., 2005).

V0 V1 V2 V3 V4 V5 V6
V0 0.905 0.068 0.020 0.005 0.002 0.000 0.000
V1 0.163 0.543 0.249 0.039 0.007 0.001 0.000
V2 0.112 0.470 0.318 0.082 0.017 0.000 0.000
V3 0.058 0.413 0.372 0.135 0.018 0.004 0.000
V4 0.071 0.357 0.381 0.190 0.000 0.000 0.000
V5 0.000 0.500 0.000 0.500 0.000 0.000 0.000
V6 0.000 0.000 0.000 0.000 0.000 0.000 0.000
Open in a new tab

• We develop a model of kinesin and dynein motors suitable for use at the cargo level.

• We propose that motor “pausing” is obstruction/ensnarement followed by detachment.

• We find that motor count can potentially explain fast versus slow transport.

• We make several experimentally testable predictions based on this result.

3.5 Effect of multiple motors

Based on the final parameters, which were specified to reproduce Brown average velocities for kinesin and dynein with a single motor and to reproduce the fastest fast transport (i.e. 4.7 μm/s), we could simulate the effect of number of motors attached to a cargo and trying to bind and process along nearby microtubules (Figure 2). These simulations were kept simplistic, assuming equal load sharing among motors, instant cargo stop with a single obstructed motor (but also instant negative load on that motor by those still processing), and no other interaction between motors, so as to minimize unintended confounds in our examination of the basic conceptual goal of this work.

Figure 2.

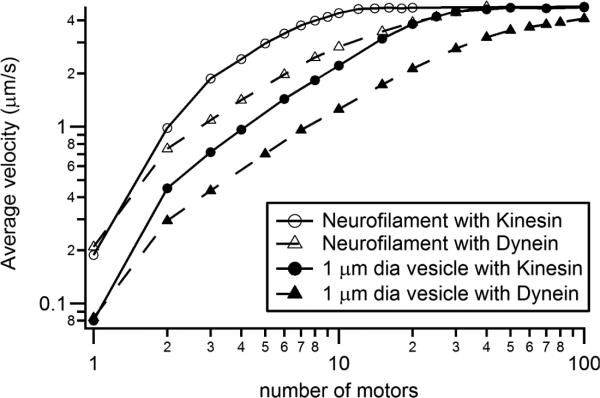
Figure 2

Open in a new tab

Profile of average velocity as a function of the number of motors.

It is apparent that multiple motors synergistically combine to dramatically increase average velocity. Thus, two kinesin average 5-6 times faster than a single kinesin and two dynein average 3-4 times faster than a single dynein. As mentioned in the predictions section, this large factor is due to a much lower unbinding rate when other motors are not pulling on obstructed motors. The factors diminish with increasing motor count with the overall factor being 11-12 at four motors versus one for kinesin, and 6-7 at four dynein motors to one. At high motor counts kinesin reaches a maximum while dynein continues to slowly increase.

4. Conclusion

We have developed a cargo-level motor model suitable for both kinesin and dynein that spans the velocity range of fast and slow transport solely by changing the number of motors attached to the cargo. We conclude from this that our proposition that axonal transport is accomplished by a single, large spectrum of axonal transport velocities by multi-motor transport, is plausible. That is, fast and slow transport may not be two modes of transport, but rather are simply single versus multi-motor transport. Simulations of the presented motor models suggest that individual in-vivo cargo-attached motors may spend as little as 5% of their time processing along a microtubule with the remainder being spent either obstructed or unbound to a microtubule. It is not surprising then that we find that multiple motors of the same type, working together to move a cargo, can achieve average velocities 20 to 30 times faster than single motor average velocities.

Supplementary Material

NIHMS657296-supplement.docx (561.4KB, docx)

  • We develop a model of kinesin and dynein motors suitable for use at the cargo level.

  • We propose that motor “pausing” is obstruction/ensnarement followed by detachment.

  • We find that motor count can potentially explain fast versus slow transport.

  • We make several experimentally testable predictions based on this result.

Acknowledgements

This study was funded by National Institute of Health grants NS081426, NS069616 and NS062200. The funding agency had no role in the design and conduct of the study, collection, management analysis and interpretation of the data; preparation, review or approval of the manuscript; or decision to submit the manuscript for publication.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Brown A, Wang L, Jung P. Stochastic simulation of neurofilament transport in axons: the “stop- and-go” hypothesis. Mol Biol Cell. 2005;16:4243–55. doi: 10.1091/mbc.E05-02-0141. doi:E05-02-0141 [pii] 10.1091/mbc.E05-02-0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Coppin CM, Pierce DW, Hsu L, Vale RD. The load dependence of kinesin's mechanical cycle. Proc Natl Acad Sci U S A. 1997;94:8539–44. doi: 10.1073/pnas.94.16.8539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Craciun G, Brown A, Friedman A. A dynamical system model of neurofilament transport in axons. J Theor Biol. 2005;237:316–22. doi: 10.1016/j.jtbi.2005.04.018. doi:S0022-5193(05)00182-7 [pii] 10.1016/j.jtbi.2005.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Dixit R, Ross JL, Goldman YE, Holzbaur EL. Differential regulation of dynein and kinesin motor proteins by tau. Science. 2008;319:1086–9. doi: 10.1126/science.1152993. doi:1152993 [pii] 10.1126/science.1152993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Elluru RG, Bloom GS, Brady ST. Fast axonal transport of kinesin in the rat visual system: functionality of kinesin heavy chain isoforms. Mol Biol Cell. 1995;6:21–40. doi: 10.1091/mbc.6.1.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gao YQ. A simple theoretical model explains dynein's response to load. Biophys J. 2006;90:811–21. doi: 10.1529/biophysj.105.073189. doi:S0006-3495(06)72269-X [pii] 10.1529/biophysj.105.073189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gazzola M, Burckhardt CJ, Bayati B, Engelke M, Greber UF, Koumoutsakos P. A stochastic model for microtubule motors describes the in vivo cytoplasmic transport of human adenovirus. PLoS Comput Biol. 2009;5:e1000623. doi: 10.1371/journal.pcbi.1000623. doi:10.1371/journal.pcbi.1000623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kam N, Pilpel Y, Fainzilber M. Can molecular motors drive distance measurements in injured neurons? PLoS Comput Biol. 2009;5:e1000477. doi: 10.1371/journal.pcbi.1000477. doi:10.1371/journal.pcbi.1000477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kerssemakers J, Howard J, Hess H, Diez S. The distance that kinesin-1 holds its cargo from the microtubule surface measured by fluorescence interference contrast microscopy. Proc Natl Acad Sci U S A. 2006;103:15812–7. doi: 10.1073/pnas.0510400103. doi:10.1073/pnas.0510400103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kunwar A, Tripathy SK, Xu J, Mattson MK, Anand P, Sigua R, Vershinin M, McKenney RJ, Yu CC, Mogilner A, Gross SP. Mechanical stochastic tug-of-war models cannot explain bidirectional lipid-droplet transport. Proc Natl Acad Sci U S A. 2011;108:18960–5. doi: 10.1073/pnas.1107841108. doi:10.1073/pnas.1107841108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Kural C, Kim H, Syed S, Goshima G, Gelfand VI, Selvin PR. Kinesin and dynein move a peroxisome in vivo: a tug-of-war or coordinated movement? Science. 2005;308:1469–72. doi: 10.1126/science.1108408. doi:10.1126/science.1108408. [DOI] [PubMed] [Google Scholar]
  12. Kuznetsov AV. Analytical solution of equations describing slow axonal transport based on the stop-and-go hypothesis. Central European Journal of Physics. 2011;9:662–673. [Google Scholar]
  13. Kuznetsov AV. An analytical solution describing the propagation of positive injury signals in an axon: effect of dynein velocity distribution. Comput Methods Biomech Biomed Engin. 2013;16:699–706. doi: 10.1080/10255842.2011.632376. doi:10.1080/10255842.2011.632376. [DOI] [PubMed] [Google Scholar]
  14. Kuznetsov IA, Kuznetsov AV. Modeling anterograde and retrograde transport of short mobile microtubules from the site of axonal branch formation. J Biol Phys. 2014;40:41–53. doi: 10.1007/s10867-013-9334-8. doi:10.1007/s10867-013-9334-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Li Y, Jung P, Brown A. Axonal transport of neurofilaments: a single population of intermittently moving polymers. J Neurosci. 2012;32:746–58. doi: 10.1523/JNEUROSCI.4926-11.2012. doi:10.1523/JNEUROSCI.4926-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mallik R, Carter BC, Lex SA, King SJ, Gross SP. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–52. doi: 10.1038/nature02293. doi:10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
  17. Mitchell CS, Lee RH. A quantitative examination of the role of cargo-exerted forces in axonal transport. J Theor Biol. 2009;257:430–7. doi: 10.1016/j.jtbi.2008.12.011. doi:S0022-5193(08)00652-8 [pii] 10.1016/j.jtbi.2008.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Mitchell CS, Lee RH. Cargo distributions differentiate pathological axonal transport impairments. J Theor Biol. 2012;300:277–91. doi: 10.1016/j.jtbi.2012.01.019. doi:S0022-5193(12)00027-6 [pii] 10.1016/j.jtbi.2012.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mizuno N, Narita A, Kon T, Sutoh K, Kikkawa M. Three-dimensional structure of cytoplasmic dynein bound to microtubules. Proc Natl Acad Sci U S A. 2007;104:20832–7. doi: 10.1073/pnas.0710406105. doi:10.1073/pnas.0710406105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Peter SJ, Mofrad MR. Computational modeling of axonal microtubule bundles under tension. Biophys J. 2012;102:749–57. doi: 10.1016/j.bpj.2011.11.4024. doi:10.1016/j.bpj.2011.11.4024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ross JL, Shuman H, Holzbaur EL, Goldman YE. Kinesin and dynein-dynactin at intersecting microtubules: motor density affects dynein function. Biophys J. 2008;94:3115–25. doi: 10.1529/biophysj.107.120014. doi:S0006-3495(08)70468-5 [pii] 10.1529/biophysj.107.120014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wang L, Brown A. Rapid intermittent movement of axonal neurofilaments observed by fluorescence photobleaching. Mol Biol Cell. 2001;12:3257–67. doi: 10.1091/mbc.12.10.3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Yu W, Baas PW. Changes in microtubule number and length during axon differentiation. J Neurosci. 1994;14:2818–29. doi: 10.1523/JNEUROSCI.14-05-02818.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zadeh KS, Shah SB. Mathematical modeling and parameter estimation of axonal cargo transport. J Comput Neurosci. 2010;28:495–507. doi: 10.1007/s10827-010-0232-9. doi:10.1007/s10827-010-0232-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS657296-supplement.docx (561.4KB, docx)

RESOURCES