A linkage disequilibrium perspective on the genetic mosaic of speciation in two hybridizing Mediterranean white oaks

Abstract

We analyzed the genetic mosaic of speciation in two hybridizing Mediterranean white oaks from the Iberian Peninsula (Quercus faginea Lamb. and Quercus pyrenaica Willd.). The two species show ecological divergence in flowering phenology, leaf morphology and composition, and in their basic or acidic soil preferences. Ninety expressed sequence tag-simple sequence repeats (EST-SSRs) and eight nuclear SSRs were genotyped in 96 trees from each species. Genotyping was designed in two steps. First, we used 69 markers evenly distributed over the 12 linkage groups (LGs) of the oak linkage map to confirm the species genetic identity of the sampled genotypes, and searched for differentiation outliers. Then, we genotyped 29 additional markers from the chromosome bins containing the outliers and repeated the multilocus scans. We found one or two additional outliers within four saturated bins, thus confirming that outliers are organized into clusters. Linkage disequilibrium (LD) was extensive; even for loosely linked and for independent markers. Consequently, score tests for association between two-marker haplotypes and the ‘species trait' showed a broad genomic divergence, although substantial variation across the genome and within LGs was also observed. We discuss the influence of several confounding effects on neutrality tests and review the evolutionary processes leading to extensive LD. Finally, we examine how LD analyses within regions that contain outlier clusters and quantitative trait loci can help to identify regions of divergence and/or genomic hitchhiking in the light of predictions from ecological speciation theory.

Introduction

The acknowledgment that major genes could drive the process of speciation (Wu, 2001), as opposed to the prevailing view of whole genome isolation (Mayr, 1963), soon led to the acceptance of the porous nature of genomes and to the concept of heterogeneous genomic divergence (Schluter, 2001; Gavrilets and Vose, 2005; Turner et al., 2005; Nosil et al., 2009; Ellegren et al., 2012). Several non-exclusive factors can potentially contribute to the genetic mosaic that is created during the process of population divergence and speciation. These include exogenous and/or endogenous drivers of divergent selection (Rundell and Price, 2009; Schluter, 2009); genetic drift (Ohta, 1992); variable mutation and recombination rates (Hedrick, 2005; Noor and Feder, 2006; Nachman and Payseur, 2012); chromosomal structure (Rieseberg, 2001; Strasburg et al., 2012); or the genomic distribution and size effects of genes under selection (Orr, 2005; Rogers and Bernatchez, 2007; Michel et al., 2010).

The best-studied evolutionary process contributing to the genetic mosaic of speciation is divergent selection, whose effects have been summarized on the basis of linkage among genetic markers (Nosil et al., 2009). Loci under divergent selection and neutral loci tightly linked to them should exhibit greater levels of divergence than expected under neutrality (Beaumont and Nichols, 1996; Schlötterer, 2002; Beaumont and Balding, 2004; Foll and Gaggiotti, 2008). Hitchhiking effects can extend far along the chromosomes and persist despite high recombination rates (Charlesworth et al., 1997; Via and West, 2008), thus contributing to greater differentiation at loosely linked neutral loci than at completely unlinked neutral loci. Finally, divergent selection can have indirect, yet widespread, effects on heterogeneous genomic divergence by reducing genome-wide effective inter-population gene flow (Barton and Bengtsson, 1986; Gavrilets, 2004), thus facilitating neutral divergence by genetic drift.

One of the most controversial issues, from both theoretical expectations and empirical results, is the creation and maintenance/growth of the genomic regions of divergence during speciation with gene flow (Hoffmann and Rieseberg, 2008; Feder and Nosil, 2010; White et al., 2010; Yeaman and Whitlock, 2011; Nachman and Payseur, 2012; Nosil and Feder, 2012; Feder et al., 2012b; Narum et al., 2013). Via (2009, 2012) proposed that strong divergent selection acting on a few loci generates an inter-population process, which she called divergence hitchhiking (DH), that is characterized by reduced inter-population recombination and gene flow. Only reduced recombination between groups around divergently selected genes would contribute to the length of the DH regions. In addition, divergent selection causes some reduction in realized gene exchange across the entire genome because the diverging phenotypic traits are selected against in the alternative environments when they occur in migrants, F1 hybrids or recombinants. This process has been named genomic hitchhiking (GH) and can facilitate divergence across the genome, even for unlinked loci (Feder et al., 2012b; Via, 2012).

Linkage disequilibrium (LD) is a powerful tool for studying the genomic architecture of ecological speciation, including the detection of divergently selected markers, the analysis of the length and location of differentiation regions, or the search for associations between LD and signatures of divergent selection (Goicoechea et al., 2012; Hohenlohe et al., 2012; Nosil, 2012; Rogers et al., 2013). However, examples of LD estimates are relatively rare in the ecological speciation literature. We would expect a change of this trend now that new methods have been developed for the genetic analysis of species in the wild (Buerkle and Lexer, 2008; Payseur, 2010; Gompert et al., 2012; Malek et al., 2012), and that next-generation sequencing provides enough markers for extensive LD analyses in model and non-model organisms (Hohenlohe et al., 2012; Gagnaire et al., 2013). In a previous study, we showed that LD among loosely linked nuclear simple sequence repeats (nSSRs) could successfully detect footprints of divergent selection between two European white oaks (Goicoechea et al., 2012). In the present work, we extend such approach to gain additional insights into the evolutionary forces shaping the genetic mosaic of speciation in this group of species. We selected two hybridizing Mediterranean oaks to demonstrate the efficacy of our method, which could complement the bi-allelic marker studies currently developed in a wide range of organisms.

It is broadly accepted that sister species from recent evolutionary radiations are most appropriate to analyze the genetic mosaic of speciation, as they avoid the confounding effects of secondary contact and/or post-speciation differentiation (Via, 2012; Feder et al., 2012a; but see Hendry, 2009; for some drawbacks). In comparison, heterogeneous genomic divergence from species originated in older evolutionary radiations remains largely unknown, even if this knowledge may be of interest to some evolutionary questions such as the duration of DH footprints on LD, or how much divergence is attained before reproductive isolation is complete.

The Fagaceae family includes several genera with contrasting evolutionary records. Although some of them comprise very few species (Chrysolepis, Notholithocarpus and Trigonobalanus), others (Castaneopsis, Lithocarpus and Quercus) have experienced extensive radiations (Manos et al., 1999, 2001). In particular, the genus Quercus underwent several evolutionary radiations from the the mid-Miocene until the early Pliocene (Axelrod, 1983; Manos and Stanford, 2001; Hubert et al., 2014), which created most of the 400 species actually found in the Northern Hemisphere. The European white oaks are best known by the two temperate species Quercus petraea and Quercus robur, which are widely distributed and have been the subject of many genetic studies providing a large amount of genomic resources (Kremer et al., 2012; Plomion and Fievet, 2013). However, the Mediterranean basin is home to over two-dozen little studied white oak species (Amaral Franco, 1990; Denk and Grimm, 2010), many of them with restricted distribution ranges and little economic importance, but with a prominent ecological role. These species show evidences of recurrent and ongoing gene flow, as indicated by the sharing of chloroplast DNA variants with strong biogeographic structure (Olalde et al., 2002; Petit et al., 2002) and by the occurrence of hybrid/admixed trees in sympatric populations (Valbuena-Carabaña et al., 2005; Curtu et al., 2007; Lepais and Gerber, 2011). Furthermore, all our data suggest their genomes maintain a large degree of synteny (Casasoli et al., 2006; Bodénès et al., 2012).

In this study, we analyzed nearly 100 SSRs from two hybridizing white oaks whose distributions are restricted to the western Mediterranean basin, Quercus faginea Lamb. and Quercus pyrenaica Willd. The two species have a complementary distribution in the Iberian Peninsula (south-west vs north-east), which is related to their preferences for basic or acidic soils, respectively (Blanco et al., 1997). Interspecific differences related to ecological divergence also include leaf morphology (ovate with serrate edges in Q. faginea vs deeply lobed in Q. pyrenaica), pubescence (glabrous vs densely pubescent) and cuticle composition (thick waxy cuticle vs thin cuticle). Flowering phenology, an ecological character with pleiotropic effects on pre-zygotic reproductive isolation, also shows large between-species differences: Q. pyrenaica is the latest white oak to flower in the Iberian Peninsula, approximately 1 month later than Q. faginea (Blanco et al., 1997).

The main objective of our study was to analyze the LD patterns in the genetic mosaic of speciation from the two hybridizing Mediterranean white oaks, to search for selection footprints that could shed light on their evolutionary history. We first ascertained the phenotype–genotype relationships and described the landscapes of genetic diversity and interspecific differentiation, based on a set of expressed sequence tag-SSRs (EST-SSRs). After controlling for null alleles and demographic history, we searched for markers putatively under selection and analyzed the haplotype patterns of interspecific differentiation. We then review several confounding effects on neutrality tests and possible causes for the extensive LD. Finally, we discuss the significance of the LD pattern as a signature of either DH or GH, while addressing several concerns from the ecological speciation literature, in particular, the establishment of a link between ecologically driven adaptation and reproductive isolation.

Materials and methods

Sampling and genotyping

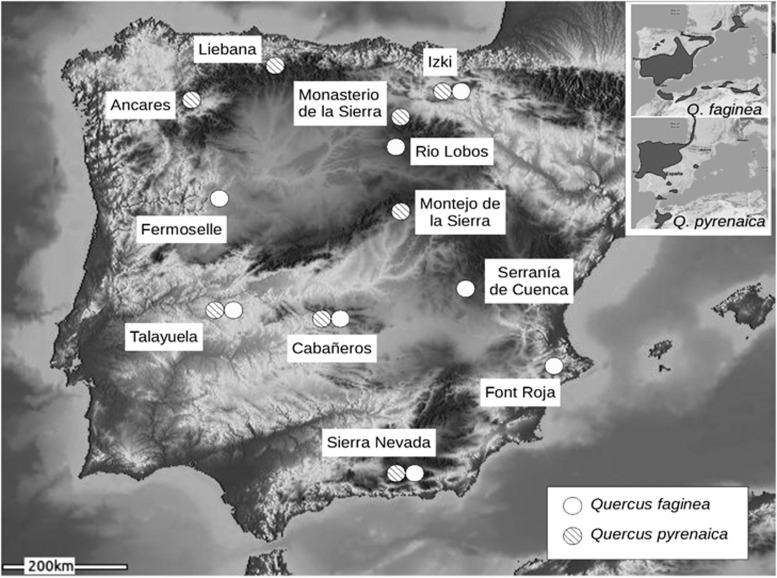
The genetic variability of the two Mediterranean white oaks (Q. faginea Lamb. and Q. pyrenaica Willd.) was sampled across the largest part of their ecological and geographical distributions (Figure 1). Interspecific population pairs were collected from four locations, although only two sympatric populations were sampled (Cabañeros and Talayuela, in Central Spain), the other two pairs representing close populations from each species (Izki and Sierra Nevada). All trees were geo-referenced using a portable global positioning system. Ninety-six trees from each species were sampled across eight locations, including 12 genotypes from each. Supplementary File 1 provides details of the forest structures at the sampling sites.

Figure 1.

Sampling localities for the eight populations from each of the two oak species analyzed in this study. The inset shows approximate global species distributions in Western Europe and North Africa.

The EST-SSRs markers used in this study were selected from available European white oaks linkage (Bodénès et al., 2012) and bin maps (Durand et al., 2010;), whereas the nSSRs were selected from multilocus scans previously carried out in Q. petraea and Q. robur (Scotti-Saintagne et al., 2004b; Goicoechea et al., 2012). Part of our data set was used in Bodénès et al. (2012), with the only intention of providing a proof of concept on the subject of the EST-SSRs transferability to the Mediterranean white oaks. Lab details about DNA extractions and purifications, PCR amplifications, electrophoretic methods and the binning of alleles, were provided on that publication.

Ninety-eight SSRs (90 EST-SSRs and 8 nSSRs) were genotyped in all trees following a two-step strategy. First, we selected 69 markers evenly distributed across the 12 linkage groups (LGs) of the oak genetic map. Subsequently, we genotyped 29 additional markers to saturate five regions from four LGs harboring putatively selected loci (in LGs #2, 3, 8 and 12). We hypothesized that DH would produce clustering of outliers (Via and West, 2008; Via, 2009); therefore, we expected to find a larger proportion of new outliers among the 29 additional markers.

Supplementary File 2 provides a full description of the markers used in this study, including the LGs they map to, whether they were used in the first or second genotyping round, the repeat motifs, the PCR primer sequences and the respective annealing temperatures. It also shows PCR product size ranges, as well as diversity and inbreeding coefficient estimates for each marker within each species.

Null-alleles estimates

MICRO-CHECKER v.2.2.3 (van Oosterhout et al., 2004) was used to analyze the likely presence of null alleles, or PCR artifacts apparently resulting in null alleles (such as peak stuttering and/or short allele dominance), in the 16 sampled populations. Departures from panmixia that could potentially result in overall homozygote excess, such as assortative mating, were discarded by checking that the homozygote excess was general over most allelic classes.

FREENA (Chapuis and Estoup, 2007) was used to evaluate the influence of null alleles on the interspecific fixation index (F_ST) estimates. The ENA estimates of F_ST (that is, using a data set ‘Excluding Null Alleles', which means allele frequencies do not sum up to 1) were obtained for 60 markers that showed significant inbreeding coefficients (F_IS) in the overall Q. faginea and Q. pyrenaica samples (see below) and they were compared with the F_ST estimates obtained assuming no null alleles were present.

Population structure

STRUCTURE v.2.3.3 (Pritchard et al., 2000) was used to analyze the genetic structure in the samples using all 98 markers. Inferences were based on the linkage model with correlated allele frequencies (Falush et al., 2003) and a unique drift rate from the ancestral population(s). We ran three independent chain replicates of 7.5 × 10⁵ iterations following a burn-in period of 10⁵ iterations, for a fixed number of populations (K=1–17). STRUCTURE likelihood and summary statistics plots were used to check the model convergence. The post-hoc criterion from Evanno et al. (2005) was then applied to determine the most likely number of clusters, and a final chain of 2 × 10⁶ iterations, following a burn-in period of 10⁵ iterations, was run to increase the accuracy of the ancestry coefficients, which were plotted with DISTRUCT (Rosenberg, 2004).

Genetic diversity and differentiation

Parameters of genetic diversity and differentiation were obtained with trees showing <12.5% admixture (that is, pure-species data set). That percentage corresponds to the mean admixture from second-generation backcrosses (BC2); it is large enough to avoid statistical noise (mean admixture in BC3 would be 6.25%), and has been previously used to identify pure species among hybridizing oaks (Goicoechea et al., 2012; Guichoux et al., 2013).

Allelic richness (AR) was estimated according to El Mousadik and Petit (1996), with a rarefacted sample size of 75 trees per species. Observed heterozygosities (Ho) were directly estimated from the frequencies of observed heterozygotes, unbiased estimates of the expected heterozygosities (He) were obtained according to Nei (1987) and the effective numbers of alleles (AE) were obtained according to Kimura and Crow (1964). FSTAT (Goudet, 2001) was used to detect significant deviations from Hardy–Weinberg proportions by permuting alleles among individuals within samples (16 000 permutations) and comparing the inbreeding coefficient values from the permuted data sets to the observed F_IS values.

The fixation index G_ST (Nei, 1987), a weighted average of F_ST over all extant alleles (Nei, 1973), was used to measure interspecific differentiation for historical reasons. However, both G_ST and F_ST have a negative dependence on within-group heterozygosity that causes them to approach zero when diversity is high, even if populations are completely differentiated (Hedrick, 2005; Jost, 2008). Therefore, we also used Jost's D, a multiplicative partitioning of diversity based on the effective number of alleles (Jost, 2008). Unbiased estimates of the two differentiation parameters were calculated with SMOGD (Crawford, 2010), using 1000 bootstrapped samples to calculate their variances and their 95% confidence intervals.

Among populations, within species, differentiations (F_ST) were estimated with a hierarchical analysis of molecular variance and their significances were tested using a non-parametric approach with 16 000 permutations (Excoffier et al., 1992). Computations were made with ARLEQUIN v3.5 (Excoffier and Lischer, 2010).

Recent demographic history

Demography can confound both outlier and LD tests. Therefore, we performed two tests to analyze the recent demographic history of both Mediterranean white oaks. The analyses were carried out with the pure-species data set containing only the neutral loci (that is, 79 markers, see below), and separately for SSRs with di- and tri/hexa-nucleotide repeat motifs, as the mutation patterns were different for those two classes.

First, the T₂ statistic in BOTTLENECK v.1.2.02 (Cornuet and Luikart, 1996) was used to examine the recent demographic history within each of the two oak species. T₂ represents the deviation of the sample gene diversity from the gene diversity expected for the observed number of alleles in the sample (k). T₂ is expected to be 0 under mutation-drift equilibrium in a constant-size population. Positive T₂ (He excess) indicates a recent bottleneck, whereas negative T₂ (He deficiency) is consistent with a recent population expansion. We computed T₂ under the two-phase model of microsatellite mutation, using 90 and 70% strict stepwise mutations to cover a realistic scenario. Wilcoxon signed rank tests were used to test the significance of the He excess or deficiency across loci against equilibrium expectations (Piry et al., 1998).

The SSRs mutation model allows evaluation of the effects of recent population expansion on different measures of variability (that is, heterozygosity and variance of allele sizes). Thus, homozygosity (probability of size identity) and genetic variance (variance of allele sizes) can lead to different θ estimates. Such differences between the θ estimates can be quantified by their ratio, the imbalance index β (equation 16 in Kimmel et al. 1998). We used the estimator

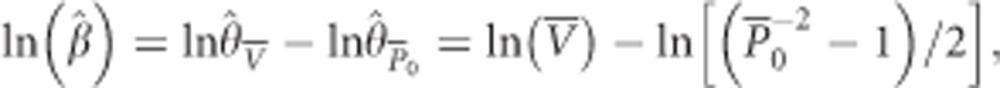where 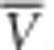and 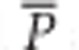are estimates of the genetic variance and homozygosity, averaged over loci (see Kimmel et al., 1998, for further details). A negative value of the imbalance index estimator indicates mutation-drift equilibrium before the expansion, whereas a positive value suggests a bottleneck preceded the expansion.

Outlier tests

These tests were carried out on the pure-species data set. The Bayesian framework of BAYESCAN (Foll and Gaggiotti, 2008), an extension to the original BAYESFST method developed by Beaumont and Balding (2004) that uses a coalescent approach, was used to identify positive and balancing selection outliers. Briefly, the allele frequencies from each sub-population were modeled with a multinomial-Dirichlet distribution and the shared ancestries within sub-populations were modeled with population-specific F_ST coefficients closely related to Wright's (1951) F_ST parameter. Selection was introduced by decomposing the locus–population-specific F_ST coefficients into a population-specific component (β) shared by all loci, and a locus-specific component (α) shared by all populations (see equation 3 in Foll and Gaggiotti, 2008). The probability of each α being different from zero (that is, significant) was then computed by the Bayes Factors of the models with and without such coefficients. A final refinement, recently incorporated into BAYESCAN, is the introduction of q-values to control the false discovery rate. BAYESCAN inferences were drawn separately for markers with di- and tri/hexa-nucleotide motifs, as recommended by the software authors for markers with different mutation rates.

BAYESCAN was designed to test heterozygosity differences among groups and thus, it is not likely that it can detect selection footprints affecting the allelic variance (or the gain/loss of rare alleles). For that reason, and to compare a coalescent-based with a non-coalescent method, we also used the SSR-specific test statistics lnRV and lnRH to search for positive selection outliers (Schlötterer, 2002; Kauer et al., 2003). Briefly, the variances in the number of repeats and heterozygosity distributions were fitted to standardized normal curves. Markers in the distribution tails (2.5%) were then taken as putative outliers. These two SSR-specific methods complement each other in the search for positive selection signatures, such as the heterozygosity drop and the reduction of rare alleles. The MSA software (Dieringer and Schlötterer, 2003) was used to perform the analyses, using 16 000 bootstrapped replicates to generate the normal distributions for the repeats and heterozygosity variances. The analyses were run first with the set of 69 initial markers to identify regions containing putative outliers, and then extended to the full data set (98 markers).

Positive selection outliers were plotted on the corresponding LGs from the bin maps developed for Q. robur (Durand et al., 2010). Furthermore, most markers (with the exception of six EST-SSRs, three of them outliers) were placed in a composite linkage map constructed in this study (see next section).

Haplotype tests

We assumed collinearity between the European white oaks genomes to assess the genomic organization of the genotyped loci. We used several available linkage maps established for Q. petraea and Q. robur (Bodénès et al., 2012 and references therein) to assemble a composite consensus map with the aid of the R library LPmerge (Endelman and Plomion, 2014). We are aware that violations of the collinearity assumption could have important implications for some interpretations of our results. However, the extremely large degree of macro-synteny and macro-collinearity observed between Q. petraea and Q. robur, as well as between Castanea and Quercus (Casasoli et al., 2006; Bodénès et al., 2012), together with the large genome similarity among the European white oaks, would argue in favor of the assumption. Indeed, linkage maps from Q. petraea and Q. robur show some non-linear relationships (for example, Bodénès et al., 2012), but we believe their most likely explanation is variation in cross-over rates among different crosses and among male and female individuals. Furthermore, even if the two Mediterranean oaks would show some micro-synteny and collinearity differences, these would become almost irrelevant on the basis of the LD results (see below).

Haplotypic analyses were also performed on the pure-species data set. LD was first analyzed genome-wide with the aid of score tests for association (Schaid et al., 2002) between haplotypes and the species genetic assignments (that is, as indicated by STRUCTURE results). The score tests are an extension to the trend in proportions tests (Armitage, 1955), which are commonly used to compare haplotype frequencies between cases and controls in association studies (Devlin and Roeder, 1999). The analyses were performed using the ‘haplo.stats' library (Sinnwell and Schaid, 2009) under the R environment (R Development Core Team, 2011). For each LG, we obtained 10 000 maximum likelihood estimates of the haplotype reconstructions using a modified expectation-maximization algorithm (Excoffier and Slatkin, 1995; Schaid et al., 2002) and the solutions with the largest likelihoods were retained for further analyses. Score tests were obtained for consecutive two-marker haplotypes from the 12 LGs with the function ‘haplo.score.slide', which uses a sliding-window approach. For this analysis, we used several thresholds of minimum haplotype counts (8, 10, 12 and 15, depending on the LGs), which should avoid introducing bias because of rare haplotypes. We also used the sliding-window approach with consecutive three-marker haplotypes to further characterize the LD patterns in two LGs displaying divergent ecological quantitative-trait loci (QTLs) in the vicinity of outlier clusters (LG2 and LG12). In such instances, the minimum haplotype counts permitted in the analyses had to be lowered to 5 and 6, respectively. Finally, we used the function ‘haplo.score' to investigate whether highly significant associations were caused by haplotypes being associated to one or both species. For this analysis, we used minimum haplotype counts of 10.

Fine-scale LD was analyzed within species and LG with MIDAS v.1 (Gaunt et al., 2006), a software package providing both numerical estimates and graphical representations of all inter-allelic associations for multiallelic markers. MIDAS uses an expectation-maximization algorithm (Hill, 1974) for two-marker haplotype inferences; it takes into account the sign of the observed inter-allelic disequilibria; that is, whether D′ is larger or smaller than 0 (D′_ij=D_ij/D_max and D_max=min [p_i(1−q_j),(1−p_i)q_j] when D_ij>0 or D_max=min [p_iq_j,(1−p_i)(1−q_j)] when D_ij<0), and it uses a Pearson's chi-square to test the significance of the null hypothesis of random association (D_ij=0) between pairs of alleles at the two loci (Zapata et al., 2001). Yate's continuity correction was applied to all significance tests, although we are aware of its tendency to overcorrect (Sokal and Rohlf, 1981). Therefore, we also provided the original Pearson's tests, with the true significances probably lying somewhere in between. LD was also computed among markers from different LGs that contained outlier clusters, as inter-allelic associations among alleles from different clusters could characterize ecological speciation, at least in some organisms (Hohenlohe et al., 2012).

Results

Population structure and differentiation

This section is fully described in Supplementary File 3. Here, we provide the main results only. Evidence for null alleles affected all 16 sampled populations and 35 out of the 98 markers. However, significant effects of null alleles' frequencies on the bulked interspecific F_ST estimates were restricted to very few markers (Supplementary Figure S3-1). The Bayesian clustering method classified the samples in two groups that corresponded to the phenotypic species (Supplementary Figures S3-2 and S3-3), although approximately 10% of the trees showed evidence of admixture (contemporary gene flow). Heterozygosity (He) and AR were similar in both species, with di-nucleotide SSRs showing much larger values than tri/hexa-nucleotide SSRs (Supplementary File 2). Differentiation levels varied broadly between the two parameters used to estimate it (D and G_ST) and among markers (Supplementary Figures S3-4 and S3-5). However, both parameters indicated a genome-wide interspecific differentiation, with only 9 out of 98 markers showing nonsignificant differentiation between the two oak species (their confidence intervals included 0). Differentiation among populations, within species, was very low for both species. However, the weighted average over loci F_ST was significant in Q. faginea.

Signals of recent demographic events

Estimated values of the T₂ statistic suggested recent population expansions in both oak species (Supplementary File 4, Supplementary Table S4-1). The results did not vary when di- or tri/hexa- nucleotide SSRs were analyzed separately. The only exception concerned the analysis of the tri/hexa-nucleotide SSRs from Q. pyrenaica assuming 70% stepwise mutations, as the nonsignificant Wilcoxon ranked test suggested a constant size population under mutation-drift equilibrium. The hypothesis of recent population expansions in these two oak species is also supported by known historical events concerning human populations (see ‘Confounding effects on neutrality testing'). On the other hand, the imbalance index estimates (lnβ) were negative in all cases (Supplementary Table S4-2), suggesting that both oak species were at mutation-drift equilibrium before the expansions took place.

Identification of selection outliers

The Bayesian multilocus scan detected four balancing selection outliers, two of them on different chromosome bins from LG2 (WAG032 and ZQP104) and one each in LG4 and LG5 (POR029 and VIT021, respectively). Furthermore, four markers from different LGs (LG #2, 3, 8 and 12) were detected as positive selection outliers. Supplementary Figure S5-1 summarizes the BAYESCAN results for markers with di- and tri/hexa-nucleotide repeat motifs separately.

Multilocus scan tests based on the differences in the observed numbers of repeats and heterozygosities (lnRV, lnRH), were conducted initially with the subset of 69 evenly spaced markers. Eight markers distributed on six bins from five LGs (LG #2, 3, 8, 11 and 12) were identified as candidates for divergent selection, or hitchhiking effects caused by nearby divergent selection (boxed and in regular type in Figure 2, filled circle outliers in Supplementary Figures S5-2a and S5-2b). From those, two markers (VIT031.1 and PIE202) contained a large number of null alleles that biased their F_ST estimates (Supplementary Figure S3-1) and possibly caused false positives in the lnRH test. The genotyping of 29 additional markers, selected from the five chromosome bins harboring the rest of the outliers, resulted in six additional outliers from four different bins (boxed and in bold type in Figure 2, open circle outliers in Supplementary Figures S5-2a and S5-2b). Overall, these results suggest that positive selection outliers are clustered within the genome.

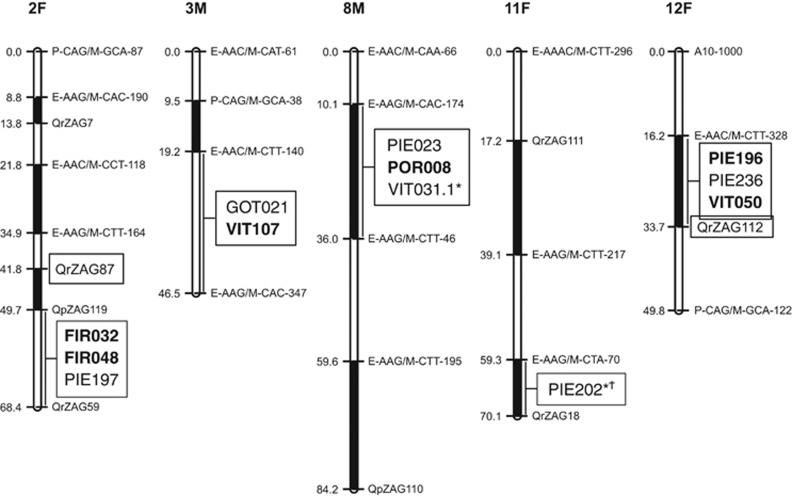
Figure 2.

Positions of the divergent selection outliers (boxes) detected by the lnRV and lnRH tests, in the LGs of the oak bin maps (F, female bin map; M, male bin map). Outliers from the initial multilocus scan with 69 markers are in regular type, whereas outliers from the 29 additional markers selected from bins known to contain at least one outlier are in bold type. The asterisks (*) designate markers with a high frequency of null alleles. The cross (†) indicates that the PIE202 bin was not genotyped with additional markers. Bin limits and markers at their edges as in Durand et al. (2010).

Contrary to classical results from genome scans with single-nucleotide polymorphism data (for example, Andrew and Rieseberg, 2013), not all the SSR outliers in our work belong to the top-rank values of the G_ST (or F_ST) distribution. The BAYESCAN and lnRH outliers fit rather well to this expectation (Supplementary Figures S5-1 and S5-2b), as only two bi-allelic hexa-nucleotide SSRs show larger F_ST values than the outliers (note that VIT031.1 and PIE202 probably are false positives). However, lnRV outliers often showed low F_ST values (Supplementary Figure S5-2a). This was not a surprising result. Indeed, it could be anticipated on the basis of the small effects that the gain/loss of rare alleles has on F_ST. Outliers did not belong to the top-rank values of the D distribution either, which can be explained by the lack of relationship between D and F_ST for markers with high heterozygosity.

Haplotype analyses: genetic association and LD

A composite linkage map was constructed (Figure 3), on the basis of the existing Q. petraea and Q. robur linkage maps, using a newly developed map merging approach (Endelman and Plomion, 2014). The composite map contains just the markers used in this study plus LG ends, which should help to clarify the relative positions of the markers on a single reference map. The first results obtained from this map were the positions of several non-outlier markers dispersed within the outlier clusters, a result that can be explained by the DH hypothesis as ancestral shared polymorphisms (Smadja et al., 2008; Via, 2012; Via et al., 2012).

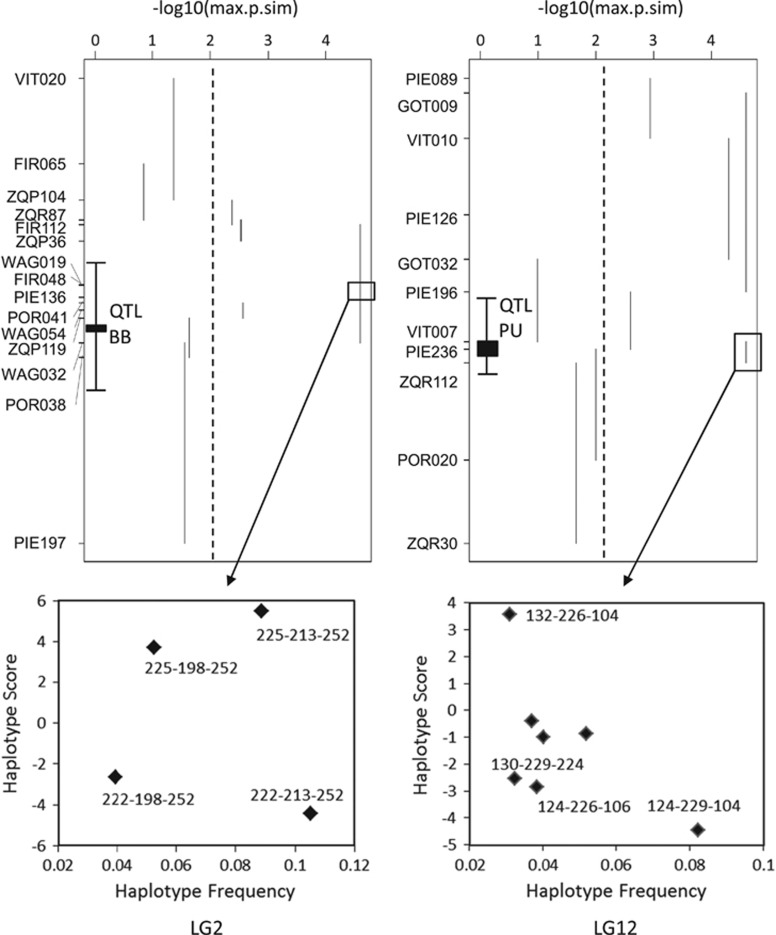
Figure 3.

Score tests for association between consecutive two-marker haplotypes and the binary character ‘species' (sliding-window analysis). The plots to the right of each LG show the association P-values (logarithmic scale) for each segment. The dotted lines mark the significance limit (P=0.01). Probabilities equal to 0 were arbitrarily assigned logarithmic values of 5.5 (should be ∞). Bold type markers correspond to positive selection outliers, whereas balancing selection outliers were identified with an asterisk. LG ends that were not genotyped in our study (markers with smaller font size) have been included for reference.

Approximately 60% of the markers were at Hardy–Weinberg disequilibrium within each species (Supplementary File 2), potentially hindering LD and genetic association estimates. However, the two common LD statistics D and r (and hence D′ and r²) can be approximately estimated without assuming random mating (Rogers and Nuff, 2009). Based on this premise, the score tests from two-marker haplotypes showed a large degree of significant associations (Figure 3). Significant score tests were not restricted to the vicinity of positive selection outliers, but they often extended to whole LGs (LGs #1, 6, 7 and 12), even if some of them did not contain any outliers. Several LGs showed large stretches of significant and nonsignificant associations (LGs #2, 3, 8 and 11). By contrast, LGs #5, 9 and 10 only showed weak associations, whereas LG4 did not show any significant association. Overall, the LD/association analysis suggested a genome-wide differentiation between the two Mediterranean white oaks, although substantial variation within LGs and across the genome was also observed.

Score tests with haplotypes composed by growing number of markers should help to delimitate the regions where LD is highest and therefore the likely regions under selection (Sinnwell and Schaid, 2009). Score tests for three-marker haplotypes (Figure 4) showed one peak of highly significant associations centered on the outlier FIR048 in LG2, close to a prominent bud burst QTL. Two distinct peaks were observed in LG12, one of them centered around the outliers ZQR112-PIE236, in the region corresponding to a pubescence QTL, and the other in a large region without outliers. Three-marker haplotype-specific scores showed that different haplotypes were significantly associated to both species (Figure 4), thus suggesting true divergent selection.

Figure 4.

Score tests for association between consecutive three-marker haplotypes from LG2 and LG12, and the character ‘species'. The association P-values (logarithmic scale) are shown by vertical lines spanning the positions of the three-marker haplotypes. Dotted lines show the significance limits (P=0.01). Probabilities equal to 0 were assigned logarithmic values of 4.5 (should be ∞). Markers on the Y axes were placed according to genetic distances in the composite map. The positions of the bud burst (BB) and pubescence (PU) QTLs were approximately projected into the SSRs map with the aid of shared markers. The two bottom charts show three-marker haplotype-specific scores from two regions that contain outliers, QTLs involved in ecological divergence and highly significant associations: WAG019-FIR048-PIE136 (LG2) and VIT007-PIE236-ZQR112 (LG12). Positive and negative scores indicate associations to Quercus faginea and Q. pyrenaica, respectively; whereas labeled haplotypes show significant associations.

Fine-scale LD analyses indicated rather generalized significant inter-allelic associations, even among markers located far apart within LGs, both with and without Yate's continuity correction (Supplementary File 6, Supplementary Figures S6-1 and S6-2, respectively). Indeed, Yate's correction drastically diminished the number of alleles at disequilibrium, but long-distance LD remained in most LGs from both species. LD among markers located on different LGs harboring outlier clusters (LG #2, 8 and 12) showed several associations among outliers located on different chromosomes (Supplementary File 7,Supplementary Figures S7-1 and S7-2, for analyses with and without Yate's correction, respectively). However, such results did not indicate preferential LD among the outliers. In fact, non-outlier markers from different LGs often showed more significant inter-allelic associations than the outliers themselves (that is, LG2-LG8 in Supplementary Figure S7-1).

Discussion

The number of markers used in this study is small compared with the capabilities of current next-generation sequencing technologies (see Nosil and Feder, 2012; Narum et al., 2013; and references therein) and the resulting landscapes of differentiation are rather coarse. However, SSRs have some virtues that may counterbalance the difficulty to genotype a large number of markers in a large number of individuals, as well as their homoplasy-related problems. Thus, SSRs can carry selection footprints affecting both the heterozygosity and the allelic variance, whereas bi-allelic markers can only show selection signatures affecting heterozygosity. On the other hand, the large number of alleles has advantages for LD analysis and associated micro-evolutionary inferences. Further, the time to the most recent common ancestor in coalescent simulations could be longer for SSRs than for bi-allelic markers under selection, which could have impacts on the age of the events that can be inferred from both types of markers.

In the following sections, we first tackle possible confounding effects on neutrality tests and discuss several evolutionary causes for the extensive LD observed in our data. Then, we relate the observed LD patterns to signatures of either DH or GH, while addressing several concerns arising in the ecological speciation literature (Hendry, 2009; Faria et al., 2013). These include the suitability of old radiations to analyze ecological speciation, the occurrence of repeated evolution and, most importantly, the establishment of the link between divergent adaptation and reproductive isolation. Indeed, other steps would be needed to draw unequivocal evidence of ecological speciation (that is, functional analysis or experimental manipulation). However, we show that our results are largely consistent with expectations from ecological speciation.

Confounding effects on neutrality testing

Demographic histories, the trajectories of populations over time, have a profound impact on selection inferences (Wall et al., 2002; Tenaillon et al., 2004; Thornton and Andolfatto, 2006; Tenaillon et al., 2008). The analysis of the demographic scenario showed evidence of recent population expansions, a hypothesis that is supported by the abandonment of traditional uses brought upon by the industrial revolution and the resulting population growths experienced by these oaks (Valbuena-Carabaña and Gil, 2013). Population expansions carry the risk that neutral mutations arising in the front of a wave of expansion accumulate to high frequencies, thus leading to false positives (Excoffier and Ray, 2008). However, the clustering of outliers observed in our data (Figures 2 and 3) suggests that neutral mutations had no such impact in our study.

False positives concerns have led to continuous improvements in genome scanning methods, such as accounting for population structure (Excoffier et al., 2009), or the use of formal tests to distinguish outliers from non-outliers in Bayesian frameworks (Foll and Gaggiotti, 2008). Despite such advances, there is no clear indication of best practices, at least when SSRs are used. The assumptions underlying the different scanning methods can result in distinct power to detect selection footprints from diverse sets of scenarios (Beaumont, 2005). Furthermore, the scanning methods have been mostly designed to detect selection signatures affecting heterozygosity, hence F_ST, whereas selection footprints on microsatellite loci can affect both the heterozygosity and the gain/loss of rare alleles. Summarizing differences in allele frequencies among populations with F_ST puts too much emphasis on heterozygosity, which is little affected by the gain/loss of rare alleles. Therefore, using a neutrality test based on the genetic variance can be essential to exploit SSRs information on selection signatures. In this study, it was re-assuring that three out of four positive selection outliers detected by the coalescent-based approach implemented in BAYESCAN were also identified as outliers by the lnRV-lnRH tests. In comparison, only one out of the nine outliers detected with the lnRV test was also detected with BAYESCAN. Note that we do not expect F_ST-based genome scan methods can detect such genetic variance outliers, except if a drop in heterozygosity accompanied the loss of rare alleles (such as we observed for ZQR112). On the other hand, the lnRV test detected at least twice as many outliers as either lnRH or BAYESCAN. This could be related to the larger variances of the lnRV than the lnRH estimates (Kauer et al., 2003), but it could also reflect the large mutation rate of microsatellites. Thus, the heterozygosity drop caused by divergent selection should recover fast under the large mutation rates characterizing SSRs, whereas the loss of rare alleles footprint should last longer and can be used, therefore, to infer older events. Some indication this could be the case comes from the mixtures of lnRV and lnRH outliers in three out of four outlier clusters, which makes difficult to support the large variances of the lnRV estimates resulted in false positives.

A final confounding source is brought by the coupling hypothesis (Bierne et al., 2011), a mechanism that can cause failure to detect local adaptation outliers because of the coupling of neutral genes with genes responsible for clines formation. However, the coupling hypothesis would only impact the discovery of the actual genes under selection, whereas the goal of identifying chromosomal regions containing outlier clusters would not be affected. Moreover, the range-wide sampling strategy implemented in our study, including different environments and forest structures (Supplementary File 1), was designed to enhance the detection of globally divergent genes, while losing power to reveal within-species variation. Thus, our sampling strategy should avoid complications derived both from the coupling hypothesis and from differential introgression with other species of the same evolutionary radiation (Gosset and Bierne, 2013).

Evolutionary causes of long-distance and background LD

LD was unexpectedly high in our study, with extensive and long-distance LD among genetic markers from the same LGs, and background levels of LD among markers from different LGs. This pattern is similar to a recent survey of the genome-wide LD among next-generation sequencing markers in the model species Gasterosteus aculeatus (Hohenlohe et al., 2012). Similarities between the two studies extend to the large fecundity and elevated effective population sizes of oak and stickleback populations, which should favor low LD or even its absence. Some differences between the two studies are the directionality of speciation in the sticklebacks (from marine toward freshwater populations) and the demographic histories of both groups of species.

Stochastic evolutionary processes seem most appropriate to explain extensive LD patterns, as they affect all the genome similarly. Gene flow and admixture, including mixing of populations, is one of the main candidates to explain our results. Theoretical work predicts that if selection maintains allele frequencies differences at several loci in different populations, or if drift caused populations to differentiate, then gene flow would result in significant LD (Nei and Li, 1973; Ohta, 1982; Slatkin, 2008). This is a likely scenario for populations/species having gone through repeated sequences of expansions and retreats during the glacial cycles. However, the Bayesian clustering did not find any significant inter-population differences in our data (Supplementary Figure S3-3). In spite of this, the increased number of markers with significant inbreeding coefficients (F_IS) in the bulked data (Supplementary Table S2) compared with the individual populations (Supplementary Table S3-1) suggests that mixing of populations could contribute, to some extent, to the observed LD patterns. For that reason, we also measured inter-population differentiation, within species, with a hierarchical analysis of molecular variance (Supplementary Table S3-2). Fixation index estimates from such analyses should have large sampling variances and coefficients of variation as a consequence of the small number of individuals sampled per population, although the large number of loci used in our study should compensate, to a certain degree, their precision (Kalinowski, 2005). Therefore, we expect average within-species F_ST should not depart greatly from Supplementary Table S3-2 estimates. We observed a significant differentiation only among Q. faginea populations, which in principle could increase background and long-distance LD levels in this species. However, the similarity between the LD patterns from both species would argue that mixing of differentiated populations cannot be the only cause for the observed LD patterns.

Selfing and small population sizes create inbreeding and could potentially raise the LD estimates. However, the elevated outcrossing rates observed in the oaks (Ritland et al., 1995; Bacilieri et al., 1996; Sork et al., 2002), together with the large effective population sizes caused by wind pollination (anemophily), suggest inbreeding is small in our study system. On the other hand, null alleles affect the inbreeding coefficient (F_IS) and we cannot discard their impact on LD even if null alleles rarely affected the F_ST estimates, an issue that remains to be explored.

A demographic history of current or pre-expansion bottlenecks could also contribute to extended LD patterns (Wall et al., 2002; Wang et al., 2004; Tenaillon et al., 2008). However, our data are not compatible with such models (Supplementary Tables S4-1 and S4-2). The recurrent bottleneck expansion model (Schaper et al., 2012), which is well suited to the demographic history of the European flora during the Quaternary, can be also excluded because it should have an impact on the imbalance index estimates that we did not observe. Thus, our results suggest that bottlenecks were not strong enough to drastically affect population sizes, or that the expansion periods were long enough to recover mutation-drift equilibrium.

Indeed, there are other evolutionary mechanisms that could explain extended LD patterns (such as segregating chromosomal rearrangements, Rieseberg, 2001; Hoffman and Rieseberg, 2008; or epistatic selection linked to post-zygotic reproductive barriers, Coyne and Orr, 2004; Presgraves, 2010; Janoušek et al., 2012 and so on), but all of them are speculative in relation to our data. Consequently, we prefer to leave this question open. On the other hand, the background LD suggests caution is needed for interpreting the association study and the LD patterns. For that reason, we discarded low-frequency haplotypes in the association analyses and used the Yate's over-correction in the fine-scale LD study. These measures seemed to produce the expected outcome, as the parallelism observed between the multilocus scans and the association profiles strongly argue that background LD had not undesirable effects in our study.

Looking at the genetic mosaic of speciation through the LD lens

Current knowledge of the European white oaks microevolution has increased rapidly during the last decade. In particular, genes and/or QTL responsible for divergent ecological adaptations have been mapped and characterized (Saintagne et al., 2004; Porth et al., 2005: Parelle et al., 2007; Brendel et al., 2008; Roussel et al., 2009; Le Provost et al., 2011), reproductive isolation barriers have been analyzed in detail (Gailing et al., 2005; Abadie et al., 2012; Lepais et al., 2013) and long-range haplotypic LD, a mechanism capable of physically linking both types of genes, seems to be the rule around putatively selected loci (Goicoechea et al., 2012). These are the three basic requirements for ecological speciation (Rundle and Nosil, 2005; Nosil, 2012), although other speciation types may also be possible for these oaks. Ecological character displacement after secondary contact can be probably ruled out, because sympatric population pairs usually show similar or lower phenotypic differentiation than allopatric pairs. However, non-adaptive diversification may have had an important role in this evolutionary radiation, at least in the origin of the allospecies (sensu Amadon, 1966) found in the three southern European peninsulas, or during the long bottleneck periods corresponding to glaciation cycles. Furthermore, homoploid hybrid speciation seems the most likely origin of some oak species (for example, Quercus subpyrenaica; Himrane et al., 2004), and other types of reticulate evolution cannot be discarded. Therefore, we analyzed the LD patterns to search for genomic footprints that could shed light on the evolutionary history of the two oak species targeted in this study.

Clustering of differentiation outliers

Clustering of F_ST outlier loci around QTLs that are involved in ecologically based reproductive isolation was first quantified by Via and West (2008), who estimated that DH regions could reach 20 cM within the genome of the pea aphid Acyrthosiphon pisum. Later studies involving other species pairs, together with next-generation sequencing markers, apparently failed to find the outlier clusters (for example, in threespine sticklebacks by Hohenlohe et al., 2010; in manakins by Parchman et al., 2013); or their patterns were interpreted as opposed to DH expectations (for example, in sunflowers by Renaut et al., 2013). However, the threespine stickleback data were reinterpreted by Via (2012) to support the existence of DH regions in such species, and a similar reinterpretation could be likely made for the other studies.

Our sampling of genetic markers from the genomes of the two Mediterranean white oaks was specifically designed to identify outlier clusters, as we eventually did (Figures 2 and 3). The proportion of outliers found among the markers selected from bins known to carry at least one outlier almost trebled the proportion of outliers detected during the initial random sampling (6/29=0.21 vs 6/69=0.087; considering VIT031.1 and PIE202 were false positives), thus confirming the utility of our two-step procedure. Outlier clusters from Q. faginea and Q. pyrenaica spanned at least 10 cM on LG2 and LG12, although the clusters could be longer because two additional outliers (FIR032 and VIT050) could not be placed within the composite map although they belong to the appropriate bins from LGs #2 and 12 (Figure 2). Our approach to cluster detection was necessarily different from the (quasi)-random sampling of the genomes made possible by high-throughput genotyping or genome re-sequencing (see Nosil and Feder, 2012; Narum et al., 2013). Therefore, the cluster definitions need to take into account the different scales of genome coverage if comparisons between both types of studies are to be made. Data from Renaut et al. (2013) clearly illustrate this issue, as the 0.3–0.6 cM outlier clusters from their study must be different to the 20 cM clusters used to define DH (Via and West, 2008; Via, 2009) and the 10 cM clusters found in this study. One concern regarding outlier clusters is co-variation among linked loci (Nosil and Feder, 2012; Faria et al., 2013). We rejected the view that co-variation could be an issue in our data, even if we did not carry out a formal test to examine it. There are two reasons that support such a conclusion. First, clustered outliers contain markers with different selection signatures (heterozygosity deficiency versus rare alleles' differences). We do not expect co-variation among markers from these two classes because the gain/loss of rare alleles has little effect on heterozygosity. Similarly, non-outlier markers interspersed among outliers should not present co-variation with F_ST outliers because they are not affected in their heterozygosities.

Relationship between outliers clusters and DH regions

Inferring whether the outlier clusters from the two Mediterranean oaks truly represent DH regions is not straightforward. First, the age of our study system can make us wonder whether outliers represent divergent selection regions, or whether they signal to recent selective sweeps from either species because of local adaptations. Once this is solved, we need to establish a link between ecological divergence and reproductive isolation, either by (i) demonstrating the existence of an ecologically divergent gene with pleiotropic effects on reproductive isolation; or (ii) demonstrating the existence of two linked genes, one responsible for ecological divergence and the other causing reproductive isolation (Schluter, 2000; Nosil, 2012).

Several reasons suggest that outliers are not footprints of recent sweeps within each species, but they were caused by divergent selection (selection acting on both species simultaneously, in different directions). First, the patterns of LD around outlier loci are similar in both species (high LD) and score tests show certain haplotypes are significantly associated to each species (Figure 4). On the contrary, LD and association footprints from a recent selective sweep for local adaptation would affect one species only. Second, three outlier clusters are involved in repeated evolution within the genus Quercus. Thus, the nSSR ZQR87 (in LG2) is also involved in the divergence between the European temperate white oaks Q. petraea and Q. robur (Goicoechea et al., 2012). Two other markers, the nSSR ZQR112 (in LG12) and the EST-SSR GOT021 (in LG3), were identified as positive selection outliers between pairs of species from three different botanical sections within the genus Quercus. ZQR112 is highly differentiated between two different species pairs within the white oaks, section Quercus (Q. petraea-Q. robur, Scotti-Saintagne et al., 2004b; and Q. faginea-Q. pyrenaica, this study) and between two species from the section Ilex (Q. alnifolia-Q. coccifera; Neophytou et al., 2011). GOT021, on the other hand, has been detected as an outlier in the section Quercus (this study) and in the North American oaks, section Lobatae (Q. ellipsoidalis-Q. rubra; Lind and Gailing, 2013). In the two instances that we were able to analyze the LD patterns around such outliers, ZQR87 and ZQR112 in the temperate oaks Q. petraea-Q. robur, we found that haplotypes were also associated to both species, thus suggesting selection at/near those markers was divergent too (Goicoechea et al., 2012). Such repetitive patterns between-species pairs with different evolutionary trajectories suggest the action of multiallelic genes involved in reproductive isolation, such as those causing crossing incompatibilities. Third, the range-wide sampling strategy in our study should avoid detecting outliers from recent local adaptations, unless a global selective advantage allows their fast spreads throughout the species ranges. Finally, the long outlier clusters associated with divergent QTLs (see below) and the presence of non-outliers within the clusters seem better explained by divergent selection than by recent sweeps in either species.

Colocalization of outliers and ecologically relevant QTLs is considered an integrative approach for linking ecological divergence to reproductive isolation (Rogers and Bernatchez, 2007; Via et al., 2012; Faria et al., 2013). There is no genetic or QTL maps from the two Mediterranean oaks tackled in this study. However, macro and micro-synteny within the European white oaks should allow the use of the QTL maps from Q. petraea-Q. robur to draw conclusions about some characters that may be involved in the speciation of the two Mediterranean oaks. LG2 outliers found in this study colocalize with one of the two most important QTLs for bud flush (Saintagne et al., 2004; Scotti-Saintagne et al., 2004a; Derory et al., 2010), which is maintained in several crosses (Gailing et al., 2005). Bud flush in oaks is an adaptive ecological trait that is entirely correlated with flowering time (Duccousso et al., 1996) and has pleiotropic effects on pre-zygotic reproductive isolation via assortative mating (Savolainen et al., 2006). Thus, the LG2 region seems to bear all the requirements for DH: an ecologically divergent QTL with pleiotropic effects on reproductive isolation and a cluster of outlier markers.

On the other hand, LG12 outliers colocalize with a QTL for leaves pubescence (Saintagne et al., 2004). Leaves differences from the two Mediterranean oaks have an obvious ecological meaning, as the small, cuticle-bearing leaves from Q. faginea are an adaptation to dry environments, while the large, pubescent leaves from Q. pyrenaica offer better adaptation to mountain conditions. A second gene causing reproductive isolation that were physically linked to the QTL, or else an unlikely pleiotropic effect of pubescence on reproductive isolation, would be needed to infer ecological speciation, and therefore DH, in this LG (Schluter, 2000; Nosil, 2012).

Interestingly, the association patterns observed in Figure 4 point toward the involvement of a single chromosomal region in LG2 divergence, coincident with the outliers cluster and the phenology QTL. This result fits to the hypothesis of a single gene with pleiotropic effects on ecological divergence and reproductive isolation on LG2; although the presence of two linked genes cannot be discarded. Association patterns from LG12 three-marker haplotypes, on the other hand, showed two regions with highly significant association scores (Figure 4). One of such regions is coincident with the outliers cluster and the pubescence QTL, relating it to ecological divergence. The other region has not been associated to outliers nor QTLs, but it should contain a gene involved in reproductive isolation in order to infer ecological speciation in this LG. We do not have any evidence of the existence of such gene(s) yet, but the draft sequence of the European white oaks genome that is being prepared for release (Plomion et al., in preparation) will help to solve such doubts.

Haplotype differentiation unlinked to outliers

Indirect genome-wide effects of divergent selection on inter-groups divergence have become known as ‘GH' (Feder et al., 2012b). GH is caused by genome-wide effects of divergent selection on the effective number of migrants, and its magnitude is proportional to the survival probability of the migrants, their mating success, and the survival probability and the mating success of the F1. These terms have multiplicative effects and their product depresses gene flow equally across the entire genome (Via, 2009, 2012).

Score tests for association allowed us to analyze the landscapes of differentiation from all 12 oak LGs on the basis of two-marker haplotypes, even if it was at coarse resolution (Figure 3). Such landscapes point toward a general genomic divergence that seems largely independent from outlier loci. In fact, the long regions of haplotype differentiation we observed across entire LGs that did not show any evidence of positive selection outliers (LG1, LG6 and possibly LG7) strongly argue in favor of a mechanism like GH. This result illustrates the power of LD for analyzing the genetic mosaic of speciation, as obtaining a similar conclusion from single marker analyses would require genotyping a very large number of markers.

The different evolutionary mechanisms involved in the formation of DH and GH regions suggest they could have different impacts on the landscapes of differentiation. In terms of selection signatures, DH accounts for divergence coupled to selective sweeps within populations, whereas GH accounts for divergence by drift. This can be related to the parameters used to measure differentiation in the following way. Jost's D accounts for divergence (populations/species moving toward different alleles), whereas the fixation index G_ST (or F_ST) accounts for divergence that exhibits selective sweeps within populations (reduced within-population diversity). Thus, a discrepancy between D and G_ST would suggest strong between-group divergence and weak within-group selection intensity, whereas congruence between D and G_ST would insinuate strong selection both between and within groups. Then, one may wonder whether discrepancies between D and G_ST could be a signature of GH, whereas congruence between D and G_ST may witness DH.

Mathematically, D is defined as:

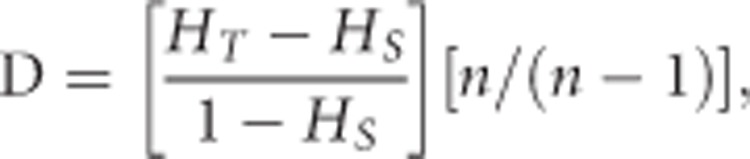(equation 11 in Jost, 2008)

which can be written in terms of G_ST as

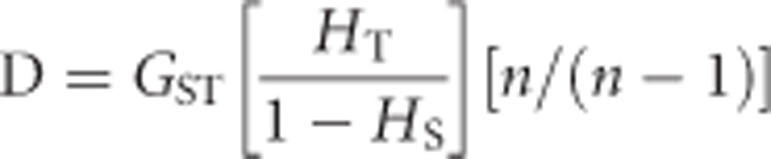If H_S is low (that is, selective sweeps within populations) and n=2 (as in our study system), then

Therefore, for D being similar to G_ST, H_T should be approximately 0.5, which is the total heterozygosity (H_T) for two sub-populations fixed at a different allele each. Indeed, the relationship holds for larger values of n, as the product of the second and third terms of the right-hand side of the equation will always be 1 when each population is fixed at a different allele (and their sampling sizes are equal). This relationship also shows that when H_S=0, D=G_ST=1.

The pair-wise comparisons between the D and the G_ST values from the markers analyzed in our study failed to show such a clear trend (Supplementary Figure S3-6). Positive selection outliers only showed similar D and G_ST estimates at low differentiation values (PIE197, PIE023 and POR008), the only exception being marker GOT021 that had similar D and G_ST values for a differentiation >0.2. Differences between the two estimators were intermediate for another five divergent selection outliers (ZQR87, VIT107, PIE236, ZQR112 and VIT050), and they were rather large for the last three (FIR048, FIR032 and PIE196). On the other hand, the long regions of haplotype differentiation unlinked to outlier loci (LG# 1, 6 and 7) showed some very different D and G_ST values, but they also showed some similar ones (for example, FIR040 on LG1, POR024 and POR027 on LG6, and FIR030 and VIT009 on LG7). Such deviations are not unexpected in our system, as the simple model outlined above could be affected by several factors, such as the ages of the selected alleles (or the age of the study system), the levels of standing variation, or differences in the mutation rates among SSRs. Indeed, it would be interesting to test if our hypothesis holds in model systems from younger evolutionary radiations.

Overall, our data and interpretations appear consistent with sympatric ecological speciation. However, ecological speciation can commence within dozens of generations (Hendry et al., 2007), which raises the need to take into account the length of the speciation events in the European white oaks for a thorough interpretation of the results. If the European white oaks radiation occurred during the early Pliocene, as it is suggested by recent phylogenetic data (Hubert et al., 2014), our study system must have undergone >4 million years and approximately 1–1.5 × 10⁵ generations of incomplete reproductive isolation. During this time, there have been multiple cycles of population expansions and retreats that offered ample opportunities both for secondary contacts and allopatric speciation, as well as for changes in the rates of intraspecific migration and drift. Thus, it becomes very difficult to ascertain whether the genetic mosaic of speciation is the result of ecologically driven reproductive isolation, or whether co-adapted genetic backgrounds have co-existed through the multiple cycles of the Quaternary glacial history (Bierne et al., 2013). It is also possible that a two-phase sequence (allopatry followed by sympatry or parapatry) may be particularly conducive to ecological speciation (Rundle and Nosil, 2005; Grant and Grant; 2008), or that different geographical contexts may reinforce each other, even multiple times, during the course of ecological speciation (Feder et al., 2005). Pushing this line of thinking a little further, the chances are that most radiations contain episodes of adaptive and non-adaptive diversification (Rundell and Price, 2009) and that different speciation types may reinforce each other for the acquisition of intrinsic and extrinsic reproductive barriers.

Conclusions

Our study highlights the possibility to analyze selection footprints in the genetic mosaic of speciation from an old evolutionary radiation, by using the LD patterns among a sparse set of genetically mapped EST-SSRs and other mapping resources. Outlier loci signaled the regions with positive selection footprints and LD patterns indicated that selection was divergent (affects the two species in different directions). Colocalization between outliers and ecologically divergent QTLs suggested that divergent selection may be ecologically driven. Finally, we were able to provide the link between ecologically driven divergent selection and reproductive isolation, at least in one case. Flowering phenology is an ecological character probably under divergent selection in our study system and causes pre-zygotic isolation via assortative mating.

Our study challenges the points of view suggesting that old radiations are not appropriate to study ecological speciation because early footprints of divergent selection would disappear within a growing differentiation background. We have shown that our strategy to sample the genome is appropriate to find outlier clusters, which are expected to contribute to DH. Furthermore, we also found long regions of single marker and haplotype differentiation unrelated to outlier loci, which insinuated the action of GH. Finally, the different evolutionary forces involved in the formation of DH and GH regions, allowed us to relate them to the similarity/differences between the fixation index (G_ST) and an absolute differentiation measurement (D). Our data are fully consistent with expectations from the ecological speciation theory. However, other evolutionary scenarios are possible, especially complex ones, which could create similar LD patterns in the genetic mosaic of speciation.

Data archiving

The data used in this study are available at the Dryad Digital Repository doi:10.5061/dryad.np29h. We will also make them available at the Quercus Portal website https://w3.pierroton.inra.fr/QuercusPortal/.

The authors declare no conflict of interest.