Abstract
The evolution of mate choice is a function of the heritability of preference. Estimation in the laboratory is typically made by presenting a female with a limited number of males. We show that such an approach produces a downwardly biased estimate, which we term the heritability of choice. When preference is treated as a threshold trait then less biased estimates are obtained particularly for preferences based on the relative value of the preferred trait. Because females in the wild typically survey on average less than five males we argue that the heritability of choice may be more meaningful than the heritability of preference. The restricted number of males surveyed can lead to a reduction in the phenotypic variance of the preferred trait in the group of males selected by the females if the phenotypic variance in preference is equal to or less than the phenotypic variance in the referred trait. If the phenotypic variance in preference exceeds that of the preferred trait then the opposite occurs. A second effect of the restricted number of males sampled is that females are likely to mate initially with males that are not the most preferred. The failure to find the most preferred male may account for the common observation of multiple matings and extra-pair copulations. We suggest that current explanations for polyandry need to take this failure into account.
Introduction
While the idea of sexual selection dates back to Darwin, the quantitative assessment of its evolution with respect to mate preference really began with Fisher (1930) and was developed more fully in the framework of quantitative genetics by Lande (1981). Lande's model and subsequent quantitative genetic models for the evolution of female preference assume that a female has access to the entire male population with no limit to the number of males that can be sampled before a choice is made (Lande, 1981; Kirkpatrick, 1982; Nichols and Butlin, 1989; Pomiankowski and Iwasa, 1993). In these models, a female with preference x inspects males and mates with a male with trait y with some probability, given by the preference function, P(y|x). An alternative model follows the same rule except that the female's probability is modified by the average male trait value, generating a relative preference.
In both cases, there is a second parameter which Lande calls ‘tolerance' that modulates the width of the preference function and which Gray and Cade (1999) call ‘choosiness'. In his analysis, Lande (1981) assumed that preference was a heritable trait whereas choosiness was not. Note that this theoretical definition differs from that of Jennions and Petrie (1997, p286) who define ‘choosiness' more loosely as ‘the effort or energy that an individual is prepared to invest in assessing mates, in terms of both the number of mates sampled and the amount of time spent examining each mate.
The evolution of preference in these models is determined in part by the heritability of preference, which has an important role through its influence on the likelihood of Fisher's runaway process (Lande, 1981) and through its effect on the genetic correlation between preference and the preferred trait, which in turn determines the rate of coevolution between these two traits (Kirkpatrick and Barton, 1997; Roff and Fairbairn, 2014).
Whereas numerous studies have examined what traits are preferred (Gibson and Langen, 1996), few have estimated the heritability of preference (Table 1; Wagner, 1998; Schielzeth et al., 2010). In these studies, the authors almost invariably use the term ‘preference' for the parameter measured, but the terms ‘responsiveness' (Collins and Carde, 1989, 1990) or ‘choice' also appear (Rodriguez and Greenfield, 2003; Qvarnström et al., 2006 and Husby et al., 2012, both referring to the same population). As discussed below, we distinguish between preference and choice, choice being what is actually measured in the trials (Heisler et al., 1987; Wagner, 1998) and preference being a genetic component of the preference function. We therefore characterize the studies listed in Table 1 as measuring choice rather than preference.
Table 1. Review of studies that estimate the heritability of female preference.
| Species | Order | Na | Cue typeb | Genetic modelc | Mean | s.d. or s.e.d | ne | Study |
|---|---|---|---|---|---|---|---|---|
| No choice trials | ||||||||
| Drosophila melanogaster | Diptera | 1 | Male | Isofemale | 0.80 | 0.16 | 4 | Narraway et al. (2010) |
| Sepsis cynipsea | Diptera | 1 | Male | Half-sib | 0.37 | 1 | Muhlhauser and Blanckenhorn (2004) | |
| Pectinophora gossypiella | Lepidoptera | 1 | Synthetic | Selection | 0.16 | 0.02 | 1 | Collins and Carde (1990)f |
| Choice trials | ||||||||
| Taeniopygia guttata | Passeriformes | 2 | Male | Full-sib | 0.10 | 0.14 | 1 | Schielzeth et al. (2010) |
| Gasterosteus aculeatus | Gasterosteiformes | 2 | Male | Full-sib | 0.43 | 0.37 | 1 | Bakker (1993) |
| Utetheisa ornatrix | Lepidoptera | 2 | Male | OP | 0.51 | 0.11 | 1 | Iyengar et al. (2002) |
| Drosophila bunnanda | Diptera | 2 | Male | Half-sib | nag | na | na | McGuigan et al. (2008) |
| Achroia grisella | Lepidoptera | 2 | Synthetic | Half-sib | 0.21 | 0.13 | 1 | Jang and Greenfield (2000) |
| Taeniopygia guttata | Passeriformes | 8 | Male | Animal | 0.03 | 0.05 | 3 | Forstmeier et al. (2004) |
| Poecilia reticulata | Cyprinodontiformes | 12 | Male | Half-sib | 0.05 | 0.08 | 14 | Brooks and Endler (2001) |
| Poecilia reticulata | Cyprinodontiformes | 5 | Male | Selection | 0.00 | 0.09 | 2 | Hall et al. (2004) |
| Nauphoeta cinerea | Blattodea | 2 | Male | Threshold | 1.02 | 0.28 | 1 | Moore (1990) |
| Drosophila simulans | Diptera | 2 | Male | Threshold | 0.26 | 0.11 | 1 | Sharma et al. (2010) |
| Cadra cautella | Lepidoptera | 2 | Synthetic | Threshold | −0.03 | 0.06 | 1 | Allison et al. (2008) |
| Teleogryllus oceanicus | Orthoptera | 2 | Synthetic | Threshold | 0.00 | 0.00 | 3 | Simmons (2004) |
| Pectinophora gossypiella | Lepidoptera | Multiple | Synthetic | OP | 0.26 | 0.25 | 6 | Collins and Carde (1989) |
| Achroia grisella | Lepidoptera | Multiple | Synthetic | Half-sib | 0.23 | 0.11 | 8 | Zhou et al. (2011) |
| Achroia grisella | Lepidoptera | Multiple | Synthetic | Full-sib | 0.31 | 0.13 | 2 | Rodriguez and Greenfield (2003)f |
| Gryllus texensis | Orthoptera | Multiple | Synthetic | OP | 0.40 | 0.11 | 2 | Gray and Cade (1999) |
| Free-ranging population | ||||||||
| Ficedula albicollis | Passeriformes | Unknown | NA | Animal | 0.05 | 0.01 | 2 | Husby et al. (2012)f |
| Ficedula albicollis | Passeriformes | Unknown | NA | Animal | 0.03 | 1 | Qvarnström et al. (2006)f | |
Except where noted (footnote f), authors define the trait as ‘preference'.
N: Number of males presented to a female. ‘Multiple' refers to the set of synthetic cues used to estimate female preference.
Refers to whether female is presented with one or more males or with a synthetic cue (pheromone, song).
Animal=animal model. OP=offspring on parent regression.
Standard error presented when there was only one estimate, otherwise standard deviation of estimates.
Number of estimates.
Collins and Carde (1989) define the response as ‘increased responsiveness', while Rodriguez and Greenfield (2003), Qvarnström et al. (2006) and Husby et al (2012) use the term ‘choice'.
Genetic variance but not heritability of preference estimated.
The studies listed in Table 1 can be conveniently divided into three broad categories: no-choice trials, choice trials and estimates from free-ranging populations (Table 1). As females are typically (but not universally) the sex exhibiting a preference, for simplicity we describe these in terms of females being the choosy sex. In no-choice trials, females are presented with a single male and some index of acceptance for this male is measured. Often this is some aspect of attention, orientation or movement toward the male, but it may also be resistance to male courtship or mounting attempts. These behaviors are then used as measures of female choice. In choice trials, females are presented with several males or synthetic cues, which may be presented simultaneously or sequentially (sometimes a combination of both). Female choice is then defined as the phenotype of the male or synthetic cue selected. Female choice was similarly defined as the phenotype of the male selected in a free-ranging population of the collared flycatcher, Ficedula albicollis, although the number of males the female surveyed was not known (Qvarnström et al., 2006; Husby et al., 2012).
Quantitative genetic models of mate selection assume that the preference trait, x, is normally distributed with some heritability h2. The heritability estimated by the choice trials, which we term the heritability of choice, may be a biased estimate of the heritability of the preference trait x because only a limited number of males are available to the female. With a limited sample of males, a female is unlikely to be able to compare the full range of available male phenotypes and so she may ultimately choose a male whose phenotype does not match her most preferred phenotype. This introduces sampling error into the variance in choice, which will cause estimates of the heritability of choice to underestimate the true heritability of preference.
A limitation on the number of males sampled also applies under natural conditions because females in wild populations are likely to have access to relatively few males. Field estimates of the number of males surveyed in 20 species averaged only 4.5 (Roff and Fairbairn, 2014), suggesting a very limited survey of the male population by each female. As in laboratory choice trials, this limited sampling means that a female is unlikely to be able to choose a male whose phenotype matches her most preferred phenotype. Thus, in the wild as in the laboratory, sampling variance in choice is likely to reduce the heritability of choice relative to the underlying heritability of preference.
It is typically assumed that the variance in preference is likely to be less than the variance in the preferred trait, which theoretically should lead to a reduction in the variance of the preferred trait. The relative variance of preference and the preferred trait can have a very significant effect on the equilibrium heritabilities of the two (Roff and Fairbairn, 2014). A limited sample of males will likely effect the extent to which the variance in the preferred trait is reduced or enlarged by female choice and hence evolutionary change in the heritabilities.
In this study, we address three questions based on the limited sampling of potential mates either in the experimental arena or in a natural population: first, to what extent is the estimate of the heritability of choice a biased estimate of the heritability of preference; second, how does the statistical power to detect genetic variation in preference vary according to the number of males sampled by a female; third, to what extent is the phenotypic variance in the preferred trait affected by the number of males sampled and the relative size of the variance in preference?
Materials and methods
Preference functions examined
We examine three types of preference functions: absolute preference, relative preference and threshold preference. The first two are based on the models described by Lande (1981). A female mates with a given male with a probability P(y|x), where y is the male trait (that is, preferred trait) value and x is the female preference value. Females with an absolute preference mate with a male with probability
 |
where v is female ‘choosiness', which Lande terms the ‘tolerance' of the female, with choosiness decreasing as v increases (that is, as the width of the tolerance function increases). Thus, females with an absolute preference mate with the highest probability with males whose trait value exactly equals the female's preference (that is, x=y). Lande (1981) assumed that x and y are normally distributed in the population with fixed heritabilities. The female choosiness parameter was assumed to be a constant, though it is possible that this parameter could also be genetically variable, in which case we would have to consider the two heritabilities and the genetic correlation between them. In the present paper, we shall assume only a single parameter, absorbing v into x and y (that is, our new variables are x=x/υ and y=y/υ). We shall assume that a female can correctly assess the male's trait value, in which case when presented with a sample of males a female will mate with the male for whom P(y|x) is the largest, that is, she chooses the male for which (y−x)2 is the smallest.
The relative preference function is defined as
 |
In this model, a female is most likely to accept a male whose trait value is x+y*: thus, females with a positive x prefer males with trait values greater than y*, whereas females with a negative x prefer males with a trait value less than y*. Note that in this model x is not preference per se but for simplicity we shall throughout this paper refer to x as the preference. Lande (1981) set y* as the mean preferred trait value of the total population of males surviving after natural selection acts. However, in an experimental setup (almost certainly also in the wild) a female only has information on the sample of males she is presented with, and so we set y* as the mean trait value equal to the mean of the males she surveys. As with the absolute preference function we absorb v and assume that a female can accurately gauge the male's trait value; thus, she will select the male for which (y−[x+y*])2 is the smallest. Females were then assigned the value y or y−y*: as better estimates were obtained using the latter, we only report these results.
Lande (1981) considered a third type of preference function that he called the psychophysical model
If both y and x are positive then a female will prefer the male with the largest value of the preferred trait in the group that she samples. Thus, female choice will be independent of y, the female preference in the case where a female is presented with a set of males simultaneously. Under the experimental design explored in the present paper this leads to female's simply choosing the largest male value and we have therefore not considered this model.
The third preference function examined in the present paper assumes that there are two types of males and that females have a preference for one or the other. This difference may be naturally occurring, as in the two color morphs of the sulfur butterfly, Colias eurytheme (Sappington and Taylor, 1990), though in this case mate selection appears to be based on the different pheromones of the two morphs (but see Papke et al., 2007 for evidence on UV reflectance). A similar situation is found in the wing dimorphic sand cricket, Gryllus firmus, in which females, by their preference for males that sing the most, preferentially favor micropterous males over macropterous males (Crnokrak and Roff, 1995). Alternatively, the difference may be imposed by the experimenter by presenting two stimuli, such as two pheromones (Allison et al., 2008) or two synthetic songs (Simmons, 2004). The quantitative genetic model for this preference function is the threshold model in which it is assumed that there exists some normally distributed trait, called the liability (=x), and a threshold that determines the phenotypic expression of the liability: females with liabilities below the threshold prefer one morph whereas females above the threshold prefer the other.
Simulation model
We used an individual variance components model (Roff and Fairbairn, 2014; Roff, 2010) to generate a full sib design with no dominance variance or maternal effects. Briefly, the simulation was constructed as follows: first, sire and dam breeding values for female preference were generated from a random normal distribution, 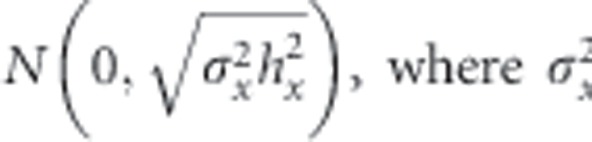 is the heritability of preference. The offspring genetic values were calculated as
is the heritability of preference. The offspring genetic values were calculated as
where xi,j is the phenotypic preference of the jth offspring from the ith family, Bi is the breeding value for the ith full sib family, gi,j is the genetic deviation of the jth offspring from the ith family, drawn from a random normal distribution
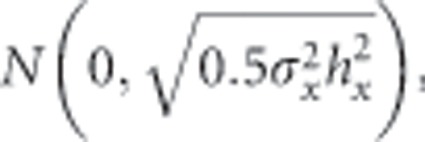 |
is the environmental deviation of the jth offspring from the ith family, drawn from a random normal distribution
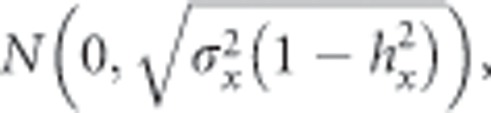 |
, Next, the phenotypic values of n males were generated from a random normal distribution N(0,1). The program then iterated through these males, for each determining the probability, P, of the female accepting the male using equations (1) or (2), and accepting the male with the largest P.
Each simulation consisted of 50 families with 10 females per family. We used this combination as it is not unreasonably large and gives a satisfactory heritability estimate when the actual trait value is known. We also did the analysis with 100 sires and 10 females per family: as would be expected from theory, this decreased the standard errors and increased the power but did not affect the bias. The heritability of preference was varied from 0.1 to 0.9 with, as noted above, the phenotypic trait mean set at zero and variance at one. For convenience, we set the mean preference and the mean preferred trait at zero: any difference between the mean preference and the mean of the preferred trait would be evident by a statistical comparison between the male values and the estimated values for the female and could be removed by subtraction of the two means. A difference in means could potentially affect the phenotypic variance of the males selected by the females but in the absence of sufficient information on what differences might be expected and because the primary focus of this paper is on the bias introduced by presenting a female with a limited number of males we do not consider this issue in the present analysis. To set the variance, we extracted data from the literature on the relative phenotypic variance of preference to the preferred trait. The ratios for the four species for which such data are available (Gryllus texensis, Achroia grisella, Colias eurythem and Ficedula albicollis) were 1.2, 1.63, 0.8 and 1.0, respectively (sources: Gray and Cade, 1999; Zhou et al., 2011; Sappington and Taylor, 1990; Qvarnström et al., 2006). Thus for these four species the phenotypic variance in preference is similar to the variance in the preferred trait. It is typically assumed that the variance in preference is likely to be less than the variance in the preferred trait, but it is also possible that the variance in preference is greater than that of the preferred trait (Roff and Fairbairn, 2014). To examine the effect of the relative size of the phenotypic variance of preference, we ran our analyses with the variance in the preferred trait set at 1 and the variance in preference at 0.5, 1 or 2. The variance in preference did not affect the bias in the heritability estimate of preference (for example, average bias differed by less than 2%) or the statistical power but did affect the variance in the selected males. Therefore, we present the results for the combination of mean equal to zero and variance of preference equal to 0.5 and 2 only for the effect on the variance in the selected males. Similarly, for convenience only, and without loss of generality, we assigned the threshold at zero, thus making the population consist of equal types of female.
Each female was presented with N randomly chosen males from the male distribution. Females choose among these N males according to the ‘best-of-N' rule (Janetos, 1980). For the absolute and relative preference functions N was varied from 2 to 20 and the male's trait value assigned to the female according to the protocol described above. With the threshold model each female was assumed to be presented with two males, one of either morph: if her liability fell below the threshold she selected the morph designated as 0 and if her liability fell above the threshold she selected the morph designated as 1.
For each combination we ran 1000 simulations to ascertain the average value of the correlation between the female's preferred male and the one she actually chose, the percentage bias and statistical power of a test for significant genetic variation among families.
Heritability estimation
Heritability of preference for the absolute and relative preference functions was estimated from a one-way ANOVA (Roff, 1997) using the assigned male value as the female's preference. It is clear from the outset that assigning a female's preference based on only two males will give a relatively poor estimate compared with, say, 10 males. As described above, we denote two types of heritability; the first is the ‘true' heritability in the sense that it is the heritability of x, the preference, and the second is the ‘apparent' heritability, that is, choice, in that it is the heritability given that a female surveys N males. The heritability of choice will be a biased estimate of the heritability of preference (x) and will typically be biased downwards.
The heritability of relative preference estimated in the above manner is incorrect as even with a large N the estimate is not that of x but a function of x. In this case we used three approaches to estimate the heritability of x: first, we used the assigned male value, second the assigned male value minus the mean of the sample from which this male came and third the threshold transformation. The basis of the threshold transformation is that if there exists a transformation that will normalize a set of data then the threshold model will itself be an appropriate alternate transformation (Roff, 2001). To use this method, we divide the data set into two halves of approximately equal size (in the present case this is done using the mean or the median: as the results did not differ we present the results using the mean) and code one set of data as zeroes and the other as ones. We then treat the data as described below for the threshold preference function. The heritability of x in the relative preference function is the heritability of the liability of the transformed data. The threshold transformation can also be used for the absolute preference function: in this case, it has the potential advantage of being less biased but the disadvantage of an increased standard error arising from converting the data to a binomial variable (Roff, 2001).
The heritability of the liability for the threshold preference function was estimated in the usual manner: that is, the heritability on the 0,1 scale, h20,1, was estimated using a one-way ANOVA and then corrected to the underlying scale by
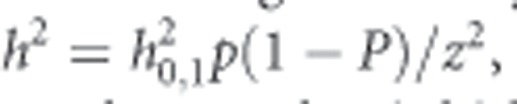 |
where P is the proportion of females selecting one of the male morphs (which one is arbitrary) and z is the ordinate on the standardized normal curve that corresponds to the probability P (Roff, 1997).
We estimated statistical power as the proportion of simulations at each combination that gave a significant result (that is, probability less than 0.05) in the one-way ANOVA.
Results
To what extent is the estimate of the heritability of choice a biased estimate of the heritability of preference?
With two males per female the average correlation (
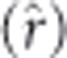 |
) between the preference and the value of the male actually chosen is low (0.45–0.65) for both preference functions (top row, Figure 1). The correlation rises rapidly with the number of males sampled and reaches 90% with six males sampled. Given uncertainty in the number of available mates a female might make her mating decision based on the first two males encountered. In this case, because the correlation between the male she most prefers and the one actually chosen is low (Figure 1), her first chosen male may be substantially different from her most preferred. If she then encounters four more males, given that the correlation between her preference and the ‘best' value among six males is close to 0.9, it is likely that one of these will be closer to her preference than her original choice. Consequently, we might expect her to engage in extra-pair copulation or multiple mating.
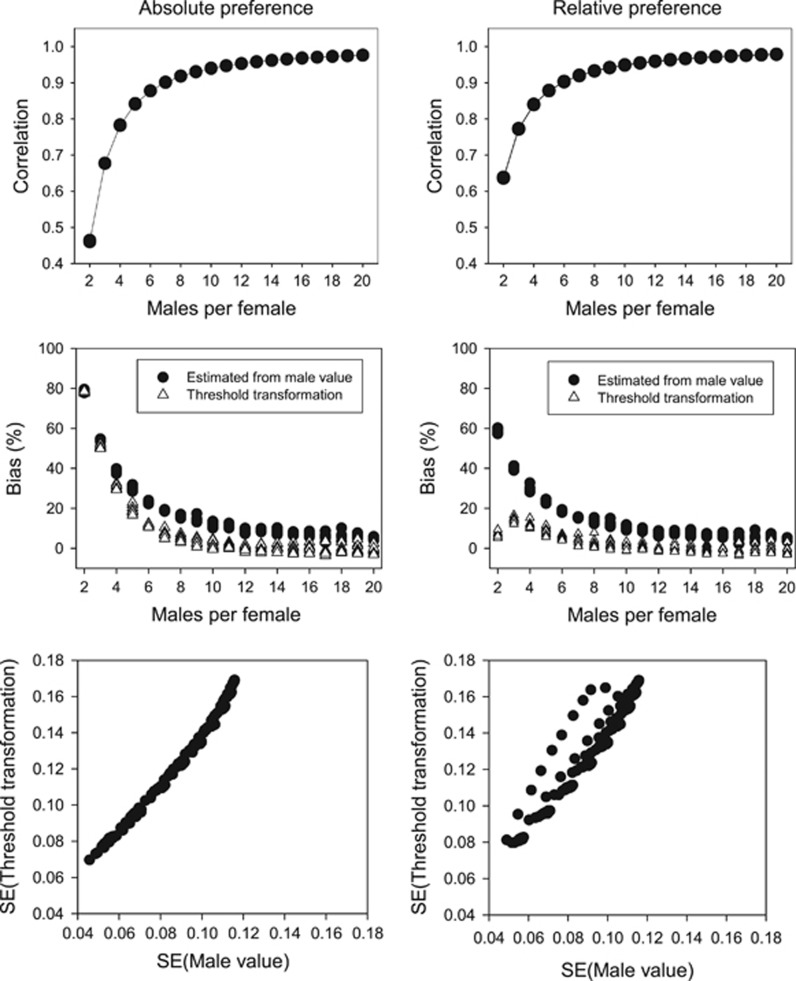
Figure 1.
Top row: Correlation between the female's true preference and that assigned to her. Middle row: Mean percentage bias, 100(h2−apparent h2)/h2, of the apparent heritability of preference. Each point is the mean of 1000 replicates. Bottom row: Standard error of the heritability using threshold transformation vs that using male value or adjusted value (y−y*). All values of h2 (0.1–0.9) are plotted.
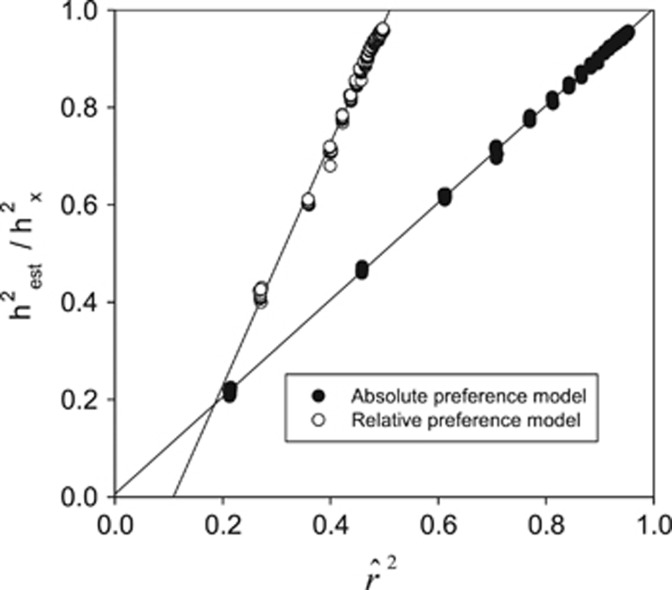
The low correlation when a small number of males is sampled is reflected in a substantial downward bias in the heritabilities (middle row, Figure 1). The bias in the estimated heritability is a result of measurement error resulting from the restricted sampling of males. This is clearly shown for the absolute preference function in which inspection of the graph suggests that bias is approximately one minus the squared correlation, a relationship verified by regression analysis (Bias=0.995−0.989
r=0.999, P<0.0001, where Bias is a proportion). Rearranging the equation Bias=1−
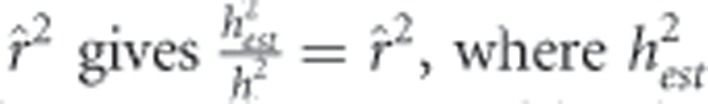 |
is the estimated heritability. This relationship is well supported by the simulated data (
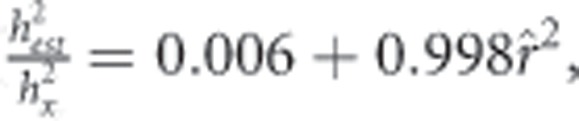 |
r=0.9998, Figure 2). Because the heritability of preference is a function of x in the relative preference function the relationship is slightly more complex, the empirical relationship being
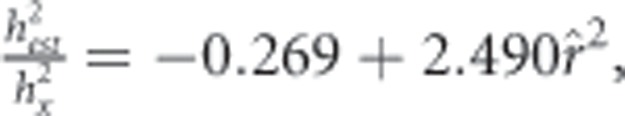 |
r=0.9975, Figure 2).
Figure 2.
 |
The heritability estimate of preference was biased downwards by 57–78% with two males per female and decreased as the number of males per female was increased (Figures 1, 2, 3). Percent bias was independent of the true heritability of preference (x). Heritabilities based on the estimated female value were biased downwards by approximately 10% when 10 males per female were used and were still 5% at N=20. For the absolute preference function, the threshold transformation did not reduce the bias at very low numbers of males per female but more or less eliminated it by N=10. For the relative preference function, except for the region 3–6 males sampled, the threshold virtually eliminated bias even at low numbers of males sampled per female (triangles in Figure 2). (We have not been able to ascertain why the percent bias is somewhat lower for two males than for 3–6 males.) As previously noted, the threshold transformation leads to an increased standard error, being around 30% for the absolute preference function and about 60% for the relative preference function (bottom row, Figure 1).
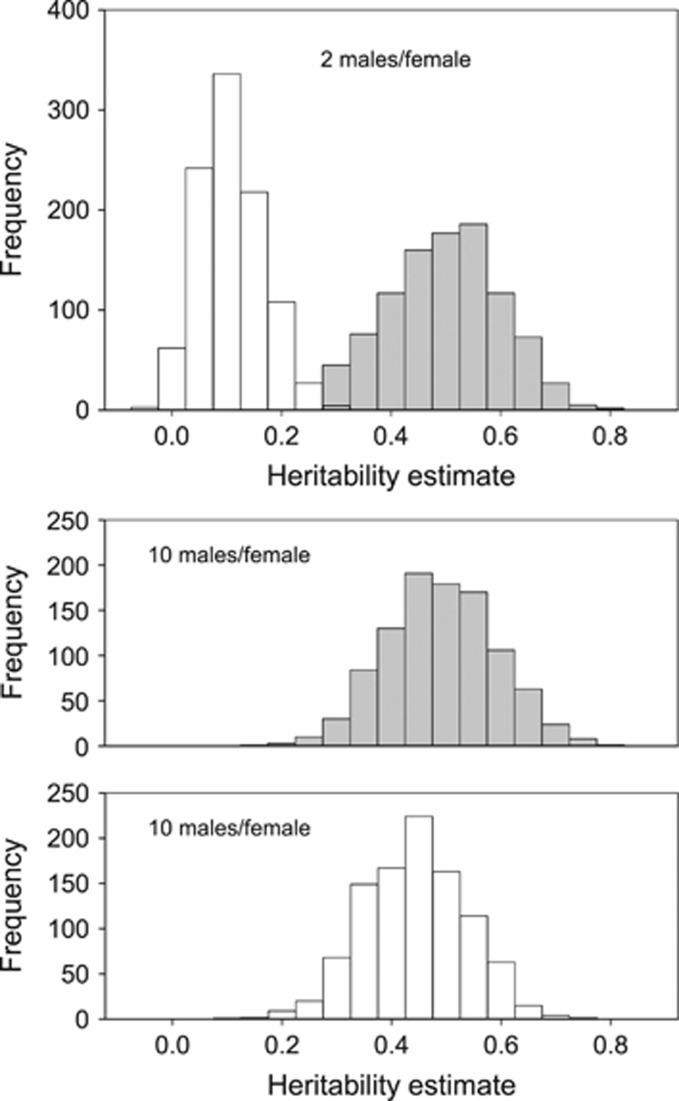
Figure 3.
Illustrative examples of the bias in the absolute preference function when females were presented with 2 (top panel) or 10 (lower panels) males per female. Results are for a single combination (1000 replicates) in which heritability of preference (x) was set at 0.5. White histograms show estimated heritability based on the assigned male value. Gray histograms show the estimate obtained using the actual preference value of each female.
The mean percentage bias in the estimation of the heritability for the threshold preference function did not vary with the heritability and was always very low, averaging only −1.6%.
How does the statistical power to detect genetic variation in preference vary according to the number of males sampled by a female?
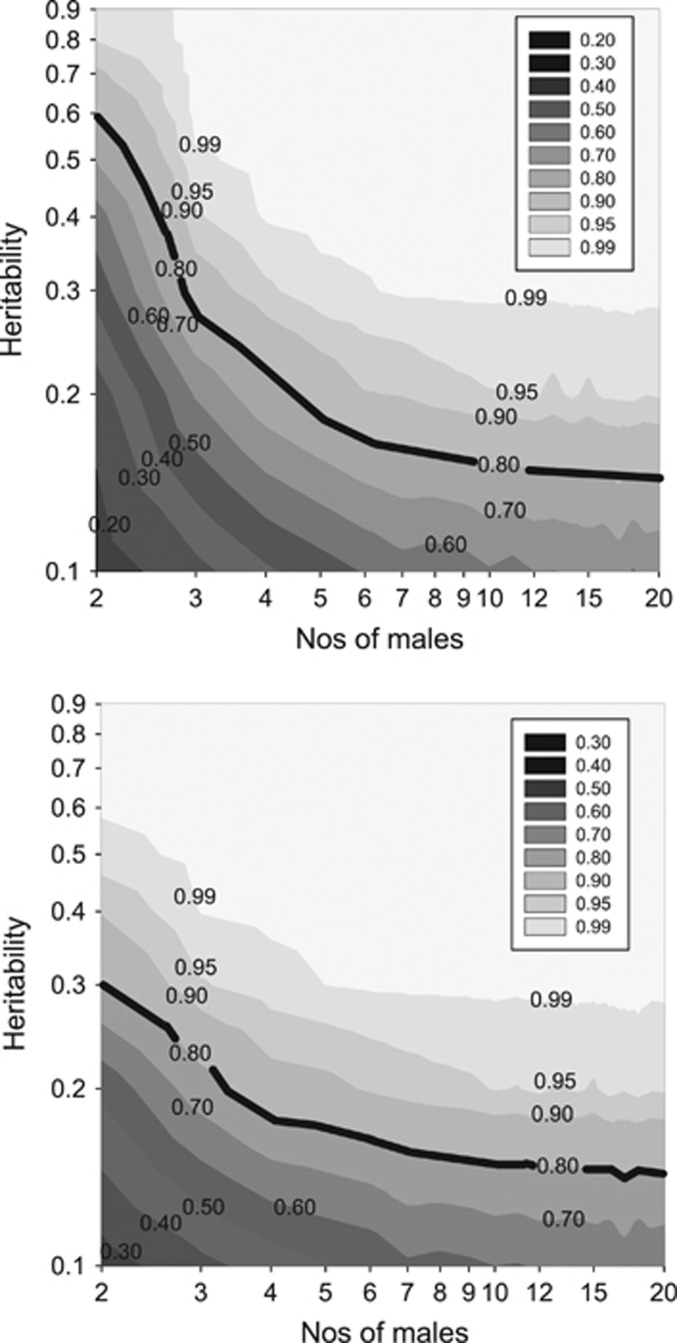
For the power analyses, we used both the assigned male trait value and the data divided into 0,1 categories: as the highest power was achieved using the assigned male value we present only these results. In contrast to the lack of an effect of heritability on the percentage bias, statistical power was coupled to both the number of males surveyed and the heritability of the female preference trait (Figure 4). A minimum acceptable power for behavioral research is taken to be 80% (Cohen, 1988), which requires either a relatively high heritability or large N. Although there may be a large bias regardless of the heritability, it is still possible to detect significant genetic variance: for example, under the absolute preference function the sample size used in the present simulations will detect a significant genetical effect more than 80% of the time when only two males per female are used and the heritability exceeds 0.6 (Figure 4). There is a larger parameter space over which power exceeds 80% for the relative preference function than the absolute preference function (Figure 4).
Figure 4.
Contour plots of statistical power for the absolute (top) and relative (bottom) preference functions. Solid black line shows 80% power isocline.
To what extent is the phenotypic variance in the preferred trait affected by the number of males sampled and the relative size of the variance in preference?
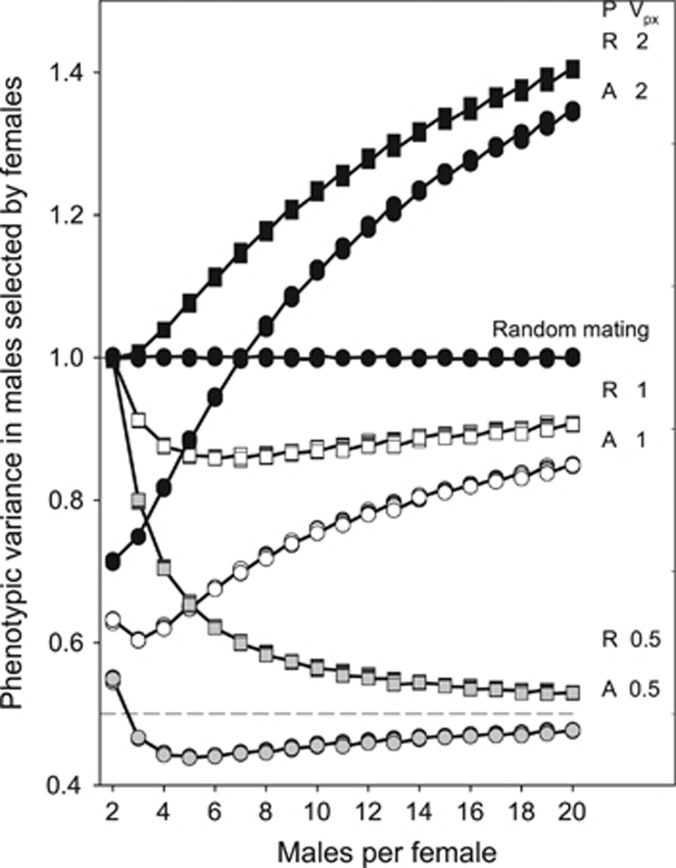
When the phenotypic variance in preference was equal to or less than that of the preferred trait the variance in the males selected by the females was reduced and remained substantially less even with 20 males per female (Figure 5). In contrast, when the phenotypic variance in preference was twice that of the preferred trait the variance in the males selected by the females was increased (Figure 5). In all cases, the phenotypic variance of the selected males asymptotically approaches the phenotypic variance of preference (verified by increasing the number of males sampled up to 1000).
Figure 5.
The variance in the preferred (male) trait in the group of males selected by the females as a function of the number of males per female, the preference function (A=absolute, R=relative) and the phenotypic variance in preference (Vpx). Results for random mating simulations are also shown. The phenotypic variance in the preferred trait in the total population was set to 1 in all cases. All heritability combinations are plotted.
Discussion
The present analysis shows that the correlation between the actual female preference value and that of the male she selects is a monotonically rising function of the number of males sampled with a very low correlation when less than four males are sampled. With the absolute preference function the correlation approaches 1 asymptotically as was also found by Benton and Evans (1998). The imprecise match between a female's true preference and that assigned to her using the male's value is reflected in a substantial downward bias in the estimated heritability of preference. Unless a female surveys a large number of males the heritability of choice will be substantially smaller than the heritability of preference. There may also be other factors that reduce the heritability of preference, such as environmental interactions (Hedrick and Dill, 1993; Jennions and Petrie, 1997; Callander et al., 2013). In this case, the genetic basis of preference is better viewed as a reaction norm than a single trait and analysis using the animal model may be most appropriate (Roff and Wilson, 2014).
The threshold transformation reduces the bias in the heritability estimate but at the cost of an increased standard error. If the preferred trait is dichotomous then the female preference function can be modelled as a threshold function and a binary choice experiment is sufficient with the threshold model giving an unbiased estimate of the heritability of preference.
Most laboratory estimates of female preference based on attraction to a particular male have used 2–6 males per female (Table 1), which means that the measured heritability of choice may significantly underestimate the heritability of preference. Heritability of preference in the seven studies (six species) based on measuring the attraction of females (or males) to two or more males (or females) in the laboratory range from 0 (guppy, Hall et al., 2004) to 0.51 (moth, Iyengar et al., 2002), with a mean of 0.19: given the low number of males the true heritabilities are probably underestimated by 40–80%. Estimates based on response to synthetic cues (3 species, 4 studies) show less variation (0.23–0.40) and average 0.30 (s.d.=0.08). With the exception of the study on the Texas field cricket, Gryllus texensis, the female preference is based on a response threshold rather than the highest preference and is likely to suffer from the same problem of underestimating the heritability of preference. The estimate for the Texas field cricket was made by use of synthetic songs differing only in pulses per trill to obtain the preference function as measured by the orientation of the female (Gray and Cade, 1999). For each female, the most preferred song was that which elicited the strongest response. The function so obtained is probably a reasonable representation of a preference function in that it included both the most preferred song (=x) and choosiness (spread of the preference curve). The heritability of preference averaged 0.40 (s.e.=0.11) but choosiness showed no additive genetic variance. Based on the probable underestimation of the apparent heritabilities, it is likely that the overall average of the heritability of preference in the species studied is around 0.4, as found in the Texas field cricket.
The approach employed by Gray and Cade (1999) assumes that the synthetic cue used is the primary or sole cue used by the female to choose among males. However, cues chosen by a female may be hierarchical in nature and if a particular cue is lower in the hierarchy then experimental results may be misleading. For example, females of the sand cricket, Gryllus firmus are primarily attracted to the relative call duration of a male and secondarily by some component of its song (Roff et al., 2003). At this time whether this is a single component or a mix of several has not been resolved, though there is some evidence that frequency might be important (Mitra et al., 2011). Thus, a plausible scenario is that females first rank males according to their relative call duration and then resolve ties by difference in song components. The type of experiment used by Gray and Cade (1999) could, therefore, suggest a higher importance of a song component in mate selection than would occur under natural conditions.
The appropriate number of males presented to a virgin female in an experimental system will depend upon the specific question being addressed. On the one hand, we might choose to use many males per female to estimate the actual heritability of preference for the first mate accepted. However, this heritability might actually be misleading if under natural conditions females of the species in question typically survey only a few males. In this case, the heritability of choice may be a more relevant measure. Field estimates on 20 species for the number of males surveyed average only 4.5 with a median of only 2.9 (Roff and Fairbairn, 2014). Thus, the estimates of the heritability of choice obtained from laboratory experiments while not being unbiased estimates of the heritability of preference may be estimating the heritability of choice that is likely to be found in free ranging populations. Of particular interest in this regard is the estimate of female preference in a wild population of the collared flycatcher, Ficedula albicollis. In this species, female preference is for male forehead patch size and, as in the present simulations, her preference was taken to be the patch size of her observed mate. The heritability of forehead patch size was estimated to be 0.38 (±0.03) and that of female preference for this trait was estimated as 0.03 (±0.01; Qvarnström et al., 2006). The number of potential mates a female surveys is not known but in a related species, the pied flycatcher, Ficedula hypoleuca, females choose among, on average, 2.3 (s.d.=1.5) males (Dale and Slagsvold, 1996). The present analysis suggests that the heritability estimated for the collared flycatcher will underestimate the heritability of preference by as much as 80%. Even after accounting for this large bias, the heritability of preference is unlikely to be greater than 0.1.
If in a population females routinely assay a few males and we are interested in how this affects the evolution of the preferred trait then we might focus upon the heritability of choice, whereas, if we are interested in addressing how the number of males assayed affects the evolution of the preferred trait then we would need to estimate the heritability of preference. The heritability of preference can be estimated, at least approximately, from an experiment that uses a single number of males by simply using the simulation described in the present paper to ask what heritability of preference would generate the heritability of choice observed in the experiment. Estimates of the heritability of choice for other numbers of males can then be derived using that heritability of preference.
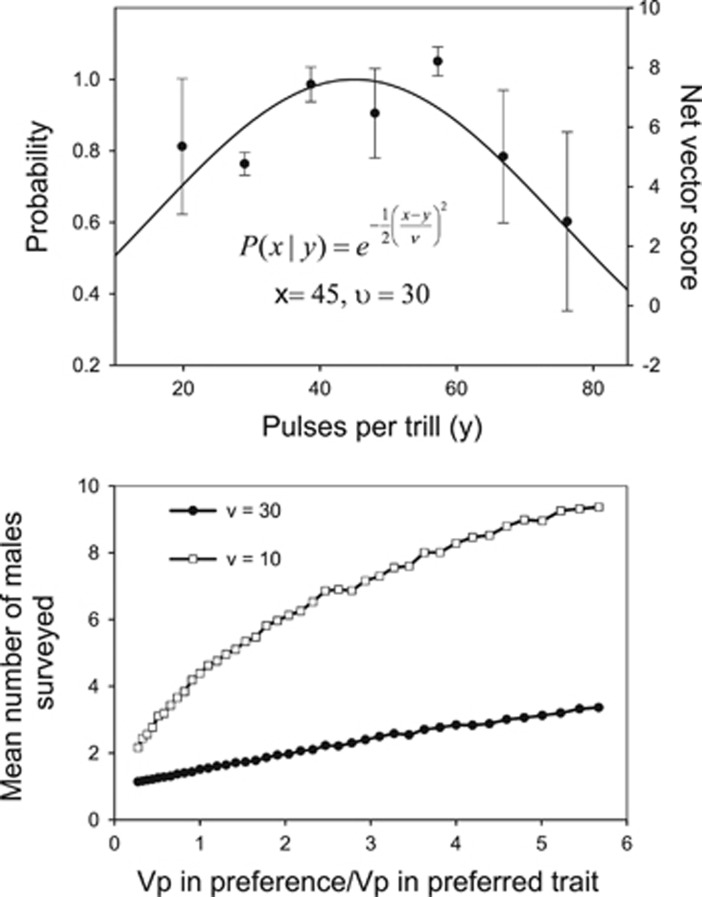
In the present analysis, we have assumed that a female is able to survey a fixed number of males simultaneously and then make a decision, a sampling scheme known as the ‘best-of-N' rule (Janetos, 1980). The general assumption, as used in the present analysis, is that a female can accurately judge male quality and thus her pick will be the closest to her own preference. This is a deterministic mode of choice that is actually at variance with the quantitative genetic models (for example, Lande, 1981; Pomiankowski and Iwasa, 1993; Kirkpatrick, 1996). In these models, choice is a probability function such that any male could be selected by a female. A biologically realistic interpretation of these probabilistic models is that a female samples males sequentially and only moves on to another male if the present male is rejected (an alternate model is that a female uses the best-of-N, where n is the entire population of males). Given this mode of choice the number of males sampled before a female accepts a male will depend upon the phenotypic means and variances in preference and the preferred trait, and the choosiness of the female. To determine whether a realistic set of parameter values could generate the small number of males typically sampled by females we used data on the Texas field cricket given by Gray and Cade (1999). We assumed an absolute preference function and fitted it ‘by eye' to the exemplar preference function given in Gray and Cade (Figure 5: to do this we assumed that the net vector score of the female could be directly equated with preference function). We set the population mean preference and preferred trait at 45 pulses per trill (which was the modal family mean value for G. texensis), the choosiness parameter, ν, at 30, which roughly matched the exemplar (Figure 6). The variance in preference and the preferred trait were initially set equal, which is consistent with the data reported in Gray and Cade (1999). We then varied the variance in preference and used the following simulation to generate the expected number of males sampled for the given variance. We generated a single female trait x by drawing at random from a normal distribution with mean 45 and the given variance. Next, we generated a male value, y, by drawing at random from the same normal distribution. Using these two values we calculated using equation 1 the probability, say P, that the female would accept the male. To determine whether she actually did accept the male we generated a random number from a uniform distribution between 0 and 1: if this number was less than P then the female accepted the male, otherwise that male was rejected and another male generated. The process was continued until a male was accepted and the entire procedure replicated 10 000 times for each variance. We also repeated the entire procedure assuming more choosy females by setting ν=10. As would be expected, the average number of males sampled increased with the phenotypic variance (Figure 6). The observed variance in G. texensis was 441 (ratio=1), which corresponds to 1.5 males per female for ν=30 and 4.4 for ν=10, both values that are commonly observed (Roff and Fairbairn, 2014). We are not suggesting that either of these is the number that female G. texensis typically sample, merely that realistic parameter values do generate the sampling regime observed in natural populations. Thus, a model of sequential sampling using the absolute preference function is a realistic biological model.
Figure 6.
Top: Exemplar female response graph from Gray and Cade (1999) with absolute preference function (solid curve) fitted ‘by eye'. Data plotted are the mean±s.d. responses of a single female as a function of the number of pulses per trill. Female response was measured as a net vector score of directed phonotaxis toward the male calling song. Bottom: Mean number of males surveyed, N, as a function of the ratio of the phenotypic variance in preference to the phenotypic variance in the preferred trait, where 1 is the observed ratio. See text for details of simulation.
How sequential sampling will affect the estimate of the heritability of preference is not clear. On the one hand, if N is large then a female using the best-of-N rule will generally get closer to her preferred male than using sequential sampling (this can be seen by simply considering the limit in which N is equal to population size). Thus, for large N sequential sampling will produce a more biased estimate than best-of-N. However, for very small N, say n=2, the best-of-N rule produces a large bias but sequential sampling that results in only two males being sampled is a consequence of the female's preference being satisfied and hence probably a reduced bias. The consequences of sequential sampling or one of the other suggested modes of choice (reviewed in Roff, 2015) can be explored using the same approach as used here for best-of-N.
In lekking species, the opportunity exists for simultaneous comparison, although even here the actual number appears to be relatively low: at least 10 of the species reported in Roff and Fairbairn (2014) could be called lekking species and for these the mean number of males surveyed averaged 3.9 (range 1.7–7.5). Thus, whether males are selected using a deterministic or probabilistic preference function the male selected is likely to be not what the female would most prefer. This finding has significant consequences not only for the estimation of the heritability of preference, but also for the influence of sexual selection on the heritability of the preference trait and the likelihood of multiple mating.
If the number of males sampled is less than 10 or the phenotypic variance in preference is equal to or less than the phenotypic variance in the preferred trait, then the phenotypic variance in the males selected by the females will be reduced. This will create stabilizing selection and selection for a reduced variance in males, as posited in the Lek paradox. An important and new finding in the present analysis is that this reduction occurs even if the variances are equal. The data for the four species described earlier suggest that phenotypic variances in preference are equal to or larger than the phenotypic variances in the preferred traits, suggesting that reduction in the variance of the preferred trait has not occurred, despite the likelihood that the variance in selected males is reduced. Several possible resolutions of the Lek paradox have been proposed (Kotiaho et al., 2008). The present analysis and that of Roff and Fairbairn (2014) suggests two other possible reasons why the heritability of the preferred trait is not reduced. First, if the variance in preference is greater than the variance in the preferred trait then mate choice can inflate the heritability of the preferred trait. A detailed analysis of this hypothesis has shown that the critical variances are the genetic rather than the phenotypic variances (Roff and Fairbairn, 2014).
The second reason is that the present analysis predicts that females are likely to mate multiply. The reason for this is that a consequence of females choosing from within a restricted number of males is that they select males that are not likely to have the most preferred phenotype. If females are typically mating first with males that do not measure up to their highest preference, then they are likely to accept males that they encounter later that are closer to their highest preference. This leads to multiple mating and increased phenotypic variance of the preferred trait. Multiple mating is common in natural populations and has been well documented in insects (Arnqvist and Nilsson, 2000), birds (Schmoll, 2011), fish (Coleman and Jones, 2011), reptiles (Uller and Olsson, 2008) and mammals (Wolff and Macdonald, 2004). A variety of adaptive (Jennions and Petrie, 2000; Neff and Svensson, 2013) and non-adaptive (Forstmeier et al., 2014) hypotheses have been put forward for multiple mating but we propose here that multiple mating may frequently result simply as a consequence of females having a limited sample of males to choose from. Given the observed number of mates typically surveyed, we predict that multiple mating will be a natural consequence of sampling error in female choice of initial mates (or male choice where males are the choosy sex) in mate-choice mating systems.
The present analysis shows that a distinction must be made between the heritability of preference and the heritability of choice. Both traits are of importance in the evolution of preferred traits but the latter may be the most relevant. However, experiments to estimate the heritability of choice should match the number of males presented to the female with the number that she typically encounters in nature. On the other hand, exploration of the possible evolutionary trajectories under scenarios in which the number of mates sampled differs from that presently observed is possible only if the heritability of preference is known. Changing population densities, as might occur as a consequence of global warming, which would likely lead to a change in mate availability, could dramatically alter the evolution of mate choice. An important consequence of limited sampling is the likelihood of multiple mating, which we propose is an alternative hypothesis for its occurrence.
Data Archiving
There were no data to deposit.
Acknowledgments
This work was supported by funding from NSF IOS-1353463. We are very grateful for the constructive comments of the four reviewers.
The authors declare no conflict of interest.
References
- Allison JD, Roff DA, Carde RT. Genetic independence of female signal form and male receiver design in the almond moth, Cadra cautella. J Evol Biol. 2008;21:1666–1672. doi: 10.1111/j.1420-9101.2008.01595.x. [DOI] [PubMed] [Google Scholar]
- Arnqvist G, Nilsson T. The evolution of polyandry: multiple mating and female fitness in insects. Anim Behav. 2000;60:145–164. doi: 10.1006/anbe.2000.1446. [DOI] [PubMed] [Google Scholar]
- Bakker TCM. Positive genetic correlation between female preference and preferred male ornament in sticklebacks. Nature. 1993;363:255–257. [Google Scholar]
- Benton TG, Evans MR. Measuring mate choice using correlation: the effect of female sampling behaviour. Behav Ecol Sociobiol. 1998;44 (2:91–98. [Google Scholar]
- Brooks R, Endler JA. Female guppies agree to differ: phenotypic and genetic variation in mate-choice behavior and the consequences for sexual selection. Evolution. 2001;55:1644–1655. doi: 10.1111/j.0014-3820.2001.tb00684.x. [DOI] [PubMed] [Google Scholar]
- Callander S, Hayes CL, Jennions MD, Backwell PRY. Experimental evidence that immediate neighbors affect male attractiveness. Behav Ecol. 2013;24:730–733. [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. Lawrence Erlbaum Associates, Inc.: Hillsdale, New Jersey; 1988. [Google Scholar]
- Coleman SW, Jones AG. Patterns of multiple paternity and maternity in fishes. Biol J Linn Soc. 2011;103:735–760. [Google Scholar]
- Collins RD, Carde RT. Heritable variation in pheromone response of the pink-bollworm, Pectinophora-gossypiella (Lepidoptera, Gelechiidae) J Chem Ecol. 1989;15:2647–2659. doi: 10.1007/BF01014723. [DOI] [PubMed] [Google Scholar]
- Collins RD, Carde RT. Selection for increased pheromone response in the male pink-bollworm, Pectinophora-gossypiella (Lepidoptera, Gelechiidae) Behav Genet. 1990;20:325–331. doi: 10.1007/BF01067799. [DOI] [PubMed] [Google Scholar]
- Crnokrak P, Roff DA. Fitness differences associated with calling behaviour in the two wing morphs of male sand crickets. Gryllus firmus. Anim Behav. 1995;50:1475–1481. [Google Scholar]
- Dale S, Slagsvold T. Mate choice on multiple cues, decision rules and sampling strategies in female pied flycatchers. Behaviour. 1996;133:903–944. [Google Scholar]
- Fisher RA. The Genetical Theory of Natural Selection. Claredon Press: Oxford; 1930. [Google Scholar]
- Forstmeier W, Coltman DW, Birkhead TR. Maternal effects influence the sexual behavior of sons and daughters in the zebra finch. Evolution. 2004;58:2574–2583. doi: 10.1111/j.0014-3820.2004.tb00885.x. [DOI] [PubMed] [Google Scholar]
- Forstmeier W, Nakagawa S, Griffith SC, Kempenaers B. Female extra-pair mating: adaptation or genetic constraint. TREE. 2014;29:456–464. doi: 10.1016/j.tree.2014.05.005. [DOI] [PubMed] [Google Scholar]
- Gibson RM, Langen TA. How do animals choose their mates. TREE. 1996;11:468–470. doi: 10.1016/0169-5347(96)10050-1. [DOI] [PubMed] [Google Scholar]
- Gray DA, Cade WH. Quantitative genetics of sexual selection in the field cricket, Gryllus integer. Evolution. 1999;53:848–854. doi: 10.1111/j.1558-5646.1999.tb05378.x. [DOI] [PubMed] [Google Scholar]
- Hall M, Lindholm AK, Brooks R. Direct selection on male attractiveness and female preference fails to produce a response. BMC Evol Biol. 2004;4:1–10. doi: 10.1186/1471-2148-4-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick AV, Dill LM. Mate choice by female crickets is influenced by predation risk. Anim Behav. 1993;46:193–196. [Google Scholar]
- Heisler IL, Anderson MB, Arnold SJ, Boake CRB, Borgia G, Hausfater G, et al. 1987The evolution of mating preferences and sexually selected traits: group reportIn: Bradbury JW, Andersson MB (eds)Sexual Selection: Testing the Alternatives John WileyChichester; 96–118. [Google Scholar]
- Husby A, Schielzeth H, Forstmeier W, Gustafsson L, Qvarnström A. Sex chromosome linked genetic variance and the evolution of sexual dimorphism of quantitative traits. Evolution. 2012;67:609–619. doi: 10.1111/j.1558-5646.2012.01806.x. [DOI] [PubMed] [Google Scholar]
- Iyengar VK, Reeve HK, Eisner T. Paternal inheritance of a female moth's mating preference. Nature. 2002;419:830–832. doi: 10.1038/nature01027. [DOI] [PubMed] [Google Scholar]
- Janetos AC. Strategies of female mate choice - a theoretical-analysis. Behav Ecol Sociobiol. 1980;7:107–112. [Google Scholar]
- Jang YW, Greenfield MD. Quantitative genetics of female choice in an ultrasonic pyralid moth, Achroia grisella: variation and evolvability of preference along multiple dimensions of the male advertisement signal. Heredity. 2000;84:73–80. doi: 10.1046/j.1365-2540.2000.00631.x. [DOI] [PubMed] [Google Scholar]
- Jennions MD, Petrie M. Variation in mate choice and mating preferences: A review of causes and consequences. Biol Rev Camb Phil Soc. 1997;72:283–327. doi: 10.1017/s0006323196005014. [DOI] [PubMed] [Google Scholar]
- Jennions MD, Petrie M. Why do females mate multiply? A review of the genetic benefits. Biol Rev. 2000;75:21–64. doi: 10.1017/s0006323199005423. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick M. Sexual selection and the evolution of female choice. Evolution. 1982;36:1–12. doi: 10.1111/j.1558-5646.1982.tb05003.x. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick M. Good genes and direct selection in evolution of mating preferences. Evolution. 1996;50:2125–2140. doi: 10.1111/j.1558-5646.1996.tb03603.x. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick M, Barton NH. The strength of indirect selection on female mating preferences. Proc Nat Acad Sci USA. 1997;94:1282–1286. doi: 10.1073/pnas.94.4.1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotiaho JS, Lebas NR, Puurtinen M, Tomkins JL. On the resolution of the lek paradox. TREE. 2008;23:1–3. doi: 10.1016/j.tree.2007.09.012. [DOI] [PubMed] [Google Scholar]
- Lande R. Models of speciation by sexual selection on polygenic traits. Proc Nat Acad Sci USA. 1981;78:3721–3725. doi: 10.1073/pnas.78.6.3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuigan K, Van Homrigh A, Blows MW. Genetic analysis of female preference functions as function-valued traits. Am Nat. 2008;172:194–202. doi: 10.1086/588075. [DOI] [PubMed] [Google Scholar]
- Mitra C, Wagner WE, Zera AJ, Tolle AE. Variation in singing behaviour among morphs of the sand cricket, Gryllus firmus. Ecol Ent. 2011;36:152–160. [Google Scholar]
- Moore AJ. The inheritance of social-dominance, mating-behavior and attractiveness to mates in male Nauphoeta-Cinerea. Anim Behav. 1990;39:388–397. [Google Scholar]
- Muhlhauser C, Blanckenhorn WU. The quantitative genetics of sexual selection in the dung fly Sepsis cynipsea. Behaviour. 2004;141:327–341. [Google Scholar]
- Narraway C, Hunt J, Wedell N, Hosken DJ. Genotype-by-environment interactions for female preference. J Evol Biol. 2010;23:2550–2557. doi: 10.1111/j.1420-9101.2010.02113.x. [DOI] [PubMed] [Google Scholar]
- Neff BD, Svensson EI. Polyandry and alternative mating tactics. Philos Trans R Soc Lond B Biol Sci. 2013;368 doi: 10.1098/rstb.2012.0045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols RA, Butlin RK. Does runaway sexual selection work in finite populations. J Evol Biol. 1989;2:299–313. [Google Scholar]
- Papke RS, Kemp DJ, Rutowski RL. Multimodal signalling: structural ultraviolet reflectance predicts male mating success better than pheromones in the butterfly Colias eurytheme L. (Pieridae) Anim Behav. 2007;73:47–54. [Google Scholar]
- Pomiankowski A, Iwasa Y. Evolution of multiple sexual preferences by Fisher‘s runaway process of sexual selection. Proc R Soc B Biol Sci. 1993;253:173–181. [Google Scholar]
- Qvarnström A, Brommer JE, Gustafsson L. Testing the genetics underlying the co-evolution of mate choice and ornament in the wild. Nature. 2006;441:84–86. doi: 10.1038/nature04564. [DOI] [PubMed] [Google Scholar]
- Rodriguez RL, Greenfield MD. Genetic variance and phenotypic plasticity in a component of female mate choice in an ultrasonic moth. Evolution. 2003;57:1304–1313. doi: 10.1111/j.0014-3820.2003.tb00338.x. [DOI] [PubMed] [Google Scholar]
- Roff DA. Evolutionary Quantitative Genetics. Chapman and Hall: New York; 1997. [Google Scholar]
- Roff DA. The threshold model as a general purpose normalizing transformation. Heredity. 2001;86:404–411. doi: 10.1046/j.1365-2540.2001.00844.x. [DOI] [PubMed] [Google Scholar]
- Roff DA. Modeling Evolution: An Introduction to Numerical Methods. Oxford Univ. Press: Oxford; 2010. [Google Scholar]
- Roff DA.2015The evolution of mate choice: a dialogue between theory and experiment Ann NY Acad Sci(in press). [DOI] [PubMed]
- Roff DA, Crnokrak P, Fairbairn DJ. The evolution of trade-offs: geographic variation in call duration and flight ability in the sand cricket, Gryllus firmus. J Evol Biol. 2003;16:744–753. doi: 10.1046/j.1420-9101.2003.00570.x. [DOI] [PubMed] [Google Scholar]
- Roff DA, Fairbairn DJ. The evolution of phenotypes and genetic parameters under preferential mating. Ecol Evol. 2014;4:2759–2776. doi: 10.1002/ece3.1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roff DA, Wilson AJ.2014Quantifying genetic by environmental interactions in laboratory systemsIn: Hunt J, Hosken DJ (eds)Genotype-by-Environment Interactions and Sexual Selection Wiley-Blackwell; 101–136. [Google Scholar]
- Sappington TW, Taylor OR. Disruptive sexual selection in Colias-eurytheme butterflies. Proc Nat Acad Sci USA. 1990;87:6132–6135. doi: 10.1073/pnas.87.16.6132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schielzeth H, Bolund E, Forstmeier W. Heritability of and early environment effects on variation in mating preferences. Evolution. 2010;64:998–1006. doi: 10.1111/j.1558-5646.2009.00890.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmoll T. A review and perspective on context-dependent genetic effects of extra-pair mating in birds. J Ornithol. 2011;152:265–277. [Google Scholar]
- Sharma MD, Tregenza T, Hosken DJ. Female mate preferences in Drosophila simulans: evolution and costs. J Evol Biol. 2010;23:1672–1679. doi: 10.1111/j.1420-9101.2010.02033.x. [DOI] [PubMed] [Google Scholar]
- Simmons LW. Genotypic variation in calling song and female preferences of the field cricket Teleogryllus oceanicus. Anim Behav. 2004;68:313–322. [Google Scholar]
- Uller T, Olsson M. Multiple paternity in reptiles: patterns and processes. Mole Ecol. 2008;17:2566–2580. doi: 10.1111/j.1365-294X.2008.03772.x. [DOI] [PubMed] [Google Scholar]
- Wagner WE. Measuring female mating preferences. Anim Behav. 1998;55:1029–1042. doi: 10.1006/anbe.1997.0635. [DOI] [PubMed] [Google Scholar]
- Wolff JO, Macdonald DW. Promiscuous females protect their offspring. TREE. 2004;19:127–134. doi: 10.1016/j.tree.2003.12.009. [DOI] [PubMed] [Google Scholar]
- Zhou YH, Kelly JK, Greenfield MD. Testing the Fisherian mechanism: examining the genetic correlation between male song and female response in waxmoths. Evol Ecol. 2011;25:307–329. [Google Scholar]