Decomposition of surface EMG signals from cyclic dynamic contractions

Abstract

Over the past 3 decades, various algorithms used to decompose the electromyographic (EMG) signal into its constituent motor unit action potentials (MUAPs) have been reported. All are limited to decomposing EMG signals from isometric contraction. In this report, we describe a successful approach to decomposing the surface EMG (sEMG) signal collected from cyclic (repeated concentric and eccentric) dynamic contractions during flexion/extension of the elbow and during gait. The increased signal complexity introduced by the changing shapes of the MUAPs due to relative movement of the electrodes and the lengthening/shortening of muscle fibers was managed by an incremental approach to enhancing our established algorithm for decomposing sEMG signals obtained from isometric contractions. We used machine-learning algorithms and time-varying MUAP shape discrimination to decompose the sEMG signal from an increasingly challenging sequence of pseudostatic and dynamic contractions. The accuracy of the decomposition results was assessed by two verification methods that have been independently evaluated. The firing instances of the motor units had an accuracy of ∼90% with a MUAP train yield as high as 25. Preliminary observations from the performance of motor units during cyclic contractions indicate that during repetitive dynamic contractions, the control of motor units is governed by the same rules as those evidenced during isometric contractions. Modifications in the control properties of motoneuron firings reported by previous studies were not confirmed. Instead, our data demonstrate that the common drive and hierarchical recruitment of motor units are preserved during concentric and eccentric contractions.

over the past 3 decades, since the report by LeFever and De Luca (1982), there have been various attempts at developing algorithms for automatically decomposing the electromyographic (EMG) signal into its constituent motor unit action potential (MUAP) trains (MUAPTs). The work was motivated by interest in studying the behavioral characteristics of motor units during a muscle contraction. The intent of this automated approach was and remains to provide the firing description of numerous simultaneously active motor units. More recently, EMG decomposition algorithms have evolved from decomposing intramuscular recordings to decomposing the surface EMG (sEMG) signal. Present algorithms (De Luca et al. 2006; Nawab et al. 2010) can identify far more than the five MUAPTs per contraction that could be studied previously by conventional intramuscular electrode techniques.

To date, all reported approaches have been limited to analyzing EMG signals obtained during isometric contractions, where the muscle fibers are kept at or near a constant length. Under this condition, variability in the shapes of the MUAPs occurs gradually and in relatively small increments, limiting the complexity of the EMG signal. During dynamic contractions, the relative movement of the electrode and the signal source alters the amplitude and frequency characteristics of the MUAPs during the contraction, thereby additionally complicating the process of MUAP shape recognition.

To be sure, studies performed under the restriction of isometric contraction have brought forth some deeper and clearer understanding of motor unit control such as the common drive property (De Luca et al. 1982b; De Luca and Erim 1994) and the onion skin property (De Luca et al. 1982a; De Luca and Contessa 2012; De Luca and Hostage 2010). However, with the exception of postural muscles and some small muscles stabilizing joints, most muscles contract anisometrically during mobile activities. Thus, to study the control strategies of the nervous system during movement involving concentric and eccentric contractions, an algorithm that is capable of decomposing the sEMG signal during dynamic contractions is required.

This report describes an innovative method for decomposing the sEMG signals obtained during cyclic contractions of elbow flexion/extensions and during knee and ankle flexion/extension during gait.

METHODS

Approach

The decomposition of the sEMG signal from dynamic (anisometric) contractions poses significant challenges not present in isometric contractions. The dominant issue concerns the substantial variation in the shape and amplitude of the MUAPs throughout a contraction. The variations are a consequence of the change in the relative position of the electrodes located on the surface of the skin, which remains stable, and the source of the action potentials on the muscle fibers, which changes as the muscle shortens and lengthens. The variation in the space between the electrode and the source influences the amount of spatial filtering that is incurred by the action potential as it radiates to the surface of the skin.

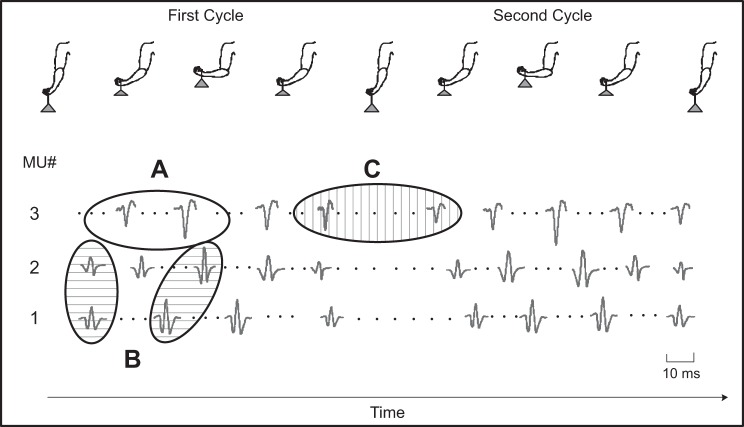
In this study, we limit the development of the algorithm to a cyclic contraction where the modifications of the MUAPs are to a great extent repeated from cycle to cycle, simplifying the identification process. Nonetheless, even in a cyclic contraction, the identification process must overcome challenges. We anticipated three potential difficulties that may arise when decomposing signals recorded during cyclic dynamic contractions. As the length of the muscle increases or decreases, it is possible that the MUAPs undergo an intracycle shape change. This morphing is illustrated in Fig. 1A. Because MUAPs may change within a cycle, it is also possible that MUAPs from two different motor units may be dissimilar within one segment of a cycle but become substantially similar in another segment of the same cycle. This intracycle morphing is illustrated in Fig. 1B. As an additional challenge, MUAPs of the same motor unit may change between cycles, even when the joint angle is at the same position. We refer to this modification as an intercycle shape change, illustrated by Fig. 1C. Collectively, these potential challenges could lead to a greater propensity for motor unit identification errors in which action potentials from a MUAPT are either missed or incorrectly classified as belonging to another motor unit.

Fig. 1.

Anticipated challenges that are likely present when decomposing surface electromyographic (sEMG) data acquired during cyclic dynamic contractions. Real motor unit (MU) action potential (MUAP) data for 3 different MUs are shown from the biceps brachii muscle of a subject recorded during 2 consecutive 5-s elbow flexion/extension contraction cycles while holding an 8-lb weight. Three potential challenges are identified by the oval outlines: A, intracycle shape change (no shading); B, intracycle shape similarity (horizontal bar shading); and C, intercycle shape change (vertical bar shading).

The ability of the algorithm to track the morphing of the MUAP shapes and discriminate MUAPs from different motor units is made possible by the analysis of four channels of sEMG signals obtained by four differential combinations from the five pin electrodes described in De Luca et al. (2006), the details of which are summarized in the Experiments in Support of Algorithm Development section of methods. Each MUAP is represented by a different characteristic shape in the sEMG signal of each channel. The pattern of the morphing progression is distinct in each channel, thus providing a means for tracking the morphing progression of each MUAP.

Algorithm Development

The main components of the algorithm developed for decomposing sEMG signals from dynamic contractions are shown in the block diagram of Fig. 2. The algorithm is an outgrowth of our previous algorithm designed for decomposing sEMG signals from isometric contractions (De Luca et al. 2006; Nawab et al. 2010). The algorithm can be conceptually divided into two distinct stages. The first deals with the problem of identifying uncontaminated action potentials of different motor units within the sEMG signal that is otherwise dominated by superposition. The algorithms for identifying uncontaminated action potentials are organized around the maximum a posteriori probability classifier introduced by LeFever and De Luca (1982). In the second stage, the detected MUAPs are used to identify automatically the constituent action potentials within superposition. Specifically, the algorithm identifies a subset of MUAPs that occur within a given superposition and then determines the precise location of each MUAP such that the superposition energy can be accounted for with a high degree of accuracy.

Fig. 2.

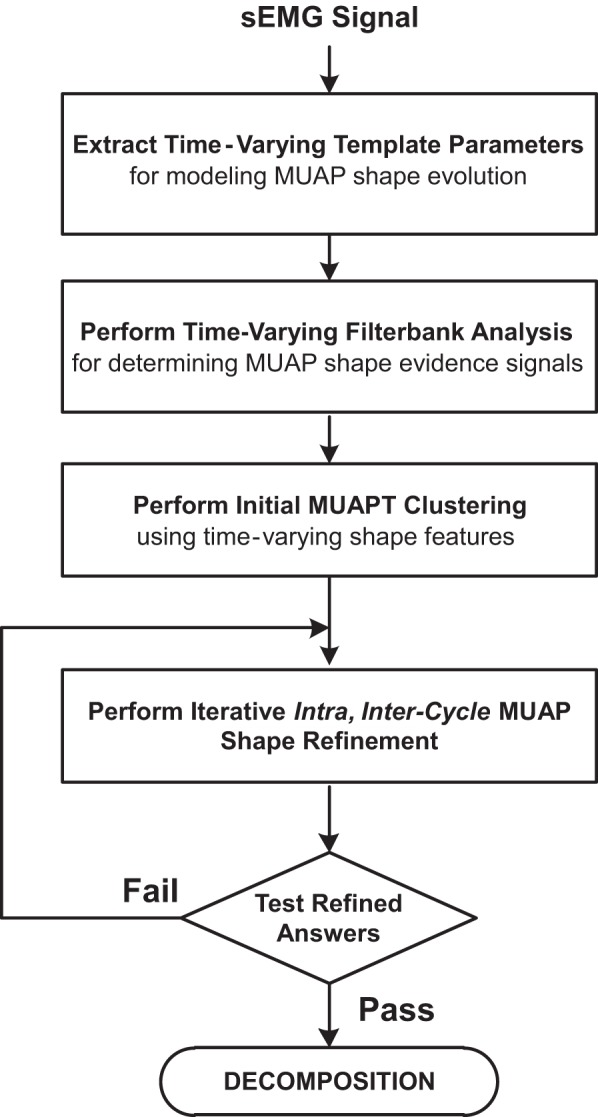
Flow diagram of the different functional components of the algorithm developed for decomposing sEMG signals acquired from cyclic dynamic contractions.

The algorithm for decomposing the sEMG signal from cyclic contractions was evolved in a piecemeal fashion. Adjustments were made as the complexity of the sEMG signals increased incrementally by challenging the algorithm with data from staircase trajectories of discrete steps at different contraction angles, then from single-cycle dynamic contractions, and ultimately by multicycle dynamic contractions.

Staircase trajectory.

Changes that occur to the sEMG waveform as the muscle length changes were introduced incrementally by this trajectory. Modifications to the algorithm were advanced gradually by analyzing the algorithm output for sEMG signals from staircase trajectories with increasingly smaller increments in contraction angle between each force plateau. We focused on two main issues: 1) tracking the evolution of MUAP shapes across steps of different contraction angles; and 2) providing incremental recruitment identification capability when the joint angle changes from one plateau to the next.

The first issue of MUAP shape evolution was addressed by modifying the maximum a posteriori probability classifier used to identify the MUAPs of each motor unit. In its initial form, the classifier was applied to sEMG signals obtained from isometric contractions during which changes in MUAP shapes tend to occur relatively gradually and in small increments over contractions of relatively long duration (De Luca 1984; Roy et al. 2007). For the present application, we modified the classifier to account for MUAP shape evolution that may occur with changes in contraction angle by implementing more adaptive MUAP-matching criteria. Specifically, we define an n-dimensional acceptance region that identifies MUAPs of the same motor unit based on local occurrences of uncontaminated MUAP shape parameters. The acceptance region of each motor unit is updated with the classification of each additional uncontaminated MUAP occurrence to account for changes in MUAP shape parameters that may occur as a function of time and contraction angle.

To address the second issue of incremental recruitment identification, we used components of our isometric contraction algorithm designed to identify motor unit recruitment during isometric changes in contraction force and adapted them to detect motor unit recruitment that occurs during dynamic changes in contraction angle. Specifically, the problem of incremental recruitment identification was addressed by adding an iterative search procedure: subsets of MUAPs are processed one at a time until the mean energy of the residual sEMG signal satisfies an adaptive threshold [see Nawab et al. (2010) for more details]. This approach allows the algorithm to examine thoroughly a reduced-complexity data set of MUAPs with fewer superpositions.

Single-cycle trajectory.

The algorithm was enhanced to account for intracycle shape changes (Fig. 1A) and intracycle shape similarities (Fig. 1B) that may occur during single-cycle anisometric contractions. Statistical classifiers derived from machine learning algorithms were combined with the time-varying maximum a posteriori probability classifier used for identifying MUAPs during staircase contractions. Specifically, we evaluated parametric changes in MUAP shapes by performing a detailed examination of the firing-to-firing continuity. A nearest neighbor classifier (Duda et al. 2000) was then designated to differentiate intracycle shape changes based on these MUAP shape parameters. Additional strategies designed to avoid incorrect classification of MUAPs were implemented based on the mathematical formulation of multiobject tracking (Vapnik 1999), an effective image-processing technique. This formulation establishes profiles of shape evolution that enable the algorithm to retrieve up-to-date shape parameters at any given time. We tested these algorithmic constructs by implementing different combinations of continuity constraints on variable features and by incorporating adaptive signal processing mechanisms into the algorithms for situation-dependent selection of combinations of continuity constraints on variable features.

Multicycle trajectory.

To decompose the sEMG signal acquired during multicycle contractions, we made additional modifications to our algorithms to account for the anticipated possibility of intercycle shape changes, illustrated in Fig. 1C, by formulating a relaxed version of the shape continuity requirements at the juncture between adjacent cycles. Specifically, the modified algorithm permits the maximum a posteriori probability classifier discrimination criteria to encompass a greater acceptance region for each motor unit during the pre- and posttransition cycles. To mitigate the susceptibility of incorrectly classifying MUAPs, we employed MUAP profile evolution discrimination based on the multiobject tracking approach implemented during single-cycle contractions. This approach works because shape similarities that are localized in the vicinity of an intercycle transition can be discriminated using the evolution of parametric changes in MUAP shapes across the entirety of individual cycles. To strengthen the robustness of this strategy further, cyclostationary signal analysis (Gardner 1994) was employed to augment the shape evolution of the involved cycles. This rigorous mathematical framework is capable of detecting the cycle-to-cycle repeatability of shape evolution trajectories and provides more robust discrimination of MUAPs from different motor units across each cycle.

Validation.

We used two approaches to validate the results of the algorithm. The first was the decompose-synthesize-decompose-compare (DSDC) method introduced by Nawab et al. (2010) and improved by De Luca and Contessa (2012). The second was the two-source method introduced by Mambrito and De Luca (1984).

DSDC METHOD.

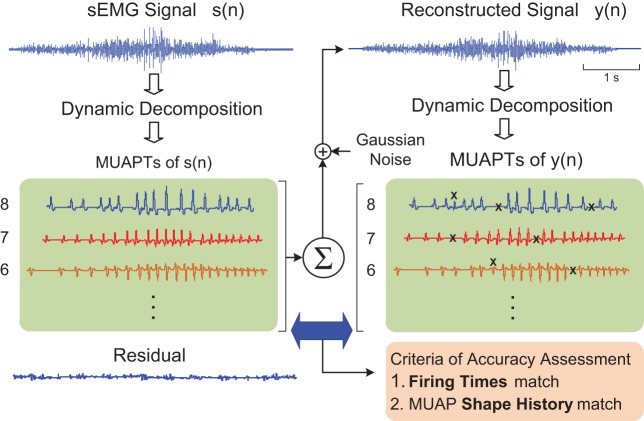
The DSDC method, initially developed for sEMG decomposition performed under isometric conditions, underwent adaptation for anisometric contractions. The details are presented in the diagram in Fig. 3. The method evaluates errors by decomposing a realistic synthesized sEMG signal and comparing the extracted MUAPTs with the MUAPTs known within the synthesized signal. The synthesized signal is composed of MUAPTs obtained from the decomposition of a recorded sEMG signal and randomized band-limited, time-varying Gaussian noise equal in root mean square to that of the residual of the recorded sEMG decomposition. To account for the changes in the shape and/or amplitude of the MUAPs throughout the anisometric contraction, we added a shape profile algorithm containing a full history of the MUAP shape and the firing times. The realistic synthesized signal was decomposed to obtain the firing instances and the time-varying MUAP shapes. Two different metrics of the decomposition performance were obtained: 1) the robustness of timing detection, calculated by how well the occurrence time of each firing instance extracted from the synthesized signal compares with the timing of the corresponding firing instance known within the signal; and 2) the robustness of shape profile tracking, calculated by how well the MUAP shapes extracted from the synthesized signal match the shape history of the MUAPs known within the signal.

Fig. 3.

A diagram illustrating the decompose-synthesize-decompose-compare (DSDC) method used to assess the accuracy of the decomposition algorithm. A recorded sEMG signal s(n) is decomposed to identify its MUAP trains (MUAPTs). A reconstructed signal y(n) is synthesized by summing together the real MUAPTs from s(n) and time-varying Gaussian noise for which the variance is set equal to that of the residual signal from the decomposition. The reconstituted signal y(n) is then decomposed and compared with the MUAPTs within the synthesized signal. The Xs indicate discrepancies between the MUAPTs of y(n) and s(n), which are designated as errors based on a comparison of the MU firing times and MUAP shapes.

TWO-SOURCE METHOD.

We supplemented the DSDC validation with the two-source method. Two sensors were placed near each other so that the sEMG signal detected by each sensor contained the MUAPTs from some common motor units. The sEMG signals from the sensors were recorded simultaneously and decomposed, and the firing instances of the common MUAPTs were compared. Further details of these validation tests are presented in Kline and De Luca (2014). We performed this test on all three muscles but succeeded in obtaining common MUAPTs only in the biceps brachii for the flexion/extension protocol. In the tibialis anterior and vastus lateralis muscles, no common MUAPTs could be located during gait.

Experiments in Support of Algorithm Development

Five subjects (3 men and 2 women, mean age 32.8 ± 12.6 yr, range 24–55 yr) participated in this study. All subjects were in good health and were screened for musculoskeletal or neurological disorders using a health questionnaire. Each of the subjects read, stated he/she was provided with a description of the procedure, and signed informed consent forms approved by the Boston University Institutional Review Board and the Western Institutional Review Board before participating in the study.

Two protocols were performed on all of the subjects. One was an elbow flexion/extension protocol, and the other was a gait protocol. For the elbow protocol, the subjects were seated with their shoulder in the neutral position, holding an 8-lb weight. Subjects were first instructed to flex their elbow to produce a staircase trajectory in which they maintained brief isometric contractions (plateaus) at specified intervals or steps between full elbow extension and 135° flexion. Three staircase conditions were tested to provide an increasing number of transitions between plateaus, which were sustained for progressively shorter durations: 4 steps (33.8, 67.5, 101.3, 135°) of 10-s duration each; 8 steps (16.9, 33.8, 50.6, …, 135°) of 5-s duration each; and 12 steps (11.3, 22.5, 33.8, …, 135°) of 3-s duration each. An electrogoniometer affixed to the elbow provided real-time feedback to the subject by displaying the joint motion of the subject with respect to a tracing of the target trajectory. The subjects were then instructed to complete a single cycle of flexion and extension of the elbow from 0 to 90° at two constant velocities: 30 and 45°/s. Finally, subjects were instructed to repeat each of the single-cycle contractions 8 times continuously.

For the gait study, subjects were instructed to walk on a level surface within the laboratory for 8 steps at 2 different speeds: 40 and 60 steps per minute. A metronome set to the desired cadence was used to assist the subject. A practice session was included for both protocols before the data acquisition. The total number of contractions for each of the conditions is summarized in Table 1.

Table 1.

Motor unit decomposition yield and accuracy

Contraction					Average Accuracy, %
Category	Muscle	Trajectory	Number of Contractions	Average MU Yield	DSDC	Two-Source
Staircase	Biceps brachii	4 Steps, 10-s plateau	4	21 ± 5	93.6 ± 2.5
		8 Steps, 5-s plateau	4	22 ± 7	92.3 ± 3.4
		12 Steps, 3-s plateau	4	25 ± 6	90.4 ± 3.5
Single cycle	Biceps brachii	Elbow flexion/extension 30°/s	10	9 ± 4	88.1 ± 2.4
		Elbow flexion/extension 45°/s	10	6 ± 2	85.6 ± 2.6
Multicycle	Biceps brachii	Elbow flexion/extension 30°/s	10	12 ± 7	91.4 ± 2.1	90.5 ± 1.0
		Elbow flexion/extension 45°/s	10	10 ± 6	89.3 ± 2.4	89.0 ± 1.3
	Tibialis anterior	Gait 40 steps per minute	9	18 ± 8	92.2 ± 3.3
		Gait 60 steps per minute	9	11 ± 5	90.5 ± 3.2
	Vastus lateralis	Gait 40 steps per minute	9	13 ± 9	86.4 ± 3.1
		Gait 60 steps per minute	9	10 ± 7	85.1 ± 3.8

Summary of motor unit (MU) action potential train yield achieved by the decomposition algorithm developed for cyclic dynamic contractions and accuracy measured by the decompose-synthesize-decompose-compare (DSDC) and 2-source test methods. Results (average ± SD) are for the entire data set across all subjects and are presented separately for the different contraction categories, muscle groups, and trajectories.

Surface EMG signals were acquired from the dominant biceps brachii during the elbow flexion/extension protocol and from both the dominant vastus lateralis (a knee extensor) and the dominant tibialis anterior (an ankle flexor) during the gait protocol. The subject's skin was prepared by cleansing with an alcohol swab and by removing the superficial dead skin with multiple tape peels. A dEMG sensor array, consisting of five cylindrical electrodes (0.5-mm diameter) arranged in the four corners and middle of a 5-mm square, was located on the surface of the skin at the approximate middle of the muscle belly, following the guidelines of Zaheer et al. (2012) for maximizing signal fidelity and motor unit yield. Signals from four pairs of the electrodes were differentially amplified and band-pass filtered from 20 to 450 Hz. All signals were acquired using a Delsys Bagnoli multichannel acquisition system and sampled at 20 kHz per channel to provide necessary resolution for the template-matching within the algorithms. Data were stored on a computer for offline analysis. For additional details regarding the recording procedure, refer to De Luca et al. (2006).

Joint displacement was recorded from the elbow and the ankle using goniometers having a resolution of ±0.5°. Foot switches were attached bilaterally to the heel and toe areas of the foot to record temporal gait parameters. Signals were conditioned and sampled at 200 Hz. Recordings of the sEMG data were synchronized with the ankle goniometer and footswitch data using a trigger pulse.

RESULTS

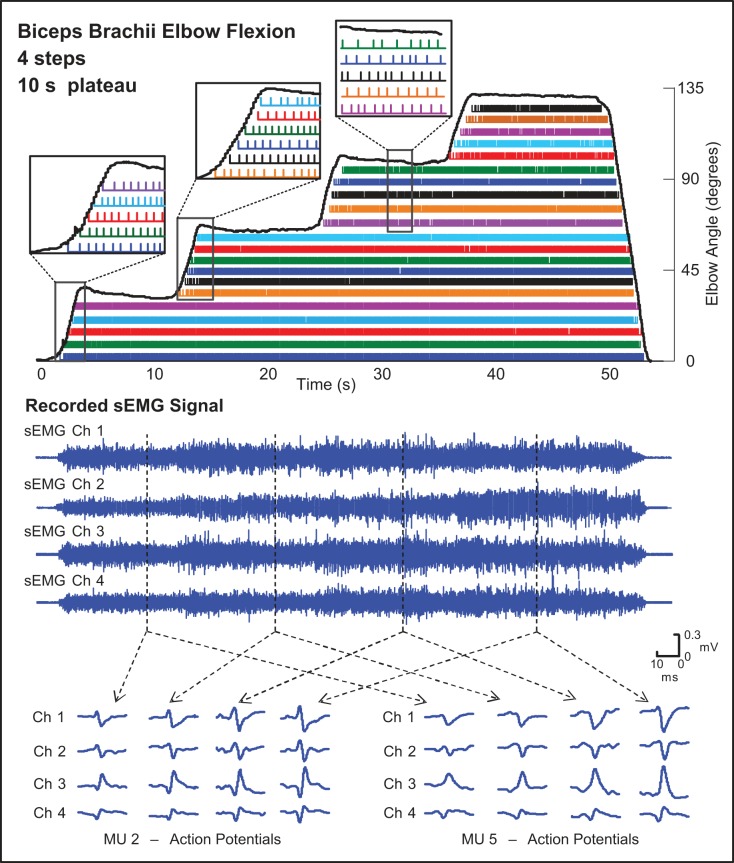
The performance of the algorithm is summarized in Table 1. For the staircase protocol, mean motor unit yield ranged from 21 to 25 MUAPTs. Verification of motor unit decomposition using the DSDC test resulted in accuracies that ranged from 90.4 to 93.6%. Figure 4 provides an example decomposition result for a staircase protocol from the biceps brachii muscle of 1 subject. Each of the sequential colored bars contains the firing instances of the same MUAPT. The MUAPs detected in each of 4 channels of the recorded sEMG signal are shown for 2 typical motor units at different joint angles of contraction. The data convey that MUAP changes appear to occur progressively and more in amplitude than in shape. The algorithm was able to track these changing MUAPs and discriminate between the MUAPs of different motor units as the joint angle changed throughout the contraction. The algorithm was also able to track the recruitment of new MUAPTs for each change in elbow flexion angle. Furthermore, no previously recruited MUAPT dropped out when the elbow position changed.

Fig. 4.

Decomposition results from a staircase trajectory contraction from 1 subject acquired from the biceps brachii muscle during elbow flexion/extension with an 8-lb weight. The staircase trajectory ranged from 0 to 135° of elbow flexion with 4 increments or “steps” of 10-s duration each. The firing instances of different MUs are identified by differently colored bars. Typical MUAPs identified in each of the 4 channels (Ch) of the recorded sEMG signal are shown for 2 example MUs at different joint angles throughout the contraction. The callout boxes identify the recruitment and firing patterns of MUs during the transition period between steps. The solid black lines represent the elbow angle measured from an electrogoniometer. Assessed accuracy was 93.6%.

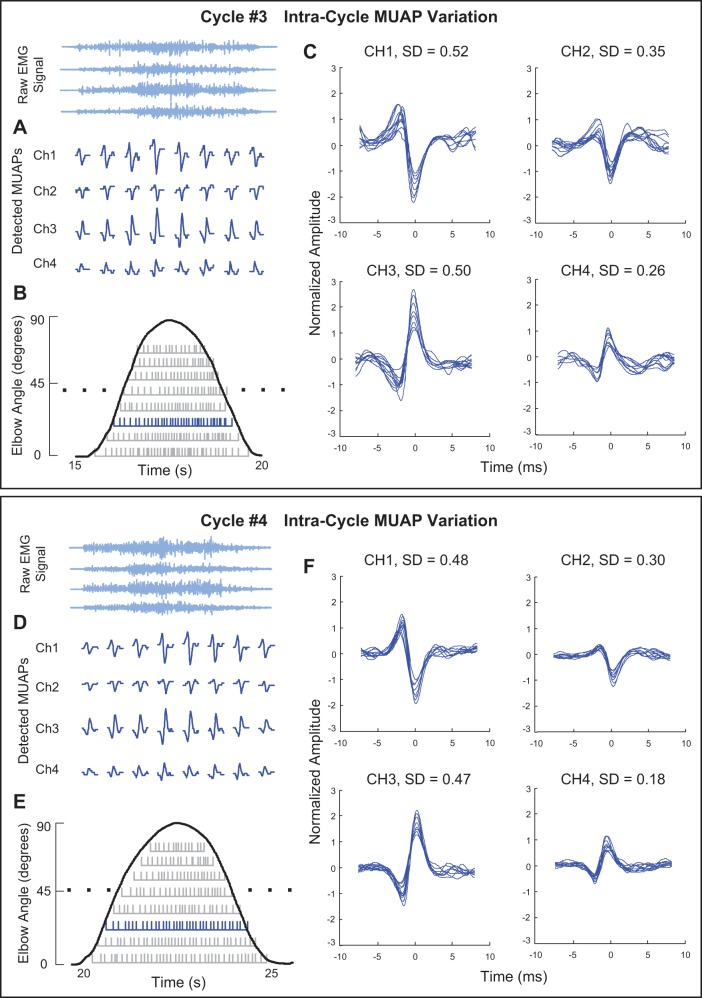
The sEMG signals from single-cycle contractions of the biceps brachii muscle yielded fewer MUAPTs than were obtainable for the staircase contractions (Table 1). A typical example of MUAP shapes and their firing instances during a single cycle of elbow flexion and extension is shown in the top plot of Fig. 5. The top plot presents the action potentials (Fig. 5A) and the firing instances (Fig. 5B) of MUAPT 3, depicted in blue, from the four channels of the decomposed sEMG signal during cycle 3 of the eight-cycle flexion/extension sequence. The bottom plot presents similar data for the same motor unit from cycle 4 of the flexion/extension sequence. Within each of the two cycles, the MUAPs appear to change progressively and mostly in amplitude as the contraction angle varies. These changes are made evident in Fig. 5, C and F, when the MUAPs observed in each channel are overlaid and normalized with respect to the MUAP for which the peak amplitude is the lowest among all action potentials belonging to the MUAPT. When comparing the MUAPs across cycles, it is also apparent that the shapes of the same MUAPs remain relatively invariant and could be tracked by our algorithm from one cycle to the next.

Fig. 5.

Decomposition results for data acquired from the biceps brachii muscle during the 3rd (Cycle #3, top plot) and 4th (Cycle #4, bottom plot) cyclic contractions of multicycle elbow flexion and extension (0–90°). The plots include an example of typical changes in the MUAP shape from MUAPT 3 for the 4 channels of data acquired from the sensor (A and D), the firing instances of 8 MUAPTs (gray bars) derived from the decomposition algorithm for each of the cyclic contractions (B and E), and superimposed MUAP waveforms for each of the 4 channels (C and F). The standard deviation (SD) of the MUAP amplitude, normalized as a percentage of the smallest action potential of the MUAPT, is presented for each channel in C and F.

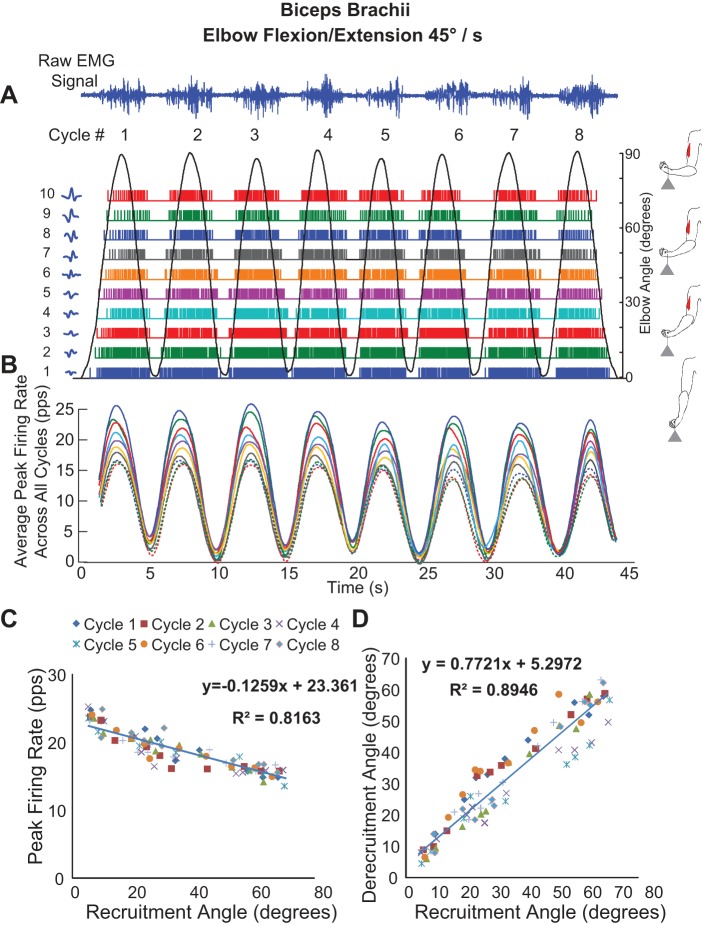
The sEMG signals from multicycle contractions of the biceps brachii muscle yielded significantly higher (equal variance t-test, P < 0.001) numbers of MUAPTs than for single-cycle contractions (Table 1). Figure 6A shows the firing instances of MUAPTs derived from 8 cyclic flexion/extension contractions of the biceps brachii muscle performed at 45°/s. The recruitment and derecruitment of the motor units may be seen as the elbow angle changes periodically. MUAPTs identified in the 1st flexion/extension cycle were identified consistently in subsequent cycles. The average yield ranged from 5 to 21 (mean 12 ± 7) MUAPTs for the 30°/s contraction and 3 to 18 (mean 10 ± 6) MUAPTs for the 45°/s contraction. Note that for this set of contractions the decomposition verification was performed with both the DSDC method and the 2-source method. The results from the 2 methods were strikingly similar. For the DSDC method, the accuracy ranged between 88.6 and 94.5% (mean 91.4 ± 2.1%) for the 30°/s contractions and 85.2–92.7% (mean 89.3 ± 2.4%) for the 45°/s contractions. For the 2-source method, the average accuracy was 90.5% for the 30°/s contractions and 89.0% for the 45°/s contractions.

Fig. 6.

Decomposition of sEMG data recorded from 1 subject during a multicycle contraction of the biceps brachii muscle (8 cycles) during repetitive elbow flexion/extension at an angular velocity of 45°/s. A: the sEMG signals and firing instances of MUAPTs derived from decomposing these signals are shown for changes in elbow angle (black sinusoidal line). The MUAP waveform templates obtained at recruitment are shown adjacent to the y-axis for each train. B: the mean firing rate values of the firing instances shown in A (MUAPTs 1–7 are shown as solid colored lines, and MUAPTs 8–10 are shown as dotted colored lines). C: the peak firing rate values are plotted vs. the angle at which the MUAPT was recruited and derecruited. The results of a linear regression analysis of the data are shown. D: the angle at which each MU is recruited is plotted vs. the angle at which it is derecruited. The results of a linear regression analysis of the data are shown. pps, Pulses per second.

Figure 6B presents the mean firing rate values of the firing instances shown in Fig. 6A. Note that the firing rates of all of the MUAPTs oscillate in unison. The firing rate curve of each MUAPT is computed by low-pass filtering the impulse train of firings with a unit-area Hanning window of 2-s duration. The values do not all reach 0 when the motor units stop firing as indicated in Fig. 6A due to the filtering influence on the firing instances. For additional details on the filtering procedure, refer to De Luca et al. (1982a). When the peak firing rate values are plotted vs. the angle at which they are recruited (Recruitment Angle in Fig. 6C), a linear regression analysis reveals an inverse relationship (r² = 0.82). When the angle at which each motor unit is recruited is plotted vs. the angle at which it is derecruited (Derecruitment Angle in Fig. 6D), a linear relationship (r² = 0.89) with a slope <1 (0.77) is found.

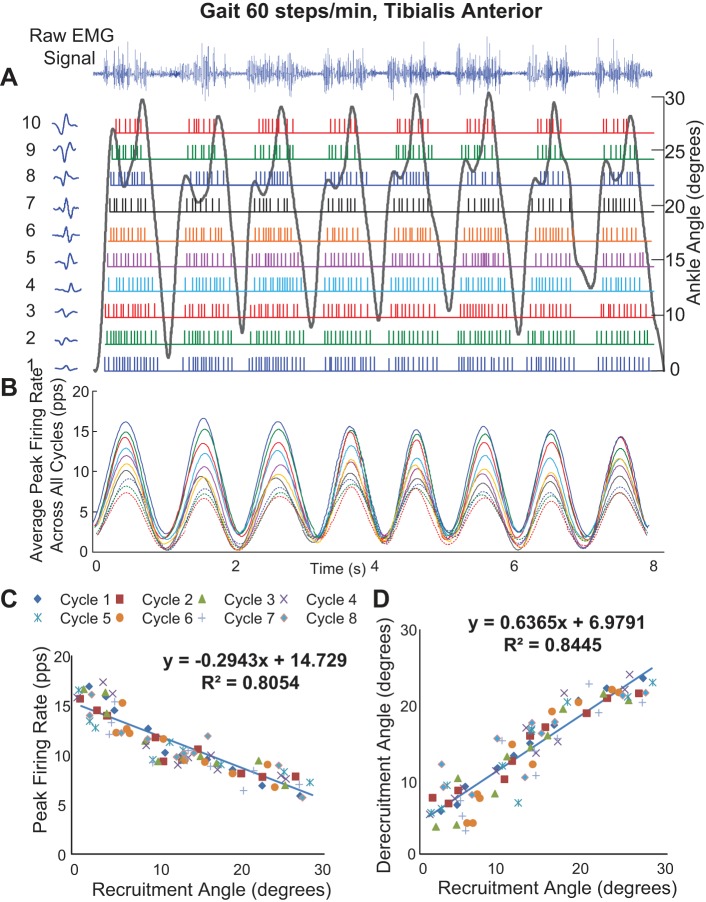
Figure 7 shows the firing behavior of MUAPTs extracted from the sEMG signal of the tibialis anterior muscle during eight successive gait cycles for a representative subject. Again, all of the MUAPTs are successively identified throughout the full sequence of the steps, including in cases where the angle profile differs, as in the last two steps. Even during gait, the firing rates are modulated in unison (Fig. 7B), and the relationship between the peak firing rate and the joint angle at which recruitment occurs is inversely linear (r² = 0.81; Fig. 7C), whereas the relationship between the derecruitment and recruitment is positively correlated (r² = 0.84; Fig. 7D).

Fig. 7.

Decomposition of sEMG data recorded from the tibialis anterior muscle from 1 subject during 8 gait cycles for a walking speed of 60 steps per minute. A: the sEMG signals and firing instances of MUAPTs derived from decomposing these signals are shown for changes in ankle angle (black line). The MUAP waveform templates at recruitment are shown adjacent to the y-axis for each train. B: the mean firing rate values of the firing instances shown in A (MUAPTs 1-7 are shown as solid colored lines, and MUAPTs 8-10 are shown as dotted colored lines). C: the peak firing rate values are plotted vs. the angle at which the MUAPT was recruited and derecruited. The results of a linear regression analysis of the data are shown. D: the angle at which each MU is recruited is plotted vs. the angle at which it is derecruited. The results of a linear regression analysis of the data are shown.

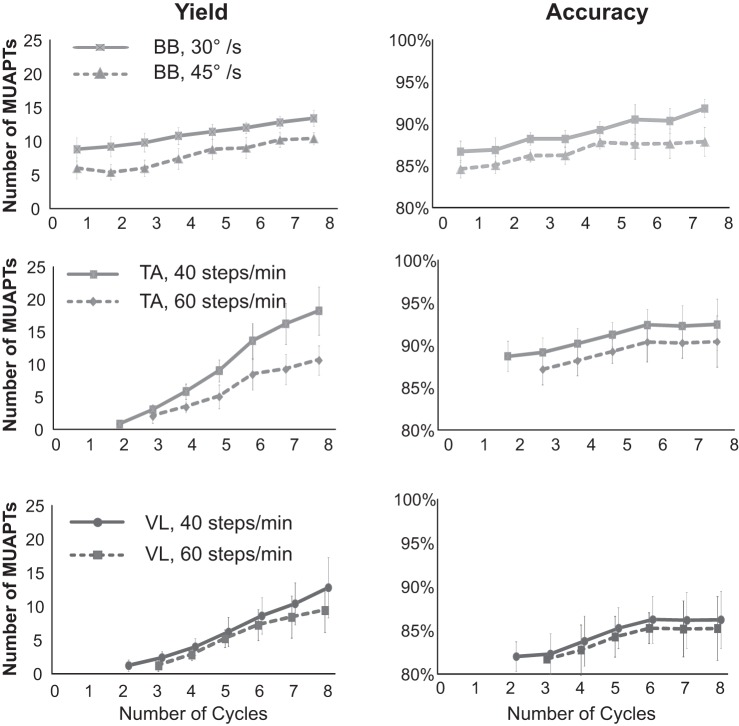
The accuracy and yield of the decomposition increased as the number of cycles increased from 1 to 8 (Fig. 8). The increase in accuracy was greater for the contractions performed at lower speeds, and the rate of improvement with repeated cycles was reduced after six cycles.

Fig. 8.

Decomposition algorithm performance is shown as a function of contraction cycle for the 3 muscles studied (BB, biceps brachii; TA, tibialis anterior; and VL, vastus lateralis). Data for each contraction cycle is plotted as mean values with SD bars for all subjects tested for all contractions. Data are plotted separately for the 2 different elbow contraction speeds (top plots) and walking speeds (2 bottom plots). Accuracy is calculated using the DSDC method.

DISCUSSION

This first attempt at decomposing sEMG signals collected during anisometric contractions has produced an algorithm that performs well for the tested cyclic contractions. It is now possible to interrogate the control of motor units during dynamic activities that address issues of movement, not only force as was previously restricted by the decomposition of the sEMG signal from isometric contractions. In its present form, the algorithm begins to provide insight into the behavior of motor units during cyclic contractions. Further improvements should increase versatility to less constrained contractions and possibly allow for investigations during a variety of functional activities or athletics.

For this study, we limited the frequency of the contractions to those that would be performed during common daily activities. It is apparent that the accuracy and the yield are both influenced by the frequency of the contraction, but we did not explore a wider range of frequencies and amplitudes, as it was beyond the intention of developing this phase of the algorithm.

The present algorithm achieved accuracy values of 92.2% and MUAPT yields of up to ∼20. During gait, where the cycles are on the order of 2-s duration (Fig. 7), the accuracy and yield are poor in the 1st cycle but improve substantially as the number of cycles increases. In its current form, the performance of the algorithm improves in accuracy up to 6 cycles, and the yield improves up to 8 cycles and possibly more.

We were able to extract MUAPTs from the sEMG signals recorded during dynamic contractions in part because our algorithm makes no assumptions about the characteristics of the MUAPs or the statistics of the motor-unit firing instances. This inherent ability is unique among decomposition techniques. Other algorithms, such as the convolution kernel compensation (CKC) technique developed by Holobar and Zazula (2003, 2004, 2007), are based on blind-source separation signal processing principles. Their approach relies on several assumptions including that the motor units have stationary MUAPs throughout the duration of a contraction. However, MUAPs are known to be nonstationary during isometric contractions [as evidenced by Bertram et al. (1995), De Luca (1984), Fortune and Lowery (2009), Juel (1988), and Roy et al. (2007) among others] and during cyclic dynamic contractions (shown by Fig. 5). Other decomposition approaches, including the CKC method and an algorithm developed by Parsaei and Stashuk (2013), rely on the assumption that the active motor units produce statistically independent firing instances. Nevertheless, ample evidence again has shown that motor units manifest correlated fluctuations in their firing rates known as common drive during isometric contractions [as documented by De Luca et al. (1982b), De Luca and Erim (1994), Farina et al. (2014), and Laine et al. (2013) among others]. The lack of statistical independence between MUAPTs has been demonstrated more recently by us (De Luca and Kline 2014) using rigorous statistical analyses and is further evidenced by the correlated firing rates observed during cyclic dynamic contractions in Figs. 6 and 7 of this study. In contrast to decomposition algorithms proposed by others, ours is not restricted by any mathematical underlying assumption that limits its usefulness.

The accuracy of our decomposition results was measured predominantly using the DSDC validation algorithm. We (Kline and De Luca 2014) have provided evidence demonstrating that the DSDC validation overcomes the drawbacks of other validation approaches. Independent verification of our decomposition algorithm for isometric contractions has been provided in four separate reports by Hu et al. (2013a,b,c, 2014) using three different methods. Hu et al. (2013a,b) confirmed that the MUAPs identified by the decomposition algorithm were similar in shape to those obtained by trigger-averaging the MUAPs from the sEMG signal. Hu et al. (2013a,c) demonstrated that the firing instances obtained by our decomposition algorithm were resolved accurately within 0.6–2 ms. Hu et al. (2013b, 2014) provided visual verification that our decomposition algorithm yields MUAPTs with an average accuracy of 95%.

In the case of the multicycle contractions of the elbow, the decomposition results were also verified by the two-source method. (This was the only protocol that provided usable data.) The measurement of accuracy for both methods was remarkably similar, providing further corroboration of the accuracy with which motor-unit firings can be extracted by our decomposition algorithm during cyclic dynamic conditions.

As expected, the MUAPs are altered as the length of the muscle changes during dynamic contractions. However, it was advantageous to find that within a cycle the alterations in the MUAP occurred progressively and were more in amplitude than in shape. This is evident in Fig. 4 and Fig. 5, A and C. The fact that the amplitude of the MUAPs tended to increase as the biceps brachii muscle shortened in length was likely a consequence of progressive changes in the position of the electrode relative to the underlying muscle fibers. We further noted that the shape of the MUAPs appeared to be relatively invariant across cycles, as seen when comparing Fig. 5C with Fig. 5F, indicating that the anticipated challenge of intercycle MUAP variability was not as prevalent in our data set. Our dynamic decomposition algorithms were able to track MUAPs within and across cycles of changing joint angle and discriminate the changing MUAPs from different motor units successfully.

Neurophysiology

Our observations thus far indicate that the activation of motor units during cyclic contractions is similar in behavior to that during isometric contractions. The presence of the onion skin that has been reported by De Luca et al. (1982a) and De Luca and Erim (1994) in isometric linearly increasing force contractions, in which a hierarchical inverse relationship exists between the order in which the motor units are recruited and the firing rate of motor units, was also found in the behavior of the firing rates of the cyclic contractions. This may be seen in Figs. 6B and 7B where the firing rates of earlier recruited motor units are greater than the later recruited motor units at any time and at any angle. This inverse relationship has been interpreted as an “operating point” that remains invariant for the motoneurons in a pool, which are modulated by the excitation to the pool when changes in muscle contraction force are required (De Luca and Hostage 2010). The current findings support the notion that the motoneurons are controlled by this operating point regardless of whether the muscle length is held constant (isometric) or changes to produce movement (anisometric). Although we did not measure the contractile force in these experiments, the force required by the muscle to maintain a fixed load during a flexion/extension contraction is related to the joint angle. Therefore, when the peak firing-rate was regressed against the angle at which the motor units were recruited, there was an inverse linear relationship (Figs. 6C and 7C). When the angle of derecruitment was regressed against the angle of recruitment, there was a linear relationship with a slope <1 (0.77 in Fig. 6D and 0.64 in Fig. 7D). When De Luca and Hostage (2010) regressed the derecruitment threshold vs. the recruitment threshold of the force during isometric contractions, the slope was found to be >1. The difference may not necessarily represent dissimilarity in the motor unit behavior under the two different paradigms. It may be due to the rate of the decreasing force at the end of the contraction sequence. The cyclic contractions decelerated over a 2-s duration, whereas the isometric contractions decelerated over a 5-s duration.

We also found strong evidence for the common drive behavior of motor units, first reported by De Luca et al. (1982b) for isometric contractions and now first shown for dynamic cyclic contractions in Figs. 6B and 7B. Average peak firing rates of concurrently active MUAPTs fluctuate in unison and with the cyclic profile of the contraction. Our previous reports of the common drive behavior were derived from the fact that short-term fluctuations in mean firing rates of different MUAPTs during sustained isometric contractions were highly correlated. A similarly high degree of correlation was observed during cyclic movement (Figs. 6B and 7B). These data indicate that common drive is a control scheme that likely governs motor unit behavior across the spectrum of voluntary contractions.

In all of the 58 cyclic contractions from 3 muscles in the upper and lower limb, we found no examples of motor unit recruitment reversals during the eccentric and concentric phase of the oscillatory contraction nor did we find any reversal in the sequential periods of the cyclic contractions. Our observations are in agreement with those of Garland et al. (1996), Sogaard et al. (1996), Laidlaw et al. (2000), and Stotz and Bawa (2001), who found no difference in the recruitment order during shortening and lengthening contractions. We found that the same motor units were recruited during the shortening and lengthening of muscles in subsequent cycles, indicating that there was no change in the control strategy during eccentric and concentric contractions. Our observations do not support the interpretation of Nardone et al. (1989), who concluded that some motor units are recruited only during lengthening contractions. In the contractions we studied, we found no systematic differences in the control of motor units among isometric, concentric, and eccentric contractions.

GRANTS

This work was supported by the National Institute of Neurological Disorders and Stroke Grant 2-R44-NS-077526-03.

DISCLOSURES

C. J. De Luca is the President of Delsys, Inc., the company that developed the technology for decomposing the sEMG signals.

AUTHOR CONTRIBUTIONS

C.J.D.L. and S.H.N. conception and design of research; S.H.R. performed experiments; S.-S.C., S.H.R., and J.C.K. analyzed data; C.J.D.L., S.-S.C., and S.H.R. interpreted results of experiments; C.J.D.L., S.-S.C., and S.H.R. prepared figures; C.J.D.L., S.-S.C., S.H.R., and J.C.K. drafted manuscript; C.J.D.L., S.-S.C., S.H.R., J.C.K., and S.H.N. edited and revised manuscript; C.J.D.L., S.-S.C., S.H.R., J.C.K., and S.H.N. approved final version of manuscript.