Abstract
Smoothly graded muscle contractions depend in part on the precision and reliability of motoneuron action potential generation. Whether or not a motoneuron generates spikes precisely and reliably depends on both its intrinsic membrane properties and the nature of the synaptic input that it receives. Factors that perturb neuronal intrinsic properties and/or synaptic drive may compromise the temporal precision and the reliability of action potential generation. We have previously shown that developmental nicotine exposure (DNE) alters intrinsic properties and synaptic transmission in hypoglossal motoneurons (XIIMNs). Here we show that the effects of DNE also include alterations in spike-timing precision and reliability, and spike-frequency adaptation, in response to sinusoidal current injection. Current-clamp experiments in brainstem slices from neonatal rats show that DNE lowers the threshold for spike generation but increases the variability of spike-timing mechanisms. DNE is also associated with an increase in spike-frequency adaptation and reductions in both peak and steady-state firing rate in response to brief, square wave current injections. Taken together, our data indicate that DNE causes significant alterations in the input-output efficiency of XIIMNs. These alterations may play a role in the increased frequency of obstructive apneas and altered suckling strength and coordination observed in nicotine-exposed neonatal humans.
Keywords: intrinsic properties, motoneuron, nicotine, development, spike-timing precision, spike-timing reliability
motoneuron spike trains are characterized by high variability between successive interspike intervals under conditions of naturally occurring synaptic input and also when cells are stimulated with DC or sinusoidal currents of varying frequency (Beierholm et al. 2001). This phenomenon has been studied in terms of spike-timing precision and reliability, which refers, respectively, to the temporal consistency of repetitive spiking, and the dependability of spiking, in response to a repetitive, stereotyped synaptic input (Sejnowski and Paulsen 2006; van Brederode and Berger 2008). Together, spike-timing precision and reliability are presumed to play an important role in establishing synchronous network output by increasing the probability that populations of neurons will respond with fidelity to common synaptic input (Beierholm et al. 2001; Usrey and Reid 1999). The mechanisms that underlie spike-timing precision and reliability are poorly understood but could be due to varying synaptic activity or to intrinsic membrane properties that determine the threshold for spike generation (Beierholm et al. 2001; Sejnowski and Paulsen 2006; Usrey and Reid 1999).
Recent studies in neonatal rodents have shown that nicotine exposure in utero and after birth via breast milk [developmental nicotine exposure (DNE)] alters hypoglossal motoneuron (XIIMN) excitability, intrinsic membrane properties. and excitatory synaptic transmission (Jaiswal et al. 2013; Pilarski et al. 2011). Accordingly, we hypothesize that DNE, by changing the development of one or several of these fundamental properties, will alter the precision and reliability of action potential generation in response to dynamic synaptic inputs. To test this hypothesis we used whole cell current-clamp recordings from XIIMNs in 400-μm brainstem slices from neonatal rats that were either saline or nicotine exposed in utero. Cells were subjected to sinusoidal current injections at nine different frequencies and three different amplitudes.
In addition, we studied motoneuron responses to static, square wave current injections to examine the influence of DNE on spike-frequency adaptation. Spike-frequency adaptation has been studied in neurons throughout the brain, including XIIMNs (Powers et al. 1999; Sawczuk et al. 1997, 1995; Viana et al. 1995), and is defined as a steady decline in discharge rate despite a constant level of injected current. Interestingly, in the neonatal brainstem smaller neurons show more spike-frequency adaptation than larger neurons (Koizumi et al. 2013), and DNE may be associated with a reduction in hypoglossal motoneuron size (Pilarski et al. 2011). From these observations one might predict that the cells from DNE animals would show more spike-frequency adaptation than control cells.
Our data show that in response to sinusoidal current injections, DNE cells fire action potentials earlier in the cycle, show increased spike-timing variability, generate fewer spikes per cycle, and show significant but complex differences in the relation between the probability of spiking and the frequency and amplitude of the injected currents. Additionally, DNE cells displayed more spike-frequency adaptation during static, square wave current injections. Taken together, these observations indicate that DNE alters the precision and reliability of spike generating mechanisms in XIIMNs. Potential implications for network synchronization and muscle force output are discussed.
MATERIALS AND METHODS
Animals.
The Institutional Animal Care and Use Committee at the University of Arizona approved all animal procedures as well as housing protocols. DNE was achieved by implanting a 28-day osmotic mini-pump (Alzet, Cupertino, CA) subcutaneously into pregnant Sprague-Dawley dams as described previously (Huang et al. 2004, 2010; Jaiswal et al. 2013; Luo et al. 2004, 2007; Pilarski and Fregosi 2009; Pilarski et al. 2011). The pump was loaded with either nicotine bitartrate (6 mg·kg−1·day−1) or physiologic saline. Implantations occurred on approximately embryonic day 5 (E5), and pregnancies continued to natural parturition. Nicotine exposure continued via breast milk after birth.
Data from 27 neonatal animals of either sex were used, ranging in age from postnatal day (P)1 to 4. Twenty-eight of 34 recorded motoneurons yielded complete data sets and were evenly split between control and DNE preparations. Data reported here came only from those 28 cells. Of those, 14 were from 13 nicotine-exposed pups, and the other 14 cells were from either saline-exposed sham animals (11 cells from 5 pups) or unexposed animals (3 cells from 3 pups). The unexposed group did not undergo any surgery or pump implantation, and since there were no differences between these cells and the cells from saline-exposed sham animals, the data were combined into a single control group and will be referred to as such throughout the rest of this article.
Plasma cotinine levels.
As in humans, rats metabolize nicotine within an hour, either to cotinine or by renal elimination (Sastry et al. 1995). In contrast, cotinine has a half-life of 20–24 h in the rat. Since blood levels of nicotine and cotinine are positively correlated, cotinine is a commonly used marker of nicotine exposure (Florescu et al. 2009). Accordingly, blood was collected during dissection in 7 saline-exposed and 23 nicotine-exposed neonates ranging in age from P0–P5 (see Fig. 2). Following decapitation, blood was collected in heparinized Eppendorf tubes, centrifuged at 5,000 g for 5 min, and the plasma stored at −20°C. Plasma cotinine was measured with a solid phase, competitive ELISA (CalBiotech Kit CO096D). Ten-microliter plasma and cotinine standards were added to wells (96-well plate) coated with anti-cotinine antibody, followed by addition of 100 μl horseradish peroxidase enzyme conjugate, and then incubated for 60 min at room temperature in the dark. After six washes in distilled water, 100 μl tetramethyl benzidine was added to each well, followed by 30-min incubation, at room temperature and in the dark. The reaction was stopped with 100 μl stop solution, the optical density (OD) was determined in an ELISA reader at a wavelength of 450 nM, and values were calculated from the standard curve. All six standards and samples from the saline-exposed animals were assayed in duplicate, while samples from the nicotine-exposed animals were analyzed in triplicate.
Fig. 2.
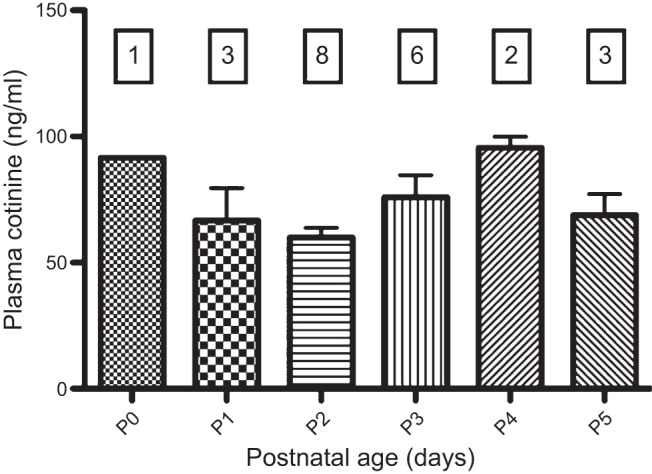
Plasma cotinine levels in nicotine-exposed neonates. As stated in results, cotinine levels were zero in saline-exposed animals, and the data are not shown. ANOVA did not detect any differences in cotinine as a function of postnatal age (F = 2.18, P = 0.1150). Numbers in boxes represent the number of animals studied at each age.
Medullary slice preparation.
Pups of either sex were collected at random from their litters and weighed. Animals were anesthetized on ice until nonresponsive to paw pinch, and decerebrated at the coronal suture. They were then eviscerated to expose the vertebral column and ribcage as well as the remaining central nervous system, moved to a dissection dish, and covered with chilled (4–8°C) and oxygenated (95% O2-5% CO2) artificial cerebrospinal fluid (aCSF), composed of (in mM): 120 NaCl, 26 NaHCO3, 30 glucose, 1 MgSO4, 3 KCl, 1.25 NaH2PO4, and 1.2 CaCl2, with pH adjusted to 7.4 and osmolarity of 300–325 mosM. The spinal cord and medulla/pons were extracted from the remaining tissue, and any tissue rostral to the pontomedullary junction was removed. The preparation was pinned to a cutting block, rostral surface up, for serial microsectioning in a Vibratome (VT1000; Leica). Transverse medullary slices were taken until the most rostral hypoglossal nerve (XIIn) rootlets were near the surface of the tissue. Two 400-μm slices were then taken to capture all or a majority of the hypoglossal motor nucleus. The slices were transferred to fresh aCSF that was continuously oxygenated with 95% O2-5% CO2 and allowed to equilibrate at room temperature for a minimum of 1 h before recording commenced. Slices were then transferred to the recording chamber and perfused with aCSF at 27°C.
Electrophysiology.
The dynamic properties of XII motoneurons were examined using whole cell patch-clamp techniques. Cells were visualized with an Olympus BX-50WI fixed-stage microscope (×40 water-immersion objective, 0.75 numerical aperture) with infrared and differential interference contrast optics and a video camera (C25400-07, Hamamatsu). Recordings were made using glass pipettes (3–6 MΩ) pulled from thick-walled borosilicate glass capillary tubes (OD: 1.5 mm; ID: 0.75 mm) and filled with the following (in mM): 135 K-gluconate, 4 KCl, 10 HEPES, 5 ATP (Mg2+ salt), 0.375 GTP, and 12.5 phosphate creatine, with pH adjusted to 7.2 and osmolarity of 275–300 mosM. In some recordings, the pipette contained 1% wt/vol Neurobiotin Tracer (Vector Laboratories) to fill cells for morphological analysis for a separate study. Liquid junction potentials were not corrected.
Protocols.
All recordings were made in current-clamp mode, using a dynamic current injection protocol consisting of nine sinusoidal input frequencies of 1, 2, 4, 6, 8, 10, 13, 16, and 20 Hz. The duration of each protocol was adjusted to keep the number of cycles at each input frequency constant. Three different sine wave amplitudes were studied at each of the input frequencies: 25, 150, and 250 pA. To avoid complications due to differences in spike threshold, the current threshold for action potential generation was determined with square wave current steps. A DC offset was then computed so that the injected sinusoidal current was above each cells' spike threshold half the time and below threshold half the time, as follows:
Thus, as sine wave amplitude increased, we decreased the applied DC offset. The different injected frequencies and amplitudes were randomized to mitigate order effects. To determine spike-frequency adaptation, square wave current steps 1 s in duration were injected into the cell until depolarization block occurred. We increased the current steps by either 20 or 50 pA, though no effect of step amplitude on indices of adaptation was seen (see below).
In addition to passive and active membrane properties, spike-timing precision depends on the spatial and temporal characteristics of the synaptic inputs bombarding the cell at any point in time. As a result, studies of spike-timing precision sometimes include a background of Gaussian distributed white noise to mimic naturally occurring synaptic inputs (Beierholm et al. 2001; Brunel et al. 2001; Fetz and Gustafsson 1983; Fuhrmann et al. 2002; Sejnowski and Paulsen 2006). Since previous studies have shown that DNE alters background excitatory (Pilarski et al. 2011) and inhibitory (Miura et al. 2006) synaptic input, we chose to simplify the analysis by studying the cells without the addition of white noise. We suggest that future studies could examine the influence of DNE on spike-timing precision in models that include synaptic noise. However, the challenge will be selecting the appropriate quantity and quality of the synaptic noise so that inputs converging on both DNE and control cells are accurately mimicked.
Data analysis.
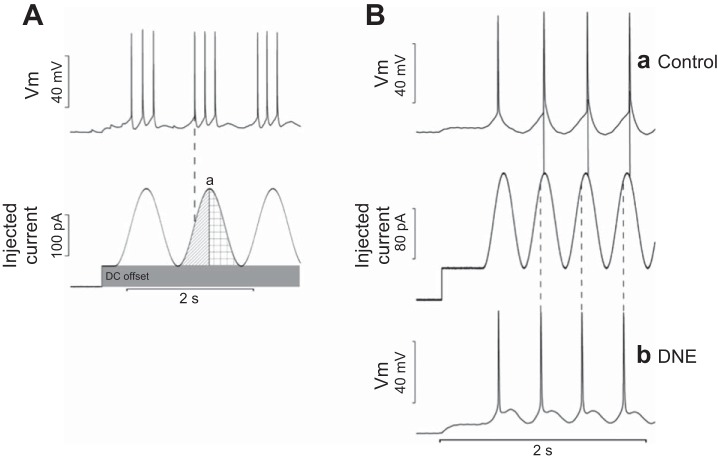
Analysis of dynamic current injections was performed offline using custom scripts written in Matlab (Mathworks, Natick, MA). To analyze the effects on spike-timing precision, we calculated phase angle, jitter, and phase error. For all measurements, the first cycle was ignored to exclude the effects of the initial depolarization. Phase angle was defined as the location, in degrees, of the first action potential of a given cycle, where the peak of the sine wave was defined as 0° (Fig. 1A, point a). An action potential that occurs before the peak would have a negative phase angle (indicated by the vertical dashed line in the initial half of the sine wave cycle in Fig. 1A), and one that occurs after the peak would have a positive phase angle (checkerboard pattern in the latter half of the sine wave cycle in Fig. 1A). Jitter measures the variability of action potential firing expressed in milliseconds and was calculated using the latency from the initial trough of the sine wave (−180° from the peak) to the onset of the first action potential. The standard deviation of these latencies across all cycles is defined as the jitter. Phase error is the variability of action potential firing expressed in degrees. To determine phase error, the latency terms from the jitter analysis were converted from milliseconds to degrees, creating phase angles. Variability of the phase angles (phase error) was calculated by taking the standard deviation of all phase angles across all cycles. The reason for including two measurements of spike-timing variability is because jitter is forced to decrease with an increase in sine wave input frequency, while phase error is independent of input frequency.
Fig. 1.
A: measurement of spike-timing precision and reliability. The top trace displays membrane voltage (Vm) of a patch-clamped hypoglossal motoneuron (XIIMN) responding to the injected current profile seen in the bottom trace. Sinusoidal current injections were delivered at amplitudes of 25, 150, or 250 pA. The DC offset (shaded area, bottom trace) was determined before injection of sinusoidal current patterns and varied between cells, as explained in materials and methods. DC offset adjustment was made to position the cells firing threshold at the midpoint of the sinusoidal current amplitudes. The peak of the sinusoidal current injection cycle (point a) was defined as 0° for analysis. A pre-peak position is defined by the diagonal bar shading, and spikes falling here have negative phase angles. Spikes occurring after the peak (defined by the crosshatch shading) would have positive phase angles. The dashed line shows that the 1st spike in the 2nd burst falls before the peak of the sine wave and therefore has a negative phase angle. B: comparison of typical responses to sinusoidal current injection in control and developmental nicotine exposure (DNE) XIIMN. Ba: phase-locked XIIMN from a control animal (top trace), which generates action potentials at the peak of the injected sinusoidal current waveform (middle trace) or just after it (solid vertical lines connect action potential onset to the corresponding sine wave). Bb: phase-locked XIIMN from a DNE animal. Note that the action potentials occur well before the peak of the sine wave (vertical dashed lines), consistent with a negative phase angle.
To analyze the effects of DNE on spike-timing reliability, the mean number of action potentials per sine wave cycle, the probability of a successful cycle, and the number of spikes per successful cycle were calculated for all input frequencies and current amplitude. A successful cycle was defined as any cycle having at least one action potential. Any frequency at which a cell fired only one action potential per input cycle was considered to be phase locked (Brody and Hopfield 2003; Fellous et al. 2001; Johnson 1980; Lavine 1971). The range of frequencies at which this occurs has been termed the preferred frequency range (Fellous et al. 2001; Pike et al. 2000), although this term has also been used to denote the frequency at which a spike falls perfectly in phase with the peak of the sine wave (Fuhrmann et al. 2002).
To quantify spike-frequency adaptation, we measured the spike frequency during the first 0.25 s of each current step (finitial) and subtracted the frequency measured over the last 0.25 s of the same current step (fsteady-state). Adaptation analysis was performed offline using a custom script written with Spike2 software (CED, Cambridge, UK). A second script was used to analyze the resting membrane potential and the input resistance of all cells. Input resistance was calculated as the change in voltage divided by the magnitude of a hyperpolarizing current step. The current threshold for action potential firing was measured as the voltage associated with the first evoked spike during the static f-I protocol.
Adaptation analysis included data from cells that received current steps of either 20 or 50 pA. The smaller amplitude step was used for cells that had low maximum current thresholds, as a way to increase the resolution of this measurement. However, to ensure that there was no effect of current step amplitude on the rate of adaptation, the adaptation rate of each cell and at each level of injected current was measured. We then averaged the adaptation rates computed in 100-pA epochs, extending from 0- to 99 pA to 900 to 999 pA. Thus, for cells receiving 20-pA steps (Control: n = 9; DNE: n = 6), we computed five adaptation rates in each of the 100-pA epochs, while only two adaptation rates in each step could be computed in cells subjected to the 50-pA steps (Control: n = 5; DNE: n = 8).
Statistics.
Statistical analysis was done using the software program R (R Foundation for Statistical Computing, Vienna, Austria). For resting membrane potential, input resistance, current threshold, weight, and age, t-tests were performed to compare control and DNE animals. Statistical analysis of the dynamic current injection data, including all measures of spike-timing precision and reliability, was performed by three factor ANOVA (treatment, sine wave frequency, sine wave amplitude) and Tukey's post hoc tests. For spike-frequency adaptation data, mean adaptation rates were compared using a two factor ANOVA (treatment and current step amplitude), followed by Tukey's post hoc tests. To determine if plasma cotinine levels depend on postnatal age, we used one-way ANOVA. Data in all figures and tables are the means ± SE unless indicated otherwise. Data are considered statistically significant if P ≤ 0.05.
RESULTS
Weight, age, plasma cotinine levels, and passive membrane properties of XIIMNs in each treatment group.
The passive properties of XIIMNs, including input resistance, resting membrane potential and the current and voltage thresholds at which spiking was initiated in response to static current injection did not differ between treatment groups (Table 1). The average weight and age of the animals in the two treatment groups were also similar (Table 1). Plasma cotinine levels in the nicotine-exposed neonates are shown in Fig. 2. Cotinine levels in saline-exposed animals were not detectable, and the data are not shown. Cotinine levels in nicotine-exposed neonates were statistically the same across all ages, ranging from 60–92 ng/ml. This compares favorably with the average cotinine level (88 ng/ml) in the umbilical cord blood of newborns whose mothers that smoked, on average, 95 cigarettes/wk (Berlin et al. 2010). Interestingly, the mean plasma cotinine concentration in the mothers, measured at delivery, was just slightly higher (106 ng/ml). Thus our dosing regimen provides fetal nicotine levels that are similar to those observed in the newborns of pregnant human smokers.
Table 1.
Analysis of hypoglossal motoneuron passive membrane properties and the weight and age of the control and DNE animals used
| Control | DNE | P Value | n (Control:DNE) | |
|---|---|---|---|---|
| Input resistance, MΩ | 161.6 ± 24.4 | 143.64 ± 26.9 | 0.62 | 14:14 |
| Resting membrane potential, mV | −58.2 ± 3.6 | −58.6 ± 4.2 | 0.94 | 14:14 |
| Current threshold, pA | 72.9 ± 20.6 | 123.6 ± 28.3 | 0.16 | 14:14 |
| Voltage threshold, mV | −46.2 ± 3.0 | −42.7 ± 3.7 | 0.46 | 14:14 |
| Weight, g | 8.1 ± 0.8 | 9.7 ± 0.7 | 0.13 | 8:13 |
| Age, day | 1.9 ± 0.3 | 2.5 ± 0.3 | 0.16 | 8:13 |
All values represent the means ± SE. P values derived from Student's t-test comparing control and developmental nicotine exposure (DNE) cells for each variable. n (Control:DNE) represents the number of animals for control and DNE, respectively. Note that a smaller number of control animals were used, as multiple motoneurons were studied in some animals.
Spike-timing precision.
Phase angle, jitter, and phase error were chosen as indices of spike-timing precision. Summary statistics for each variable are shown in Table 2. Phase angle represents the position of the first spike of a cycle relative to the peak of the injected sinusoidal current. Figure 1B shows a representative comparison of spike trains recorded from a XIIMN from a control (Fig. 1Ba, top trace) and DNE animal (Fig. 1Bb, bottom trace). Note that the control cell spiked either just before or just after the peak of the sine wave (solid vertical lines), while the cell from the DNE animal always spiked before the peak (dashed vertical lines), indicating a negative phase angle. The average calculated phase angles were strongly dependent on input frequency, changing from negative to positive as input frequency increased (Fig. 3), with each level of current evoking a similar range of phase angles across the input frequencies that we used (Fig. 3). Importantly, we found a significant treatment effect, with DNE motoneurons firing earlier in the cycle than control cells at current injection amplitudes of 150 (P < 0.001) and 250 pA (P < 0.001) (Figs. 1 and 3 and Table 2) but not at 25 pA (P = 0.97). These effects were statistically uniform across the frequency range, as ANOVA did not reveal a treatment:frequency interaction (Table 2). An interesting result of this analysis is that the preferred frequency (i.e., a phase angle of zero, horizontal dashed line in Fig. 3) was higher in the DNE cells, as indicated by the rightward shift of the curves at 150 and 250 pA. In addition, there was a significant interaction between frequency and current injection amplitude for cells in both treatment groups, indicating that a phase angle of zero occurred at progressively higher input frequencies as current amplitude increased (Table 2 and Fig. 3).
Table 2.
ANOVA table values for spike-timing precision and reliability variables
| Treatment | Frequency | Current | Treatment × Frequency | Treatment × Current | Frequency × Current | |
|---|---|---|---|---|---|---|
| Phase angle | (1, 42.0, <0.001) | (8, 242.5, <0.001) | (2, 49.2, <0.001) | (8, 1.7, 0.10) | (2, 9.0, <0.001) | (16, 4.2, <0.001) |
| Jitter | (1, 1.4, 0.23) | (8, 34.1, <0.001) | (2, 154.7, <0.001) | (8, 0.6, 0.81) | (2, 1.9, 0.15) | (16, 11.7, <0.001) |
| Phase error | (1, 3.3, 0.07) | (8, 27.3, <0.001) | (2, 578.9, <0.001) | (8, 0.7, 0.72) | (2, 10.2, <0.001) | (16, 10.7, <0.001) |
| Spikes per cycle | (1, 4.7, 0.031) | (8, 146.2, <0.001) | (2, 35.9, <0.001) | (8, 1.9, 0.062) | (2, 0.1, 0.89) | (16, 3.4, <0.001) |
| Probability of Success | (1, 0.3, 0.56) | (8, 95.8, <0.001) | (2, 234.4, <0.001) | (8, 1.7, 0.099) | (2, 10.5, <0.001) | (16, 17.3, <0.001) |
| Spikes per successful cycle | (1, 4.9, 0.027) | (8, 131.9, <0.001) | (2, 17.3, <0.001) | (8, 1.9, 0.063) | (2, 0.6, 0.55) | (16, 4.8, <0.001) |
Columns represent main factors and interactions measured using a three-way ANOVA. Each cell displays the degrees of freedom (df), F value (F), and P value (P), displayed as (df, F, P).
Fig. 3.
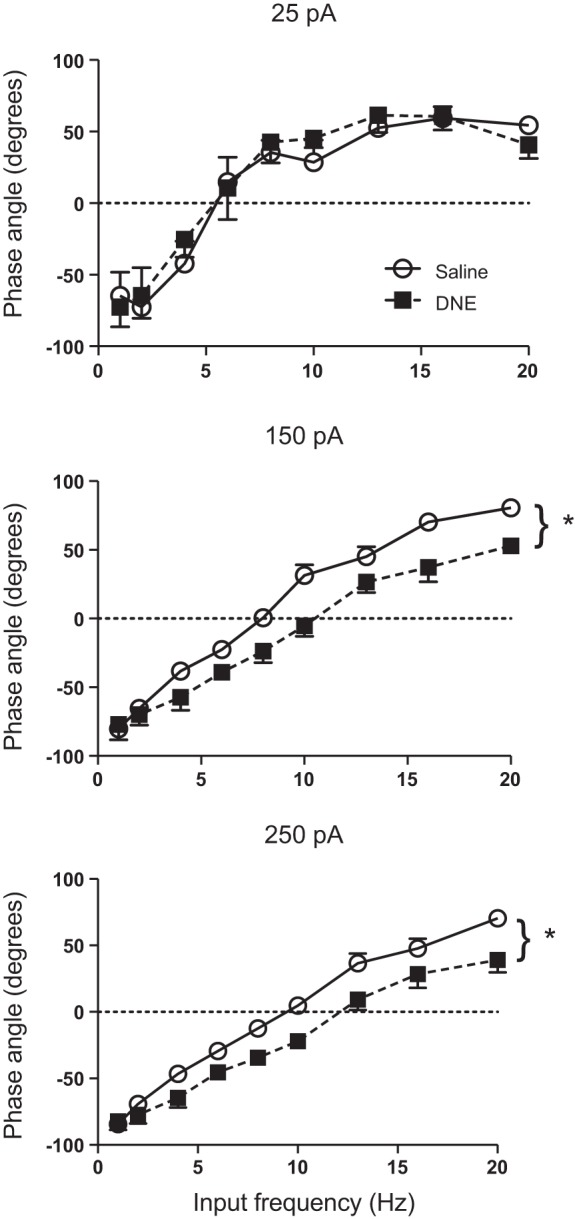
Influence of current, input frequency, and treatment on phase angle. Phase angle becomes progressively more positive with increasing input frequency at all 3 amplitudes. At higher current injection amplitudes, DNE neurons (■) fire significantly earlier than the control motoneurons (○). *P < 0.05, DNE vs. control. See results and Table 2.
As explained in materials and methods, jitter represents the variability of spike timing measured in milliseconds. Across all current injection amplitudes, jitter decreased with increasing sine wave frequency, reaching a plateau near 5 Hz (Fig. 4). Increasing the current injection amplitude also reduced jitter, most notably at lower input frequencies, consistent with the significant frequency:current interaction (Table 2 and Fig. 4). However, no treatment effects for jitter were seen at any level of sinusoidal current injection amplitude, or input frequency (Table 2 and Fig. 4).
Fig. 4.
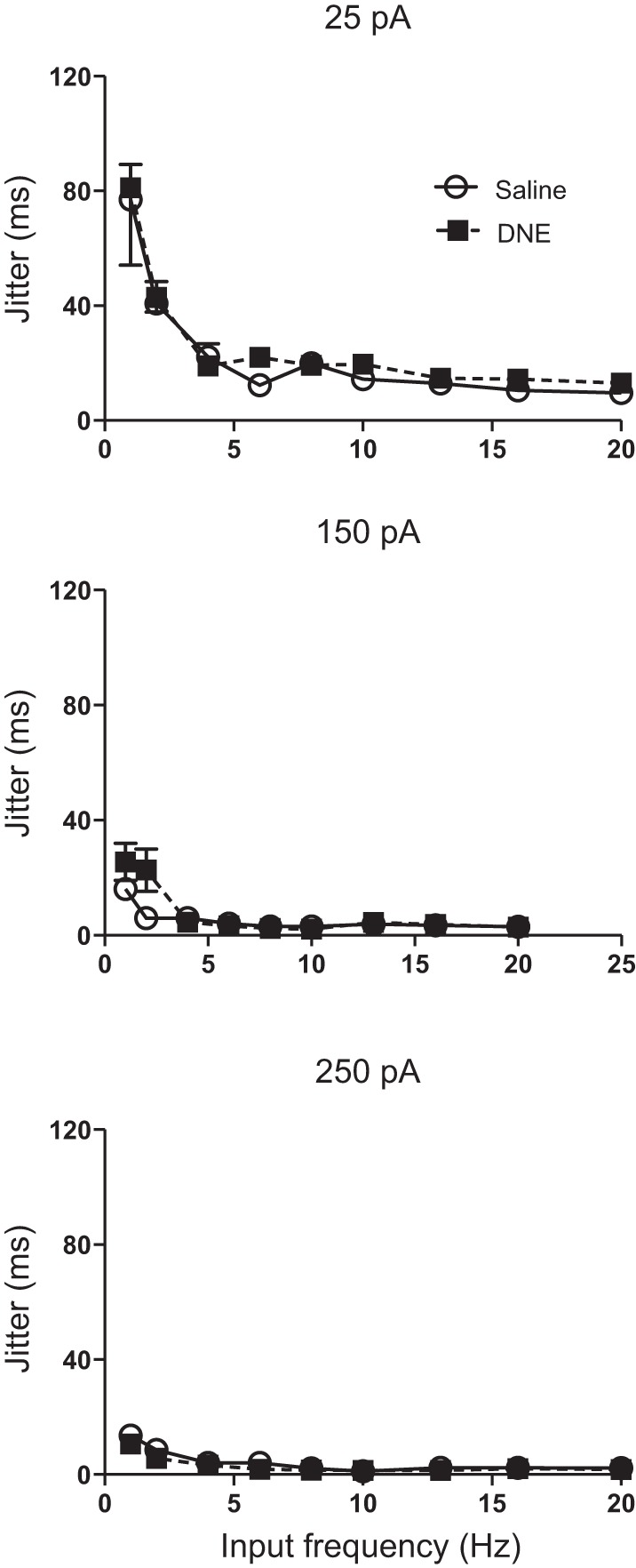
Influence of current, input frequency, and treatment on jitter. Jitter decreases with increasing input frequency at all current amplitudes, and is highest at a current injection amplitude of 25 pA. DNE did not significantly alter jitter at any current amplitude or sine wave frequency. DNE cells, ■; control cells, ○.
Phase error also measures the variability of spike timing but is independent of the cycle length. Although the ANOVA did not reveal an overall treatment effect for phase error (F = 3.3; P = 0.071; Table 2), there was a significant current:treatment interaction, indicating that treatment effects depend on current injection amplitude (Table 2). Indeed, post hoc analysis revealed a significant treatment effect at the 25-pA current injection level, whereby DNE neurons show a greater phase error compared with neurons from control cells (P < 0.001; Fig. 5). There were no treatment effects at 150 (P = 0.98) or 250 pA (P = 0.82), as shown in Fig. 5. Phase error also varied significantly with current and input frequency, and there was a significant interaction between these variables (Table 2 and Fig. 5). Phase error increased monotonically as a function of input frequency at 25 pA but decreased markedly and showed much less frequency dependence as the amplitude of injected current rose, consistent with greater precision at high levels of injected current (Fig. 5).
Fig. 5.
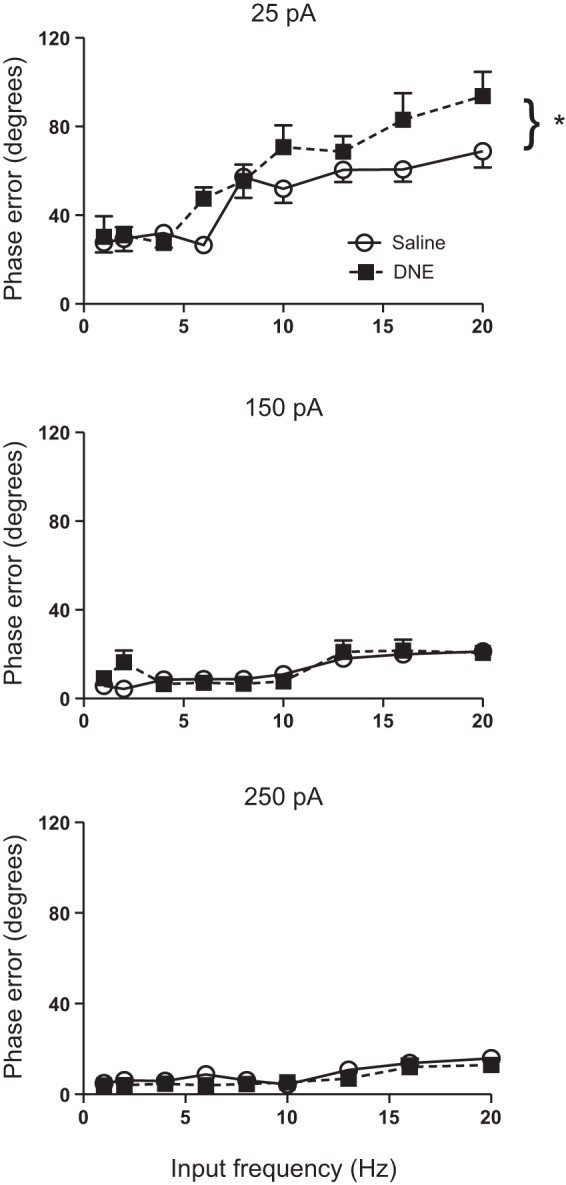
Influence of current, input frequency, and treatment on phase error. Phase error increases with increasing input frequency and drops markedly as current injection amplitude increases. DNE cells (■) had significantly larger phase error at the lowest current injection amplitude compared with control cells (○). Treatment effects were not observed at the medium and high sinusoidal current injection amplitudes. *P < 0.05, DNE vs. control.
Spike-timing reliability.
To assess changes in the reliability of motoneuron spiking, the number of spikes per sine wave cycle, the probability of a successful cycle (i.e., the percentage of cycles that evoked at least one action potential) and the number of spikes per successful cycle were measured, with the summary statistics shown in Table 2. For the number of spikes per cycle, ANOVA revealed significant treatment, frequency, and current effects, as well as a significant frequency:current interaction. Because there was no interaction between treatment and frequency or treatment and current (Table 2), the treatment effect is by definition independent of both variables. Examination of the data (Fig. 6), however, suggests that the treatment effect is occurring only at the two lowest frequencies and only at current amplitudes of 150 and 250 pA. Examination of Fig. 6 also shows that, in both treatment groups, the number of spikes per cycle declines markedly as input frequency rises and that higher amplitude current injections are associated with more spikes per cycle. Moreover, the preferred frequency, defined as the frequency that evokes one spike per cycle (e.g., horizontal dashed line in Fig. 6), increases as a function of sine wave amplitude and appears to be identical in both treatment groups.
Fig. 6.
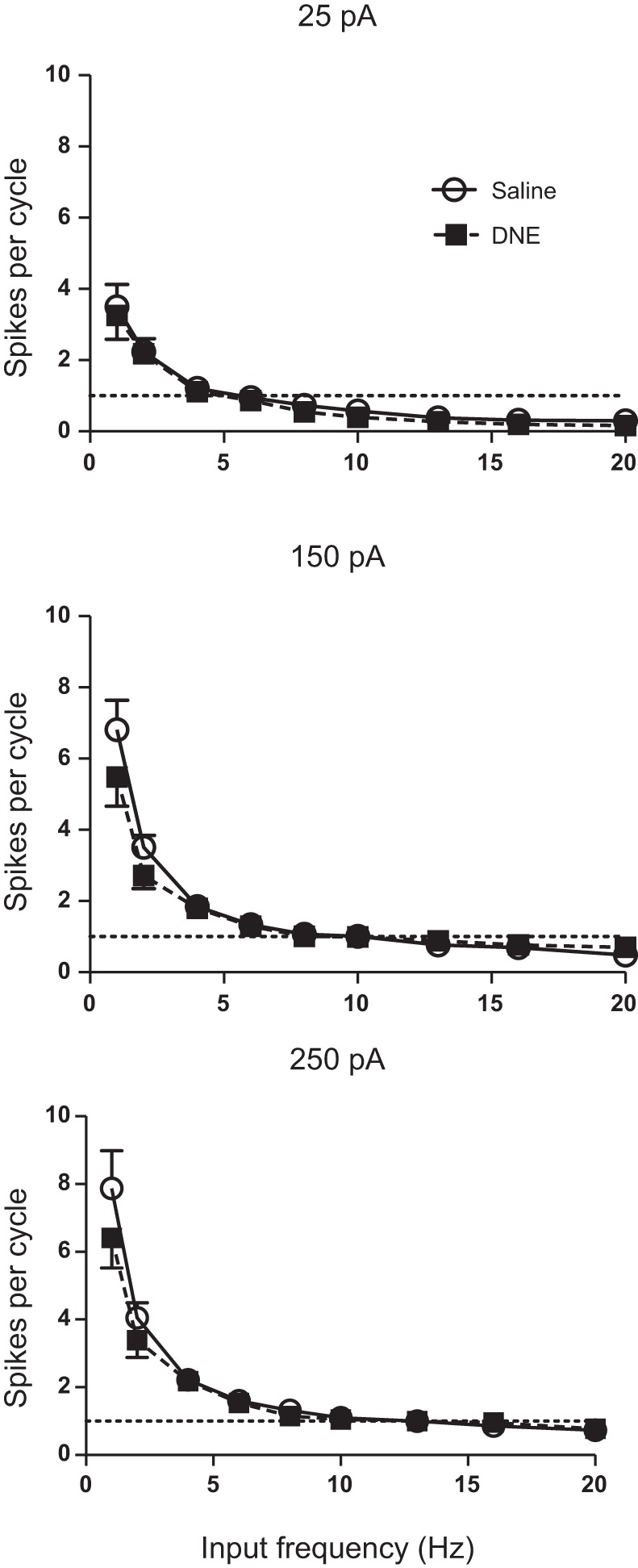
Influence of current, input frequency, and treatment on the number of spikes per sine wave cycle. The number of spikes per cycle decreases steeply with increasing input frequency and increases with increasing current injection amplitude. There was a significant treatment effect, with DNE cells (■) generating fewer spikes per cycle than control cells (○), but only at the 2 lowest input frequencies and at the 2 highest levels of injected current (see results). The region of phase locking (1 spike per sine wave cycle, horizontal dashed line) increased progressively with increases in sine wave amplitude.
Measurement of the probability of a successful cycle showed that motoneurons became less successful with increasing input frequency at all three current injection amplitudes (Fig. 7). However, the range at which cells could be considered highly successful, which we defined as a probability of 90% or above, did increase with increasing current injection amplitude. This range extended from 1 to 4 Hz at 25 pA, 1 to 10 Hz at 150 pA, and 1 to 13 Hz at 250 pA. ANOVA revealed significant frequency and current effects, but no overall treatment effects (Table 2). However, there was a significant treatment:current interaction, but no interaction between treatment and frequency. Thus treatment effects depend on current injection amplitude, but are independent of input frequency (Table 2 and Fig. 7). Interestingly, the treatment effect was significant only at 25 pA, with DNE cells less successful than control cells (Fig. 7). There was also a significant interaction between input frequency and current injection amplitude, with frequency having less effect on the probability of a successful cycle as current injection amplitude increased (Fig. 7).
Fig. 7.
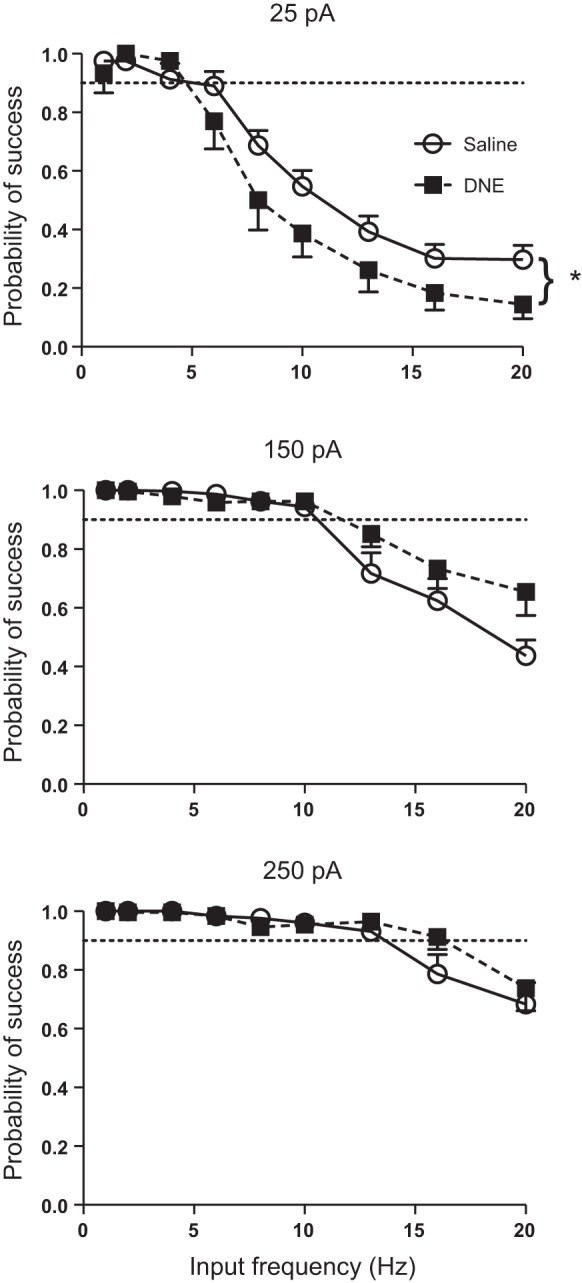
Influence of current, input frequency, and treatment on the probability of a successful cycle. The probability of a successful cycle increases with current injection amplitude in all cells. DNE has complex effects on the probability of successful spiking as a function of current injection frequency and amplitude. There was no overall treatment effect but a significant interaction between treatment and current injection amplitude (Table 2). As explained in text, post hoc analysis showed that at an amplitude of 25 pA, DNE cells (■) are less likely to spike in a given cycle compared with control cells (○). However, at 150 pA DNE cells appear more likely to spike at the higher input frequencies, although this difference is not significant. Points lying above the horizontal dashed line are considered to have a high probability of generating a spike, as explained in results.
We also examined the number of spikes per successful cycle, as this analysis corrects for the effects of skipped cycles (Fig. 8). As shown in Table 2, there were significant treatment, frequency, and current effects, and a significant frequency:current interaction. However, there were no significant interactions between treatment and current or treatment and frequency, indicating that the effects of DNE are independent of both current and frequency. Similar to spikes per cycle (Fig. 6), closer inspection of the data in Fig. 8 reveals that the treatment effect is most likely occurring only at the lowest input frequencies and only at input current amplitudes of 150 and 250 pA.
Fig. 8.
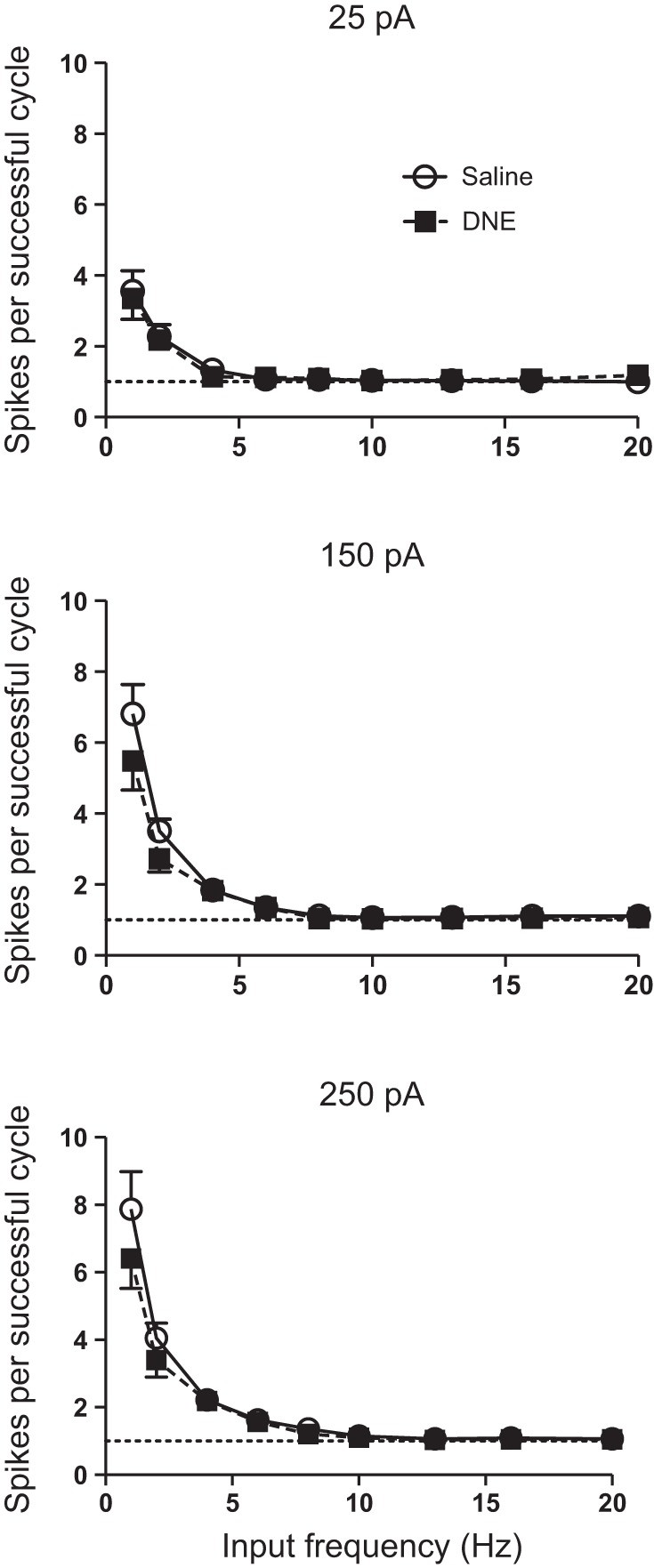
Influence of current, input frequency and treatment on the number of spikes per successful cycle. When the number of spikes per cycle is normalized to include only successful cycles, DNE cells (■) have slightly fewer spikes than control cells (○). Because there was no treatment:frequency interaction (Table 2), the treatment effect is independent of frequency. However, examination of the data clearly shows that the differences occurred only at the 2 lowest frequencies, and at the 2 highest levels of injected current. See text for further explanation.
Spike-frequency adaptation.
We examined spike-frequency adaptation in XIIMNs using static, square wave current step injections (Fig. 9A). The index of adaptation for a given current step was determined by subtracting the steady-state firing rate from the initial firing rate at each level of injected current (shaded regions in Fig. 9A). Because we applied step increments of 20 or 50 pA, we first ran a two-way ANOVA to look for interactions between treatment and current step amplitude. ANOVA confirmed that step amplitude had no effect on our index of spike-frequency adaptation in either control (9.2 ± 0.25 Hz for 20-pA steps, vs. 8.7 ± 0.46 Hz for 50-pA steps; P = 0.959) or DNE cells (10.6 ± 0.45 Hz for 20-pA steps vs. 10.7 ± 0.48 Hz for 50-pA steps; P = 0.99). Accordingly, we computed the average adaptation rate for all current step levels for all motoneurons in each treatment group. As shown in Fig. 9B, DNE cells showed higher levels of adaptation than control cells (control, 9.0 ± 0.24 Hz; DNE, 10.5 ± 0.36 Hz; P = 0.00085).
Fig. 9.
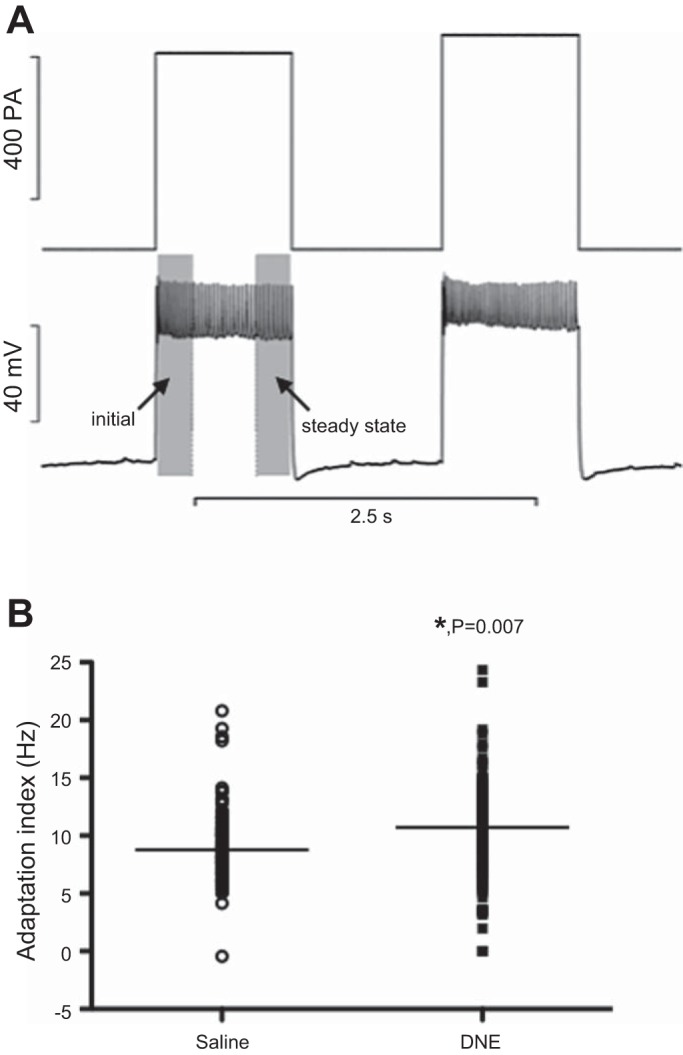
Spike-frequency adaptation in XIIMNs from control and DNE preparations. A: representative trace showing a motoneuron's response (bottom traces) to square wave current injections (top traces). For each current step, the mean frequency of the 1st and last one-quarter second was measured (finitial and fsteady-state, respectively), and spike-frequency adaptation was calculated as: adaptation (Hz) = finitial − fsteady-state. This index was calculated for all current steps that were associated with continuous firing throughout the 1-s step. B: adaptation values (in Hz) for every level of injected current and for all motoneurons studied. DNE motoneurons showed a significantly higher spike-frequency adaptation compared with control cells. The horizontal bars show the median adaptation index in each treatment group. *P = 0.007, DNE vs. control.
The average steady-state discharge frequency, computed as the average frequency across the last 250 ms of each current step (Fig. 9A), also differed between treatment groups (control, 22.3 ± 0.92 Hz; DNE, 18.5 ± 0.73 Hz; P = 0.0013). The initial discharge frequency did not differ between treatment groups (31.4 ± 0.9 Hz for control vs. 29.0 ± 0.8 Hz for DNE; P = 0.054).
DISCUSSION
We studied the effects of DNE on the dynamic properties and spike-frequency adaptation of XIIMNs. A neuron's dynamic properties, such as spike-timing precision and reliability, are thought to be crucial for establishing network oscillatory function and efficiency in cortical neurons (Mainen and Sejnowski 1995; Sejnowski and Paulsen 2006). Our findings in neonatal rodents show that DNE is associated with a significant shift in the timing of action potentials in response to sinusoidal current injection. In addition, DNE cells displayed a lower likelihood of successfully discharging action potentials in response to low amplitude current injections and showed increased spike-frequency adaptation. These alterations in spike-timing precision, reliability, and spike train dynamics in XIIMNs suggest that if central nervous system development is delayed by DNE, this could lead to altered neural control of tongue muscles. More generally, these observations provide important clues for future studies examining the influence of DNE on the development of motor systems.
Influence of DNE on XIIMN spike-timing precision and reliability.
Across the frequency range that we tested, DNE cells fired earlier in the sine wave cycle (a shift to lower phase angles) at injected current levels of 150 and 250 pA (Fig. 3), consistent with increased excitability. These observations are consistent with our earlier study showing that DNE motoneurons had a lower action potential threshold when subjected to square wave current injections (Pilarski et al. 2011). However, we also showed that DNE motoneurons had a lower probability of successful spiking (defined as the frequency range at which the probability of success was 90% or above; Fig. 7, dashed line) at a current injection amplitude of 25 pA (Fig. 7). Although this appears to contradict our earlier work (Pilarski et al. 2011), we suggest that at 25 pA the cells were very close to firing threshold and thus unstable. This is supported by our observation that DNE cells had a greater phase error at 25 pA compared with control cells (Fig. 5, see below) consistent with instability. Also, in the present study we adjusted the baseline membrane potential to just below the firing threshold, while in the earlier study current injections were initiated from the cell's resting membrane potential. Moreover, there are no doubt differences in the response to sinusoidal current injections, compared with the 1-s, square wave current steps used in the earlier study. The lack of a treatment effect at 150 and 250 pA likely reflects the fact that all cells were considerably more successful as current injection amplitude increased, consistent with the work of (van Brederode and Berger 2008). Indeed, the range of highly successful spiking extended to 5 Hz at 25 pA and to 10 and 15 Hz as current was increased to 150 and 250 pA. Interestingly, the data at 25 pA may be the most physiologically relevant, as over 90% of the excitatory postsynaptic currents recorded from XIIMNs in rhythmic brainstem slices are between 10 and 60 pA (Pilarski et al. 2011). Finally, we also found a very small but significant treatment effect in the number of spikes per cycle, although this effect appears to exist only at input frequencies of 5 Hz or less (Fig. 6). Nevertheless, this finding is consistent with an increase in the gain of the injected current-spike-frequency relation in response to square wave current injections that we observed previously (Pilarski et al. 2011).
Analysis of phase angle has also been used to define a preferred frequency, which is the frequency associated with a phase angle of zero (Fig. 3). A computational model of a small number of interconnected neurons, all with an identical preferred frequency, was shown to synchronize at an input frequency a bit below the preferred frequency of the neurons, due to synaptic delays in the network (Fuhrmann et al. 2002). Synchronous network oscillations are believed to underlie a variety of rhythmic behaviors and are thought to be important for coordinating the activity of populations of motoneurons and enhancing muscle force production (Beierholm et al. 2001; Funk and Parkis 2002). Here we showed that the DNE motoneurons had a higher preferred frequency than the control cells (right shift in the phase angle-frequency curves in Fig. 3), suggesting that higher input frequencies would be required to synchronize the hypoglossal motoneuron pool in DNE animals. In rhythmic brainstem slices, XIIMNs are activated during the inspiratory phase of the respiratory cycle by excitatory synaptic input from the pre-Bötzinger complex, the presumed central pattern generator for breathing. In previous studies we found that the baseline frequency of XIIMN population output in rhythmic brainstem slices is unaltered by DNE, suggesting that the baseline bursting rhythm of the central pattern generator is not altered by DNE (Jaiswal et al. 2013; Pilarski et al. 2011). However, synchronization of intraburst, synaptically driven action potential discharge may be compromised in DNE animals since their XIIMNs have a higher preferred frequency. This could lead to decreased force output and/or poorly coordinated tongue muscle contractions.
A very interesting and unexpected observation is the qualitative difference that input frequency exerts on jitter and phase error in XIIMNs. Although jitter fell markedly as input frequency rose (fig. 4), phase error increased as a function of input frequency (Fig. 5). Studies in cortical neurons suggest that jitter or other time-dependent measures of variability decrease with high frequency synaptic inputs and increase when the inputs are delivered at low sine wave frequencies or with DC stimulation (Beierholm et al. 2001; Mainen and Sejnowski 1995). Our measures of jitter are consistent with these observations. However, the increase in phase error (which is a time-independent measure) shows that increased input frequency is associated with increased variability of motoneuron spiking. This indicates that spiking is more precise at low rather than high input frequencies. This is consistent with data shown for one representative XIIMN in a study by van Brederode and Berger (2008; their Fig. 7A4). Thus, the influence of input frequency on spike train variability depends on whether it is measured with a time-dependent variable such as jitter or a time-independent index such as phase error; this is not trivial, as the two indexes lead to directionally opposite conclusions regarding the influence of DNE on spike-timing precision. Interestingly, the increase in phase error observed here at high input frequencies may explain the increased coefficient of variation of the interspike interval in respiration-related genioglossus muscle motor unit spike trains when respiratory drive was increased with elevated carbon dioxide (John et al. 2005).
Influence of DNE on spike-frequency adaptation.
Spike-frequency adaptation has been demonstrated in motoneurons for decades (Granit et al. 1963) and has been demonstrated consistently in XIIMNs (Haddad et al. 1990; Lape and Nistri 2000; Mosfeldt Laursen and Rekling 1989; Powers et al. 1999; Sawczuk et al. 1995, 1997; Viana et al. 1995; Zeng et al. 2005). XIIMNs typically display adaptation in three phases over a 60-s step of current injection: initial adaptation, defined as the sharp decline over the first few interspike intervals; early adaptation, which lasts approximately through the first second and has a much shallower slope; and late adaptation, which is defined as the gradual decline in firing rate that lasts throughout the remainder of the 60-s current injection period (Sawczuk et al. 1995). Here, we focused on the early adaptation phase, as we were interested in motoneuron responses to brief rather than prolonged changes in synaptic input. DNE motoneurons showed a significant increase in spike-frequency adaptation, as a result of a greater reduction in discharge rate over both the initial and last one-quarter second of the 1-s square wave current injection protocol that we used. As indicated above, our earlier study (Pilarski et al. 2011) showed that XIIMNs from DNE animals had a lower firing threshold and also an increase in the gain of the injected current-firing rate relation. However, in that study we also showed that motoneurons from control cells continued to increase their firing rate up to an injected current level of 1,479 pA. In contrast, the DNE cells either stopped spiking altogether or generated a few truncated spikes at an average injected current of 594 pA (see Fig. 5 in that study). This may contribute to the increased spike-frequency adaptation revealed in the present study. For example, changes in the inactivation parameters of voltage-sensitive Na+ currents or a persistent inward current could increase the propensity for depolarization block.
Potential mechanisms.
Taken together, our observations suggest that DNE alters the conductance of ion channels that underlie the cell's response to depolarizing input. An in vitro and computational analysis of neocortical pyramidal neurons (Fuhrmann et al. 2002) showed that increasing the maximum potassium conductance caused an increase in the preferred frequency, similar to the right-shift in the phase angle-frequency relation that we saw with DNE (Fig. 3). Fuhrmann et al. suggested that this might reflect modulation of potassium conductances that contribute to the spike after-hyperpolarization (Steriade et al. 1993). Nucleus accumbens neurons from nicotine-addicted mice showed a reduced after-hyperpolarization and hyperexcitability, due to a decrease in potassium conductance mediated by large-conductance Ca2+-activated K+ channels (BKCa) (Ma et al. 2013). Inhibition of apamin-sensitive, small conductance calcium-activated potassium channels (SK channels) decreased spike-frequency adaptation by reducing the Ca2+-dependent afterhyperpolarization of medium duration (mAHP) in neonatal (Lape and Nistri 2000; Viana et al. 1995) and adult (Powers et al. 1999) XIIMNs. DNE may, therefore, alter the expression or functional efficacy of SK channels, which are well suited to influence firing frequency by altering the trajectory of repolarization. Moreover, open SK channels would increase spike-frequency adaptation, as mentioned above (Lape and Nistri 2000; Powers et al. 1999; Viana et al. 1995). Furthermore, neuromodulators such as acetylcholine are known to reduce spike-frequency adaptation (Katz and Frost 1997; Stiefel et al. 2008; Tang et al. 1997), suggesting that the manipulation of cholinergic signaling by DNE alters potassium channel expression and/or function in XIIMNs by unknown mechanisms. Together, alterations in the after-hyperpolarization, spike-frequency adaptation, and preferred frequency of individual neurons are predicted to have significant consequences for synchronization of oscillatory firing in populations of neurons (Fuhrmann et al. 2002).
It is important to note that our studies investigated the response of motoneurons to current injected into the cell body, yet activation in vivo would involve synaptic inputs to both dendritic and somatic regions. Classical studies of motoneuron physiology (Binder et al. 1996) revealed a correlation between the action potential threshold in response to somatic current injection and that evoked by natural synaptic input. Thus there is ample precedent for assessing motoneuron functional properties with somatic current injection. Nevertheless, it will be essential to investigate the effects of DNE on motoneuron responses to natural synaptic drive.
In conclusion, our experiments show that DNE alters spike-timing precision and reliability and spike-frequency adaptation, adding to an expanding volume of literature indicating that DNE has significant effects on the input-output properties of XIIMNs. Importantly, this dynamic current injection analysis provides information about a neuron's ability to respond precisely and faithfully to oscillatory inputs and to relay this information in a manner that promotes the formation of synchronous network activity. The cellular and molecular mechanisms by which DNE alters the input-output relation of motoneurons are unknown, but the present data provide important clues for future investigations.
GRANTS
This research was supported by National Institute of Child Health and Human Development Grant 1R01-HD-071302 and American Heart Association Grant 12GRNT12050345.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: G.L.P. and R.F.F. conception and design of research; G.L.P. and A.M.F. performed experiments; G.L.P. and A.M.F. analyzed data; G.L.P., R.B.L., and R.F.F. interpreted results of experiments; G.L.P. prepared figures; G.L.P. drafted manuscript; G.L.P., R.B.L., and R.F.F. edited and revised manuscript; R.F.F. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Seres Cross for expertly implanting the osmotic minipumps.
REFERENCES
- Beierholm U, Nielsen CD, Ryge J, Alstrom P, Kiehn O. Characterization of reliability of spike timing in spinal interneurons during oscillating inputs. J Neurophysiol 86: 1858–1868, 2001. [DOI] [PubMed] [Google Scholar]
- Berlin I, Heilbronner C, Georgieu S, Meier C, Spreux-Varoquaux O. Newborns' cord blood plasma cotinine concentrations are similar to that of their delivering smoking mothers. Drug Alcohol Depend 107: 250–252, 2010. [DOI] [PubMed] [Google Scholar]
- Binder MD, Heckman CJ, Powers RK. The physiological control of motoneuron activity. In: Handbook of Physiology. Exercise: Regulation and Integration of Multiple Systems. Bethesda, MD: Am Physiol Soc, 1996, sect. 12, 1996, p. 3–53 [Google Scholar]
- Brody CD, Hopfield JJ. Simple networks for spike-timing-based computation, with application to olfactory processing. Neuron 37: 843–852, 2003. [DOI] [PubMed] [Google Scholar]
- Brunel N, Chance FS, Fourcaud N, Abbott LF. Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys Rev Lett 86: 2186–2189, 2001. [DOI] [PubMed] [Google Scholar]
- Fellous JM, Houweling AR, Modi RH, Rao RP, Tiesinga PH, Sejnowski TJ. Frequency dependence of spike timing reliability in cortical pyramidal cells and interneurons. J Neurophysiol 85: 1782–1787, 2001. [DOI] [PubMed] [Google Scholar]
- Fetz EE, Gustafsson B. Relation between shapes of post-synaptic potentials and changes in firing probability of cat motoneurones. J Physiol 341: 387–410, 1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florescu A, Ferrence R, Einarson T, Selby P, Soldin O, Koren G. Methods for quantification of exposure to cigarette smoking and environmental tobacco smoke: focus on developmental toxicology. Ther Drug Monit 31: 14–30, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhrmann G, Markram H, Tsodyks M. Spike frequency adaptation and neocortical rhythms. J Neurophysiol 88: 761–770, 2002. [DOI] [PubMed] [Google Scholar]
- Funk GD, Parkis MA. High frequency oscillations in respiratory networks: functionally significant or phenomenological? Respir Physiol Neurobiol 131: 101–120, 2002. [DOI] [PubMed] [Google Scholar]
- Granit R, Kernell D, Shortess GK. Quantitative aspects of repetitive firing of mammalian motoneurones, caused by injected currents. J Physiol 168: 911–931, 1963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddad GG, Donnelly DF, Getting PA. Biophysical properties of hypoglossal neurons in vitro: intracellular studies in adult and neonatal rats. J Appl Physiol (1985) 69: 1509–1517, 1990. [DOI] [PubMed] [Google Scholar]
- Huang YH, Brown AR, Costy-Bennett S, Luo Z, Fregosi RF. Influence of prenatal nicotine exposure on postnatal development of breathing pattern. Respir Physiol Neurobiol 143: 1–8, 2004. [DOI] [PubMed] [Google Scholar]
- Huang YH, Brown AR, Cross SJ, Cruz J, Rice A, Jaiswal S, Fregosi RF. Influence of prenatal nicotine exposure on development of the ventilatory response to hypoxia and hypercapnia in neonatal rats. J Appl Physiol 109: 149–158, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaiswal SJ, Pilarski JQ, Harrison CM, Fregosi RF. Developmental nicotine exposure alters AMPA neurotransmission in the hypoglossal motor nucleus and pre-Botzinger complex of neonatal rats. J Neurosci 33: 2616–2625, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John J, Bailey EF, Fregosi RF. Respiratory-related discharge of genioglossus muscle motor units. Am J Respir Crit Care Med 172: 1331–1337, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DH. The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones. J Acoust Soc Am 68: 1115–1122, 1980. [DOI] [PubMed] [Google Scholar]
- Katz PS, Frost WN. Removal of spike frequency adaptation via neuromodulation intrinsic to the Tritonia escape swim central pattern generator. J Neurosci 17: 7703–7713, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koizumi H, Koshiya N, Chia JX, Cao F, Nugent J, Zhang R, Smith JC. Structural-functional properties of identified excitatory and inhibitory interneurons within pre-Botzinger complex respiratory microcircuits. J Neurosci 33: 2994–3009, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lape R, Nistri A. Current and voltage clamp studies of the spike medium afterhyperpolarization of hypoglossal motoneurons in a rat brain stem slice preparation. J Neurophysiol 83: 2987–2995, 2000. [DOI] [PubMed] [Google Scholar]
- Lavine RA. Phase-locking in response of single neurons in cochlear nuclear complex of the cat to low-frequency tonal stimuli. J Neurophysiol 34: 467–483, 1971. [DOI] [PubMed] [Google Scholar]
- Luo Z, Costy-Bennett S, Fregosi RF. Prenatal nicotine exposure increases the strength of GABA(A) receptor-mediated inhibition of respiratory rhythm in neonatal rats. J Physiol 561: 387–393, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Z, McMullen NT, Costy-Bennett S, Fregosi RF. Prenatal nicotine exposure alters glycinergic and GABAergic control of respiratory frequency in the neonatal rat brainstem-spinal cord preparation. Respir Physiol Neurobiol 157: 226–234, 2007. [DOI] [PubMed] [Google Scholar]
- Ma L, Wu YM, Guo YY, Yang Q, Feng B, Song Q, Liu SB, Zhao DQ, Zhao MG. Nicotine addiction reduces the large-conductance Ca(2+)-activated potassium channels expression in the nucleus accumbens. Neuromol Med 15: 227–237, 2013. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science 268: 1503–1506, 1995. [DOI] [PubMed] [Google Scholar]
- Miura M, Ishii K, Aosaki T, Sumikawa K. Chronic nicotine treatment increases GABAergic input to striatal neurons. Neuroreport 17: 537–540, 2006. [DOI] [PubMed] [Google Scholar]
- Mosfeldt Laursen A, Rekling JC. Electrophysiological properties of hypoglossal motoneurons of guinea-pigs studied in vitro. Neuroscience 30: 619–637, 1989. [DOI] [PubMed] [Google Scholar]
- Pike FG, Goddard RS, Suckling JM, Ganter P, Kasthuri N, Paulsen O. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J Physiol 529: 205–213, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilarski JQ, Fregosi RF. Prenatal nicotine exposure alters medullary nicotinic and AMPA-mediated control of respiratory frequency in vitro. Respir Physiol Neurobiol 169: 1–10, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilarski JQ, Wakefield HE, Fuglevand AJ, Levine RB, Fregosi RF. Developmental nicotine exposure alters neurotransmission and excitability in hypoglossal motoneurons. J Neurophysiol 105: 423–433, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers RK, Sawczuk A, Musick JR, Binder MD. Multiple mechanisms of spike-frequency adaptation in motoneurones. J Physiol (Paris) 93: 101–114, 1999. [DOI] [PubMed] [Google Scholar]
- Sastry BV, Chance MB, Singh G, Horn JL, Janson VE. Distribution and retention of nicotine and its metabolite, cotinine, in the rat as a function of time. Pharmacology 50: 128–136, 1995. [DOI] [PubMed] [Google Scholar]
- Sawczuk A, Powers RK, Binder MD. Contribution of outward currents to spike-frequency adaptation in hypoglossal motoneurons of the rat. J Neurophysiol 78: 2246–2253, 1997. [DOI] [PubMed] [Google Scholar]
- Sawczuk A, Powers RK, Binder MD. Spike frequency adaptation studied in hypoglossal motoneurons of the rat. J Neurophysiol 73: 1799–1810, 1995. [DOI] [PubMed] [Google Scholar]
- Sejnowski TJ, Paulsen O. Network oscillations: emerging computational principles. J Neurosci 26: 1673–1676, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, McCormick DA, Sejnowski TJ. Thalamocortical oscillations in the sleeping and aroused brain. Science 262: 679–685, 1993. [DOI] [PubMed] [Google Scholar]
- Stiefel KM, Gutkin BS, Sejnowski TJ. Cholinergic neuromodulation changes phase response curve shape and type in cortical pyramidal neurons. PLoS One 3: e3947, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang AC, Bartels AM, Sejnowski TJ. Effects of cholinergic modulation on responses of neocortical neurons to fluctuating input. Cereb Cortex 7: 502–509, 1997. [DOI] [PubMed] [Google Scholar]
- Usrey WM, Reid RC. Synchronous activity in the visual system. Annu Rev Physiol 61: 435–456, 1999. [DOI] [PubMed] [Google Scholar]
- van Brederode JF, Berger AJ. Spike-firing resonance in hypoglossal motoneurons. J Neurophysiol 99: 2916–2928, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viana F, Bayliss DA, Berger AJ. Repetitive firing properties of developing rat brainstem motoneurones. J Physiol 486: 745–761, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng J, Powers RK, Newkirk G, Yonkers M, Binder MD. Contribution of persistent sodium currents to spike-frequency adaptation in rat hypoglossal motoneurons. J Neurophysiol 93: 1035–1041, 2005. [DOI] [PubMed] [Google Scholar]