Shear stress is normalized in glomerular capillaries following ⅚ nephrectomy

Abstract

Loss of significant functional renal mass results in compensatory structural and hemodynamic adaptations in the nephron. While these changes have been characterized in several injury models, how they affect hemodynamic forces at the glomerular capillary wall has not been adequately characterized, despite their potential physiological significance. Therefore, we used intravital multiphoton microscopy to measure the velocity of red blood cells in individual glomerular capillaries of normal rats and rats subjected to ⅚ nephrectomy. Glomerular capillary blood flow rate and wall shear stress were then estimated using previously established experimental and mathematical models to account for changes in hematocrit and blood rheology in small vessels. We found little change in the hemodynamic parameters in glomerular capillaries immediately following injury. At 2 wk postnephrectomy, significant changes in individual capillary blood flow velocity and volume flow rate were present. Despite these changes, estimated capillary wall shear stress was unchanged. This was a result of an increase in capillary diameter and changes in capillary blood rheology in nephrectomized rats.

endothelial cells sense and respond to changes in fluid flow and shear stress to maintain normal physiological function, and altered endothelial mechanotransduction has been implicated in the development of disease (8). Shear stress at the interface between flowing blood and the endothelial glycocalyx is transmitted to the endothelial cells, resulting in various cellular responses (38, 39). Acute increases in shear stress in the systemic circulation result in vasodilation, while chronic changes in fluid shear stress lead to vessel remodeling to maintain wall shear stress at relatively constant levels (18, 22). However, the role of fluid shear stress in glomerular capillary remodeling has not been well studied in the context of chronic renal injury.

Changes in single-nephron hemodynamics have been characterized in a number of disease models. In the setting of chronic kidney disease, loss of functional nephrons often leads to hyperfiltration in remnant nephrons (6, 15). In nephrectomized rats, this process is characterized by a two- to threefold increase in plasma flow and single-nephron glomerular filtration rate (SNGFR) in remnant nephrons (3, 5, 9, 29, 40). In the absence of compensatory mechanisms, increased flow would result in a comparable increase in shear stress at the wall of the glomerular capillaries. However, compensatory hypertrophy of remnant nephrons accompanies many chronic renal diseases (10, 14, 20). Following partial nephrectomy in rats, the number of glomerular capillary segments, average capillary length, and total capillary surface area increase (1, 27).

Despite the well-established hemodynamic and structural adaptations in the nephron following injury, how these alter the mechanical microenvironment in vivo is not clear. Our current understanding of the role of mechanical stimulation of glomerular endothelial cells comes largely from in vitro studies of perfused, isolated glomerular endothelial cells. Glomerular endothelial cytoskeletal organization, endothelial nitric oxide synthase (eNOS) signaling, nitric oxide production, and electrical resistance are altered in cultured cells grown under physiological levels of fluid shear stress compared with cells grown in static culture (4). Chronic exposure to shear stress in glomerular endothelial cells decreased NF-κB activation and platelet-derived growth factor B (PDGF-B) expression (12). Despite the seemingly important role of fluid flow in glomerular endothelial cell function, the effects of disease-related changes in renal blood flow on shear stress in the glomerulus has not yet been characterized.

Intravital multiphoton imaging of the kidney has emerged as a powerful tool to evaluate kidney function and disease (13, 17, 26, 30). Here, we use intravital microscopy to directly measure red blood cell (RBC) velocity in the glomerular capillaries of healthy and injured rats. We then used previously established theoretical models and experimental data regarding blood rheology in small tubes and vessels to estimate the shear forces at the glomerular capillary wall in health and disease. This approach permits estimation of shear stress in glomerular capillaries from direct measurements of blood flow and structural characterization in individual glomerular capillaries.

Understanding the mechanical microenvironment of the nephron is critical to understanding the role of mechanotransduction in progression of kidney disease. However, little experimental data exist on the shear stress on glomerular endothelial cells in vivo, especially in the setting of renal dysfunction. The goal of this work was to measure injury-induced changes in individual capillary blood flow and estimate hemodynamic forces at the glomerular capillary wall in healthy animals to determine whether changes in single-nephron blood flow due to loss of functional nephron mass had a significant and potentially physiologically meaningful impact on the hemodynamic forces on glomerular capillaries. We found that despite significant changes in renal hemodynamics 2 wk following injury, glomerular vascular remodeling as well as changes in the rheological properties of blood acted to maintain shear stress at the glomerular capillary wall at relatively constant levels. Additionally, there were no measureable differences in the hemodynamic parameters immediately following injury.

MATERIALS AND METHODS

Animals.

All experiments were conducted in accordance with National Institutes of Health guidelines and were approved by the Institutional Animal Care and Use Committee. Male Simenson Munich-Wistar rats were anesthetized using isoflurane. Blood pressure was monitored by cannulating the femoral artery. Intravenous access was obtained in the jugular vein. Animals were hydrated during imaging by intravenous infusion of normal saline at 1.5 ml/h. One set of animals underwent ⅚ nephrectomy (5/6 Nx) performed 2 wk before imaging. The right kidney was removed, and two branches of the renal artery were occluded in the left kidney. The left kidney was externalized immediately before imaging through a small flank incision (34). Before imaging, a small blood sample was taken and systemic hematocrit was measured by centrifugation.

Imaging.

The animals were moved to the microscope stage, and the externalized kidney was placed in contact with a glass-bottom dish filled with normal saline. Blood pressure, heart rate, body temperature, and stage temperature were monitored continuously during imaging, and temperature was maintained at 37 ± 1°C using a warming pad. Imaging was performed on an Olympus FV1000 multiphoton microscope. Surface glomeruli were first identified under low magnification (×20). Line scans of capillary blood flow were obtained using a ×60 water-immersion objective (NA 1.2) as described previously (35). The number of individual glomeruli that were imaged in each experimental group were 50, 33, and 19 for control, 5/6 Nx (t = 0), and 5/6 Nx (t = 2 wk), respectively. Line scans were taken in 3–6 capillaries/glomeruli for a total number of capillary scans of 225, 155, and 95 for control, 5/6 Nx (t = 0), and 5/6 Nx (t = 2 wk), respectively.

RBC velocity.

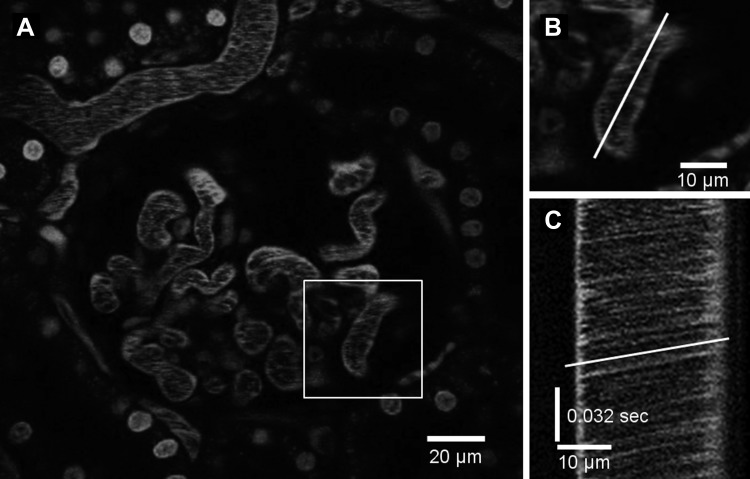
To measure axial or centerline RBC velocity in the glomerular capillaries, animals were injected with 150-kDa rhodamine-labeled dextran (TdB Consultancy, Uppsala, Sweden). This fluorescent-labeled macromolecule distributes into plasma and is not appreciably cleared by the kidney. Figure 1A shows a single glomerulus following injection of rhodamine-dextran. Line scans were obtained as close as possible to the centerline of each capillary segment (Fig. 1B). In the line scan images, RBCs appear as dark streaks (Fig. 1C), the slopes of which correlate with the RBC velocity as described previously (19, 25, 41).

Fig. 1.

A: fluorescence micrograph of a glomerulus after injection of high-molecular-weight (150 kDa) rhodamine-dextran. Cell nuclei are stained with Hoechst. B: line scan location for generating the time-distance image. C: line scan image of time (t) − distance (d). The black streaks indicate red blood cells moving through the vessel. The slope of the streaks (white line) is used to calculate the centerline velocity.

Cross-sectional velocity, volume flow rate, and wall shear rate.

According to the Fahraeus effect, the RBC velocity in small vessels is higher than that of plasma due to the tendency of the cells to move to the center of the flow path. The ratio of the average blood velocity (v_b) to the average cell velocity (v_c) is equal to the ratio of the hematocrit in the vessel (H_T) to the discharge hematocrit (H_D). In single-file flow, the measured centerline velocity (v_cl) is equal to the average cell velocity. We assumed single-file flow for vessels with diameter (D_T) <12 μm. The average cross-sectional blood velocity is then given by Eq. 1.

$${\mathrm{v}}_{\mathrm{b}}=\frac{{\mathrm{H}}_{\mathrm{T}}}{{\mathrm{H}}_{\mathrm{D}}}{\mathrm{v}}_{\mathrm{c}\mathrm{l}}$$ (1)

Given the technical difficulty of determining instantaneous tube and discharge hematocrits, we estimated H_T/H_D as a function of vessel diameter using the Papenfuss and Gross (28) least-squares fit of the Albrecht et al. (2) in vitro data for blood flow through narrow glass tubes.

$$\frac{{\text{H}}_{\text{T}}}{{\text{H}}_{\text{D}}}=0.5\left[1+e^{-0.633\left(\frac{D_{\text{T}}}{D*}-1\right)}\right]$$ (2)

where D^* is the smallest diameter vessel that a RBC can pass through without altering its surface area. This is calculated from the following relationship

$${(D*)}^3-\frac{3\mathit{A}\mathrm{c}}{\pi }D*+\frac{12}{\pi }V\mathrm{c}$$ (3)

where cell surface area (A_c) and cell volume (V_c) were taken as 137 μm² and 60 μm³, respectively.

For larger vessels (>20 μm) where multiple cells moving at different velocities occupy a cell-rich core that is surrounded by a cell-free layer, H_T/H_D has been shown to increase to unity at vessel diameters ∼300 μm (2), and the relationship between centerline velocity and average cross-sectional blood velocity is reasonably well estimated by v_b= 0.625v_cl (23). Little experimental or theoretical data exist for the transition between these two flow regimes. As such, we simply assumed a linear increase in H_T/H_D to unity at 300 μm and v_b/v_cl to 0.625 at 20 μm as a function of vessel diameter for 12 μm < D_T < 20 μm. While this is an oversimplification, the vast majority of the vessels examined in both the normal and injury groups were <12 μm in diameter.

The volume flow rate (Q) was calculated as the product of the average cross-sectional velocity and the cross-sectional area as determined from direct measurements of the capillary diameters assuming a circular cross section. Wall shear rate (γ˙) was calculated according to Eq. 4

$$\dot{\gamma }=\frac{32Q}{\pi D^3}$$ (4)

Estimating wall shear stress.

To estimate the capillary wall shear stress, the apparent viscosity in the vessel was calculated based on the Fahraeus-Lindquvist effect. We estimated the apparent viscosity using the relationship between vessel diameter and relative viscosity developed by Pries et al. (31). This requires an instantaneous value for the discharge hematocrit. As mentioned previously, this is technically challenging in vivo. We estimated H_D by assuming the linear relationship between H_T and systemic hematocrit (H_sys) as described previously (24). The discharge hematocrit was then calculated using the previously determined H_T/H_D ratio. The apparent relative viscosity was then calculated as a function of H_D and D_T according to the in vivo viscosity law (31). The apparent viscosity (μ_app) was then calculated by multiplying the relative apparent viscosity by the plasma viscosity, which was taken as 1.24 cP. Finally, shear stress (τ) was calculated using Eq. 5.

$$\tau ={\mu }_{\text{app}}\dot{\gamma }$$ (5)

Statistical analysis.

The changes in blood pressure and hematocrit between the injury and control groups were evaluated using a t-test. The effect of 5/6 Nx on vessel diameter, RBC velocity, cross-sectional velocity, volume flow rate, apparent viscosity, wall shear rate, and wall shear stress immediately and 2 wk post-Nx was analyzed using linear mixed-models analysis. Statistical analyses were performed using R version 3.1.2 (http://www.rstudio.com). A two-sided significance level of 5% was required for consideration as statistically significant.

RESULTS

Blood pressure and hematocrit.

Blood pressure was elevated at 2 wk post-Nx. Systolic pressure in control animals was 109 ± 4 mmHg (n = 8) vs. 126 ± 6 mmHg (n = 9) in the 5/6 Nx (t = 2 wk) group (P = 0.007). Systemic hematocrit dropped significantly at 2 wk following injury from 42 ± 2% in the control group to 35 ± 1% (P = 0.004) in the injury group.

Injury led to increased capillary diameter and average cross-sectional blood velocity.

The average vessel diameter and blood velocity are given in Fig. 2. Mean diameter for control animals was 8.7 ± 0.5 μm. There was no significant change immediately following nephrectomy (8.6 ± 0.3 μm), but at 2 wk post-Nx the mean capillary diameter increased to 10.1 ± 1.3 μm. There was no statistically significant change in average cross-sectional blood velocity immediately following 5/6 Nx. Average blood velocity for control animals was 0.09 ± 0.02 and 0.10 ± 0.04 cm/s immediately following 5/6 Nx. The average blood velocity at 2 wk post-Nx increased significantly to 0.14 ± 0.04 cm/s.

Fig. 2.

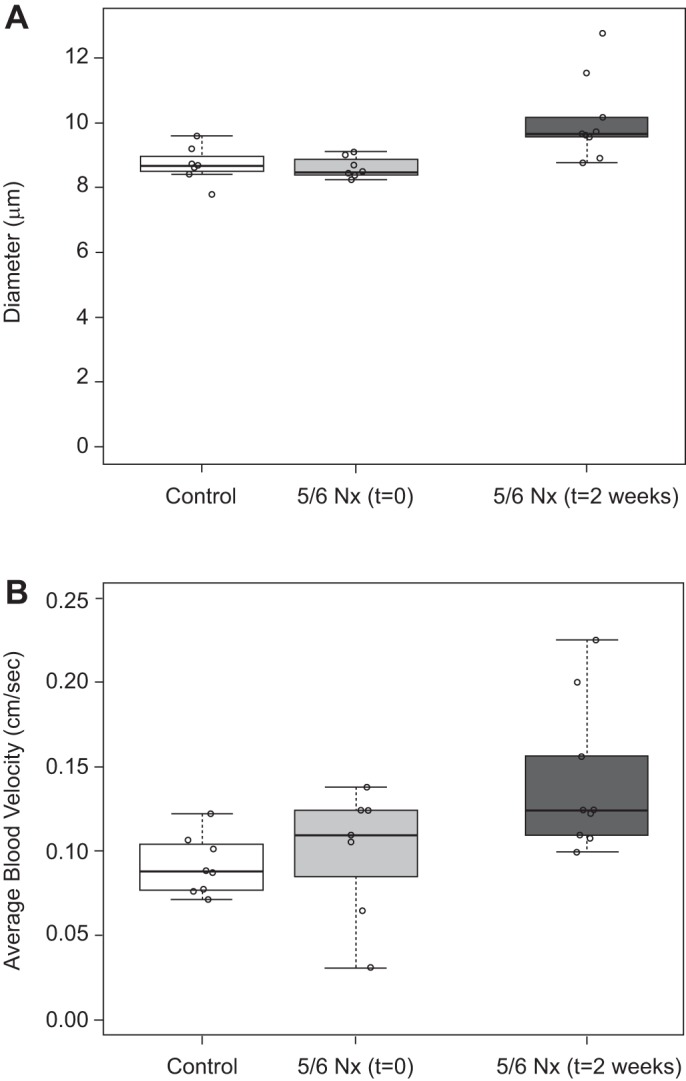
Glomerular capillary diameter (A) and average blood velocity (B) in rats before, immediately after, and 2 wk after ⅚ nephrectomy (5/6 Nx). Diameter and blood velocity increased significantly at 2 wk but not immediately following injury (t = 0). Individual data points on the box plot are the mean value for individual animals.

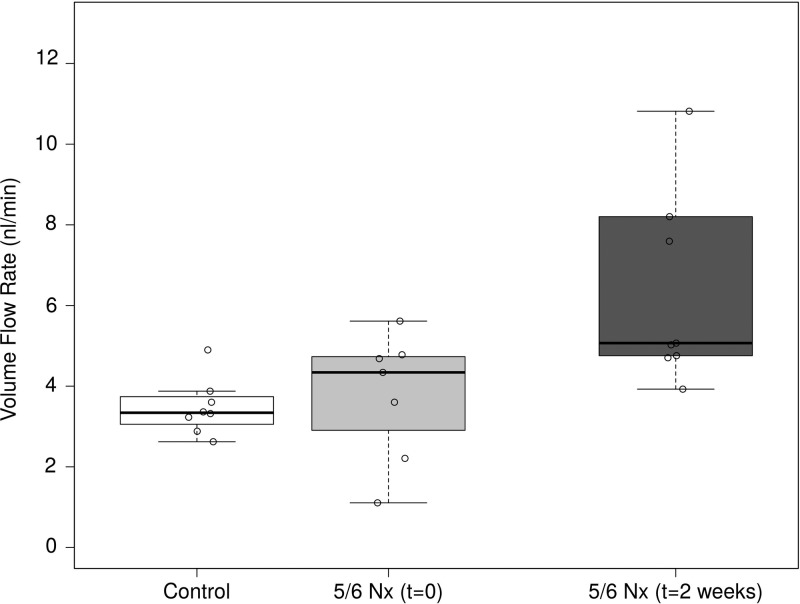
Injury led to increased volume flow rate.

Increases in both the average blood velocity and cross-sectional area led to a significant increase in the volume flow rate of blood in glomerular capillaries 2 wk following 5/6 Nx (Fig. 3). The average volume flux approximately doubled from 3.47 ± 0.70 nl/min in control animals to 7.28 ± 3.77 nl/min in the injury group. There was significant variability in the volume flow in each vessel. This is partially due to variability in the vessel diameter, with larger vessels exhibiting generally higher flow rates.

Fig. 3.

Volume flow rate in glomerular capillaries following 5/6 Nx. Volume flow rate increased significantly at 2 wk following injury but not immediately following injury.

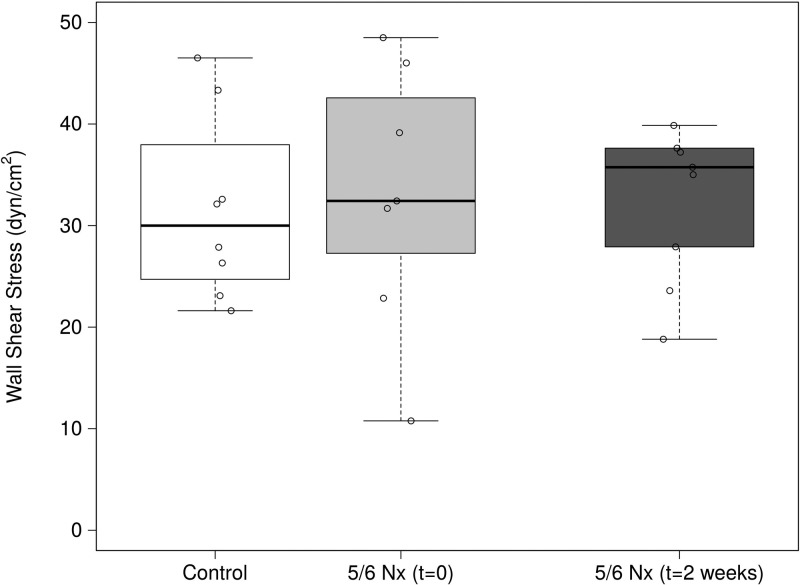
Injury did not affect wall shear stress.

There was a slight, but statistically significant increase in wall shear rate 2 wk following injury. Based on Eq. 2, the shear rate is a function of volume flow rate and vessel geometry. The increase in vessel diameter partially normalized the shear rate, but the large increase in volume flux resulted in a small increase in shear rate from 875 ± 195 s⁻¹ in control animals to 1,169 ± 340 s⁻¹ 2 wk after nephrectomy (P = 0.03). When the change in apparent viscosity is taken into account, the resulting wall shear stress remained unchanged 2 wk following 5/6 Nx (Fig. 4).

Fig. 4.

Wall shear stress in glomerular capillaries immediately after and 2 wk following 5/6 Nx. Despite the increase in volume flow, there was no statistically significant change in shear stress. This was a result of increased vessel diameter and decreased apparent viscosity.

A summary of the measured and calculated parameters are shown in Table 1. No significant changes were observed in any of the measured or calculated parameters immediately following injury. At 2 wk following injury, the vessel diameter, axial RBC velocity, blood velocity, apparent viscosity, and wall shear rate were all significantly different. The competing effects of blood flow, apparent viscosity, and capillary diameter had balanced effects on wall shear stress such that it remained unchanged after injury.

Table 1.

Glomerular capillary structural, hemodynamic, and rheological properties

	Control (n = 8)	5/6 Nx (t = 0; n = 7)	5/6 Nx (t = 2 wk; n = 9)
Diameter, μm	8.7 ± 0.5	8.6 ± 0.3 (NS)	10.1 ± 1.3* (P = 0.002)
Centerline cell velocity, cm/s	0.17 ± .03	0.18 ± .07 (NS)	0.26 ± 0.08* (P < 0.001)
Average blood velocity, cm/s	0.09 ± 0.02	0.10 ± 0.04 (NS)	0.14 ± 0.04* (P < 0.001)
Volume flow rate, nl/min	3.47 ± 0.70	3.76 ± 1.59 (NS)	7.28 ± 3.77* (P < 0.001)
Wall shear rate, s−1	875 ± 195	935 ± 356 (NS)	1,169 ± 340* (P = 0.03)
Apparent viscosity, cP	3.48 ± 0.28	3.49 ± 0.30 (NS)	2.85 ± 0.24* (P < 0.001)
Wall shear stress, dyn/cm2	31.7 ± 9.1	33.1 ± 13.2 (NS)	34.3 ± 9.9 (NS)

Values are means ± SD. Nx, nephrectomy; NS, no significant difference from control.

^*Statistically significant difference from control (P < 0.05).

DISCUSSION

Renal hyperfiltration and compensatory hypertrophy are well-established consequences of reduced renal mass. Despite significant changes in renal hemodynamics and their consequences for the progression of renal disease, we previously had limited insight into whether these changes translate into altered hemodynamic forces at the glomerular capillary wall. To investigate this further, we performed matched structural and blood flow analysis in individual glomerular capillaries and used these data to estimate capillary wall shear stress.

We observed a significant increase in capillary diameter following injury. Varying changes in capillary diameter following 5/6 Nx have been reported in previous studies, with one study showing no statistical difference in vessel diameter (1), while another showed an increase in vessel diameter similar to our findings (7). These studies were performed in Sprague-Dawley rats as opposed to the Munich Wistar strain. The diameter data were also obtained from histological sections, and the fixation procedure may have had an effect on the tissue structure. Since our data was collected in live animals, tissue preparation is excluded as a potential source of error in structural characterization. Other factors potentially contributing to differences between our results and those of others include details of the surgical procedures or the diet of animals following injury.

A limited number of studies have evaluated renal hemodynamics immediately following nephrectomy. One study by Sigmon et al. (36) showed an increase in renal blood flow of ∼8% immediately following unilateral nephrectomy that was mediated by NO. Any change in single-nephron blood flow and/or vasodilation that precedes renal hypertrophy could result in a transient change in the shear stress sensed by glomerular capillary endothelial cells. To investigate whether changes in blood flow in ⅚ nephrectomy could have an effect on glomerular capillary hemodynamics immediately following injury, we measured RBC velocity and vessel diameter within 2 h after injury. There was no observed change in vessel diameter, RBC velocity, or volume flow rate. After estimating wall shear rate and wall shear stress, there was no statistically significant difference between control animals and those that were evaluated immediately following injury. Based on these data, there is no indication that there are significant changes in renal hemodynamics or hemodynamic forces at the glomerular capillary wall in the early phase after ⅚ nephrectomy.

At 2 wk following injury, there were significant increases in both the mean axial RBC velocity and blood volume flow rate. Despite more than doubling of the mean volume flux, there was no significant change in the estimated wall shear stress. This stability results from the canceling effects of three factors. The first and most predominant is the increase in vessel diameter. Since shear stress scales with the cube of diameter, even small increases in vessel diameter have a significant impact on wall shear stress. The other two issues are related to the viscous properties of blood. The in vivo viscosity law predicts a strong relationship between effective viscosity and vessel diameter. Therefore, small changes in diameter result in a significant difference in apparent blood viscosity. Finally, the decrease in the systemic hematocrit in the 5/6 Nx (t = 2 wk) group also acts to decrease the estimated apparent viscosity based on the relationship between systemic hematocrit and microvessel hematocrit. The combination of structural alteration in the glomerular capillary and the size-dependent viscous properties of blood acts to normalize the wall shear stress in the glomerular capillaries 2 wk after ⅚ nephrectomy.

The only previous studies that we are aware of that attempted to estimate the shear stress at the glomerular capillary wall were mathematical network models by Lambert et al. (21) and Remuzzi et al. (32). The Remuzzi analysis, which was based on a full histological reconstruction of a rat glomerulus, resulted in a mean capillary wall shear stress of 23 dyn/cm². This model was based on a combination of theoretical analysis and in vitro data to estimate apparent viscosity. More recent data have shown that the apparent viscosity in vivo is significantly higher than what would be estimated from measurements in smooth-walled tubes under similar conditions (31). It has been suggested that this is due to a combination of in vivo effects that include the influence of the endothelial glycocalyx in determining flow resistance in small-diameter vessels (11). Additional factors that likely contribute to the difference in vivo compared with in vitro include irregularities in the microvessel diameter (16) and network effects due to vessel branching (31).

Estimating shear stress in glomerular capillaries is complicated by several factors. The microcirculation both in the kidney and in other microvascular networks is characterized by a high degree of heterogeneity with regard to both volume flux and hematocrit. Microvascular parameters like tube hematocrit and apparent viscosity have not been well studied in the kidney microcirculation. Here, we attempted to estimate these parameters using a combination of in vitro data and in vivo data from other microvascular networks. The application of microvascular parameters based on data obtained in other vascular systems is far from ideal, but the lack of data from the glomerular vasculature required some extrapolation. Consequently, additional experimental and theoretical work specific to the glomerular capillary network may lead to a more accurate estimation of the shear stress at the glomerular capillary wall. In addition, intravital two-photon microscopy is confined to imaging superficial glomeruli due to limited tissue penetration depth. Any differences in blood flow in deeper glomeruli would not be captured using this technique. Finally, the analysis presented here is effectively measuring the fluid shear stress at the interface between the blood flow and endothelial glycocalyx. The endothelial glycocalyx transmits that force to the endothelial cell, resulting in an altered cell response (38, 39). It is clear that a number of disease states alter the permeability properties of the glomerular endothelial glycocalyx (33, 37) and may alter the transmission of force to the glomerular endothelial cells. This could be a potential mechanism by which endothelial mechanotransduction may be altered even in a setting of unchanged wall shear stress.

Despite these limitations, this analysis illustrates several important points. The lack of altered blood flow parameters in individual glomerular capillaries in the phase immediately following injury suggests that the response to renal injury is not likely dominated by short-term vasomotor responses, but rather by long-term adaptations. In the chronic-injury phase, there are significant increases in blood velocity and volume flow rate, but shear stress is maintained at relatively constant levels as a result of two main factors. First, structural remodeling results in increased capillary diameter that acts to decrease the wall shear stress. This is a similar compensatory mechanism to that observed in other vascular networks. Second, the increase in vessel diameter combined with the decrease in the systemic hematocrit following injury result in a corresponding decrease in the estimated apparent blood viscosity that acts to decrease the wall shear stress. Finally, shear stress in the glomerular capillaries is likely higher than what has been previously predicted based on the observation that apparent viscosity is significantly higher in vivo than what is predicted purely from in vitro data and theoretical analysis.

GRANTS

This work was funded by a grant from the National Institutes of Health (K01 DK092357) and the George M. O'Brien Center for Advanced Renal Microscopic Analysis (P30 DK079312) at Indiana University Medical School.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: N.F. provided conception and design of research; N.F., R.M.S., and S.B.C.-B. performed experiments; N.F., R.M.S., and A.B. analyzed data; N.F. interpreted results of experiments; N.F. and A.B. prepared figures; N.F. drafted manuscript; N.F., B.A.M., and W.H.F. edited and revised manuscript; N.F., B.A.M., and W.H.F. approved final version of manuscript.