Calculating Optical Absorption Spectra of Thin Polycrystalline Organic Films: Structural Disorder and Site-Dependent van der Waals Interaction

Abstract

We propose a new approach for calculating the change of the absorption spectrum of a molecule when moved from the gas phase to a crystalline morphology. The so-called gas-to-crystal shift Δ_m is mainly caused by dispersion effects and depends sensitively on the molecule’s specific position in the nanoscopic setting. Using an extended dipole approximation, we are able to divide Δ_m= −QW_m in two factors, where Q depends only on the molecular species and accounts for all nonresonant electronic transitions contributing to the dispersion while W_m is a geometry factor expressing the site dependence of the shift in a given molecular structure. The ability of our approach to predict absorption spectra is demonstrated using the example of polycrystalline films of 3,4,9,10-perylenetetracarboxylic diimide (PTCDI).

Introduction

Thin films of conjugated organic molecules are essential building blocks in organic and hybrid optoelectronics. These films are typically characterized by a nanocrystalline structure. Planar or bulk heterojunctions are realized either by different organic molecules or by combination with inorganic semiconductors or metal oxides such as ZnO and TiO₂.¹⁻³ The energetic alignment of the ground and excited states of the different materials governs the efficiency of charge separation and the open-circuit voltage in photovoltaic cells and, similarly, the injection of charge carriers and energy transfer dynamics in light-emitting devices.⁴⁻⁶ Hence, it is essential to understand in detail how structural disorder and site-dependent interactions affect the energetic properties of organic thin films.

When a molecule m is moved from the gas phase into a crystalline morphology, its optical transition energies undergo the so-called gas-to-crystal shift. This shift is due to (i) Coulomb coupling of static charge distributions, (ii) inductive polarization shifts, (iii) excitonic shifts, (iv) dispersion shifts caused by the interaction between higher excited transition densities of the molecule m and surrounding molecules, and (v) charge transfer states coupling to Frenkel exciton states.

In this manuscript, we show that absorption spectra of nanocrystalline molecular films are dominated by dispersive shifts (iv). These shifts are typically assumed to be constant for all molecules of the system which is true in a bulk crystal where all constituents feel the same infinitely large environment. However, in a nanoscopic morphology, the dispersion becomes site-dependent. It will strongly depend on whether the molecule is situated close to the surface or deep within the nanocrystallite. We will introduce in the following an efficient computation scheme to calculate the site-dependent level shift and demonstrate its capability by explaining optical absorption spectra of a series of thin nanocrystalline films of 3,4,9,10-perylenetetracarboxylic diimide (PTCDI) of different crystallite size. Figure 1 shows a typical absorption spectrum of a thin PTCDI film grown by molecular beam deposition. The spectral shape is characterized by a distinct double-structure that does not resonate with the features of the isolated molecule in solution (see Figure 1). We will show in the following that the two features are due to molecules experiencing distinctively different environments.

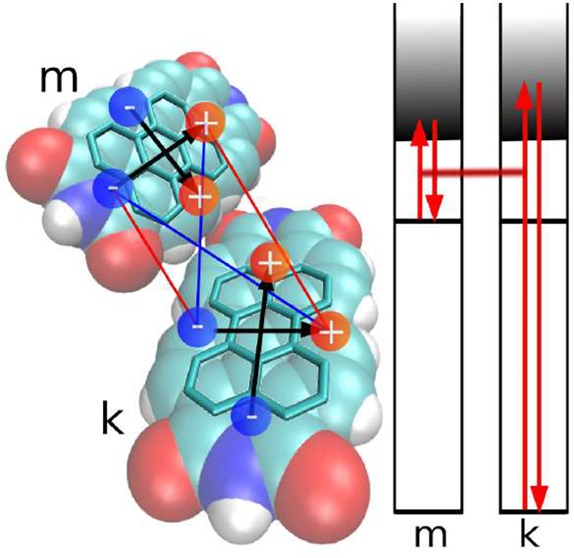
Figure 1.

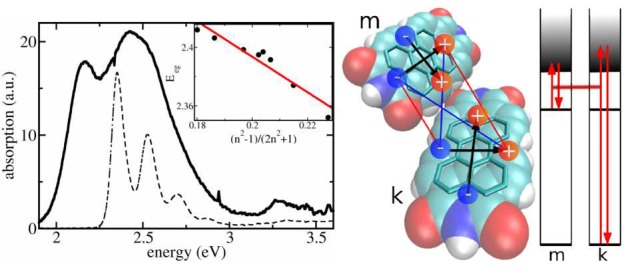
Left panel: Room temperature absorption spectra of different PTCDI systems. Solid line: PTCDI film vacuum-deposited on Al₂O₂. The nominal thickness is 12 nm. Dashed line: PTCDI monomer in toluene solution. The inset shows the S_0,ν=0 → S_1,ν=0 transition energy for the PTCDI derivate N,N′-bis(1-hexylheptyl)perylene-3,4:9,10-bis(dicarboximide) in nonpolar solvents with different refractive indices n: pentane (n = 1.36), hexane (n = 1.38), nonane (n = 1.41), dodecane (n = 1.42), cyclohexane (n = 1.43), hexadecane (n = 1.43), tetrachloromethane (n = 1.46), and benzene (n = 1.50). Red line: linear fit. Right panel: Space-filling model of two PTCDI molecules. The carbon bondings establishing the π-electron system are highlighted. The positive and negative partial charges of an extended dipole model for higher electronic transitions of type ξ are indicated. Their interaction represents the position and orientation dependent excitonic coupling between molecule m and molecule k. The depicted interaction constitutes V(m∥,k⊥). A scheme of coupled virtual transitions giving rise to the dispersive shift ΔE_me(k), eq 1, is presented as well. Shown is the transition of molecule m into a higher level f and the transition of a molecule k of the surrounding from its ground state to the higher level f′.

Model

We start the description of the system by defining the electronic states φ_ma and related energies E_ma of an isolated molecule at site m and in state a. In the most naive picture, singly excited states now follow from the standard Frenkel exciton Hamiltonian H_exc = ∑_m,n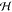mn|ϕ_m⟩⟨ϕ_n|, where the ground state energy E₀ = ∑_mE_mg = 0 is shifted to the origin of the energy scale.

Here, we have defined the molecular product states ϕ_m with molecule m in the first excited state φ_me and all other molecules in the ground state φ_ng. The overall ground state ϕ₀ is given by the product of all molecular ground states φ_ng. The diagonal and off-diagonal part of the Hamiltonian matrix 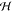_mn represent the excitation energies 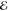_m = E_me −E_mg and the resonant excitonic coupling terms 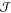_mn, respectively. A proper rescaling of all elements of 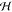_mn may account for the dispersion effects, but a more microscopic picture is desirable. We note that site-dependent dispersive energy shifts have been calculated for aggregates of Rydberg atoms in ref (10). Here, we suggest a method that is capable of calculating those shifts for molecular aggregates.

In the following, we will directly compute the site-dependent shifts Δ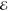_m = ΔE_me – ΔE_mg of the excitation energy 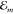. Here, the individual level shifts ΔE_ma with a = g, e arise from the nonresonant Coulomb coupling of molecule m with all its surrounding molecules. They can be written as ΔE_ma = ∑_kΔE_ma(k), where the contribution due to the coupling to molecule k is given in second order perturbation theory by^13,14

1

The expression includes the transition energies E_mfa = E_mf – E_ma and E_kf′g = E_kf′ – E_kg. f and f′ count all higher excited energy levels (f, f′ > e), and J_mk(ag, f′f) is the Coulomb coupling between the electronic transition density ρ_fa^(m)(r) of molecule m and the electronic transition density ρ_f′g(r′) of molecule k (cf. Figure 1).⁸ Equation 1 illustrates that the site dependence of the dispersion originates from the dependence of the J_mk(ag, f′f) on the position of molecule m relative to molecule k. Since the summation of the two energy differences in the denominator is always more than 1 order of magnitude larger than the coupling of transition densities, eq 1 represents a good approximation for the energy shift ΔE_ma(k).

The rigorous evaluation of eq 1 for a large molecule like PTCDI in a complex environment like a nanocrystalline film according to eq 1 is a formidable task. Instead, we utilize a simplified treatment based on the well-established extended dipole approximation for computation of the J_mk(ag, f′f). This allows us to derive a formula for the level shifts that contains only quantities that are, at least in principle, accessible by experiment. In the extended dipole approximation, the actual transition densities are replaced by transition dipoles represented by a single negative and a single positive charge ∓q placed at a fixed distance that resembles the spatial extension of the single-molecule excitation (see Figure 1). As a consequence, the resulting distance dependence of the J_mk(ag, f′f) is more realistic as in the point dipole approximation.

The PTCDI excited states can be classified into states with transition dipoles parallel to the long molecular axis (ξ(a,f) = ∥) and perpendicular to it (ξ(a,f) = ⊥) (Supporting Information part A). The basic idea of our simplified treatment is to place the charges at the same distance for all transitions f with polarization (ξ(a,f) = ∥) and likewise for the charges corresponding to the transitions of type ξ(a,f) = ⊥. In both cases, the q(a,f) is positioned at the boundary of the π-electron system (cf. Figure 1). As a consequence, the charge q(a,f) depends on the initial state a and the excited state f and can be derived from the ratio of the respective transition dipole moment and the intercharge distance.

We verified this approximation by performing extensive electronic structure computations for a large number of excited states by comparing the Coulomb coupling matrix elements J_mk obtained by the extended dipole approximation with the exact value based on atomic-centered partial transition charges (Supporting Information part A). The mean error is below 5% for all excited states that have been considered. The extended dipole approximation allows us to factorize the interaction matrix element J_mk(ag, f′f) = q(a,f)q(g,f′)V(mξ(a,f), kξ′(g,f′)) into two contributions, the effective charges q(a,f), q(g,f′) and the distance dependence of the interaction of extended dipoles V(mξ(a,f), kξ′(g,f′)), i.e., the interaction of a pair of unit charges of opposite sign at molecule m and k. The V(mξ(a,f), kξ′(g,f′)) still depend on the transitions af, gf′ via ξ(a,f), ξ′(g,f′).

If the different states f, f′ lie sufficiently close in energy, we may average over the two different transition dipole directions by introducing |V_mk|² = ∑_ξ, ξ′|V(mξ, kξ′)|²/4. Our electronic structure calculations of the higher excited states support this approximation. As a consequence, the V_mk becomes independent of the states f, f′ and hence J_mk(ag,f′f) ≈ q(f)q(f′)V_mk.

Finally, the site-dependent transition energy shift of molecule m can be written as

2

with

3

and W_m = ∑_kV_mk².

While W_m can be interpreted as a geometry factor determined by the structure of the nanocrystalline film, the Q-factor is specific to the molecule under consideration and accounts for transition energies and strengths of all its excited states f. The Q-factor cannot directly be calculated; however, it can be obtained experimentally from an independent absorption measurement of an amorphous film of randomly orientated molecules. The obtained value of Δ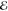_m is identified with Q⟨W_m⟩, where the angle brackets represent the disorder average. The thus obtained Q-factor can then be used to calculate site-dependent energy shifts for any given nanostructured environment.

Before simulating PTCDI absorption spectra, we provide an experimental estimate of the expected magnitude of the level shift. To this end, we measured absorption spectra placing the molecules in various nonpolar environments (see Figure 1). Since PTCDI is not well soluble, we perform the experiment with the related molecule N,N′-bis(1-hexylheptyl)perylene-3,4:9,10-bis(dicarboximide) whose UV/vis spectrum perfectly coincides with that of PTCDI, as the alkyl substituents do not affect the π-electron system. The shift of the transition energy 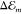with respect to the gas phase excitation energy E_gp is related to the solvent’s refractive index n at optical wavelengths via 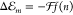with f(n) = (n² – 1) /(2n² + 1).^14,15 The expression originates from the solvation energy of a point dipole in a spherical cavity surrounded by a homogeneous continuum.¹⁵ We will refer to this relation as the continuum solvent approximation (CSA). A fit of the measured S_0,ν=0 → S_1,ν=0 transition energy as a function of the solvent’s refractive index (cf. inset of Figure 1) yields 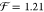eV and E_gp = 2.64 eV. For a thin polycrystalline PTCDI film, a refractive index n_PTCDI = 1.96 is reported.^16,17 Application of CSA predicts a rather substantial level shift of 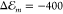meV with respect to E_gp which is in the range of the observed spectral changes (cf. Figure 1).

Experimental

The optical constants of PTCDI are measured in situ during deposition on KBr substrates by differential reflectance spectroscopy (DRS) in a thickness range between 0.1 and 5 monolayers (ML) using a home-built setup comprising a tungsten lamp and an Ocean Optics HR 4000 spectrometer connected to the deposition chamber via optical fibers. For thin films deposited on transparent substrates the DRS signal under normal incidence is proportional to the imaginary part of the films dielectric function Im(ϵ):¹⁸ DRS = ΔR/R ≈ −{8πd/λ}{Im(ϵ)/(1 – ϵ_KBr)}.

Information on the thin film morphology is obtained by atomic force microscopy performed in situ with an Omicron UHV AFM/STM controlled by a Matrix system. PTCDI films deposited on KBr(100) reveal steps with heights of 7 Å at sub-ML coverage (see Figure 2), indicating that the molecules do not lie flat on the surface but are tilted like in the bulk crystal.¹¹ The arrangement of the molecules in these planes as obtained by MD simulations is depicted in Figure 2. Increasing the coverage, the thin film morphology is characterized by formation of small, slightly elongated crystallites with no preferred single in plane orientation (see Figure 2).

Figure 2.

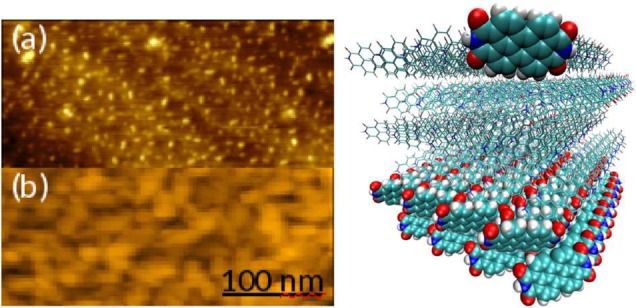
Left panel: AFM images of PTCDI deposited on KBr(100). The film thicknesses are (a) 0.2 ML and (b) 4.9 ML. The height scales are 1.5 and 6 nm, respectively. Right panel: Cross section of PTCDI monolayers. The PTCDI structure was obtained from a 1 ns MD simulation of a cube of 4.5 nm edge length, starting from the structure according to crystallographic data.¹¹ Highlighted are one PTCDI molecule at the crystallite surface and the first two monolayers (shown via space-filling models). In a single monolayer there is one molecule per unit cell; the PTCDI unit cell of the bulk crystal containing two molecules¹¹ is observed when at least two monolayers are present. All figures were produced with VMD.¹²

In order to calculate the W_m and the excitonic coupling matrix elements 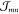, a precise knowledge of the morphology (size distribution and orientation of grains) and arrangement of PTCDI molecules in nanocrystalline domains is required. However, the experimental determination of the exact structure of the present PTCDI film is beyond the scope of this work. Instead, we performed extensive MD simulations of a set of 216 PTCDI molecules forming periodic cubic crystallites of maximal edge length of 4.5 nm in order to obtain possible PTCDI crystal configurations (see Supporting Information part B).

Results

We now apply the new methodology to explain the optical spectra of nanocrystalline PTCDI films. It is important to note that both the resonant excitonic coupling (iii) (which causes a mixing of states) and the nonresonant interactions (iv) (which are responsible for the level shifts) contribute to the observed changes in the spectrum when going from the isolated molecule to the polycrystalline thin film. It was shown in ref (7) that charge transfer states coupling to Frenkel exciton states (v) change the absorption curve only slightly for PTCDA crystals. Such a small effect was reproduced in our own calculations using the parameters given in ref (7). For the sake of clarity we will neglect charge transfer states in this work. Also, Coulomb coupling of static charge distributions (i) is found to be small (<5 meV) and thus inductive polarization shifts (ii) have been neglected (Supporting Information parts A and C).

Thus, for the derivation of absorption spectra, three more factors have to be accounted for, that is, the computation of the resonant excitonic coupling 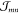, the screening of 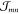, and the vibronic coupling from an MD generated molecular conformation. The screened 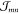have been computed via transition partial charges and respective screening factors⁹ as is explained in detail in Supporting Information part D. With the MD derived geometry, we obtain maximal values of 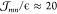meV. As resonant excitonic coupling is rather weak in PTCDI nanocrystallites, site-dependent level shifts must thus be mainly responsible for the large observed spectral changes (see Figure 1).

To account for vibronic coupling, only a single vibrational progression per molecule (Huang–Rhys factor of 0.62) is taken into account. This has been found sufficient for modeling the PTCDI monomer spectrum.¹⁹ The single particle approximation²⁰ is used to derive an electron–vibrational Hamilton matrix where a single vibronically (labeled by ν) excited molecule couples to surrounding molecules in the vibrational ground state.

Exciton states are constructed as Φ_α= ∑_m,νc_α(m,ν)χ_meνϕ_m, where χ_meν is the total vibrational wave function with vibrational excitations in the excited state of molecule m and the c_α(m,ν) denote the respective expansion coefficients. The absorption line shape follows as the sum over all exciton levels α with transition energies E_α weighted by the respective oscillator strengths |∑_m,νc_α(m,ν)d_m|². Finally, Gaussian broadening of typically 0.15 eV (full width at half-maximum) is introduced for all transitions. The value is deduced from the experimental absorption line width for 0.1 ML film coverage (see Figure 3).

Figure 3.

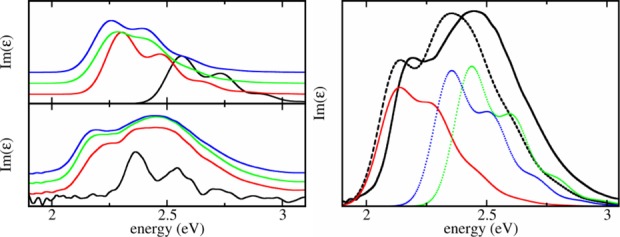
Left: Computed absorption line shapes assuming perfect two-dimensional films (upper panel) and measured (lower panel) absorption line shapes of different thicknesses of a PTCDI film (see text for details). Red: 1 ML. Green: 3 ML. Blue: 5 ML (4.9 ML for the experiment). The calculated black line shows the calculation for a single PTCDI molecule on the surface, according to the geometry of Figure 2. The measured black line shows the spectrum for 0.1 ML coverage, where the molecules are assumed to lay flat on the KBr surface. Right: A partly inhomogeneous film is assumed. Full black line: experimental spectrum for a 4.9 ML film of PTCDI on KBr. Dashed black line: calculated spectrum of a nanocrystalline film of nominally 5 ML thickness. For details on the structure, see text. Red line: calculated spectrum of a crystalline film composed of 5 ML arranged as in Figure 2. Dotted lines: calculated spectra for two types of thin films consisting of regular arranged small crystallites each containing 12 molecules; see Supporting Information part E for details.

The calculations have been done considering the conformation shown in Figure 2. The spectra calculated for the first one, three, and five monolayers (MLs) of the cube, assuming a perfect crystalline film, are depicted in Figure 3. We checked that the exciton spectrum does not further change when increasing the size of the system in directions parallel to the KBr surface. The dispersive energy shifts have been computed assuming periodic boundary conditions in the directions parallel to the KBr surface. Setting the theoretical shift 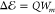equal to the experimentally obtained 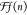, the Q-factor was calculated for the 5 ML thick, perfect film as Q = 3.2 eV Ų.

The dispersive molecular energy shifts due to interaction with the KBr surface have been approximated as follows. For a single molecule on a large PTCDI block the dispersive shift may be calculated as described above and interpreted as interaction between a single PTCDI molecule and a homogeneous dielectric which is proportional to the factor f(n). In this way, the interaction with the KBr surface can be treated. Since a single PTCDI on a PTCDI bulk is shifted by 0.1 eV, and the refractive indices of PTCDI and KBr are n_PTCDI = 1.96 ¹⁶ and n_KBr = 1.55, respectively, we estimate an energy shift of ΔE_PTCDI(KBr) = 0.075 eV for a PTCDI molecule on KBr. Since the molecules in the second ML (7 Å apart from the surface) show only a small dispersive energy shift due to interaction with the PTCDI bulk, we neglect respective energy shifts of all PTCDI molecules that are not directly located on the surface.

Calculated and experimental Im(ϵ) spectra are compared in Figure 3 for different PTCDI coverages. Both the calculated and experimental 1 ML spectra are red-shifted compared to the 0.1 ML spectra. This red-shift increases with increasing coverage. The trend is clearly seen considering the narrow feature in the experimental spectra. As already noted above, the calculations indicate that this shift is due to dispersion interaction. The large difference between experimental and calculated spectrum at 0.1 ML coverage is due to the fact that in the calculations we assume tilted molecules according to Figure 2. In the actual 0.1 ML film, the molecules most likely lay flat on the surface and receive thus a stronger red-shift.

The experimental thin film spectra display, besides the just discussed narrow feature, a broad band in the energy range between 2.3 and 2.8 eV which is absent in the calculated spectra where instead a vibrational progression similar to the monomer spectrum is observed. We conclude that the measured films consist not only of perfectly grown layers.

Instead, the line shape suggests that the spectrum is a superposition of spectra of a perfectly grown crystalline phase (feature at ∼2.1 eV) and a more loosely packed, rather disordered phase (broad band between 2.3 and 2.8 eV). The spectral weight of the two contributions implies that the proportion of well ordered and disordered phases is about the same.

To model the experimental spectra, an additional disordered phase is considered consisting of small crystallites (12 molecules) with a packing density reduced by 50% (see Supporting Information part E for structural details). The Q-parameter is recalculated taking into account the size distribution of the crystallites in the film. Because of the fact that the average over the W_m is smaller in a disordered film, setting Q⟨W_m⟩_m equal to the experimentally obtained 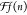yields a larger Q = 4.26 eV Ų. Because of the larger Q-value, the line shape for the perfect crystalline phase in Figure 3 (right panel) is red-shifted with respect to that in Figure 3 (left panel) where a perfect crystal was assumed. Finally, to simulate the experimental absorption spectrum, the average is taken over a mixture of ordered and disordered phases (Figure 3). Agreement with the experimental spectrum is obtained when assuming that the PTCDI film consists of 53% of the orderd phase. The small red-shift of the calculated curve by about 0.05 eV may be due to errors when deriving the parameters 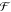and E_gp.

The only free “parameter” used in the calculations is the structure of the disordered film (its ratio with respect to the ordered phase is fixed by the integral over the line shapes). A reduction of the packing density by about 30% results in a blue-shift of at least 0.2 eV with respect to the spectrum of a perfect crystalline film. As obviously many different configurations contribute to the experimental spectrum in the range between 2.3 and 2.8 eV, the vibronic progression is smeared out leading to a broad and unstructured absorption band.

Conclusions

In summary, we introduced a new approach for calculating the optical absorption spectra of organic polycrystalline thin films. In particular, a novel relation for molecular excitation energy shifts due to dispersion effects of the environment has been derived. The obtained formulas allow for the determination of site-dependent level shifts of a molecule in a given nanoscale environment. On that basis, we were able to explain a distinct double structure of the S₀ → S₁ transition in the absorption spectrum of PDCTI films by the coexistence of two molecular phases. Large crystals where most molecules are located in the interior give rise to the component on the low-energy side, while the blue-shifted broad unstructured feature is due to a phase of loosely packed small aggregates experiencing a weaker gas-to-crystal shift, as most molecules reside at or close to the surface. We note that our results explain the absorption features as disorder induced dispersive effects due to nonresonant excitonic coupling. In previous works these features are explained by strong resonant excitonic coupling that transfers oscillator strength to the vibrational satellites (see refs (21) and (22)). While a fully quantitative analysis of the film morphology is beyond the scope of this work, our findings emphasize that an explicit consideration of the local energy structure is mandatory to understand the optical properties of molecules in nanoscaled solid-state systems.

Supporting Information Available

Electronic structure calculations in part A, MD simulations in part B, comments on the neglect of inductive polarization shifts in part C, computation of excitonic coupling using partial transition charges in part D, and description of our model of the small aggregates in more detail in part E. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Status

^∥ The authors mourn the loss of Fritz Henneberger who passed away on February 1, 2015.