A New Drug Combinatory Effect Prediction Algorithm on the Cancer Cell Based on Gene Expression and Dose–Response Curve

Abstract

Gene expression data before and after treatment with an individual drug and the IC₂₀ of dose–response data were utilized to predict two drugs' interaction effects on a diffuse large B-cell lymphoma (DLBCL) cancer cell. A novel drug interaction scoring algorithm was developed to account for either synergistic or antagonistic effects between drug combinations. Different core gene selection schemes were investigated, which included the whole gene set, the drug-sensitive gene set, the drug-sensitive minus drug-resistant gene set, and the known drug target gene set. The prediction scores were compared with the observed drug interaction data at 6, 12, and 24 hours with a probability concordance (PC) index. The test result shows the concordance between observed and predicted drug interaction ranking reaches a PC index of 0.605. The scoring reliability and efficiency was further confirmed in five drug interaction studies published in the GEO database.

Cancer is a serious and highly prevalent disorder that is triggered by a complex interplay of genetic factors. Drugs designed to act against individual molecular targets can't usually combat the multigenic disorder disease.1,2 Combination drugs that impact multiple targets simultaneously are better at controlling complex disease systems than the single drug. Drug-combination therapy has showed greater cell growth inhibition and population than either agent alone in cancers, which has been reported in many researches.3,4 Compared to the single drug therapy, multidrug therapy is less prone to drug resistance and risk,2 and has less toxicity in small combining doses,5 as well as a higher therapeutic effect.6–8 It has become gradually the standard of care in cancer therapeutic areas.3,9 Generally, combinatorial drug effects could be classified into three types: additive, synergism, and antagonism: (i) When the effect of the drug combination is equal to that of the sum of the effects of the individual components, it is defined as additive; (ii) Synergistic action refers to the drug combinatory effect exceeding the additive effect of two individual components; (iii) Antagonism action refers to a reduced combinatory effect when compared with the effect of the most effective individual substance.10 It remains a challenge to predict drug combinatory effects from two single drugs' effect. Our current understanding of the drug interaction mechanics in multidrug therapy is more or less drug targeted-based.1,11 During the drug discovery process, predicting the drug combination effect in vitro heavily relies on the experiment. However, testing all possible combinations in vitro in cancer is not feasible due to the large combinatorial search space. Computational prediction may assist in identifying potential drug combination effects at the molecular level, such as an integrating method by molecular and pharmacological data,4 a machine learning-based prediction of drug–drug interactions (DDIs) by integrating drug phenotypic, therapeutic, chemical, and genomic properties,12 and large-scale pharmacogenomic screens of cancer cell lines.13 These methods are promising strategies to predict unknown DDIs. However, these methods can't solve the key problem: how to detect and compare the dose response between the single and the combination drugs. The drug dose eventually needs to balance the benefit and risk from its efficacy and toxicity. On the other hand, some other methods emerged which were based on pathways of gene sets. These methods advanced our understanding about the drug responsive cellular processes.14,15 However, because of the potential knowledge bias of existing pathway databases, some critical genes may well not have been annotated for their functions and associated pathways. Hence, their roles in DDIs will be missed in these pathway-based approaches. Therefore, we hypothesize that drug responsive gene expression data are the most powerful and unbiased approach in predicting DDIs. In our study, we designed a new score schema to predict the drugs combination effect based on gene expression and their dose–responsive curve in cancer cell lines.

In 2006, Gustavo Stolovitzky and Andrea Califano founded the Dialogue on Reverse Engineering Assessment and Methods (DREAM) project. DREAM's purpose was to provide a reliable and reproducible platform to compare a large number of computational biology methods based on golden standard data. The inspiration for the DREAM project came from the success of the Critical Assessment of Structure Prediction (CASP) competition.16 During the CASP competition, contestants were challenged to predict the final structure of a protein when given the amino acid sequence.17 DREAM7-4 subchallenge 2 problem (DREAM7-4-2) asked the participating teams to predict the interactive activity of pairs of compounds in the OCI-LY3, a diffuse large B-cell lymphoma (DLBCL) cell line.18,19 Figure 1 describes the task overview. All contestants were given the gene expression data after separating treatments with 14 individual drugs at time intervals of 6, 12, and 24 hours in triplicate. The cells were also treated with dimethyl sulfoxide (DMSO) as controls. Dose–response curves of 9 out of 14 single drugs at 24 hours were also given. Using these curves, IC₂₀ (20% inhibitory concentration) values were determined. Each contestant team was asked to predict pairwise drug interactions ordered from the most synergistic to the most antagonistic.19

Figure 1.

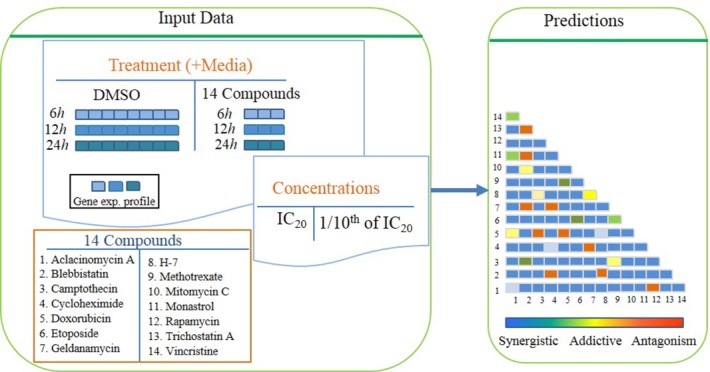
Overview of DREAM7-4 task. OCI-LY3 cell lines are treated with 14 different drugs at two different drug concentrations (IC₂₀ at 24 and 48 hours, where IC₂₀ is defined as concentration of drug needed to kill 20% of cells). The gene expression profiles (GEP) of the cells in different drugs were generated in triplicate at three different timepoints (6, 12, 24 hours) and the GEP of the cells in DMSO treated was eight times at the same timepoints. In addition, the drug–response curve from single agent treatment of OCI-Ly3 is also given. The challenge is to use the provided data to predict the order of efficacy of 91 pairs of drug combinations from the most synergistic to the most antagonistic.

In this study we hypothesize that these changes in gene expression after exposure of a drug can be used to predict these drug interaction effects. In particular, two drugs having significantly differentiated gene expression changes, where a number of specific genes in the same direction (up or down) will have a synergistic effect. The more specific genes affected in the same direction will be directly correlated to a higher synergistic effect. Conversely, the more specific genes affected in opposite directions will be directly correlated to a higher antagonistic effect. Our research attempts to infer the synergistic or antagonistic effect from two drugs based on the above biological assumption. A novel drug interaction scoring algorithm was then developed. There are some factors that remain unknown in influencing the prediction performance for the drugs interaction. One factor is the optimal drug exposure time for the drug responsive gene expression measurement; and the other factor is the core gene set selection, which include genes that are responsible for drug interaction prediction. In this work these two problems were extensively investigated using the dose–responsive curves and the gene expression data of the single drug response from the OCI-LY3 DLBCL cell line of DREAM7-4-2. Finally, the performance of our drug interaction score and its biological assumption was evaluated in five published GEO databases from six drug interaction studies.

RESULTS

Overview

Our method hypothesizes that a single drug effect on the OCI-LY3 cell can be attributed to the expression change from a particular set of genes, i.e., core genes set. The synergistic/antagonistic effects between a pair of drugs was derived and predicted from this core genes set. Figure 2 shows the whole drug interaction prediction process in detail. It has three parts: (i) the drug interaction scoring and prediction in the core genes set (left side of Figure 2); (ii) the drug interaction calculation from the observed dose response curve (right side of Figure 2); (iii) the probabilistic concordance (PC) index calculation between the experimental drug interaction ranking and the predicted drug interaction ranking (the bottom of Figure 2). The drug interaction prediction algorithm is the essential part of the study. It includes seven steps (left side of Figure 2): (1) Input data is prepared, including the gene expression profiles of all samples in different drug treatment groups and the DMSO control group; (2) quality control analysis is conducted. It uses principle components analysis (PCA) to identify and remove outlier samples; (3) differential expression genes are identified between drug treatment and DMSO through ANOVA method; (4) core genes set is selected (see Figure 3), including the whole genes set, the drug sensitive genes set, the drug sensitive minus drug nonsensitive genes set, and the known drug target genes set; (5) calculate the drug interaction score; (6) store the prediction result for each drug pair; (7) the scoring algorithm comprises all drug pairs, and all the predicted drug interactions were ranked from the most synergistic to the most antagonistic. The drug interaction calculation from the observed dose response curve (right side of Figure 2), includes three steps: (a) Calculate the expected fractional inhibition f_xy from two individual drugs' IC₂₀; (b) measure the f_AB from the cell treated with two drugs together; (c) calculate and rank the drug interaction index, excess over bliss(eob), from f_xy and f_AB, collectively.

Figure 2.

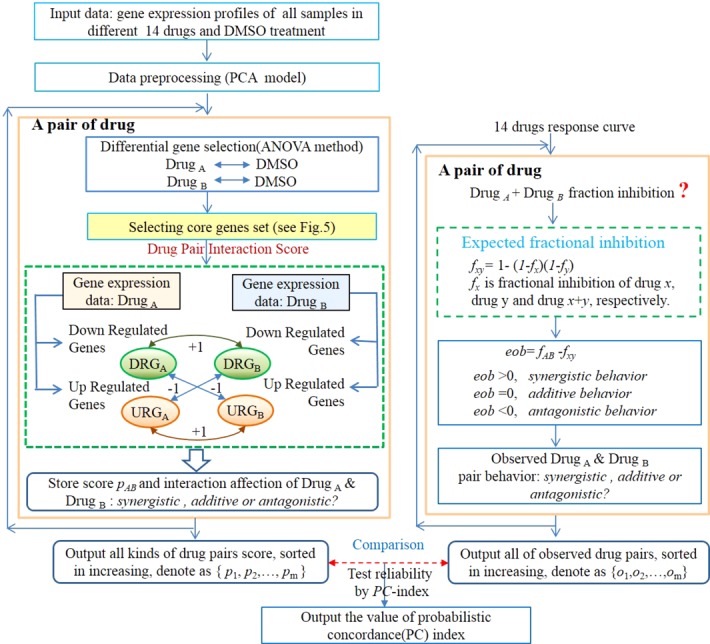
Schematics of data processing. The data processing flow included three parts: (1) The drug interaction scoring by its gene expression on the left; (2) the drug interaction observation by calculation of single drug response curve, which is shown on the right; (3) the calculation of the PC index of which the comparison between the scoring prediction and the result of the observed experiment, which is shown on the bottom.

Figure 3.

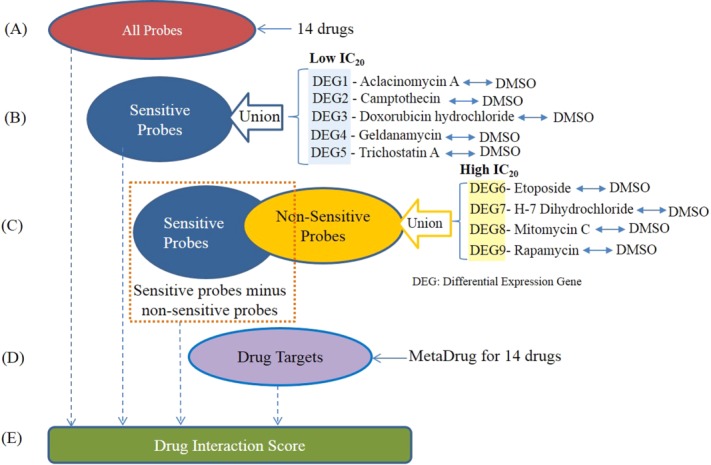
Core gene selection is used to determine the effectiveness of synergism for all the 91 possible two drug combinations. (a) All possible gene probes are used. (b) The gene set is determined by selecting all the sensitive probes from the union of all five low IC₂₀ drugs. (c) The third set is determined by subtracting the union of all nonsensitive differentially expressed gene probes from the four high IC₂₀ drugs. (d) The fourth scheme only selects the drug targeted gene probes reported in MetaDrug database. (e) The genes set of a–d will take part in the drug interaction score respectively to test the reliability of the drug combination.

Data preprocessing

PCA is conducted first for the quality control of gene expression data. PCA achieves the dimensionality reduction by finding new axes, i.e., principal components (PCs), where top PCs can account for the majority of variance in the data.20 In general, PC₁ and PC₂ represent the highest of the variance in data among all the PCs; here they are routinely used to express the main intrinsic factor of samples variance. Supplementary Figure 1 shows the preprocessing result of gene expression by using PCA for outliers' recognition. It can be seen that there were two outlier samples from the drug-treated groups: mitomycin C (denoted as TH001_AP_100427_01C_E02 in experience) and H-7 (dihydrochloride, denoted as TH001_AP_100427_01C_H09 in experience). They were far away from all the other samples, hence they were removed from the follow-up analysis. Therefore, drug-treated groups of mitomycin and dihydrochloride have only two replicates, while the other drugs have three.

Core gene selection is an essential part of our drug interaction algorithm development. When the cell is treated with different compounds, their impact on cell growth will be channeled through a set of genes. This gene set is so called the core gene set. In this study, four different sets of core genes are proposed (see description in Methods and Figure 3). The first set includes every probe set in the Affymetrix array (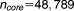). The second core gene set includes all of the drug-sensitive gene probes from five drugs (aclacinomycin A, camptothecin, doxorubicin hydrochloride, geldanamycin, and trichostatin A) with low IC₂₀ (the core genes number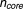= 12500, 9000, 9862 for 6, 12, and 24 hours, respectively). The third core gene set is the drug-sensitive gene probes from five drugs of low IC₂₀ minus the nonsensitive gene probes, where the nonsensitive gene probes are from the other four drugs (etoposide, H-7 dihydrochloride, mitomycin C, and rapamycin) with high IC₂₀ (the core genes number= 2567, 4004, 3204 for 6, 12, and 24 hours, respectively). The fourth core gene set is derived from the drug targets reported in MetaDrug (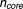= 80).21

Time-dependent analysis of the drug interaction prediction based on four different sets of core genes

The drug interaction scores are calculated at three different timepoints after the drug treatment, 6, 12, and 24 hours for all 91 drug combinations in 14 compounds. The ranked scores are compared to observed interaction scores (i.e., eob) through the normalized PC index. A higher PC index represents a better concordance between the observed drug interaction and the predicted drug interaction. The highest score is 0.90 here, not 1.00, because of the noise of the experimental data. Figure 4 shows the comparison result of the drug interaction prediction in four sets of core genes at 6, 12, and 24 hours. It can be observed that the gene expression after a 12-hour drug treatment had a better performance than the 6- and 24-hour timepoints because of its high PC index in four different probes set, and the PC index reaches the largest value of 0.605. In addition, the performance of the sensitive probes is better than the other three core gene selections at 12 hours.

Figure 4.

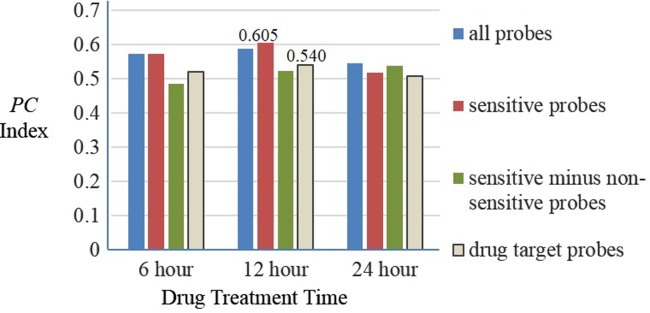
Comparison result of the drug interaction prediction for four sets of core genes at different times. The y-axis is the probabilistic concordance-index (PC index) and shows that the concordance between the predictions result and the gold standard at 6, 12, and 24 hours.

Gene expression based probe selection vs. known drug target-based probe selection

These two core gene selection schemes are based on two totally different assumptions. Gene expression-based probe selection is a purely discovery-based approach, whereas drug target-based probe selection is a candidate target approach. It focuses on the known protein targets of the drugs from the MetaDrug database.21,22 According to our time-dependent analysis of drug interaction prediction between these two core genes set selection schemes, the gene expression based on the drug-sensitive core gene set outperformed the target gene core set at any timepoint of 6, 12, and 24 hours. After 12 hours of drug treatment, the PC index of the drug sensitivity core set has a PC index of 0.605, while the drug target score has a PC index of 0.540 (Figure 4). These results confirm our hypothesis that the discovery-oriented and less biased drug sensitive core gene set outperforms the knowledge-driven and potentially biased drug target core gene set for DDI prediction.

Drug interaction prediction

Using the drug sensitivity core gene set after 12 hours drug treatment, a score was calculated for each drug pair. Ranks are assigned to drug pairs using these scores. The final scores range from +24.06% (most synergistic) to –2.33% (most antagonistic). Whenever drug combinations had the same score, a higher ranking is given to the drug pair that has a greater number of total genes affected by the two drugs. Table 1 is a list of drug combinations with their ranks in terms of synergism. The most synergistic pair has the highest rank. The pair with the most antagonistic effect has the lowest rank. Each pair that results in lower ranking than the trichostatin A & vincristine combination has a positive score and will have a synergistic effect in silico. All pairs that result in scores higher than the trichostatin A & vincristine pair will have an antagonistic effect in silico.

Table 1.

Ranking of pairwise drug combinations based on the gene expression profiling scoring, discussed in the Methods

Drug combination	Rank	Observed ranking (gold standard)
Camptothecin & H-7	1	10
Camptothecin & Trichostatin A	2	56
Cycloheximide & H-7	3	9
Cycloheximide & Rapamycin	4	78
Geldanamycin & Rapamycin	5	47
Camptothecin & Doxorubicin	6	16
Camptothecin & Etoposide	7	15
Cycloheximide & Trichostatin A	8	37
Doxorubicin & Etoposide	9	24
Monastrol & Rapamycin	10	48
Camptothecin & Methotrexate	11	62
Monastrol & Trichostatin A	12	18
Camptothecin & Mitomycin C	13	5
H-7 & Trichostatin A	14	19
Rapamycin & Trichostatin A	15	60
Geldanamycin & H-7	16	31
Camptothecin & Cycloheximide	17	59
Doxorubicin & Mitomycin C	18	4
Etoposide & Mitomycin C	19	3
Etoposide & Trichostatin A	20	11
H-7 & Rapamycin	21	27
Cycloheximide & Monastrol	22	12
Etoposide & Rapamycin	23	83
Doxorubicin & Trichostatin A	24	8
Cycloheximide & Etoposide	25	69
Doxorubicin & Rapamycin	26	87
Blebbistatin & Rapamycin	27	57
Camptothecin & Monastrol	28	67
Blebbistatin & H-7	29	7
Methotrexate & Trichostatin A	30	55
Geldanamycin & Trichostatin A	31	58
Etoposide & Methotrexate	32	76
Geldanamycin & Monastrol	33	75
Doxorubicin & H-7	34	1
Etoposide & H-7	35	6
Mitomycin C & Trichostatin A	36	13
Aclacinomycin A & H-7	37	26
Etoposide & Monastrol	38	90
Geldanamycin & Vincristine	39	29
Blebbistatin & Cycloheximide	40	85
Cycloheximide & Mitomycin C	41	17
Methotrexate & Mitomycin C	42	28
H-7 & Mitomycin C	43	2
H-7 & Monastrol	44	14
Aclacinomycin A & Geldanamycin	45	61
Cycloheximide & Methotrexate	46	64
H-7 & Vincristine	47	43
Blebbistatin & Monastrol	48	21
Aclacinomycin A & Vincristine	49	49
Rapamycin & Vincristine	50	42
Methotrexate & Monastrol	51	35
Aclacinomycin A & Rapamycin	52	65
Blebbistatin & Doxorubicin	53	72
Doxorubicin & Methotrexate	54	73
Cycloheximide & Doxorubicin	55	68
Doxorubicin & Monastrol	56	91
Cycloheximide & Geldanamycin	57	81
Cycloheximide & Vincristine	58	38
Aclacinomycin A & Doxorubicin	59	53
Blebbistatin & Geldanamycin	60	39
Doxorubicin & Geldanamycin	61	46
Blebbistatin & Camptothecin	62	88
Blebbistatin & Trichostatin A	63	80
Blebbistatin & Methotrexate	64	52
Aclacinomycin A & Blebbistatin	65	74
Blebbistatin & Vincristine	66	30
Mitomycin C & Rapamycin	67	66
Blebbistatin & Mitomycin C	68	34
Aclacinomycin A & Camptothecin	69	86
Monastrol & Vincristine	70	20
Mitomycin C & Monastrol	71	82
Trichostatin A & Vincristine	72	50
Blebbistatin & Etoposide	73	79
Aclacinomycin A & Mitomycin C	74	22
Doxorubicin & Vincristine	75	41
Methotrexate & Vincristine	76	25
Aclacinomycin A & Methotrexate	77	77
Mitomycin C & Vincristine	78	70
Aclacinomycin A & Etoposide	79	45
Aclacinomycin A & Monastrol	80	23
Aclacinomycin A & Cycloheximide	81	33
Etoposide & Vincristine	82	32
Geldanamycin & Mitomycin C	83	63
Camptothecin & Vincristine	84	51
Etoposide & Geldanamycin	85	44
Aclacinomycin A & Trichostatin A	86	84
Methotrexate & Rapamycin	87	40
Geldanamycin & Methotrexate	88	54
H-7 & Methotrexate	89	36
Camptothecin & Geldanamycin	90	71
Camptothecin & Rapamycin	91	89
Compound pair with additive activity (IC36)	Trichostatin A & Vincristine

Ranking is from most synergistic to most antagonistic. Trichostatin A & vincristine showed a purely additive effect.

Drug interaction scoring algorithm validation using GEO datasets

Six drug interactions were reported in five published GEO datasets (Supplementary File 2). Both the single drug responsive gene expression profiles and their combinatory effect gene expression profiles are available. In order to verify the sensitive genes set of a single drug, the main factor for the synergistic or the antagonistic contribution is the combination drug efficacy. The consistency of differentially expressed genes is compared between a single drug and combinatory drug treatment. Our score algorithm in Figure 5 assumes that the combinatory effect of two drugs is more consistent with the concordance between two single drug effects if they are synergistic than they are not. In Table 2, it can be seen that among six drug pairs three drug pairs have an additive effect, and the other three pairs have a synergy effect. Column (A) of Table 2 displays the number of differentially expressed genes by the combinatory effect of two drugs. Column (B) shows how many genes in column (A) had the same directional differential expression from both the single drug treatments, which is the primary assumption in our algorithm (Figure 5). Column (C) presents the ratio of (B) over (A), i.e., a concordance ratio. It is interesting to see that the additive drug pairs have a concordance rate (0.46, 0.34, 0.50), while the synergistic drug pairs have a higher concordance rate (0.51, 0.54, 0.73). These results support that the synergistic drug interaction has a stronger concordance rate than the additive drug interaction.

Figure 5.

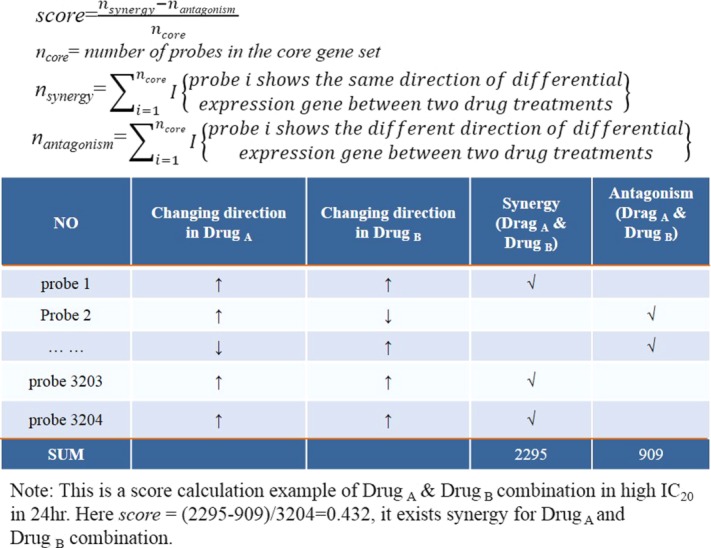
The scoring scheme of the drug combination effect based on analyzing gene expression data. The score formula and a specific calculation processing of Drug A and Drug B at high IC₂₀ in 24 hours is given.

Table 2.

Concordance between drug combinatory effect in experiment and the concordance ratio

Data sets	Cancer type	Drug combination	Drug interaction affection in biology experience	Differential expressed genes by the combinatory effect of two drugs (A)	The genes number of the same variation direction (B)	Concordance ratio (C)
GSE45587	Neuroblastoma	All-trans retinoic acid & valproic acid	The treatment of valproic acid is augmented by all-trans retinoic acid (Additive)	6965	3212	0.46
GSE11550	Melanoma	Elesclomol & paclitaxel	Drug combination has significant effect in cancer (Additive)	5578	1903	0.34
GSE43452	Glioblastoma	Temozolomide & Y.15 (FAK inhibitor)	Combination can significantly reduce tumor growth (Additive)	6479	3249	0.50
GSE33366	Breast cancer	Tamoxifen & BMS754807	Synergy	5191	2664	0.51
GSE33366	Breast cancer	Letrozole & BMS754807	Synergy	3440	1843	0.54
GSE6914	Nonsmall cell lung cancer	Bexarotene & gemcitabine	Resensitized (Sysnergy)	4587	3368	0.73

DISCUSSION

Multidrug combinations are thought to attack drug resistance in cancer. By utilizing treatments involving more than one drug, it is thought that one drug will kill the cells resistant to the other drug and the other drug will kill the cells resistant to the first drug; thereby, the combination drugs treatment prevents the regrowth of the disease with resistance to the current therapy.9,23 This method has been very popular for fighting cancer.24 However, testing all possible combination in vitro in cancer is not feasible due to the large combinatorial search space. DREAM7-4 provided a platform to develop models that predict the synergistic/antagonistic activity of drug pairs in the OCI-LY3 cell line.19 We are one of 31 contestants for the DREAM7-4 challenge. In this work, based on the gene expression profile of before and after treatment of a single drug and its dose–responsive curve, a novel drug interaction scoring algorithm was developed to predict the synergistic or the antagonistic effects of two drug combinations in cancer. Fourteen drugs and their combinatory experiments in a DLBCL cancer cell were investigated. The drugs' interaction effect was scored by counting the differentially expressed genes in the core gene set that went in either the same or the opposite direction between two drug treatments under their IC₂₀s. The prediction scores were compared with the observed drug interaction data at 6, 12, and 24 hours with a PC index. The test result shows that the drug-sensitive gene set can achieve the best prediction result and its PC index equals 0.605, which was extremely close to the best prediction PC index = 0.613 in the DREAM7-4-2 challenge. In addition, using only the known drug targets cannot provide comparable drug interaction prediction performance, as the core gene sets do, which were drug-responsive genes selected from whole genome differential expressed genes. Finally, our score schema is validated by using drug interaction data collected from the GEO. Using the additional gene expression data after the combined two exposures, we found that differentially expressed genes in the synergistic drug interaction pairs had higher concordance rates than those of additive drug interaction pairs. This study provides a valuable drug-combinatory effect predictive model that can screen synergistic drug interaction pairs from single drugs' gene expression profiles.

Our current best drug interaction performance, a PC index of 0.605, is still far from the optimal prediction, 0.90. There are strategies that will likely improve the drug interaction prediction. First, our current best core gene set, drug-sensitive genes, are only based on five sensitive drugs. We believe more sensitive drugs and their responsive genes will help to improve the prediction. Second, our current drug interaction prediction algorithm is not a truly supervised method; it is based on a biological assumption of concordantly differentially expressed genes between single drugs and their combinations. We still expect to design a more proper supervised machine learning algorithm combining our method to gain better performance in the future. Third, the current scoring scheme is a highly simplified method, which does not differentiate or weight the highly or lowly expressed genes. It is worthwhile to investigate the drug interaction prediction performance with more sophisticated methods. Finally, a drug interaction net provides us a new view to obtain drug combination efficiency by integrating molecular, therapy, and pharmacological data.4,23,25 Based on a drug network and multiple data merging technology, looking for the core genes set by drug-targeted and disclosing the rule between the drugs and the genes from DDIs will provide us much clinic direction for cancer treatment in the future, as will also be our goal in the next study.

METHODS

Cell culture, drug treatment, and gene expression profiling

The diffuse large B-cell lymphoma (DLBCL) cell line was obtained from the University Health Network (Toronto, Canada) and was cultured under standard conditions (37°C in humidified atmosphere, with 5% CO₂) in Iscove's modified Dulbecco's medium (IMDM) supplemented with 10% fetal calf serum (FCS). Each drug was titrated in the OCI-LY3 cell line in a 20-point titration curve. Cell viability following drug treatment was determined using the CellTiter-Glo (Promega, Madison, WI). An IC₂₀ value for each drug was calculated using Dose Response Fit and Calculate ECx (epirubicin, cisplatin, and Xeloda) components from the Pipeline Pilot Plate Data Analytics collection. For drugs for which more than 20% viability reduction could not be reached, a default concentration of 100 μM was used. For generation of gene expression profiles, the OCI-LY3 cells were seeded in tissue culture-treated 96-well plates at a density of 50,000 cells per well (100 μL) and treated at the IC₂₀ concentrations of each of the drugs at 24 and 48 hours. In the assay, three timepoints (6, 12, and 24 hours) were analyzed for gene expression profiling. All profiles were generated in triplicate biological replicates except DMSO-treated samples, which were hybridized in octuplicate since they were used as internal controls for each timepoint. To confirm viability data at each step, identical plates were produced and cell viability assessed using the CellTiter-Glo reagent (Promega). Total RNA was isolated with the Janus automated liquid handling system (Perkin Elmer, Boston, MA) using the RNAqueous-96 Automated Kit (Ambion, Austin, TX), quantified by a NanoDrop 6000 spectrophotometer and quality checked with an Agilent Bioanalyzer. 300 ng of each of the samples with RIN value >7 were converted to biotinylated cRNA with the Illumina TotalPrep-96 RNA Amplification Kit (Ambion) using a standard T7-based amplification protocol and hybridized on the Human Genome U219 96-Array Plate (Affymetrix, Santa Clara, CA). Hybridization, washing, staining, and scanning of the array plates were performed on the GeneTitan instrument (Affymetrix) according to the manufacturer's protocols. The drugs for which IC₂₀ values were reported includes aclacinomycin A, camptothecin, doxorubicin hydrochahloride, geldanamycin, trichostatin A, etoposide, H-7 dihydrochloride, mitomycin C, and rapamycin. For blebbistatin, cycloheximide, methotrexate, monastrol, and vincristine, IC₂₀ values were not reported. All of the detailed information has been provided by the DREAM project.18,19

Experimental determination of synergy

For each drug, IC₂₀ was determined (as described above) at 60 hours following drug treatment by measuring cell viability and generating a dose–response curve. Each drug combination was then tested at the respective IC₂₀ (or 100 μM) concentration of the individual drugs in five replicates. All drugs and combinations are diluted in DMSO, with a final DMSO concentration of 0.4%. Cells were placed at a density of 2,000 cells per well in 384-well plates and drugs were added at 12-hour intervals after seeding by drug transfers of serially diluted drugs. Assay plates were then incubated for 60 hours followed by addition of 25 μL of CellTiter-Glo (Promega) at room temperature. Plates were read on Envision (Perkin Elmer) using an enhanced luminescence protocol.

Data available for drug interaction prediction and validation

The experimental data were generated by the NCI-nominated lab, and each competition team receives the data and conducts the computation. The single drug treated and untreated gene expression data at 6, 12, and 24 hours were used. Only 9 out of 14 drug dose-responsive curves are used for developing the drug combinatory synergy predictive model. Among these nine drugs, five drugs are highly sensitive (IC₂₀ <1 μM), and the other four are not sensitive (IC₂₀ >10 μM). The predictive performance is then compared to the observed drug interaction data measured by the Excess over Bliss (called eob, see the following description).

Gene expression-based drug combinational effect model

Drug-induced differential gene expression

All gene expression samples were normalized with the Robust Multichip Averaging (RMA) normalization method using the Bioconductor package in R.26 At each timepoint of drug treatment, differential gene expression analysis was conducted between treated samples and DMSO samples. The analysis of variance method (ANOVA) was used to analyze the differences between group means and their associated procedures (such as "variation" among and between groups). It is useful in comparing (testing) two or more means (groups or variables) for statistical significance. Here the differentially expressed gene probe selection was selected by ANOVA statistical analyses between DMSO and drug treatment samples (using the ANOVA function in R), with P < 0.05 regarded as the significant threshold.

Core gene set selection

To test our hypothesis correction, four schemes of core gene set selection were selected (Figure 3). Differentially expressed genes for all drugs were identified by comparing their drug treatment samples with control (DMSO) samples. All differentially expressed gene probe with a significant P value (P ≤ 0.05) were combined in each IC₂₀ at 24 hours after drug treatment. The first scheme simply selects all the probes (Figure 3a). The second scheme selects only the sensitive probes derived from the union of all the differentially expressed gene probes from five low IC₂₀ drugs (Figure 3b). The third scheme selects the sensitive probes to five low IC₂₀ drugs, but not the nonsensitive probes. The nonsensitive probes are derived from the union of all the differentially expressed gene probes from the four high IC₂₀ drugs (Figure 3c). The second and third schemes are used in determining which probes can be kept as different sets used in determining synergism. The fourth scheme only selected the drug targeted gene probes reported in MetaDrug (Figure 3d). The drug targets are reported in Supplementary Table 1.

The drug interaction score is constructed based on a scoring scheme presented in Figure 5. The denominator of the score is the number of core gene probes. The core gene selection follows the previous point. Then the synergy score between two drugs is the number of gene probes that are consistently up- or downregulated (i.e., showing the same direction of gene expression change) after the drug treatment. The antagonism score is calculated as the number of the genes showing the reversed regulation direction. The drug interaction score is the synergistic score minus the antagonism score normalized by the number of core gene probes. In Figure 5, a specific calculated example for the score of Drug A and Drug B is shown in IC₂₀ 24 hours. The probe changing direction in Drug A or Drug B is decided by the ANOVA statistical analyses result between the DMSO group and the drug treatment group.

Excess over Bliss as a measurement for synergy

The Bliss additivism (or Bliss independence) model27 predicts that if the i-th pair drug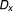 and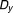, with experimentally measured fractional inhibitions 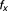and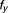, have an additive effect, then the expected fractional inhibition,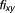, induced by their combination should be:

Here the IC is 20%,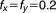,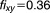. Excess over Bliss is determined by computing the difference in fractional inhibition induced by its observed value of Drug A and Drug B combination 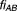and expected fractional inhibition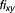

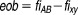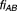is a ratio with the observed cell viability after drug combination treatment in time 60 hours to the ones of before single drug treatment plus. When the drug pair for, it has an additive behavior, whereas the drug pair with positive (or negative)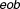 values has synergistic (or antagonistic) behavior. In fact, here the propagation of errors using the standard error mean of fractional inhibitions is used to compute the standard error of the mean.

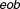Scoring using probabilistic concordance index

In order to calculate the concordance between predicted and observed ranks of drug-pairs, a concordance index (c-index) is designed to compute the proportion of concordance between them to quantify the quality of ranking of all predictions. To compute the c-index, we first rank the observed drug pairs and the predicted drug pairs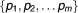 from most synergistic to most antagonistic for each of the possible pairwise combinations. A score 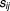is computed as follows:

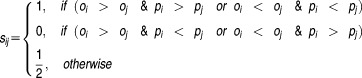and define the concordance index as

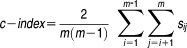Where m is the number of drug pairs, in DREAM7-4-2 problem, 14 drugs have m = 91 pairs. Quantification using the c-index assumes that there is no ambiguity in the observed rankings, and therefore both the prize and penalty for concordance and discordance is extreme. The above design method is for a specific discrete event. When it becomes a continual description in large events, the concordance index expectation can be expressed by the following formula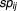; we called it the probabilistic concordance-index (PC-index) to measure the concordance between the observed and the predicted in large events.

where erf' is an error function defined as eob is excess over Bliss, sem is the standard error of the mean excess over Bliss. The probabilistic concordance (PC) index is thus defined as:

For a specific event, when the predicted and the observed list of drug pairs are entirely concordant, the c-index can reach a maximum score of 1. But due to noise in the large data, the PC-index is less than 1, even for the average experimentally measured eob in practice. In our study, all of the challenge results and other test results find that the maximum PC−index (PC_max) is 0.90. The minimum PC−index (PC_min) corresponds to a prediction with exactly the opposite order compared to the average experimentally measured eob. Note that PC_min=1−PC_max. Hence, the normalized PC−index is defined as:

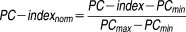Drug interaction data from GEO

We identified five datasets from the GEO database (http://www.ncbi.nlm.nih.gov/geo/). Their accession numbers are GSE45587, GSE11550, GSE43452, GSE33366, and GSE6914. These five datasets contain six drug interaction pairs (Supplement DataGEO.doc).

Conflict of Interest/Disclosure

The authors state that there is no conflict of interest. As an Associate Editor for CPT:PSP, LL was not involved in the review or decision process for this article.

Author Contributions

L.L., C.P.G., P.S.A., and L.C. wrote the article; L.L. and C.P.G. designed the research; L.L. and A.S. performed the research; C.P.G., P.S.A., A.S., and L.C. analyzed the data.

Supplemental Information

Supplemental information includes two programming codes of the key modeling, five dataset and 12 result files, and detailed information can be found in the supplemental description files.

Acronyms

Abbreviation	Definition
CASP	critical assessment of structure prediction
c-index	concordance index
DDI	drug–drug interaction
DLBCL	diffuse large B-cell lymphoma
DMSO	dimethyl sulfoxide
DREAM	dialogue on reverse engineering assessment and methods
ECx	epirubicin, cisplatin and xeloda
eob	excess over bliss
FCS	fetal calf serum
IC	inhibitory concentration
IMDM	Iscove's modified Dulbecco's medium
PC-index	probability concordance index
PCs	principal components
PCA	principal component analysis
RMA	robust multichip averaging

Study Highlights

WHAT IS THE CURRENT KNOWLEDGE ON THIS TOPIC?

• ✓ It is known that many cancers develop resistance to treatment involving one drug alone. Drug combination therapy can actually become synergistic in their killing power, resulting in a smaller amount of drugs needed for successful treatment.

WHAT QUESTION DID THIS STUDY ADDRESS?

• ✓ What is the best way to predict drug interaction on a specific cell line? Using gene expression data before and after treatment of individual drugs and their IC₂₀ values, it is possible to predict the synergistic power of drug–drug combinations with relatively high accuracy.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

• ✓ Gene expression data seems to be one of the most important features in predicting DDI. Our core gene selection and gene expression-based synergy score performs well in predicting the drug combinatory synergy.

HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS

• ✓ The development of treatments for individuals can be made more effective by utilizing the gene expression data of biopsies of the patient's tumor response shortly after individual drug exposures.

Supporting Information

Additional supporting information may be found in the online version of this article.