On the Effects of Thermal History on the Development and Relaxation of Thermo-Mechanical Stress in Cryopreservation

Abstract

This study investigates the effects of the thermal protocol on the development and relaxation of thermo-mechanical stress in cryopreservation by means of glass formation, also known as vitrification. The cryopreserved medium is modeled as a homogeneous viscoelastic domain, constrained within either a stiff cylindrical container or a highly compliant bag. Annealing effects during the cooling phase of the cryopreservation protocol are analyzed. Results demonstrate that an intermediate temperature-hold period can significantly reduce the maximum tensile stress, thereby decreasing the potential for structural damage. It is also demonstrated that annealing at temperatures close to glass transition significantly weakens the dependency of thermo-mechanical stress on the cooling rate. Furthermore, a slower initial rewarming rate after cryogenic storage may drastically reduce the maximum tensile stress in the material, which supports previous experimental observations on the likelihood of fracture at this stage. This study discusses the dependency of the various stress components on the storage temperature. Finally, it is demonstrated that the stiffness of the container wall can affect the location of maximum stress, with implications on the development of cryopreservation protocols.

INTRODUCTION

Ice formation is known to be harmful to cells, structured tissues, and organs [1-5]. Vitrification suppresses ice formation and serves as an important alternative to conventional cryopreservation (vitreous in Latin means glass). Cryopreservation via vitrification is considered the only alternative to long-term preservation of large-size biological specimens. Vitrification is facilitated by the use of cryoprotective agents (CPAs) and high cooling rates in order to avoid crystallization. One of the most significant limiting factors to the development of successful cryopreservation techniques for large-size specimens is the development of thermo-mechanical stress, potentially compromising the structural integrity of the specimen.

The high cooling rates required to facilitate vitrification result in significant thermal gradients within a large-size sample, where each layer of the material may display a different tendency to contract. Since adjacent layers of the material cannot overlap, thermal stress develops, making the resulting strain compatible. If this stress exceeds a critical threshold, permanent damage may occur with fracture formation as its most dramatic outcome [6,7]. It follows that, the magnitude of the resulting thermo-mechanical stress elevates with the increasing size of the specimens.

Several studies have investigated the formation of fractures in cryopreserved materials and their dependency on the employed thermal protocols [8-12]. Fractures have been observed in mouse blastocysts [8], blood vessels [9,11], Mexican fruit flies [10], as well as CPA in the absence of biological specimens [11,12]. Pegg and co-workers [9] showed that fractures in cryopreserved arteries generally formed during the initial stages of rewarming, and that fractures could be prevented by lowering the rewarming rate while below −100°C. Kasai and co-workers [8] and Rajamohan and Leopold [10] further suggested that the tendency to fracture can be reduced by both lowering the initial rewarming rate and the final cooling rate. These studies suggest that an optimal thermal protocol should involve two-stage cooling, with rapid cooling to prevent crystallization followed by slower cooling to avoid fracturing, and consistently two-stage rewarming, with slow warming followed by rapid warming. Cryogenic protocols of similar nature are common practice in cryopreservation [13,14], where the specific rates are often explored by trial and error.

Rabin and Steif [15,16] presented a mathematical model for calculating the developing stresses in an inward freezing problem of classical cryopreservation. This model assumes that the unfrozen region, being a low-viscosity material, can only sustain hydrostatic pressures but cannot support deviatoric stresses. The main contribution in that study is that the deviatoric stress must be zero at the freezing front but that the deviatoric stress at the melting front may be non-zero. This outcome of modeling provides an explanation for the counterintuitive experimental observation that factures often develop at the beginning of the rewarming phase, when the stress reaches its peak value.

The domain does not crystallize during cryopreservation via vitrification but, instead, over a limited temperature range the viscosity increases dramatically by 12 orders of magnitude, from a liquid-like to a solid-like material. Instead of having two distinct regions as in classical cryopreservation, possibly modeled as a low viscous fluid and a linear-elastic solid, in vitrification the material may be modeled from an engineering mechanics perspective as having three regions, characterized as a low viscous fluid, a transition region, and a highly viscous material—practically a solid. Additionally, since there is no crystallization, the large volume expansion associated with water changing to ice does not occur during vitrification. Nevertheless, the modeling approach in [15,16] remains applicable and the analysis of vitrification protocols calls for further investigation—the subject matter of the current study. Beyond temperature gradients within the domain, thermal stress may also develop in response to differential thermal strain between the CPA and its container [17,18]. This effect is further investigated in the current study in the context of vitrification.

As part of an ongoing effort to investigate thermo-mechanical effects in cryopreservation [6,11,17-23,24-26], the current study aims at investigating the potential contribution of including a temperature-hold step in cryopreservation protocols, in order to facilitate annealing and thereby reducing the risk to structural damage. The current study focuses on large-size specimens, where thermo-mechanical stress may lead to structural failure. While large-size per se may commonly refer to specimens measuring a few millimeters or more in the context of cryobiology, large-size in the analysis of thermo-mechanical stress may have a different, outcome-dependent meaning. In the current study we refer to large-size specimens as specimens that exhibit steep temperature gradients which can give rise to significant stresses, possibly reaching the strength of the material. Hence, the term large size is associated with the with the temperature non-uniformity within the specimen along the thermal history, which may not be known a priori. The vast experimental evidence summarized above supports the notion of such a relationship, white the current theoretical study is designed to explore it.

MODELING

Due to the high viscosity of the CPA within the temperature range relevant to the development of thermo-mechanical stress, heat transfer in the domain is assumed solely by conduction:

$$\rho C_p\stackrel{.}{T}=\nabla \cdot (k\nabla \mathrm{T})$$ (1)

where T is temperature, ρ is density, C_p is specific heat capacity, and a superposed dot represents a time derivative. Note that heat generation due to viscous dissipation is negligible compared with changes in energy due to heat flow. This has important computational implications as the temperature field can be computed first, without consideration of stresses, and then the stresses are computed while taking into account the temperature field.

Material Model

The viscosity of a CPA increases with the decreasing temperature until it acts as solid at very low temperatures, which is modeled as a viscoelastic fluid. Following the simplest approach that captures such behavior, the CPA is modeled as a so-called Maxwell fluid, where the total strain rate is the sum of strain rates due to elastic deformation, viscous flow, and thermal expansion. For uniaxial tension in a lumped-capacity system (uniform temperature distribution) this relation is given by:

$$\stackrel{.}{\epsilon }=\frac{1}{E}\frac{d\sigma }{dt}+\frac{\sigma }{3\eta }+\beta \frac{dT}{dt}$$ (2)

where ε̣ is the total strain-rate, σ is the stress, E is the Young’s Modulus, η is the viscosity, and β is the coefficient of linear thermal expansion. Since the viscosity is temperature-dependent, the viscous portion of the strain rate dominates its elastic portion at high temperatures. Conversely, the elastic portion dominates the viscous portion at low temperatures, while at mid-range temperatures both responses are significant.

A non-uniform temperature distribution will give rise to a general state of stress, not necessarily limited to uniaxial tension or compression. The material model for the creep strain rate given by Eq. (2) is generalized following a standard approach in mechanics as follows:

$${\stackrel{.}{\epsilon }}_{creep}=\frac{\mathbf{S}}{2\eta }$$ (3)

where S is the deviatoric stress tensor, corresponding to the stress tensor with the hydrostatic pressure removed. The elastic strain rate is related to the stresses by the isotropic elastic relation:

$${\stackrel{.}{\epsilon }}_{elastic}=\frac{1}{E}[(1+\nu )\stackrel{.}{\sigma }-\nu \mathbf{I}\cdot tr\left(\stackrel{.}{\sigma }\right)]$$ (4)

where ν is the Poisson ratio, I is identity tensor, and tr $\left(\stackrel{.}{\sigma }\right)$ is the trace of the stress rate tensor. Finally, the container of the CPA is assumed to behave linear-elastically, with its own elastic properties.

Finite Element Solution

Figure 1 displays a simplified vial, which will be used in this study. This geometry is representative of a wide class of cryopreservation applications, and is simulative of recent experimental investigations using cryomacroscopy [27]. Two general cases are investigated in this study, (A) a reduced problem where wall effects are negligible, and (B) a combined problem of container and CPA.

Figure 1.

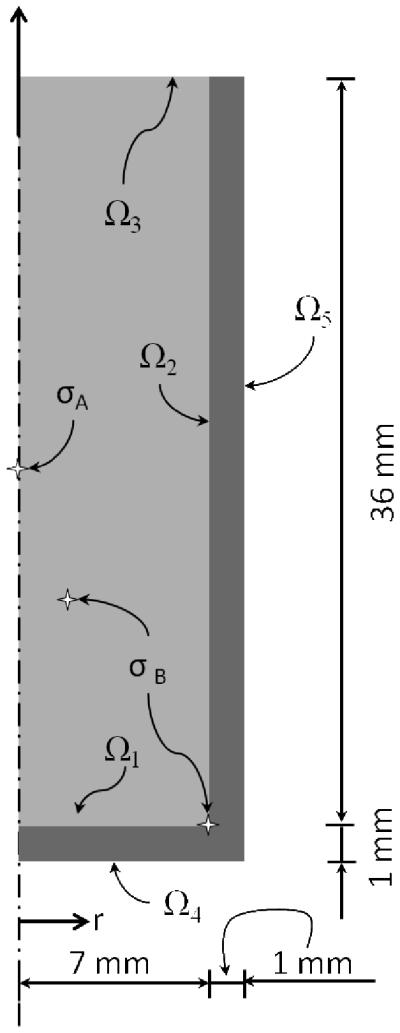
Schematic illustration of the axisymmetric model used for FEA in the current study for two key cases: (Case A) CPA in the absence of a container, where identical temperature boundary conditions are imposed on Ω₁, Ω₂, and Ω₃; and (Case B) CPA contained within a cylindrical vial, where identical temperature boundary conditions are imposed on Ω₄ and Ω₅, while thermal insulation is assumed on Ω₃, consistent with [27]. In both cases zero normal stress is assumed on the outer most surfaces. In Case B, continuity in temperature and displacement are assumed on Ω₁ and Ω₂. Also illustrated for the purpose of discussion the maximum principle-stress points, σ_A and σ_B, for Cases A and B, respectively.

The coupled thermal-stress problem is solved with the commercial finite element code Abaqus (Dassault Systèmes, Inc.). The heat transfer and displacement problems use identical meshes consisting of 8-noded, axisymmetric, quadrilateral DCAX8 elements for heat transfer and CAX8H for displacement calculations. For Case B, 1451 elements are used to geometrically model the CPA subdomain and 190 elements are used for the container, while 414 elements in total are used for Case A. The reduced number of elements in Case A is associated with the simplified CPA boundary condition (Fig. 1).

Material Properties

The material property values used in the current study are listed in Table 1. Due to limited availability of relevant CPA properties and due to its high relevancy to vitrification, the CPA cocktail VS55 is used as a model for material properties. In one case study, properties of the CPA dimethyl sulfoxide (DMSO) and the CPA cocktail DP6 are additionally used. VS55 and DP6 have drawn significant attention in recent years for vitrification of large-size specimens, and have been comprehensively characterized by the current research team. DP6 is a cocktail of 234.4 g/**doubt**f DMSO (3M), 228.3 g/f propylene glycol (3M), and 2.4 g/f HEPES in EuroCollins solution.VS55 is a cocktail of 242.1 g/f DMSO (3.1M), 168.4 g/f propylene glycol (2.2M), 139.6 g/f formamide (3.1M), and 2.4 g/f HEPES. The two cocktails are similar, with the exception of the exclusion of formamide from DP6. Beyond being a classical CPA and a key ingredient in both cocktails, the 7.05M DMSO has been demonstrated as a reference solution for the study of thermo-mechanical stress [19].

Table 1.

Physical properties used in this study [19-24,29,35-41]

Property	Material	Value	Source
Viscosity	VS55	η = 1.21 × 104 Pa-s;−100°C < T η = 4.2783 × 10−23 e−0.6091T Pa-s; −140°C < T < −100°C η = 4.63 × 1014 Pa-s; T ° −140°C	[29]
	7.05M DMSO	η = 1.77 × 104 Pa-s;−110°C < T η = 2.8190 × 10−27 e−0.6447T; −147°C < T < −110°C η = 4.06 × 1014 Pa-s; T < −147°C	[29]
	DP6	η = 5.11 × 104 Pa-s;−100°C < T η = 5.6503 × 10−23 e−0.6207T; −137°C < T < −100°C η =4.82 × 1014 Pa-s; T < −137°C	[29]
Glass Transition Temperature (DSC)	VS55	−123°C	[19]
	7.05M DMSO	−132°C	[30]
	DP6	−119°C	[19]
Density	VS55	1100 kg/m3	[35]
	Container	1075 kg/m3	[36]
Thermal Conductivity	VS55	0.3 W/m−°C	[37]
	Container	−0.01274T + 0.02 W/m°C	[38]
Specific Heat	VS55	2400 J/kg−°C	[39]
	Container	03.936T + 1121.1 J/Kg−°C	[36]
Thermal Expansion	VS55	1.1 × 10−4 °C−1	[19-21,23]
	Container	0.7 × 10−4 °C−1	[40]
Young’s Modulus	VS55	800 × 106 Pa	[22,24]
	Container	3.45 × 109 Pa	[41]
Poisson’s Ratio	VS55	0.25	Assumed
	Container	0.35	[41]

With the exception of viscosity, all CPA properties used in the current analysis are temperature independent, which simplifies the analysis. Consistent with recently published studies to explain cryomacroscopy observations [28], the container material properties are assumed similar to polystyrene. Despite all of the work that has been done, some material property data for VS55 is still unavailable. The density of VS55 was assumed to be the same as 8.4M DMSO (which is known) since they have the same solute concentration. Additionally, the poisson’s ratio of VS55 was assumed to be 0.25, which is typical of elastic solids.

Due to the high temperature dependency of the CPA viscosity, changing twelve orders of magnitude in the relevant temperature range for vitrification, special steps were taken to ensure stability and convergence of the FEA analysis in a realistic computer run time. At the beginning of cooling, when the viscosity is extremely low, extremely short time steps would be required in order to ensure stability within the simulation. Conversely, at extremely low temperatures, the viscosity is so high that the material simply acts elastically. In order to simplify the solution, a piecewise functional form was used to approximate the viscosity behavior, as listed in Table 1 [29].

While every attempt was made to select the most representative property values for the current study, results of this study are considered somewhat qualitative rather than quantitative for the following reasons: (i) some material properties are not readily available and, therefore, are estimated; (ii) some material properties have been assigned constant values rather than capturing their true temperature-dependent behavior in order to simplify the analysis; (iii) the one term (Maxwell) viscoelastic model that has been chosen for this study may be too simplistic to fully capture the full behavior for a given CPA; and, (iv) the selection of VS55 as a representative CPA cocktail is a choice of practice, where other cocktails may exhibit somewhat different values. Nevertheless, the physical modeling in the current study is believed by the authors to generate realistic level of stresses, and comparison between the different cases are believed to provide credible guidelines on how to reduce the level of stress in similar protocols. By comparing the effects of the various thermal protocols, it should be possible to determine which protocols are likely to minimize stress (and thus the likelihood to fracture) in comparison with the others.

Thermal History at the Boundary

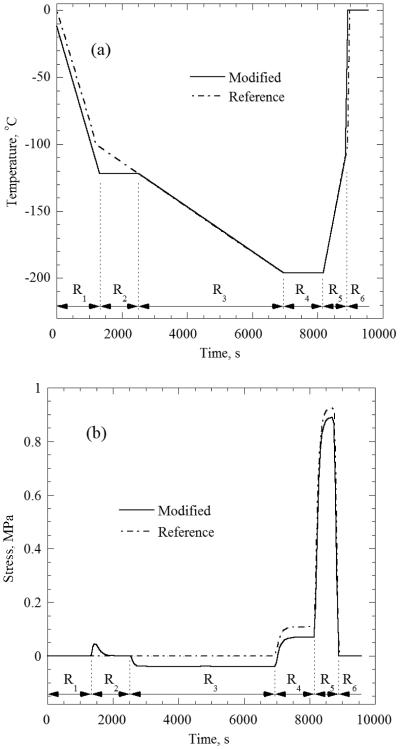
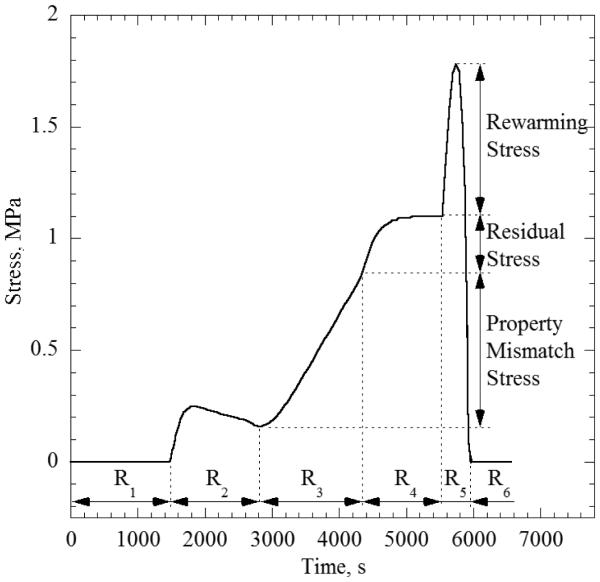
The goal of this study is to investigate how the thermal history affects stresses and, thus, the likelihood to fracture, for which a variety of temperature boundary conditions are compared. Consistent with cryopreservation practices [1-3], a reference thermal history at the boundary is displayed in Fig. 2(a), combining five stages (labeled as R₁, R₃, R₄, R₅, and R₆). The reference thermal history at the boundary consists of (R₁) fast cooling at a rate of 5°C/min from room temperature (20°C) down to an intermediate temperature of −100°C, (R₃) slow cooling at a rate of 1°C/min down to the storage temperature of −196°C (liquid nitrogen boiling), (R₄) hold time of 20 min at the storage temperature, (R₅) slow rewarming at a rate of 7.5°C/min up to an intermediate temperature of −100°C, and (R₆) fast rewarming at a rate of 100°C/min back to room temperature. The R₁ and R₆ cooling/rewarming rates were chosen so that the entire specimen would exceed the critical cooling/rewarming rate for VS55, which is estimated to be 2.5°C/min and 50°C/min respectively [30,31]

Figure 2.

The key thermal histories used in the current study and the corresponding principle stress for the case of uncontained CPA (Case A): (a) the thermal history imposed on the external boundary (Fig. 1), where the modified protocol includes an annealing stage; and (b) the corresponding principle stress at the center of the domain, subject to data shifted in time such that both data sets have a common onset of rewarming in stage R5—the stage in which maximum stress is found.

There has been some speculation that an intermediate stage of temperature hold at the vicinity of glass transition would be favorable in reducing stresses, by facilitating annealing or stress relaxation. In order to investigate this proposed practice, an additional thermal history at the boundary is investigated, combining an intermediate temperature hold before cryogenic storage. The latter thermal history is referred to as the modified thermal history, and the additional temperature hold is labeled R₂, as displayed in Fig. 2(a). The modified thermal history extends the cooling rate of R₁ to a lower temperature of −122°C, combined with a hold time of 1200 sec, to potentially facilitate stress relaxation. The remainder of the modified protocol is essentially the same as the reference one. The temperature selection of −122°C is not arbitrary but is related to the glass transition process. Noday et al. [29] have measured viscosity values of 10¹⁰ and 10¹² Pa-s at temperatures of −122.4 and −129.9°C, respectively (the temperature at which the viscosity gets to a value of 10¹² P-s is one common definition of glass transition). DSC studies indicate an intermediate glass transition temperature of −123°C [29].

In order to investigate the effects of each parameter of the modified case, the different stages are methodically varied from the above nominal values. For the four cooling/rewarming stages (R₁, R₃, R₅, and R₆), four rate variations are further investigated, having slopes of either one fourth, one half, twice, or quadruple the above nominal values. For the annealing stage (R₂), four hold temperature variations are studied, at +4°C, +2°C, −2°C, and −4°C of the nominal value listed above. For the storage stage (R₄), four additional storage temperatures are selected at −140°C, −150°C, −160°C, and −170°C. Recall that the glass transition temperature for VS55 is −123°C and any of the above storage temperatures can be conveniently achieved in the vapor phase storage above liquid nitrogen (common practice in cryopreservation). Finally, the duration of the temperature hold stages (R₂ and R₄) was varied between the different cases to ensure thermal equilibrium at the end of each respective stage. In practice, the material was assumed thermally equilibrated when temperature non-uniformity of less than 0.1°C was achieved at each respective case.

RESULTS AND DISCUSSION

This study is theoretical by nature, encapsulating the underlying principles of thermo-mechanical stress in viscoelastic materials, as they pertain to experimental observations collected in previous studies. The current study does not include in vitro experiments, but is intended to lay out a foundation for future design of in vitro investigations. Given the virtually endless combinations of experimental variables and the cost of experimentation, such a systematic approach to future studies is deemed essential. In a parallel study, polarized light and photoelasticity principles are also explored to augment the design of such future investigations [32]. With this approach in mind, the discussion below starts with thought experiments explaining the key features of stress development in typical cryopreservation cases, and gradually advances to more complex case studies, which may be studied experimentally in a progressive manner.

Thought Experiments

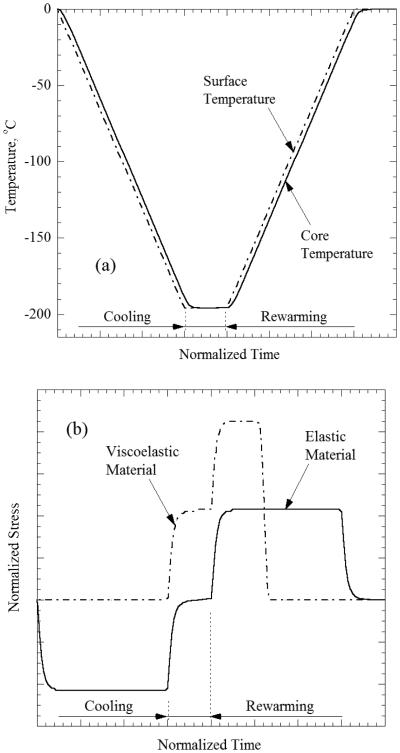
The ideas presented in [15,16] are fundamental to the understanding of stress development during cryopreservation via vitrification, so they will be adapted here to illustrate the effects of a thermal protocol on thermal stress in a simple thought experiment. Consider a very long cylinder with temperature-independent material properties, initially at a uniform temperature. Starting at room temperature, the boundary is cooled at a constant rate down to a storage temperature of −196°C, held there for some period of time, and then rewarmed at a constant heating rate back to room temperature. During cooling, a temperature gradient will develop, where the outside is colder than the inside. At storage, this gradient will decay towards thermal equilibrium, while during rewarming, the opposite temperature gradient will develop, with the outer surface warmer than the inside. If the material would be an elastic solid throughout the process, then the outside would undergo tension during cooling and correspondingly the inside would undergo compression. With thermal equilibrium, the material would return to a stress-free state at the storage temperature. Finally, from similar arguments, the outside would undergo compression while the inside undergoes tension during rewarming. Through this thought experiment, the stress state of the material is dependent only upon the instantaneous thermal gradient.

Consider another thought experiment where the viscosity of the material transitions smoothly from a low viscous fluid at high temperatures to a highly viscous material at low temperature, with such a high viscosity value that it can be considered solid for all practical applications. Stress relaxation occurs so quickly at high temperatures that, despite the developing temperature gradients during cooling, the material is initially cooled stress free. Further assume that the temperature gradient in the material develops in the same manner during cooling, whether the material behaves linear elastically or viscous. As the material approaches the storage temperature, the vitrified material is stress free, has a thermal gradient built in, but now responds elastically due to the low temperature. So, as the thermal gradient equilibrates, stresses build with tension on the inside and compression on the outside. Thus, at storage temperature, the material has a built in residual stress. This residual stress is equal in magnitude and opposite in direction when compared to the stress that developed in the equivalent purely elastic body during cooling. So, residual stresses left in the body at storage temperature are dependent on the thermal gradient which formed during cooling, hence the current stress state is thermal-history dependent. Finally, as the material rewarms, the inside undergoes additional tension on top of the residual tension and the outside undergoes additional compression. These stresses then disappear as the temperature becomes warm enough to allow for stress relaxation (as the material transitions from elastic solid to viscous fluid). As described in [15,16], this additional tension at the onset of rewarming, coupled with the fact that brittle materials such as glasses tend to fail due to tensile stress explains theoretically why CPAs are most likely to fracture at the onset of rewarming, as seen empirically in [8-12].

In practice, many thermal protocols consist of two-stage cooling (fast then slow), storage, and then two-stage rewarming (slow then fast). One can see why this approach may be effective based on the stress history analysis above. Since gradients that form within the liquid phase have no effect on stress, the cooling rate can initially be high; at lower temperatures, as the material begins transitioning towards a more elastically dominated response, lower cooling rates are beneficial because their smaller temperature gradients result in lower stresses at storage. Additionally, the material reacts elastically at the initial stages of rewarming, so slow rewarming is needed in order to reduce stress, but as the material transitions from elastic solid to viscous fluid, faster warming will not lead to higher stresses. The initially high cooling rate and the terminal high rewarming rate are required to suppress crystallization, when the viscosity is low. Hence, high tendency to crystalize and high potential to significant thermal stress mostly reside in complementary parts of the cryopreservation protocol. It is the transition between the different regimes that is critical to the analysis in the current study.

These concepts are qualitatively illustrated in Fig. 3, where two infinite cylinders, having the same thermal and mechanical properties are exposed to identical thermal histories. The material that behaves linear elastically displays zero stress each time the temperature equilibrates. The viscoelastic material (vitrified material) displays residual stress at cryogenic storage, increased stress upon rewarming, and relaxation of stress at higher temperatures by means of viscous flow.

Figure 3.

Qualitative results of a thought experiment subject to simplified boundary conditions in Case A: (a) the expected thermal history at the center of the domain subject to imposed temperature on the outer surface; and (b) the corresponding principle (also axial) stress at the center of the domain for both an elastic and viscoelastic material models.

Fractures tend to form in brittle materials due to maximum principal stress. The maximum principal (also tensile) stress in the CPA in Case A (no container) always occurs in the axial direction at the geometric center of the specimen. For this reason, all stress history plots for CPA simulations in the current study are taken from that location unless specified otherwise. Finding the location of maximum stress in Case B (with container) is somewhat more complicated as described below.

CPA Simulations – Case A

Figure 2(b) displays the axial stress history at the center of the sample for both the reference and modified thermal histories for Case A (no container). The stress due to the reference boundary condition is consistent with the thought experiment described above (see Fig. 3). To summarize, there is zero stress state during cooling, residual tensile stress develops during thermal equilibration at storage temperature, additional tensile stress at the onset of rewarming, and stress relaxation as the sample transitions back into a viscous fluid. The maximum stress due to the modified thermal history is somewhat lower and the stress history is more complex: a “blip” in stress during annealing at R₂, and compression during cooling in R₃. These effects are explained below. The maximum stress in Fig. 2(b) is of the order of 1 MPa, which is similar in magnitude to the stress-to-fracture in prior experimental investigations [33]. Results of other case studies below indicate even higher predicted stresses, which suggest possible fracturing for the corresponding thermal histories.

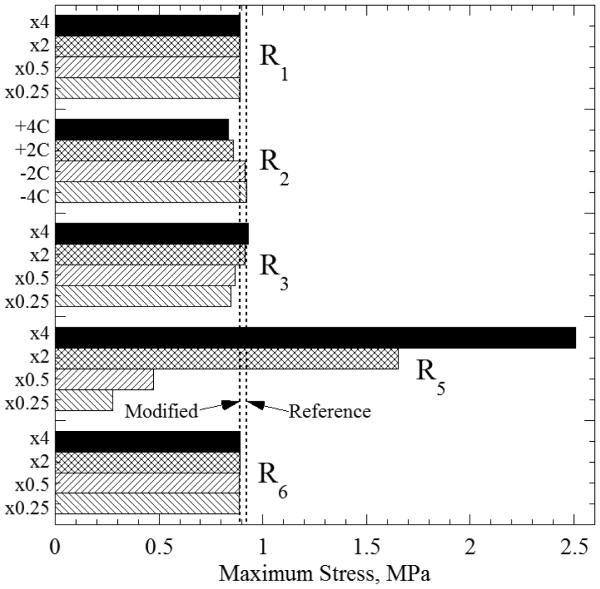
Figure 4 displays the maximum tensile stress for select boundary conditions and additional numerical detail is summarized in table 2. Sections R₁ and R₆ occur exclusively at high temperatures, where viscosity is low enough to allow for instantaneous stress relaxation. As a result, the cooling rate in neither section has an appreciable effect on the maximum tensile stress, nor for that matter do they have any appreciable effect on the stress state anywhere in the material. Empirical studies have shown that neither of these sections have an appreciable effect on the likelihood to fracture [8-10].

Figure 4.

Maximum tensile stress for the general Case A of the modified protocol (stress relaxation stage included) for variable boundary conditions. In each special case, only one parameter is varied at a time, while the maximum stress is always found in R5, qualitatively consistent with Fig. 2.

Table 2.

Summary of thermal-history parameters and the resulting maximum stresses for the cases compared in Fig. 4.

Protocol Section	Description	Label	Value	Maximum Stress, kPa
R1	Initial cooling rate, °C/min	×0.25 ×0.5 Modified ×2 ×4	1.25 2.5 5 10 20	893 893 890 893 893
R2	Annealing temperature, °C	+4 +2 Modified −2 −4	−118 −120 −122 −124 −126	924 914 890 858 835
R3	Final cooling rate, °C/min	×0.25 ×0.5 Modified ×2 ×4	0.25 0.5 1 2 4	846 868 890 915 933
R5	Initial rewarming rate, °C/min	×0.25 ×0.5 Modified ×2 ×4	1.875 3.75 7.5 15 30	279 473 890 1,653 2,508
R6	Final rewarming rate, °C/min	×0.25 ×0.5 Modified ×2 ×4	25 50 100 200 400	888 888 890 892 891

The maximum tensile stress is highly dependent on the rewarming rate in section R₅, as can be seen in Fig. 4. At these low temperatures, the CPA is so viscous, that it acts like an elastic solid. Thus, the stress due to R₅ is directly dependent on the current thermal gradient. Faster rewarming rates lead to higher tensile stresses and slower rates lead to lower stresses. By reducing the rewarming rate in R₅ to 25% of its reference value the additional stress at the onset of rewarming can be reduced by 75%. Multiple studies [8-10] have noted that the likelihood to fracture seems to be highly dependent on the rate of the initial rewarming—this effect is borne out by the current model.

Temperature hold at a suitable level can noticeably reduce the maximum tensile stress. To the best of the authors’ knowledge, this study pioneers the investigation of this effect in the context of cryopreservation, while providing insight into the subtle role of the annealing temperature. It is apparent from Figs. 4 and 5 that a lower annealing temperature leads to lower maximum tensile stress. Also, a lower annealing temperature leads to higher compressive stresses during the R₃ section. The change in stress associated with thermal equilibration at the storage temperature is the same in all cases and depends upon the cooling rate R₃; the response in this stage is fully elastic. Maximum stress variation with the annealing temperature is associated with how much stress arose when the temperature gradient first develops in R₃, with the stress range being compressive in this process. If the hold stage is at a sufficiently low temperature, the behavior is akin to the thought experiment for a fully elastic material: the material responds predominantly elastically to the development of the thermal gradient in R₃ and equilibration at storage largely reverses the stress, bringing the storage stress to zero. If the hold stage is at too high temperature, when the viscosity is still relatively low, little stress accompanies the development of the thermal gradient in R₃ (equilibration produces tensile stress at storage like the thought experiment for viscous material transitioning to solid). At intermediate hold temperature level, some stresses arise with the development of the thermal gradient in R₃ and equilibration always producing the same increase in stress, which brings the storage stress to intermediate levels.

Figure 5.

Stress history for variable annealing temperatures (stage R2) in Case A. Datasets have been shifted in time such that all have a common onset of rewarming in stage R5—the stage in which maximum stress is found.

Admittedly, lower annealing temperatures lead to slower stress relaxation and, thus, they require longer stress relaxation times (seen in Fig. 5). An anneal temperature of −26°C seems appropriate for a glass transition temperature of −129.9°C [29] (viscosity equals 10¹² Pa-s). This requires a relatively long relaxation time of approximately one hour, while reducing the residual stress at storage by 86% when compared to the reference case. In comparison, achieving a similar reduction in stress merely by slowing the R₃ cooling rate would require excessively slow rates of about −0.25°C/min, elongating the cryopreservation protocol by 5 to 6 hours.

A limit appears to the extent in which the maximum stress can be reduced by lowering the annealing temperature, when compared with the reference case. All the above scenarios presume zero stresses at the commencement of R₃, which would be true only if the viscosity is still high enough in R₂ that annealing can occur. Otherwise residual stress from temperature gradients from the R₁ stage can further contribute to the residual stress at storage. To summarize, if a temperature hold is to be beneficial, it must occur within a certain temperature range. At too high temperatures (above, for example, −100°C), the stress relaxation occurs quickly enough during R₃ that residual stress at storage is unaffected by the annealing and is indistinguishable from the stress state due to the reference boundary condition. If the hold temperature R₂ is too low, relaxation is too slow and there is insufficient time to relax the stresses induced by equilibrating the temperature gradient from R₁; the stress at storage can be as high as if the cooling were performed entirely at the high rate R₁ down to storage. Ideally, the anneal takes place at an intermediate temperature that results in low residual stress following a relatively short temperature-hold time.

Note that the stresses prior to equilibration at the storage temperature are tensile at the exterior of the specimen, which can potentially exceed the strength of the material and induce cracking (glassy materials tend to fail due to tension). Hence, an upper limit to R₃ cooling rate exists beyond which fractures would occur. Conversely, the maximum tensile stress during rewarming occurs at the geometric center.

The attention is now shifted to viscosity near glass transition. The logarithmic slope of the viscosity with temperature is similar for all three solutions analyzed [29], where the primary difference between the datasets is in a temperature shift corresponding to the different glass transition temperatures. Hence, the maximum tensile stress for all three viscosity functions is essentially the same as long as the annealing temperature is also shifted accordingly (−8.2°C for DMSO and +2.73°C for DP6). While the material properties for the different solutions may vary [19-23,25,34], unlike the simplified assumption in the current analysis, the thermal protocol strategy to minimize stress would still work in all cases as long as the R₂ annealing temperature is shifted appropriately.

Simulations for CPA and Container – Case B

Case B models stresses that develop in many realistic cryopreservation protocols, such as in a recent cryomacroscopy study [27]. Here, the top surface is assumed to be thermally insulated, which is consistent with negligible heat transfer rate from the CPA upper surface to an air gap above it. This assumption corresponds to free convection above the CPA as opposed to high forced convection of the outer walls. The stress history in the CPA within the container essentially follows the same process as in Case A, with an additional effect resulting from the mechanical interaction between the container and the solution after it has entered into the elastic-dominant state, as schematically displayed in Fig. 6.

Figure 6.

Stress history for CPA within a container with the three stress components clearly labeled. The stress history was chosen so as to make each component clearly visible. Also, note how the stress relaxation in R2 is slower when compared to the stress relaxation for a CPA without a container.

The CPA and the container tend to contract at different rates consistent with their thermal expansion coefficient values, with the CPA tending to contract more. Due to continuity in displacement at the CPA-container interface, the container prohibits the CPA from contracting as much as unconstrained contraction would yield (Case A), and so the entire CPA domain goes into a state of tensile stress. This effect may intensify the overall tensile stress that would otherwise develop in the absence of a container.

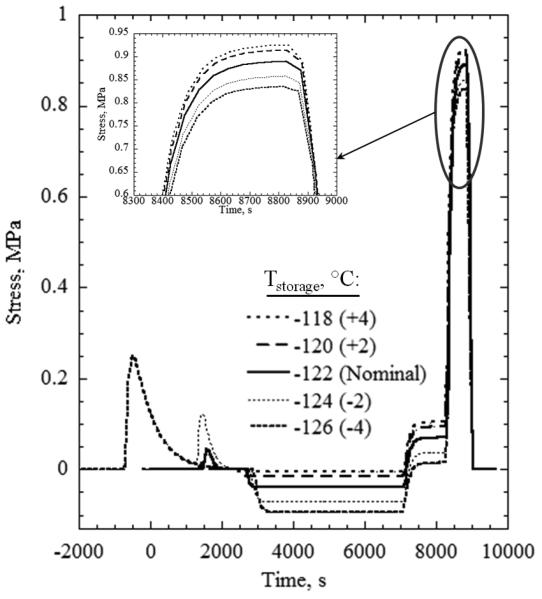
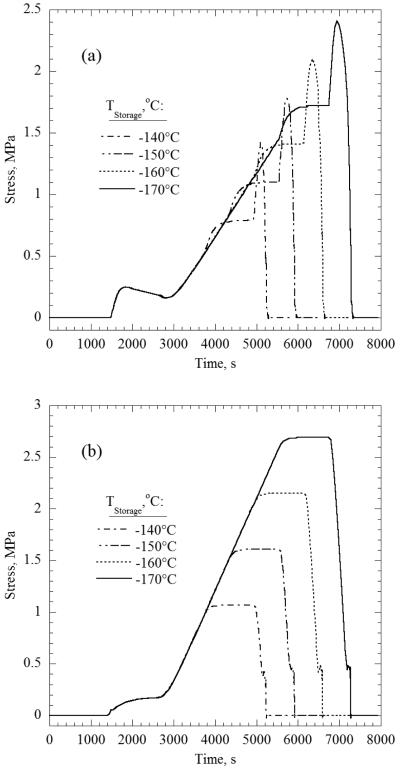
One strategy to minimize the added stress imposed by the container is to reduce its ability to restrain the CPA. A container with a lower Young’s modulus or a thinner wall is more compliant, and thus less able to constrain the solution against thermal contraction. A different strategy could be to select a container material with thermal expansion coefficient closer to that of the CPA and, thereby, lower the thermal strain difference between CPA and container. While all of these approaches could reduce the maximum tensile stress in the CPA, the current investigation is focused on the thermal boundary conditions, and so the strategy adopted here is to vary the boundary conditions instead of modifying the material properties or geometry. For example, minimizing the differential thermal strain between the two materials by elevating the storage temperature reduces the stress level.

The location of maximum stress in Case A was always at the geometric center due to symmetric boundary conditions. Due to asymmetric wall effects and thermal boundary conditions in Case B, the location of the maximum stress is now shifted off center. The location of the maximum stress was found in one of two locations, depending on the thermal boundary condition (see Fig. 1). When the stress due to differential thermal strain dominates, the maximum stress is found where the base is connected to the wall. Alternatively, when the stress due to thermal gradients (i.e. residual stress at storage and additional stress upon rewarming) are more significant, then the location of maximum stress will be offset down and to the right from the geometric center. Fig. 7 displays the differences between the stress histories at these two locations. Using Fig. 6 as a guide, one can clearly see the distinct stress modes in Fig. 7(a), while only the stresses due to differential thermal strain are visible near the container wall as shown in Fig. 7(b).

Figure 7.

(a) Stress history at the location offset from the center for the R4 variations, and (b) stress history at the bottom right corner for the R4 variations; see σ_B in Fig. 1.

Comparing the results displayed in Fig. 7 with those displayed in Figs. 4 and 6 it can be concluded that, due to the restraining effects of the container, the rate of stress relaxation in Case B is significantly slower than in Case A. This means that annealing times at R₂ for a given temperature take significantly longer than for CPA without a container (over 100 min vs. approximately 13 min at −120°C for the particular container properties and geometry used in the current study). Even partial annealing can reduce the maximum residual tensile stress, as long as the portion of stress in R₂ which did not relax is smaller than the residual stress that would be generated due to the thermal gradients in R₃. However, this significantly slower annealing time makes the benefits of annealing more ambiguous and dependent upon the particular system geometry, container material, and cryopreservation protocol.

SUMMARY AND CONCLUSION

Investigating the effects of the thermal history on the resulting mechanical stress has been the subject of several previous studies and is a staple of efforts to cryopreserve large-size samples. The current study focused on annealing effects, subject to varying thermal history parameters, such as the rate of cooling, rewarming, and storage temperature. Several independent empirical studies have reported on fractures in cryopreserved materials, subject to mechanical stress levels similar to those simulated in the current study. Consequently, empirical studies have suggested that the likelihood to fracture is strongly dependent upon the cooling rate when approaching cryogenic storage (R₃) and the subsequent initial rewarming rate (R₅). The current study provided explanations for those previous observations and further insight into the affecting mechanisms. This study theoretically investigated—for the first time—the effects of annealing, and how it can reduce stress while minimizing its dependence on the cooling rate.

Theoretical results suggest that the residual tensile stress at storage can be reduced by 86% compared with the reference by using low temperature annealing, and that additional stress upon the onset of rewarming can be reduced by 75% by using a slower rewarming rate. Additionally, it was shown that provided that the thermal gradients are fully developed before crossing the glass transition region, the maximum tensile stress is independent of the storage temperature. Finally, it was shown that for the three CPA solutions where viscosity data exists, the viscosity value is not particularly important as long as the annealing temperature is appropriately shifted with respect to the glass transition temperature.

Some of the mechanical effects present in CPA within a container were elucidated in this study. Firstly, it was shown that stresses due to thermal gradients are controlled by the initial rewarming rate (R₅) and by either the annealing time and temperature (R₂) or the cooling rate (R₃). Additionally, it was demonstrated that stresses due to differential thermal strain between CPA and container are dependent on the storage temperature. Also, the parameters that affect the location of maximum stress for CPA within a container were discussed, while the restraining effects of the container on the rate of stress relaxation were investigated. Based on these observations, the authors suggest the following guidelines when developing a cryopreservation thermal protocol: (i) use a container that is as compliant as possible, such as an FEP bag; (ii) if this is not practical, storage temperature should be as high as possible (though still below the glass transition region); (iii) an annealing stage appears to be a better way of lowering residual stress than using slow cooling rates with a compliant container, but slow cooling rates may be more effective for cryopreservation within a rigid container; (iv) annealing significantly reduces stress when carried out at a few degrees above glass transition; (v) stresses are highly dependent upon the initial rewarming rate, with very slow rewarming up to an intermediate temperature drastically lowering maximum tensile stress; and, (vi) thermo-mechanical analyses of specific container geometry and materials can be used as an effective tool to further reduce the likelihood to structural damage during cryopreservation.

While the critical stress threshold below which fractures will not form may be difficult to evaluate, by learning which boundary conditions minimize stress and what the most significant driving forces are, it is plausible to design more effective thermal protocols for the benefit of cryopreservation practice

Highlights.

• Simulation of mechanical stress effects due to thermal protocols on vitrifying CPA

• Reducing initial rewarming rate reduces mechanical stress

• A temperature hold near glass transition temperature reduces mechanical stress

• When employing a temperature hold near glass transition, slow cooling rates have almost no effect

• Initial cooling and final rewarming rates have no effect on mechanical stress

• Rigid containers drastically increase mechanical stress