ODF RECONSTRUCTION IN Q-BALL IMAGING WITH SOLID ANGLE CONSIDERATION

Abstract

Q-ball imaging (QBI) is a high angular resolution diffusion imaging (HARDI) technique which has been proven very successful in resolving multiple intravoxel fiber orientations in MR images. The standard computation of the orientation distribution function (ODF, the probability of diffusion in a given direction) from q-ball uses linear radial projection, neglecting the change in the volume element along the ray, thereby resulting in distributions different from the true ODFs. For instance, they are not normalized or as sharp as expected, and generally require post-processing, such as sharpening or spherical deconvolution. In this paper, we consider the mathematically correct definition of the ODF and derive a closed-form expression for it in QBI. The derived ODF is dimensionless and normalized, and can be efficiently computed from q-ball acquisition protocols. We describe our proposed method and demonstrate its significantly improved performance on artificial data and real HARDI volumes.

1. INTRODUCTION

Diffusion-weighted magnetic resonance imaging (DWMRI) provides valuable information about the fiber architecture of neural tissue by measuring the diffusion of water molecules in three-dimensional (3D) space. The microscopic diffusion function may be measured by using the model-free diffusion spectrum imaging (DSI) [1], which is the direct Fourier inversion of the diffusion signal. This technique is time intensive, as it measures the diffusion signal on a 3D Cartesian lattice. Thus, an alternative approach based on sampling only on a spherical shell (or multiple ones) has been proposed, referred to as high angular resolution diffusion imaging (HARDI) [2]. The spherical shell, being a 2D manifold, includes a number of measurement points which grows quadratically with the desired angular resolution, as opposed to cubically with the spatial resolution in the entire 3D lattice of DSI.

While the 3D probability density function (PDF) of the diffusion is helpful in studying the tissue microstructure, the orientation distribution function (ODF) – the marginal probability of diffusion in a given direction – is the quantity of interest for mapping the orientation architecture of the tissue. Q-ball imaging (QBI), [3], is a widely used ODF reconstruction scheme for HARDI, based on a spherical tomographic inversion called the Funk-Radon transform. This technique's simplicity and its ability to resolve intravoxel fiber orientations have made it popular for fiber tracking and characterizing white matter architecture. A number of recently proposed methods have turned QBI into a very efficient and robust technique [4]–[6].

However, the definition of the ODF currently used in QBI is different from the actual marginal PDF of diffusion in a constant solid angle. The former is a linear radial projection of the PDF, which does not take into account the quadratic growth of the volume element with respect to its distance from the origin (see Sec. 2.1 and Fig. 1 for more details). This inaccurate formulation generally distorts the ODF, and has created the need for postprocessing such as manual normalization and sharpening.

Fig. 1.

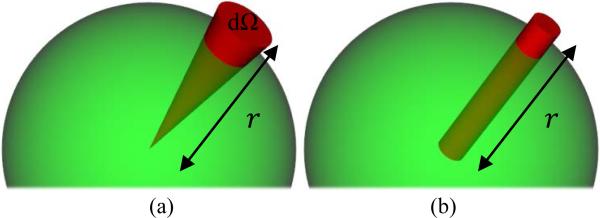
Radial integration of the PDF, (a) in a cone of constant solid angle (i.e., the factor r² is considered), and (b) by linear projection (i.e., inaccurately without the factor r²).

In this paper, we re-derive the ODF expression for QBI via Fourier analysis, this time starting from the proper definition of the ODF in constant solid angle. We show that this results in an inherently normalized and dimensionless expression. In addition, we illustrate through our experiments that the ODFs are sufficiently sharp and that multiple fiber orientations are better resolved. Furthermore, by making use of the spherical harmonic basis, we demonstrate that the implementation of the new expression is as straightforward as that of the currently used (inaccurate) formula, or maybe even simpler, considering that further sharpening is not really necessary.

In Sec. 2 we describe the foundation of our mathematical derivation, along with a brief version of the proof, and also provide an implementation scheme. Experimental results are presented in Sec. 3, and Sec. 4 concludes with a review of the contributions.

2. METHODS

2.1. General ODF Definition

The PDF of the diffusion of water molecules, $P\left(\stackrel{\rightharpoonup }{r}\right)$, gives the displacement probability $P\left(\stackrel{\rightharpoonup }{r}\right)dv$ of a molecule, initially the origin, to be in the infinitesimal volume dv located at $\stackrel{\rightharpoonup }{r}$ after a certain amount of time. We assume this function to be symmetric (i.e. $P(-\stackrel{\rightharpoonup }{r})=P\left(\stackrel{\rightharpoonup }{r}\right)$), which is the quite common assumption in DWMRI. The PDF cnab be presented in Cartesian coordinates with $\stackrel{\rightharpoonup }{r}={(x,y,z)}^T$ and dv = dxdydz. However, for mapping the orientation architecture of the tissue, the representation which mostly interests us is in the standard spherical coordinates, parameterized by with (r, θ, ϕ), where $\stackrel{\rightharpoonup }{r}=r\widehat{u}$, with û(θ, ϕ) = (sin θ cos ϕ, sin θ sin ϕ, cos θ)^T being the unit direction vector. The volume element in this case is dv = r²drdΩ with dΩ = sin θ dθdϕ being the infinitesimal solid angle element.

We note by ODF(û)dΩ the probability of diffusion in the direction û through the solid angle dΩ, which can be computed by integrating the displacement probabilities, i.e., $P\left(\stackrel{\rightharpoonup }{r}\right)dv=P\left(r\widehat{u}\right)r^{2}drd\Omega$, for all magnitude r, while keeping û constant:

$$ODF\left(\widehat{u}\right)d\Omega ={\int }_{r=0}^{r=\infty }P\left(R\widehat{u}\right)r^{2}drd\Omega$$

or simply:

$$ODF\left(\widehat{u}\right)={\int }_0^{\infty }P\left(r\widehat{u}\right)r^{2}dr$$ (1)

The above definition, which is normalized and dimensionless, is the integral of the probability values in a cone of “very small” constant solid angle (Fig. 1(a)). This correct definition was used for instance by the authors of [1] in DSI, where $P\left(\stackrel{\rightharpoonup }{r}\right)$ was first computed from the diffusion data via Fourier inversion and then integrated to calculate the ODF, and also in [7]–[8] for diffusion tensor imaging (DTI), where the ODF was analytically computed. However to the best of our knowledge, the expression for ODF reconstruction so far used in HARDI, and specifically QBI [3], is different from Eq. (1), in the sense that the integral is not weighted by the important (and mathematically correct) factor r² (Fig. 1(b)).¹ Without including this factor, the radial projection gives an artificial weight to $P\left(\stackrel{\rightharpoonup }{r}\right)$ which is, respectively, too large and too small for points close to and far from the origin.² Moreover, the ODF will not be necessarily normalized or dimensionless,³ and an additional normalization factor will be required.

As an example intended for comparison, we compute the ODFs with and without r² in the case of DTI, with the following standard Gaussian PDF:

$$P\left(\stackrel{\rightharpoonup }{r}\right)=\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}{\mid D\mid }^{\frac{1}{2}}}{e}^{-\frac{1}{2}{\stackrel{\rightharpoonup }{r}}^T{D}^{-1}\stackrel{\rightharpoonup }{r}}$$

where D is the covariance matrix. The computed ODFs are:

$$\begin{array}{cc}\hfill OD{F}_{with{r}^2}\left(\widehat{u}\right)=& \frac{1}{4\pi {\mid D\mid }^{\frac{1}{2}}{\left({\widehat{u}}^T{D}^{-1}\widehat{u}\right)}^{\frac{3}{2}}}\hfill \\ \hfill OD{F}_{without{r}^2}\left(\widehat{u}\right)=& \frac{1}{Z}\frac{1}{4\pi {\mid D\mid }^{\frac{1}{2}}{\left({\widehat{u}}^T{D}^{-1}\widehat{u}\right)}^{\frac{1}{2}}}\hfill \end{array}$$

where Z is the normalization constant that subsequently needs to be computed and added to ODF_{without r²} (û) (see[3]). An example of this pair of ODFs is illustrated in Fig. 2. No min-max normalization is used in any of the figures.

Fig. 2.

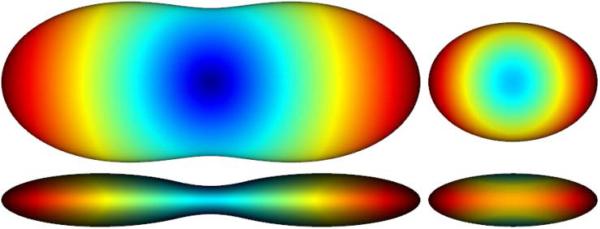
DTI example of ODF reconstruction (with {10, 5, 1} as the diagonal entries of the tensor), shown from two view angles, (left) with the factor r², (right) without the factor r² and after normalization. Note how less sharp the latter is and how incompletely it represents the true structure of the ODF.

Next, we derive a closed-form expression for the ODF in QBI using the correct r²-weighted integral.

2.2. Q-ball Imaging ODF Reconstruction

We present here a brief version of the proof for the ODF expression in QBI. The complete proof is provided in [9].

Let $E\left(\stackrel{\rightharpoonup }{q}\right)$ be the 3D Fourier transform of $P\left(\stackrel{\rightharpoonup }{r}\right)$. Theoretically, we know that E(0)=1, since the zero frequency of a PDF is its integral over the entire space, which is equal to 1. In addition, we have the values of $E\left(\stackrel{\rightharpoonup }{q}\right)$ measured on a q-ball, i.e., the frequencies with constant norm $\mid \stackrel{\rightharpoonup }{q}\mid =q_0$, as $\tilde{E}\left(\widehat{u}\right)≔E\left(q_0\widehat{u}\right)=\frac{s\left(\widehat{u}\right)}{s_0}$, where S(û) is the HARDI signal and S₀ is the base-line image.

Our mathematical derivation is based on the following two relatively simple yet fundamental facts from Fourier analysis:

• The Fourier transform of $P\left(\stackrel{\rightharpoonup }{r}\right){\mid \stackrel{\rightharpoonup }{r}\mid }^2$ is $-{\nabla }^{2}E\left(\stackrel{\rightharpoonup }{q}\right)$, where ∇² is the Laplacian operator.

• For a symmetric function $f:{\mathbb{R}}^3\to \mathbb{R}$ with the 3D Fourier transform $F\left(\stackrel{\rightharpoonup }{q}\right)$, and for the arbitrary unit vector û, we have ${\int }_0^{\infty }f\left(r\widehat{u}\right)dr=\frac{1}{8{\pi }^2}{\iint }_{{\widehat{u}}^{\perp }}F\left(\stackrel{\rightharpoonup }{q}\right)d^2\stackrel{\rightharpoonup }{q}$, where ${\widehat{u}}^{\perp }$ is the plane perpendicular to û.

Combining the two above statements with Eq. (1) leads to

$$ODF\left(\widehat{u}\right)=-\frac{1}{8{\pi }^2}{\iint }_{{\widehat{u}}^{\perp }}{\nabla }^{2}E\left(\stackrel{\rightharpoonup }{q}\right)d^2\stackrel{\rightharpoonup }{q}$$

Now, without loss of generality, we choose our coordinates such that ẑ = û, thus ${\widehat{u}}^{\perp }$ is the q_x-q_y plane. We then use the following expansion for the Laplacian in spherical coordinates (q,θ,ϕ):

$${\nabla }^{2}E=\frac{1}{q}\frac{{\partial }^2}{\partial q^2}\left(qE\right)+\frac{1}{q^2}{\nabla }_b^{2}E$$

where ${\nabla }_b^2$ is the Laplace-Beltrami operator which is independent of the radial component q, and is defined as ${\nabla }_b^{2}E=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\mathrm{sim}\theta \frac{\partial E}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}E}{\partial {\varphi }^2}$. The surface integral on the q_x-q_y plane is computed by fixing $\theta =\frac{\pi }{2}$ and choosing the surface element $d^2\stackrel{\rightharpoonup }{q}=qdqd\varphi$, as follows:

$$\begin{array}{c}\hfill ODF\left(\widehat{z}\right)=-\frac{1}{8{\pi }^2}{\int }_0^{2\pi }{\int }_0^{\infty }{\nabla }^{2}E\left(\stackrel{\rightharpoonup }{q}\right)qdqd\varphi \hfill \\ \hfill ODF\left(\widehat{z}\right)=-\frac{1}{8{\pi }^2}{\int }_0^{2\pi }{\int }_0^{\infty }\left(\frac{1}{q}\frac{{\partial }^2}{\partial q^2}\left(qE\right)+\frac{1}{q^2}{\nabla }_b^{2}E\right)qdqd\varphi \hfill \end{array}$$

One can verify that the integral of the first term is independent of $E\left(\stackrel{\rightharpoonup }{q}\right)$ and its derivatives:

$${\int }_0^{2\pi }{\int }_0^{\infty }\left(\frac{1}{\mathrm{q}}\frac{{\partial }^2}{\partial q^2}\left(qE\right)\right)qdqd\varphi =-2\pi E\left(0\right)=-2\pi$$

Therefore:

$$ODF\left(\widehat{z}\right)=\frac{1}{4\pi }-\frac{1}{8{\pi }^2}{\int }_0^{2\pi }{\int }_0^{\infty }\frac{1}{q}{\nabla }_b^{2}E\left(\stackrel{\rightharpoonup }{q}\right)dqd\varphi$$

while while $\theta =\frac{\pi }{2}$ is kept constant in the integration.

To compute the integral of the second term, the values of $E\left(\stackrel{\rightharpoonup }{q}\right)$ are required for the entire q-space, which except for the time-consuming DSI modality, are not available. Thus, we need to approximate $E\left(\stackrel{\rightharpoonup }{q}\right)$ from the values measured on the q-ball. In this work, we consider the following radial mono-exponential model:

$$E\left(q\widehat{u}\right)\cong E{\left(q_0\widehat{u}\right)}^{\frac{q^2}{q_0^2}}=\tilde{E}{\left(\widehat{u}\right)}^{\frac{q^2}{q_0^2}}$$

where q₀ is the radius of the q-ball. This type of interpolation has been previously used and discussed in [10]–[11].⁴ After applying the mono-exponential assumption and a few more steps of calculations, the following ODF expression can be derived:

$$ODF\left(\widehat{z}\right)=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}{\int }_0^{2\pi }{\nabla }_b^2\ln (-\ln \tilde{E}\left(\widehat{u}\right))d\varphi$$

Finally, rewriting the expression independently of the choice of the axes, the following analytical formula can be shown to hold for the ODF:

$$ODF\left(\widehat{u}\right)=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}FRT\left\{{\nabla }_b^2\ln (-\ln \tilde{E}\left(\widehat{u}\right))\right\}$$ (2)

where FRT is the Funk-Radon transform [12], defined as:

$$FTT\left\{f\left(\widehat{u}\right)\right\}≔{\iint }_{{\widehat{u}}^{\perp }}f\left(\stackrel{\rightharpoonup }{w}\right)\delta (\mid \stackrel{\rightharpoonup }{w}\mid -1)d^2\stackrel{\rightharpoonup }{w}$$

with δ(·) being the Dirac delta function.

We can see that the above ODF expression is dimensionless and intrinsically normalized, as the integrals of the first and second terms over the sphere are 1 and 0, respectively. This is in contrast to the ODF formula originally used in QBI, i.e., $\frac{1}{Z}FRT\left\{\tilde{E}\left(\widehat{u}\right)\right\}$, where a normalization factor Z was needed.

2.3. Implementation

Our implementation of the ODF reconstruction makes use of the spherical harmonic (SH) basis, $Y_k^m\left(\widehat{u}\right)$, which is common for the analysis of HARDI data. The steps taken here to numerically compute Eq. (2) are similar to those described in [5], except that no regularization or sharpening is performed (regularizations will further improve the results). Particularly, we use the real and symmetric modified SH basis introduced in [5], where SH functions are indexed by a single parameter j corresponding to k_j and m_j. We first employ a minimum least square scheme to compute the modified SH coefficients c_j of the double logarithm of the signal, such that

$$\ln (-\ln \tilde{E}\left(\widehat{u}\right))\approx \sum _{j=1}^R{c}_j{Y}_j\left(\widehat{u}\right)$$

where R=(l+1)(l+2)/2, with l being the order of the SH basis (we chose l=4 throughout our experiments). Next, since the SH elements are eigenfunctions of the Laplace-Beltrami operator, we compute ${\nabla }_b^2\ln (-\ln \tilde{E}\left(\widehat{u}\right))$ by multiplying the coefficients c_j by their corresponding eigenvalues, −k_j(k_j+1). Then, as suggested in [5], the Funk-Radon transform is computed by multiplying the coefficients by 2πP_kj(0), where P_k(·) is the Legendre polynomial of degree k, with $P_k\left(0\right)=(-1)\frac{k}{2}\frac{1\times 3\times \cdots \times (k-1)}{2\times 4\times \cdots \times k}$ for even k. Finally, since $Y_1\left(\widehat{u}\right)=\frac{1}{2\sqrt{\pi }}$, the SH coefficients of the ODF are derived as

$$c_j^{\prime }=\{\begin{array}{cc}\frac{1}{2\sqrt{\pi }}\hfill & j=1\hfill \\ -\frac{1}{8\pi }{(-1)}^{\frac{k_j}{2}}\frac{1\times 3\times \cdots \times (k_j+1)}{2\times 4\times \cdots \times (k_j-2)}{c}_j\hfill & j>1\hfill \end{array}\phantom{\}}$$

As can be seen, by taking advantage of the SH framework, this implementation is as straightforward as the one introduced in [5] for the original QBI ODF formula, or even simpler if no further sharpening is to be performed.

3. RESULTS AND DISCUSSION

To validate our approach, we first show results using artificial data. We simulated fiber crossing by generating diffusion images from the sum of two exponentials, $\tilde{E}\left(\widehat{u}\right)=(e^{-{\widehat{u}}^T{D}_1\widehat{u}}+e^{-{\widehat{u}}^T{D}_2\widehat{u}})∕2$, where D₁ is a diagonal matrix with diagonal entries (17, 3, 3), and D₂ is D₁ rotated about the y-axis by a varying angle. The ODFs were reconstructed in the fourth order SH basis from 76 diffusion directions, uniformly sampled on the sphere. The results are shown in Fig. 3, for three different methods: our proposed framework, the original (standard) QBI, and the original QBI followed by Laplace-Beltrami sharpening, $(1-\lambda {\nabla }_b^2)$, with parameter λ=0.2.⁵ As can be seen, our method resolves the crossings starting at about 45°, compared to about 60° by the other two methods.

Fig. 3.

Experimental results on synthetic data with fiber crossing, using: (top) our proposed technique, (middle) original QBI after normalization, and (bottom) original QBI with Laplace - Beltrami sharpening.

We also tested our method on two real HARDI datasets; first on the physical phantom in [13], which was constructed from excised rat spinal cords and designed to have crossing tracts (90 diffusion images at b=1300 s/mm²), and then on human brain data [14] (200 diffusion images at b=3000 s/mm²). The ODFs were reconstructed with the fourth order SH basis using three approaches: our proposed method, the original (standard) QBI, and the original QBI followed by Laplace-Beltrami sharpening with parameters 0.5 for the rat data and 0.8 for the brain data. Results are superimposed on the generalized fractional anisotropy (GFA) map and demonstrated in Fig. 4. (Note that the ODFs are shown as they are; no min-max normalization is used in any of the figures.) Our method (left) produces sharper and more accurate ODFs than the original QBI (middle). Although sharpening (right) enhances the original QBI ODFs considerably in anisotropic tissue, it causes significant instability in isotropic regions (e.g. the background of the rat phantom and the CSF in the human brain data), in contrast to our technique which preserves isotropy fairly well. For human brain dataset, we show the intersection of three fiber bundles: internal capsule (IC)/corona radiata (CR), radiations of the corpus callosum (CC), and superior longitudinal fasciculus (SLF).

Fig 4.

Reconstructed ODFs from rat spinal cord phantom (top) and human brain (bottom), shown on the GFA map, using: (left) our proposed technique, (middle) original QBI after normalization, and (right) original QBI with Laplace-Beltrami sharpening.

4. CONCLUSIONS

We derived a new ODF formula for q-ball imaging, which is based on the proper definition of the ODF in constant solid angle. A closed-form expression for the ODF, dimensionless and normalized, was derived from a single q-shell by means of Fourier analysis. We presented a brief version of the proof, and an efficient implementation based on spherical harmonics parameterization was proposed. We have validated the technique with artificial data and tested it on real HARDI volumes. We have recently extended this work to multiple q-shells, further improving the results [9].