Multiple q-Shell ODF Reconstruction in q-Ball Imaging

Abstract

Q-ball imaging (QBI) is a high angular resolution diffusion imaging (HARDI) technique which has been proven very successful in resolving multiple intravoxel fiber orientations in MR images. The standard computation of the orientation distribution function (ODF, the probability of diffusion in a given direction) from q-ball uses linear radial projection, neglecting the change in the volume element along the ray, thereby resulting in distributions different from the true ODFs. A new technique has been recently proposed that, by considering the solid angle factor, uses the mathematically correct definition of the ODF and results in a dimensionless and normalized ODF expression from a single q-shell. In this paper, we extend this technique in order to exploit HARDI data from multiple q-shells. We consider the more flexible multi-exponential model for the diffusion signal, and show how to efficiently compute the ODFs in constant solid angle. We describe our method and demonstrate its improved performance on both artificial and real HARDI data.

1 Introduction

Diffusion-weighted magnetic resonance imaging (DWMRI) provides valuable information about the fiber architecture of neural tissue by measuring the diffusion of water molecules in three-dimensional (3D) space. The diffusion function may be measured by using the model-free diffusion spectrum imaging (DSI) [1], which is the direct Fourier inversion of the diffusion signal. This technique is however time intensive, as it measures the diffusion signal on a 3D Cartesian lattice. Thus, an alternative approach based on sampling on one or multiple spherical shells has been proposed, referred to as high angular resolution diffusion imaging (HARDI) [2].

While the 3D probability density function (PDF) of the diffusion is helpful in studying the tissue microstructure, the orientation distribution function (ODF) – the marginal probability of diffusion in a given direction – is the quantity of interest for mapping the orientation architecture of the tissue. Q-ball imaging (QBI), [3], is a widely used ODF reconstruction scheme for HARDI, based on a spherical tomographic inversion called the Funk-Radon transform. This technique’s simplicity and its ability to resolve intravoxel fiber orientations have made it popular for fiber tracking and characterizing white matter architecture. Moreover, a few works have suggested exploiting data from multiple q-shells to benefit from the high signal-to-noise ratio (SNR) and high angular contrast-to-noise ratio (CNR) of the data acquired at respectively low and high b-values, [3]-[5]. Using multiple q-shells also allows us to employ richer models for the diffusion signal, as discussed in this paper.

Nonetheless, with the exception of our previous paper [6] and a very recent parallel and independent work [7] (the differences will be detailed in Sec. 2.2), the definition of the ODF used in QBI has been different from the actual marginal PDF of diffusion in a constant solid angle. It has been computed as a linear radial projection of the PDF, which does not take into account the quadratic growth of the volume element with respect to its distance from the origin (see Sec. 2.1 for details). This inaccurate formulation generally distorts the ODF, and has created the need for post-processing such as manual normalization and sharpening [8].

We recently proposed, [6], a new ODF expression for QBI which is derived from the proper definition of the ODF in constant solid angle. We showed that the computed ODF is inherently normalized and dimensionless, producing without any post-processing, sharp ODFs with improved resolution of multiple fiber orientations. In this paper, we extend this work by deriving a general formulation for multiple q-shell QBI. We demonstrate the improvement achieved by considering the information from multiple q-shells, and using richer multi-exponential models.

In Sec. 2 we describe the foundation of our mathematical derivation, along with a brief version of the proof, and also provide an implementation scheme. Experimental results are presented in Sec. 3, along with a brief discussion.

2 ODF Computation in Solid Angle: Multiple q-Shell Formulation

2.1 General ODF Definition

The PDF of the diffusion of water molecules, $P(\stackrel{\rightharpoonup }{r})$, gives the displacement probability $P(\stackrel{\rightharpoonup }{r})\mathit{d\upsilon }$ of a molecule, initially placed at the origin, to be in the infinitesimal volume dυ located at $\stackrel{\rightharpoonup }{r}$ after a certain amount of time. We assume this function to be symmetric (i.e. $P(-\stackrel{\rightharpoonup }{r})=P(\stackrel{\rightharpoonup }{r})$), which is a quite common assumption in DWMRI. The PDF is represented in the standard spherical coordinates, (r, θ, ϕ), with the displacement vector $\stackrel{\rightharpoonup }{r}=r\widehat{u}$ and the unit direction vector û(θ, ϕ) = (sin θ cos ϕ, sin θ sin ϕ, cos θ)^T. The volume element in this case is dυ = r² drdΩ with dΩ = sin θ dθdϕ being the infinitesimal solid angle element.

We denote by ODF (û)dΩ the probability of diffusion in the direction û through the solid angle dΩ, which is computed by integrating the displacement probabilities, i.e., $P(\stackrel{\rightharpoonup }{r})\mathit{d\upsilon }=P(r\widehat{u})r^2\mathit{drd}\mathrm{\Omega }$, for all magnitude r, while keeping û constant:

$$\mathit{ODF}(\widehat{u})={\mathit{\int }}_0^{\infty }P(r\widehat{u})r^2\mathit{dr}$$ (1)

The above definition, which is normalized and dimensionless, is the integral of the probability values in a cone of “very small” constant solid angle. This correct definition was used for instance by the authors of [1] in DSI, where $P(\stackrel{\rightharpoonup }{r})$ was first computed from the diffusion data via Fourier inversion and then integrated to calculate the ODF. However to the best of our knowledge, the expression for ODF reconstruction so far used in QBI [3], (except for our previous work [6] and a very recent parallel and independent paper [7], both for single q-shell) is different from Eq. (1), in the sense that the integral is not weighted by the important (and mathematically correct) factor r². Without including this factor, the radial projection gives an artificial weight to $P(\stackrel{\rightharpoonup }{r})$ which is, respectively, too large and too small for points close to and far from the origin. Moreover, the ODF will not be necessarily normalized or dimensionless, and manual normalization will be required.

Next we derive a closed-form ODF expression in multiple q-shell QBI using the correct r² -weighted integral.

2.2 Q-ball Imaging ODF Reconstruction

In this section, we derive the ODF expression in multiple q-shell QBI, and present a brief proof of the derivation.

Let $E(\stackrel{\rightharpoonup }{q})$ be the 3D Fourier transform function of $P(\stackrel{\rightharpoonup }{r})$. Theoretically, we know that E(0) = 1, since the zero frequency of a PDF is its integral over the entire space, yielding 1. In addition, we have the values of $E(\stackrel{\rightharpoonup }{q})$ measured on M different q-balls, i.e., the frequencies with constant norm $|\stackrel{\rightharpoonup }{q}|=q_i$, i = 1, …, M, as ${\stackrel{\sim }{E}}_i(\widehat{u}):=E(q_i\widehat{u})=\frac{S_i(\widehat{u})}{S_0}$, where S_i(û) is the HARDI signal on the i^th q-ball and S₀ is the base-line image.

Our mathematical derivation is based on the following two relatively simple yet fundamental facts from Fourier analysis:

• The Fourier transform of $P(\stackrel{\rightharpoonup }{r})|\stackrel{\rightharpoonup }{r}{|}^2$ is $-{\nabla }^{2}E(\stackrel{\rightharpoonup }{q})$, where ∇² is the Laplacian operator.

• For a symmetric function f : ℝ³ → ℝ with the 3D Fourier transform function $F(\stackrel{\rightharpoonup }{q})$, and for the arbitrary unit vector û, we have that ${\mathit{\int }}_0^{\infty }f(r\widehat{u})\mathit{dr}=\frac{1}{8{\pi }^2}\mathit{\int }{\mathit{\int }}_{{\widehat{u}}^{\perp }}F(\stackrel{\rightharpoonup }{q})d^2\stackrel{\rightharpoonup }{q}$, with û^⊥ being the plane perpendicular to û.

Combining these statements with Eq. (1) leads to

$$\mathit{ODF}(\widehat{u})=-\frac{1}{8{\pi }^2}\mathit{\int }{\mathit{\int }}_{{\widehat{u}}^{\perp }}{\nabla }^{2}E(\stackrel{\rightharpoonup }{q})d^2\stackrel{\rightharpoonup }{q}$$

Now, without loss of generality, we choose our coordinates such that ẑ = û, thus making û^⊥ the q_x-q_y plane. We then use the following expansion for the Laplacian in spherical coordinates, (q, θ, ϕ):

$${\nabla }^{2}E=\frac{1}{q}\frac{{\partial }^2}{\partial q^2}(\mathit{qE})+\frac{1}{q^2}{\nabla }_b^{2}E$$

where ${\nabla }_b^2$ is the Laplace-Beltrami operator, which is defined independently of the radial component q, as ${\nabla }_b^{2}E=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial E}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}E}{\partial {\varphi }^2}$. The surface integral on the q_x-q_y plane is computed by fixing $\theta =\frac{\pi }{2}$ and using the expression $d^2\stackrel{\rightharpoonup }{q}=\mathit{qdqd\varphi }$

$$\begin{array}{lll}\mathit{ODF}(\widehat{z})& =& -\frac{1}{8{\pi }^2}{\mathit{\int }}_0^{2\pi }{\mathit{\int }}_0^{\infty }{\nabla }^{2}E(\stackrel{\rightharpoonup }{q})\mathit{qdqd\varphi }\\ & =& -\frac{1}{8{\pi }^2}{\mathit{\int }}_0^{2\pi }{\mathit{\int }}_0^{\infty }\left(\frac{1}{q}\frac{{\partial }^2}{\partial q^2}(\mathit{qE})+\frac{1}{q^2}{\nabla }_b^{2}E\right)\mathit{qdq\; d\varphi }\end{array}$$

The integral of the first term can be seen to be constant and independent of $E(\stackrel{\rightharpoonup }{q})$,

$${\mathit{\int }}_0^{2\pi }{\mathit{\int }}_0^{\infty }\left(\frac{1}{q}\frac{{\partial }^2}{\partial q^2}(\mathit{qE})\right)\mathit{qdq\; d\varphi }=-2\mathit{\pi E}(0)=-2\pi$$

Therefore,

$$\mathit{ODF}(\widehat{z})=\frac{1}{4\pi }-\frac{1}{8{\pi }^2}{\mathit{\int }}_0^{2\pi }{\mathit{\int }}_0^{\infty }\frac{1}{q}{\nabla }_b^{2}E(\stackrel{\rightharpoonup }{q})\mathit{dq\; d\varphi }$$

while $\theta =\frac{\pi }{2}$ is kept constant in the integration.

To compute the integral of the second term, the values of $E(\stackrel{\rightharpoonup }{q})$ are required in the entire q-space, which are in general – except for the time-consuming DSI modality – not available. Thus, we need to approximate $E(\stackrel{\rightharpoonup }{q})$ from the values measured on the q-balls. In this work, we consider the following radial multi-exponential model [9],

$$E(q\widehat{u})\cong \sum _{k=1}^N{\lambda }_k(\widehat{u}){\alpha }_k{(\widehat{u})}^{q^2}$$

with the constraints

$$\begin{array}{lll}0& <& {\alpha }_k(\widehat{u}),{\lambda }_k(\widehat{u})<1\\ & & \sum _{k=1}^N{\lambda }_k(\widehat{u})=1\end{array}$$ (2)

where Eq. (2) comes from the fact that E(0) = 1.¹ Once the values of λ_k and α_k are estimated (see Sec. 2.3), they can be used in the following ODF expression, which is obtained by a few more steps of calculation,

$$\mathit{ODF}(\widehat{z})=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}{\mathit{\int }}_0^{2\pi }{\nabla }_b^2\sum _{k=1}^N{\lambda }_k(\widehat{u})\ln (-\ln {\alpha }_k(\widehat{u}))\mathit{d\varphi }$$

Finally, rewriting the expression independent of the choice of the axes, the following analytical formula can be derived for the ODF:

$$\mathit{ODF}(\widehat{u})=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}\mathit{FRT}\left\{{\nabla }_b^2\sum _{k=1}^N{\lambda }_k(\widehat{u})\ln (-\ln {\alpha }_k(\widehat{u}))\right\}$$ (3)

where $\mathit{FRT}\{f(\widehat{u})\}:=\mathit{\int }{\mathit{\int }}_{{\widehat{u}}^{\perp }}f(\stackrel{\rightharpoonup }{w})\delta (|\stackrel{\rightharpoonup }{w}|-1)d^2\stackrel{\rightharpoonup }{w}$ is the Funk-Radon transform [3].

The above ODF expression is dimensionless and intrinsically normalized, since the integrals of the first and second terms over the sphere are respectively 1 and 0. This is in contrast to the (single q-shell) ODF formulas used in original QBI, i.e., $\frac{1}{Z}\mathit{FRT}\{{\stackrel{\sim }{E}}_1(\widehat{u})\}$, and also in [7], where a normalization factor Z is needed. Additional differences can be observed in the approach presented here and in [6], compared to [7]. As demonstrated here, integration of the radial part of the Laplacian on the plane always results in a constant without requiring any model for the diffusion signal. Yet, [7] uses the Bessel approximation of the Dirac delta function which yields a variable (sometimes negative) term. As for the integral of the tangential term of the Laplacian, we use the exponential model that is particularly consistent with E(0) = 1, in contrast to [7] that assumes the tangential term to be zero outside the q-ball, leading to an expression similar to Laplacian-Beltrami sharpening.

2.3 Parameter Estimation

In order to approximate the diffusion signal in a direction û by a weighted sum of N exponentials, we need to estimate the 2N parameters λ_k (û) and α_k (û), for k = 1, …, N. We continue this subsection considering a fixed direction, and therefore drop the notation (û). To estimate the aforementioned parameters, at least 2N − 1 independent equations – besides Eq. (2) – are required, which can be obtained from the HARDI signals measured on M q-balls, for M ≥ 2N − 1. Numerical optimization approaches such as the trust region algorithm, [10], may be employed to solve this non-linear system in the most general case. Here, however, we discuss two special cases with closed-form analytical solutions.

The mono-exponential assumption (N = 1) requires measurement on at least M = 1 q-ball. As it has been shown in [6], M = 1 leads to λ₁ = 1 and ${\alpha }_1={\stackrel{\sim }{E}}_1^{\frac{1}{q_1^2}}$ ². Furthermore, if measured values are provided on more than one q-balls and the mono-exponential model is still desired, one can fit the best exponential by computing the average Apparent Diffusion Coefficient ( $\mathit{ADC}:=-\frac{1}{b}\ln \frac{S}{S_0}$) across all the q-shells.

Another practical case of great interest arises when we consider the richer bi-exponential model (N = 2, see for example [11]) to reconstruct the ODFs from (at least) M = 3 q-shells. Parameterizing the problem in terms of b-values, $b_i=\tau q_i^2$, and choosing the physical units such that the diffusion time τ = 1 (see also Footnote ²), we obtain (for M = 3) the following system of equations for each direction:

$$\begin{array}{c}\lambda {\alpha }^{b_i}+(1-\lambda ){\beta }^{b_i}={\stackrel{\sim }{E}}_i,i=1,2,3\\ 0<\alpha ,\beta ,\lambda <1\end{array}$$

An analytical solution can be derived for the particular and reasonable case when the sequence 0, b₁, b₂, b₃ is an arithmetic progress.³ We describe this solution here, along with some regularization that guarantees the parameters to remain within the correct range.⁴ Without loss of generality, let us assume α ≥ β, and also choose the physical units such that, b₁ = 1, b₂ = 2, and b₃ = 3. Then,

$$\lambda {\alpha }^i+(1-\lambda ){\beta }^i={\stackrel{\sim }{E}}_i,i=1,2,3$$

We first define and calculate the following two quantities:

$$A:=\frac{\alpha +\beta }{2}=\frac{{\stackrel{\sim }{E}}_3-{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_2}{2({\stackrel{\sim }{E}}_2-{\stackrel{\sim }{E}}_1^2)},B:=\frac{\alpha -\beta }{2}=\sqrt{{\left(\frac{{\stackrel{\sim }{E}}_3-{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_2}{2({\stackrel{\sim }{E}}_2-{\stackrel{\sim }{E}}_1^2)}\right)}^2-\frac{{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_3-{\stackrel{\sim }{E}}_2^2}{{\stackrel{\sim }{E}}_2-{\stackrel{\sim }{E}}_1^2}}$$

The parameters are afterward computed as follows:

$$\alpha =A+B,\beta =A-B,\lambda =\frac{1}{2}+\frac{{\stackrel{\sim }{E}}_1-A}{2B}$$

However, we still need to ensure that they are real and in the correct ranges. One can verify that these conditions are satisfied by enforcing the following constraints:

$$\begin{array}{c}0<{\stackrel{\sim }{E}}_3<{\stackrel{\sim }{E}}_2<{\stackrel{\sim }{E}}_1<1,{\stackrel{\sim }{E}}_1^2<{\stackrel{\sim }{E}}_2,{\stackrel{\sim }{E}}_2^2<{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_3\\ {\stackrel{\sim }{E}}_3-{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_2<{\stackrel{\sim }{E}}_2-{\stackrel{\sim }{E}}_1^2+{\stackrel{\sim }{E}}_1{\stackrel{\sim }{E}}_3-{\stackrel{\sim }{E}}_2^2\end{array}$$

Thus, we can obtain the optimal values of α, β, and λ, by initially projecting Ẽ_is onto the subspace defined by these inequalities,⁵ and then computing the parameters.

2.4 Implementation

Our implementation of the ODF reconstruction from the estimated values of λ_k (û) and α_k (û) makes use of the spherical harmonic (SH) basis, $Y_l^m(\widehat{u})$, which is common for the analysis of HARDI data. The steps taken here to numerically compute Eq. (3) are similar to those described in [8]. Particularly, we use the real and symmetric modified SH basis introduced in [8], where SH functions are indexed by a single parameter j corresponding to l_j and m_j. We adopt a minimum least square scheme to compute a set of modified SH coefficients, c_j, such that ${\sum }_{k=1}^N{\lambda }_k(\widehat{u})\ln (-\ln a_k(\widehat{u}))\approx {\sum }_{j=1}^R{c}_j{Y}_j(\widehat{u})$, where R = (L + 1)(L + 2)/2, with L being the order of the SH basis (we chose L = 4 throughout our experiments). Next, since the SH elements are eigenfunctions of the Laplace-Beltrami operator, we compute ${\nabla }_b^2{\sum }_{k=1}^N{\lambda }_k(\widehat{u})\ln (-\ln a_k(\widehat{u}))$ by multiplying the coefficients c_j by their corresponding eigenvalues, −l_j(l_j + 1). Then, as suggested in [8], the Funk-Radon transform is computed by multiplying the coefficients by 2πP_lj(0), where P_l(·) is the Legendre polynomial of degree l, with $P_l(0)={(-1)}^{\frac{l}{2}}\frac{1\times 3\times \cdots \times (l-1)}{2\times 4\times \cdots \times l}$ for even l. Finally, given that $Y_1(\widehat{u})=\frac{1}{2\sqrt{\pi }}$, the SH coefficients of the ODF are derived as

$$c_j^{\prime }=\{\begin{array}{cc}\frac{1}{2\sqrt{\pi }}& j=1\\ -\frac{1}{8\pi }{(-1)}^{\frac{l_j}{2}}\frac{1\times 3\times \cdots \times (l_j+1)}{2\times 4\times \cdots \times (l_j-2)}{c}_j& j>1\end{array}$$

The implementation of the proposed formula for the true ODF is as straightforward as the one introduced in [8] for the original ODF formula.

3 Results and Discussion

To demonstrate the advantages of exploiting multiple q-shells in QBI, we first show the experimental results on an artificial example which consists of large diffusion values in two orthogonal directions. We synthesized diffusion images by sampling the sum of two exponentials, $E(\stackrel{\rightharpoonup }{q})=({|\sin \varphi |}^{q^2/2}+{|\cos \varphi |}^{q^2/2})/2$, on seven q-shells (b = q² = 1,2, …, 7) and in 76 directions, uniformly distributed on the hemisphere. Figure 1 illustrates the ODFs reconstructed from single q-shells for different b-values, three q-shells with mono-exponential model, and three q-shells with bi-exponential model. As can be observed, for the data acquired at low b-values (b = 1,2,3), the bi-exponential model using three q-shells is the only method correctly resolving the horizontal and vertical ODF peaks, corresponding to the strong ADC values in those directions (ϕ = 0°, 90°, 180°, 270°). It should be noted, however, that the drawback of such a more general model is its lesser robustness to noise, as low order models are often more robust (e.g., computing the average of a signal is more robust than estimating the actual signal). ODFs are shown as they are; no min-max normalization is used in any of the figures. Dark red represents negative values.

Fig. 1.

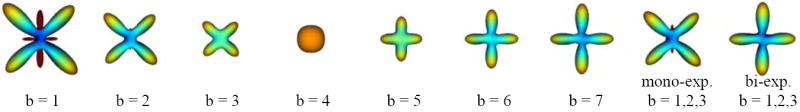
Results of the ODF reconstruction on synthetic data. Note how the bi-exponential model correctly resolves the maxima of the ODF from low b-values.

We also tested our method on the real HARDI dataset introduced in [12]. An anesthetized young Macaca mulatta monkey was scanned using a 7T MR scanner (Siemens) equipped with a head gradient coil (80mT/m G-maximum, 200mT/m/ms) with a diffusion weighted spin-echo EPI sequence. Diffusion images were acquired (twice during the same session, and then averaged) over 100 directions uniformly distributed on the sphere. We used three b-values of 1000, 2000, and 3000 s/mm², TR/TE of 4600/65 ms, and the voxel size of 1×1×1 mm³. The ODFs were reconstructed from the three q-shells using both mono-exponential and bi-exponential methods, and also from the single q-shells individually. Figure 2 depicts the results on a coronal slice through the centrum semiovale area, superimposed on the fractional anisotropy (FA) map. Note how using the bi-exponential method allows for more clear recovery of certain fiber bundles, such as callosal radiations and corticospinal tract, and better resolution of crossing areas (see outlined regions in Fig. 2). Figure 2 (top, right) is the only subfigure illustrating results by the original QBI (without r²).

Fig. 2.

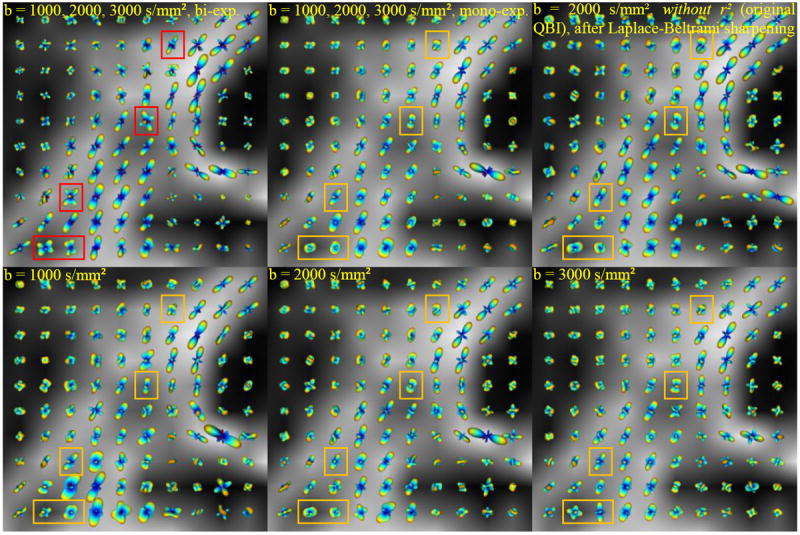
Reconstructed ODFs from the real brain data, shown on the FA map. The bi-exponential model ODFs (top, left) have been scaled down 1.5 times for better comparison. All the ODFs except those in (top, right) have been reconstructed considering the factor r²