Measuring Brain Connectivity: Diffusion Tensor Imaging Validates Resting State Temporal Correlations

Abstract

Diffusion tensor imaging (DTI) and resting state temporal correlations (RSTC) are two leading techniques for investigating the connectivity of the human brain. They have been widely used to investigate the strength of anatomical and functional connections between distant brain regions in healthy subjects, and in clinical populations. Though they are both based on magnetic resonance imaging (MRI) they have not yet been compared directly. In this work both techniques were employed to create global connectivity matrices covering the whole brain gray matter. This allowed for direct comparisons between functional connectivity measured by RSTC with anatomical connectivity quantified using DTI tractography. We found that connectivity matrices obtained using both techniques showed significant agreement. Connectivity maps created for a priori defined anatomical regions showed significant correlation, and furthermore agreement was especially high in regions showing strong overall connectivity, such as those belonging to the default mode network. Direct comparison between functional RSTC and anatomical DTI connectivity, presented here for the first time, links two powerful approaches for investigating brain connectivity and shows their strong agreement. It provides a crucial multi-modal validation for resting state correlations as representing neuronal connectivity. The combination of both techniques presented here allows for further combining them to provide richer representation of brain connectivity both in the healthy brain and in clinical conditions.

Introduction

Resting state temporal correlations (RSTC) between fMRI time-courses of distant brain regions were first observed [1] between contralateral motor cortices and later between other regions known to be strongly functionally connected, such as auditory and visual areas [2], language [3] and working memory systems [4]. The recognition of the importance of the default mode network (DMN) [5] and its anti-correlated counterpart the task positive network increased interest in resting correlations as a tool for defining functional systems in the working human brain. Not only are RSTC useful to improve the basic understanding of normal working brain, but their modifications e.g in the DMN are found in several clinical conditions [6–12]. Converging indirect evidence for the neuronal origin of resting state correlations in the fMRI timecourses is coming mainly from studies of physiology of MRI signal such as [13–15] on awake and anesthetized humans [16, 17]as well as monkeys [18] and are best reviewed in [19, 20], The basic physiological mechanism is still not well understood and the interpretation of changes of its intensity as representing modification of neural connections and information flow between brain regions remains uncertain. If, as is widely believed, the RSTC represents important information on neuronal connectivity between distant brain regions, these regions must use neuronal connections to carry the associated information flow. To allow for such communication between nodes of brain networks there must be a white matter fiber path connecting them. This pathway does not have to be direct, but nevertheless one expects that functional connectivity must in some manner be dependent on the strength of the relevant anatomical neuronal connection. It is therefore important to investigate similarities between connectivity measures obtained from the analysis of RSTC and anatomical measures of strength of neuronal connectivity.

In this paper we compare the strength of anatomical and functional connectivity. We expected that the connectivity measures obtained using resting correlations would be consistent with those obtained independently using diffusion tensor imaging (DTI). Such agreement would support the hypothesis that RSTC measures inter-regional connectivity.

Both DTI and temporal correlations in resting state fMRI offer the potential to investigate the neuronal connectivity of the working human brain. DTI measures the integrity of white matter tracts, while RSTC examines the similarities between spontaneous fluctuations that occur over time in distal gray matter areas. Both techniques use MRI scanning, but are independent, use different imaging sequences and employ different physical principles and physiological effects. Because those two techniques measure different aspects of neuronal connectivity, much can be learned by comparing how well they agree and where and why they differ.

Diffusion tensor imaging is based on analysis of the inhomogeneity of water diffusion. Multiple MRI images are taken that measure the ability of water to diffuse along different gradient directions. These measurements allow calculation of the diffusion tensor used to measure local anisotropy (usually expressed as fractional anisotropy, FA) that can be understood as representing the local “strength” of white matter nerve bundles. This tensor can be also used find the dominant direction of diffusion and thus to track white matter tracts in DTI tractography [21, 22]. DTI is widely used to investigate white matter fiber connectivity and thus the anatomical structure of distant brain connections. While local anisotropy measures are successfully used quantitatively, fiber tracking is most often used in a qualitative, descriptive manner. The quantification is performed successfully[23, 24] for specified white matter tracts but has not been employed in a global approach to investigate whole brain connectivity.

RSTC is now often used to quantify the strength of brain connectivity, yet little is understood about why and how such correlations represent the actual strength of neuronal connectivity between any given regions. While the presence of connecting neuronal fibers (anatomical connectivity) is necessary for regions to interact, the strength of functional connectivity can presumably be modulated in various mental states and does not have to be directly related to anatomical strength of fiber bundles that can be observed via DTI. For example the first and most prominent connections observed with resting state correlations were those connecting left and right motor cortex, and those regions are connected by direct white matter fibers.

The need to combine anatomical and functional connectivity has been recognized e.g. in [20], the excellent review of current work is found in the review [25]. The related work [26] was limited to neighboring gyri and found only weak trends towards agreement between techniques; so far no one has been able to compare them globally.

This paper presents a novel approach in which we use DTI tractography to estimate the strength of anatomical connection for any two voxels in the brain. We show how both techniques can be used to create a global gray matter connectivity matrix that provides a quantitative measure of connectivity strength for any two gray matter voxels in standard brain space. Such matrices can be compared spatially within subjects to compute how well they agree for any given subject or in comparison between average composite maps. The comparison can be also made between subjects, any pair of voxels or of regions can be analyzed across a subject population.

The agreement between both measures provides an important cross validation, as both techniques are still being developed and neither has been well established as a working tool for neuroscience. Having established the overall omnibus agreement between them, the local or population differences between connectivity measures can provide insights into a specific connectivity deficit, to characterize it as related to anatomical circuit disruption or to functional impairment of neuronal connectivity caused e.g. by neurotransmitter imbalances, failure of specific brain regions to activate, etc.

Methods

Subjects

Data was collected from 41 carefully screened healthy individuals aged 28±10 years, 23 male, who were participating as normal controls in various cognitive experiments approved by the Hartford Hospital IRB. Subjects were free of psychiatric disorders, as assessed by the SCID[27], were neurologically normal, not substance abusers and had signed informed consents.

Imaging

MR imaging was performed using a 3T Siemens Allegra scanner (Siemens, Erlangen, Germany). T1 structural images were collected for anatomical co registration and segmentation. Resting state data were collected during one run of 210 images at TR/TE 1500/28 msec, flip angle 65°, FOV 24 × 24 cm, 64 × 64 matrix, 3 by 3 mm in plane resolution; 5 mm slice thickness, 30 slices. DTI was performed using a twice-refocused spin echo [28]; TR/TE=5800/87 msec, FOV=20 cm, acquisition and reconstruction matrices = 128×96 and 128×128, 8 averages, diffusion sensitizing orientations in 12 directions with one b₀, b=1000 s/mm2, 45 contiguous axial slices with 3 mm section thickness. Data processing was performed using SPM2[29], DtiStudio (Johns Hopkins University, Baltimore, MD; http://cmrm.med.jhmi.edu) (for fiber tracking) and in-house software written using MATLAB.

Brain Segmentation

Standard SPM2 segmentation tool was used to segment each subject’s brain into three components representing gray matter, white matter and cerebrospinal fluid (CSF). Individual masks were converted into standard space with 4×4×4 mm resolution and composite masks were created for white and gray matter, each covering top 5000 voxels that were found most consistently in individual brain segmentations.

Resting State Data Analysis

The preprocessing of the resting state data generally followed that of [30, 31]. The first 5 images were dropped, data were motion corrected using SPM2, the remaining data were band-pass filtered to remove signal of frequencies higher than 0.1 Hz (non BOLD signal, mostly cardiac and respiratory noise) and frequencies lower than 0.005 Hz (mostly signal drift due to scanner instabilities). The data were intensity normalized for each slice (e.a. the intensity of each slice image was divided by its mean), motion corrected and spatially normalized to a standard template using SPM 2. Images were smoothed using Gaussian filter of FWHM 4mm and resampled to a resolution of 4mm³. Brain segmentation of the T1 data was performed for each subject using SPM2 tool and brain was divided into 3 components of white and gray matter and CFS. The correlation between time courses was calculated for all 5000×5000 voxel pairs within gray matter. The correlation was estimated using GLM model that removed 6 motion estimates. The final resting correlation map was transformed to a Z-distribution using Fisher’ transform. The distribution was fitted to a Gaussian and adjusted to a zero-centered normal distribution as in [32, 33].

Diffusion Tensor Imaging Data Analysis

Tractography was performed using DTIstudio software package. Fiber tracts were detected using standard FACT algorithm with stop criteria of FA > 0.25 and turning angle of 70 degrees. In average 40,000 fibers were detected for a single subject. After calculating fiber tracts, the fiber coordinates were normalized into standard space. Using SPM2, a nonlinear transformation was computed between the B0 image and the provided Montreal Neurologic Institute T2 template and the transformation was applied to each fiber coordinate.

While fiber tracking was performed in whole brain, the calculation of DTI connectivity matrix was limited to white matter only. White matter was defined my mask created for each study using standard SPM2 segmentation algorithm. To quantify the strength of anatomical connectivity between any two white matter voxels, we counted all tracts connecting them identified during the tractography step. This created a first order matrix of direct connectivity. Multiplying this matrix by itself creates a second matrix that counts all possible paths that can be built using two connected tracts. Further multiplications yields matrices counting any longer paths. The final outcome was calculated by summing the number of paths of each length (up to 8 segments) with a weighting that heavily penalized more indirect paths. The connectivity measure C_DTI(x,y), for any given voxel pair was then defined as the sum of contributions from all path lengths:

$${\mathrm{C}}_{\text{DTI}}(\mathrm{x},\mathrm{y})={\sum }_{\mathrm{i}=1:\mathrm{N}}2^(\text{-N})log(1+{\mathrm{C}}_{\mathrm{N}}(\mathrm{x},\mathrm{y})),$$

where C_N is number of paths of length connecting voxels x and y.

The inclusion of paths of various lengths has a twofold purpose. It allowed for the possibility of multisynaptic connections and also provided a statistical remedy for the problem of fibers crossing and or touching. If fibers are crossed or are closer than image resolution, the fiber tracking algorithm may stop (if crossed fibers cause the fractional anisotropy to be higher than set threshold), or can lead to tracking along the wrong fiber. Even if only one of possible fibers is detected in a region of crossing, the other will be included as higher order paths build of all fibers reaching the point of crossing. The weighting causes connectivity measures for voxels that can be connected by path of any length to be significantly larger that those than require higher number of segments. This lowers the possibility of false positives, as the connections that are composed of large number of segments that are more likely be artifactual are given a low connectivity value. Their inclusion does not change the status of more direct fibers as mostly connected but it expands the area in the connectivity space that is estimated. Even with as many as eight fibers allowed to form a path, only between 30% and 70% of voxels pairs are assigned a non-zero connectivity estimate.

The weighting factors that heavily favor the direct connections are working to ensure that the multi-path procedure allows to estimate connectivity for voxel pairs that are not connected by direct path, but its connectivity estimates are substantially lower that those of voxels connected by more direct path. We have checked that changing the length of path to a smaller value is not changing the main results of this paper. Even if only direct fiber path are included the main correlation between DTI and functional connectivity maps remain highly significant and while connectivity maps show less voxels, the regions shown as most strongly connected in multi path maps presented here are still shown as the main connected regions.

White matter - gray matter transition

An important problem in comparing the two methods here is that they are focused on different tissues; DTI fiber tracking estimates nerve fiber location by analysis of constraints to water diffusion occurring in white matter, while resting correlation between fMRI time courses is based on BOLD effects observed in gray matter. To resolve this problem we incorporated brain segmentation using standard SPM tools. We estimated DTI connectivity only for white matter and resting state only for gray matter. Given the final goal of estimating the strength of connectivity between cortical gray matter areas, we had to calculate the DTI connectivity for any given pair of gray matter voxels. The gray matter connectivity matrix for DTI was calculated from the white matter connectivity matrix as follows. For each gray matter voxel we have defined the neighborhood of closest white matter voxels. To define the size of this neighborhood for any given gray matter voxel, we found the nearest white matter voxel. The distance to this voxel was then increased by one voxel size (4mm) to create the neighborhood radius size (defined separately for each gray matter voxel). The white matter neighborhood was defined by all white matter within this radius. On average, this neighborhood had a radius of 12 mm and consisted of 5 white matter voxels. In some cases this led to inclusion of white matter voxels that were somewhat distant to our target gray matter voxel, but the rule was based on the premise that even gray matter voxels embedded far from the nearest white matter fibers have to gather input from some most proximate white matter fibers.

The resulting DTI connectivity matrix has a non Gaussian distribution; it was positively skewed and had a high (25–75%) proportion of zeros. We did not estimate the significance of individual DTI maps, the significance of all presented results was estimated using the between subject variance.

Geometrical distance correction

Both techniques outlined above tend to break down for proximate voxels. Resting correlations are elevated due to scanner-introduced correlations between nearest neighbors, interpolations and spatial smoothing. DTI based connectivity for gray matter relies on finding nearest white matter neighbors that were found on average 7 mm apart. For this reason we excluded all voxel pairs located closer than 24 mm from the analysis. Even for larger distances, both measures decreased with increasing distance and thus show strong negative correlation with distance; this correlation may introduce a false similarity. We corrected for this in two ways. All correlations between resting and anatomical connectivity were calculated as partial correlations with geometrical distance removed. In other analyses, such as relationships between mean functional and anatomical connectivity (as plotted in figure 4), data were binned for equal distance and later averaged between distances.

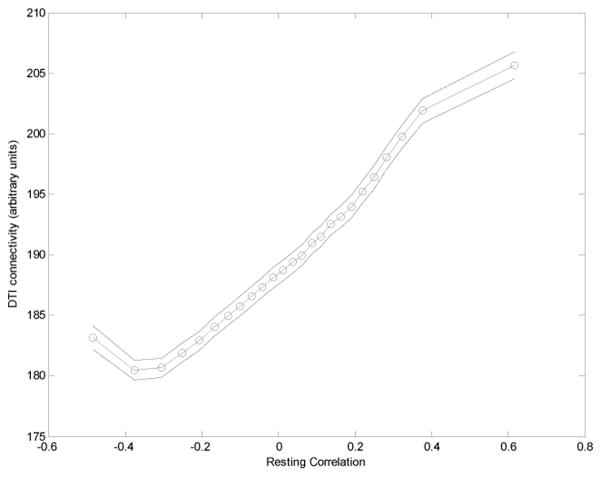
Figure 4.

Mean DTI estimated anatomical connectivity as a function of mean functional resting state connectivity. The whole connectivity matrix was divided based in the resting connectivity values into 25 bins The average value of DTI connectivity of each of those bins is plotted against mean resting connectivity. It is apparent that anatomical connectivity (measured by DTI) increases for most of the range, with exception of the lowest resting connectivity bin. This suggests that it is the resting connectivity and not its absolute value that corresponds to the actual functional connectivity, that negative resting connectivity should not be interpreted as representing real functional connectivity.

Regions of Interest

While most of the analysis was performed on global 5000×5000 connectivity matrices a set of Regions of Interest (ROI) was defined to allow for comparison of ROI seeded connectivity map such as shown on Figure 3 and to quantify the strength of ROI connectivity in ROIs presented in Table 3, 26 ROIs were defined to cover most of the gray matter using the WFU_PickAtlas free software [34] (http://www.ansir.wfubmc.edu) without modification. The sizes and Talairach coordinates of ROIs are presented Table 1.

Figure 3.

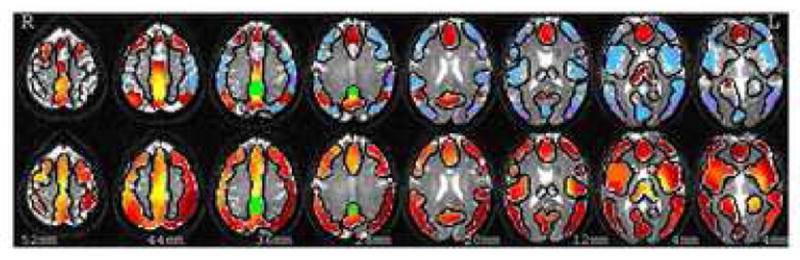
This illustrates connectivity maps for the posterior cingulate cortex (PCC). The top row represents the functional map based on the resting correlation analysis thresholded at p<0.001 (uncorrected). The bottom row shows the strength of anatomical connectivity estimated using DTI tractography. The connection between vACC and PCC can be seen in both maps. Green color represents the seed region.

Table 3.

Mean intensities for connectivity maps calculated for each predefined ROI used as a seed region.

ROI name	mean resting connectivity	Mean DTI connectivity	Mean correlation (individual subjects)	Correlation between composite maps
Angular_L	−0.027#	12.10#	0.06	0.39
Angular_R	0.008*	46.31	0.11**	0.43
CingAnt	0.018**	64.26*	0.23**	0.55
CingPost	−0.020	91.58*	−0.01	0.24
Cingulate	0.084**	96.33*	0.23**	0.52
Cuneus	−0.049##	37.13#	0.12**	0.45
IFG_L	0.004**	38.86#	0.10**	0.35
IFG_R	0.003*	65.69	0.21**	0.38
IPL_L	0.009**	15.55#	0.10**	0.45
IPL_R	0.047**	69.21	0.14**	0.42
Insula_L	0.051**	84.94*	0.17**	0.49
Insula_R	0.047*	63.95	0.25**	0.47
Lingual	−0.075#	34.08#	0.15**	0.45
MFG_L	0.008*	56.47	0.15**	0.42
MFG_R	0.011*	71.72*	0.25**	0.47
MOcG_L	−0.171#	38.36#	−0.04	−0.11
MOcG_R	−0.123#	13.56#	−0.01	−0.14
MTG_L	−0.067#	35.40#	0.07*	0.26
MTG_R	−0.040#	19.27#	0.08**	0.36
MedFG	0.005	67.37	0.20**	0.45
Postcentral_L	0.003	27.37#	0.09**	0.32
Postcentral_R	0.019*	90.23*	0.15**	0.31
Precuneus	0.032*	68.14	0.14**	0.53
TG_L	−0.035#	22.51#	0.10**	0.39
TG_R	−0.018	48.86	0.15**	0.35
Thalamus	0.023	113.63*	0.22**	0.58

First two columns represent the mean (averaged between all subject, across the brain) strength of anatomical (DTI) and functional (RSTC) connectivity. Those connectivity strengths were compared to the mean of whole brain gray matter as a null hypothesis. Significantly increased correlation is represented as ** for p<0.001, and * for p<0.01 significance levels. Correlations significantly smaller than mean are marked as ^## p<0.001 and ^# p<0.01. The third column represents the spatial or increased correlation between connectivity maps calculated for each subject separately and compared to null hypothesis of zero correlation. The fourth column shows correlations between composite (averaged between subjects) maps of connectivity. Spatial correlations are calculated as partial correlation with effect of geometrical distance excluded.

Table 1.

The anatomically defined regions with Talairach coordinates of its center and sizes.

ROI name	X=	Y=	Z=	Size (mm^3)
Angular L	−46	−62	36	1040
Angular R	45	−60	37	1168
CingAnt	0	31	17	1376
CingPost	0	−47	33	480
Cingulate	0	−22	45	1248
Cuneus	5	−77	26	1216
IFG L	−45	22	12	1976
IFG R	45	22	12	1864
IPL L	−52	−43	39	1032
IPL R	50	−42	38	760
Insula L	−40	−5	3	1568
Insula R	40	−7	4	1648
Lingual G.	5	−70	−1	1032
Middle FG L	−35	33	31	2496
Middle FG R	34	31	32	2256
Med. Occ FG L	−44	−76	4	832
Med. Occ FG R	44	−77	4	832
Middle TG L	−53	−47	5	1976
Middle TG R	53	−50	6	1624
Medial FG	−1	34	28	3168
Postcentral L	−54	−25	36	1104
Postcentral R	54	−26	35	672
Precuneus	2	−62	50	1168
Sup. Temp G L	−54	−22	8	656
Sup. Temp G R	54	−20	8	664
Thalmus	0	−21	5	592

Results

Overall connectivity matrix agreement

The agreement between Resting State and DTI connectivity matrices was calculated for each subject by calculating the partial correlation between anatomical and functional 5000×5000 connectivity matrices with geometrical distance removed.

Analyzed for each subject individually correlation between both methods was significant at p<0.00001 for 39 out of 42 subjects, the average Pearson r -value was 0.18 ± 0.10. In the group between-subjects correlation analysis this effect was found to be highly significant (p< 0.0001 (T=5.6 N=41). This correlation was found using whole correlation matrices, and realatively low r-value can be understood because it includes significant voxel to voxel variablility and all voxel pairs that have very weak or nonexistent neuronal connectivity but still exibit non-zero resting correlations.

To better evaluate the contribution coming from voxel pairs that can be connected using fiber path built from less than 9 fibers we subdivided whole DTI connectivity matrix into subsets depending of the shortest multi-fiber path that can connect them. Table 2 presents sizes of those subsets, mean values of both connectivity measures and the correlation between resting and functional connectivity calculated for each component separately. First important observation is that even using as long as 8 fiber long paths only 31% of all possible voxel pairs can be connected. Next one can see that even for the weakest connected component the correlation between functional and resting connectivity is substantial. This correlation is increasing for stronger connections up to voxel pairs connected by shorter fiber path up to 2 fibers, and then begins to falls down. This last dip is most likely caused by the saturation effect, there may be not much variance in connectivity measures between voxels that are most strongly connected. The mean resting connectivity for each component is increasing only slightly but monotonically across whole range of components.

Table 2.

Connectivity matrix can be subdivided into components defined by shortest possible fiber path connecting voxel pairs. The size, mean DTI and Resting connectivity and the mean correlation between resting and DTI connectivity are presented. Clearly inclusion of voxel pairs that can only be connected by a multi-fiber path is extending the connectivity measures to obtained covareage of substantial part of whole connectivity space. Even the 8^th component composed of weakly connected voxel pairs that require 8 consecutive fibers to connect them still shows substantial correlation with resting correlation connectivity estimate.

Shortest path (Fibers #)	Component size (% of conn. matrix)	DTI conn.	Rest conn.	DTI-Rest correlation
1	1	154	0.562	0.26
2	2	150	0.549	0.34
3	5	127	0.547	0.40
4	6	100	0.546	0.40
5	8	81	0.543	0.33
6	4	46	0.540	0.35
7	3	26	0.538	0.23
8	2	10	0.537	0.13
No fiber path	69	0	0.530	0

Overall agreement between seeded connectivity maps

To better understand the extent of the agreement between both connectivity matrices we analyzed the spatial agreement between their columns, representing the connectivity maps created using each individual voxel as a seed region. Each voxel seeds two connectivity maps, one for each technique. Thus, spatial correlation between those maps measures the agreement between both connectivity measures originating at this voxel. Such spatial correlation maps calculated for each subject were combined using the between-subject variance for a significance estimate. Results are presented on Figure 1. Voxels at p<0.05 are represented by yellow or red when they showing significant correlation between maps from two modalities. One can observe that most of the gray matter voxels create significantly similar connectivity maps with the exception of right middle occipital gyrus.

Figure 1.

Map of the correlation between Resting State and anatomical connectivity maps. Each activated voxel represents a seed for which anatomical and functional originating connectivity maps are significantly similar. Red color represents voxels at p<0.05 and yellow p<0.001. Most of gray matter is found to seed connectivity maps that agree significantly. In this and following figure the Talairach slices presented are at z= 52 to −4 mm, with skip of 8mm.

Another representation of this correlation is presented in Table 3 where correlation is calculated between maps seeded in anatomically defined regions of interest; this was significant for all but 4 of 26 regions.

Global Connectivity Maps

As it is not possible to illustrate the entire multi-dimensional connectivity matrix, we chose several representations of global connectivity strength. The mean global connectivity maps are presented in Figure 2. For each matrix we calculated a map of average connectivity by averaging constituent columns of the matrix, so that each voxel represents the mean strength of all connections from this voxel to all other 5000 gray matter voxels. Both connectivity and resting connectivity matrices were calculated for each subject separately and the significance calculated for resting connectivity using between-subject comparisons thresholded at p<0.001 uncorrected. For display purposes the anatomical connectivity matrix (positively defined) was normalized and thresholded to leave the same number of activation voxels. Those regions that are strongly connected are similar, with the main exception being in insular regions, that are more functionally connected but show weak anatomical connection in the left hemisphere and in thalamus, which has strong anatomical but no corresponding functional connectivity.

Figure 2.

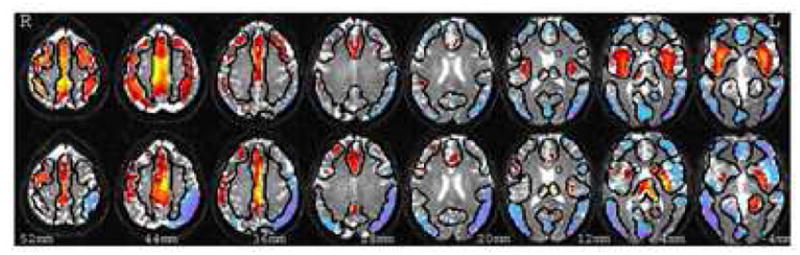
Maps of mean connectivity (voxel intensity shows average of connectivity measure between this voxel and all other gray matter voxels). The upper row represents functional connectivity calculated from resting state correlations. Significance was estimated from between-subject variance p<0.001. The lower row represents the (positively defined) anatomical connectivity normalized to zero mean for better comparison.

The regions showing strongest overall connectivity overlap for both techniques and are also those showing the strongest spatial correlation, shown as yellow in figure 1. This would be expected if both techniques measure connectivities originating from the same neuronal origin and stronger overall connectivity allows the similarity to become more significant if the signal to noise level is stable.

Region of Interest Analysis

Table 3 Shows mean resting and anatomical connectivity between each anatomically defined region and whole brain. The last column represents the spatial correlation between the resting and DTI maps seeded by this region.

Nearly all regions (22 out of 26) show highly significant (p<0.001) correlation between maps from both modalities. As a general rule, regions that are most strongly connected to the rest of the brain produce correlation maps that are most correlated between modalities.

To show the example of similarities between connectivity maps, figure 3 presents resting and anatomical connectivity maps for one of the defining regions of the default mode network, the posterior cingulate cortex. The main portions of the Default Mode Network can be seen in the resting connectivity map. Inspection of these regions shows that resting connectivity is underlined by anatomical connectivity, regions with high positive resting connectivity have increased anatomical connectivity, while regions with negative resting connectivity (that are sometimes viewed as showing functional connectivity as well) have lowest anatomical connectivity.

Interregional discrepancies between Functional and Anatomical connectivity

While there is an significant overall agreement between both measures of connectivity the ROI analysis can show interregional connections that exhibit disruption of this agreement. Mean value of connectivity maps for voxel connecting any two regions of interest was rank ordered to detect region pairs for which the connectivity measure do not agree. The high resting connectivity and low anatomical connectivity was observed most prominently for connection linking Right and Left Inferior Frontal Gyri (IFG), as well as those linking right to left Insula and for connections between left and right IFG and Right Angular Gyrus. The interpretation of this discrepancy is not obvious. Since tracts connecting those regions are passing through tight white matter regions with multiple fiber crossing and “kissing” the low anatomical connectivity may possible be an artifact caused by use of deterministic tracking algorithm for detecting primary fibers that may not be completely compensated by adding multi-fiber paths. Another possible explanation may be that resting connectivity may be artificially inflated for contra lateral regions due to similarities in their location in vasculature tree.

High anatomical connectivity and low resting connectivity was noted for connection between left Insula and left medial occipital frontal gyrus as well as for connection between left Insula and Medial Frontal Gyrus (MFG). This finding as well as the surprisingly strong connection between left Insula and PCC observed in lower row on figure 3 may be an artifact caused by the proximity of Insula to uncinate fasiculus that may be not connected to insula but may represent the closest white matter to several of insular gray matter voxels and thus may artificially inflate the DTI based estimate of the connectivity of insula. Another possible explanation for the fact that functional connectivity is lower than anatomical connectivity for those region pairs, maybe the presence of localized negative temporal correlations, like those reported in [31], that lower the estimate of functional connectivity. This effect would have to be localized since the findings reported in the following paragraph show that overall, globally, negative correlations tend to not represent anatomical connectivity.

Positive and negative resting correlations

To further characterize the relationship between both methods we analyzed their correlations as a function of resting connectivity. We divided the connectivity matrix into 25 bins of similar resting correlation. In Figure 4 we plotted the mean DTI connectivity for each resting correlation bin. One can see near-monotonic increases across most of the range, with a small deflection for lowest (most negative) values of resting connectivity. This means that resting connectivity predicts anatomical connectivity not only for connections that stand out as the most significant but across most of the brain, with the possible exception of the most strongly negative resting correlations, which display a rise in the anatomical connectivity.

Discussion

Overall agreement for within subject and averaged analysis

Our results show significant agreement between DTI and resting connectivity estimates of strength of connectivity. As predicted, this agreement is stronger for regions showing high connectivity (by either measure). Anatomical connectivity increases with resting connectivity across most of the range of resting correlations, with the possible exclusion of about 4% of voxel pairs with smallest (most negative) resting correlations were it rises slightly. This suggests that not only connections with highest values of resting connectivity represent neuronal connectivity. In the bulk of range of resting connectivity values that are usually interpreted as representing random Gaussian noise, resting connectivity is still influenced by the same resting correlation mechanism.

Both the mean connectivity maps (Figure 2) and also maps showing connectivity of individual regions (such as Figure 3) show remarkable similarity across both techniques. Overall agreement is highest for regions with strongest connectivity, suggesting that discrepancies between maps are mostly due to noise, but that those discrepancies may also represent a more subtle connectivity relationship. That is, while in general stronger anatomical connectivity is associated with (i.e. predicts, causes or allows for) stronger functional connectivity, not all connections obey that precise pattern. Some of the differences may originate from the different sensitivities of both techniques and when recognized can be employed to enhance the connectivity analysis. For example, lack of functional connectivity observed in the thalamus may be caused by the weak sensitivity of resting correlation in inferior portions of the brain, where additional noise due to cardiac and respiratory related brain pulsation is most prominent. Other differences seen in Table 3 are seen mostly in the connectivity of left IFG and left IPL. Values there are significantly above average for resting connectivity and significantly below average for anatomical connectivity. Further analysis of such discrepancies can allow us to characterize connectivity in an improved and more multidimensional manner, encompassing both anatomical and functional components.

While the general agreement we delineate tends to support the validity of both techniques, it is also of great interest to examine where the connectivity estimates from these methods differ; in fact this is where conjunction of both approaches can be most useful. In longitudinal studies of normal or pathological development, as well as in comparing populations, divergence between DTI and resting correlation connectivity may help understand the biological substrate of changes. While both methods assess particular aspects of overall brain connectivity, a dominant decrease of DTI connectivity would suggest white matter abnormality, while conversely, resting state connectivity deficits may indicate network problems possibly originating in dysfunction of crucial network nodes, altered neurotransmitter levels or deviant function, rather than in direct signal propagation.

Conclusions

Anatimical connectivity measures agrees with resting connectivity but does not explain it compeletely

Results show a strong similarity between brain connectivity estimates obtained from two very different imaging techniques. This agreement reaches far beyond the fact that both techniques show connectivity in major systems such as the default mode network or the motor-sensory system. The agreement between connectivity maps is very high for strongly connected regions and weaker (but still significant) for most other region pairs. This observation supports the widely accepted but not well proven hypothesis that the resting state correlations do represent the strength of neuronal connections in working brain. At the same time it validates the technique of integrating DTI detected fibers tracts that was introduced in this study to create global DTI based connectivity matrix of gray matter.

Most of the negative resting state correlations represent a decrease in the anatomical connectivity

Anatomical connectivity increases for most of the range of resting connectivity, with the possible exception of small negative tail, where it begins to rise again for most negative correlations. The voxel pairs exhibiting the negative resting correlation are characterized by very low DTI anatomical connectivity. This suggests that negative resting correlations may not represent actual negative synchronicity between spontaneous fluctuations but may be an effect of global normalization and simply represent left tail of random distribution of noise. The preprocessing approach used here and in typical analyses of resting state data may be overzealous in eliminating potential artifacts through normalization for mean intensity on a slice or volume basis. It is possible that global distribution of correlation values after the exclusion of artifacts does not resemble a Gaussian distribution of random noise, with only increased tails representing the “real” neuronal connectivity, but that neuronal connectivity is present and causing positive correlation over most of the brain.

Potential for clinical applications

DTI is widely used to help assess multiple white matter diseases. It has also been used to show deficiencies of white matter integrity in multiple conditions including schizophrenia[35], autism[36], Alzheimer’s Disease and mild-cognitive impairment (MCI) [37]. Measures of resting connectivity have not been yet as widely applied, but have also been shown decreases in conditions such as Alzheimer’s Disease and MCI[9], autism[8] attention deficit disorder[38] and schizophrenia[7]. Demonstrating the anatomical underpinning of such resting correlations helps to underpin this measurement as a valid tool to investigate brain networks and their impairments.

The future utility for clinical applications will come from the combination of both techniques. Since the method of quantification of DTI connectitivity proposed here was design mostly to asses the connectivity of gray matter for the direct comparison with functional connectivity it lacks high spatial resolution that can be obtained from DTI measurements. It can be still applied to analyze the relative strength of DTI and functional between cortical region of interest. Alternatively a more focused measure of DTI connectivity may be devised that will retain more of its high spatial correlation to allow for more detailed voxel level comparison. This may allow one to go beyond characterizing certain conditions as being generally related to impaired brain connectivity. For example if DTI based measurements of connectivity are lowered it suggests the impairment of fiber tracts and thus weakened neuronal connections. Reduced functional connectivity in the absence of reduction of anatomical connectivity would point to impaired network nodes that fail to utilize existing but impaired neuronal connections effectively. Direct combination of both methods can also be used to improve the specifity of defining regions of interest that are to be investigated in functional activation studies that reaching beyond localization and to description of network function.