A Systematic Review of Methodology: Time Series Regression Analysis for Environmental Factors and Infectious Diseases

Abstract

Background: Time series analysis is suitable for investigations of relatively direct and short-term effects of exposures on outcomes. In environmental epidemiology studies, this method has been one of the standard approaches to assess impacts of environmental factors on acute non-infectious diseases (e.g. cardiovascular deaths), with conventionally generalized linear or additive models (GLM and GAM). However, the same analysis practices are often observed with infectious diseases despite of the substantial differences from non-infectious diseases that may result in analytical challenges. Methods: Following the Preferred Reporting Items for Systematic Reviews and Meta-Analyses guidelines, systematic review was conducted to elucidate important issues in assessing the associations between environmental factors and infectious diseases using time series analysis with GLM and GAM. Published studies on the associations between weather factors and malaria, cholera, dengue, and influenza were targeted. Findings: Our review raised issues regarding the estimation of susceptible population and exposure lag times, the adequacy of seasonal adjustments, the presence of strong autocorrelations, and the lack of a smaller observation time unit of outcomes (i.e. daily data). These concerns may be attributable to features specific to infectious diseases, such as transmission among individuals and complicated causal mechanisms. Conclusion: The consequence of not taking adequate measures to address these issues is distortion of the appropriate risk quantifications of exposures factors. Future studies should pay careful attention to details and examine alternative models or methods that improve studies using time series regression analysis for environmental determinants of infectious diseases.

Introduction

Time series regression analysis is one of the most common methods practiced in environmental epidemiology studies. Time series analysis usually follows one population or community throughout the study period and requires health outcome (dependent) and exposure (independent) variables measured repeatedly over time and at the fixed interval (e.g. on daily or weekly basis). In the analysis, impacts of exposures on outcomes are evaluated by comparing the changes over time in the rates of outcome occurrences and the corresponding level of exposures. Because within-one-community comparison does not require the denominator data unless the targeted population changes over time [1], the advantages of the analysis is that individual level confounders and uncertainty of the covered area for study are not considered as problems. Instead, time-varying covariates are considered important confounding factors.

Time series analysis is typically suitable for investigations on relatively direct and short-term effects of exposures. In environmental epidemiology studies, it has long been applied to assess the impacts of air pollution and meteorological variability on acute non-infectious diseases that are routinely collected in database, that is, deaths, hospital admissions or visits [2]. Conventionally, generalized linear models (GLMs) and generalized additive models (GAMs) are the standard models for the analyses [1–3].

Though time series analysis in environmental epidemiology studies has been widely used for non-infectious diseases, it is also being used for infectious diseases in the same manner. Infectious diseases are substantially different from acute non-infectious diseases (e.g. cardiovascular deaths, cardiac arrests, asthma attacks) in the nature of causal mechanisms and the population at risk. More precisely, the distinct difference from non-infectious diseases is that the incidence of infectious disease often dependent on transmissions among individuals, the presence of intermediators (e.g. vectors), and temporary or permanent immunity protection. These differences might consequently result in statistical challenges when applying infectious diseases to the conventional time series method, yet no study to date has summarized the potential considerations. The present article is a review of the literature for studies in which associations between infectious disease and environmental factors are evaluated with GLMs and GAMs, aiming to characterize the potential methodological challenges involved in the analyses. Other time-series methods developed from econometrics [4] and forecasting such as autoregressive integrated moving average (ARIMA) are not considered here because of the different modeling structure and required model components. The literature review was conducted following the guidelines of Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) [5].

Time series regression model

Here we first introduce a brief overview of the time series regression model. An outcome of interest is usually a count of disease occurrence. The outcome counts and measured exposure factors of interest should be in order of time and at the fixed interval in dataset. The most common regression model is Poisson regression model, also known as GLM with Poisson distribution, which can be expressed as follows:

Y_t~Poisson(μ_t)

log(μ_t) = ζ₀ + ζx_t + Σ_p η_pz_p,t + f(t).

where Y is the disease count at the time t, ζ₀ is the intercept, f(t) denotes the smoothing function of time to remove the effects of seasonality and long term trend, x_t represents the exposure factors, and Σ_pη_pz_p,t denotes other time-varying covariates [6]. Adjustments of seasonal variation and long term trend in a model characterize the traditional time series method and are required to differentiate their effects from the short-term associations between exposures factors and outcome of interest. For the seasonal variation adjustments, alternatively, the time stratifications and trigonometric terms (Fourier) are widely used. Further details about time series regression models are described elsewhere [6].

Method

Literature search strategy

Our aim was to summarize the characteristics of analyses of studies using GLMs or GAMs to assess associations between infectious diseases and environmental factors. We conducted systematic reviews on published articles in the online electronic database of PubMed (http://www.ncbi.nlm.nih.gov/pubmed). Since the exposure factors of our interest were particularly climate or weather, we limited our review to the climate-sensitive infectious diseases for targeted diseases in this study, that is, malaria, cholera, dengue, and influenza. In the search on PubMed, the following key designated terms were included: “weather” OR “climate” OR “temperature” OR “rainfall” OR “precipitation” OR “humidity” AND the name of each disease (“malaria”, “dengue”, “cholera” and “influenza”). For further specific identifications, studies were restricted to journal articles written in English and targeting human health outcomes through the additional filter functions of “article types”, “language” and “species” on PubMed. Publications dated from January 1st, 1995 to November 5th, 2013, identified as of December 4th, 2013, were included in the search.

Selection of articles

A total of 2,598 reports was found through the designated search on the online database. Since a large number of articles was identified, precise measures were taken for screening and eligibility assessments (Fig. 1). After the duplicates were removed, two authors screened the titles of the studies to determine whether the studies looked at associations between infectious diseases and weather or climate factors. The articles selected by either one of two authors in the title screening process were then re-assembled, and the following procedure of eligibility selections was conducted in two steps by one author. First, the abstract and method sections were examined to determine whether GLMs or GAMs were used as analysis methods, and studies apparently using irrelevant methods were discarded. In the second step, the full text of the rest of the studies was reviewed to confirm that the purpose and analysis method of each study were suitable for our literature review.

Fig. 1.

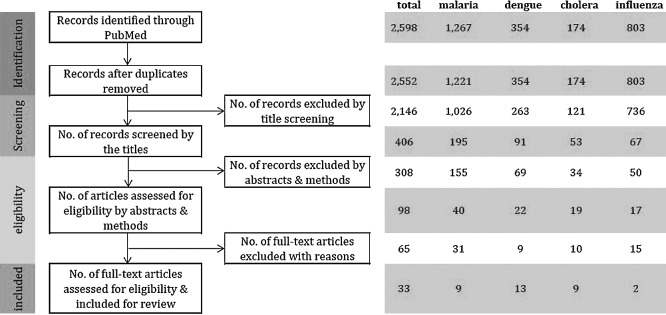
PRISMA diagram flow of systematic review.

Review schemes for study designs and analytical methods

In order to pursue the strategic reviews of analytic methodology, we have set certain schemes to investigate. The 13 schemes are as follows; author and publication year; study period; study location; age and group of targeted population; outcome of interests; exposure factors; statistical models; time unit of data; confounder controls (season, trend, and others); variation in the susceptible population; autocorrelation; lag estimate of exposure factors; overdispersion.

Results

Of the 2,598 reports initially identified by our designated electronic search on PubMed, 33 articles were selected for our review at the end of the eligibility evaluation. These 33 articles consist of 9 malaria [7–15], 13 dengue [16–28], 9 cholera [29–37], and 2 influenza [38, 39] studies (Table 1). Table 2 shows the locations in which the reviewed studies were conducted. The study locations are mostly low- and middle-income countries in tropics, as our targeted diseases, except for influenza, are most prevalent in the areas [40].

Table 1.

	Ref.	Author, year	Study period (year)	City (Country)	Exposure	Statistical model	Unit of data	Confounder control			Variation in susceptible population	Autocorrelation*	Assessed Lag*	Overdispersion
								Season	Trend	Others
Malaria	7	Kim, et al., 2012	2001–2009	the capital region (Korea)	temperature, RH, diurnal temperature range (DTR), duration of sunshine	GLM Poisson	weekly	Fourier terms	year	—	—	—	0 to 8 weeks single lag (SL) for all cliamte parameters, rainfall 0 to 60 days (SL)	Overdispersion parameter included
	8	Jusot, et al., 2011	2000–2003	Magaria (Niger)	rainfall	GAM negative binomial (NB)	daily	penalised cubic regression spline		religious celebrations, days of the week, holidays, min & max temp, RH	—	penalised cubic regression spline is to minimize the autocorrelation	0 to 40 days (SL)	NB distribution model
	9	Haque, et al., 2010	1989–2008	Rangamati district, (Bangladesh)	temperature, rainfall, humidity, normalized difference vegetation index (NDVI), SST of the Bay of Bengal, NINO3	GLM NB	monthly	month	year	—	—	AR(1) included	all (except NINO): 0 to 3 months moving average (MA), NINO3: 0 to 3, 4 to 7, 8 to 11 (MA)	NB distribution model
	10	Xiao, et al., 2010	1995–2006	Hinan (China)	temperature, rainfall, RH	Poisson regression	monthly	—	—	population	—	the cases for the previous months	0 to 3 months (SL)	—
	11	Olson, et al., 2009	1996–1999	Brazilian Amazon region	temperature, rainfall	Poisson regression	monthly	natural cubic spline		population (offset)	—	—	—	—
	12	Hashizume, et al., 2008	1982–2011	western Kenyan highlands	DMI (diapole mode index), NINO3, rainfall	GLM Poisson	monthly	month	year	population not considered since trends in malaria rates are included in the model	—	AR(1) included	0 to 6 months (SL)	included overdispersion parameter
	13	Teklehaimanot, et al., 2004	1990–2000	Ethiopia	temperature, rainfall	Poisson regression	weekly	week (of the year)	—	—	—	AR included (based on a moving average of the number of cases four, five and six weeks before)	rainfall: 4 to 12 weeks (MA) temperature: 4 to 10 weeks (MA)	—
	14	Teklehaimanot, et al., 2004	1990–2000	Ethiopia	temperature, rainfall	Poisson regression	weekly	time variable	—	district, interaction between time and district	—	—	rainfall: 4 to 12 weeks (MA) temperature: 3 to 10 weeks (MA)	—
	15	Abeku, et al., 2003	1986–1993	Ethiopia	temperature, rainfall	GLMM (mixed model)	monthly	—	—	log (numer of cases in the previous month) was included as sector-specific random effects	—	log (numer of cases in the previous month) as sector-specific random effects handles spatial and temporal autocorrelations.	rainfall: 1 and 2 months distributed lag (DL) temperature: 1 month (SL)	—
Dengue	16	Hii, et al., 2012	2000–2011	Singapore	temperature, rainfall	Poisson regression	weekly	season parameter	trend parameter	population (offset)	—	the past number of cases	12 to 24 weeks (SL)	developed Poisson regression model that allowed overdispersion
	17	Gomes, et al., 2012	2001–2009	Rio de Janeiro (Brazil)	rainfall, temperature, proportions of days in the month: mean temperature < 22(°C), 22 ≤ mean temperature < 26, 26 ≤ mean temperature	GLM Poisson & NB	monthly	—	year	population × the number of days in the month (offset)	—	—	1 and 2 months (SL)	NB distribution model
	18	Lowe, et al., 2011	2001–2009	Southeast Brazil	rainfall, temperature, Oceanic Niño Index (ONI)	GLMM NB	monthly	month	—	expected number (offest): the population × global dengue rate. cartographic, demographic, and economic variables	inclusion of unstructured random effect to be surrogate for not only population immunity, but quality of healthcare services and local health interventions	the log standardised morbidity ratio lagged by 3 months was included in the model.	temperature and rain: 3 month (MA), ONI: 4 month (SL)	NB distribution model
	19	Hashizume, et al., 2012	2005–2009	Dhaka (Bangladesh)	river levels, temperature, rainfall	GLM Poisson	weekly	Fourier terms	year	public holidays	—	AR(1) included	assessed up to 26 weeks	used generalized linear Poisson regression models allowing for overdispersion
	20	Earnest, et al., 2012	2001–2008	Singapore	temperature, rainfall, RH, ours of sunshine and hours of cloud, Southern Oscillation Index (SOI)	Poisson regression	weekly	sinusoidal terms	—	—	—	AR(2) included	0 to 12 week (SL)	included overdispersion parameter
	21	Pham, et al., 2011	2004–2008	Dak Lak province, Vietnam	temperature, duration of sunshine, rainfall, RH, larval index (household index, the container index, and the Breteau index)	Poisson regression	monthly	Seasonal components	Trend components	—	—	AR(1) included	—	—
	22	Pinto, et al., 2011	2000–2007	Singapore	rainfall, temperature, RH	Poisson regression	weekly	—	—	—	—	—	0 to 40 week (SL)	—
	23	Shang, et al., 2010	1998–2007	3 areas in Southern Taiwan (Tinan, Kaohsiung, and Pingtung)	temperature, RH, wind speed, rainfall, rainy hours, sunshine accumulation hours, sunshine rate (from sunrise to sunset), sunshine total flux, imported dengue cases	Poisson regression, and GLM NB	bi-weekly	Fourier terms	—	area, population desity	—	—	assessed 1 to 12 bi-weeks which is equivalent to 2 tp 24 weeks (SL)	NB distribution model
	24	Chen, et al., 2010	1998–2008	Taipei and Kaohsiung (Taiwan)	temperatures, rainfall intensity, RH	Poisson regression, GEE	monthly	—	—	the percentage of monthly Breteau index (BI) levels > 2 (index for the potential transmission risk)	—	—	0 to 4 months (SL)	—
	25	Tipayamongkholgul, et al., 2009	1996–2005	all provinces in Thailand	the multivariate ENSO index (MEI), the sea level pressure index (SLP), temperatures, RH, wind speed	quasi-Poisson or NB	monthly	sinusoidal terms		population (offset), province, population density	—	the cases of the previous month	1 to 12 months (SL)	used quasi-Poisson or NB
	26	Lu, et al., 2009	2001–2006	Guangzhou (China)	temperatures, rainfall, RH, wind velocity	Poisson regression, GEE	monthly	—	—		—	AR(1) included	0 to 3 months (SL)	included overdispersion parameter
	27	Johansson, et al., 2009	1986–2006	all manicipalities in Puerto Rico	temperatures, rainfall	Poisson regression	monthly	natural cubic spline on observational time		population (offest), % of population below the poverty line	—	—	temperature: 0 to 2 month (DL), rain: 1 to 2 (DL)	—
	28	Thammapalo, et al., 2005	1978–1997	73 provinces in Thailand	rainfall, rainny days, temperatures, RH	Poisson regression	monthly	Fourier terms	time in month (t) and (t)2	—	—	the lagged residual series is included	none	—
Cholera	29	Hashizume, et al., 2011	1993–2007	Dhaka (Bangladesh)	DMI, NINO3, SST and SSH of the northern Bay of Bengal	GLM negative binomial (NB)	monthly	month	year	—	not considered	lagged model residual included (Brumback method)	0–3, 4–7, 8–11 months (MA)	NB distribution model
	30	Rajendran, et al., 2011	1996–2008	Kolkata (India)	temperature, RH, rainfall	GLM, SARIMA	daily	exponential smoothing function		—	—	—	—	—
	31	Hashizume, et al., 2010	1983–2008	Dhaka (Bangladesh)	temperature, rainfall	GLM Poisson	weekly	Fourier terms	year	sampling proportion	—	—	high rain: 0–8 (MA), low rain: 0–16 (MA), temperature: 0–4 (MA)	included overdispersion parameter
	32	Paz, 2009	1971–2006	8 African countries: Uganda, Kenya, Rwanda, Burundi, Tanzania, Malawi, Zambia, and Mozambique	air temperature, sea surface temperature (the western Indian Ocean), anomaly air temperature	Poisson regression	yearly	—	—	—	—	AR1 = cor (Yt, Yt-1) is taken into account in the estimation using generalized estimating equations.	0 and 1 year (SL)	—
	33	Constantin de Magny, et al., 2008	1997–2006	Matlab (Bangladesh) and Kolkata (India)	SST, rain, chlorophyll a concetration	GLM quasi-Possion	monthly	quarter periods of a year	—	—	—	log (number of cases for the previous month)	0 and 1 month (SL)	quasi-Poisson model
	34	Martinez-Urtaza, et al., 2008	1994–2005	Peru	SST, sea height anmoaly, heat content above 20°C	GAM NB & ridge regression with penalties to identify zero-inflation	weekly	thin plate regression splines		—	—	observational time × smoothing (when autocorrelation was seen in residuals) included	1 to 5 weeks (SL)	NB distribution model
	35	Luque Fernández, et al., 2008	2003–2006	Lusaka (Zambia)	temperature, rainfall	GLM Poisson	weekly	sinusoidal terms	—	—	—	the cases for the previous week.	temperature 6 weeks (SL), rainfall 3 weeks (SL)	examined by standard errors were scaled using the square root of the Pearson chi2 dispersion.
	36	Hashizume, et al., 2008	1996–2002	Dhaka (Bangladesh)	rainfall, river level, temperature	GLM Poisson	weekly	Fourier terms	year	public holidays	—	AR(1) included	rainfall: 0 to 16 weeks (MA), river level: 0 to 4 weeks (MA)	—
	37	Huq, et al., 2005	1997–2000	5 different cities, (Bangladesh)	water temperature, air temperature, water depth, pH, rainfall	Poisson regression	bimonthly	—	—	—	—	—	0, 2, 6, 4, 8 months (SL)	—
Influenza	38	Hu, et al., 2012	2009	Brisbane (Australia)	temperature, rainfall, interaction	Poisson regression, spatiotemporal analysis (CAR)	weekly	sinusoidal terms	—	socio-economic index, population (offset), spatially structured random effect	—	AR(1) included	1 week single lag (SL)	—
	39	Jusot, et al., 2011	2009–2010	Niger	temperature, relative humidity (RH), wind speed, visibility	GAM	daily	seasonal components	trend components	day of the week, holidays, religious festival, and pilgrimage	—	—	—	—

Blanks represent unknown for the case no statements are made in articles regarding each category. Otherwise whether it was considered or how it was considered are stated in this table.

* SL: single lag, MA: moving average, DL: distribute lag, AR: auto-regressive term

Table 2.

Study locations.

Region	Countries	Number of studies (n = 33)
Africa	Burundi, Ethiopia, Kenya, Niger, Malawi, Rwanda, Tanzania, Uganda, Zambia	8
East Asia	China, Taiwan, Korea	5
Southeast Asia	Thailand, Vietnam, Singapore	6
South Asia	India, Bangladesh	8
Central/South America	Peru, Puerto Rico, Brazil	5
Oceania	Australia	1

The counts for outcome diseases of interest used in the studies were mostly in the time unit of weeks and months (29 studies). Daily and yearly counts were not as common, being only 5 and 1 studies respectively (Table 3).

Table 3.

Summary of modelling characteristics

	Number of studies (n = 33)
Unit of outcome data
Daily	3
Weekly (including bi-weekly)	13
Monthly (including bi-monthly)	16
Yearly	1
Regression models
GLM (Poisson, quasi-Poisson, negative binomial)	28
GAM (Poisson, negative binomial)	3
Mixed models	2
Control of seasonality and long term trend
Some adjustments were included in the model	25
No adjustments / not described	8
Autocorrelation
Examined / included parameters to control autocorrelation	21
No specific measures / not described	12
Lag effects of exposure
Lag effects of whether variables were assessed	28
No lag effect assessments	5

As specified in the review criteria, the regression models were GLM and GAM with different distribution models, i.e. Poisson, quasi-Poisson, and negative binomial (31 studies). The other two studies integrated mixed models. Among the studies, 18 used models allowing for overdispersion, if any, by inclusion of an overdispersion parameter or selection of different distribution models (e.g. quasi-Poisson or negative binomial).

As mentioned above, an adjustment of seasonal variation and long-term trend is part of the standard approach in the typical time-series regression. In our review, 25 of the 33 studies (76%) included terms in models that allow for seasonality and trends with natural spline functions on time, trigonometric functions, or month and year indicator variables. Other than adjustments for cyclic seasonality and long term trend effects, more than half of the reviewed studies commonly indicated considerations or attempts to control autocorrelation (21 studies). Autocorrelation adjustments may have been necessary because time series are generally subjected to high autocorrelation caused by serial correlations between observations close in time distance. In those 21 studies, the most popular method for autocorrelation controls was to incorporate autoregressive terms including lagged outcome values, the logarithm of lagged outcome values, and lagged model residuals (19 studies).

Other covariates were also included in many studies, including spatial factors if studies involved different geographical areas, population number, risk related index, and holiday indicators. In risk assessments of exposure factors, time lag effects were considered in the majority of the reviewed studies (28 studies). However, we found that the analyzed lag forms (i.e. single lag, moving average lag, or distributed lag) and the time length of lag varied by study regardless of the same targeted disease. While evaluated lag lengths were, if predetermined, often supported by literature reviews and biological plausibility, many did not provide the rationales of assessed lag lengths. In some exploratory studies, on the other hand, long lag lengths were investigated to observe the thorough exposure effects over time. Another finding in our review was, even though infectious diseases generally confer temporary or permanent immunity, the susceptible or immune population was rarely addressed in study models. No studies computed or integrated the estimated susceptible population, and a few studies instead included proxies (e.g. vaccination rate) to account for the target population’s susceptible risk.

Discussion

While time series analysis with GLMs or GAMs is the established method in environmental epidemiology research, our review brings attention to several potential issues when the same application of the traditional approach for non-infectious diseases extends to infectious diseases.

First, immune protection, which is one of the unique features of infectious diseases, can lead to rapid changes in the underlying population at risk over the course of the study period, but few studies have addressed the susceptible or immune population in their models. The information on immune population can be critical as host immune competence (intrinsic factor) and environmental (extrinsic) factors are both important contributors to seasonal disease activity [41]. In particular, the importance of the interplay of intrinsic and extrinsic factors is illustrated in one cholera study in which the developments of outbreaks is unsuccessful, even with the disease’s favorable environmental conditions when the susceptible population is small [42]. The consequence of not taking into account the susceptible population in a model is the misquantification of the effects of environmental exposures. However, since estimates of immune or susceptible individuals within a population seldom exist in data, it is often necessary to create alternative measures to increase the precision of the analysis. The alternative approaches may include, but are not limited to, reconstructing estimation of susceptible population by deterministic models (e.g. susceptible-infected-recovered models) and proxy indicators such as vaccination rates.

Secondly, while adjustments for seasonal variations and long term trends were common, one third of the reviewed articles did not include the adjustment measures in their models. The reason is unknown, yet one possible reason might be less apparent seasonal variations of disease activity. For instance, while in temperate climate regions have epidemics of influenza on a regular basis in winter time, malaria often presents a less obvious periodic pattern of seasonality. In general, adjustments for seasonality variation in the traditional time series analysis involve two important meanings, i.e. elimination of the effects of unknown time-varying covariates and realization of the regression assumption of independence. Realization of the independence assumption is a particularly important underlying regression hypothesis for time series analysis, because observations of a variable that are close in time tend to be similar and are generally correlated (i.e. autocorrelation) [1]. When seasonality is absent in the outcome data at a glance, the question may naturally arise whether there is any necessity to implement seasonal adjustments in a model. However, given the possibility of serial correlations that may naturally exist in time series data, the question of whether to include seasonal adjustments should be carefully examined using statistical validations (e.g. model fitness and residuals).

Another concern regarding autocorrelations arises when the magnitude of strength and the potential underlying cause are considered. In our literature review, inclusion of autoregressive terms in addition to seasonal adjustments to control autocorrelation was commonly observed (19 studies), which, for one reason, may imply that the adjustment of seasonality variation alone is not sufficient. In general, an imperfect control of autocorrelation suggests omissions of other significant time-varying covariates from a model [43]. However, given the characteristics of infectious diseases, a stronger autocorrelation than controlled seasonality may be induced by the actual correlation in outcome observations due to disease transmissions among individuals. In other words, the true dependence among neighboring observations can be present with infectious disease data because the number of newly infected individuals depends on the number of previously infected individuals in the population. In fact, some studies [15, 16] included autoregressive terms (e.g. a lagged outcome or logarithm of lagged outcome) to account for the dependency of infectious diseases data. This correlation is also known as “true contagion” [44], and the resulting violation of the assumption of independence will cause biases not in the regression coefficients but in the estimates of standard errors [43]. Thus, the discussion again returns to the importance of implementing adequate seasonality adjustments with statistical validations and the need for additional measures if autocorrelation in model residuals remains. In order to competently address the autocorrelation resulting from true contagion or transmissibility of infectious diseases, it might be worthwhile in the future to explore what approaches are not only statistically effective but also biologically compelling from the aspect of disease mechanisms.

Thirdly, in the process of estimating lag effects of exposure factors, the lag timings evaluated varied by studies in spite of the same targeted disease. This may be because the quantitative evidences needed to establish the optimal lag timings remains elusive with most diseases, although there might be qualitatively convincing ideas. The difficulty of estimating the optimal lag times may be especially severe in vector-borne diseases. In these diseases, the transmission mechanisms become highly complicated due to the intermediating effects of vectors which influence the strong disease seasonality [45], but they can also be highly content-dependent. For instance, the association patterns and lags of rainfall effects in malaria vary widely by region and climate conditions (e.g. whether the region is generally dry or has abundant rain) [46]. More importantly, however, time lags and association patterns can be more complicated in infectious diseases than non-infectious diseases because the mechanism of disease manifestation (e.g. incubation period) and the transmission dynamics of pathogenic microorganisms (e.g. bacteria, viruses, parasites, or fungi) play a critical role in the causal pathway. Therefore, an understanding of biological mechanisms can be of great help in estimating lags and association patterns. If no certain prior knowledge exists or complicated transmission pathways are expected, then strategic exploration approaches are required to find the optimal estimates.

Lastly, most of our reviewed studies conducted an analysis using weekly or monthly data (including bi-weekly and bi-monthly). Unlike non-infectious diseases, daily count outcomes were much less common. This relates to only certain infectious diseases, but it is worth noting that using the longer time unit of data may sometimes lead to an underestimation of risk factors when the optimal time lags of exposure effects and disease incubation periods are short (e.g. monthly data is used for analysis when the optimal exposure effects are expected in one week lag). Wherever possible, selection of the most statistically robust and biologically plausible time unit of data is desirable for analysis.

Our study has some limitations. The first is that, among all the diseases potentially linked to weather variability, only four diseases were selected for the review. As a result, we may have eliminated studies that could have delivered some insightful analytical approaches. In review of our aim to characterize the methodological trends, however, our selected diseases were probably sufficient because they consist of different types of infectious diseases including water-borne, vector-borne, and air-borne diseases. Another limitation is that GLMs and GAMs were the only targeted models, even though other methods such as autoregressive integrated moving average can also fall into the category of time series regression models. Those other time-series methods might have provided solutions for the concerns raised here, but we believe that we have looked at important issues in common with the above that deserve careful attention and awareness. In conclusion, the careful implementation of time series regression analysis is required in the study of environmental determinants of infectious diseases. Further studies are required to explore alternative models and to address methods that will improve the time series analysis.

Conflict of Interest

None to declare.