Imaging of a linear diode bar for an optical cell stretcher

Abstract

We present a simplified approach for imaging a linear diode bar laser for application as an optical stretcher within a microfluidic geometry. We have recently shown that these linear sources can be used to measure cell mechanical properties; however, the source geometry creates imaging challenges. To minimize intensity losses and simplify implementation within microfluidic systems without the use of expensive objectives, we combine aspheric and cylindrical lenses to create a 1:1 image of the source at the stretcher focal plane and demonstrate effectiveness by measuring the deformation of human red blood cells and neutrophils.

1. Introduction

Optical traps generate microscale forces useful for manipulating colloidal particles [1] and cells [2,3]. Motivating integration within microfluidic devices are the comparable pN hydrodynamic forces, the relative length scales, the ease of use and fabrication, the biocompatibility, and the low cost [4]. Because of this, microfluidics and optical forces have been combined to create optical stretchers [5–7] which impart stresses on the surface of deformable microscale objects [5–12], an approach that has seen significant recent interest because of the non-invasive nature of optical traps and the desire to measure cell mechanical properties [13,14]. Currently, the simplest linear optical stretcher employs a single inexpensive, high-power diode laser bar source [15–17] to stretch cells along the laser long axis [18–20]. In this, opposing antipodal stretching forces are generated along the linear stretcher when the beam width and length are shorter and longer than the cell size, respectively [19]. Whereas linear optical traps can be generated by other methods [21,22], the inherent geometric anisotropy characteristic to such linear diode bar sources, typically 100:1 or greater, allows for direct application as an optical stretcher. For example, a diode bar may have emitter dimensions of 1 µm by 100 to 300 µm. In linear stretcher configurations the applied stretching force varies with fast axis numerical aperture (NA), exhibiting a theoretical maximum in membrane stress at ~0.5 NA [19]. The short laser dimension (fast axis) of linear diode bar sources typically diverges at ~30°, corresponding to a 0.5 NA, while the beam typically diverges at ~10° (slow axis) along the length of the extended source. In previous reports, we have used a pair of microscope objectives to collimate the laser output and relay the image of the laser bar to the specimen plane [18,20]. In such a design, the laser source is collimated by the first microscope objective, but due to the elongated geometry of the linear source, the collimated beam continues to experience extension along the long axis. This extension continues until the beam reaches the focusing objective, where the off-axis incident light is blocked from entering the back aperture of the focusing objective, resulting in a loss of optical power and altering beam profile. Additionally, such objectives are not typically designed to function in the near-infrared (IR) spectrum, leading to losses [23]. Our previous approach experienced power losses of approximately 50% at the focal plane [19]. Also, the use of bulky microscope objectives [18,19] or aligned optical fibers [6] to generate optical stretchers make integration challenging; reduced optical component size is needed for ease of integration with microscale measurement platforms.

Here we extend previous work by describing a wavelength-specific optimized optical imaging system for a diode laser bar made from commercially available inexpensive optics. This system addresses the need for simplified optics capable of imaging an anamorphic linear diode bar source with the theoretically optimum NA while limiting loss in optical intensity and changes in beam profile associated with using microscope objectives. Here, we design an optical stretcher of 0.5 NA where aspheric lenses are used to collimate the laser output and cylindrical lenses used to correct for the extension of the source. The aspheric lenses correct for spherical aberration and offer a long working distance, thereby enabling strong cell stretching forces at significant channel depth. Additionally, we show that optical transmission is improved with near IR light compared to our previous system based on standard microscope objectives [18,19]. This approach shows enhanced stretching of human red blood cells (RBCs) and neutrophils compared to other techniques [19] and allows stretching through glass coverslips and thin polydimethylsiloxane (PDMS) layers, demonstrating increased trapping depth, independent of device thickness.

2. System description

2.1 Optical system and optimization

The challenge in designing optical traps using diode bars is the extension of the source geometry from a point to a linear source. To address this, we simulated a 1x100 µm² diode bar with a central wavelength at 1064 nm in Zemax (Zemax, LLC, Redmond, WA) with slow and fast beam axes diverging at 7° and 30°, respectively. The dimensions of this source and its emission angles are already suitable for trapping. The design criterion of the optical system is to provide 1:1 imaging with high optical transmission using commercially available, inexpensive optics. We simulated the extended source with a linear assembly of five point sources spaced 25 µm apart. Simulation was performed for the divergence of both axes separately, and yielded identical placement for optical elements in both cases, as the 30° divergence is the limiting case for our system.

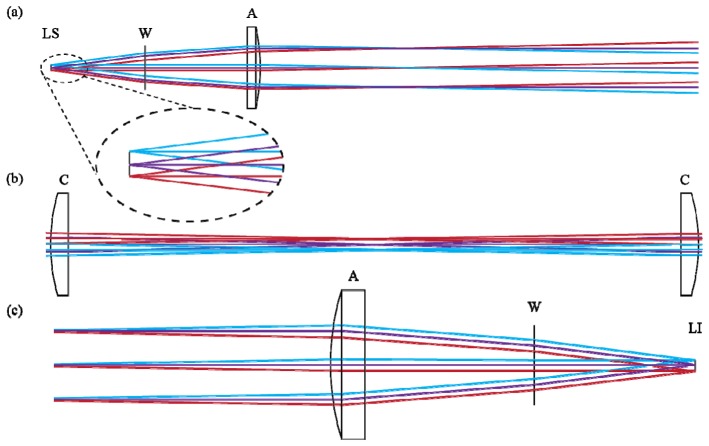
The optical simulation is illustrated in Fig. 1 and Fig. 2 . An aspheric lens forms the first element of the system and was chosen with sufficiently high NA to accommodate the 30° divergence without vignetting. The output of the diode source was collimated by placement of this aspheric lens (f = 4.51 mm, NA = 0.54, AR coated for 1064 nm) 1.6 mm from a 0.25 mm BK7 window positioned 1.1 mm from the laser. Because the source is an extended line, not a point, the light off-center of the asphere axis, while collimated, continues to extend along the plane of source extension. To correct for this overextension, a cylindrical lens of f = 100 mm is placed 120 mm from the asphere, with its optical power oriented with source extension. Maintaining 1:1 imaging of the source requires placement of an identical second cylindrical lens 197 mm from the first, together functioning as a telescope optimized for our specific wavelength. The second asphere is placed 120 mm from the telescope, forming the final image of the laser through a coverslip window 2.7 mm from the final aspheric lens. 1:1 imaging is accomplished by system symmetry about the center of the cylindrical telescope. To illustrate the function of each optical element and the beam profile in the system, cross-sections of the laser are illustrated in Fig. 1 and Fig. 2.

Fig. 1.

Illustration of the optical system parallel to the extended source axis. Not to scale. Light from the laser source (LS) passes through the BK-7 window (W) and is collimated by the first aspheric lens (A). The cylindrical lenses (C) have no optical power along this axis, leaving the beam unchanged. The beam is refocused by the second asphere (A) and passes through a coverslip window (W) before forming the laser image (LI).

Fig. 2.

Illustration of the optical system perpendicular to the extended source axis. Not to scale. Optical component labeling corresponds to Fig. 1. (a) Light from the source is collimated by the asphere, but experiences extension along the laser axis. (b) Cylindrical lenses correct for extension of the collimated light. (c) The laser is refocused by the final asphere.

Figure 1 shows the optical system as if one were looking along the extended axis of the laser, observing divergence of the fast axis at 30°. From this perspective the divergence of each of the five point sources would overlap, hiding the additional ray traces from view. Figure 1 shows the beam being fully collimated by the asphere after passing through the BK7 window. As there is no optical power in the cylindrical lenses in the plane of the fast axis, the lenses are shown as flat. The laser is then refocused through the final asphere and window.

Figure 2 illustrates the divergence of the slow axis from a perspective perpendicular to the extended laser axis. For clarity, only three of the five simulated point sources are shown. As in Fig. 1, the aspheric lens collimates the laser output (Fig. 2(a)). The ray-trace for the point source at the top (shown in cyan) and bottom (shown in red) of the extended source are collimated by the asphere but, because they are off-center from the optical axis, the collimated output is tilted relative to the optical axis, leading to extension of the collimated light. The placement of the cylindrical lens in Fig. 2(b) corrects this extension and inside the cylindrical lens telescope the beam is collimated and not extending. Refocusing begins with the second cylindrical lens and is finished by placement of the final asphere shown in Fig. 2(c).

With no windows the entire imaging system is diffraction-limited. With the BK7 window after the diode and coverslip before the sample, analysis shows that slight aberrations are evident in the beam, becoming progressively worse off-axis. Nonetheless, ray tracing indicates that the root mean square radius of the aberrated beam is only 0.6% larger then the diffraction-limited Airy radius.

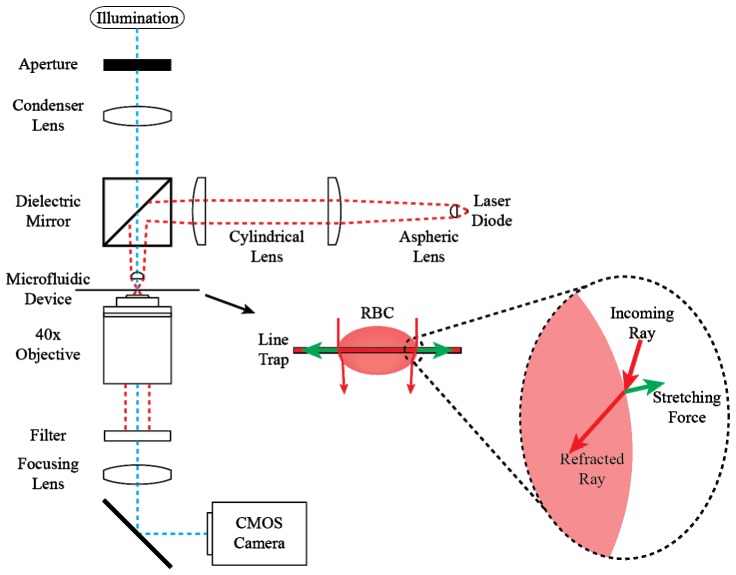
The complete optical stretching system is illustrated in Fig. 3 . In this, an image of a 1064 nm 8 W, 1x100 µm² laser diode (Lumics GmbH, Germany) is formed by two aspheric lenses (A230-C, ThorLabs, Newton, NJ) and two cylindrical lenses (LJ1567RM, ThorLabs, Newton, NJ). A broadband dielectric mirror, HR Coating: 750-1100 nm (BB1-E03, Thorlabs, Newton, NJ) is used to reflect the beam toward the final aspheric lens, which refocuses the beam at the focal plane of the imaging objective.

Fig. 3.

Optical stretching setup and generation of optical stretching force.

The sample plane is illuminated using a 200 W light source (Prior Scientific Inc., Rockland, MA). Light passes through a light guide and adapter and is focused with a 100 mm lens before passing through the dichroic mirror and the aspheric lens. Light is collected for imaging using a Zeiss LD Achroplan 40x/0,60 infinity-corrected objective. A shortpass filter with a cut-off wavelength of 900 nm (FES0900, Thorlabs, Newton, NJ) blocks the camera from laser exposure and an image produced by a 200 mm focal length lens is imaged by a Phantom v341 high-speed camera (Vision Research, Wayne, NJ) at 40 fps. Laser power was measured using a PM100D power meter and S130C photodiode power sensor (ThorLabs GmbH, Dachau, Germany) at the manufacturer-measured peak emission wavelength of 1070 nm.

2.2 Sample preparation

4.94 µm polystyrene beads (Bangs Laboratories, Inc., Fishers, IN) were used for trap visualization. Blood was collected from anonymous donors via finger-prick following an IRB-approved protocol. 2 µl of blood was diluted to 500 µl in a PBS buffer at 155 mOsm, containing 1.25% w/v sodium citrate to prevent coagulation and 0.17% w/v bovine serum albumen to prevent non-specific binding to device surfaces. Neutrophils were isolated from 4.5 ml of blood following methods outlined elsewhere [24] and an IRB-approved protocol. After isolation, the cells were suspended in a solution of Hank’s Balanced Salt Solution (Invitrogen, Grand Island, NY) and 2.4% v/v human serum albumen (Sigma, St Louis, MO).

2.3 Microfluidic device fabrication

Silicon wafer masters were fabricated using standard photolithography techniques [25]. PDMS (Slygard 184, Dow Corning, Midland, MI) was mixed in a 10:1 ratio, poured over the wafer, and placed under vacuum for approximately 1 hr for degassing. Once degassed, a silanized 48x60 mm glass coverslip was placed over the device patterns in the PDMS. The additional weight and smooth surface of the coverslip created a thin, smooth device upper surface for better laser imaging. Devices of varying thickness were poured and, after coverslip removal and exposure of the flat PDMS surface, overall device thicknesses measured 0.5 mm, 0.8 mm, and 1.0 mm. To interface tubing to the device and prevent leaking, additional PDMS was bonded to the well sections. Well holes were punched using a 0.75 mm hole punch (Ted Pella, Inc., Redding, CA) and the devices were bonded to glass coverslips via oxygen plasma.

2.4 Image processing

Image processing was performed on sequential frames with a custom C program using the OpenCV computer vision library [26]. First, noise in the image was reduced using cvSmooth. Next, the image was thresholded using cvAdaptiveThreshold, which accounts for any light gradient by weighing pixels to generate a binary image. Contours in the image were then detected using cvFindContours and fit to ellipses by cvFitEllipse2. Ellipse data was used to track contours and quantify cell deformation using percent relative stretch of the cell’s major axis diameter (A), defined as the percent difference between the stretched (A_S) and relaxed (A_R) major axis diameters, (A_S – A_R)/A_R•100%.

3. Results

3.1 Optical transmission and beam profile

We compared the power emitted from the laser diode to the power transmitted through the final aspheric lens of the system to assess transmission efficiency. Measurements predict a maximum power loss of 25% at the maximum diode current of 12,600 mA, a significant improvement over the 50% power loss of our previous method [19,20]. Beam shape was characterized with standard knife-edge methods by measuring beam profile at different positions along the beam propagation axis. The measured beam NA in air was 0.52 ± 0.04, which is in agreement with the simulated beam NA. Figure 4 shows an image of the beam shape at the objective focal plane, and of polystyrene beads trapped in solution. The dotted line indicates the position of the optical trap, corresponding to a length of 100 µm. To characterize forces, particles were trapped in flow in a channel directed perpendicular to the long trap axis. Once trapped, flow velocity was increased until particles released and trap strength estimated from viscous drag was ~40 pN at 1080 mW diode power.

Fig. 4.

Linear optical trap and trapped colloidal particles.

3.2 Cell stretching

As light refracts at a surface, a stretching force is generated by conservation of momentum (Fig. 3). By employing a linear extended laser source, stresses are induced along the length of the cell generating net opposing antipodal forces that act to elongate the cell. A detailed explanation of the generation of forces and a stress distribution has been described in previous work [19]. RBCs were used to test optical stretching in the optimized imaging system. An optical force was first applied, the stretching cell allowed to reach full deformation, and the force then removed to measure cell relaxation. To quantify cell deformation, the major axis of the ellipse fitted to each cell was used to characterize the behavior of the cells as they stretched and relaxed. Figure 5 shows the relative cell stretch as a function of total applied laser power for cells stretched between coverslips and for cells stretched under static conditions in a microfluidic device. In both cases, a linear relationship between laser power and cell stretch was observed, in agreement with previous results [19]. There was not a significant difference between cells stretched by focusing the laser through glass coverslips or through any PDMS layer. Transmission efficiencies are accounted for in Fig. 5 by plotting relative stretch data versus power emitted from the laser. Stretching data adapted from [19] is plotted in Fig. 5 for comparison.

Fig. 5.

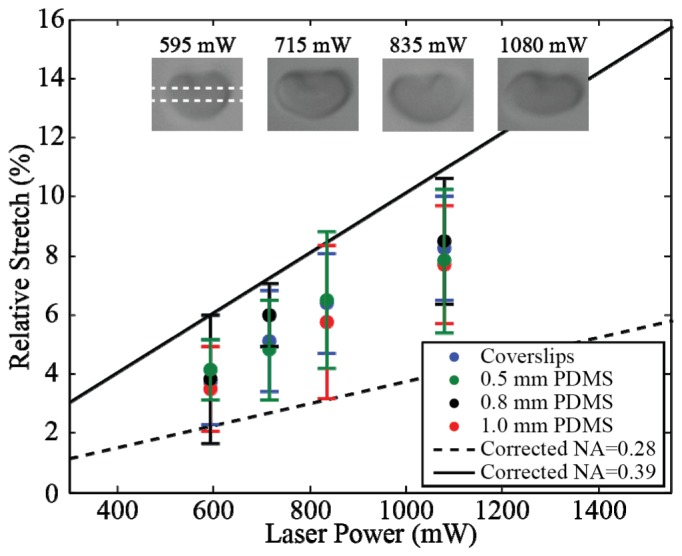
Red blood cell stretching as a function of measured diode laser power (n = 75) between coverslips (n = 29) and in 0.5 mm (n = 18), 0.8 mm (n = 12) PDMS devices. Corrected NA = 0.28 and corrected NA = 0.39 data adapted from [19]. Dotted white bar illustrates position of the optical stretcher and error bars indicate standard deviation.

A final mean for all four geometries of 8.0% cell stretch was observed at 1080 mW laser diode power, of which 808 mW is transmitted to the optical stretcher focal plane. This value represents the total power along the length of the linear stretcher, corresponding to ~8 mW/µm, well below the damage threshold for cells [2]. Using the membrane shear modulus [8] and the RBC model proposed by Evans [27], one can estimate the optical stretching force at this power to be ~30 pN, a value comparable to applied force in other reported optical stretchers [5]. Neutrophils were also observed to stretch ~4.0% (n = 10) at 55 mW/µm between glass coverslips, a stretch and optical power comparable to previously reported neutrophil stretching [28].

4. Discussion

The optical stretcher described here allows for optimized imaging of a linear diode bar laser source. As the fast axis divergence and emitter dimensions of the laser source are already appropriate for stretching, creating a 1:1 image of the laser generates an optimized stretcher. This combination of geometric anisotropy and NA, inherent to linear diode bar sources, generates opposing antipodal forces on a cell surface that act to elongate the cell along the axis of the stretcher [19]. To preserve a favorable NA with no image magnification, we employed simplified optics optimized to the diode specifications using ray tracing. The experimental results show a measured beam NA and length at the focal plane in good agreement with simulation prediction. This optimization also led to an improved light transmission of 75% compared to ~50% when using high-NA objectives [13,19,23], even with point sources. Further losses in optical intensity can be expected when imaging a linear diode laser with a single objective, as the extension of the source will cause continued extension of the collimated beam. The data presented in Sawetzki et al. [19], in which objectives were used to collimate the source, corresponds to an optical system transmission of 50%. In our imaging system, optical intensity is preserved by correcting the extension of the secondary beam axis with cylindrical lenses, allowing for maximum optical throughput. The “Corrected NA = 0.28” data was measured using a 40x objective (NA = 0.65) with a measured stretcher fast axis NA of 0.28 [19]. When compared with data for our optimized fast axis NA of 0.52, there is a significant increase in stretching effectiveness relative to the 0.28 NA of the 40x objective in both coverslip and PDMS configurations. Increasing stretching effectiveness has allowed us to deform more rigid cell systems, such as neutrophils, not previously demonstrated with linear optical stretchers.

Aspheric lenses reduce spherical aberrations present when using standard microscope objectives, as simulation predicts with the focused beam used here only 0.6% larger than the diffraction limit. To reduce spherical aberrations [29], Sawetzki et al. [19] used an oil immersion objective (NA = 1.45) to stretch with a measured stretcher NA of 0.39. Although the oil immersion objective appears capable of stretching cells more efficiently than our setup, these objectives are limited by short trapping depth and the ability to stretch only through glass coverslips [23]. By employing our optical system we demonstrate comparable stretching efficiency with an order-of-magnitude increase in trapping depth, evidenced by the ability to trap through a range of thin PDMS layers into microfluidic devices. With the ubiquitous use of PDMS in microfluidic devices, the ability to integrate optical forces without the use of bulky, expensive microscope objectives will allow for more effective miniaturization of optical stretching systems. Our technique allows for imaging optics to be decoupled from the laser focusing optics, allowing for an increased field of view and additional design options. Additionally, improved optical transmission combined with effective cell stretching in microfluidic flow devices will allow for increases in deformability assay measurement throughput.

5. Conclusion

In this work, we optimized an optical system for imaging of an anamorphic diode bar laser source for use as a linear optical stretcher. By creating an image identical to the laser source we maintained the optimized stretching NA and favorable geometry associated with the source using inexpensive, commercially available optics. Additionally, we improved optical transmission compared to microscope objectives while also correcting for source extension. We demonstrated the optical stretcher’s capabilities with RBC stretching and show results comparable to previous designs. The use of the simplified optics in this anamorphic system also resulted in increased working distance compared to microscope objectives, representing an effective, low-cost alternative to microscope objective-based optical stretching systems.