Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2015 Feb 13;6(3):815–826. doi: 10.1364/BOE.6.000815

2-D PSTD Simulation of focusing monochromatic light through a macroscopic scattering medium via optical phase conjugation

Snow H Tseng 1,*
PMCID: PMC4361436  PMID: 25798306

Abstract

By employing the pseudospectral time-domain (PSTD) simulation technique, we analyze the propagation of monochromatic light through a macroscopic scattering medium. Simulation results show that, monochromatic light can be directed through a scattering medium and focus into a narrow peak; a range of wavelengths has been simulated. Furthermore, we compare: i) focusing monochromatic light through a macroscopic scattering medium, and, ii) focusing monochromatic light through vacuum. Based upon numerical solutions of Maxwell’s equations, we demonstrate: with a fully-surrounding wavefront of specific amplitude and phase, sub-diffraction focusing can be achieved with monochromatic light, with or without the presence of a scattering medium.

OCIS codes: (290.4210) Multiple scattering, (290.7050) Turbid media

1. Introduction

Optical techniques are commonly limited to epithelial applications due to the shallow penetration depth through biological tissue structures. Increasing the penetration depth through turbid media via wavefront shaping essentially opens up new possibilities for biomedical applications. Research effort has been devoted to direct light propagation through scattering medium [1, 2]. A practical method to compensate the scattering effect of disordered media has been experimentally demonstrated by [3–6]. With a transport concept framework, the transmission matrix model based on Dorokhov’s random-matrix theory [7] is employed to analyze light propagation through scattering medium [8–11] where light propagation is described by a set of input-output relationships of correlated orthonormal channels [12–14]. The general objective is to propagate light through macroscopic scattering medium (e.g. biological tissues).

To enhance light penetration, a better understanding of the mechanism of light propagates through scattering media is needed. Due to the irregular geometry, light impinging upon a scattering medium exhibits a complex pattern of sinuous bright lines threading through space. The specific pattern depends upon the optical wavelength and the geometry of the scattering medium; the pattern complexity increases for a scattering medium with a larger refractive index (n) or a larger number density of scatterers (N). In general, the sinuous pattern resembles a network of branching water channels branching through the scattering medium (Fig. 1 ), which begs the question: Does light propagate preferentially along certain routes through a scattering medium?

Fig. 1.

Fig. 1

Open in a new tab

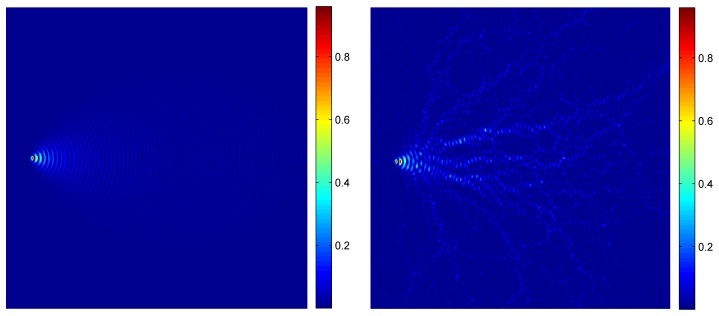
(a) Light propagation through vacuum. (b) Light propagation through a scattering medium exhibits a sinuous, complex pattern resembling a network of branching water channels.

The idea of light propagating through a scattering medium along specific routes is similar to an energy transport problem. The relationship of input-light and output-light is described by a transmission matrix. The stream-like pattern of light illuminating a scattering medium branches out forming a complex pattern with multiple routes connecting any two points. If light propagates preferentially along certain routes (e.g. the bright lines in Fig. 1(b)) through a scattering medium, it can be shown that the back-propagation of phase-conjugated light falls short to reconstruct the original outgoing light. The logic can be elaborated as follows: As depicted in Fig. 2 , between (A) the original light source and a point (B) outside the scattering medium, there are multiple routes connecting the two points. The length of each sinuous route is in general different; therefore, light propagating along different routes from B to A acquires a different a phase. Therefore, if light propagates along the sinuous bright routes as shown in Fig. 1(b), phase-conjugated light back-propagating through the scattering medium via various sinuous paths would in general be out-of-phase and fall short to perfectly reconstruct the original outgoing light profile.

Fig. 2.

Fig. 2

Open in a new tab

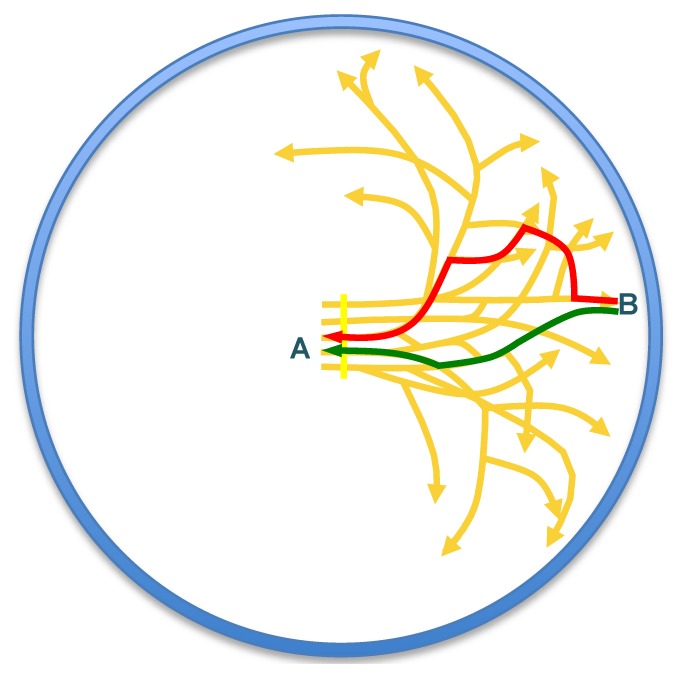
Schematics of light propagation through a scattering medium. Light propagating from A to B along different routes (e.g. green path and red path) would in general be out-of-phase due to the difference in optical path length.

2. Simulating light propagation via numerical solutions of Maxwell’s equations

To accurately account for the wave characteristics of light propagation through scattering medium, numerical solutions of Maxwell’s equations are required. A widely used simulation technique to obtain numerical solutions of Maxwell’s equations for light scattering problems is the finite-difference time-domain (FDTD) technique. Recently a two-dimensional (2-D) FDTD simulation analysis of light penetration using an ultrasound modulated guide star has been reported [15], where light propagation through a region of 60-μm-by-100-μm is modeled. However, due to the intense computations involved, the FDTD technique falls short to model macroscopic light scattering problems. Here we employ the pseudospectral time-domain (PSTD) technique [16]; the PSTD algorithm is computationally economic and advantageous for modeling large-scale light scattering problems [17]. Effort has been devoted to improving the PSTD technique for light scattering simulations [18]. While achieving comparable accuracy as the conventional FDTD, the PSTD reduces the computer storage and the running-time by approximately for large electromagnetic wave interaction models in D dimensions that does not have geometric details or material inhomogeneities smaller than one-half wavelength [16]. The temporal derivatives are calculated using a central difference scheme, whereas the spatial derivatives are calculated using discrete Fourier transforms:

{∂E∂x|i}=−F−1{jkx⋅F{Ei}}, (1)

where E is the electric vector field, kx is the wave number, and the Fourier transform is represented by F. Since computer calculations are based on discrete numbers, discretization of the continuous electromagnetic fields is necessary. According to the Nyquist sampling theorem, the spatial derivatives calculated in Eq. (1) is of spectral accuracy (meaning as accurate as it can get with the given information), allowing the PSTD technique, with a coarse grid of two spatial samples per wavelength, to achieve similar accuracy as the finite-difference time-domain (FDTD) technique (FDTD requires 20 spatial samples per wavelength.) The coarse spatial grid points enables simulating large-scale optical phenomena with economic computational memory. In addition, an anisotropic perfectly matched layer absorbing boundary condition [19] is implemented to absorb all outgoing waves. If all outgoing waves never re-interact with the medium, the light scattering simulation can be considered as practically isolated in vacuum.

In this manuscript, we model propagation of a fully-surrounding, CW wavefront through a macroscopic scattering medium to a target position inside the scattering medium. All the simulations reported in this manuscript are two-dimensional (2-D) simulations of TM waves: Electric field (Ez) is polarized in the z- direction, and the magnetic field (H→=Hxxˆ+Hyyˆ) and propagation of light lie in the x-y plane. Instead of a coupled-dipole numerical approach where dielectric cylinders are modeled as idealized point dipole radiators [20], we analyze light propagation through scattering medium via grid-based, PSTD numerical solutions of Maxwell’s equations to accurately account for the wave characteristics of light. With a spatial resolution of 0.33 μm and temporal resolution Δt = 0.05 fs, the propagation of CW light with a wavelength of λ = 1 μm is modeled. A 1800-by-1800 simulation grid is employed to model a 600 μm by 600 μm space. The scattering medium is modeled as a cluster of N randomly positioned, non-absorbing, dielectric cylinders with refractive index n. For each simulation, a total of 240,000 time-steps (12 ps) are simulated. Each simulation takes typically ~8 hours to run with 16 computing cores of an Intel 2.66 GHz processor.

3. Methods

To model the back-propagation of phase-conjugated light through a scattering medium, we employ the PSTD technique to simulate light propagation through a scattering medium. We model a finite-width, CW light source embedded inside a macroscopic scattering medium. The electromagnetic field of a finite-width, sinusoidal CW plane-wave is added into space inside the scattering medium as a “soft source” to avoid artificial scattering of a hard source. By inserting a piece-wise continuous segment of incident field into the simulation to model a localized CW light source, the segment of electromagnetic field is locally piecewise continuous with minimal discontinuities at the edge, which suffices to maintain numerical stability of the PSTD algorithm [21]. Time-wise, the CW light source is added into the simulation at every time step with a sinusoidal period corresponding to the frequency of the light source. By periodically adding CW light electromagnetic field into the PSTD simulation as a piecewise continuous field, a localized, finite-width, sinusoidal CW plane-wave embedded inside a large-scale light scattering simulation can be modeled in the PSTD simulation.

We model a fully surrounding CW wavefront of specific amplitude and phase converging upon a scattering medium, as depicted in Fig. 3 . The amplitude and phase are obtained by phase-conjugating the CW outgoing light originating from a virtual light source positioned at the target position. The simulation is performed in two stages: forward scenario (Fig. 3(a)) and playback scenario (Fig. 3(b)). In the forward scenario, a CW finite-width plane wave is generated from a virtual light source and propagates through the scattering medium; the amplitude and phase are randomized as light multiply scatters through irregular geometry of the scattering medium. The amplitude and phase of light exiting the scattering medium are recorded and later used to generate the phase-conjugated light in the playback scenario. In the playback scenario, a ring-shaped wavefront positioned outside the scattering medium is employed to generate a fully-surrounding wavefront converging inwards via phase-conjugation. The propagation of phase-conjugated light through a macroscopic scattering medium can be accurately modeled by the forward scenario and playback scenario.

Fig. 3.

Fig. 3

Open in a new tab

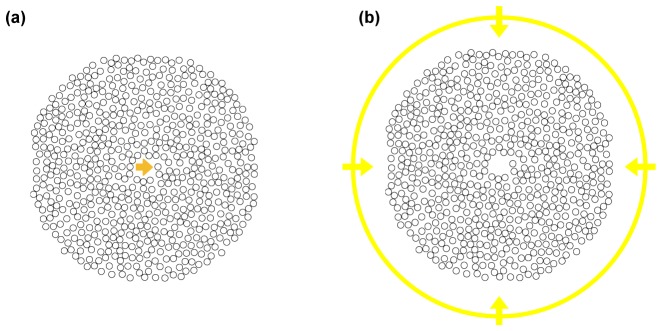
Propagation of OPC light is modeled in two stages: (a) Forward scenario: a CW light source embedded at the center of a 40-μm-diameter empty region centered inside a scattering medium consisting of 630 randomly-positioned (minimum edge-to-edge spacing of 0.5 μm), 10-μm-diameter dielectric (n = 1.6) cylinders. (b) Playback scenario: amplitude and phase of the CW outgoing wave is recorded and phase-conjugated to form a circular wavefront converging through the scattering medium.

4. Modeling the back-propagation of phase-conjugated light

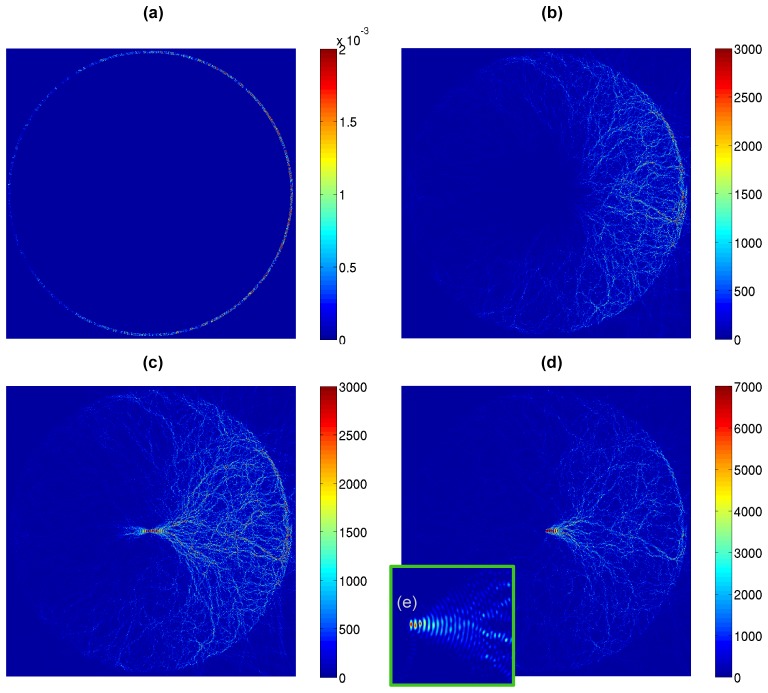
We investigate the possibility of propagating light through a macroscopic scattering medium to a target position via multiple scattering. Recently, a simulation analysis has been reported by Carminati et al. [20] where a scattering medium (cylindrical region of radius R = 1.91 μm) is modeled by a cluster of idealized point dipoles. Here we model this problem on a macroscopic scale (~300x300 times larger). Instead of treating each scatterer as an idealized point dipole, we model the scattering medium via a grid-based PSTD simulation where the geometry is specified by the refractive index n as a function of x and y of the entire simulation space. As shown in Fig. 4 , we demonstrate a large-scale simulation of CW light propagation through a scattering medium to a target position with dimensions 1200 μm by 1200 μm. A CW plane wave (wavelength λ = 1 μm) with a cross-sectional width of 5 μm is generated atthe center of the simulation. The scattering medium consists of 22,222 non-absorbing, randomly-positioned, 5-μm-diameter dielectric cylinders closely-packed (minimum edge-to-edge spacing of 0.5 μm) within a cylindrical region with a diameter of 1160 μm; the scattering mean free path is 6.86 μm, the optical thickness is 169, and the strength of disorder (morphological disorder [22]) is 0.0619. A fully surrounding, CW wavefront converging upon the scattering medium is shown in Fig. 4(a). As light propagates through the scattering medium, a stream-like pattern of bright lines threading towards the center is exhibited (Fig. 4(b)). Maximum amplitude is reached as light converges at the center (target position). Simulation results show that phase-conjugated light back-propagates through the scattering medium and focuses coherently.

Fig. 4.

Fig. 4

Open in a new tab

( Media 1 (850.7KB, MOV) ) Simulating CW, fully-surrounding, phase-conjugated light impinging upon a scattering medium. The scattering medium consists of 22,222 non-absorbing, randomly-positioned, 5-μm-diameter dielectric cylinders closely packed within a circular region of 1160 μm diameter; the scattering mean free path is 6.86 μm, the optical thickness is 169, and the strength of disorder is 0.0619. The λ = 1 μm CW light is generated with the phase-conjugated, CW amplitude and phase of outgoing light recorded in the forward scenario. a) A ring-shaped, CW wavefront of light is generated periodically. b) At t = 1 ps, light propagates through the scattering medium via multiple scattering, c) At t = 1.5 ps, light converges at the center and then diverges outward. (d) A soft sink technique is employed to eliminate the outgoing light, leaving only the incoming light component. A zoomed-in view of (d) is shown in (e).

5. Analyzing back-propagated light reaching the target position

To quantitatively analyze the propagation of light through a scattering medium, we model light scattering through an absorption-less scattering medium. The cross-sectional electric field Ez profile measured at the target position is compared. In an ideal situation where light perfectly back-propagates and reconstructs the original outgoing light profile at the target position, light continues to propagate through the target position and diverge outwards (like a light source illuminating in the opposite direction of the original light source.) Eliminating the outgoing light component is necessary to quantify the impinging light component [23]. Based upon the linearity of the Maxwell’s equations, we employ a soft sink simulation technique [24] to subtract out only the outgoing light component. Analogous to the soft source in the forward scenario, a soft sink is implemented by adding a finite-width CW plane wave propagating in the opposite direction with the precise amplitude but 180-degree out of phase. As shown in Fig. 4(c), a fully-surrounding, phase-conjugated light converges at the target position then continues to diverge outwards; the field profile at the target position is broadened as the impinging light and diverging light interfere with each other. The added outgoing wave cancels out only the outgoing light component while leaving the incoming light component intact, as shown in Fig. 4(d).

By subtracting out the outgoing light component, the incoming light component can be quantitatively analyzed. A cross-sectional profile of the forward or back-propagated CW propagating light is measured along the white dashed line at the center of the simulation grid (as shown in Figs. 5(a) and 6(a) ). The total energy of the forward and the total energy of the back-propagated light profiles are normalized to 1, respectively. The spot size of the forward and back-propagated light can be quantified by calculating the full-width-at-half-maximum (FWHM) of the measured profile. The reconstruction of the back-propagated light can be quantified by calculating the root-mean-square error of the back-propagated light profile relative to the forward propagated light profile.

Fig. 5.

Fig. 5

Open in a new tab

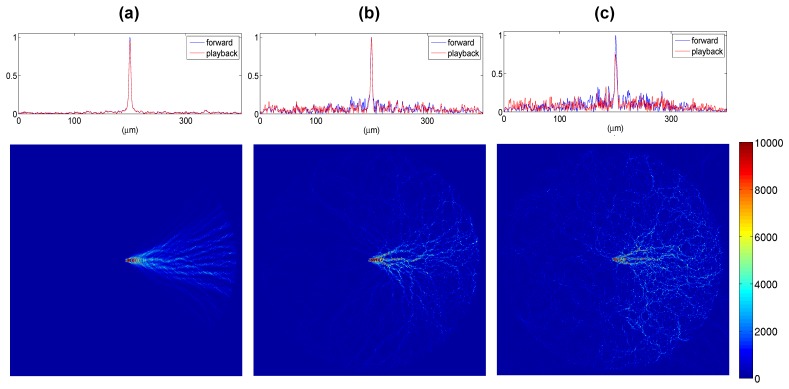
Simulation of light (λ = 4 μm) back-propagated through a scattering medium consisting of 1600 6-μm-diameter dielectric cylinders, each with a refractive index (a) n = 1.05, (b) n = 1.2, (c) n = 1.3, respectively. Inset-figures: Regardless of n, the back-propagated light converges coherently and reconstructs the original light profile (FWHM peak width ~4 μm as measured along the white dashed line at the center).

Fig. 6.

Fig. 6

Open in a new tab

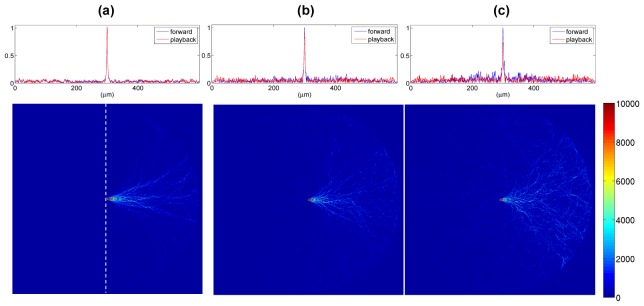
Simulation of light (λ = 4 μm) back-propagated through a 560-μm-diameter scattering medium consisting of N 2.4-μm-diameter dielectric (n = 1.2) cylinders, where (a) N = 3000, (b) N = 9000, and (c) N = 16356, respectively. Inset-figures: Regardless of N, the back-propagated light converges coherently and reconstructs the original light profile (FWHM peak width ~4 μm as measured along the white dashed line at the center).

Here we simulate light propagation through a scattering medium of various optical thicknesses. The back-propagation of light for varying the refractive index (n) (Fig. 5) and the number density (N) (Fig. 6) of the scattering medium are analyzed. In Fig. 5, the scattering medium consists of 1600 randomly positioned, uniform, 6-μm-diameter dielectric (refractive index n) cylinders clustered (with a minimum spacing of 0.5 micron) within a 360-μm-diameter area; for λ = 4 μm and refractive index n = 1.2, the scattering mean free path is 5.05 μm, and optical thickness is 71.29. With the phase-conjugated amplitude and phase recorded in the forward scenario, a CW light (wavelength λ = 4 μm) propagates from outside a scattering medium inwards while exhibiting a sinuous, stream-like pattern. If light propagates preferentially along certain routes, back-propagation of light in general would be out-of-phase due to difference in optical path length. Yet, as shown in Figs. 5 and 6, regardless of the refractive index (n) or the number density (N), the CW wavefront converges coherently and reconstructs the original light profile.

6. Focusing monochromatic phase-conjugated light through a scattering medium

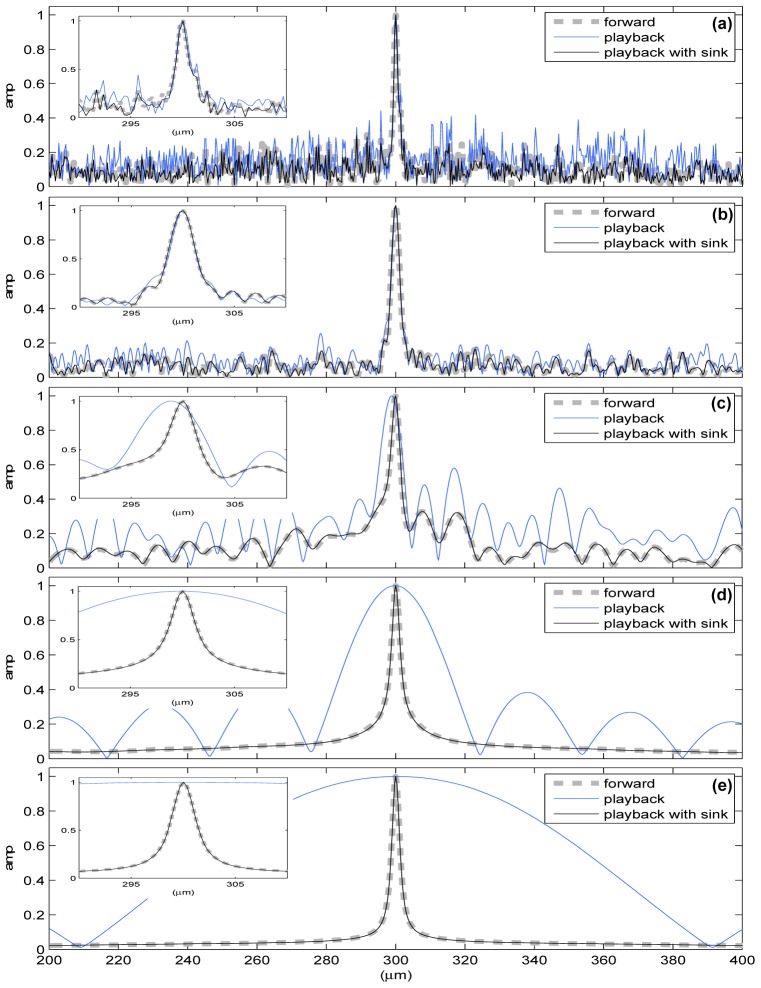
Recently it has been reported that wideband light is crucial for the sub-diffraction focusing phenomenon [20, 25]; here we simulating this phenomenon for CW, monochromatic phase-conjugated light. With a grid-based PSTD simulation, we model light impinging upon a scattering medium consisting of 1600 randomly positioned, 6-μm-diameter dielectric (n = 1.2) cylinders clustered in a 180-μm-radius area. A 4-μm-wide aperture is embedded at the center of the scattering medium. Various wavelengths are simulated: (a) 1 μm, (b) 4 μm, (c) 16 μm, (d) 64 μm, and (e) 256 μm. For λ = 1 μm and refractive index n = 1.2, the scattering mean free path is 8.29 μm, and the optical thickness of the scattering medium is 43.40. Light emitted from the aperture scatters through the scattering medium and propagates outwards. The amplitude and phase are recorded at a distance of 290 μm from the center. As shown in Fig. 7 ( Media 2 (3.7MB, MOV) ), with a fully-surrounding wavefront, the phase-conjugated light back-propagates through the scattering medium and focuses at the center; the cross-sectional amplitude profile of light at the center of the simulation is measured and compared. The FWHM of each forward peak is: (a) 1.3 μm, (b) 3.0 μm, (c) 4.0 μm, (d) 3.1 μm, (e) 3.0 μm, respectively. Before eliminating the outgoing field component the root-mean-square error is: (a) 9.5%, (b) 4.97%, (c) 15.5%, (d) 29.5%, and, (e) 46.7%, respectively; after eliminating the outgoing light component, the root-mean-square error is: (a) 3.05%, (b) 0.58%, (c) 0.40%, (d) 0.24%, and, (e) 0.19%, respectively. Evidently the peak width of the forward light and back-propagated light are identical. As shown in Fig. 7, with a fully-surrounding, CW wavefront of specific amplitude and phase, monochromatic light can be focused through a scattering medium to a narrow peak, regardless of the wavelength.

Fig. 7.

Fig. 7

Open in a new tab

( Media 2 (3.7MB, MOV) ) Simulation of light back-propagated through a scattering medium to a narrow peak. The scattering medium consists of 1600 randomly positioned, 6-μm-diameter dielectric (n = 1.2) cylinders. A 4-μm-wide plane-wave light source (wavelength λ) is embedded at the center of the scattering medium. From top to bottom: (a) λ = 1 μm, (b) λ = 4 μm, (c) λ = 16 μm, (d) λ = 64 μm, (e) λ = 256 μm, respectively. In each subplot, the forward propagation light profile (gray dashed line) is compared to the back-propagated light (blue line) and the back-propagated light with a soft sink to eliminate the outgoing light component (black line). A zoomed-in view is shown in each inset-figure. Before eliminating the outgoing field component the root-mean-square error is: (a) 9.5%, (b) 4.97%, (c) 15.5%, (d) 29.5%, and, (e) 46.7%, respectively; after eliminating the outgoing light component, the root-mean-square error is: (a) 3.05%, (b) 0.58%, (c) 0.40%, (d) 0.24%, and, (e) 0.19%, respectively. The peak width at FWHM is: (a) 1.7 μm, (b) 3.0 μm, (c) 4.1μm, (d) 3.7 μm, (e) 3.0 μm, respectively. It is clear that the peak width of the forward light and back-propagated light profiles are identical.

7. Focusing light through vacuum

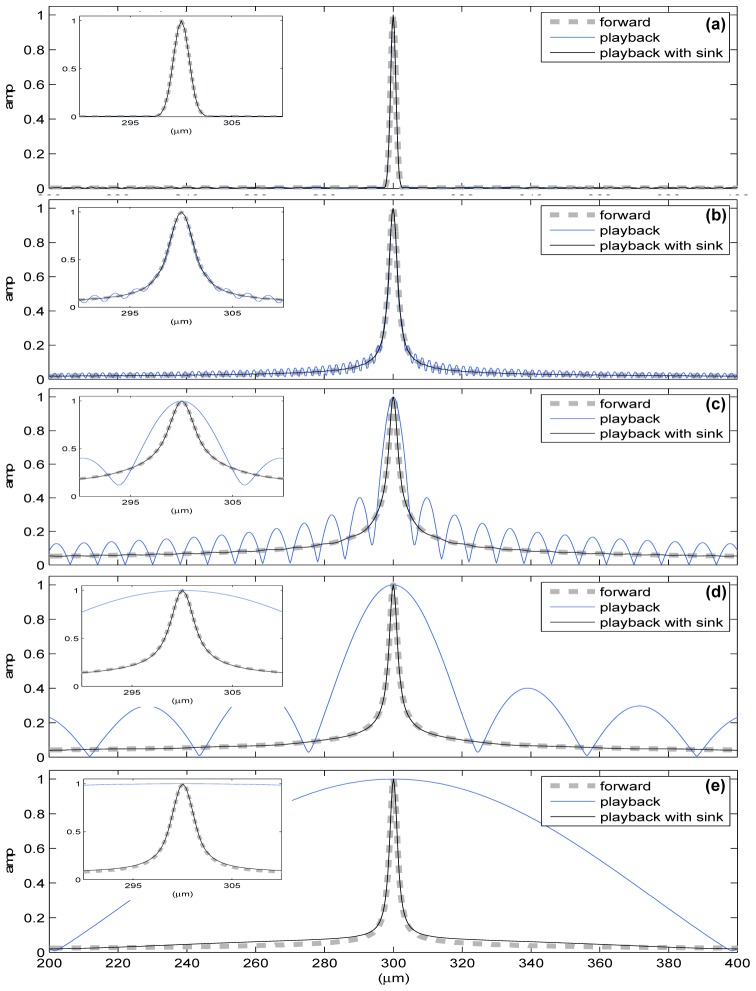
Next, we model back-propagation of light with a fully-surrounding wavefront (wavelength λ) without the presence of a scattering medium. The dimensions of the simulation are 600 μm by 600 μm; a 4-μm-wide aperture is embedded at the center of the simulation. Various wavelengths (λ) are simulated: (a) 1 μm, (b) 4 μm, (c) 16 μm, (d) 64 μm, and (e) 256 μm. The amplitude and phase are recorded at a distance of 290 μm from the center. With a fully-surrounding wavefront, the phase-conjugated light back-propagates through space; the cross-sectional amplitude profile of light at the center of the simulation is measured and compared. In general, light is irregularly scattered from the scattering medium and causes interference everywhere. As a result, the emerging light profile is asymmetric as it is the superposition of: (i) a perfect Gaussian light profile emerging from the soft source, and, (ii) the interference from irregularly scattered light of the entire scattering medium. Before eliminating the outgoing field component the root-mean-square error is: (a) 0.23%, (b) 1.84%, (c) 9.32%, (d) 30.29%, and, (e) 65.68%, respectively; after eliminating the outgoing light component, the root-mean-square error is: (a) 0.17%, (b) 0.089%, (c) 0.20%, (d) 0.208, and, (e) 0.17%, respectively. Evidently the peak width of the forward light and back-propagated light are identical. As shown in Fig. 8 ( Media 3 (1.7MB, MOV) ), with a fully-surrounding wavefront of specific amplitude and phase, light can be focused through vacuum to a narrow peak, regardless of the wavelength. Together, Figs. 7 and 8 clearly show that the sub-diffraction focusing phenomenon [1] can be achieved with or without the presence of a scattering medium.

Fig. 8.

Fig. 8

Open in a new tab

( Media 3 (1.7MB, MOV) ) Simulation of light back-propagated through vacuum to a narrow peak. A 4-μm-wide plane-wave light source (wavelength λ) is embedded at the center of the simulation. From top to bottom: (a) λ = 1 μm, (b) λ = 4 μm, (c) λ = 16 μm, (d) λ = 64 μm, (e) λ = 256 μm, respectively. In each subplot, the forward propagation light profile (gray dashed line) is compared to the back-propagated light (blue line) and the back-propagated light with a soft sink to eliminate the outgoing light component (black line). A zoomed-in view is shown in each inset-figure. Before eliminating the outgoing field component the root-mean-square error is: (a) 0.23%, (b) 1.84%, (c) 9.32%, (d) 30.29%, and, (e) 65.68%, respectively; after eliminating the outgoing light component, the root-mean-square error is: (a) 0.17%, (b) 0.089%, (c) 0.20%, (d) 0.208, and, (e) 0.17%, respectively. The FWHM is: (a) 1.8 μm, (b) 3.3 μm, (c) 5 μm, (d) 3.6 μm, (e) 3.1 μm, respectively. It is clear that the peak width of the forward light and back-propagated light profiles are identical.

Convergence analyses are presented in Fig. 9 to justify the simulation results. In principle, an ideal simulation can be achieved with an infinitely long simulation time and an infinitely large simulation space. However, in practice we can only model a finite number of time-steps and a finite size simulation space. Analysis of the temporal convergence and spatial convergence of the simulation are performed. As shown in Fig. 9(a), the accuracy of the simulation increases with increased simulation time, which is closer to the CW steady state. On the other hand, to model light phase-conjugated in the far field, the OPC region has to be far enough from the scattering medium so that light scattered into arbitrary directions impinges the OPC region at normal incidence. As shown in Fig. 9(b), the accuracy of the simulation increases with increased distance between the scattering medium and the OPC region, where the outgoing light impinges the OPC region at near normal incidence. The temporal and spatial convergence analyses presented in Figs. 9(a) and 9(b) show that the simulations reported in this manuscript is robust and accurate.

Fig. 9.

Fig. 9

Open in a new tab

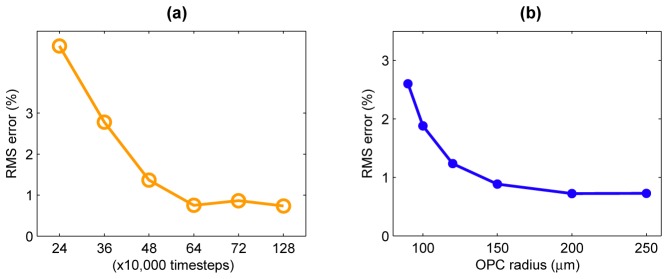
Convergence analyses of the simulation. With a soft sink to eliminate the outgoing light component, the impinging light profile reconstructed from back-propagated light is compared to the original outgoing light in the forward scenario. The accuracy of the simulation increases with: (a) increased number of simulation time-steps (CW steady state), and, (b) increased distance between the OPC region and the scattering medium, where outgoing light impinges the OPC region at near normal incidence.

8. Summary

By means of a grid-based PSTD simulation, we analyze light propagation through an absorption-less, scattering medium of macroscopic dimensions (up to 1200 μm by 1200 μm). Simulation results show that phase-conjugated light propagates and focuses through scattering media coherently; the sinuous, stream-like pattern of bright lines (Fig. 1(a)) is the result of constructive interference rather than actual pathways through which light propagates.

Recent simulation research reported achieving sub-diffraction focusing through a scattering medium with broadband light [20, 25]; in this manuscript, we demonstrate sub-diffraction focusing can be achieved with monochromatic phase-conjugated light; various wavelengths of light has been simulated. Simulation results show that, with specific amplitude and phase, CW light can propagate through a macroscopic scattering medium and focus into a narrow peak. Furthermore, to analyze the effect of scattering, we compare: i) focusing monochromatic light through a macroscopic scattering medium (Fig. 7), and, ii) focusing monochromatic light through vacuum (Fig. 8). Based upon numerical solutions of Maxwell’s equations, we demonstrate with a fully-surrounding wavefront of specific amplitude and phase, sub-diffraction focusing can be achieved with monochromatic light, with or without the presence of a scattering medium.

Acknowledgments

This research is supported by the Taiwan National Science Council Grant NSC-99-2112-M-002-016-MY3, NSC-102-2112-M-002-020, and National Taiwan University grant NTU-ERP-103R89086. We thank Yingmin Huang and Changhuei Yang for insightful discussions.

References and links

  • 1.Lerosey G., de Rosny J., Tourin A., Fink M., “Focusing beyond the diffraction limit with far-field time reversal,” Science 315(5815), 1120–1122 (2007). 10.1126/science.1134824 [DOI] [PubMed] [Google Scholar]
  • 2.Vellekoop I. M., Lagendijk A., Mosk A. P., “Exploiting disorder for perfect focusing,” Nat. Photonics 4(5), 320–322 (2010). 10.1038/nphoton.2010.3 [DOI] [Google Scholar]
  • 3.Xu X., Liu H., Wang L. V., “Time-reversed ultrasonically encoded optical focusing into scattering media,” Nat. Photonics 5(3), 154–157 (2011). 10.1038/nphoton.2010.306 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Wang Y. M., Judkewitz B., Dimarzio C. A., Yang C. H., “Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light,” Nat. Commun. 3, 928 (2012). 10.1038/ncomms1925 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Fiolka R., Si K., Cui M., “Parallel wavefront measurements in ultrasound pulse guided digital phase conjugation,” Opt. Express 20(22), 24827–24834 (2012). 10.1364/OE.20.024827 [DOI] [PubMed] [Google Scholar]
  • 6.Tay J. W., Lai P. X., Suzuki Y., Wang L. V., “Ultrasonically encoded wavefront shaping for focusing into random media,” Sci. Rep. 4, 3918 (2014). 10.1038/srep03918 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Edelman A., Rao N. R., “Random matrix theory,” Acta Numer. 14, 233–297 (1999). 10.1017/S0962492904000236 [DOI] [Google Scholar]
  • 8.Kim M., Choi W., Yoon C., Kim G. H., Choi W., “Relation between transmission eigenchannels and single-channel optimizing modes in a disordered medium,” Opt. Lett. 38(16), 2994–2996 (2013). 10.1364/OL.38.002994 [DOI] [PubMed] [Google Scholar]
  • 9.Choi W., Mosk A. P., Park Q.-H., Choi W., “Transmission eigenchannels in a disordered medium,” Phys. Rev. B 83(13), 134207 (2011). 10.1103/PhysRevB.83.134207 [DOI] [Google Scholar]
  • 10.Mosk A. P., Lagendijk A., Lerosey G., Fink M., “Controlling waves in space and time for imaging and focusing in complex media,” Nat. Photonics 6(5), 283–292 (2012). 10.1038/nphoton.2012.88 [DOI] [Google Scholar]
  • 11.Park J.-H., Park C., Yu H., Park J., Han S., Shin J., Ko S. H., Nam K. T., Cho Y.-H., Park Y., “Subwavelength light focusing using random nanoparticles,” Nat. Photonics 7(6), 454–459 (2013). 10.1038/nphoton.2013.95 [DOI] [Google Scholar]
  • 12.Kim M., Choi Y., Yoon C., Choi W., Kim J., Park Q. H., Choi W., “Maximal energy transport through disordered media with the implementation of transmission eigenchannels,” Nat. Photonics 6(9), 583–585 (2012). 10.1038/nphoton.2012.159 [DOI] [Google Scholar]
  • 13.Hillman T. R., Yamauchi T., Choi W., Dasari R. R., Feld M. S., Park Y., Yaqoob Z., “Digital optical phase conjugation for delivering two-dimensional images through turbid media,” Sci. Rep. 3, 1909 (2013). 10.1038/srep01909 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Yu H., Hillman T. R., Choi W., Lee J. O., Feld M. S., Dasari R. R., Park Y., “Measuring large optical transmission matrices of disordered media,” Phys. Rev. Lett. 111(15), 153902 (2013). 10.1103/PhysRevLett.111.153902 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Hollmann J. L., Horstmeyer R., Yang C., DiMarzio C. A., “Analysis and modeling of an ultrasound-modulated guide star to increase the depth of focusing in a turbid medium,” J. Biomed. Opt. 18(2), 025004 (2013). 10.1117/1.JBO.18.2.025004 [DOI] [PubMed] [Google Scholar]
  • 16.Liu Q. H., “Large-scale simulations of electromagnetic and acoustic measurements using the pseudospectral time-domain (PSTD) algorithm,” IEEE Trans. Geosci. Rem. Sens. 37(2), 917–926 (1999). 10.1109/36.752210 [DOI] [Google Scholar]
  • 17.Tseng S. H., Ting W. L., Wang S. J., “2-D PSTD Simulation of the time-reversed ultrasound-encoded deep-tissue imaging technique,” Biomed. Opt. Express 5(3), 882–894 (2014). 10.1364/BOE.5.000882 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Munro P. R. T., Engelke D., Sampson D. D., “A compact source condition for modelling focused fields using the pseudospectral time-domain method,” Opt. Express 22(5), 5599–5613 (2014). 10.1364/OE.22.005599 [DOI] [PubMed] [Google Scholar]
  • 19.Gedney S. D., “An anisotropic perfectly matched layer-absorbing medium for the truncation of FDTD lattices,” IEEE Trans. Antenn. Propag. 44(12), 1630–1639 (1996). 10.1109/8.546249 [DOI] [Google Scholar]
  • 20.Pierrat R., Vandenbem C., Fink M., Carminati R., “Subwavelength focusing inside an open disordered medium by time reversal at a single point antenna,” Phys. Rev. A 87(4), 041801 (2013). 10.1103/PhysRevA.87.041801 [DOI] [Google Scholar]
  • 21.Huang Y., Tsai C., Tseng S. H., “PSTD simulation of the continuous-wave optical phase conjugation phenomenon,” (in review).
  • 22.Choi S. H., Kim Y. L., “Hybridized/coupled multiple resonances in nacre,” Phys. Rev. B 89(3), 035115 (2014). 10.1103/PhysRevB.89.035115 [DOI] [Google Scholar]
  • 23.de Rosny J., Fink M., “Overcoming the Diffraction Limit In Wave Physics Using a Time-Reversal Mirror and a Novel Acoustic Sink,” Phys. Rev. Lett. 89(12), 124301 (2002). 10.1103/PhysRevLett.89.124301 [DOI] [PubMed] [Google Scholar]
  • 24.Huang Y., Hung Y., Tseng S. H., “An optical Target to eliminate impinging light in a light scattering simulation,” Comput. Phys. Commun. 185(10), 2504–2509 (2014). 10.1016/j.cpc.2014.05.027 [DOI] [Google Scholar]
  • 25.Steel M. J., Marks B., Rahmani A., “Properties of sub-diffraction limited focusing by optical phase conjugation,” Opt. Express 18(2), 1487–1500 (2010). 10.1364/OE.18.001487 [DOI] [PubMed] [Google Scholar]

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES