Optimal wavelength combinations for near-infrared spectroscopic monitoring of changes in brain tissue hemoglobin and cytochrome c oxidase concentrations

Abstract

We analyze broadband near-infrared spectroscopic measurements obtained from newborn piglets subjected to hypoxia-ischemia and we aim to identify optimal wavelength combinations for monitoring cerebral tissue chromophores. We implement an optimization routine based on the genetic algorithm to perform a heuristic search for discrete wavelength combinations that can provide accurate concentration information when benchmarked against the gold standard of 121 wavelengths. The results indicate that it is possible to significantly reduce the number of measurement wavelengths used in conjunction with spectroscopic algorithms and still achieve a high performance in estimating changes in concentrations of oxyhemoglobin, deoxyhemoglobin, and oxidized cytochrome c oxidase. While the use of a 3-wavelength combination leads to mean recovery errors of up to 10%, these errors drop to less than 4% with 4 or 5 wavelengths and to even less than 2% with 8 wavelengths.

1. Introduction

Near-infrared spectroscopy (NIRS) has long been recognized as a promising tool for noninvasive and real-time assessment of tissue oxygenation and metabolism. Wavelength-dependent optical attenuation signals can be resolved to extract information on biological chromophores that directly reflect the oxygenation, hemodynamic, and metabolic state of tissue site under investigation. Large penetration depth of infrared light allows for analysis of breast, muscle, and brain tissues, opening up the possibility of a wide range of clinical applications [1–4].

The potential use of NIRS as a neuromonitoring modality is particularly appealing. Numerous experimental and clinical studies have been carried out to delineate the biological basis of optical signals obtained from healthy and injured brain. These studies present sound evidence that NIRS-derived changes in chromophore concentrations can act as markers of cerebral physiology and pathology; the results offer significant insights into the feasibility of NIRS for observation of functional activation [5,6], detection of autoregulation or metabolic failure during routine surgery or after brain injury [7,8], and assessment of impending neurological damage due to hypoxia-ischemia (HI) in adults or neonates [9–11].

The main chromophores of interest in neuro-optical research are oxyhemoglobin, deoxyhemoglobin, and cytochrome c oxidase. While oxyhemoglobin and deoxyhemoglobin provide information on cerebral circulation and intravascular oxygenation, the redox state of cytochrome c oxidase is considered to be a key indicator of cellular oxygen metabolism [12–16]. Hence, a complete analysis of cerebral health is critically dependent on the ability to concurrently monitor the time course of any changes associated with all these three chromophores. As an important example, our group has recently demonstrated the significance of combined hemoglobin and cytochrome c oxidase measurements for assessment of neonatal brain injury [8].

The modified Beer-Lambert law forms the mathematical basis of spectroscopic algorithms that relate wavelength-dependent optical attenuation signals to changes in chromophore concentrations [12,17]. In theory, extraction of information on three chromophores requires measurements at only three wavelengths. Yet, such a minimalistic approach is prone to physical noise and cross-talk artifacts that may lead to inaccurate quantification of changes in chromophore concentrations and misinterpretation of experimental or clinical data. This is especially pertinent to analysis of brain signals; the cerebral concentration of cytochrome c oxidase is about an order of magnitude less compared to those of oxyhemoglobin and deoxyhemoglobin and can therefore be easily masked by the latter two chromophores [12–15]. As a general strategy, NIRS instruments are designed to collect optical attenuation signals at a multitude of wavelengths. When measurements at a large number of wavelengths are fed into spectroscopic algorithms, any detrimental effects of physical noise and cross-talk are expected to diminish. The use of many more wavelengths than necessary, however, implicates complex instrumentation that inevitably translates into bulky and costly systems. It is thus important to minimize redundancy but still ensure a robust analysis scheme through a detailed investigation into optimal wavelength combinations for cerebral monitoring.

In this study, we analyze time-dependent cerebral NIRS signals obtained from a total of 18 newborn piglets subjected to transient HI. Our system can provide measurements at 1-nm intervals between 780 and 900 nm, and we first quantify changes in chromophore concentrations using all 121 wavelengths; these results are hereafter referred to as the gold standard. We aim to significantly reduce the number of wavelengths by identifying optimal combinations that are most likely to provide accurate concentration information. Since an exhaustive search among 121 wavelengths can be computationally prohibitive due to large time complexity, we employ the genetic algorithm (GA), a popular method for solving optimization problems, to perform a heuristic search for 3-, 4-, 5-, and 8-wavelength combinations that give rise to the least possible estimation errors when compared to the gold standard. More specifically, the primary aims of this work are to (i) quantify the significance of the number of wavelengths used in conjunction with spectroscopic algorithms and (ii) suggest various combinations of discrete wavelengths for resolving changes in hemoglobin and cytochrome c oxidase concentrations. The end results of our study lay the groundwork for a guided transition to simpler NIRS systems that are more practical and cost-effective.

2. Methods

2.1 Cerebral NIRS measurements

The study described here was based on a well-established animal model of human neonatal HI and involved newborn piglets aged less than 24 h. The piglet NIRS data used have been presented in a recent publication by Bainbridge et al. [11]. As outlined therein, all experiments were carried out in accordance with UK Home Office Guidelines. Each piglet was anesthetized and surgically prepared for transient HI. Both common carotid arteries were isolated at the level of the fourth cervical vertebra and encircled by remotely controlled vascular occluders. HI was induced by remotely inflating these occluders and simultaneously lowering the fractional inspired oxygen to subnormal levels. Deflating the occluders and restoring the fractional inspired oxygen to normal levels ended the HI insult.

Transmission mode NIRS measurements were obtained with an in-house broadband system that has been detailed elsewhere [11]. An optode positioned stereotactically against the left side of the piglet head delivered light from a stabilized tungsten halogen source. The detector optode was placed against the right side of the head and directly across the source optode such that a line joining the two optodes passed through the center of the brain. Intensity spectra between 650 and 980 nm were continuously recorded before, during, and after HI using a charge-coupled device with an approximate dispersion of 1 nm per pixel and an effective resolution of less than 5 nm. These spectra were then converted into a time series of wavelength-dependent attenuation changes via a reference spectrum. Measurements from 18 different piglets produced a total of 18 datasets for further analysis.

2.2 Quantification of changes in cerebral chromophore concentrations

The modified Beer-Lambert law can be used to relate attenuation measurements to changes in cerebral chromophore concentrations. Since the total concentration of cytochrome c oxidase remains constant over the time course of our experiments [5,10,15], this law can be formulated as

$$\left[\begin{array}{c}\Delta A({\lambda }_1)\\ \Delta A({\lambda }_2)\\ \begin{array}{c}.\\ .\\ .\end{array}\\ \Delta A({\lambda }_n)\end{array}\right]=\left[\begin{array}{ccc}\beta ({\lambda }_1){\epsilon }_{Hb{O}_2}({\lambda }_1)& \beta ({\lambda }_1){\epsilon }_{HHb}({\lambda }_1)& \beta ({\lambda }_1){\epsilon }_{oxCCO-redCCO}({\lambda }_1)\\ \beta ({\lambda }_2){\epsilon }_{Hb{O}_2}({\lambda }_2)& \beta ({\lambda }_2){\epsilon }_{HHb}({\lambda }_2)& \beta ({\lambda }_2){\epsilon }_{oxCCO-redCCO}({\lambda }_2)\\ \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ .\end{array}\\ \beta ({\lambda }_n){\epsilon }_{Hb{O}_2}({\lambda }_n)& \beta ({\lambda }_n){\epsilon }_{HHb}({\lambda }_n)& \beta ({\lambda }_n){\epsilon }_{oxCCO-redCCO}({\lambda }_n)\end{array}\right]\left[\begin{array}{c}\Delta [Hb{O}_2]\\ \Delta [HHb]\\ \Delta [oxCCO]\end{array}\right],$$ (1)

where ΔA(λ₁) through ΔA(λ_n) are the attenuation changes measured at n different wavelengths λ₁ through λ_n, β(λ₁) through β(λ_n) are the respective differential pathlengths, and ∆[HbO₂], ∆[HHb], and ∆[oxCCO] denote changes in concentrations of oxyhemoglobin, deoxyhemoglobin, and oxidized cytochrome c oxidase. Note that ε_HbO2 and ε_HHb represent the specific extinction coefficients of oxyhemoglobin and deoxyhemoglobin, whereas ε_{oxCCO−redCCO} represents the difference between the specific extinction coefficients of oxidized and reduced forms of cytochrome c oxidase.

Our analysis initially employed a total of n = 121 wavelengths spaced at 1-nm intervals between 780 and 900 nm. The values of ε_HbO2, ε_HHb, and ε_{oxCCO−redCCO} were obtained from [12]. A baseline optical pathlength was first estimated using the second differential of the 840-nm water feature and assuming a fixed cerebral water content of 85% [11]; wavelength-dependent correction factors were then applied to calculate β(λ₁) through β(λ_n) [9,11,17–19]. The differential pathlengths calculated for all 18 datasets averaged to 24.3 cm at 780 nm and to 19.8 cm at 900 nm, implying a ~19% decrease over the wavelength range considered. Solving Eq. (1) in a least-squares sense for each time point of a dataset generated the corresponding concentration changes in the piglet brain over the experimental period. It is important to point out that ∆[HbO₂], ∆[HHb], and ∆[oxCCO] are defined to be zero at the first measurement point such that the subsequent time-dependent changes are all relative to this first measurement. As indicated before, these results obtained with n = 121 wavelengths represent the gold standard values that can be used for benchmarking purposes [12].

2.3 GA-based search for optimal wavelength combinations

The most straightforward method to determine k optimal wavelengths for cerebral monitoring is to test all possible k-element combinations out of n = 121 wavelengths and to identify the combination that produces the smallest estimation errors when benchmarked against the gold standard. Even though such an exhaustive search is feasible for small k, the number of possible combinations to process, ⁿC_k, increases very rapidly with increasing k resulting in a prohibitively large time complexity. We hence resort to a GA-based approach in order to expedite the search through an optimization scheme.

Extensive details on the formulation and implementation of the GA can be found in [20]. Briefly, this is a heuristic that mimics biological evolution, which is effectively a method for searching among a larger number of possible solutions. The algorithm begins by creating a random initial population of individual solutions. At each step, three main operators are used to create the next generation from the current population. The selection operator selects parents that contribute to the next generation; individuals that conform better to a predetermined fitness criterion are generally selected as parents. Best-fit or elite individuals are also automatically passed to the next generation. The crossover operator combines two parents to create potentially superior children. Finally, the mutation operator applies random changes to individual parents and thereby adds to diversity. Over successive generations, the population evolves toward an optimal solution. A schematic diagram of the overall algorithm is provided in Fig. 1 .

Fig. 1.

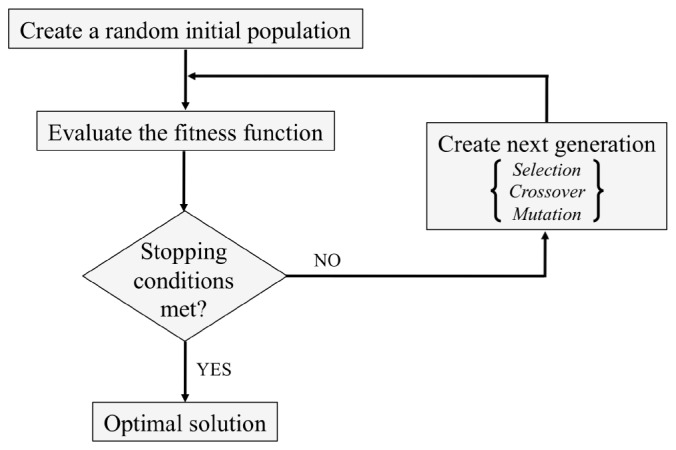
Schematic diagram of the GA. Evolution over successive generations through the selection, crossover, and mutation operators leads to an optimal solution.

In the context of our study, individual solutions are k-element wavelength combinations, where k = 3, 4, 5, or 8. The fitness function to be minimized is the normalized root mean square error (NRMSE_k) defined as

$$NRMS{E}_k=\sqrt{\frac{{\displaystyle \sum _{i=t_1}^{t_2}{\displaystyle \sum _{j=1}^3{\left(\Delta {[c_j]}_k(i)-\Delta {[c_j]}_n(i)\right)}^2}}}{{\displaystyle \sum _{i=t_1}^{t_2}{\displaystyle \sum _{j=1}^3{\left(\Delta {[c_j]}_n(i)\right)}^2}}}}.$$ (2)

Here, c_j represents the jth chromophore with j = 1, 2, and 3 corresponding to HbO₂, HHb, and oxCCO, respectively. Concentration changes estimated with a given k-wavelength combination at time point i are denoted by ∆[c_j]_k(i), whereas the gold standard results obtained with all n = 121 wavelengths are denoted by ∆[c_j]_n(i). Note that NRMSE_k is computed only over the period of HI. Hence, time indices t₁ and t₂ roughly indicate the start and end of this period.

The GA routine employed in this work has been implemented in MATLAB^® (The MathWorks, Inc., Natick, MA) using the Global Optimization Toolbox. The selection function was specified to be ‘Stochastic uniform’, whereas the crossover and mutation functions were custom written. As detailed in [21], special efforts were made to fine-tune user-defined parameters such as the population size and the number of generations and to refine stopping conditions for optimized convergence. It is also important to note that the resolution of our NIRS system led to an additional search constraint: the interval between successive wavelengths in a given combination was set to be at least 5 nm. Since the algorithm is random in nature, multiple runs were conducted for each case under consideration and the output with the minimum NRMSE_k was recorded. For k = 8, the number of runs required to ensure convergence to the global minimum with a precision of 10⁻⁴ was empirically determined to be 200. The very same number of runs was then used for all k to maintain consistency.

We performed our GA-based search for optimal wavelength combinations on a per-piglet basis. Analysis of each dataset separately proved advantageous in revealing the extent of inter-subject variability. The results were then partitioned into k = 3, 4, 5, or 8 clusters using the k-means clustering algorithm provided in the Statistics Toolbox of MATLAB^®. For this algorithm, the distance measure was specified to be ‘squared Euclidean’, the maximum number of iterations allowed was 100, and the number of replicates with random starting points was set to 20.

3. Results

3.1 Cerebral monitoring during transient HI

Figure 2 shows a sample dataset of NIRS attenuation changes over the wavelength range of 780-900 nm and the corresponding gold standard values of ∆[HbO₂], ∆[HHb], and ∆[oxCCO]. Spectral measurements have a 1-min time resolution, but only a selected few are displayed for clarity [Fig. 2(a)]. The concentration changes, on the other hand, are plotted at 1-min intervals with pre-HI, HI, and post-HI periods clearly labeled [Fig. 2(b)]. For this piglet, time point i = t₁ = 20 marks the beginning of HI, whereas time point i = t₂ = 66 marks the end of HI. The results are representative of the general trends observed in all our datasets: HI is associated with an increase in [HHb] and a decrease in [HbO₂] and [oxCCO]. After the insult is removed, a recovery back toward pre-HI values ensues.

Fig. 2.

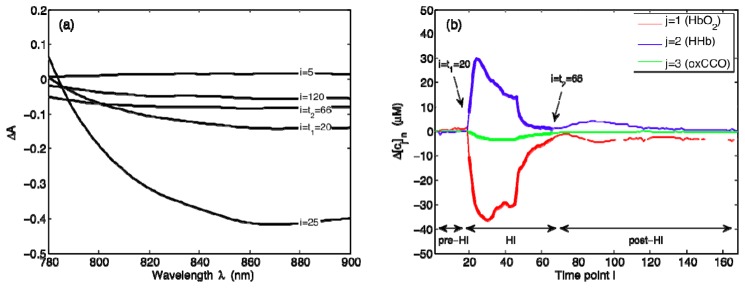
NIRS-based quantification of changes in cerebral chromophore concentrations. (a) Sample ∆A measurements at selected time points i, and (b) gold standard values of Δ[c_j], where c_j represents the jth chromophore with j = 1, 2, and 3 corresponding to HbO₂, HHb, and oxCCO, respectively. Time points i are in minutes. For this representative dataset, i = t₁ = 20 marks the beginning of HI and i = t₂ = 66 marks the end of HI.

3.2 GA results

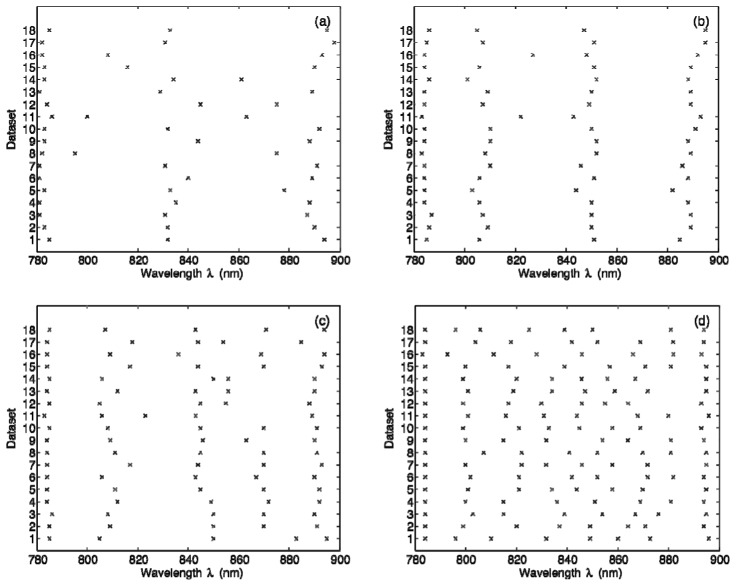
Figure 3 shows the results of our GA-based search for optimal wavelength combinations. The wavelengths obtained for all 18 datasets are displayed separately for k = 3, 4, 5, and 8 [Figs. 3(a)–3(d)]. Note that NRMSE_k values achieved for different piglet datasets average to 0.0135 for k = 3, 0.0068 for k = 4, 0.0048 for k = 5, and 0.0022 for k = 8.

Fig. 3.

GA-derived optimal wavelength combinations for (a) k = 3, (b) k = 4, (c) k = 5, and (d) k = 8. The results are displayed separately for all 18 datasets.

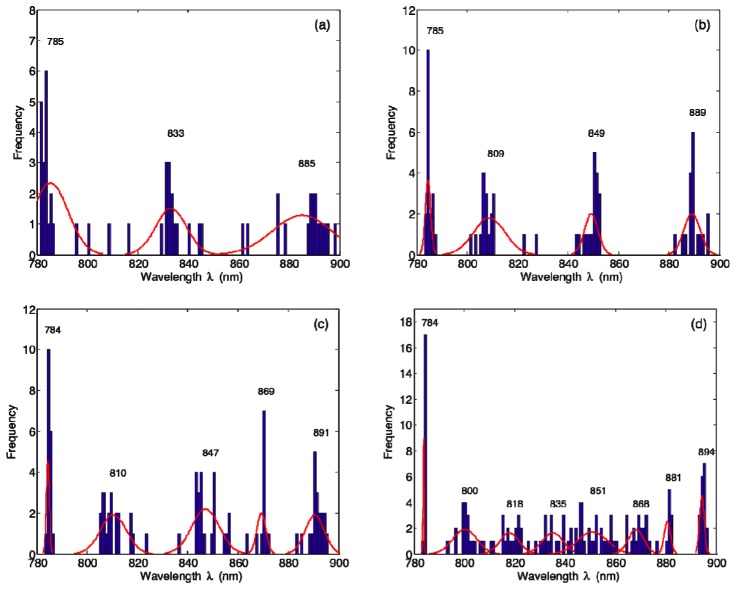
Our GA results are plotted in Fig. 4 as histograms of binned wavelengths, again separately for k = 3, 4, 5, and 8 [Figs. 4(a)–4(d)]. The results of k-means clustering applied to GA-derived wavelengths are shown in Table 1 , where the centroid positions and within-cluster standard deviations of point-to-centroid distances have been rounded to the nearest integer. These clustering results are also displayed in Fig. 4 as Gaussian curves overlaid on the histograms; each curve has been normalized to the mean frequency of its respective cluster.

Fig. 4.

Histograms of GA-derived optimal wavelength combinations for (a) k = 3, (b) k = 4, (c) k = 5, and (d) k = 8. The results of k-means clustering applied to GA-derived wavelengths are displayed as Gaussian curves overlaid on the histograms; these curves have been generated using the values reported in Table 1 and each has been normalized to the mean frequency of its respective cluster.

Table 1. Results of k-means clustering applied to GA-derived wavelengths. Centroid positions are reported along with within-cluster standard deviations of point-to-centroid distances, all rounded to the nearest integer.

k		Centroid wavelengths ± within-cluster standard deviations (nm)
3		785 ± 8	833 ± 7	885 ± 10
4		785 ± 1	809 ± 6	849 ± 3	889 ± 3
5		784 ± 1	810 ± 5	847 ± 5	869 ± 2	891 ± 4
8		784 ± 0	800 ± 3	818 ± 3	835 ± 4	851 ± 6	868 ± 5	881 ± 1	894 ± 1

Figure 5 presents an overlay of the centroid wavelengths reported in Table 1 and the specific extinction coefficients ε_HbO2, ε_HHb, and ε_{oxCCO−redCCO} over the wavelength range of 780-900 nm. It appears that the wavelengths for each k evenly span the entire spectral range with no particular grouping pattern. There is also no evidence of any correlation between these clustering results and the spectral profiles of the extinction coefficients.

Fig. 5.

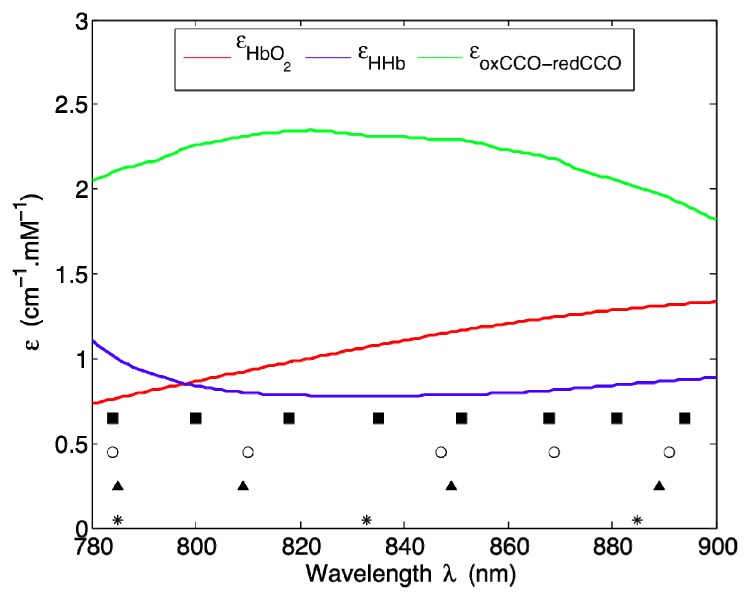
Overlay of the centroid wavelengths listed in Table 1 and the specific extinction coefficients ε_HbO2, ε_HHb, and ε_{oxCCO−redCCO} over the wavelength range of 780-900 nm.

3.3 Performance assessment of GA results

It is important to verify that the centroid wavelengths listed in Table 1 can indeed provide a common basis for accurate quantification of concentration information. Figure 6 exemplifies how the estimated changes in cerebral chromophore concentrations differ from the gold standard values when these k-wavelength combinations are used in conjunction with Eq. (1). Note that the dataset considered here is the same as the one shown in Fig. 2 and the estimation errors are plotted only over the period of HI. It is obvious that ∆[HbO₂], ∆[HHb], and ∆[oxCCO] differ significantly from their gold standard counterparts for k = 3, but the errors tend toward zero as k increases [Figs. 6(a)–6(c)]. Similar trends are observed for other datasets as well.

Fig. 6.

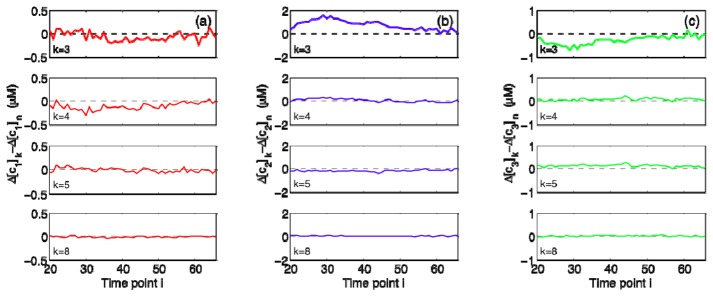
Estimation errors for ∆[c_j], where c_j represents the jth chromophore with j = 1, 2, and 3 corresponding to (a) HbO₂, (b) HHb, and (c) oxCCO, respectively. Time points i are in minutes. The dataset considered here is the same as the one shown in Fig. 2 and the errors for each k-wavelength combination listed in Table 1 are plotted only over the period of HI.

We use four different error metrics to present an overall performance assessment of the wavelength combinations listed in Table 1. The first metric is NRMSE_k defined in Eq. (2). The other three are percent absolute errors (PAE_k) for ∆[HbO₂], ∆[HHb], and ∆[oxCCO] averaged over HI time points. Table 2 provides the means and standard errors of these metrics computed over all 18 datasets. The results point to diminishing errors with increasing k; the standard errors reported suggest that this behavior is consistent across all the datasets considered.

Table 2. Error metrics computed for each k-wavelength combination listed in Table 1. The means and standard errors reported for NRMSE_k and time-averaged PAE_k are over all 18 datasets.

			Time-averaged PAEk for ∆[cj]
k		NRMSEk	j = 1 (HbO2)	j = 2 (HHb)	j = 3 (oxCCO)
3		0.0342 ± 0.0034	2.83% ± 0.70%	5.09% ± 0.67%	10.03% ± 1.10%
4		0.0133 ± 0.0012	1.30% ± 0.26%	2.42% ± 0.40%	3.25% ± 0.40%
5		0.0102 ± 0.0014	1.09% ± 0.25%	1.77% ± 0.34%	3.06% ± 0.51%
8		0.0052 ± 0.0007	0.46% ± 0.08%	1.17% ± 0.24%	1.48% ± 0.13%

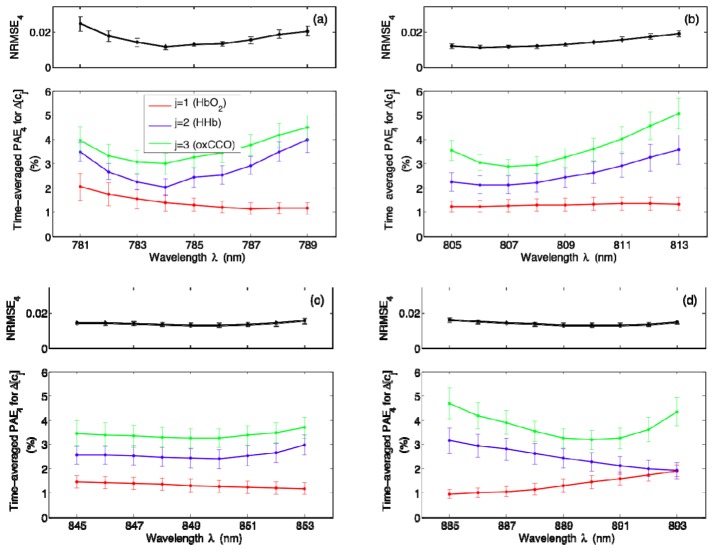
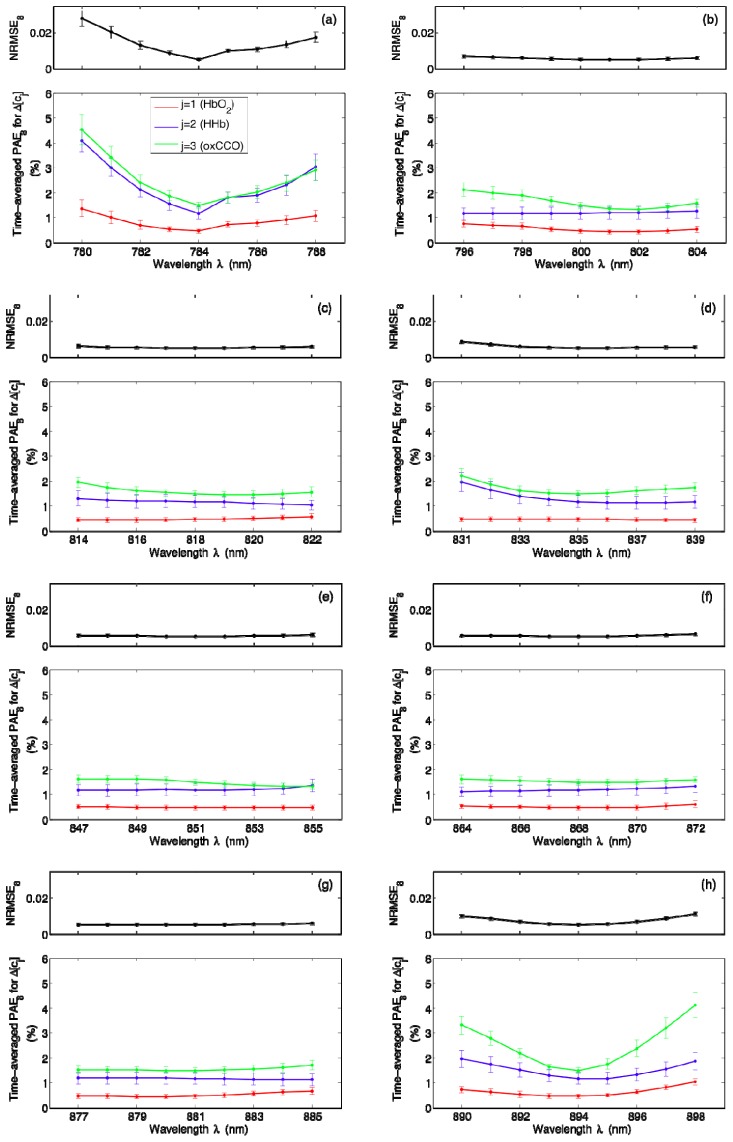
In order to determine how sensitive our NIRS algorithm is to any small shifts from the centroid wavelengths, we perturb each wavelength one at a time up to ± 4 nm while keeping other wavelengths fixed and we compute the error metrics corresponding to these new combinations. The results for k = 4 are displayed in Fig. 7 , where the means and standard errors plotted are over all 18 datasets. It is clear that small shifts can indeed lead to changes in estimation errors; time-averaged PAE₄ for ∆[oxCCO] appears to be quite prone to shifts in individual wavelengths [Figs. 7(a), 7(b), and 7(d)], whereas time-averaged PAE₄ for ∆[HbO₂] is mostly characterized by a relatively flat wavelength profile [Figs. 7(b) and 7(c)]. Figure 8 shows a similar set of results for k = 8. Although time-averaged PAE₈ for ∆[HHb] and ∆[oxCCO] are especially prone to small shifts from the first and last centroid wavelengths [Figs. 8(a) and 8(h)], perturbing intermediate wavelengths does not seem to cause significant deterioration in algorithm performance as evidenced by negligible changes in all of the error metrics presented [Figs. 8(b)–8(g)].

Fig. 7.

Wavelength dependence of NRMSE₄ and time-averaged PAE₄ for ∆[c_j], where c_j represents the jth chromophore with j = 1, 2, and 3 corresponding to HbO₂, HHb, and oxCCO, respectively. Each of the four wavelengths listed in Table 1 is perturbed one at a time up to ± 4 nm and the resulting error metrics are plotted in (a)–(d). The means and standard errors shown are over all 18 datasets.

Fig. 8.

Wavelength dependence of NRMSE₈ and time-averaged PAE₈ for ∆[c_j], where c_j represents the jth chromophore with j = 1, 2, and 3 corresponding to HbO₂, HHb, and oxCCO, respectively. Each of the eight wavelengths listed in Table 1 is perturbed one at a time up to ± 4 nm and the resulting error metrics are plotted in (a)–(h). The means and standard errors shown are over all 18 datasets.

4. Discussion

A major goal of the study presented here was to reveal the significance of wavelength optimization for resolving changes in brain tissue chromophore concentrations. Our main findings can be outlined as follows: (i) the optimal 3-wavelength combination gives reasonable results for ∆[HbO₂] and ∆[HHb], but not for ∆[oxCCO], (ii) increasing the number of wavelengths to 4, 5, and 8 can lead to a ~2-, 3-, and 7-fold improvement in estimation accuracy, respectively, and (iii) the optimal 8-wavelength combination is highly recommended for simultaneous assessment of ∆[HbO₂], ∆[HHb], and ∆[oxCCO].

Wavelength optimization is undoubtedly a requisite for designing efficient and high-performing optical monitoring and imaging tools. Various strategies have recently been proposed to identify optimal wavelength combinations for analysis of different tissue sites using NIRS or other optical modalities. These include adoption of analytical or model-driven performance metrics to minimize chromophore cross-talk and to maximize separability [22–29], recursive elimination of extraneous wavelengths [30], and implementation of GA-based search routines that can be applied to experimental, clinical, or model-generated data [31]. Our group has collected a significant amount of cerebral NIRS measurements from newborn piglets over the past several years; this has motivated us to implement a GA-based routine and to perform a heuristic search for wavelength combinations that can provide accurate information on HI-induced changes in cerebral chromophore concentrations. In order to verify that the routine we implemented was indeed capable of identifying wavelength combinations with the least possible estimation errors, we carried out an exhaustive search for k = 3 over all possible combinations. Both methods generated the same output, offering evidence into the validity of our GA-based optimization approach.

Overall, the GA results plotted in Fig. 3 point to different optimal wavelength combinations for different piglet datasets, but a high degree of clustering around the centroid wavelengths is evident in all the histograms presented in Fig. 4. Consistently small within-cluster standard deviations listed in Table 1 are also in line with this observation. We can hence conclude that even though inter-subject variability is inevitable, the centroid wavelengths are likely to represent spectral positions that are most suitable for cerebral monitoring in general. Note that as illustrated in Fig. 5, all three cerebral chromophores have broad spectral profiles. It is thus not possible to visually inspect the wavelength dependence of specific extinction coefficients and directly infer which wavelength combinations can be used to best resolve these chromophores. This serves as yet another justification for the systematic approach we adopted for our optimization study.

It has been previously reported that the performance of spectroscopic algorithms can be greatly improved by increasing the number of measurement wavelengths [12]. The results of our analysis are in full agreement with this assertion. The trends depicted in Fig. 6 and the error metrics listed in Table 2 indicate that the use of a 3-wavelength combination is not sufficient for simultaneous assessment of ∆[HbO₂], ∆[HHb], and ∆[oxCCO]. Incorporation of additional wavelengths leads to a consistent decrease in NRMSE_k and time-averaged PAE_k; the level of accuracy achieved with k = 8 is especially promising as it appears that concentration changes can all be recovered with mean errors of less than 2%. These findings reveal the redundancy associated with the use of all 121 wavelengths and provide guidelines for refined cerebral measurements. As is evident from Figs. 7 and 8, the centroid wavelengths listed in Table 1 can indeed be considered to be optimal, especially when their respective within-cluster standard deviations are small due to a high degree of clustering. In such cases, small shifts from the centroid wavelengths can negatively affect the performance of NIRS algorithms. It is also important to note that time-averaged PAE_k for ∆[oxCCO] tends to be particularly sensitive to wavelength perturbations; the mean values for k = 4 and 8 are characterized by up to a ~2- and 3-fold increase, respectively, over a range of ± 4 nm. This is not surprising since the inherently low cerebral concentration of cytochrome c oxidase renders the recovery of ∆[oxCCO] most challenging.

In fact, there has been much debate on how reliable it is to quantify ∆[oxCCO] from cerebral NIRS signals in the presence of significantly higher concentrations of oxyhemoglobin and deoxyhemoglobin. It has been claimed that chromophore cross-talk, insufficient separability due to physical noise, and any concurrent changes in scattering can all give rise to spurious ∆[oxCCO] traces [12,22]. Yet, recent studies disprove these claims and establish ∆[oxCCO] as a NIRS-derived indicator of the redox state of mitochondrial cytochrome c oxidase and hence as a brain-specific optical biomarker of cerebral metabolic status [5,8–11,14,15,32,33]. Also note that our study employs a restrictive wavelength range of 780-900 nm; exclusion of shorter wavelengths helps to enhance the contribution of cytochrome c oxidase to attenuation signals [14]. Further, this chromophore is expressed predominantly in deeper brain regions [5,10] that are thoroughly probed with our transmission mode measurements.

Currently, there are no commercial NIRS instruments that measure ∆[oxCCO]. Early-generation systems of the NIRO series, namely the NIRO-1000, 500, and 300 (Hamamatsu Photonics K.K., Hamamatsu City, Japan), enabled measurement of ∆[oxCCO], but these systems are no longer available [34]. The NIRO-1000 used 6 wavelengths (780, 808, 830, 847, 867, and 911 nm), while the NIRO-500 used 4 wavelengths (775, 810, 870, and 904 nm); a comparative assessment of the performance of these two systems in resolving ∆[oxCCO] can be found in [12]. The NIRO-300 was also a 4-wavelength system that typically used 775, 810, 850, and 910 nm [35,36]. The particular choice of wavelengths was mainly dictated by the availability of laser sources at the time of development of these instruments and attempts were made to equally distribute the wavelengths across the near-infrared range from 770 nm and above. Current research instruments for measuring ∆[oxCCO], on the other hand, are broadband systems [5,8,10,11,37,38].

From a practical viewpoint, our proposed NIRS wavelengths are well within the range of what is available from LED sources made of AlGaAs-type materials. The results of our optimization study can hence be readily applied to develop compact and cost-effective NIRS systems capable of resolving ∆[HbO₂], ∆[HHb], and ∆[oxCCO]. It is also important to note that the potential ease of implementation was the main reason for limiting the analysis presented to combinations of a maximum of 8 wavelengths; the use of more populous combinations would raise feasibility issues and defeat the original purpose of our work. After all, the optimal 8-wavelength combination yields the desired level of accuracy for monitoring HI-induced changes in cerebral chromophore concentrations.

On a related matter, the level of accuracy required for quantification of ∆[HbO₂], ∆[HHb], and ∆[oxCCO] largely depends on the specific clinical application under consideration. For example, changes in chromophore concentrations during functional activation are usually an order of magnitude less compared to changes due to physiological insults such as hypoxia, hypocapnia, and hypercapnia. In addition, even though a sub-μM accuracy may be sufficient for ∆[HbO₂] and ∆[HHb], an extra order of magnitude is needed for ∆[oxCCO]. This can be achieved with the optimal 8-wavelength combination, making our results potentially applicable to various clinical contexts. We intend to carry out further validation tests in order to assess whether the results presented here generalize to other measurement systems and to other clinically relevant models.

As a final remark, we point out that even though our GA-based approach is an effective strategy for data-driven wavelength optimization, a simulation-based extension of this study is likely to prove useful in interpreting the empirical results obtained. The Monte Carlo method [39–41] can provide a flexible modeling framework to simulate specific experimental or clinical conditions and to assess the contribution of each of the three chromophores to attenuation signals at different wavelengths. There is no doubt that such a comprehensive sensitivity analysis will be instrumental in revealing the physical basis of optical measurements obtained from brain tissues.

5. Conclusions

In summary, the research presented here highlights the importance of a systematic approach to identifying optimal wavelength combinations for NIRS-based cerebral monitoring. Our analysis indicates that the optimal 3-wavelength combination (785, 833, and 885 nm) leads to mean errors of up to 10% in estimating ∆[HbO₂], ∆[HHb], and ∆[oxCCO]. Increasing the number of wavelengths to 4 (785, 809, 849, and 889 nm) or 5 (784, 810, 847, 869, and 891 nm), however, reduces mean errors to less than 4%. The optimal 8-wavelength combination (784, 800, 818, 835, 851, 868, 881, and 894 nm) is quite promising with mean errors of less than 2%. These results suggest that it is possible to significantly reduce the number of measurement wavelengths used in conjunction with spectroscopic algorithms and still achieve a high performance in estimating changes in cerebral chromophore concentrations. Such a design simplification is expected to improve the clinical adaptability and utility of NIRS systems.