Summary
Motions are essential for protein function, and knowledge of protein dynamics is a key to our understanding the mechanisms underlying protein folding and stability, ligand recognition, allostery, and catalysis. In the last two decades, NMR relaxation measurements have become a powerful tool for characterizing backbone and side chain dynamics in complex biological macromolecules like proteins and nucleic acids. Accurate analysis of the experimental data in terms of motional parameters is an essential prerequisite for developing physical models of motions in order to paint an adequate picture of protein dynamics. Here I describe in detail how to use the software package DYNAMICS that was developed for accurate characterization of the overall tumbling and local dynamics in a protein from nuclear spin-relaxation rates measured by NMR. Step by step instructions are provided and illustrated through analysis of 15N relaxation data for protein G.
Keywords: Relaxation, protein dynamics, order parameter, spectral density, dipolar coupling, chemical shift anisotropy, CSA, overall tumbling, rotational diffusion tensor, monomer-dimer equilibrium
1. Introduction
Proteins are molecular nanomachines. Understanding of how they work requires detailed knowledge of not only their three-dimensional structure but also of various motions that take place in a protein and the roles they play in protein’s folding and stability, ligand recognition, allostery, and catalysis. NMR is perhaps the most powerful analytical tool in structural biology, because it is capable of providing site-specific information on the structure, dynamics, and electronic environment of essentially any nucleus in a molecule, even as complex as a protein or nucleic acid. Moreover, solution NMR methods allow studies of molecules in their native milieu, the reporter groups used do not cause any structural perturbations, and the applied magnetic fields are still so weak compared to the thermal energy that they do not affect molecular structure or dynamics.
Recent decades witnessed a burst in NMR studies of protein motions (reviewed in (1)). A popular reporter group for protein dynamics studies has been the N-H group, for several reasons, most importantly: 1H-15N is an isolated spin-pair (to a good approximation), conveniently located in the backbone and abundant in proteins which, combined with the oftentimes good spread of NMR signals in the 1H-15N correlation spectra, allows almost complete coverage of a protein sequence (except prolines), and 15N enrichment is relatively easy and affordable. There is growing interest in developing and extending the NMR methodology (see e.g. (2, 3)) to understand motions in other groups in a protein, both in the backbone (CO, C'-Cα, CαHα) and in the side chains (e.g. methyl groups).
The underlying concept of NMR being a sensitive tool for accessing equilibrium protein dynamics is that nuclear spin relaxation is caused by modulation (by the overall and internal motions) of the magnetic field sensed by a nucleus under observation. This field is a result of magnetic interactions (dipolar and scalar) with the magnetic moments of surrounding nuclei and of perturbations in the electronic environment of the nucleus, resulting in the shielding effect. All of these mechanisms contribute to nuclear-spin relaxation, albeit to a different extent. Modulation of dipolar coupling can be caused by reorientation of the internuclear vector as well as variation in its length. For a bonded pair of atoms, bond vibrations are usually very fast (on the NMR time scale) and therefore do not contribute to nuclear-spin relaxation rates directly (except for an altered effective bond length). Likewise, the effect of motions on the chemical shift (shielding) tensor could be envisioned as a reorientation of the tensor, as well as a modulation of its principal components. The former contributes in a similar way as reorientation of the dipolar coupling while the latter could lead to the so-called conformational (or chemical) exchange contributions to relaxation. Note that unlike the dipolar coupling, the shielding tensor generally is not axially symmetric; however, a fully anisotropic tensor can always be presented as a sum of two axially symmetric tensors, and for each of them the above statement applies.
I will not describe in this chapter how relaxation rates are measured, this information can be found in various sources, e.g. (4). Instead, here I focus on how these rates can be analyzed.
1.1 The underlying equations
The experimental spin relaxation parameters (longitudinal and transverse relaxation rates, R1 and R2, and the steady-state heteronuclear NOE) are directly related to power spectral densities, J(ω), which are Fourier transforms of the corresponding correlation functions describing reorientations of the internuclear vector of interest. In the case of the backbone amide 15N nucleus, the major sources of 15N spin relaxation are modulations by motions of (i) the dipole-dipole interaction (=dipolar coupling) of the nuclear magnetic moment of 15N with that of the directly bonded 1H, and (ii) the anisotropy of the 15N chemical shift tensor (CSA). The standard equations read:
| (1) |
| (2) |
| (3) |
Here d = −(μo/(4π)γHγNh/(4πrHN3) is the strength of the 15N-1H dipolar coupling, c = −ωN·CSA/3, ωH and ωN are the resonance frequencies of 1H and 15N, respectively, and Rex is the conformational exchange contribution (if any) to measured R2. These equations assume that the effects of reorientational motion on the 1H-15N dipolar interaction and on the 15N CSA can be described by the same auto-correlation function. Corrections to the above equations that account for noncollinearity of these two interactions are discussed in (5).
Eqs 1–3 provide the basis for extracting information on protein dynamics from NMR relaxation measurements. Given the experimental data, the primary objectives here are (i) to determine the spectral densities J(ω) and, most importantly, (ii) to translate them into an adequate physical picture of protein dynamics. As it is generally impossible to determine all parameters of complex motions from a limited set of measurements, the latter objective requires adequate theoretical models of motion that can be obtained from comparison with molecular dynamics simulations (e.g. (6–8)). Nevertheless, accurate analysis of experimental data (objective (i)) is an essential prerequisite for such a comparison.
Extracting the spectral densities directly from Eqs 1–3 is problematic because this system of equations in underdetermined: the number of unknowns (d, c, J(ω)’s, and possibly Rex) exceeds the number of available experimental data (e.g. (9)). A widely accepted way to circumvent this problem, the so-called “model-free” approach (10, 11), is based on a rather simple parameterization of the spectral density function by approximating the correlation function describing local dynamics as mono-exponential
| (4) |
In this parameterization, τloc has the meaning of the correlation time of the bond’s motion, and the angular amplitude of bond reorientations is characterized by the so-called squared order parameter, (S2), a dimensionless measure of the amplitude on a scale from 0 to 1: S2=0 for unrestricted bond motions, while S2=1 when this motion is completely restricted. Assuming that the strength of the dipolar coupling (d) and the 15N CSA term (c) are known, this leaves only two fitting parameters (three if Rex is present), S2 and τloc, to be determined for each residue, because the overall tumbling of the molecule is described by a small number of global parameters (see below).
It was found however, that analysis of 15N relaxation data in proteins sometimes requires a more complex, dual-exponential parameterization (the so-called “extended model-free” model (12)):
| (5) |
This correlation function represents a superposition of two independent motions "fast” and “slow”, characterized by the corresponding order parameters (Sfast2 and Sslow2) and correlation times (τfast and τslow) and occurring on entirely separated time scales: τfast ≪ τslow. Note that for consistency with Eq.4, here I introduced the generalized order parameter S2 that represents the total amplitude of the combined motion: S2 = Sslow2 Sfast2. In this chapter I will refer to the model-free characteristics of local motion (S2, τloc or Sfast2, τfast,S2, τslow) as well as Rex as microdynamic parameters. Various parameterizations of the correlation function Cloc(t) will be referred to as models of local motion.
If there is no correlation between the local dynamics and the overall rotational diffusion of a molecule, as assumed in the model-free approach, the total correlation function that determines J(ω) and hence the rates of 15N relaxation (Eqs. 1–3) can be written in the following form
| (6) |
where Covrl(t) is the autocorrelation function describing the overall tumbling of a rigid molecule characterized by the (generally anisotropic) rotational diffusion tensor D͇ (13, 14). In the simplest case of isotropic overall tumbling with a correlation time τc, . In the case of rotational anisotropy, the expressions for Covrl(t) are more complex and depend on the bond’s orientation with respect to the diffusion tensor frame (see e.g. (15)). The corresponding equations can be found, for example, in (13, 14, 16). Recall that Fourier transforms of C(t) give the power spectral densities J(ω) in Eqs 1–3. For example, in the case of isotropic rotation diffusion, combining Eqs 4 and 6 gives
| (7) |
and 1/τe = 1/τc + 1/τloc.
Numerous studies in the last two decades (by NMR relaxation, as well as MD simulations, e.g. (6, 7)) revealed quite restricted backbone motions in well-ordered regions (secondary structure) in proteins, with the amplitudes of S2~0.87, whereas significantly lower S2 (reflecting greater amplitudes) are often observed in the flexible unstructured regions, such as loops and termini. Likewise, the associated time scales (τloc or τfast) are in the 1–100 ps range for protein-core elements and slower, up to several nanoseconds (τslow) in the flexible parts, possibly reflecting concerted motion of several residues or segments.
It should be pointed out that the information about protein motions is limited by the time window imposed by the overall tumbling. Being unrestricted, the overall tumbling eventually averages both the dipolar- the CSA-related energies to zero, such that there is essentially nothing left for slower motions to modulate, except for the principal values of the dipolar or chemical shift tensors. The latter modulation manifests itself in the so-called chemical- or conformational exchange processes, which provide access to motions slower than τc and have been studied quite extensively recently (e.g. (17)).
In this chapter I describe the use of computer program DYNAMICS(18, 19) designed to extract parameters characterizing protein motions from NMR-measured spin-relaxation parameters. For convenience, italic Arial font is used throughout the text to indicate the names of the parameters in DYNAMICS. Courier font is used to indicate Matlab commands and screen output messages; the lines containing Matlab commands throughout this chapter begin with the Matlab prompt (≫).
2. Description of DYNAMICS software
2.1 Highlights of the program DYNAMICS
DYNAMICS is a computer program for model-free analysis of spin relaxation data. The current version of the program (version 3.0) includes the following features
Overall tumbling. All possible models of the overall rotational diffusion are allowed: isotropic, axially symmetric, and fully anisotropic. The overall rotational diffusion tensor can be an input variable, but can also be determined simultaneously with the model-free analysis of the relaxation data.
Multiple-field data. Simultaneous or separate analysis of experimental data from measurements at multiple magnetic fields. Data sets at various fields do not have to be complete.
Chemical shift anisotropy. The CSA can be treated as uniform (fixed) or site-specific, the program also allows determining site-specific CSA values simultaneously with data analysis.
Monomer-dimer equilibrium. The program allows data analysis when the molecule of interest exists in a fast dynamic equilibrium between monomeric and dimer states.
2.2 The overall organization of the program
The overall organization of DYNAMICS is depicted in the flowchart in Figure 1. The program is written in Matlab (The MathWorks, Inc); the current version of the program is compatible with Matlab versions 6.5 and newer. It will be assumed here that the user is familiar with very basic Matlab commands that allow loading and saving data and navigation to the desired folder/directory.
Figure 1.
Flowchart of the program DYNAMICS
2.3 Treating the overall rotational diffusion of a molecule
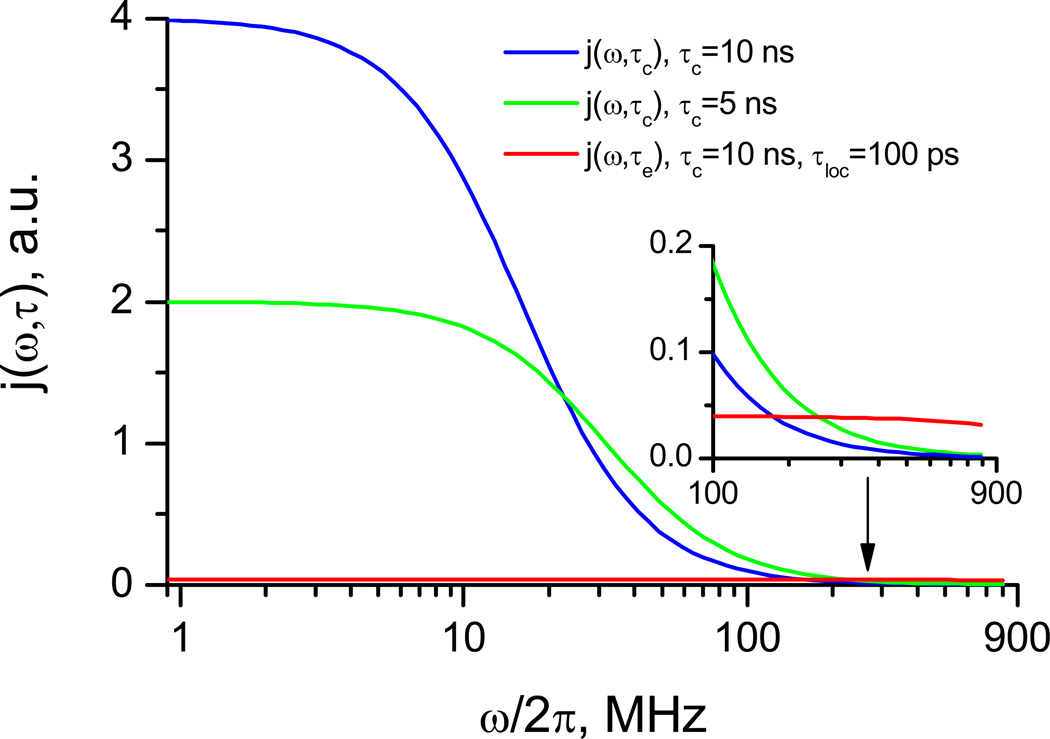
As shown in Figure 2, the contribution to the spectral density function from the overall tumbling is quite substantial (if not dominant), and often overshadows that from local motions. As our main goal here is to characterize internal motions, accurate treatment of the overall tumbling is absolutely critical for accurate analysis of the local dynamics in a protein (20). Thus, the first and foremost step in relaxation data analysis is to determine, and “subtract”, the contribution from the overall tumbling. Significant attention in the past was paid to developing tools for accurate analysis of the overall rotational diffusion (16, 21–28).
Figure 2.
Relative contributions to the power spectral density J(ω) from the overall tumbling and local motion. Shown as a function of frequency ω are j(ω,τc) (see Eq 7) for τc = 5 ns (green) and 10 ns (blue), and j(ω,τe) for τloc = 100 ps and τc =10 ns (red). The factors S2 and (1–S2) are not included.
In principle, the overall rotational diffusion can also be characterized simultaneously with the analysis of local dynamics, and in fact, DYNAMICS includes a mechanism for doing this (see Sections 3.2, 3.3). However, beyond the simplest case of isotropic tumbling, this determination becomes less straightforward and can require significant effort, as multiple parameters need to be optimized manually,. Therefore, if protein atom coordinates are available, the most straightforward and reliable way to characterize the overall rotational diffusion is directly from relaxation data and separately from (and prior to) the analysis of local motions. The underlying reason for this is based on the fact that, for well-defined structural regions in a protein, the “reduced” relaxation rates R1’ and R2’ are both proportional (to a good approximation) to the squared order parameter. (The “reduction” is achieved by subtracting from Eqs 1–2 the contributions from the high-frequency components, J(ωH) and J(ωH±ωN), of the spectral density function, e.g. (27)) Thus the R2’/R1’ratio is S2-independent, and the determination of the overall motion can be de-convoluted (hence performed separately) from the analysis of local protein dynamics (22, 26, 27, 29). Moreover, as discussed in (26, 27, 29, 30), the R2’/R1’ratio is independent of site-specific variations in the actual values of d and c (Eqs 1–2), and therefore depends solely on the structure of a protein (i.e. orientations of the NH bonds with respect to the diffusion tensor axes) and on the diffusion tensor itself (22).
This concept is implemented in the computer program RotDif (26) available online from our website: http://gandalf.umd.edu/FushmanLab/. The use of this program is illustrated in (26–28), therefore we do not describe these steps in detail here. Briefly, the RotDif program uses NH-vector coordinates and relaxation rates, R1, R2, as well as NOE (if available) as input parameters, and outputs the principal components of the diffusion tensor D͇ (Dx, Dy, Dz) along with the orientation (given by the Euler angles α, β, and γ) of the principal axes of the tensor with respect to the protein coordinate frame. The output also includes the overall rotational correlation time τc (=TAUc) and the anisotropy of the tensor (Dz/Dx, Dz/Dy), to be directly entered as input to DYNAMICS. For the B3 domain of protein G (GB3), used here as an example, RotDif analysis of 15N relaxation data measured at 14.1 T (600 MHz 1H frequency) yielded the following characteristics of the (axially symmetric) diffusion tensor: D‖≡Dz=6.05±0.44 10−7 s−1, D⊥≡Dx=Dy =4.45±0.15 10−7 s−1, α=90° ±8°, β=70° ±10°, which give τc =3.34 ±0.14 ns and the anisotropy D‖/D⊥=1.36±0.09. The results at other fields are very similar (19).
2.4 Selection of the appropriate model for local motion
At the heart of the DYNAMICS program is the model selection algorithm, which, based on how a particular model of local motion fits experimental data, selects the most appropriate model. It is similar to the approach described in (31) and is based on the Occam’s razor principle, in that the simplest model that fits the data is considered sufficient. All models of local motion used in DYNAMICS are listed in Table 1. The model selection process starts with the simplest model, LS_00, and first determines if it is acceptable, i.e. the following two criteria are satisfied: (1) the model yields physically reasonable values of the microdynamic parameters (in this case, 0 ≤ S2 ≤1, but more generally for all models: 0 ≤ S2, Sfast2≤1; τloc, τfast >5 ps; 100 ps <τslow <τc, and Rex ≥ σR2) and (2) it provides a reasonable fit to the experimental data, i.e. passes the goodness-of-fit test (32). If this model is acceptable, the program proceeds to the next-level-complexity models (in this case, LS_tl and LS_ex) and applies the same acceptance rules as above. If any of these models are acceptable and yield lower residuals of fit (χ2) than the lower-complexity model (in this case, LS_00), the program uses the F-statistics test to determine if this improvement in the fit is genuine and reflects a better-fit model or merely reflects the greater number of fitting parameters (32). This is possible because the models being tested are nested: each higher complexity model retains the same parameters as the lower complexity model and introduces an additional parameter. If neither model provides a better fit than LS_00, the latter model is accepted, and the program moves to the next residue. If not, the program proceeds to higher complexity models and so on. The program keeps increasing the level of complexity until the number of fitting parameters (Npar) reaches the number of experimental data (Ndat) for a given residue, hence the number of degrees of freedom (df = Ndat -Npar) becomes 0. Note that when df=0, the F-statistics test does not work. In this case we implement a simple rule: if χ2 < 0.01, the model is accepted. This is somewhat arbitrary, and therefore selection of a model with df=0 (e.g. LS_tx or CL_00 for a set of R1, R2, NOE measured at a single field) should be taken with some caution.
Table 1.
Microdynamic parameters for the various models of local motion used in DYNAMICS.
| Modela |
S2 or Sslow2b |
τloc or τslowb |
Sfast2 | τfast | Rex | #expc | Npard | Indexe |
|---|---|---|---|---|---|---|---|---|
| LS_00 | Vf | 0 | 1 | N/A | 0 | 1 | 1 | 0 |
| LS_tl | V | V | 1 | N/A | 0 | 1 | 2 | 1 |
| LS_ex | V | 0 | 1 | N/A | V | 1 | 2 | 2 |
| LS_tx | V | V | 1 | N/A | V | 1 | 3 | 3 |
| CL_00 | V | 0 | V | V | 0 | 2 | 3 | 4 |
| CL_tl | V | V | V | V | 0 | 2 | 4 | 5 |
| CL_ex | V | 0 | V | V | V | 2 | 4 | 6 |
| CL_tx | V | V | V | V | V | 2 | 5 | 7 |
| Matlab name | S2g | TAUloc orTAUslb | S2f | TAUf | Rex |
The name of the corresponding model of local motion as used in DYNAMICS
Naming convention used in DYNAMICS: the corresponding motional parameters in the mono-exponential model are S2 and τloc, whereas in the double-exponential (“extended”) model these parameters are called Sslow2 and τslow.
The number of exponentials in the corresponding correlation function of local motion (see Eqs 4 and 5)
The total number of fitting parameters in a given model
“V” indicates that the corresponding parameter is present in a given model and is fitted (not fixed); N/A = not applied
The name of the corresponding Matlab variable in DYNAMICS output. Note that in the case of “extended” models the reported S2 value is in fact S2 = Sfast2 × Sslow2
It could happen that none of the models of local motion for a given residue pass the goodness-of-fit test because of a poor fit or underestimated experimental errors, resulting in χ2 values higher than the acceptance level. In this case, if at least one model yielded a physically meaningful set of microdynamic parameters, the lowest-χ2/df model that satisfies the latter criterion is selected, and the residue will be marked as belonging to the NOMOD category. If none of the models yield a physically meaningful solution, the residue is marked as program-excluded residue (EXCL category), and DYNAMICS will output a message: no model found, at all.
2.5 Running DYNAMICS
2.5.1 Getting started
All the scripts and functions of DYNAMICS package come in a single compressed file. When you uncompress it (using one of the standard programs) it will by default put all the content of the package in a folder called dynamics.
I recommend that you run all the analysis from the directory containing your relaxation data, which is separate from the dynamics directory: this will prevent you from ‘littering’ the latter with output files that DYNAMICS creates automatically (see Section 3.5). For this you will need to add the dynamics directory to your Matlab path, for example by using the following command:
≫path(path,’c:/MyMatlab/dynamics’)
(here I assumed that all DYNAMICS scripts are located in the folder c:/MyMatlab/dynamics on your computer).
2.5.1 Before you run the program
Navigate to your data directory and load all required input parameters (Table 2) into the Matlab workspace (use Matlab function load for this). Make sure that all of the parameters are in the proper format and units as specified in Table 2. The auxiliary program pdb2nh (see Section 3.6.1) will help you retrieve NH-vector coordinates from the protein coordinate file.
Table 2.
Input parameters for DYNAMICS
| Parameter or data array name (case sensitive) |
The meaning | Data format/structure | Required? |
|---|---|---|---|
| freq | 1H frequency, in MHz, could be several (Nfreq) frequencies, if data at multiple fields | vector of length Nfreqa | Yes |
| r11 (if single field) or several arrays r11, r12, etc generally: r1i where i=1,2,…,Nfreq | R1 data for Nres residues at a given frequency i | Array Nresb ×3: [Residue# R1c σR1c] |
Yes |
| r21 (if single field) or several arrays r21, r22, etc generally: r2i where i=1,2,…,Nfreq | R2 data for Nres residues at frequency i | Array Nres×3: [Residue# R2c σR2c] |
Yes |
| r31 (if single field) or several arrays r31, r32, etc generally: r3i where i=1,2,…,Nfreq | NOE data for Nres residues at frequency i | Array Nres×3: [Residue# NOE σNOE] |
Yes |
| vNH | NH-vectors (normalized) for Nres residues | Array Nres×4: [Residue# x y zd] |
Only for anisotropic diffusion models (kovrl=1 or −1) |
| csa | CSA values for Nres residues | Array Nres × 3: [Residue# CSAe σCSAe] |
Only for fixed site-specific CSA (kcsa=−1). If kcsa=0, the program will ask you |
| TAUc | Overall rotational correlation time, σc, in ns | Scalar or vector | Yes. If TAUc is missing in the workspace, the program will ask you to input it manually |
| Dz2Dx, Dy2Dx | Ratios of the principal values of the diffusion tensor (Dz/Dx, Dy/Dx) | Scalars | Only for anisotropic diffusion models (kovrl=1 or −1). The program will ask you to input them manually |
| alpha, beta, gamma | Euler angles {α,β,γ}, in degrees that define the orientation of the diffusion tensor axes with respect to the protein coordinate frame | Scalars or vectors | Only for anisotropic diffusion models (kovrl=1 or −1). The program will ask you to input them manually |
| Ct, Kd | Molar concentration of the protein (Ct) and the dimer’s dissociation constant (Kd), both in mM | Scalars | Only for monomer-dimer equilibrium model (kovrl=2). The program will ask you to input them manually |
| kovrl | Flag indicating various rotational diffusion models | =0 for isotropic (default); =1 for axially symmetric; =−1 for fully anisotropic; =2 for monomer-dimer equilibrium |
Only for non-isotropic motion, otherwise set to 0 by default |
| kcsa | Flag for selecting various CSA options | =0 for fixed uniform CSA (default); =−1 for fixed site-specific CSA; =1 to fit site-specific CSA |
Only for non-uniform CSA model, set to 0 by default |
| kplot | Flag to suppress (0) or allow (1) visual output in a form of data plots | =0 =1 (default) |
Only for suppressing plot, otherwise set to 1 by default |
| kfig | Flag controlling figure numbers for plotting the results | =0 open a new figure (default); =−1 plot to the same figure; otherwise figure #=kfig |
Only to output to a specific figure#, otherwise set to 0 by default |
| ML_ver | Matlab version | e.g. for Matlab version 7.01, ML_ver = 7.0 | Set manually or let the program determine |
Nfreq= number of frequencies in the freq list
Nres= number of residues in the list. If data for some residues are unavailable, do not include these residues in the list or use NaN (see footnote c)
The values of relaxation rates R1, R2 and their experimental errors, σR1, σR2, should be in 1/sec, the values of NOE and the experimental error, σNOE, are dimensionless. If for a given residue the relaxation parameter (R1, R2, or NOE) is not available, input NaN (“non-assigned-number”) in the corresponding position (second column) in the array.
x,y,z should be coordinates of a unit vector in the direction of the NH bond (can be obtained by running an auxiliary program pdb2nh, see Section 3.6.1)
CSA values and their errors (σCSA) should be in ppm
2.5.2 Run-time dialog
To start the program type the following command in the Matlab Command window:
≫dynamics
If you added the dynamics directory to the Matlab path, you can type this command directly from your data directory (recommended). At the start, the program performs preliminary analysis of the input data and outputs on the screen various estimates of the overall rotational correlation time and the statistics of the distribution of the R2/R1 ratios. Here is an example of such output for 15N relaxation data at 14.1 Tesla (1H frequency = 600.13 MHz) for GB3 (19). We will use these data throughout this chapter. If relaxation data at more than one field are included, the analysis and the output will be done for each field separately.
----------------------600.13MHz----------------------
TOTAL: MEAN=2.2131 SD(MEAN)=0.12582 TAU= 3.3506
L&S : MEAN=2.1806 SD(MEAN)=0.062933 TAU(MEAN)= 3.2995
MEAN(TAU)= 3.2981 SD_TAU= 0.098668
TAUmc= 3.3001 SD_TAUmc= 0.11508
resid. with the R2/R1 within MEAN +/− SD : 37
resid. with the R2/R1 above MEAN + SD : 9
resid. with the R2/R1 below MEAN − SD : 5
The purpose of this analysis is to estimate the overall rotational correlation time (as , (33)) and to count, in the spirit of (34), how many residues have the R2/R1 ratio within one standard deviation (SD) from the mean R2/R1 value. These residues are expected to fit into the “standard” Lipari & Szabo model (10, 11). Residues with the R2/R1 ratio more than one standard deviation below the mean value could require the Rex term (see Eq 2), while those residues that have R2/R1 more than one standard deviation above the mean value might need the “extended” model-free model (12).
At the start the program plots the experimental data (R2, R1, NOE, and residue-specific CSAs, if applicable) as a function of residue number (see Figs. 3 and 4). This output can be suppressed by setting kplot to 0 (or any number other than 1).
Figure 3.
Output of DYNAMICS analysis of backbone motions in GB3 from 15N relaxation data at 600 MHz. (A) Input data; (B) the results of analysis assuming isotropic overall tumbling with TAUc=3.33ns; and (C) the results of analysis assuming anisotropic (axially symmetric) overall tumbling with TAUc=3.33 ns and other diffusion tensor characteristics presented in Section 2.3. A uniform 15N CSA value of −174.2 ppm was assumed throughout the protein. The circles on the “model” plot in B indicate residues that fall into the NOMOD category.
Figure 4.
Output of DYNAMICS analysis of backbone motions in GB3 from 15N relaxation data at five magnetic fields. (A) Input data. (B-C) the results of analysis assuming (axially symmetric) anisotropic overall tumbling (B) with a uniform (fixed) CSA=-174.2 ppm (as in Fig. 3) and (C) site-specific CSAs obtained simultaneously with the microdynamic parameters from fitting these relaxation data. The circles on the “model” plots indicate residues that fall into the NOMOD category.
The run-time dialog that follows is shown step-by-step below. Note that many questions that appear on the screen have a default answer (indicated in the square brackets): this answer will be assumed if you press ENTER, and if the question was about a parameter involved in computations, the program will output a message confirming that the corresponding value was assumed.
Input a CSA value [−160] ==>
This line appears if kcsa is set to 0 (default), i.e. a fixed uniform CSA value will be used. Input the desired value (only numeric input) or simply press ENTER: in this case CSA=−160 ppm will be assumed. Note that if kcsa was set to −1, a list of fixed (site-specific) CSA values must exist in the workspace, otherwise the program will output an error message and exit.
If you did not define TAUc value(s), the program will ask you
Input TAUc value(s) (in ns) ==>
Here you can input a single value (e.g. 3.3) or a list of values, e.g. [3.28 3.3 3.32].
If you selected the isotropic rotational diffusion model (i.e. kovrl was set to 0 on undefined), the program will proceed to actual model-free analysis and model selection on a residue by residue basis (see below). However, if the anisotropic diffusion model was selected (i.e. kovrl was set to −1 or 1), additional input requests will appear.
In case kovrl was set to 1, you will see the following messages
<<<<<<<<<<< axially symmetric model selected >>>>>>>>>>> Input the Dz/Dx ratio (Dz/Dx <=0 -stop) [1]==>
Enter the actual value of the ratio (in the case of axial symmetry, it is the same as D‖/D⊥).
Input a range of BETA values [0:10:90]==>
Enter a range of β values, if you want to screen different orientations of the diffusion tensor, or just a single value (for example, the output of RotDif analysis).
Input the ALPHA angle [0]==>
Enter the value of angle α, in degrees.
Input a starting BETA angle [0]==>
If you entered a single β value when answering the BETA-question above, re-enter it here. Otherwise enter a single value of β that you want to start with. Note that the β value you enter in this line will be used first, even if you entered a different value or a range of values above. You will be then given the option to proceed with the above-entered β values.
If kovrl was set to −1, the dialog will be similar, except that you will see the following message
<<<<<<<<<<< anisotropic model selected >>>>>>>>>>>
and in addition to the questions listed above you will be asked to enter Dz/Dy and the angle γ:
Input Dy/Dx ratio [1]==> Input the GAMMA angle [0]==>
If you selected the monomer-dimer equilibrium model (18) (i.e. kovrl=2), you will be asked to input the total protein concentration and the dissociation constant (both in mM) prior to starting the analysis:
<<<<<<<<<< monomer-dimer equilibrium >>>>>>>>>>> Input protein concentration (in mM) ==> Input the dissociation constant, Kd (in mM) ==>
The program will then compute and output the [monomer]/[dimer] molar ratio and proceed to the data analysis (as described above for the isotropic tumbling option).
After all required parameters (depending on the overall tumbling model) have been entered, the program will start model-free analysis. This analysis is performed on a per-residue basis, and for each residue the program outputs the results in the following format (these data are taken from the GB3 analysis):
res# 48 LS_tx -model, S2= 0.74325 TAUloc= 0.015475 Rex= 0.10926 chi2= 5.904e- 006 res# 49 LS_00 -model, S2= 0.78293 TAUloc= 0 Rex= 0 chi2= 0.61294 res# 50 CL_00 -model, S2= 0.7772 TAUsl= 1.9757 Rex= 0 S2f= 0.85552 TAUf= 0 chi2= 4.6997e-009 res# 52 LS_tl -model, S2= 0.8388 TAUloc= 0.0064478 Rex= 0 chi2= 2.6929e-005 res# 55 LS_tl -model, S2= 0.80301 TAUloc= 0.016452 Rex= 0 chi2= 0.48655
The models of local motion and the corresponding parameters are defined in Table 1; chi2 represents the residuals of fit (χ2) for a given residue. In addition to numeric output, DYNAMICS visualizes/plots some of the results of the latest run on the screen (see examples in Figs. 3 and 4): the relevant microdynamic parameters (e.g. S2, τloc, Rex) and the selected local motion model (represented by its Index, see Table 1). As mentioned above, the plot option can be suppressed by the user by setting kplot = 0. If CSA was among the fitting parameters (i.e. kcsa=1), the output also shows the resulting CSA values.
After completing a run through all non-excluded residues, the program outputs a summary of the results (see Section 2.5.3) and either continues the calculations for all other TAUc and/or β values (if there is more than one value for each of these parameters), or stops and waits for user’s input. If the isotropic tumbling model was selected (kovrl=0 or 2), the message on the screen will read:
Input TAUc (TAUc <= [0] - break)==>
Entering a positive number will trigger another round of calculations with this TAUc value, whereas zero or a negative number will be interpreted as the signal to proceed to exit or error analysis. Note that the latest positive TAUc value will be taken as the final/accepted value and used for error analysis. If the TAUc value that you want to accept is not the latest one, you need to re-enter the desired value, let the program run through all residues again (this is quite fast anyway), and only after that enter 0 or a negative TAUc to exit or proceed to error analysis.
In the case of anisotropic tumbling (kovrl = −1 or 1), the message on the screen reads
Satisfied? (1-yes(calc.err), [0]-cont.(beta-range), 2-man.input, -1- stop/exit)==>
Enter 1 here to proceed to error analysis, 0 to continue computations with other β values (if more than one β value was entered above), 2 if you want to return to manual input of the diffusion tensor parameters (see above), and −1 to exit the program.
If you choose to exit the program, it will automatically remove unnecessary (run-time) variables from the workspace and finish.
If you choose to proceed to error analysis, the program will ask you to select the method of error estimation:
Choose MC simulation of exper.data(0) or fitted params(1 or 2(vis=on)) ==>
Selecting option 0 will generate synthetic experimental data (assuming normally distributed noise with the standard deviation σR1, σR2, or σNOE), and for each set of generated data will perform the fit using the same model of local motion as selected for the real data. By default, 500 runs will be performed for each residue, and the standard deviation will be displayed and included in the ERR array and in the final report RESERR. If you select option 1, the program will determine experimental errors using the constant χ2-boundaries method (32), which assumes that the residuals of fit are distributed according to a χ2 distribution, and therefore a deviation of the fitted parameters from the optimal value by one standard deviation would result in a specific increase in χ2 that depends on the number of fitting parameters (e.g. Δχ2 =1, 2.3 or 3.53 for Npar=1, 2 or 3, respectively). Thus the program determines the confidence boundaries for the fitted parameters by generating their values randomly and keeping only those values that led to Δχ2 below the corresponding threshold. By default, the simulation runs until 500 generated points fall into the defined Δχ2 region. This method is usually faster, except for those rare cases when the errors in fitting parameters are extremely small. You can visualize the confidence regions for selected parameters if you select option 2. As the error estimation proceeds, the program will output on the screen the results (standard deviation, SD) for every residue and, after it is finished, will also update the results plot with error bars. If you choose options 1 or 2 in the isotropic tumbling mode, the program will present you with an option to vary TAUc together with the other parameters such that the estimated errors reflect the possible uncertainty in τc as well. However, since τc is not a fitting parameter, this option should be used for evaluation purposes only.
After the program run is finished, you can save the results that you want to keep by using Matlab’s save command, for example:
>> save results.mat RESERR NOMOD EXCL TAUCHI ANISO
This will save RESERR, NOMODEL, and other parameters listed in that command line to a Matlab file results.mat (which stores data in a binary format). If you want to save your results in ascii format (to be easily opened by a text editor or any spreadsheet program), type:
>> save results.dat RESERR –ascii
Type help save to see other saving options that Matlab provides. See also the description of DYNAMICS’s automatic saving feature in Section 3.5.
2.5.3 Understanding the output
DYNAMICS outputs the results of the analysis on the screen, both in numerical format and as plots, and stores them in several output parameters/arrays, summarized in Table 3.
Table 3.
Output parameters created by program DYNAMICS
| Parameter | Meaning and data format |
|---|---|
| NOMOD | List of residues in the NOMOD category (see Section 2.4), i.e. residues for which none of the models of local motion passed the goodness-of-fit test (χ2 too high), although at least one model provides a physically meaningful set of microdynamic parameters |
| EXCL | List of residues that have been excluded by the program because none of the tested models of local motion are able to provide a physically meaningful set of microdynamic parameters (see Section 2.4) |
| RES | The results of fit in the following format (array Nres × 10): [Residue# τc S2 τloc Rex Sfast2 τfast model-Index χ2 CSA] |
| ERR | The results of error analysis in the following format (array Nres × 7): [Residue# δτc δS2 δτloc δRex δSfast2 δτfast] |
| RESERR | Combined results of fit (RES) and error analysis (ERR) in the following format (array Nres × 16): [Residue# τc δτc S2 δS2 τloc δτloc Rex δRex Sfast2 δSfast2 τfast δτfast model-Index χ2 CSA] |
| TAUCHI | Record of all evaluations performed during the current DYNAMICS run in the isotropic tumbling mode or monomer-dimer equilibrium (empty if anisotropic tumbling). Each line is a summary statistics for all residues, in the following format: τc, χ2(mod), Nnomod, χ2(nomod), runs, df, χ2(total), χ2(total)/df, Nexcl |
| ANISO | Record of all evaluations performed during the current DYNAMICS run in the anisotropic mode (empty matrix in the isotropic or mono-dimer equilibrium). Each line is a summary of statistics for all residues, in the following format (for axially symmetric model): τc, Dz/Dx,β,α, χ2(mod),Nnomod,χ2(nomod), runs, df, χ2(total), χ2(total)/df, Nexcl In the case of fully anisotropic tumbling model, the format is τc, Dz/Dx, Dy/Dx β,α,γ χ2(mod),Nnomod,χ2(nomod), runs, df, χ2(total), χ2(total)/df, Nexcl |
| runs | This parameter counts how many times the selected model switches between model-free and “extended” model-free models in adjacent residues along the protein sequence |
| df | Number of degrees of freedom, df = Ndat - Npar |
| chi2 | Residuals of fit, |
As discussed above, during each run the program outputs the results of analysis for each residue. In addition to the obvious issues, like the model and the actual values of the microdynamic parameters, the user should also pay attention to the residuals of fit (chi2=χ2), which are represented by the last number in each row (or the one before last if CSA is also a fitting parameter). The chi2 information is important, because it tells you how well the data fit the model. Ideally, a good fit would give chi2 values of about 1 per degree of freedom. Thus, chi2 numbers in the range of single digits (≈ df) or lower indicate a reasonable fit, whereas much higher chi2 values indicate a potential problem with data analysis for a particular residue: either the “best”-fit model is not ideal for that residue or perhaps the experimental errors are underestimated (hence elevated chi2).
In addition to results for each residue, after each run through all residues is completed, the program outputs a summary of the results of the current run, which looks like this:
NOMODEL 2 res.: 36 45 chi2 = 52.8946 TAUc= 3.33 MODEL chi2= 107.0356 runs= 14 df= 46 TOTAL Chi2= 159.9302 Chi2/df= 3.4767
The first line here is optional and appears only if there is at least one residue that falls into the NOMOD category (see Section 2.4): it lists those residues and their total chi2. The second line reports the current τc value, the total chi2 value for “MODEL” residues, i.e. those for which proper model selection was obtained, and a summary of other statistics of the results (see Table 3). The last entry in this line is the total chi2 divided by the number of degrees of freedom.
The program also summarizes similar statistics for all iterations (various TAUc values) performed so far in a form shown below for the isotropic tumbling model:
TAUc chi2mod nomod chi2nomod runs df total_chi2 totalCHI2/df nexcl 3.15 87.4701 5 72.5883 0 39 160.0584 4.1041 0 3.33 107.0356 2 52.8946 14 46 159.9302 3.4767 0 <-- 3.45 100.6942 5 157.2367 22 42 257.9309 6.1412 0
Here mod and nomod refer to MODEL and NOMOD categories, and nexcl is the number of residues in the EXCL category, i.e. for which no model could be found; the rest of the parameters are defined in Table 3. These data are also stored in array TAUCHI. The horizontal arrow on the right indicates the entry with the lowest total χ2/df.
For anisotropic diffusion model the summary table is slightly different (because of the additional overall-tumbling-related parameters) and looks like this (also saved in array ANISO, see Table 3):
TAUc Dz/Dx beta alpha --> chi2mod nomod chi2nomod runs df total_chi2 totalCHI2/df nexcl 3.33 1.36 65 90 --> 76.8789 0 0 6 49 76.8789 1.569 0 3.33 1.36 70 90 --> 78.0965 0 0 4 50 78.0965 1.5619 0
For fully anisotropic diffusion model, the summary table also includes Dy/Dx and angle gamma.
2.6 Practical examples
The examples of DYNAMICS graphics outputs showing the input 15N relaxation data for GB3 at 14.1 T (600 MHz) and the resulting microdynamic parameters and models of local motion are shown in Figure 3. The analysis was performed assuming isotropic or anisotropic overall tumbling of the protein. Differences in the microdynamic parameters and selected models of local motion illustrate the need to use an adequate model for the overall tumbling (anisotropic rotational diffusion in the case of GB3 (35)). The analysis of GB3 data measured at five fields (9.4, 11.7, 14.1, 16.4, and 18.8 T) assuming a uniform (fixed) 15N CSA or including site-specific 15N CSA as a fitting parameter is illustrated in Figure 4.
3. Miscellaneous Issues
3.1 General notes on using DYNAMICS
(1) Make sure the input list of frequencies freq contains all the pertinent 1H frequencies (magnetic fields) for the data that you want to analyze. It is critical that the order in which the frequencies are listed in the freq-list is coordinated with the second “index” in the relaxation parameters names. For example, if freq=[500, 600], then r11, r21, and r31 should be R1, R2, and NOE data at 500 MHz, respectively, while r12, r22, and r32 should be R1, R2, and NOE data at 600 MHz.
(2) Small Rex values (< 1 s−1) could be artifacts of model selection (for example, due to an inadequate overall tumbling model, as illustrated in Fig. 3) or a result of elevated 15N CSA, rather than real exchange contributions. Relaxation data at more than one magnetic field are required (analyzed separately or together) to verify the consistency of the model selection as well as that the resulting Rex term has the expected field dependence (∝ Bo2).
(3) To fit CSA values, relaxation data at more than one magnetic field are required.
(4) When conformational exchange (Rex) is present, the CSA values obtained from the analysis could be biased, since both the Rex and the CSA contributions to relaxation rates have a similar field dependence (∝ Bo2).
(5) Errors in the derived CSA values, as well as the associated errors in microdynamic parameters from such analysis (kcsa=1), can currently be calculated only using the “experimental data simulation” option.
(6) In the output RES matrix, the CSA values are included as column #10, following the χ2 values. In the output RESERR matrix the CSA values and errors in CSA are included as the last two columns (#16, 17).
(7) Even if you input a single TAUc value for the isotropic or monomer-dimer-equilibrium model, the program will run calculations for this TAUc twice. This is done to compare the results of at least two runs and, because DYNAMICS is fast, does not take too much time.
3.2 Strategy for determining the overall rotational correlation time when the structure is unknown or RotDif results are unreliable
What can one do if protein coordinates are not available? One can always use the isotropic overall tumbling model in DYNAMICS, which does not require knowledge of protein structure. However, one should be aware of the fact that the microdynamic parameters derived from such analysis could be biased by the possible oversimplification of the tumbling model used, particularly if the protein shape turns out to be far from spherical.
While RotDif provides an efficient and reliable way to determine the overall rotational diffusion tensor, it is also possible to estimate the tensor (or at least some of its characteristics) simultaneously with DYNAMICS analysis. This feature was built into DYNAMICS in the old days when RotDif was unavailable, and still remains. Here is the recipe that I recommend if you want to determine τc from 15N relaxation data at a single field.
(1) Use only residues from structurally well-defined regions (“core”) of the protein. Exclude any residues that are in highly flexible/unstructured parts (e.g. loops and termini) of your protein: they would likely require the “extended”-model-free models. You can do this based on the structure of the protein, or using only residues for which the R2/R1 ratio falls within one standard deviation from the mean (the estimates are provided at the very beginning of each DYNAMICS run). You also might want to exclude residues with noticeably high R2 values but “average” R1 values. It might be helpful to plot the R2/R1 ratio for such an analysis. The rationale for these exclusions is that at a single field there is no reliable F-statistics test for models (CL_00, LS_tx) with df=0, so you try to minimize these contributions.
(2) Start with the estimate of TAUc that DYNAMICS provides at the very beginning of the run.
(3) Run DYNAMICS once at this TAUc, and analyze the output results for various residues. Identify residues that give very high chi2, compared to the rest of residues. You will want to exclude these residues during the next run. The rationale is that these residues will dominate the total chi2, thus biasing the optimization based on the residuals of fit. For example, if the average chi2 level is in the single digits, it might be prudent to exclude residues that gave chi2 above 30–50.
(4) With the new set of residues, run DYNAMICS while varying TAUc. The goal is to find TAUc that minimizes chi2/df. This optimization could be tricky, because when the input TAUc deviates from the actual τc, the model selection procedure could compensate by choosing a different model. For example as TAUc increases, there is a tendency toward the CL_00 model, for which chi2 could be very low (recall that for that model df=0 when using data at a single field, thus the F-statistics test does not work in this case, and acceptance of this model is somewhat arbitrary). The same happens when TAUc is lower than the actual τc: the model selection will compensate by choosing LS_ex or LS_tx models (recall that for the latter df=0, hence the F-statistics does not work). This would also result in a decrease in the total number of degrees of freedom. Therefore the name of the game here is to find a TAUc value (or range) in the “middle” region, where the total chi2 is at or close to its minimum and at the same time the total df is at or close to its maximum. There might not be a clear single TAUc value, but one should remember there is always an uncertainty in τc even from RotDif analysis. Examples of such analyses are shown in Figure 5. In addition, to help deal with an artificial selection of the CL_00 model, DYNAMICS also uses another parameter, called runs (Table 3). The rationale behind it is to avoid an artificial situation when a single residue shows large-amplitude motions (this is what the extended model is usually needed for) while its neighbors do not. To avoid this, runs counts how many times the selected model switches between “LS” and ‘CL” models in adjacent residues. Naturally, one wants to minimize the number of such switches, because intuitively one would expect that large-amplitude fluctuations involve several adjacent residues in the polypeptide chain, and not just a single one.
Figure 5.
Illustration of the use of DYNAMICS to optimize τc simultaneously with model-free analysis of 15N relaxation data for GB3. (A) The analysis assumed an anisotropic tumbling model with the diffusion tensor’s anisotropy and orientation as specified in Section 2.3. (B) The analysis assumed isotropic tumbling model. The 15N CSA was set to −174.2 ppm (fixed) in both cases. Only secondary structure residues were included; in addition, residues D36 and Y45 were excluded from this analysis because of high χ2 values. Solid line in both panels shows χ2/df while the dashed line depicts the number of degrees of freedom, df. The vertical bars in the top plots show the number of residues with Rex (blue) (LS_ex and LS_tx models) or with extended model (CL_00) (red) selected for each value of TAUc, as well as the number of NOMOD residues (black). There were no NOMOD residues in the analysis in A. The RotDif analysis gives the τc value of 3.34±0.14 ns (19) (or 3.37±0.20 ns for these selected residues); a very similar value (3.36 ns) calculated from the mean R2/R1 value was reported at the beginning of the DYNAMICS run.
One should also bear in mind that the total chi2 /df (as well as chi2) is generally not a smooth function because changes in the selected model of local motion for individual residues would result in abrupt changes in the residuals of fit and df.
(5) After the TAUc value has been optimized, use this value to run DYNAMICS again, this time for all residues in the protein. You might need to do several iterations of such an analysis.
3.3 Strategy for determining the overall rotational diffusion tensor when RotDif results are unreliable
The strategy here is similar to that described in the previous section, except that (i) protein atom coordinates are required and (ii) you will need to vary several parameters as the same time. For example, for the axially symmetric model, you might want to vary Dz/Dx and the angles α and β. While doable, this optimization is not straightforward, can require significant effort, and can result in a local rather than a global minimizer. Thus I would recommend using it only when no other option is available.
3.4 Cleaning the workspace
DYNAMICS generates and keeps most of the necessary intermediate variables in the current Matlab workspace (computer memory). They are automatically removed from the workspace when the program terminates successfully. If the program run was terminated prematurely either by the user (e.g. via CTRL/C) or in case of a run-time error, these variables will remain in the workspace. This might cause an interruption in the normal program execution when you start it next time during the same Matlab session. To ensure uninterrupted program flow, it is recommended to remove the remaining intermediate variables from the computer memory before restarting DYNAMICS. Removal of only intermediate variables can be achieved by issuing the following command:
>>dynclean
3.5 Automatic saving of the results
To prevent accidental loss of the computed data, the results (RES, NOMOD, EXCL, TAUCHI, ANISO) are automatically saved to a Matlab file after completion (and acceptance) of the model-free analysis and again after error analysis (the same parameters as above plus ERR and RESERR). To reduce the chance of overwriting this file when you run DYNAMICS again, the name of the file contains the current date followed by a random number from 0 to 99, e.g. dyn16jan2011_92.mat.
3.6 Auxiliary programs
The DYNAMICS package includes several programs designed to help the user prepare data for running the calculations. Some of these programs are briefly described below. Their use and the actual command lines are not detailed here: the reader can find all relevant information in the header of each program using any text editor (e.g. Matlab editor)
3.6.1 pdb2nh
This program extracts coordinates of backbone NH vectors from a given protein atom coordinates file and normalizes these vectors (to be used as input for DYNAMICS). In case hydrogens cannot be found (e.g. crystal structure), the program builds amide hydrogens from coordinates of the heavy atoms C’, O, N, Cα in the corresponding peptide plane using conventional rules.
3.6.2 reldata, reldatae
Given all pertinent parameters of the overall and local dynamics, as well as the orientation of the NH vector (if necessary), the reldata program computes 15N relaxation rates: R1, R2, and NOE. The input options also include the ability to add random noise to the data.
The program reldatae performs the same task as reldata, but in addition also computes the longitudinal (ηz) and transverse (ηxy) cross-correlation rates between the 1H-15N dipolar interaction and 15N CSA, see e.g. (19, 36).
3.6.3 conv2temp
This program allows conversion between τc values at different temperatures, by taking into account the temperature dependence of water viscosity, see e.g. (37).
3.6.4 Demo scripts
The package includes several demo scripts, designed to help the user learn how to run DYNAMICS:
| demo_iso.m | isotropic overall tumbling |
| demo_ani.m | anisotropic overall tumbling |
| demomdeq.m | monomer-dimer equilibrium |
| demo_csa_iso.m | CSA fit + isotropic overall tumbling |
| demo_csa_ax.m | CSA fit + axially symmetric anisotropic overall tumbling |
| demo_csa_ani.m | CSA fit + fully anisotropic overall tumbling |
All “demo_csa” scripts use data at five magnetic fields and include CSA as a fitting parameter. Note that these scripts can be modified to use site-specific CSA values as an external fixed parameter (kcsa = −1) rather than as an adjustable parameter. All you need is to open this file with any text editor and uncomment (remove %) the line kcsa = −1.
Each of these scripts starts by generating synthetic sets of relaxation data using reldata.m, and then runs DYNAMICS using these data as input. Additional three text files, demo_iso.txt, demo_ani.txt, and demomdeq.txt, contain copies of the screen outputs and the dialog, to illustrate the main steps in data analysis using DYNAMICS.
Acknowledgements
The development of DYNAMICS program was supported by NIH grant GM065334. My work on this chapter has led to several modifications of the program, which hopefully made it user-friendlier, and I would like to thank the editors, Alex Shekhtman and David Burz, for being so patient with me during this process.
References
- 1.Palmer AG., 3rd NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 2.Sheppard D, Sprangers R, Tugarinov V. Experimental approaches for NMR studies of side-chain dynamics in high-molecular-weight proteins. Prog Nucl Magn Reson Spectrosc. 2010;56:1–45. doi: 10.1016/j.pnmrs.2009.07.004. [DOI] [PubMed] [Google Scholar]
- 3.Godoy-Ruiz R, Guo C, Tugarinov V. Alanine methyl groups as NMR probes of molecular structure and dynamics in high-molecular-weight proteins. J Am Chem Soc. 2010;132:18340–18350. doi: 10.1021/ja1083656. [DOI] [PubMed] [Google Scholar]
- 4.Cavanagh J, Fairbrother WJ, III, AJ P, Skelton NJ. Protein NMR Spectroscopy. San Diego: Academic Press; 1996. [Google Scholar]
- 5.Fushman D, Cowburn D. The effect of noncollinearity of 15N-1H dipolar and 15N CSA tensors and rotational anisotropy on 15N relaxation rates, CSA/DD cross correlation, and TROSY. J. Biomol. NMR. 1999;13:139–147. doi: 10.1023/a:1008349331773. [DOI] [PubMed] [Google Scholar]
- 6.Fushman D, Ohlenschlager O, Rüterjans H. Determination of the backbone mobility of ribonuclease T1 and its 2'GMP complex using molecular dynamics simulations and NMR relaxation data. J Biomol Struct Dyn. 1994;11:1377–1402. doi: 10.1080/07391102.1994.10508074. [DOI] [PubMed] [Google Scholar]
- 7.Pfeiffer S, Fushman D, Cowburn D. Simulated and NMR derived backbone dynamics of a protein with significant flexibility: A comparison of spectral densities for the <beta> ARK PH domain. J.Amer.Chem.Soc. 2001;123:3021–3036. doi: 10.1021/ja0031117. [DOI] [PubMed] [Google Scholar]
- 8.Maragakis P, Lindorff-Larsen K, Eastwood MP, Dror RO, Klepeis JL, Arkin IT, Jensen MO, Xu H, Trbovic N, Friesner RA, Palmer AG, Shaw DE. Microsecond molecular dynamics simulation shows effect of slow loop dynamics on backbone amide order parameters of proteins. J Phys Chem B. 2008;112:6155–6158. doi: 10.1021/jp077018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fushman D, Cowburn D. Nuclear magnetic resonance relaxation in determination of residue-specific 15N chemical shift tensors in proteins in solution: protein dynamics, structure, and applications of transverse relaxation optimized spectroscopy. In: James T, Schmitz U, Doetsch V, editors. Methods in Enzymology. 2001. pp. 109–126. [DOI] [PubMed] [Google Scholar]
- 10.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. J.Amer.Chem.Soc. 1982;104:4559–4570. [Google Scholar]
- 11.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J.Amer.Chem.Soc. 1982;104:4546–4559. [Google Scholar]
- 12.Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. Deviations from the simple two-parameter model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J.Amer.Chem.Soc. 1990;112:4989–4936. [Google Scholar]
- 13.Woessner D. Nuclear spin relaxaion in ellipsoids undergoing rotational brownian motion. J.Chem.Phys. 1962;37:647–654. [Google Scholar]
- 14.Favro DL. Theory of the Rotational Brownian Motion of a Free Rigid Body. Phys. Rev. 1960;119:53–62. [Google Scholar]
- 15.Ryabov YE, Fushman D. A Model of Interdomain Mobility in a Multidomain Protein. J. Am. Chem. Soc. 2007;129:3315–3327. doi: 10.1021/ja067667r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational diffusion anisotropy of human ubiquitin from 15N NMR relaxation. J. Am. Chem. Soc. 1995;117:12562–12566. [Google Scholar]
- 17.Palmer AG, 3rd, Grey MJ, Wang C. Solution NMR spin relaxation methods for characterizing chemical exchange in high-molecular-weight systems. Methods Enzymol. 2005;394:430–465. doi: 10.1016/S0076-6879(05)94018-4. [DOI] [PubMed] [Google Scholar]
- 18.Fushman D, Cahill S, Cowburn D. The main chain dynamics of the dynamin pleckstrin homology (PH) domain in solution: Analysis of 15N relaxation with monomer/dimer equilibration. J. Mol. Biol. 1997;266:173–194. doi: 10.1006/jmbi.1996.0771. [DOI] [PubMed] [Google Scholar]
- 19.Hall JB, Fushman D. Variability of the 15N Chemical Shielding Tensors in the B3 Domain of Protein G from 15N Relaxation Measurements at Several Fields. Implications for Backbone Order Parameters. J.Am.Chem.Soc. 2006;128:7855–7870. doi: 10.1021/ja060406x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fushman D, Cowburn D. Studying protein dynamics with NMR relaxation, in. In: Sarma R, Sarma M, editors. Structure, Motion, Interaction and Expression of Biological Macromolecules. Albany, NY: Adenine Press; 1998. pp. 63–77. [Google Scholar]
- 21.Blackledge M, Cordier F, Dosset P, Marion D. Precision and uncertainty in the characterization of anisotropic rotational diffusion by 15N relaxation. J.Am.Chem.Soc. 1998;120:4538–4539. [Google Scholar]
- 22.Fushman D, Xu R, Cowburn D. Direct determination of changes of interdomain orientation on ligation: use of the orientational dependence of 15N NMR relaxation in Abl SH(32) Biochemistry. 1999;38:10225–10230. doi: 10.1021/bi990897g. [DOI] [PubMed] [Google Scholar]
- 23.Fushman D, Ghose R, Cowburn D. The effect of finite sampling on the determination of orientational properties: A theoretical treatment with application to interatomic vectors in proteins. J. Am. Chem. Soc. 2000;122:10640–10649. [Google Scholar]
- 24.Dosset P, Hus JC, Blackledge M, Marion D. Efficient analysis of macromolecular rotational diffusion from heteronuclear relaxation data. J Biomol NMR. 2000;16:23–28. doi: 10.1023/a:1008305808620. [DOI] [PubMed] [Google Scholar]
- 25.Ghose R, Fushman D, Cowburn D. Determination of the Rotational Diffusion Tensor of Macromolecules in Solution from NMR Relaxation Data with a Combination of Exact and Approximate Methods - Application to the Determination of Interdomain Orientation in Multidomain Proteins. J.Magn.Reson. 2001;149:214–217. doi: 10.1006/jmre.2001.2295. [DOI] [PubMed] [Google Scholar]
- 26.Walker O, Varadan R, Fushman D. Efficient and accurate determination of the overall rotational diffusion tensor of a molecule from 15N relaxation data using computer program ROTDIF. J. Magn. Reson. 2004;168:336–345. doi: 10.1016/j.jmr.2004.03.019. [DOI] [PubMed] [Google Scholar]
- 27.Fushman D, Varadan R, Assfalg M, Walker O. Determining domain orientation in macromolecules by using spin-relaxation and residual dipolar coupling measurements. Progress NMR Spectroscopy. 2004;44:189–214. [Google Scholar]
- 28.Hall JB, Walker O, Fushman D. Characterization of the overall rotational diffusion of a protein from 15N relaxation measurements and hydrodynamic calculations. In: Downing AK, editor. Protein NMR techniques (Methods in Molecular Biology) Humana Press Inc.; 2004. pp. 139–160. [DOI] [PubMed] [Google Scholar]
- 29.Fushman D, Cowburn D. Characterization of Inter-Domain Orientations in Solution Using the NMR Relaxation Approach, in. In: Krishna NR, L B, editors. Protein NMR for the Millenium (Biological Magnetic Resonance Vol 20) Kluwer; 2002. pp. 53–78. [Google Scholar]
- 30.Fushman D. Determination of protein dynamics using 15N relaxation measurements. In: Zerbe O, editor. BioNMR in drug research. Wiley-VCH; 2002. pp. 283–308. [Google Scholar]
- 31.Mandel AM, Akke M, Palmer AGI. Backbone dynamics of E. coli Ribonuclease HI: correlations with structure and function in an active enzyme. J. Molecular Biology. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
- 32.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. NY: Cambridge University Press; 1992. [Google Scholar]
- 33.Fushman D, Weisemann R, Thüring H, Rüterjans H. Backbone dynamics of ribonuclease T1 and its complex with 2'GMP studied by two-dimensional heteronuclear NMR spectroscopy. J.Biomol.NMR. 1994;4:61–78. doi: 10.1007/BF00178336. [DOI] [PubMed] [Google Scholar]
- 34.Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studies by N15 inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 35.Hall JB, Fushman D. Characterization of the overall and local dynamics of a protein with intermediate rotational anisotropy: Differentiating between conformational exchange and anisotropic diffusion in the B3 domain of protein G. J Biomol NMR. 2003;27:261–275. doi: 10.1023/a:1025467918856. [DOI] [PubMed] [Google Scholar]
- 36.Hall JB, Fushman D. Direct measurement of the transverse and longitudinal 15N chemical shift anisotropy-dipolar cross-correlation rate constants using 1H-coupled HSQC spectra. Magnetic Resonance in Chemistry. 2003;41:837–842. [Google Scholar]
- 37.Ryabov YE, Geraghty C, Varshney A, Fushman D. An efficient computational method for predicting rotational diffusion tensors of globular proteins using an ellipsoid representation. J Am Chem Soc. 2006;128:15432–15444. doi: 10.1021/ja062715t. [DOI] [PubMed] [Google Scholar]