Fairness versus Efficiency of Vaccine Allocation Strategies

Abstract

Objectives

This research develops a framework to objectively measure the degree of fairness of any allocation rule aimed at distributing a limited stockpile of vaccines to contain the spread of Influenza.

Methods

The trade-off between the efficiency and the fairness of allocation strategies is demonstrated through an illustrative simulation study of an Influenza epidemic in Southwestern Virginia. A Susceptible-Exposed-Infectious-Recovered (SEIR) model is used to represent the disease progression within the host.

Results

Our findings show that among all the criteria considered here, the household size (largest first) combined with age (youngest first) based strategy leads to the best outcome. At 80% fairness, highest efficiency can be achieved but in order to be 100% fair, disease prevalence will have to rise by ≈1.5%.

Conclusions

This research provides a framework to objectively determine the degree of fairness of vaccine allocation strategies.

Introduction

Public health officials, when faced with scarce medical resources like limited vaccines, have primarily focused on designing allocation strategies that are efficient so that the prevalence and the intensity of infection can be minimized. If the improved efficiency helps overcome the scarcity, the problem is solved but if it persists, a set of rules is needed to prioritize individuals in a way that the distribution is fair. To evaluate the fairness of a rule, however, a systematic procedure is needed.

A variety of criteria can be applied to justify whether or not a specific allocation rule is appropriate when it comes to the distribution of a limited stockpile of vaccines. Broadly speaking, they can be categorized into two classes: efficiency and fairness. The former concentrates on how well a rule drives the system to the most efficient outcome whereas the latter focuses on how well the allocation rule addresses some fairness criteria, i.e., axioms that prescribe the relative importance of each individual based only on some of her features, which are irrelevant to the resulting outcomes. In reality, an allocation rule is often justified by both criteria. For example, in a market economy, the efficiency rule suggests that individuals should be paid their marginal contributions to the society in order to motivate them to produce the maximum output whereas fairness is covered through redistribution mechanism, such as taxes and subsidies, which transfer resources from the rich to the poor, the weak, and so on.

Researchers in public health area have extensively studied the efficiency aspects of allocations of a limited stockpile of vaccines. The “proper” or efficient distribution rules have been shown to minimize the disease prevalence, maximize quality-adjusted years, or minimize economic costs among other things [1, 2, 3]. Since all measures of efficiency are based on the outcomes of the resulting epidemic, it is straightforward to quantify the degree of efficiency for each distribution rule, post-epidemic.

The other aspect of the problem, i.e. fairness, remains insufficiently investigated in the literature. There have been very few studies that focused on the fairness of distribution strategies, and the criteria for prioritizing the most important individuals are subjective. Specifically, researchers have suggested four kinds of fairness: treating people equally, favoring the worst-off, maximizing total benefits, and promoting and rewarding social usefulness [4, 5, 6]. Given that these analyses in the literature are totally based on qualitative analysis, researchers lack a general methodology to quantitatively measure the degree of fairness of each distribution rule, and objectively assess the tradeoff between the efficiency and fairness.

The problem above leads to the main motivation for this work. This research builds a general framework, similar to the Gini coefficient, which measures income inequality, to quantify the degree of fairness given a corresponding axiom of fairness. With the help of this framework, we investigate the relationship between efficiency and fairness, of various vaccine allocation strategies during an Influenza like illness (ILI) epidemic.

Our results show that a distribution rule with a very high degree of fairness is usually harmful to the society since it is applied at the cost of efficiency; and the most efficient distribution rule turns out to be, not the fairest one. Specifically, this research finds that distribution strategies that use household-size, life cycle, and network-degree criteria, are well aligned with efficiency to a large extent. In all scenarios, in order to be 100% fair, however, some efficiency must be sacrificed. A mixed criterion based on both household-size and age does better than the individual ones.

The rest of the paper is organized as follows. Section 2 defines the framework for quantifying the degree of fairness and efficiency. Section 3 simulates a variety of distribution strategies during an ILI epidemic on a realistic social network. Section 4 discusses the empirical results and their implications, and Section 5 concludes.

The Framework to Measure Fairness

We first define the general forms of efficiency and fairness that are suitable for empirical studies.

Baseline. For an epidemic on graph G(N, T), where N is the set of vertices and T denotes all edges; for a given individual i ∈ N, f_i(G) denotes the probability of i getting infected, without any intervention.

Intervention. Now consider an intervention, i.e. distribution of a limited stockpile of L vaccines to the public. Based on a set of demographic variables X_i for each individual i, let D(X_i) ∈ [0, 1] be the probability that she gets vaccinated, such that ${\sum }_{i=1}^{\mid N\mid }D(x_i)=L$.

Let h_i(G, D) be the probability of individual i getting infected when the intervention policy depicted by function D(·) is in place.

Definition 1. Given a vector of weights W = (ω_i)_i∈N, the efficiency of policy D is defined as $E(D,W)={\sum }_{i=1}^{\mid N\mid }{\omega }_i(f_i(G)-h_i(G,D))$.

Given that the term Σω_i · f_i(G) is fixed and exogenously given, let us just focus on the value of Σω_i · h_i(G, D) while comparing the efficiency of different intervention policies. Intuitively speaking, given the corresponding weights of individuals for an intervention, the efficiency is (negatively) determined by the weighted sum of individual costs caused by the epidemic. For this reason, we define $\widehat{E}(D,W)={\sum }_{i=1}^{\mid N\mid }{\omega }_i·h_i(G,D)$ as the social cost, after applying intervention characterized by D, and focus mainly on this term in the rest of the paper.

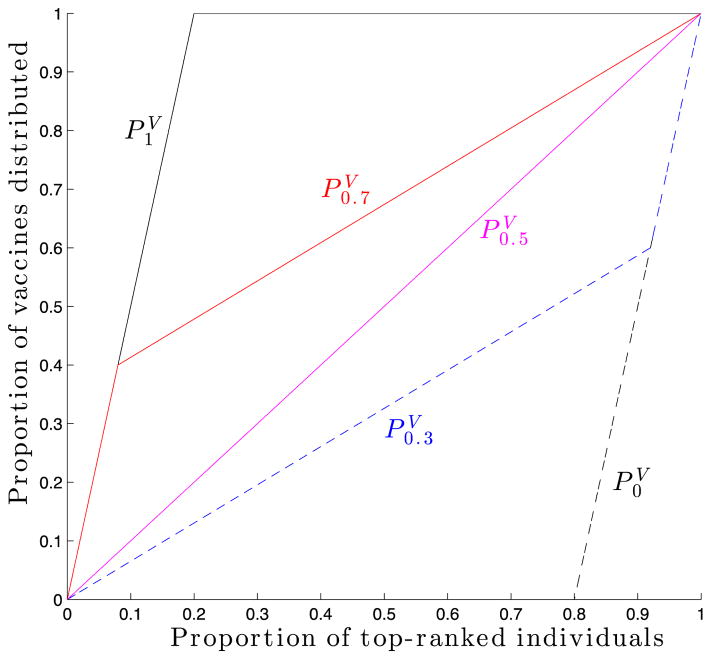
The definition of fairness of an intervention, however, is more complicated. The term “fairness” should be derived from some axiom that justifies the set of people who should get vaccinated for some righteous reasons. Formally speaking, given a function V:X_i → ℝ, an axiom of fairness characterized by V claims that individuals should get vaccinated according to their importance as determined by V. Then given V, it is easy to define the fairest distribution rule D₁(V) and the unfairest distribution rule D₀(V): First rank all V(X_i) values in descending order, the distribution rule D₁(V) will vaccinate only the first L individuals whereas rule D₀(V) vaccinates only the last L individuals. All other distribution rules that assign L vaccines to individuals in N, must reside somewhere between the fairest and the unfairest rules. To further quantify the degree of fairness for any distribution rule, we define a cumulative allocation function, P_D,V(·), for any distribution rule D and fairness axiom V: Rank all individuals in descending order of their V(X_i) values, then for fraction λ ∈ [0, 1], P_D,V(λ) tells us, in expected values, the proportion of L vaccines that have been distributed out to the first λ|N| individuals. Obviously we have P_D,V(0) = 0, P_D,V(1) = 1, and P_D,V(·) is a non-decreasing function.

P_D1,V(λ) equals $\frac{\lambda \mid N\mid }{L}$ if $\lambda <\frac{L}{\mid N\mid }$ and 1 otherwise. P_D0,V(λ) equals $\left(\lambda -1+\frac{L}{\mid N\mid }\right)\frac{\mid N\mid }{L}$ if $\lambda \ge 1-\frac{L}{\mid N\mid }$ and 0 otherwise. Any other curve of P_D,V(·) should locate between these two, and constitute a closed image with either of them. For this reason, it is reasonable to define the fairness degree of D as the relative area between curves P_D,V(·) and P_D0,V(·).

Definition 2. Given an axiom characterized by V, the fairness degree of D is the area between curves P_D,V(α) and P_D0V(α), normalized by the area between curves P_D1V(α) and P_D0,V(α), where α is the degree of fairness

Next we would like to characterize a distribution rule exclusively by its degree of fairness, but according to the above setting, for any fairness degree α ∈ (0, 1), there are infinitely many distribution rules whose fairness degree is exactly α. To make our analysis tractable, we investigate only a subclass of distribution rules, namely rules that have up to two-piece linear cumulative distribution functions. More specifically, for all distribution rules with fairness degree higher than or equal to 0.5, we work with the one that vaccinates a proportion with the highest V(X_i) values for sure and distributes the remaining vaccines to the rest uniformly randomly.

Analogously, for all distribution rules with fairness degree smaller than 0.5, we only select the one that vaccines a proportion with the smallest V(X_i) values and distributes the remaining vaccines to the rest uniformly randomly. By doing so, given any fairness degree α ∈ [0, 1], a distribution rule D_α(V) is uniquely determined, and for any P_DαV(·) we can thus write $P_{\alpha }^V(·)$ for short. For instance, in Figure 1, the area between curves $P_{0.3}^V$ and $P_0^V$ should be 30% of the area between curves $P_1^V$ and $P_0^V$.

Figure 1.

Curves for cumulative function $P_{\alpha }^V(·)$ with fairness degree α being equal to 1, 0.7, 0.5, 0.3 and 0, respectively. Only 20% of the whole population get vaccinated.

To sum up, we have introduced a general framework to measure the degree of fairness of any vaccine allocation rule. Furthermore, given any fairness degree α ∈ [0, 1], we focus on a unique allocation rule, which can be characterized exclusively by α, given the axiom of fairness V.

Experimental Methods

Next we describe the simulation methods, experimental settings, efficiency criteria as well as various axioms of fairness.

Disease Model and Simulation Setting

We use an agent-based epidemic simulation tool called EpiFast [7], to study the propagation of an Influenza-like-illness, over the social contact network of Montgomery County in Southwest Virginia. The synthetic population, representing approximately 75,000 individuals, is obtained through a detailed population synthesis process that makes it statistically indistinguishable from the US census data when aggregated to a block group level [8]. Further a detailed set of daily activities and their corresponding locations are assigned to each individual in order to generate a colocation based social contact network. The estimation of the social network is described in detail in several peer-reviewed studies [9, 10, 11].

A Susceptible-Exposed-Infectious-Recovered (SEIR) model is used to represent the disease progression within the host. This is a widely used disease model in Epidemiology. There are no deaths and births in the model, each health individual is initially assigned as susceptible; once an individual has been infected but is not infectious, she enters the incubation period and is thus labeled as exposed; after the incubation period, she becomes infectious; once an infectious individual recovers, she becomes immune to the disease and is thus labeled as recovered.

For each individual, the incubation period duration is sampled from a discrete distribution with mean 1.9 days and standard deviation 0.49 day; the infectious period duration is sampled from a discrete distribution with mean 4.1 days and standard deviation 0.89 [12]. Five infections from external sources occur within the population each day to seed the epidemic. The simulation is run for 300 days. Only 15,000 vaccines are assumed to be available which means only 20% of the population can get vaccinated. These individuals are chosen at the beginning of the simulation based on different fairness criteria. The efficacy of the vaccine is assumed to be 90%.

Recall that for any fairness degree, a proportion of vaccines are distributed to individuals with the greatest (or the smallest) V(X_i) values, and the remaining vaccines are distributed to other individuals uniformly randomly. To account for the stochasticity embedded in the random distribution part, for each degree of fairness, we run 30 simulation replicates and report the average of these results.

Efficiency Measures

We consider two standard measures of (negative) efficiency in the current work: the prevalence rate of the disease and the loss in the total number of quality days.

Disease Prevalence

Our first measure of (negative) efficiency is prevalence of disease, namely, the ratio of infected individuals in the population. This measure is widely used in practice and the literature because the prevalence of a disease can is a signal of how severely the disease is affecting the society. As a result, this measure can, to some extent, serve as a proxy for the social costs due to the disease. Under this measure, each individual is weighted equally.

Quality Days Lost

Different individuals are valued differently by the society, and thus should be assigned different weights based on their value while considering the efficiency of an intervention. We use the survey results in [13], which uses age to determine the weights of the individuals. The negative efficiency is then measured by the sum of weighted infectious days lost.

By fitting the results into a simplistic function, the weight, ω_i for each individual is given as:

$$\{\begin{array}{c}\frac{4.1}{11}[11-0.3(30-{\mathit{Age}}_i)],if{\mathit{Age}}_i\le 30,\\ max\left\{0,\frac{4.1}{11}[11-0.4({\mathit{Age}}_i-30)]\right\},if{\mathit{Age}}_i>30,\end{array}$$ (1)

Where Age_i stands for the age of individual i. This function simply claims that the 30-year-old individuals should be given the highest weight and the younger and older should be valued less important. This idea is also explained in [5] which argue that the importance of an individual should be calculated based on two considerations: how many resources have already been invested in that person and how many years are left to complete an ordinary life-cycle. The youth are weighted less because less investment has been made in them so far and the old are weighted less because they have fewer years to live to complete a life-cycle. Hence, middle-aged individuals are given the highest weights.

Further, to make the “loss in quality days” meaningful in reality, the weights are normalized by factor $\frac{4.1}{11}$ for all individuals. By doing so, ω_i for individuals in age 30 are set to be 4.1, which is exactly the average number of infection days. In other words, we take 4.1 quality days lost for an infected individual who is 30, and the quality days lost for all other individuals are set accordingly such that their relative days lost are revealed by their relative importance.

To understand the intuition behind this treatment, recall that the mean infection period in our simulation model is 4.1 days, so without lost of generality every individual is assumed to spend 4.1 days to recover from the disease. The 4.1 days for different individuals, however, may be valued differently according to their importance in the society. So we normalize the lost days of disease for individuals in age 30 as 4.1 full days and discount others’ accordingly. The probability of infection is calculated empirically for each person by averaging the health outcomes over 30 replicates. The expected number of quality days lost in an epidemic is calculated by summing up the number of days lost to infection for all individuals, weighted by their respective ω_i.

Fairness axioms

Three axioms of fairness have been investigated in this research: taxpayer, life-cycle and investment-adjusted life cycle.

Taxpayer

This axiom simply states that households who pay more taxes should be given higher priority because they financially contribute most to the society. Given that we do not have data on taxes paid by the households, we use household income as a proxy to prioritize the individuals. Formally, we have V(X_i) = HI_i, where HI_i stands for the taxes paid by the household to which individual i belongs. Note that through this axiom, we can study another widely argued but opposite fairness concern i.e. the poorest first, which is defined by V(X_i) = −HI_i. Hence an intervention with fairness α under the taxpayer axiom could also be regarded as an intervention with fairness 1 − α under the poorest first axiom.

Life-Cycle

The life-cycle axiom states that priority should be given to the youngest individuals. It is justified by the idea that all individuals have the right to go through a complete life cycle, and the youngest need to be protected most because they have lived the smallest fractions of a complete life cycle. Formally, we have here V(X_i) = −Age_i, where Age_i is individual i’s age.

Investment-Adjusted Life Cycle

This axiom states that priority should be given to middle aged individuals as stated in (1) because a substantial investment has been made and the person has many more years left to live. Formally speaking, V(X_i) = ω_i, where ω_i is as defined in equation (1).

Results and Discussion

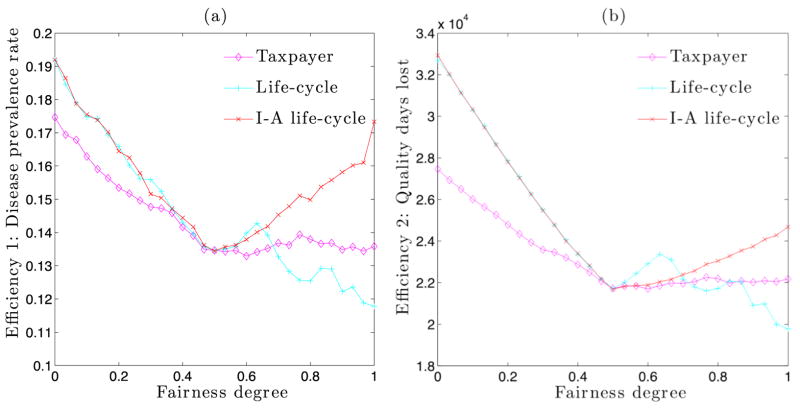
Figure 2 illustrates the relationship between the efficiency and fairness measures. Subfigure (a) shows the efficiency-fairness relationships when “disease prevalence rate” is used as the efficiency measure whereas subfigure (b) shows the same when “Quality days lost” is taken as the efficiency measure.

Figure 2.

Relationship between (negative) efficiency and fairness of vaccine allocation strategies. Subfigure (a) uses disease prevalence rate as the efficiency measure and subfigure (b) uses the quality days lost. Simulations are run on a synthetic social network of Montgomery County in Southwest Virginia. Only 20% of the population gets vaccinated. Vaccine efficacy is set at 90%.

The two subfigures show that the choice of efficiency measure does not qualitatively change the results: For the taxpayer and life-cycle fairness, both subfigures show that although an improvement in fairness is accompanied by an improvement in efficiency at low degree of fairness (below 0.5), no obvious trends exist for greater fairness degrees. More strikingly, in case of investment adjusted life cycle fairness, pursuing fairness actually harms the efficiency.

Note that, in both subfigures the curves intersect with each other at fairness degree of 0.5. This is not a coincidence; recall that according to the definition of the fairness degree of a specific distribution rule, the cumulative allocation function of the distribution rule with fairness degree 0.5 should be a straight line between points (0,0) and (1,1), i.e. curve $P_{0.5}^V$ in Figure 1. In other words, this distribution rule treats all individuals equally by allocating vaccines uniformly randomly to the society. Strictly speaking, there exist infinitely many distribution rules whose fairness degree is 0.5. After imposing the two-piece linearity requirement on the curves of cumulative allocation functions, however, the straight curve shown in Figure 1 is the unique rule for consideration. This specific distribution rule is fairness-independent; i.e. regardless of the fairness axiom, the fairness-degree-0.5 distribution rule remains the same. As stated before, we run 30 replicates for each distribution rule to deal with the randomness embedded in the selection process, and report the average of the simulation results; for all distribution rules that follow α = 0.5, the average results are statistically identical, as shown in Figure 2.

Although the curves exhibit significant variation for higher degrees of fairness, the left-hand-side of the curves share a common diminishing trend. This in turn suggests an important finding i.e. for each axiom of fairness, the inverse of it would not be a reasonable criterion. It would not make sense to give priority to older people or less invested individuals. It may be reasonable to consider, however, the inverse of the taxpayer based fairness axiom, i.e. giving priority to the poor, which is discussed below.

Vaccinate the Rich or the Poor?

Some people might argue that priority should be given to the poor people who otherwise may not be able to afford the vaccine. Our results in Figure 2 suggest that the poorest-first fairness is inconsistent with both efficiency measures. In subfigure (a), if the vaccines are distributed uniformly randomly to all individuals as in the case of α = 0.5, the expected disease prevalence is about 13.5%; however, after implementing the fairest distribution under the poorest-first axiom (i.e. the least fair choice under the taxpayer axiom), the disease prevalence increases to about 17.5%—the peak of the curve. On the other hand, the taxpayer fairness axiom neither improves the efficiency nor harms it—the right-hand-side of the corresponding curve is rather flat in both the subfigures.

Vaccinate Based on Age?

Next, we compare the results of the life-cycle and investment adjusted life-cycle based axioms. If the life-cycle principle is accepted as the axiom of fairness, pursuing the fairness of the interventions does help improve the efficiency in both cases despite some fluctuations at fairly high degree of fairness. Furthermore, the fairest distribution rule in this case leads to the most efficient result.

The result for the investment adjusted life-cycle rule, however, is more striking. Under our experimental settings, we find that assigning more weight to the middle-aged individuals and pursuing fairness harms the society both in terms of high prevalence rate as well as greater loss in the total number of quality days. Nevertheless, some researchers in the literature have argued that this kind of intervention combined with some other rules should be well aligned with efficiency [5,14].

One explanation for this could be that, assigning weights to individuals based on their investment and potential is quite different from assigning weights to them based on their relevance in the spread of an epidemic. The former mainly considers people’s values to the society whereas the latter depends on people’s positions in the social contact network. Although these two considerations may overlap to some extent, e.g. individuals in their 30s may have more social contacts than those much younger or much older, the weighting method for the investment adjusted life-cycle does not seem to be a good proxy for the connectivity in the social network.

Vaccinate Based on Network Degrees?

In a social network, individuals with the highest network-degrees or connectivity are the ones who may help propagate the epidemic by getting infected and infecting others. For this reason, it is often argued that priority should be give to the highest degree individuals [15]. On the other hand, the network degree weighted by duration, may be even more accurate because it not only accounts for the connectivity of the individual but also the duration of each contact. The problem is that even if it is a good strategy, in reality, it is hard to implement due to the lack of the availability of information on people’s contacts and their durations.

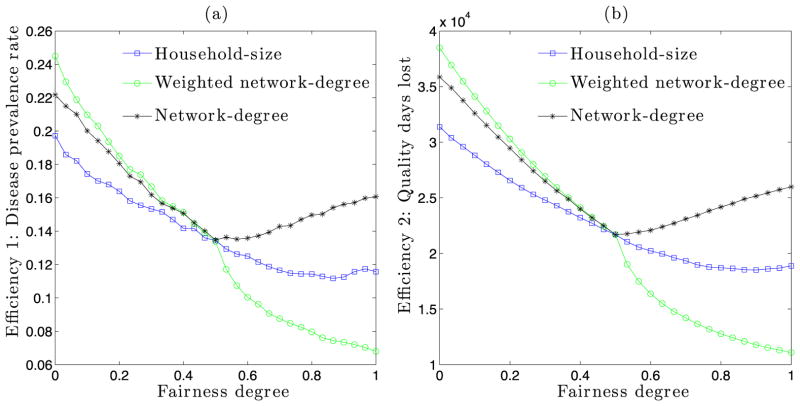
To overcome this challenge, we consider the size of the household as a proxy for the network degree and the weighted network degree. Although it represents only a subgraph of the entire social network for each individual, it is a useful proxy because it is more easily observable and implementable by policy makers. For our synthetic social network, we have complete information on each individual’s contacts, the duration of each contact as well as the household sizes. Figure 3 considers each of the options i.e. network degree, weighted network degree and the household size, to compare the trade-off between the efficiency and fairness.

Figure 3.

Relationship between (negative) efficiency and fairness of vaccine allocation strategies. Subfigure (a) uses disease prevalence rate as the efficiency measure and subfigure (b) uses the quality days lost. Simulations are run on a synthetic social network of Montgomery County in Southwest Virginia. Only 20% of the population gets vaccinated. Vaccine efficacy is set at 90%.

Figure 3 shows that the weighted network-degree based fairness is the most consistent with the measures of efficiency. The social costs in terms of prevalence and lost days continue to drop as the degree of fairness increases. The inverse of this strategy would lead to the highest social costs and level of inefficiency. Surprisingly, network-degree results are quite different from the weighted network degree results. For fairness degrees greater than 0.5, further improvement in the fairness actually reduces efficiency. This result suggests that contact durations are more important than the number of contacts in the spread of the epidemic and hence the network degree, although more observable, may not be used as a proxy for the weighted degree.

On the other hand, household size seems to be a good proxy for the weighted degree. This is because within-household contacts play an important role and represent a large part of the interaction duration for the individuals. Furthermore, data on household size is conveniently available from the census. In case of household size, fairness improves with the efficiency under both measures in Figure 3. This means that in our specific setting, if the authority has to choose a fairness principle that is implementable and leads to efficient results, it should be the household-size fairness.

Mixed Principle

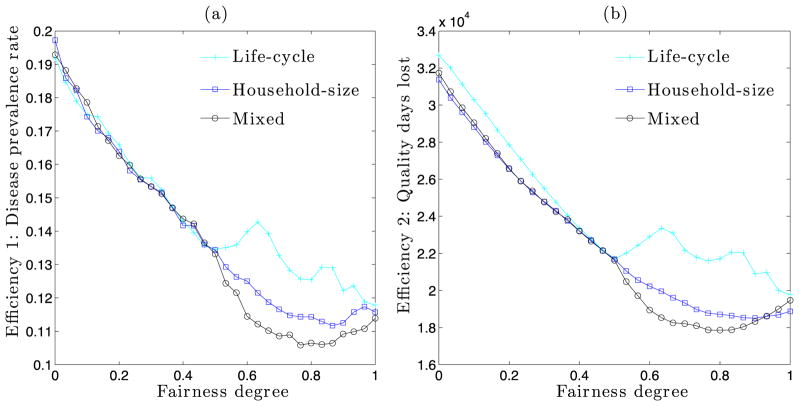
All fairness principles considered so far have been based on a single variable, but recall that in our framework, fairness could be based on a vector of demographic variables X_i. This means we should be able to evaluate if a multi-variable criteria performs better than the individual ones. In particular, the life-cycle fairness principle is the most consistent with the efficiency measures as compared to the other fairness criteria in Figure 2 and the household-size principle performs better than the others in Figure 3 and is implementable. It is possible that a combination of them performs better than either of them individually, so we design a new criterion, which gives priority to young individuals from large households.

The relationship between the mixed fairness and efficiency is illustrated in Figure 4. We also include the results of the life-cycle and household-size fairness in the same figure for comparison purposes. As shown in the figure, the mixed fairness is most well aligned with the efficiency measures. This suggests that, for our specific example, distribution rules based on the mixed fairness principle could be an ideal choice for the public health officials who aim to achieve both efficiency and fairness.

Figure 4.

Relationship between (negative) efficiency and fairness of vaccine allocation strategies. Subfigure (a) uses disease prevalence rate as the efficiency measure and subfigure (b) uses the quality days lost. Simulations are run on a synthetic social network of Montgomery County in Southwest Virginia. Only 20% of the population gets vaccinated. Vaccine efficacy is set at 90%.

Conclusions

This study contributes to the public health debate on who to protect when everyone cannot be protected, and how to prioritize the distribution of limited vaccines. Allocating limited resources is always a challenge but lives are at stake when it comes to medical resources. This paper, for the first time, provides a general framework to assess the fairness and efficiency of the public health intervention policies. It develops appropriate axioms of fairness and examines the trade-offs between the efficiency and fairness under these axioms by providing objective ways of measuring fairness. If public health authorities come up with a new distribution rule, this framework can help determine its degree of fairness and can help alleviate some of the ethical concerns.

Table 1.

Summary of Variables and Notations

L	Stockpile of vaccines
|N|	Population size
ωi	Weight of individual i while computing efficiency
Xi	Vector of demographics for individual i
V(Xi)	Individual i’s priority, given Xi and fairness characterized by V(·)
α	A generic fairness degree in interval [0,1]
D	A generic vaccine allocation rule
PD,V(·)	Cumulative allocation function given allocation rule D and fairness V(·)
D_α(V)	Uniquely determined allocation rule whose fairness degree is α, given V(·)
$P_{\alpha }^V$	Cumulative allocation function of allocation rule D_α(V)