Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Mar 17;5:9158. doi: 10.1038/srep09158

Shubnikov - de Haas oscillations, weak antilocalization effect and large linear magnetoresistance in the putative topological superconductor LuPdBi

Orest Pavlosiuk 1, Dariusz Kaczorowski 1, Piotr Wiśniewski 1,a
PMCID: PMC4361847  PMID: 25778789

Abstract

We present electronic transport and magnetic properties of single crystals of semimetallic half-Heusler phase LuPdBi, having theoretically predicted band inversion requisite for nontrivial topological properties. The compound exhibits superconductivity below a critical temperature Tc = 1.8 K, with a zero-temperature upper critical field Bc2 ≈ 2.3 T. Although superconducting state is clearly reflected in the electrical resistivity and magnetic susceptibility data, no corresponding anomaly can be seen in the specific heat. Temperature dependence of the electrical resistivity suggests existence of two parallel conduction channels: metallic and semiconducting, with the latter making negligible contribution at low temperatures. The magnetoresistance is huge and clearly shows a weak antilocalization effect in small magnetic fields. Above about 1.5 T, the magnetoresistance becomes linear and does not saturate in fields up to 9 T. The linear magnetoresistance is observed up to room temperature. Below 10 K, it is accompanied by Shubnikov-de Haas oscillations. Their analysis reveals charge carriers with effective mass of 0.06 me and a Berry phase very close to π, expected for Dirac-fermion surface states, thus corroborating topological nature of the material.

Large family of half-Heusler compounds that crystallize in a noncentrosymmetric cubic MgAgAs-type structure attracts much attention due to their remarkable magnetic and electrical transport properties1,2. Recent ab initio electronic structure calculations have predicted that several dozen of half-Heusler compounds, due to a strong spin-orbit coupling, have inverted bands requisite for topological properties3,4,5. Topological insulators (TI) constitute a new class of materials, which are insulating in the bulk, but at the same time their surface states are protected from backscattering by Z2 topology6,7,8. These surface states are theoretically described as massless Dirac fermions with linear dispersion and lifted spin-degeneracy. Such properties open new prospects for spintronic applications. In contrast to two-dimensional (2D) TIs, like HgTe, some of half-Heusler phases possess not only band inversion at an odd number of time-reversal-invariant momenta, but also may have a bulk band-gap opening under uniaxial pressure, which lowers the crystal symmetry9. In result, the rare-earth (RE) based half-Heusler compounds (REPdBi, REPtBi, REPdSb, REPtSb) may possibly form the biggest group of the three-dimensional (3D) TIs.

After the discovery of the 3D TI systems, a quest for superconductivity in materials with the non-trivial topology of electron bands started due to their potential applications in topological quantum computing10,11,12. Topological superconductor (TS) is a material characterized by protected Majorana surface states and bulk consisting of mixed-parity Cooper-pair states13,14. The first theoretically forecasted and experimentally discovered TS was Bi2Se3 doped with Cu atoms15,16. Since it remains problematic to clarify the nature of the surface Majorana fermions in the inhomogeneous crystals of CuxBi2Se3 (Ref. 17), new TS materials are sought extensively among low-carrier-density semiconductors, whose Fermi surfaces are centered around time-reversal-invariant momenta18. In this context, the superconductivity recently found in the bismuthides REPtBi: LaPtBi (Tc = 0.9 K)19, LuPtBi (Tc = 1.0 K)20, and YPtBi (Tc = 0.77 K)21,22,23 appears most attracting. Besides, the content of magnetic rare-earth may bring about other properties, such as long-range antiferromagnetic ordering or heavy fermion behavior24.

Potentially, the rare-earth palladium-bearing bismuthides REPdBi are equally interesting from the point of view of topological and superconducting properties. Magnetic and transport behaviors of these compounds have been first investigated on polycrystalline samples25,26,27,28. Most of them have been characterized as local-moment antiferromagnets (with Néel temperatures TN = 2–13 K) with electrical properties characteristic of semimetals or narrow-band semiconductors. Recently, diamagnetic YPdBi has been reported to exhibit large linear magnetoresistance (LMR) and Shubnikov-de Haas (SdH) quantum oscillations at low temperatures, and its nontrivial topological nature has been evaluated29. In turn, CePdBi has shown some features of incipient superconductivity (Tc = 1.3 K) emerging in the antiferromagnetic state (TN = 2 K), and a hypothesis on topological character of the compound has also been formulated30. Similarly, ErPdBi has been reported to show the coexistence of antiferromagnetism (TN = 1.06 K) and superconductivity (Tc = 1.22 K), and hence acclaimed as a new platform for the research of the reciprocity of magnetic order, superconductivity, and nontrivial topological states31. However, in our own study on single-crystalline ErPdBi, we could not confirm those findings because no clear-cut evidence for any intrinsic superconducting state in this material has been observed32. Most recently, superconductivity (Tc = 1.7 K) has been reported for nonmagnetic LuPdBi, accompanied by a 2D weak antilocalization (WAL) effect33. Since the latter feature is considered as a fingerprint of topological surface states, the compound was suggested to be a topological superconductor with Majorana edge states33. In this work, we present the results of our comprehensive magnetic susceptibility, specific heat and electrical resistivity measurements performed on high-quality single crystals of LuPdBi. The obtained data are here critically compared with those reported in Ref. 33.

Results

Electrical resistivity and Hall effect

The temperature dependence of the electrical resistivity, ρ, of the LuPdBi single crystal is shown in Figure 1a. From 300 K down to ≈170 K, the resistivity displays a semiconducting-like character (dρ(T)/dT < 0), then at lower temperatures ρ(T) becomes typical for metals. Such a behavior of the resistivity is common for the REPdBi compounds26,27,28,31,32. As demonstrated in Figure 1b, the overall behavior of the electrical resistivity in LuPdBi can be well described over an extended range of temperature considering two independent channels for charge transport: semiconducting- and metallic-like. The former contribution is written as ρs(T) = a exp(−Eg/kBT), where Eg is an energy gap between valence and conduction bands, while the latter one is expressed as ρm(T) = ρ0 + bT2 + cT, where ρ0 is the residual resistivity due to scattering on structural defects, the second term represents electron-electron scattering processes, while the third one accounts for scattering on phonons. The total conductance, σ(T) ≡ 1/ρ(T) is the sum σ(T) = σs(T) + σm(T), where σs(T) ≡ 1/ρs(T) and σm(T) ≡ 1/ρm(T). Fitting these expressions to the experimental data of LuPdBi in the wide temperature interval from 5 K to 300 K, yielded the parameters: a = 296 mΩcm, Eg = 11.5 meV, ρ0 = 226 mΩcm, b = 0.018 mΩcm/K2, and c = 1.72 mΩcm/K. The so-derived energy gap Eg is very close to 15.2 meV reported for LuPdBi in Ref. 25, and very similar to the values reported for other REPdBi phases26,27,28,31,32.

Figure 1. Electrical transport properties of single-crystalline LuPdBi.

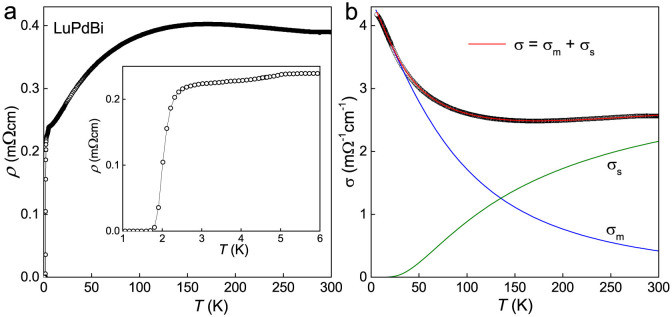
Figure 1

Open in a new tab

(a) Temperature dependence of the electrical resistivity up to 300 K. Inset: low-temperature resistivity data revealing a superconducting transition near 2 K. (b) Temperature dependence of the electrical conductivity in the normal state fitted by the function σ(T) = σm(T) + σs(T) (red line) described in the text. The metallic and semiconducting contributions are represented by blue and green curves, respectively.

It is worth noting that the temperature variation of the resistivity of LuPdBi single crystal obtained in the present work somewhat differs from that reported before by Xu et al.33, who observed a monotonous increase of the resistivity with decreasing temperature from 300 to 2 K, and attempted to analyze their ρ(T) data above 90 K in terms of 3D variable-range hoping model. However, also in that case, the transport at low-temperatures was attributed to the metallic channel (though no quantitative analysis was made).

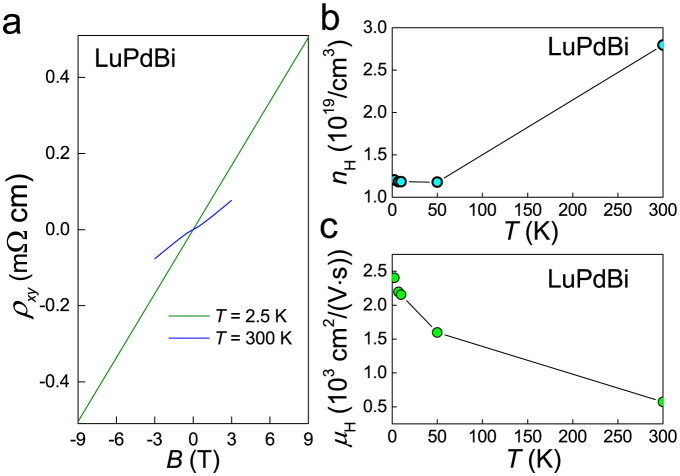
As displayed in Figure 2a, the Hall resistivity of LuPdBi measured at 2.5 K is a linear function of the applied magnetic field up to 9 T. The Hall coefficient evaluated from this data was RH = 0.0565 mΩcm/T. Almost identical magnitude of RH was derived from ρxy(B) collected at T = 4, 7, 10 and 50 K (not shown). Assuming a single parabolic band, one may estimate the Hall carrier concentration, nH, to be at low temperatures 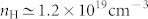Inline graphic. Above 50 K, nH was found to increase with increasing temperature and to attain at 300 K a value of 2.8 × 1019 cm−3 (see Figure 2b). In turn, as demonstrated in Figure 2c, the so-obtained Hall carrier mobility, μH, gradually decreases with increasing temperature, from the value 2404 cm2V−1s−1 at T = 2.5 K to 573 cm2V−1s−1 at 300 K.

Figure 2. Hall effect in LuPdBi.

Figure 2

Open in a new tab

(a) Magnetic field dependence of the Hall resistivity measured at 2.5 and 300 K. (b) Temperature variation of the Hall carrier concentration. (c) Temperature variation of the Hall carrier mobility.

The inset to Figure 1a displays the resistivity of single-crystalline LuPdBi at the lowest temperature studied. In agreement with Ref. 33, the compound undergoes a transition to superconducting state. The resistivity starts to drop near 2.2 K and becomes zero below 1.8 K. Using a criterion of 90% drop in the resistivity value from the point where the ρ(T) curve starts bending down, Tc = 1.9 K was determined. This value is slightly higher than Tc = 1.7 K reported before for LuPdBi (Ref. 33), and remains the highest Tc found so far for the RETBi superconductors. As can be inferred from the inset to Figure 1a, besides the superconducting phase transition, we observed a small resistivity drop below 5 K. The existence of a fairly similar anomaly in ρ(T) near this temperature has previously been reported for a few other half-Heusler bismuthides and antimonides26,34, and tentatively attributed to superconductivity of thin films of metallic Bi(Sb) located at grain boundaries, yet the actual nature of this feature remains unclear.

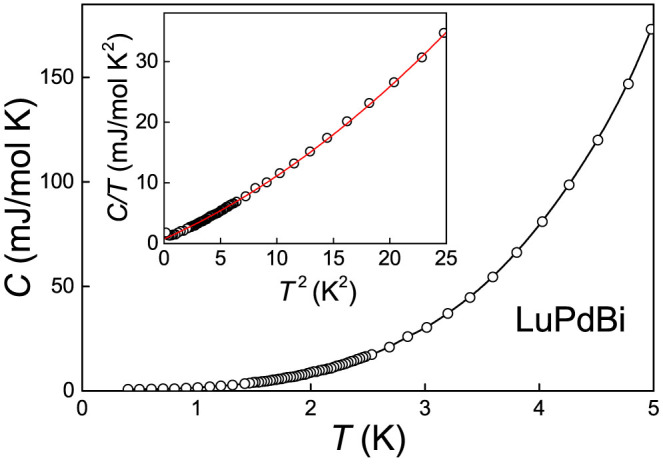
The temperature dependence of the electrical resistivity of LuPdBi measured in external magnetic fields up to 2 T is shown in Figure 3a. The width of superconducting transition increases gradually from 0.4 K at zero field to 0.7 K at 1 T. The critical temperature defined by the drop of the resistivity to 90% of its normal-state value varies with magnetic field in a manner presented in Figure 3b. The so-derived Bc2(T) dependence has a positive curvature, characteristic of two-band clean-limit type-II superconductors, like YNi2B2C, LuNi2B2C (Ref. 35) or MgB2 (Ref. 36). Though our sample exhibits the residual resistivity ratio ρ(300 K)/ρ(4 K) of only 1.8, the observation of SdH oscillations described below, indicates its very good quality, which allows us to consider the observed superconductivity to have a clean limit character. Indeed, as displayed in Figure 3b, the experimental Bc2(T) data can be well approximated in the whole temperature range by the expression 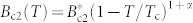Inline graphic, previously applied, e.g., to MgB2 (Ref. 36). The fitting parameter 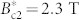Inline graphic can be considered as the upper limit for the upper critical field Bc2(0). The parameter α = 0.496(22) is significantly larger than 0.32 and 0.24 (0.25) reported for MgB2 and LuNi2B2C (YNi2B2C), respectively35,36. Using the relation 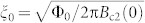Inline graphic, one obtains an estimate for the coherence length ξ0 = 17 nm. This value is about three times larger than those reported for MgB2 (Ref. 36), YNi2B2C and LuNi2B2C (Ref. 37). Nevertheless, it is still distinctly smaller than the mean free path l = 60 nm derived from the SdH data (see below) and this comparison corroborates our assumption that the superconductivity in LuPdBi occurs in the clean limit (l/ξ0 > 1). The Werthamer-Helfand-Hohenberg approximation38 provides an estimate for the orbitally limited upper critical field 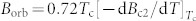Inline graphic to be 0.5 T. The Pauli limited upper critical field BP can be evaluated from the equation 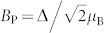Inline graphic, where the BCS energy gap Δ = 1.76 kBTc. The estimate for the measured crystal of LuPdBi is BP = 3.5 T. Thus, the Maki parameter αM = Borb/BP = 0.2 was obtained. One can conclude that the superconductivity in LuPdBi is Pauli limited. It is worthwhile recalling that the relationship Borb < Bc2 < BP was established also for the related half-Heusler superconductors YPtBi and LuPtBi (Refs. 20 and 22).

Figure 3. Superconductivity in LuPdBi.

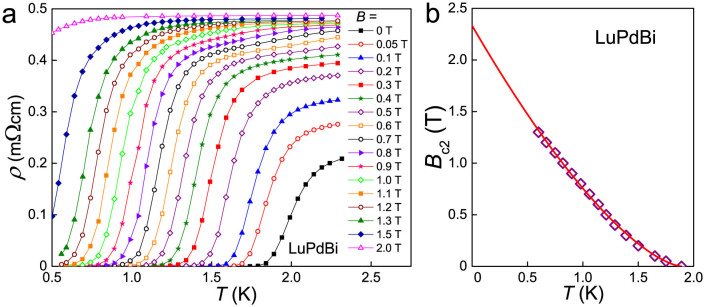
Figure 3

Open in a new tab

(a) Low-temperature dependencies of the electrical resistivity measured in different external magnetic fields. (b) Upper critical field as a function of temperature. Solid line represents the fit of the function 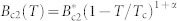Inline graphic described in the text.

Thermodynamic properties

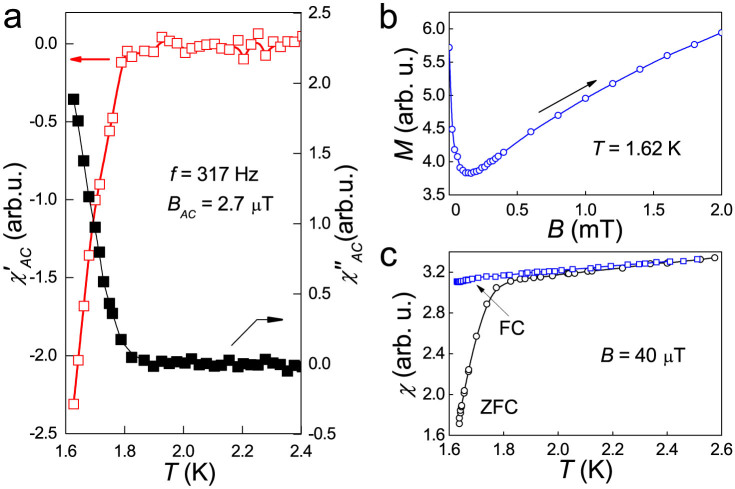
Figure 4 displays the results of magnetic measurements performed on a collection of several single crystals of LuPdBi. Both components of the AC magnetic susceptibility show clear anomalies at 1.8 K typical for a superconducting transition. The corresponding feature is seen on the temperature dependence of the DC magnetic susceptibility measured in a weak magnetic field upon cooling the sample in zero field. Comparison with the data obtained in field-cooled regime reveals superconducting current screening effect. Furthermore, the magnetization M measured at the lowest temperature T = 1.62 K attainable in our experimental setup exhibits a field variation characteristic of type-II superconductors. All these features are in concert with the electrical resistivity data and manifest the emergence of the superconducting state in LuPdBi below Tc = 1.8(1) K. From the M(B) curve presented in Figure 4b one can roughly estimate the upper limit for the lower critical field Bc1 to be of 0.05 mT. Then, the formula 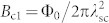Inline graphic yields the penetration depth λsc = 3629 nm.

Figure 4. Magnetic properties of single-crystalline LuPdBi.

Figure 4

Open in a new tab

(a) Temperature variations of the real and imaginary components of the AC magnetic susceptibility taken with a magnetic field of 2.7 μT alternating with a frequency of 317 Hz. (b) Field dependence of the magnetization measured at T = 1.62 K upon cooling the specimen in zero magnetic field. (c) Low-temperature dependence of the DC magnetic susceptibility recorded upon cooling the specimen in zero magnetic field (ZFC) and in an applied field of 40 μT (FC). All solid lines are guides to the eye.

As can be inferred from Figure 5, the low-temperature dependence of the specific heat of LuPdBi is featureless. In particular, no obvious anomaly is seen at the superconducting phase transition. Remarkably, analogous situation occurs for other half-Heusler superconductors: LuPtBi (Ref. 39) and YPtBi (Ref. 40). Lack of any feature in C(T) at Tc in these systems may be due to the fact that superconductivity originates from topologically protected surface states, which occupy a very small volume in relation to the volume of entire sample. The only exception is the result reported by Xu et al.33 who observed for their single crystal of LuPdBi a prominent BCS-like specific heat jump at the onset of superconductivity. A critical comment on this data can be found in Supplementary Material.

Figure 5. Heat capacity of LuPdBi.

Figure 5

Open in a new tab

Low-temperature dependence of the specific heat. Inset: specific heat over temperature ratio as a function of temperature squared. Solid red line represents the fit to the function C/T = γ + βT2 + δT4 discussed in the text.

As shown in the inset to Figure 5, below 5 K, the C/T(T) variation can be well described by the standard formula C/T = γ + βT2 + δT4 with the electronic specific heat coefficient γ = 0.75 mJ/mol K2 and the coefficients of the phonon contribution β = 0.8 mJ/mol K4 and δ = 0.02 mJ/mol K6. From the relation ΘD = (12nRπ4/5β)1/3 (R is the gas constant and n is the number of atoms per formula unit) one derives the Debye temperature ΘD = 194 K. The obtained values of γ and ΘD are close to those reported in Ref. 25: γ = 0.096(327) mJ/mol K2 and ΘD = 194.9 K but strongly disagree with the results derived for LuPdBi by Xu et al.: γ = 11.9 mJ/mol K2 and ΘD = 295 K (Ref. 33). It is worth recalling that for other nonmagnetic RETBi the values of γ are also very small: 0.1 for YPtBi (Ref. 41) and 0.06 mJ/mol K2 LuPtBi (Ref. 39).

Magnetoresistance

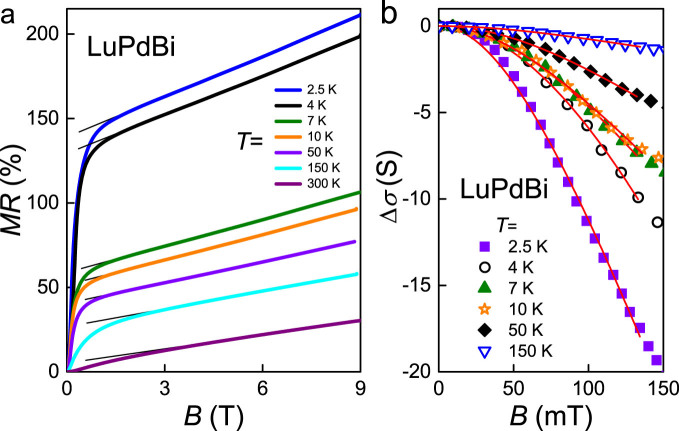
Figure 6a shows the magnetoresistance data of LuPdBi, defined as MR(B) = [ρ(B) − ρ(0)]/ρ(0)], with ρ(B) and ρ(0) denoting the electrical resistivity measured in applied field and in zero field, respectively. Remarkably, at 2.5 K, MR is as large as 210% in the strongest field of 9 T achievable in our experimental setup. With increasing temperature, MR gradually diminishes, yet even at 300 K it reaches about 30% in B = 9 T, which is a very large value. A striking feature of MR(B) is its linear nonsaturating behavior. Above a certain magnetic field (ranging from 1.5 T at 2.5 K to 3 T at 300 K), MR becomes proportional to B with a slope systematically decreasing with increasing temperature, from about 8%/T at the lowest temperatures, down to 3%/T at 300 K.

Figure 6. Transverse magnetotransport in single-crystalline LuPdBi.

Figure 6

Open in a new tab

(a) Field dependence of the magnetoresistance measured at different temperatures. Solid lines emphasize the linear behavior. (b) Low-field variations of the conductance measured at different temperatures. Solid curves represent the functions given in Eq. 1, which account for the weak antilocalization effect.

In conventional theory of metals and semiconductors, MR should grow quadratically in weak magnetic fields and then saturate in strong fields42. Linear magnetoresistance (LMR) is a phenomenon reported for narrow-gap semiconductors43,44,45, multi-layered graphene46, topological insulators47,48,49 and Dirac semimetals50,51. Two main approaches were made to understand this behavior. In their classical theory, Parish and Littlewood attributed LMR to material inhomogeneities, which give rise to sturdy spatial fluctuations in the electrical conductivity52. In turn, Abrikosov developed the quantum magnetoresistance theory53, that predicts LMR in zero-gap band systems with linear energy dispersion being in the extreme quantum limit (EQL) in which all electrons are confined to the first Landau level. The Abrikosov theory was demonstrated to work correctly for graphene46 and topological insulator Bi2Se3 nanosheets47, with topological surface states possessing a linear energy dispersion over wide temperature interval.

For single-crystalline LuPdBi, the detailed X-ray and microprobe characterization revealed a very good sample quality, which was further confirmed by the observation of SdH oscillations (see below). This prompts us to dismiss the classical theory. On the other hand, the compound shows LMR behavior virtually identical to that reported for silver chalcogenides, interpreted within the quantum magnetoresistance theory53. Moreover, the SdH data indicated that the studied crystal was in an EQL regime at temperatures up to at least 10 K. All these findings suggest that the quantum approach is perfectly applicable, and the observed LMR effect is a hallmark of Dirac-like band structure in this putative topological semimetal.

In weak magnetic fields, MR of LuPdBi displays a very abrupt rise. For example, at T = 2.5 K, MR attains a huge value of 150% already in a field of 1.5 T. Similar situation, but with lower MR increase, occurs at higher temperatures, up to 150 K. Such sharp cusps on the MR isotherms are reminiscent of a weak antilocalization (WAL) effect, which relies on destructive interference of the electron wave functions between two closed paths with time-reversal symmetry. In topologically nontrivial materials, WAL is enhanced due to ability of topologically protected surface states to collect a π Berry phase due to the helical spin polarization. Thus, the WAL effect may be considered as a manifestation of surface-state transport in LuPdBi.

Taking into account the coexistence in our LuPdBi sample of two parallel conducting channels (see Figure 1b and the discussion above), in conjunction with the plausibly topological nature of the compound, one may assume that at temperatures below ≈25 K the conductivity was almost entirely determined by the metallic channel due to the sample surface. Consequently, the sheet resistance Rs(B) of the conducting surface of the sample can be derived. Figure 6b displays the sheet magnetoconductance of LuPdBi, Δσ(B) = (1/Rs(B)) − (1/Rs(0)), where Rs(B) and Rs(0) represent the data obtained in applied field and zero field, respectively. These experimental results can be analyzed in terms of the Hikami-Larkin-Nagaoka formula54

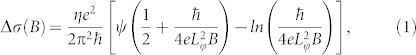graphic file with name srep09158-m1.jpg

where Lφ stands for a phase coherence length, η is a parameter depending on the strength of spin-orbit interaction and magnetic scattering, ψ(x) is digamma function, while the other symbols have their usual meanings. For T = 2.5 K, the fitted parameters are Lφ = 49.6(2.2) nm and 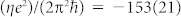Inline graphic and are comparable to Lφ ≈ 95 nm and 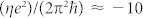Inline graphic obtained for the same compound in Ref. 33. This finding strongly supports our assumption of the 2D topological nature of the metallic conducting channel in LuPdBi. For higher temperatures, where the contribution due to the bulk channel becomes noticeable, the fits of Eq. 1 to the experimental data are still of good quality, but the value of η decreases with increasing temperature. More detailed description of the dependence of WAL parameters on temperature is given in Supplementary Material. It is worth mentioning that a similar analysis of MR(B) of LuPdBi was presented in Ref. 33, however the fitted values of η were ≈105 larger than that expected for a TI system (see also our comment in Supplementary Material).

Shubnikov-de Haas oscillations

SdH oscillations are being recognized as a powerful tool in the studies of 3D TIs9. Dirac fermions are characterized by a π Berry phase (for ordinary metals the Berry phase is equal to zero), and the phase factors of the oscillations reveal the Berry phase values for the system. Observations of SdH oscillations have been reported in some candidate topological materials from the half-Heusler family19,21,29,32. For our LuPdBi samples, SdH oscillations were well resolved at temperatures up to 10 K, hence indicating very good quality of the single crystals measured. Figure 7a shows the oscillatory component Δρxx, obtained by subtracting a background from the ρxx(B) isotherms. The oscillations are clearly periodic in 1/B, however their frequency is very low. Fast Fourier transform (FFT) analysis of these data yielded rather poor quality spectra with broad peaks corresponding to a single temperature-independent frequency ≈10 T, shown in inset to Figure 7a. Obviously, the broadness of FTT peaks comes from low frequency of the oscillations and only less than three periods covered by our measurements. In order to obtain more reliable value of the oscillation frequency fSdH we perfomed direct fitting of the standard Lifshitz-Kosevich (L-K) expression where 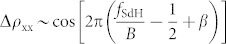Inline graphic with β being a phase shift9,55. The analysis yielded fSdH = 11.9 T and β = 0.431(2).

Figure 7. Shubnikov–de Haas oscillations in LuPdBi.

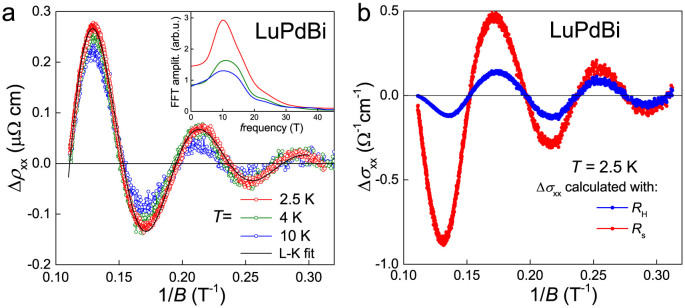
Figure 7

Open in a new tab

(a) Oscillatory component of the electrical resistivity as a function of inverse magnetic field, measured at different temperatures. Black solid line represents a fit of 2.5 K data with L-K formula. Inset: FFT spectra obtained for different temperatures. (b) Oscillatory component of longitudinal electrical conductivity at T = 2.5 K calculated with macroscopic Hall resistivity (blue line) or surface channel Hall resistivity (red line).

The oscillation frequency is related to the extremal cross section area AF of the Fermi surface through the Onsager relation 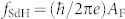Inline graphic, where 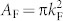Inline graphic. The value of fSdH derived for LuPdBi implies the Fermi vector kF = 0.019 Å−1 that corresponds to a 2D carrier density 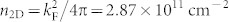Inline graphic (we assume lifted spin degeneracy). The temperature dependence of the resistivity oscillations amplitude is given by the standard L-K expression Δρxx(T) ~ λ(T)/sinh(λ(T)), where 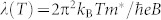Inline graphic and m* is the effective cyclotron mass55. Fitting this equation to the experimental data of LuPdBi (see Figure 8a) one obtains m* = 0.06 me, where me is the free electron mass. From the values of kF and m*, the Fermi velocity 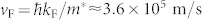Inline graphic and the Fermi energy 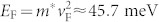Inline graphic were derived. Since calculation of the Sommerfeld coefficient for a 2D Fermi surface is impossible (it encloses zero volume), we used the formula 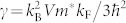Inline graphic (corresponding to spherical Fermi surface) and obtained the Sommerfeld coefficient equal to 0.003 mJ/mol K2. This value is much smaller than 0.75 mJ/mol K2 derived from the specific heat data. This finding indicates that the SdH oscillations originate from 2D states Fermi surface or from a tiny 3D Fermi surface, much smaller than the bulk one contributing to the specific heat. If the bulk states were contributing to SdH oscillations one should observe high cyclotron frequency (large kF) and/or large cyclotron mass, not seen in LuPdBi. Moreover, the Hall concentration of 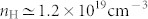Inline graphic is over 50 times larger than 2.3 × 1017 cm−3 obtained when we assumed that SdH effect originates from 3D spherical Fermi surface. Such discrepancy in the Hall and SdH concentrations further supports the conjecture that the SdH oscillations in LuPdBi originate from the surface states.

Figure 8. Analysis of the SdH oscillations in LuPdBi.

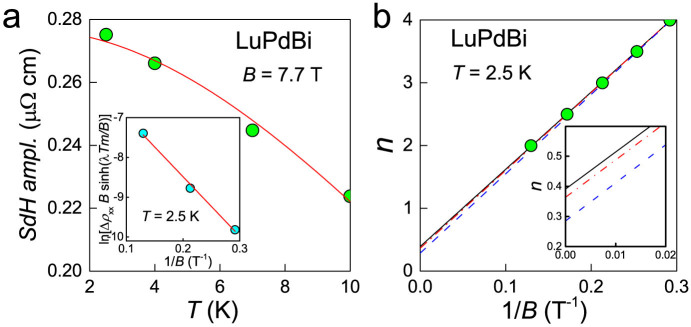
Figure 8

Open in a new tab

(a) Lifshitz-Kosevich description (solid line) of the temperature dependence of the SdH amplitude. Inset: Dingle plot for the oscillations measured at 2.5 K. Solid straight line determines the Dingle temperature (see the text). (b) Landau-level fan diagram for the SdH oscillations measured at 2.5 K. Fitted straight solid line intersecting the ordinate axis at 0.4 indicates the Berry phase very close to π. Dashed (blue) line represents the fit to extrema in conductivity Δρxx derived with macroscopic Hall coefficient, RH. Dot-dashed (red) line corresponds to Δσxx derived with Hall coefficient of surface channel Rs (see text for explanation). Inset shows the blow up of the area where the fitted lines intercept ordinate axis.

Knowing m*, one can carry out the Dingle analysis shown in the inset to Figure 8a. The lifetime τ of the carriers can be found from the Dingle temperature 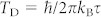Inline graphic. The slope of the linear fit to the data yielded TD = 16.9 K, which gave τ = 7.2 × 10−14 s. Ergo, the mean-free path l = vFτ = 26 nm and the surface mobility 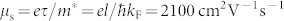Inline graphic were obtained. Metallicity parameter kFl of LuPdBi is then equal to 5.

Figure 8b presents the Landau-level fan diagram for the SdH oscillations in LuPdBi at 2.5 K. Positions of the extrema in Δρxx(1/B) are marked with circles as a function of their number (n for maxima and 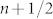Inline graphic for minima). Though the very small value of fSdH allowed to observe only five such extrema, a good linear fit could be performed, with an intercept of 0.391(26), shown as a solid black line. However, the choice of resistance ρxx or conductance σxx for Landau level indexing may be very important and yield different phase factor9. Since the Hall resistivity of LuPdBi measured at 2.5 K was ρxy(B = 9 T) = 0.54 mΩcm, that is very close to ρxx = 0.50 mΩcm, it cannot be ignored in analysis of the SdH oscillations. We thus calculated 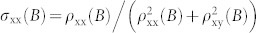Inline graphic and extracted the oscillatory component Δσxx(1/B). These data are shown as blue points in Figure 7b. Straight line fitted to the positions of their extrema (shown as dashed blue line in Figure 8b) yielded the phase factor of 0.285(40) (for clarity the datapoints are not shown).

But the case of LuPdBi is an example (which very likely can be extended to other bulk samples with topologically nontrivial states on their surface) where the oscillatory component of σxx(1/B) should be derived in a different manner. Our sample, as the temperature dependence of resistivity indicates, contains two parallel conduction channels: metallic and semiconducting (Figure 1b). At low temperatures, the latter makes negligible contribution to the conductivity, but may still play an important role in the Hall effect. However, the SdH oscillations we observe seem to originate from surface carriers. Hence, the Hall resistivity of the surface channel should be used for Δσxx(1/B) calculation. It can be easily obtained as ρs,xy(B) = RsB, where Rs is the Hall coefficient of the surface channel, which can be derived from the formula Rs = t/(en2D), where n2D is the surface carrier concentration and t is the sample thickness9. For our sample of LuPdBi, Rs = 0.0146 mΩcm/T at 2.5 K. After recalculating σxx(B) as 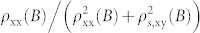Inline graphic, extracting its oscillatory component (shown with red in Figure 7b) and finding positions of its extrema on 1/B axis, we could fit another straight line resulting in the phase factor of 0.364(44) (note dot-dashed red line in Figure 8b).

Most remarkably, all the applied methods of determinig the phase factor (we believe that the electronic nature of 3D TIs is most appropriately accounted for in that employing Rs) yielded values very close to 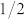Inline graphic, which was theoretically predicted for Dirac fermions. Small departure of the experimental value from 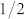Inline graphic may arise from Zeeman coupling effect56,57 or small deviation of the energy dispersion of Dirac fermions from the linear one58. Nevertheless, the observation in LuPdBi of a π Berry phase is another strong indicator of the topologically nontrivial character of the compound.

Conclusions

We synthesized high-quality single crystals and investigated the electronic properties of a putative 3D topological superconductor LuPdBi. The electrical transport in the compound was found to be driven by two parallel conducting channels: metallic and semiconducting, with the negligible contribution of the latter at low temperatures. The superconductivity emerges at Tc = 1.9 K and is characterized by the upper critical field Bc2(0) ≤ 2.3 T. It is of type II clean-limit BCS. Remarkably, no feature in the heat capacity is observed near the onset of superconducting state, which rather rules out its bulk character. Instead, we tend to attribute the superconductivity in LuPdBi to the surface states.

The compound shows the linear-in-B magnetoresistance, as high as 210% at 2.5 K and over 30% at 300 K (in magnetic field of 9 T). In low magnetic fields, there clearly occurs the weak antilocalization effect. Both features are hallmarks of the topologically protected states. Furthermore, the observed SdH oscillations yield the very small effective mass of 0.06 me and the Berry phase very close to π, in concert with the topological nature of LuPdBi, characterized by the Fermi surface sheet containing massless, extremely mobile Dirac fermions.

In summary, based on the results of our study, we postulate that at low temperatures, below about 10 K, LuPdBi effectively becomes a topological insulator, with negligible contribution of its bulk to the electronic transport and with the topological nature of its surface states being clearly reflected in the physical properties. The superconductivity in LuPdBi seems to emerge from the topologicaly protected surface states and further confirmation, both experimental and theoretical, of this conjecture is a challenging task for the future.

Methods

Material preparation

Single crystals of LuPdBi were grown from Bi flux. The elemental constituents of high purity (Lu: 99.99 wt.%, Pd: 99.999 wt.%, Bi: 99.9999 wt.%), taken in atomic ratio 1:1:12, were placed in an alumina crucible, and sealed under argon atmosphere inside a molybdenum ampule. The reactor was heated slowly up to 1300°C and kept at this temperature for 15 hours. Next, it was cooled down to 1000°C at a rate of 3°C/hour, and then to room temperature at a rate of 5°C/hour. The crucible with the charge was extracted from the molybdenum ampule, covered with another alumina crucible filled with silica wool and resealed in an evacuated quartz tube. Then, the tube was heated up to 900 K at which point the excess of Bi flux was removed by centrifugation. The crystals obtained by this technique had a shape of cubes or plates, with dimensions up to 0.5 × 0.5 × 0.5 mm3 or 0.1 × 0.5 × 3 mm3, respectively. They had metallic luster and were stable against air and moisture.

Material characterization

Powdered single crystals of LuPdBi were characterized at room temperature by powder X-ray diffraction (PXRD) carried out using an X'pert Pro PANanalitical diffractometer with Cu-Kα radiation. The crystal structure refinements and the theoretical PXRD pattern calculations were done employing the FULLPROF program59. Quality of the samples studied was also verified by single crystal X-ray diffraction (SCXRD) performed at room temperature on an Oxford Diffraction Xcalibur four-circle diffractometer equipped with a CCD camera and using Mo-Kα radiation. The SCXRD data analysis was done using the program package SHELXL-9760. The results of PXRD and SCXRD investigations are presented in Supplementary Material.

Chemical composition of the LuPdBi crystals was examined on a FEI scanning electron microscope (SEM) equipped with an EDAX Genesis XM4 spectrometer. The specimens were glued to a SEM stub using carbon tape. The crystals were found homogeneous and free of foreign phases, with the chemical compositions very close to the ideal one (for details see Supplementary Material).

Physical measurements

Electrical resistivity and Hall measurements were carried out from 0.4 K to 300 K in applied magnetic fields up to 9 T using a conventional ac four-point technique implemented in a Quantum Design PPMS platform. Dimensions of samples were: 0.010 × 0.051 × 0.227 cm3, for ρxx, and 0.0067 × 0.051 × 0.1524 cm3 for ρxy measurements. Current and voltage leads were 50 μm thick silver wires attached to the parallelepiped-shaped specimens with silver paste and additionally spot welded. The heat capacity was measured on 10.6 mg collection of single crystals, in the temperature interval 0.4–5 K by relaxation time method using also the PPMS platform. DC magnetization and AC magnetic susceptibility measurements were performed on 30.1 mg collection of single crystals, in the temperature range 1.62–2.6 K in weak magnetic fields up to 2 mT employing a Quantum Design MPMS-XL SQUID magnetometer.

Author Contributions

D.K. and P.W. designed the research project, O.P. prepared the samples, O.P. and P.W. performed the physical measurements and analyzed the data. All the authors discussed the experimental results and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Material

srep09158-s1.pdf (503.9KB, pdf)

Acknowledgments

Authors thank Dr. Marek Daszkiewicz for the X-ray characterization of single crystalline LuPdBi. The work was financially supported by the National Centre of Science (Poland) under research grant 2011/01/B/ST3/04466.

References

  1. Graf T., Felser C. & Parkin S. S. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 39, 1–50; 10.1016/j.progsolidstchem.2011.02.001 (2011). [DOI] [Google Scholar]
  2. Casper F., Graf T., Chadov S., Balke B. & Felser C. Half-Heusler compounds: novel materials for energy and spintronic applications. Semicond. Sci. Technol. 27, 063001; 10.1088/0268-1242/27/6/063001 (2012). [DOI] [Google Scholar]
  3. Lin H. et al. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 9, 546–9; 10.1038/nmat2771 (2010). [DOI] [PubMed] [Google Scholar]
  4. Al-Sawai W. et al. Topological electronic structure in half-Heusler topological insulators. Phys. Rev. B 82, 125208; 10.1103/PhysRevB.82.125208 (2010). [DOI] [Google Scholar]
  5. Chadov S. et al. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 9, 541–5; 10.1038/nmat2770 (2010). [DOI] [PubMed] [Google Scholar]
  6. Roy R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322; 10.1103/PhysRevB.79.195322 (2009). [DOI] [Google Scholar]
  7. Fu L., Kane C. L. & Mele E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803; 10.1103/PhysRevLett.98.106803 (2007). [DOI] [PubMed] [Google Scholar]
  8. Moore J. & Balents L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306; 10.1103/PhysRevB.75.121306 (2007). [DOI] [Google Scholar]
  9. Ando Y. Topological Insulator Materials. J. Phys. Soc. Jpn. 82, 102001; 10.7566/JPSJ.82.102001 (2013). [DOI] [Google Scholar]
  10. Fu L. & Kane C. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 100, 096407; 10.1103/PhysRevLett.100.096407 (2008). [DOI] [PubMed] [Google Scholar]
  11. Tanaka Y., Yokoyama T., Balatsky A. & Nagaosa N. Theory of topological spin current in noncentrosymmetric superconductors. Phys. Rev. B 79, 060505; 10.1103/PhysRevB.79.060505 (2009). [DOI] [Google Scholar]
  12. Akhmerov A., Nilsson J. & Beenakker C. Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator. Phys. Rev. Lett. 102, 216404; 10.1103/PhysRevLett.102.216404 (2009). [DOI] [PubMed] [Google Scholar]
  13. Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–67; 10.1103/RevModPhys.82.3045 (2010). [DOI] [Google Scholar]
  14. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–110; 10.1103/RevModPhys.83.1057 (2011). [DOI] [Google Scholar]
  15. Fu L. & Berg E. Odd-Parity Topological Superconductors: Theory and Application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001; 10.1103/PhysRevLett.105.097001 (2010). [DOI] [PubMed] [Google Scholar]
  16. Sasaki S. et al. Topological Superconductivity in CuxBi2Se3. Phys. Rev. Lett. 107, 217001; 10.1103/PhysRevLett.107.217001 (2011). [DOI] [PubMed] [Google Scholar]
  17. Kriener M., Segawa K., Ren Z., Sasaki S. & Ando Y. Bulk Superconducting Phase with a Full Energy Gap in the Doped Topological Insulator CuxBi2Se3. Phys. Rev. Lett. 106, 127004; 10.1103/PhysRevLett.106.127004 (2011). [DOI] [PubMed] [Google Scholar]
  18. Hsieh T. H. & Fu L. Majorana Fermions and Exotic Surface Andreev Bound States in Topological Superconductors: Application to CuxBi2Se3. Phys. Rev. Lett. 108, 107005; 10.1103/PhysRevLett.108.107005 (2012). [DOI] [PubMed] [Google Scholar]
  19. Goll G. et al. Temperature-dependent Fermi surface in CeBiPt. Europhys. Lett. 57, 233–9; 10.1209/epl/i2002-00566-9 (2002). [DOI] [Google Scholar]
  20. Tafti F. F. et al. Superconductivity in the noncentrosymmetric half-Heusler compound LuPtBi: A candidate for topological superconductivity. Phys. Rev. B 87, 184504; 10.1103/PhysRevB.87.184504 (2013). [DOI] [Google Scholar]
  21. Butch N. P., Syers P., Kirshenbaum K., Hope A. P. & Paglione J. Superconductivity in the topological semimetal YPtBi. Phys. Rev. B 84, 220504; 10.1103/PhysRevB.84.220504 (2011). [DOI] [Google Scholar]
  22. Bay T. V., Naka T., Huang Y. K. & de Visser A. Superconductivity in noncentrosymmetric YPtBi under pressure. Phys. Rev. B 86, 064515; 10.1103/PhysRevB.86.064515 (2012). [DOI] [Google Scholar]
  23. Bay T. et al. Low field magnetic response of the non-centrosymmetric superconductor YPtBi. Solid State Commun. 183, 13–7; 10.1016/j.ssc.2013.12.010 (2014). [DOI] [Google Scholar]
  24. Canfield P. C. et al. Magnetism and heavy fermion-like behavior in the RBiPt series. J. Appl. Phys. 70, 5800; 10.1063/1.350141 (1991). [DOI] [Google Scholar]
  25. Riedemann T. M. Heat capacities, magnetic properties, and resistivities of ternary RPdBi alloys where R = La, Nd, Gd, Dy, Er, and Lu. MSc thesis, Iowa State University, Ames 10.2172/251374 (1996). [DOI] [Google Scholar]
  26. Gofryk K., Kaczorowski D., Plackowski T., Leithe-Jasper A. & Grin Y. Magnetic and transport properties of the rare-earth-based Heusler phases RPdZ and RPd2Z (Z = Sb, Bi). Phys. Rev. B 72, 094409; 10.1103/PhysRevB.72.094409 (2005). [DOI] [Google Scholar]
  27. Kaczorowski D., Gofryk K., Plackowski T., Leithe-Jasper A. & Grin Y. Unusual features of erbium-based Heusler phases. J. Magn. Magn. Mater. 290–291, 573–9; 10.1016/j.jmmm.2004.11.538 (2005). [DOI] [Google Scholar]
  28. Gofryk K., Kaczorowski D., Plackowski T., Leithe-Jasper A. & Grin Y. Magnetic and transport properties of rare-earth-based half-Heusler phases RPdBi: Prospective systems for topological quantum phenomena. Phys. Rev. B 84, 035208; 10.1103/PhysRevB.84.035208 (2011). [DOI] [Google Scholar]
  29. Wang W. et al. Large Linear Magnetoresistance and Shubnikov-de Hass Oscillations in Single Crystals of YPdBi Heusler Topological Insulators. Sci. Rep. 3, 2181; 10.1038/srep02181 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Goraus J., Ślebarski A. & Fijałkowski M. Experimental and theoretical study of CePdBi. J. Phys. Condens. Matter 25, 176002; 10.1088/0953-8984/25/17/176002 (2013). [DOI] [PubMed] [Google Scholar]
  31. Pan Y. et al. Superconductivity and magnetic order in the noncentrosymmetric half-Heusler compound ErPdBi. Europhys. Lett. 104, 27001; 10.1209/0295-5075/104/27001 (2013). [DOI] [Google Scholar]
  32. Pavlosiuk O., Filar K., Wiśniewski P. & Kaczorowski D. Magnetic order and SdH effect in half-Heusler phase ErPdBi. Acta Phys. Polon. A in print (2015). [Google Scholar]
  33. Xu G. et al. Weak Antilocalization Effect and Noncentrosymmetric Superconductivity in a Topologically Nontrivial Semimetal LuPdBi. Sci. Rep. 4, 5709; 10.1038/srep05709 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Gofryk K. et al. Magnetic, transport, and thermal properties of the half-Heusler compounds ErPdSb and YPdSb. Phys. Rev. B 75, 224426; 10.1103/PhysRevB.75.224426 (2007). [DOI] [Google Scholar]
  35. Freudenberger J. et al. Superconductivity and disorder in YxLu1−xNi2B2C. Physica C 306, 1–6; 10.1016/S0921-4534(98)00354-2 (1998). [DOI] [Google Scholar]
  36. Müller K. H. et al. The upper critical field in superconducting MgB2. J. Alloys Compd. 322, L10–13; 10.1016/S0925-8388(01)01197-5 (2001). [DOI] [Google Scholar]
  37. Shulga S. et al. Upper Critical Field Peculiarities of Superconducting YNi2B2C and LuNi2B2C. Phys. Rev. Lett. 80, 1730–3; 10.1103/PhysRevLett.80.1730 (1998). [DOI] [Google Scholar]
  38. Werthamer N. R., Helfand E. & Hohenberg P. C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 147, 295–302; 10.1103/PhysRev.147.295 (1966). [DOI] [Google Scholar]
  39. Mun E. et al. Magnetic-field-tuned quantum criticality of the heavy-fermion system YbPtBi. Phys. Rev. B 87, 075120; 10.1103/PhysRevB.87.075120 (2013). [DOI] [Google Scholar]
  40. Pagliuso P. et al. Low temperature specific heat of YBiPt. APS March Meeting 2013, Baltimore, Abstract ID: BAPS.2013.MAR.B13.13 (2013).URL http://meeting.aps.org/Meeting/MAR13/Session/B13.13 Date of access: 15/01/2015 [Google Scholar]
  41. Pagliuso P. et al. Crystal-field study in rare-earth-doped semiconducting YBiPt. Phys. Rev. B 60, 4176–80; 10.1103/PhysRevB.60.4176 (1999). [DOI] [Google Scholar]
  42. Abrikosov A. Fundamentals of the theory of metals (North-Holland, Amsterdam, 1988). [Google Scholar]
  43. Petrovic C. et al. Anisotropy and large magnetoresistance in the narrow-gap semiconductor FeSb2. Phys. Rev. B 67, 155205; 10.1103/PhysRevB.67.155205 (2003). [DOI] [Google Scholar]
  44. Hu J. & Rosenbaum T. F. Classical and quantum routes to linear magnetoresistance. Nat. Mater. 7, 697–700; 10.1038/nmat2259 (2008). [DOI] [PubMed] [Google Scholar]
  45. Xu R. et al. Large magnetoresistance in non-magnetic silver chalcogenides. Nature 390, 57–60; 10.1038/36306 (1997). [DOI] [Google Scholar]
  46. Friedman A. L. et al. Quantum linear magnetoresistance in multilayer epitaxial graphene. Nano Lett. 10, 3962–5; 10.1021/nl101797d (2010). [DOI] [PubMed] [Google Scholar]
  47. Wang X., Du Y., Dou S. & Zhang C. Room Temperature Giant and Linear Magnetoresistance in Topological Insulator Bi2Te3 Nanosheets. Phys. Rev. Lett. 108, 266806; 10.1103/PhysRevLett.108.266806 (2012). [DOI] [PubMed] [Google Scholar]
  48. Shekhar C. et al. Electronic structure and linear magnetoresistance of the gapless topological insulator PtLuSb. Appl. Phys. Lett. 100, 252109; 10.1063/1.4730387 (2012). [DOI] [Google Scholar]
  49. Zhang S. X. et al. Magneto-resistance up to 60 Tesla in topological insulator Bi2Te3 thin films. Appl. Phys. Lett. 101, 202403; 10.1063/1.4766739 (2012). [DOI] [Google Scholar]
  50. He L. P. et al. Quantum transport evidence for a three-dimensional Dirac semimetal phase in Cd3As2. Phys. Rev. Lett. 113, 246402; 10.1103/PhysRevLett.113.246402 (2014). [DOI] [PubMed] [Google Scholar]
  51. Novak M., Sasaki S., Segawa K. & Ando Y. Large linear magnetoresistance in the Dirac semimetal TlBiSSe preprint arXiv:1408.2183 (2014). URL http://lanl.arxiv.org/abs/1408.2183 Date of access: 15/01/2015
  52. Parish M. M. & Littlewood P. B. Non-saturating magnetoresistance in heavily disordered semiconductors. Nature 426, 1–4; 10.1038/nature02073 (2003). [DOI] [PubMed] [Google Scholar]
  53. Abrikosov A. Quantum magnetoresistance. Phys. Rev. B 58, 2788–94; 10.1103/PhysRevB.58.2788 (1998). [DOI] [Google Scholar]
  54. Hikami S., Larkin A. I. & Nagaoka Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Prog. Theor. Phys. 63, 707–10; 10.1143/PTP.63.707 (1980). [DOI] [Google Scholar]
  55. Shoenberg D. Magnetic Oscillations in Metals (Cambridge University Press, Cambridge, 1984). [Google Scholar]
  56. Analytis J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nature Phys. 6, 960–4; 10.1038/nphys1861 (2010). [DOI] [Google Scholar]
  57. Chen J. et al. Tunable surface conductivity in Bi2Se3 revealed in diffusive electron transport. Phys. Rev. B 83, 241304; 10.1103/PhysRevB.83.241304 (2011). [DOI] [Google Scholar]
  58. Taskin A. A. & Ando Y. Berry phase of nonideal Dirac fermions in topological insulators. Phys. Rev. B 84, 035301; 10.1103/PhysRevB.84.035301 (2011). [DOI] [Google Scholar]
  59. Rodríguez-Carvajal J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B Condens. Matter 192, 55–69; 10.1016/0921-4526(93)90108-I (1993). [DOI] [Google Scholar]
  60. Sheldrick G. M. A short history of SHELX. Acta Crystallogr. A. 64, 112–22; 10.1107/S0108767307043930 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Material

srep09158-s1.pdf (503.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES