Abstract
A remarkable feature of vanadium dioxide is that it can be synthesized in a number of polymorphs. The conductivity mechanism in the metastable layered polymorph VO2(B) thin films has been investigated by terahertz time-domain spectroscopy (THz-TDS). In VO2(B), a critical temperature of 240 K marks the appearance of a non-zero Drude term in the observed complex conductivity, indicating the evolution from a pure insulating state towards a metallic state. In contrast, the THz conductivity of the well-known VO2(M1) is well fitted only by a modification of the Drude model to include backscattering. We also identified two different THz conductivity regimes separated by temperature in these two polymorphs. The electronic phase diagram is constructed, revealing that the width and onset of the metal-insulator transition in the B phase develop differently from the M1 phase.
Multi-polymorphic materials – compounds that can assume numerous, different crystal symmetries with the same chemical composition, show great promise as future electronic materials. This is because their structural diversity can give rise to a variety of electrical and optical responses that can be tuned for technological applications such as optical switches, batteries, solar cells, optical filters, spintronic devices, memory devices etc1,2,3,4. Vanadium dioxide is one of the most popular polymorphic materials that can assume several crystallographic structures5,6,7. Amongst the several stable and metastable VO2 polymorphs, monoclinic VO2(B) and monoclinic VO2(M1) are particularly interesting, as these materials display more than thousand-fold changes in conductivity with temperature8,9. Understanding polymorphism in vanadium dioxide has tremendous practical importance in the design and control of electro-optic materials for future technologies.
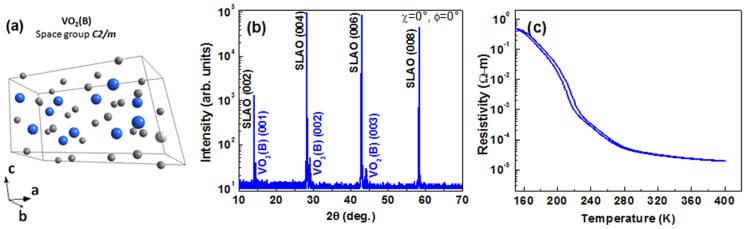
The metastable monoclinic VO2(B) adopts a structure derived from V2O5 and belongs to the space group C2/m (12) compared to the well-known VO2(M1), which takes up the space group P21/c (14)10,11,12. The crystal structure of VO2(B) is illustrated in Figure 1(a). A salient structural difference between the monoclinic phases in VO2(B) and VO2(M1) is that VO2(B) has a smaller β inter-axial angle11 (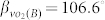 and
and 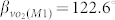 ) which may play an important role in the formation of defects and impurities in epitaxial growth of films. While metal-insulator transition (MIT) in VO2(M1) is associated with a corresponding reversible structural phase transition from a room temperature monoclinic to a high temperature tetragonal phase9,13,14,15,16, currently there is little understanding of the nature of the semimetal-to-insulator transition in VO2(B) which remains monoclinic with MIT10. It is also interesting to compare these polymorphs in context of V-V pairing mechanism, which strongly influences the conductivity pathways. VO2(M1) undergoes V-V dimerization in the monoclinic insulating phase with very short V-V bonds (~2.65 Å) creating a large dimer-to-dimer distance (~3.12 Å)14. This alternate long and short V-V separation inhibits conductivity. But when VO2(M1) undergoes a phase transition to the rutile structure all the V-V distances become the same (~2.87 Å) and do not allow the formation of dimers14. In contrast, one doesn't see a significant change of V-V distance in the B phase10. One could plainly see that, even though these VO2 polymorphs have the same chemical stoichiometry, their structures and electronic attributes are evidently distinct and a comparative study between these polymorphs is aptly motivated by an objective to get a better understanding on the correlation between MIT and structural phase transition. Furthermore, while a lot of progress has been made towards understanding the physics of metal-insulator transition in VO2(M1) by optical techniques17,18,19,20,21,22,23,24,25,26,27,28, no parallel efforts has been made so far to understand the mechanism in VO2(B). From a practical applications point of view, one of the key attractions of VO2(B) is that it is conducting at room temperature, compared to VO2(M1) which is insulating and may hold technological merits over VO2 (M1) for devices at room temperature operation8.
) which may play an important role in the formation of defects and impurities in epitaxial growth of films. While metal-insulator transition (MIT) in VO2(M1) is associated with a corresponding reversible structural phase transition from a room temperature monoclinic to a high temperature tetragonal phase9,13,14,15,16, currently there is little understanding of the nature of the semimetal-to-insulator transition in VO2(B) which remains monoclinic with MIT10. It is also interesting to compare these polymorphs in context of V-V pairing mechanism, which strongly influences the conductivity pathways. VO2(M1) undergoes V-V dimerization in the monoclinic insulating phase with very short V-V bonds (~2.65 Å) creating a large dimer-to-dimer distance (~3.12 Å)14. This alternate long and short V-V separation inhibits conductivity. But when VO2(M1) undergoes a phase transition to the rutile structure all the V-V distances become the same (~2.87 Å) and do not allow the formation of dimers14. In contrast, one doesn't see a significant change of V-V distance in the B phase10. One could plainly see that, even though these VO2 polymorphs have the same chemical stoichiometry, their structures and electronic attributes are evidently distinct and a comparative study between these polymorphs is aptly motivated by an objective to get a better understanding on the correlation between MIT and structural phase transition. Furthermore, while a lot of progress has been made towards understanding the physics of metal-insulator transition in VO2(M1) by optical techniques17,18,19,20,21,22,23,24,25,26,27,28, no parallel efforts has been made so far to understand the mechanism in VO2(B). From a practical applications point of view, one of the key attractions of VO2(B) is that it is conducting at room temperature, compared to VO2(M1) which is insulating and may hold technological merits over VO2 (M1) for devices at room temperature operation8.
Figure 1.
(a) Crystal structure of the VO2(B) polymorph. The vanadium atoms are represented by blue spheres and the oxygen atoms are represented by dark grey spheres.(b) XRD θ–2θ pattern for the VO2(B) film epitaxially grown on (001) SLAO substrate. (c) Temperature dependent resistivity of VO2(B) on SLAO measured using a traditional four point geometry.
The drastic changes in conductivity with temperature for these VO2 polymorphs are accompanied by a corresponding change in optical response, thereby making terahertz (THz) spectroscopy a viable technique to probe the nature of electronic properties in these systems. There have been several reports where THz spectroscopy has been employed to measure conductivity in VO2(M1) polymorphs25,26,29,30,31. Although metal-insulator transition materials are generally characterized by standard four-point probe method, it provides information only about dc conductivities which can be distorted by surface defects due to electrode contacts32. On the other hand, THz spectroscopy is a contactless probe, providing frequency-dependent complex conductivity in the far-infrared region. Terahertz time-domain spectroscopy (THz-TDS) allows the amplitude and phase of the THz pulse to be obtained, without the need for Kramers-Kronig analysis in the extraction of complex conductivity33,34,35. Moreover, compared to traditional steady-state dc conductivity measurements which is limited to macroscopic conductivity paths, THz spectroscopy explores electron dynamics over nanometer length scales, possibly revealing conducting phases in this scale undetectable by long-range transport measurements29. Indeed, THz spectroscopy has been used to make comprehensive optical investigations in a host of materials rich in exotic conducting phases including graphene36,37, toplogical insulators34,38, superconductors39,40,41, oxide semiconductors32,33, quantum-confined semiconductors42, and percolating systems43.
In this paper we report a systematic investigation of THz complex conductivities of 60-nm thick VO2(B) thin films deposited on (001) SrLaAlO4 (SLAO) substrate. There has been no literature report on the complex conductivities of this system. In our operational THz frequency range (0.3–2.3 THz), there are no observable optical phonon resonances of VO2(B), and hence it is possible to observe the conductivity response that arises solely from free carriers. These are then compared with that of 60-nm VO2(M1) thin films deposited on SLAO substrate. This study conclusively demonstrates clear signatures of different electronic orders in these two vanadium dioxide polymorphs.
Results
Sample growth, structural and transport characterization
The XRD spectra of VO2(B) thin film on SLAO is shown in Figure 1(b). We clearly see that the XRD reflections of VO2(B) are perfectly aligned with the substrate (azimuthal angle, χ = 0). This means that our film is highly oriented. Temperature-dependent electrical transport measurements are carried out in Physical Property Measurement system (Quantum Design) utilizing a four probe geometry. As shown in Figure 1(c), the resistivity of VO2(B) films grown on SLAO substrate undergo four orders-of-magnitude change (from 2 × 10−5 Ω-m to 0.35 Ω-m) in resistivity as the temperature changes from 400 K to 160 K, which is consistent with a previous report on VO2(B) nanorods8. There is a weak thermal hysteresis at low temperatures below 240 K.
THz-TDS
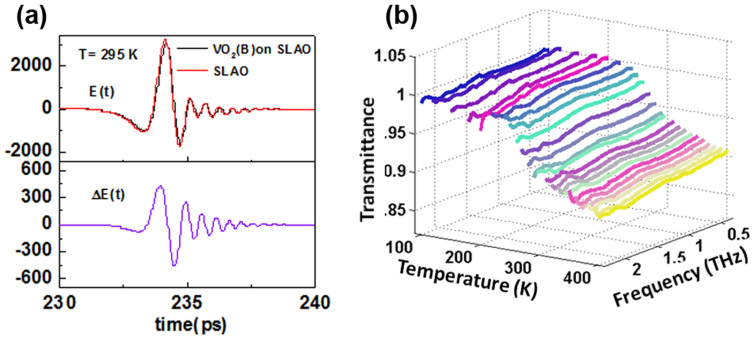
Figure 2(a) shows time-domain signal of the main THz pulse [E(t)] transmitted through the film and reference for VO2(B) thin film. After the main pulse, a weaker pulse (etalon pulse) appears due to multiple reflections in the substrate. The main THz pulse and etalon pulse are well separated in the time domain, allowing easy truncation of the time-domain data to remove the etalon pulse. All our subsequent data analysis is done on the main pulse and removal of etalon pulses does not lead to any relevant loss of information. The lower panel of Figure 2(a) is the THz absorption at 295 K by plotting the difference in the electric field time domain signal between the sample and the reference [ΔE(t)]. Fast Fourier Transform (FFT) is then performed on the time domain THz signals to obtain the amplitude and phase of the THz transmission spectra.
Figure 2.
(a) THz signals transmitted through VO2(B) film deposited on SLAO substrate compared to the transmitted signal through bare substrate at 295 K shown along with monoclinic VO2(B) cell. While the top panel describes the raw transmitted THz electric-field waveform E(t) the bottom panel represents the corresponding difference in the THz waveform ΔE(t) between the sample and the reference. (b) Evolution of the transmission spectra with temperature and frequency of VO2(B) thin film deposited on SLAO substrates during warming process.
The transmittance, T(ω) of the VO2 film is defined as the ratio between complex electric field of the THz pulse from sample (film + substrate) 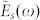 and reference (bare substrate)
and reference (bare substrate) 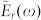 . In Figure 2(b) the frequency-dependent and temperature-dependent transmittance amplitudes through the VO2(B) film are shown. In the insulating state, at temperatures lower than the transition temperature, we find that the transmittance amplitude is close to unity. For VO2(B) film, as the temperature of the sample approaches ~240 K, there is THz absorption and a clear trend of increasing absorption at higher temperatures. The spectral shape is almost frequency independent for all runs. The frequency dependent complex refractive index
. In Figure 2(b) the frequency-dependent and temperature-dependent transmittance amplitudes through the VO2(B) film are shown. In the insulating state, at temperatures lower than the transition temperature, we find that the transmittance amplitude is close to unity. For VO2(B) film, as the temperature of the sample approaches ~240 K, there is THz absorption and a clear trend of increasing absorption at higher temperatures. The spectral shape is almost frequency independent for all runs. The frequency dependent complex refractive index 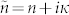 can be extracted from the experimental transmittance T(ω) by fitting the formula36,44
can be extracted from the experimental transmittance T(ω) by fitting the formula36,44
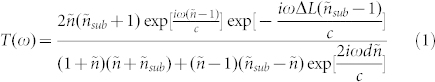 |
where 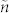 and
and 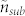 are the complex refractive indices of VO2 film and SLAO substrate, respectively, d is film thickness and ΔL is the thickness difference between sample and reference substrates and c is the speed of light in vacuum. This above equation takes into account the multiple internal reflections inside the film.
are the complex refractive indices of VO2 film and SLAO substrate, respectively, d is film thickness and ΔL is the thickness difference between sample and reference substrates and c is the speed of light in vacuum. This above equation takes into account the multiple internal reflections inside the film.
The extracted complex refractive index 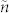 is then used to calculate the complex optical conductivity
is then used to calculate the complex optical conductivity 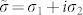 where σ1(ω) = 2nκωε0 and σ2(ω) = (ε∞ − n2 + κ2)ωε0 where ε0 is the permittivity of free space and ε∞ is the high frequency dielectric constant. For VO2(B), ε∞ is an unknown quantity and is initially set to 1. After the determination of complex conductivities, ε∞ will be used as a temperature-dependent fitting parameter in the conductivity models as discussed in the following sub-sections. On the other hand, we used ε∞ = 9 based on previous studies for determining conductivities in VO2(M1)45,46.
where σ1(ω) = 2nκωε0 and σ2(ω) = (ε∞ − n2 + κ2)ωε0 where ε0 is the permittivity of free space and ε∞ is the high frequency dielectric constant. For VO2(B), ε∞ is an unknown quantity and is initially set to 1. After the determination of complex conductivities, ε∞ will be used as a temperature-dependent fitting parameter in the conductivity models as discussed in the following sub-sections. On the other hand, we used ε∞ = 9 based on previous studies for determining conductivities in VO2(M1)45,46.
Complex conductivity of VO2(B)
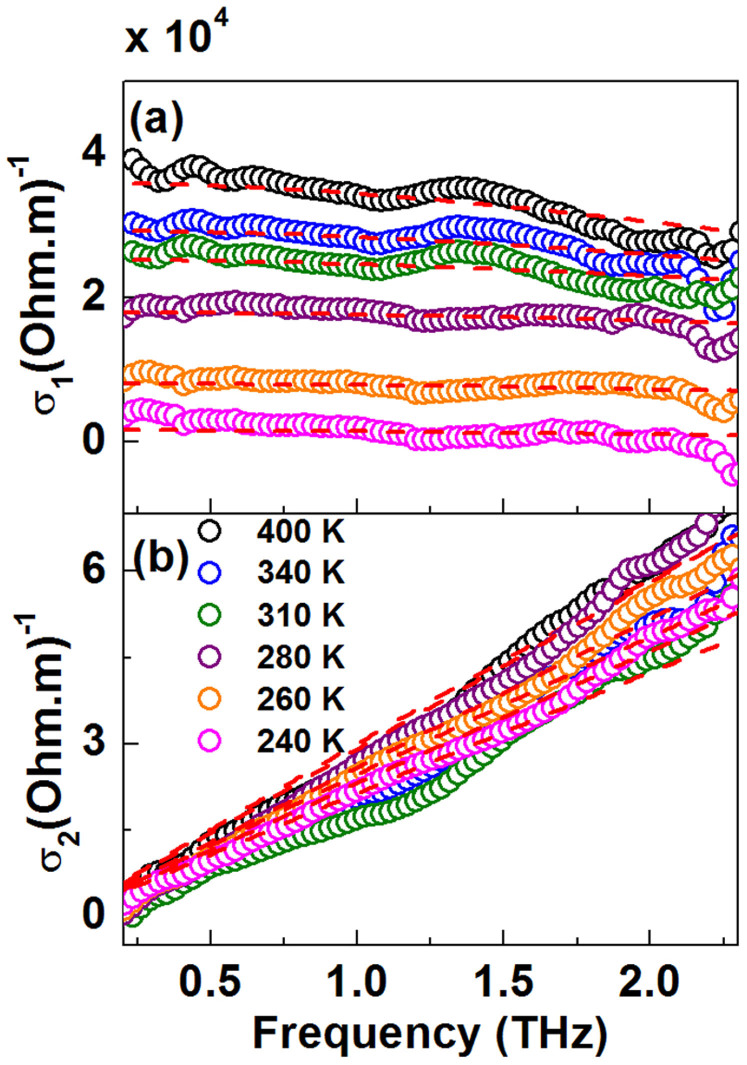
The complex optical conductivities of the VO2(B) films for temperatures ranging from 240 K to 400 K are shown in Figures 3(a) and (b) as a function of frequency during the warming process (open symbols). Below 240 K, the transmission is ~100%, giving zero real conductivity, indicating that the films are clearly insulating. The onset of a positive σ1(ω) marks the transition from an insulating regime to a conducting one. We clearly observe σ1(ω) to increase with increasing temperature throughout our frequency range. Thermal excitation of electrons into the conduction band can account for this nature, that is, a Drude response where σ1(ω) is a maximum at low frequency and decreases with increasing frequency, while σ2(ω) are zero at low frequency and increases with increasing frequency.
Figure 3.
(a) Real and (b) imaginary conductivities in the THz frequency range of VO2(B) thin films grown on SLAO with fits to the Drude model (red dash lines) shown for temperatures ranging from 240 to 400 K.
According to the Drude model, the frequency dependent complex optical conductivity is given by
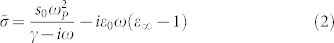 |
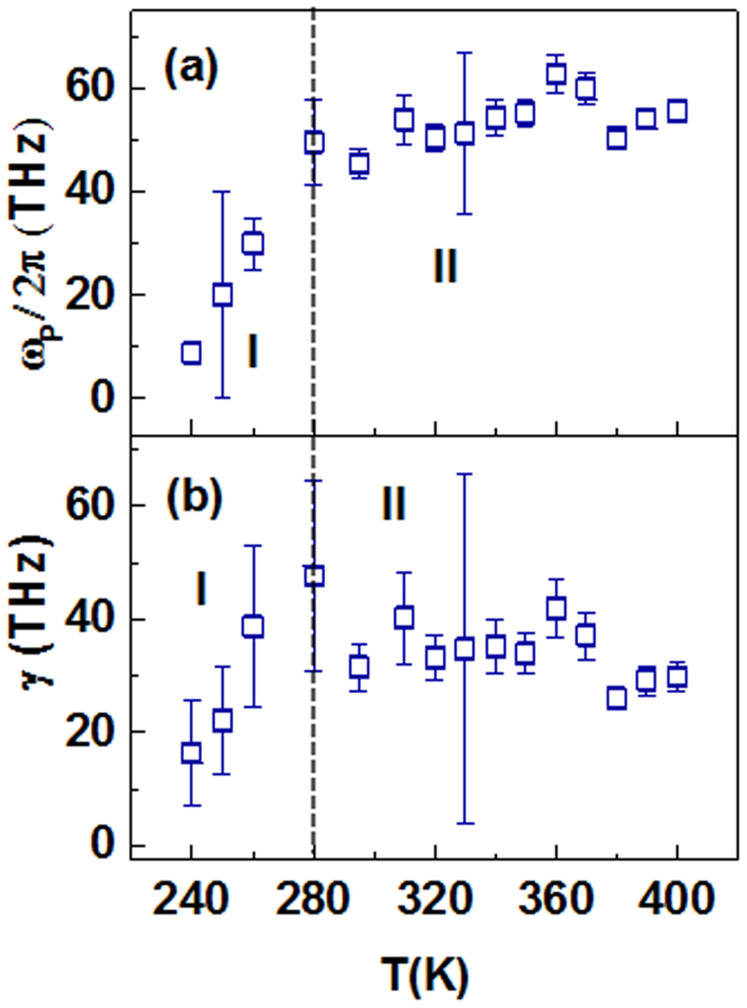
where ωP is the Drude plasma frequency, γ is the free carrier scattering rate and ε∞ is the high frequency dielectric constant as defined earlier. Both σ1(ω)and σ2(ω) at each temperature measurement are simultaneously fitted to Equation 2, as shown by the dash red lines in Figures 3(a) and (b) respectively. The fits are reasonably good for all temperatures. The fittings results of the Drude parameters are shown in Figures 4(a) and (b). The simultaneous fitting of σ1(ω) and σ2(ω) to the Drude model greatly reduces the width of the error bars of the fitted γ and ωP even though σ1(ω) is relatively featureless.
Figure 4.
Temperature dependence of (a) the plasma frequency and (b) the scattering rate, for T ≥ 240 K as estimated from the Drude fitting. The dashed lines are guide to the eye demarcating the two different electronic orders.
We observe a similar trend in both the plasma frequency and the scattering rate – both parameters increases as we increase the temperature up to ~280 K, and tends to saturate beyond 280 K. This common trend in ωP and γ describe two different temperature-dependent conductivity mechanisms. To address this issue and to make a distinction, we describe the temperature regions 240 K ≤ T ≤ 280 K and 280 K <T ≤ 400 K as conductivity regimes I and II respectively.
In regime I, ωP/2π rises from (8 ± 1) THz to (49 ± 8) THz, while in regime II this parameter has a mean value of ~ (54 ± 5) THz. The plasma frequency is closely related to the number of charge carriers (N) in the system via 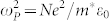 where m* is the effective mass. The scattering rate, (γ) is associated with the mobility of the carriers, (μ) via the expression γ = e/(m*μ). Without the knowledge of the carriers' effective mass, accurate values of N and μ in VO2(B) cannot be determined. In the later sub-sections, more discussions regarding the nature of m* will be presented.
where m* is the effective mass. The scattering rate, (γ) is associated with the mobility of the carriers, (μ) via the expression γ = e/(m*μ). Without the knowledge of the carriers' effective mass, accurate values of N and μ in VO2(B) cannot be determined. In the later sub-sections, more discussions regarding the nature of m* will be presented.
The Boltzmann dc conductivity σ0 can be obtained from the expression
 |
Figure 5(a) shows the calculated dc conductivity using Equation 3. The plot shows σ0 increasing with increasing temperatures, but the rate of change is significantly smaller at higher frequencies. We recall that while ωP and γ start saturating at 280 K, σ0 does not. However, for T > 280 K and T ≤ 280 K, σ0 changes with different slopes and hence can be correlated with our description of conductivity regimes I and II. If we compare, our estimated dc conductivity from the THz measurements are consistent with the electrical transport measurements shown in Figure 1(c). Figure 5(b) shows the logarithmic conductivity, ln(σ) plotted against reciprocal temperature, 1000/T. The activation energy, Ea can be estimated from the thermal activation model of dc conductivity which has the following temperature dependence
 |
where kB is the Boltzmann constant. The linear fittings of the conductivity regimes with the activation model show a good agreement. Fits to Equation 4 yields Ea (regime I) = (260 ± 30) meV, and Ea (regime II) = (47 ± 3) meV. This significant difference in activation energies supports our claim that there are two different temperature dependent conductivity mechanisms in VO2(B). In regime I, the conductivity mechanism is poor with larger activation energy, while in regime II, the conductivity is better with smaller activation energy. The presence of small activation energy in conductivity regime II shows that even at high temperatures it has not achieved a fully metallic state. The features of metal-insulator transition in VO2(B) can be understood as follows: (i) Temperatures below 200 K can be identified as a pure insulating state displaying 100% transmission in the insulating state, (ii) conducting state I is an intermediate electronic phase transition characterized by strong dependence of Drude parameters with temperature, (iii) conducting state II describes the phase after the transition is completed. The boundaries of various electronic phases driven by temperature are thus more clearly defined in the THz-TDS study compared to the electrical transport measurements where the change in resistivity is gradual and not well discernible.
Figure 5.

(a) Temperature dependence of dc conductivity of VO2(B) films on SLAO as estimated from Equation 3. (b) Logarithmic plot of conductivity ln(σ) vs reciprocal temperature 1000/T shown alongside linear fitting and the conductivity regimes I and II.
Comparison with VO2(M1)
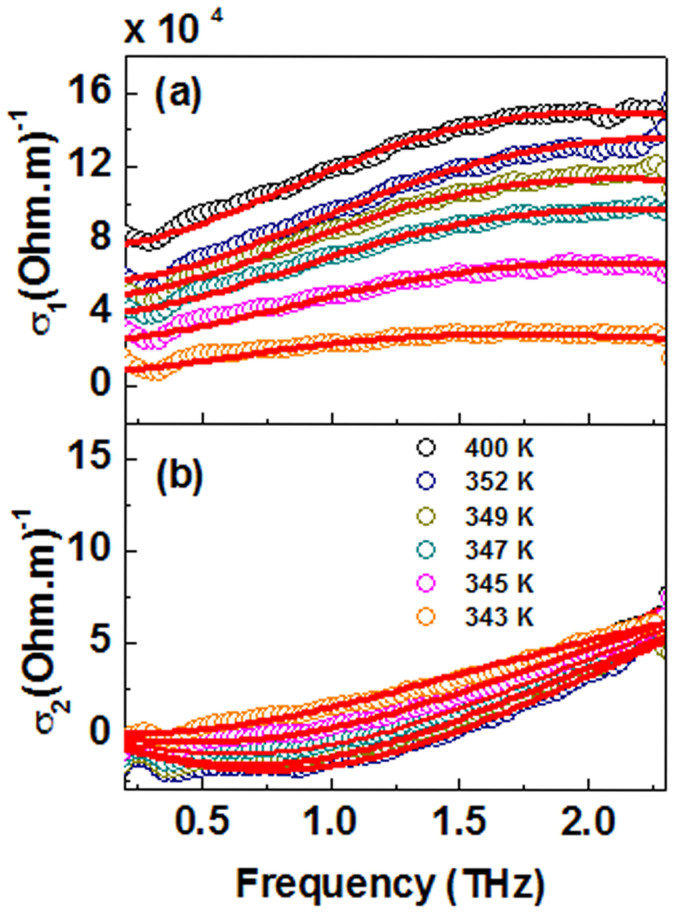
The THz conductivity spectra of 60-nm thick VO2(M1) film grown on SLAO are shown in Figure 6 plotted as the temperature of the system is gradually increased from 343 K to 400 K. In contrast to VO2(B), throughout this temperature range, σ1(ω) increases with increasing frequency, while σ2(ω) starts at zero at low frequencies, becomes negative, then crosses over to positive with increasing frequency. This is consistent with the previous reported THz studies of VO2(M1) films25,26,30.
Figure 6.
(a) Real and (b) imaginary conductivities of VO2(M1) films on SLAO with fits to the Drude-Smith model (sold red lines) for six selected temperature points in the range 343 K–400 K during the warming process.
In classical VO2(M1) systems it has been reported that the complex conductivities can be effectively modelled by Drude-Smith theory, which is a generalisation of the Drude model proposed by Smith, in order to account for the conductivity suppression due to charge localization33,43,47,48. In this polymorph, it is widely considered that the transition from a highly transparent insulating phase to an absorbing metallic phase occurs through a percolating network29,46,49. Near the threshold of this transition, phase separation and domain formation dictate the electronic pathways. The frequency-dependent optical conductivity in the Drude-Smith model is given by47
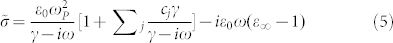 |
The additional terms described by cj represents the fraction of the carrier's initial velocity retained after j number of scattering events47. In various systems such as poor conductors, metal-insulator transition materials and various nanomaterials where the Drude-Smith model is successfully applied, only the first scattering term is considered (i.e. j = 1)30,48,50,51,52. In this scenario, carrier transport transitions from ballistic to diffusive after one scattering event, leading to complete momentum randomization47. In our fitting analysis also we will only consider the first cj term and in this case we take c1 = c. The parameter c can take up any values anywhere between 0 (free Drude carrier conduction) and −1 (full carrier backscattering)43. There have been other reports of using effective medium theory (EMT) models to fit THz conductivities of VO2(M1) with varying degrees of success29,31. Our attempts to model the optical conductivities using the effective medium models gave inconsistent results (Supplementary Information). On the other hand, as shown by the fitting lines in the Figures 6 (a) and (b), the Drude-Smith formalism given by Equation (5) when j = 1 gives excellent fits to our measured conductivities of σ1(ω) and σ2(ω). We could see that even at high temperatures the conductivity does not follow an ideal Drude behaviour which indicates that the nanogranular boundaries persist even after the transition. In highly granular systems, the Drude-Smith is much more effective in describing the effective conductivity rather than a conventional EMT models because it can describe effective conductivities of systems where grain boundaries persist even in large conducting fractions30,43. The advantage of Drude-Smith over EMT models in this scenario has been discussed by T. L. Cocker et.al30.
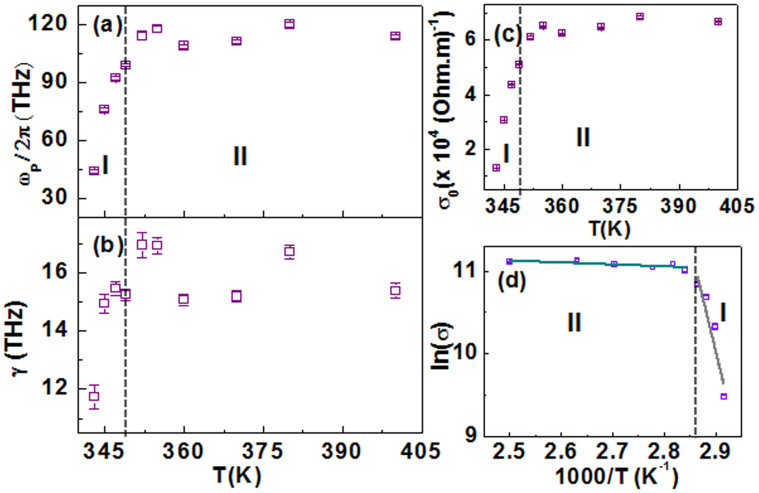
Simultaneous complex fitting of optical conductivities gives the information about the parameters ωP, γ and c. Figure 7 summarizes the ωP, γ parameters obtained from the fitting procedure as well as the dc conductivity σ0 which is given by the equation, 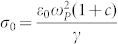 . The Drude-Smith parameters ωP and γ increase with increasing temperatures in the temperature range 343 K–349 K; above 349 K they remain largely temperature-independent. This characteristic is similar to the temperature dependence of Drude parameters in VO2(B). In the temperature range 352 K–400 K, the mean value of ωP/2π is ~ (110 ± 4) THz. The fitting parameter c lies between −0.88 and −0.75 which indicates significant carrier backscattering – an attribute of carrier localization, resulting in significant suppression of low-frequency conductivities. The temperature dependence of the fitted values of c supports the percolation picture in VO2(M1)43.
. The Drude-Smith parameters ωP and γ increase with increasing temperatures in the temperature range 343 K–349 K; above 349 K they remain largely temperature-independent. This characteristic is similar to the temperature dependence of Drude parameters in VO2(B). In the temperature range 352 K–400 K, the mean value of ωP/2π is ~ (110 ± 4) THz. The fitting parameter c lies between −0.88 and −0.75 which indicates significant carrier backscattering – an attribute of carrier localization, resulting in significant suppression of low-frequency conductivities. The temperature dependence of the fitted values of c supports the percolation picture in VO2(M1)43.
Figure 7. Temperature dependence of Drude-Smith fitting parameters:
(a) the plasma frequency, ωP/2π (b) the scattering rate, γ for T ≥ 343 K and (c) dc conductivity as estimated from Equation 3 for VO2(M1) films grown on SLAO during the warming cycle. The dashed lines separates the conductivity regimes I and II. (d) Logarithmic conductivity, ln(σ) dependence on reciprocal temperature 1000/T is shown and fitted with a linear relation.
We find that similar to ωP and γ, σ0 increases with increasing temperatures till 349 K; at higher temperatures, it attains a mean saturating value of (6.5 ± 0.3) × 104 (Ohm.m)−1. Analogous to VO2(B), we can define the temperature range of 343 K–349 K as conductivity regime I and 352 K–400 K as conductivity regime II. However in VO2(M1), σ0 remains largely temperature independent in conductivity regime II, while in VO2(B) there is a weak temperature dependence in this regime. Figure 7(d) shows the linear fitting plot of logarithmic conductivity, ln(σ) versus reciprocal temperature, 1000/T. Similar to our previous analysis of VO2(B), we can determine the activation energy of VO2(M1) from the slope of the linear relation. For VO2(M1), in the low-temperature regime I, the activation energy Ea = (2200 ± 500) meV while in the high-temperature state II, Ea = (20 ± 8) meV. The difference between the activation energies in regions I and II is much larger in VO2(M1) than in VO2(B) which is consistent with our ωP and σ0 results where the quantitative growth of these values as the system goes from regime I to II is much larger in VO2(M1) compared to VO2(B). Also, while the activation energies in regime II are similar in these VO2 polymorphs, Ea of VO2(M1) is an order of magnitude larger than that of VO2(B) in regime I. This means that in regime I, the conductivity slope is steeper in VO2(M1) and concomitantly we found a sharper rise of ωP and γ in VO2(M1) in regime I.
According to M. M. Qazilbash et. al.22, a significant enhancement of the carrier effective mass, m* (as large as 5me, where me is mass of an electron) is found in the infrared spectra, especially in the intermediary phase transition state which is analogous to our conductivity regime I. After the transition is completed (at T ~ 350 K), m* is close to 2me which is the value reported by other experiments46. Considering m* = 2me, at temperatures just above the transition (T = 352 K), we obtain the carrier density to be ~3.6 × 1020 cm−3 from the plasma frequency. In the case of Drude-Smith model, the relationship between γ and μ is modified as, 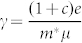 . This relationship gives μ = 11.35 cm2/(V·s) at T = 352 K in VO2(M1). Previous THz-TDS experiments on VO2(M1) reported similar values of carrier density and mobility30,31. Hall effect measurements reported similar values of carrier density at this temperature but the reported mobility is lower, which is probable as THz study does not face the challenges in Hall measurements due to low-mobility53. The fundamental difference between these two techniques is that while Hall measurement is meant for DC conductivity measurements THz-TDS is an AC measurement method. Hall measurement being a contact method requires the charge carriers to travel substantial distance across the biased electrodes but on the other hand THz-TDS captures the conductivity traversed in sub-pico second timescales resulting in ‘conductivity snap-shots'42. As a consequence, THz-TDS can give conductivity information before the carriers are trapped or recombined and as such it is quite reasonable to expect that the THz mobility would be higher than the Hall mobility. We can also compare the carrier density and the mobility parameters of VO2(M1) with that of VO2(B). By assuming m* = 2me at T = 295 K for VO2(B), which is just after the transition, the calculated values are N ≈ 6.4 × 1019 cm−3 and μ ≈ 21.9 cm2/(V·s).
. This relationship gives μ = 11.35 cm2/(V·s) at T = 352 K in VO2(M1). Previous THz-TDS experiments on VO2(M1) reported similar values of carrier density and mobility30,31. Hall effect measurements reported similar values of carrier density at this temperature but the reported mobility is lower, which is probable as THz study does not face the challenges in Hall measurements due to low-mobility53. The fundamental difference between these two techniques is that while Hall measurement is meant for DC conductivity measurements THz-TDS is an AC measurement method. Hall measurement being a contact method requires the charge carriers to travel substantial distance across the biased electrodes but on the other hand THz-TDS captures the conductivity traversed in sub-pico second timescales resulting in ‘conductivity snap-shots'42. As a consequence, THz-TDS can give conductivity information before the carriers are trapped or recombined and as such it is quite reasonable to expect that the THz mobility would be higher than the Hall mobility. We can also compare the carrier density and the mobility parameters of VO2(M1) with that of VO2(B). By assuming m* = 2me at T = 295 K for VO2(B), which is just after the transition, the calculated values are N ≈ 6.4 × 1019 cm−3 and μ ≈ 21.9 cm2/(V·s).
It has been reported that the first-order phase transition in VO2(M1) takes place via percolation where metallic domains embedded in a matrix of insulating phase starts nucleating sporadically as temperature is increased. When the temperature reaches the metal-insulator transition temperature TMI, the domains become well connected to form a percolating path in this inhomogeneous composite medium. The Drude-Smith model has been applied to various percolating systems where inhomogeneity in conductivity contributes of a non-zero backscattering parameter c. On the other hand VO2(B) can be described by a simple Drude model, although it is a poor conductor in comparison to VO2(R). The fact that VO2(R) cannot have an ideal Drude behavior can be explained by its granular origin, intrinsic inhomogeneity. In VO2(B) we cannot see evidence of inhomogeneous phase separation or percolating transport from the THz study and thus shows a good Drude fit. The explanation for this difference between the polymorphs is two-fold — first, VO2(B) is a more uniform film in the context of epitaxial growth with lesser roughness and hence no backscattering. VO2(M1) on the other hand, has a more grainy morphology due to the larger β inter-axial angle (Supplementary Information). Second, the activation energy is larger in VO2(B) in the conducting state and so the number of thermally activated carriers are smaller.
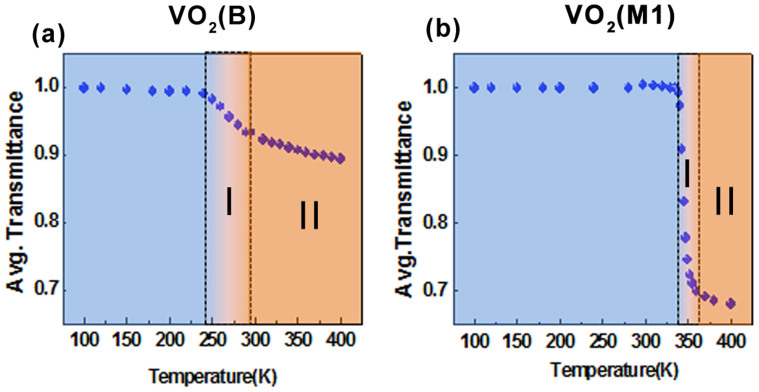
Furthermore, the narrow intermediate state of VO2(M1), which falls in our conductivity regime I, is a strongly correlated phase marked by enhanced mass and an optical pseudo-gap before crossing over to a rutile metallic state as indicated by several optical measurements including infrared spectroscopy, ellipsometry and femtosecond pump-probe measurements22,23,49,54. It is also possible that in the intermediate state of VO2(B), electronic correlations may play a significant role in this intermediate transition state. The rich electronic phase diagram of these vanadium dioxide polymorphs can be summarized from our THz transmission spectra as illustrated in Figure 8.
Figure 8.
Normalized and frequency-averaged THz transmission of (a) VO2(B) and (b) VO2(M1) thin films as a function of temperature during the warming process. These values are normalised to the transmission at 100 K. The blue colour regions represent the insulating phases while the pure conducting phases are coloured orange. The two dotted lines mark the intermediate transition state. The conductivity regimes I and II as described in the previous discussions are also labelled.
Discussion
In conclusion, we have used THz spectroscopy to measure the temperature-dependent complex optical conductivity of vanadium dioxide polymorphs. In our operational frequency range (0.3–2.3) THz, VO2(B) exhibits no phonon modes and the onset of Drude conductivity behaviour arrives for temperatures higher than 240 K. On the other hand, in VO2(M1) the THz conductivity can be better described by the Drude-Smith model. Key parameters of carrier dynamics (i) plasma frequency (ωP) and (ii) scattering rate (γ) are obtained by fitting to the Drude (in VO2(B)) and Drude-Smith in (VO2(M1)) models. Interestingly, our THz analysis revealed that like in VO2(M1), VO2(B) also transforms from an insulating system to a conducting system but is mediated by a much broader intermediate state with the transition onset much closer to room temperature making it more suitable than the widely studied VO2(M1) for optoelectronic devices operating at room temperature. Our study also demonstrates that these polymorphs can also be used as temperature-controlled THz frequency modulators. While the sharp phase transition in VO2(M1) is suitable for digital-like THz modulation, the broad phase transition in VO2(B) offers analog-like continuous modulation of THz spectra very similar to W-doped VO2(M1)55. THz conductivity study is a fascinating subject of research from viewpoints of phase transitions in these systems. We show that THz spectroscopy is an excellent method of studying polymorphism in materials.
Methods
Sample growth
Pulsed Laser Deposition is used to fabricate the various VO2 polymorph thin films by ablating a commercial Vanadium single crystal (100) orientated target on the SLAO (001) substrate. The growth temperature is 500°C and the oxygen pressure is varied from 5 × 10−3 to 7 × 10−3 Torr. By systematic control of oxygen growth pressure and pulse laser frequency, the various phases of VO2 are stabilized. Detailed growth conditions study has been reported in a previous study56.
XRD and AFM
The θ–2θ diffraction data measurements are done on a Bruker D8 Discover diffractometer CuKα1 (λ = 1.54 Å). Temperature-dependent electrical transport measurements are carried out in Physical Property Measurement system (Quantum Design) utilizing a four probe geometry. The surface morphology analysis of the various films are characterized on an atomic force microscope (AFM, Dimension V, Veeco).
THz-TDS
THz transmission spectra measurements of the VO2 films are carried out using the TeraView Spectra 3000 THz-TDS system, incorporated with a Janis ST-100-FTIR cryostat. The operational temperature range of the cryostat is 10 K to 450 K. In this system low temperature-grown GaAs films is used for the generation and detection of THz waves. THz time-domain data of VO2 films are taken with respect to the signal transmitted through the bare substrate as a reference. Optical properties of the bare SLAO substrate are determined by THz-TDS, with vacuum as the reference signal. The complex refractive index, 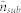 of SLAO substrate is obtained to be
of SLAO substrate is obtained to be 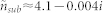 and almost temperature and frequency-independent, and thus is a very suitable THz transparent material in our operational temperature and frequency range. The cryostat is equipped with a vertical motorized stage with a resolution of 2.5 μm which is used to control the back and forth motion between the sample and reference positions.
and almost temperature and frequency-independent, and thus is a very suitable THz transparent material in our operational temperature and frequency range. The cryostat is equipped with a vertical motorized stage with a resolution of 2.5 μm which is used to control the back and forth motion between the sample and reference positions.
The aperture diameter used is 7 mm which allowed for an accurate measurement of the THz signal for frequencies as low as 0.3 THz. For each sample and reference run, 900 THz traces are taken in 3 minutes. The thickness difference between the film substrate and the bare substrate (reference), must be taken into account in our subsequent analysis57. The sample is kept in a high vacuum (~10−6 mbar) for all our experiments.
Author Contributions
T.V. and E.E.M.C. conceived the project. J.L., T.V. and E.E.M.C. designed the research and E.E.M.C. supervised the project. A.S. fabricated the samples and conducted electrical measurements. H.R. took X.R.D. measurements. J.L. performed the AFM measurements. THz-TDS data were taken by J.L. and C.L. and analyzed by J.L. and E.E.M.C. The manuscript was prepared by J.L. and E.E.M.C. with assistance from T.V., C.L. and A.S. All the authors contributed to discussion on the results for the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
We thank the NUSNNI-NanoCore at the National University of Singapore, Singapore and National Research Foundation (NRF), Singapore, under the Competitive Research Program (CRP) “Tailoring Oxide Electronics by Atomic Control” NRF2008NRF-CRP002-024, CRP “Interface Science and Technology” NRF-CRP4-2008-04, National University of Singapore (NUS) cross-faculty grant and FRC (ARF Grant No. R-144-000- 278-112), MOE Tier 1 RG13/12 and MOE2014-T1-001-056 for the financial support. We also acknowledge the funding support from the Singapore NRF through the Singapore-Berkeley Research Initiative for Sustainable Energy (SinBeRISE) CREATE Programme.
References
- Rao Popuri S. et al. VO2 (A): Reinvestigation of crystal structure, phase transition and crystal growth mechanisms. J.Sol. St. Chem. 213, 79–86 (2014). [Google Scholar]
- Wu C., Wei H., Ning B. & Xie Y. New Vanadium Oxide Nanostructures: Controlled Synthesis and Their Smart Electrical Switching Properties. Adv. Mater. 22, 1972–1976 (2010). [DOI] [PubMed] [Google Scholar]
- Mattioli G., Filippone F., Alippi P. & Amore Bonapasta A. Ab initio study of the electronic states induced by oxygen vacancies in rutile and anatase TiO2. Phys. Rev. B 78, 241201 (2008). [Google Scholar]
- Mai L. et al. Nanoscroll Buffered Hybrid Nanostructural VO2(B) Cathodes for High-Rate and Long-Life Lithium Storage. Adv. Mater. 25, 2969–2973 (2013). [DOI] [PubMed] [Google Scholar]
- Galy J. A Proposal for (B) VO2-(A) VO2 Phase Transition: A Simple Crystallographic Slip. J. Solid State Chem. 148, 224–228 (1999). [Google Scholar]
- Katzke H., Tolédano P. & Depmeier W. Theory of morphotropic transformations in vanadium oxides. Phys. Rev. B 68, 024109 (2003). [Google Scholar]
- Oka Y., Yaob T. & Yamamoto N. Structural Phase Transition of VO2(B) to VO2(A). J. Mater. Chem. 1, 815–818 (1991). [Google Scholar]
- Corr S. A. et al. VO2(B) nanorods: solvothermal preparation, electrical properties, and conversion to rutile VO2 and V2O3. J. Mater. Chem. 19, 4362 (2009). [Google Scholar]
- Zylbersztejn A. Metal-insulator transition in vanadium dioxide. Phys. Rev. B 11, 4383–4395 (1975). [Google Scholar]
- Oka Y., Yao T., Yamamoto N., Ueda Y. & Hayashi A. Phase Transition and V4+-V4+ pairing in VO2(B). J. Sol. St. Chem. 105, 271 (1993). [Google Scholar]
- Leroux C., Nihoul G. & Tendeloo G. V. From VO2(B) to VO2(R): Theoretical structures of VO2 polymorphs and in situ electron microscopy. Phys. Rev. B 57, 5111 (1998). [Google Scholar]
- Liu J., Li Q., Wang T., Yu D. & Li Y. Metastable Vanadium Dioxide Nanobelts: Hydrothermal Synthesis, Electrical Transport, and Magnetic Properties. Angew. Chem. 43, 5048–5052 (2004). [DOI] [PubMed] [Google Scholar]
- Imada M., Fujimori A. & Tokura Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998). [Google Scholar]
- Goodenough J. B. The Two Components of the Crystallographic Transition in VO2. J. Solid State Chem. 3, 490 (1971). [Google Scholar]
- Nakano M. et al. Collective bulk carrier delocalization driven by electrostatic surface charge accumulation. Nature 487, 459–462 (2012). [DOI] [PubMed] [Google Scholar]
- Jeong J. et al. Suppression of Metal-Insulator Transition in VO2 by Electric Field-Induced Oxygen Vacancy Formation. Science 339, 1402–1405 (2013). [DOI] [PubMed] [Google Scholar]
- Okazaki K. et al. Photoemission study of the metal-insulator transition in VO2/TiO2(001): Evidence for strong electron-electron and electron-phonon interaction. Phys. Rev. B 69, 165104 (2004). [Google Scholar]
- Liu M. et al. Symmetry breaking and geometric confinement in VO2: Results from a three-dimensional infrared nano-imaging. Appl. Phys. Lett. 104, 121905 (2014). [Google Scholar]
- Ruzmetov D., Senanayake S. & Ramanathan S. X-ray absorption spectroscopy of vanadium dioxide thin films across the phase-transition boundary. Phys. Rev. B 75, 195102 (2007). [DOI] [PubMed] [Google Scholar]
- Koethe T. C. et al. Transfer of Spectral Weight and Symmetry across the Metal-Insulator Transition in VO2. Phys. Rev. Lett. 97, 116402 (2006). [DOI] [PubMed] [Google Scholar]
- Tao Z. et al. Decoupling of Structural and Electronic Phase Transitions in VO2. Phys. Rev. Lett. 109, 166406 (2012). [DOI] [PubMed] [Google Scholar]
- Qazilbash M. M. et al. Mott Transition in VO2 Revealed by Infrared Spectroscopy and Nano-Imaging. Science 318, 1750–1753 (2007). [DOI] [PubMed] [Google Scholar]
- Kim H.-T. et al. Monoclinic and Correlated Metal Phase in VO2 as Evidence of the Mott Transition: Coherent Phonon Analysis. Phys. Rev. Lett. 97, 266401 (2006). [DOI] [PubMed] [Google Scholar]
- Cavalleri A., Dekorsy T., Chong H., Kieffer J. & Schoenlein R. Evidence for a structurally-driven insulator-to-metal transition in VO2: A view from the ultrafast timescale. Phys. Rev. B 70, 161102 (2004). [Google Scholar]
- Kübler C. et al. Coherent Structural Dynamics and Electronic Correlations during an Ultrafast Insulator-to-Metal Phase Transition in VO2. Phys. Rev. Lett. 99, 116401 (2007). [DOI] [PubMed] [Google Scholar]
- Hilton D. et al. Enhanced Photosusceptibility near Tc for the Light-Induced Insulator-to-Metal Phase Transition in Vanadium Dioxide. Phys. Rev. Lett. 99, 226401 (2007). [DOI] [PubMed] [Google Scholar]
- Jones A. C., Berweger S., Wei J., Cobden D. & Raschke M. B. Nano-optical Investigations of the Metal-Insulator Phase Behavior of Individual VO2 Microcrystals. Nano lett. 10, 1574–1581 (2010). [DOI] [PubMed] [Google Scholar]
- Quackenbush N. F. et al. Nature of the Metal Insulator Transition in Ultrathin Epitaxial Vanadium Dioxide. Nano lett. 13, 4857–4861 (2013). [DOI] [PubMed] [Google Scholar]
- Jepsen P. et al. Metal-insulator phase transition in a VO2 thin film observed with terahertz spectroscopy. Phys. Rev. B 74, 205103 (2006). [Google Scholar]
- Cocker T. L. et al. Terahertz conductivity of the metal-insulator transition in a nanogranular VO2 film. Appl. Phys. Lett. 97, 221905 (2010). [Google Scholar]
- Mandal P., Speck A., Ko C. & Ramanathan S. Terahertz spectroscopy studies on epitaxial vanadium dioxide thin films across the metal-insulator transition. Opt. Lett. 36, 1927 (2011). [DOI] [PubMed] [Google Scholar]
- Baxter J. B. & Schmuttenmaer C. A. Carrier dynamics in bulk ZnO. I. Intrinsic conductivity measured by terahertz time-domain spectroscopy. Phys. Rev. B 80, 235205 (2009). [Google Scholar]
- Baxter J. B. & Schmuttenmaer C. A. Conductivity of ZnO Nanowires, Nanoparticles, and Thin Films Using Time-Resolved Terahertz Spectroscopy. J. Phys. Chem. B 110, 25229 (2006). [DOI] [PubMed] [Google Scholar]
- Tang C. S. et al. Terahertz conductivity of topological surface states in Bi1.5Sb0.5Te1.8Se1.2. Sci. Rep. 3, 3513; 10.1038/srep03513 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd-Hughes J. & Jeon T.-I. A Review of the Terahertz Conductivity of Bulk and Nano-Materials. J. Infrared, Millimeter, Terahertz Waves 33, 871–925 (2012). [Google Scholar]
- Zou X. et al. Terahertz Conductivity of Twisted Bilayer Graphene. Phys. Rev. Lett. 110, 067401 (2013). [DOI] [PubMed] [Google Scholar]
- George P. A. et al. Ultrafast Optical-Pump Terahertz-Probe on epitaxial graphene. Nano lett. 8, 4248–4251 (2008). [DOI] [PubMed] [Google Scholar]
- Valdés Aguilar R. et al. Terahertz Response and Colossal Kerr Rotation from the Surface States of the Topological Insulator Bi2Se3. Phys. Rev. Lett. 108, 087403 (2012). [DOI] [PubMed] [Google Scholar]
- Bilbro L. S. et al. Temporal correlations of superconductivity above the transition temperature in La2 − xSrxCuO4 probed by terahertz spectroscopy. Nature Phys. 7, 298–302 (2011). [Google Scholar]
- Frenkel A., Gao F., Liu Y., Whitaker J. F. & Uher C. Conductivity peak, relaxation dynamics, and superconducting gap of YBa2Cu3O7 studied by terahertz and femtosecond optical spectroscopies. Phys. Rev. B 54, 1355 (1996). [DOI] [PubMed] [Google Scholar]
- Valdés Aguilar R. et al. Pair-breaking effects and coherence peak in the terahertz conductivity of superconducting BaFe2 − 2xCo2xAs2 thin films. Phys. Rev. B 82, 180514 (2010). [Google Scholar]
- Ulbricht R., Hendry E., Shan J., Heinz T. F. & Bonn M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 83, 543–586 (2011). [Google Scholar]
- Walther M. et al. Terahertz conductivity of thin gold films at the metal-insulator percolation transition. Phys. Rev. B 76, 125408 (2007). [Google Scholar]
- Duvillaret L., Garet F. & Coutaz J. L. A Reliable Method for Extraction of Material Parameters in Terahertz Time-Domain Spectroscopy. IEEE J. Sel. Top. Quantum Electron. 2, 739 (1996). [Google Scholar]
- Barker A., Verleur H. & Guggenheim H. Infrared Optical Properties of Vanadium Dioxide Above and Below the Transition Temperature. Phys. Rev. Lett. 17, 1286–1289 (1966). [Google Scholar]
- Choi H. S., Ahn J. S., Jung J. H., Noh T. W. & Kim D. H. Mid-infrared properties of a VO2 film near the metal-insulator transition. Phys. Rev. B 54, 4621 (1996). [DOI] [PubMed] [Google Scholar]
- Smith N. Classical generalization of the Drude formula for the optical conductivity. Phys. Rev. B 64, 155106 (2001). [Google Scholar]
- Turner G. M., Beard M. C. & Schmuttenmaer C. A. Carrier Localization and Cooling in Dye-Sensitized Nanocrystalline Titanium Dioxide. J. Phys. Chem. B 106, 11716–11719 (2002). [Google Scholar]
- Qazilbash M. et al. Infrared spectroscopy and nano-imaging of the insulator-to-metal transition in vanadium dioxide. Phys. Rev. B 79, 075107 (2009). [Google Scholar]
- Cooke D. et al. Transient terahertz conductivity in photoexcited silicon nanocrystal films. Phys. Rev. B 73, 193311 (2006). [Google Scholar]
- Němec H., Kužel P. & Sundström V. Far-infrared response of free charge carriers localized in semiconductor nanoparticles. Phys. Rev. B 79, 115309 (2009). [Google Scholar]
- Zou X. et al. Temperature-dependent terahertz conductivity of tin oxide nanowire films. J. Phys. D: Appl. Phys. 45, 465101 (2012). [Google Scholar]
- Ruzmetov D., Heiman D., Claflin B., Narayanamurti V. & Ramanathan S. Hall carrier density and magnetoresistance measurements in thin-film vanadium dioxide across the metal-insulator transition. Phys. Rev. B 79, 153107 (2009). [Google Scholar]
- Qazilbash M. et al. Correlated metallic state of vanadium dioxide. Phys. Rev. B 74, 205118 (2006). [Google Scholar]
- Karaoglan-Bebek G., Hoque M. N. F., Holtz M., Fan Z. & Bernussi A. A. Continuous tuning of W-doped VO2 optical properties for terahertz analog applications. Appl. Phys. Lett. 105, 201902 (2014). [Google Scholar]
- Srivastava A. et al. Selective Growth of Single Phase VO2(A, B and M) Polymorph Thin Films. Appl. Phys. Lett. Mater. 3, 026101 (2015). [Google Scholar]
- Kadlec C. et al. Temperature and electric field tuning of the ferroelectric soft mode in a strained SrTiO3/DyScO3 heterostructure. Phys. Rev. B 80, 174116 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information